Part 1 is here: statistic.html. Comments to John Beaudoin have been moved here: beaudoin.html.
In November 2024 Nicolas Hulscher, Michael Cook, Raphael Stricker, and Peter McCullough published a paper titled "Excess Cardiopulmonary Arrest and Mortality after COVID-19 Vaccination in King County, Washington": https://www.opastpublishers.com/open-access-articles/excess-cardiopulmonary-arrest-and-mortality-after-covid19-vaccination-in-king-county-washington.pdf.
The first author Nicolas Hulscher is the "foundation administrator" of McCullough Foundation, and he runs the Twitter account of McCullough Foundation.
Raphael Stricker is possibly the main person who popularized the hoax about Morgellons disease, and he was one of the two advisory board members of Morgellons Disease Foundation, which was founded by Mary Leitao who coined the term Morgellons disease. Stricker was prescribing ivermectin as a treatment for Morgellons before 2020. He was kicked out of academia in 1990 after he falsified data in a study about HIV, and afterwards he worked as an associate director of a penis enlargement clinic. In 2021 Stricker also authored a paper about hydroxychloroquine together with Peter McCullough and Harvey Risch, who are both members of the chief medical board of the Wellness Company. TWC's chief marketing officer used to be Christopher Alexander, whose bio says that he is "recognized as a leader in disinformation, misinformation, and counter-propaganda campaigns".
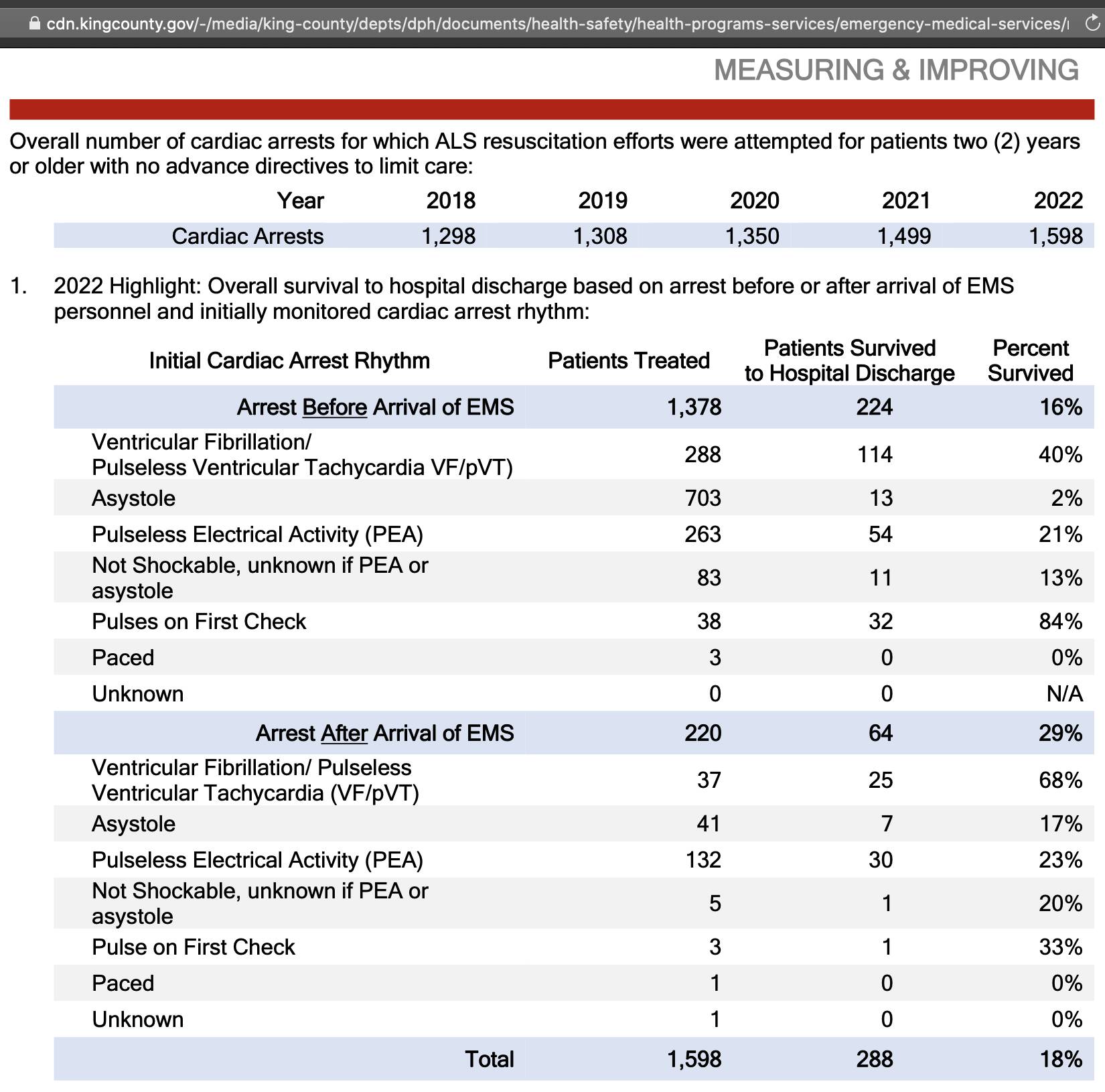
King County is the most populous county of the Seattle metropolitan area. Hulscher and his coauthors compiled the data from yearly PDFs published by the Emergency Medical Services Division of King County. For example the data for 2022 was shown in this table from the annual report for 2023: [https://kingcounty.gov/en/dept/dph/health-safety/health-centers-programs-services/emergency-medical-services/reports-publications]

The cardiac arrest cases that were included in the report were
defined as "cardiac arrests for which ALS
resuscitation efforts were attempted for patients two (2) years or older
with no advance directives to limit care". Hulscher seems to have
calculated the number of cardiac arrest deaths by multiplying the number
of cases with the rounded percentage of patients who didn't survive,
which gave him a figure of 1121 deaths in 2022 (from
1350*(100-17)/100). However he could've derived the exact
number of deaths by simply subtracting the number of survived patients
from the number of treated patients, so for example 1350 minus 234
would've given him the exact figure of 1116 deaths in 2020.
Hulscher also incorrectly entered the survival rate in 2021 as 18% even though it should've been 16%, but I didn't find other errors in his Table 1 when I compared it to the original PDF reports:
| Hulscher Table 1 | Original PDFs | |||||
|---|---|---|---|---|---|---|
| Year | Treated | Survived | Died | Treated | Survived | Died |
| 2005 | 1124 | 190 (17%) | 934 | |||
| 2006 | 993 | 174 (18%) | 819 | |||
| 2007 | 1035 | 191 (18%) | 844 | |||
| 2008 | 1046 | 199 (19%) | 847 | |||
| 2009 | 1072 | 206 (19%) | 866 | |||
| 2010 | 1069 | 218 (20%) | 851 | |||
| 2011 | 1047 | 223 (21%) | 824 | |||
| 2012 | 1134 | 252 (22%) | 882 | |||
| 2013 | 1135 | 235 (21%) | 900 | |||
| 2014 | 1246 | 267 (21%) | 979 | |||
| 2015 | 1114 | 20% | 891 | 1114 | 221 (20%) | 893 |
| 2016 | 1228 | 24% | 933 | 1228 | 288 (24%) | 940 |
| 2017 | 1215 | 21% | 960 | 1215 | 251 (21%) | 964 |
| 2018 | 1298 | 22% | 1012 | 1298 | 289 (22%) | 1009 |
| 2019 | 1308 | 19% | 1059 | 1308 | 253 (19%) | 1055 |
| 2020 | 1350 | 17% | 1121 | 1350 | 234 (17%) | 1116 |
| 2021 | 1499 | 18% | 1229 | 1499 | 242 (16%) | 1257 |
| 2022 | 1598 | 18% | 1310 | 1588 | 288 (18%) | 1300 |
| 2023 | 1697 * | 18% * | 1392 * | 1669 | 311 (19%) | 1358 |
Above I marked Hulscher's cells for 2023 with an asterisk because Hulscher et al. calculated them as a linear projection of the data for 2021 and 2022. In the real data for 2023 that was published in September 2024, the number of deaths was slightly lower than Hulscher's projected number of deaths for 2023:

I think Hulscher should've just omitted 2023 from his paper instead of including projected data for 2023, or in his plots he should've somehow visually differentiated the projected data from actual data.
On the website of Emergency Medical Services Division of King County, there's annual PDF reports going back to 2003, but the reports for 2003 and 2004 are missing the table which shows the number of treated cardiac arrest patients.
Hulscher misleadingly only included data from 2015 onwards in his paper. He used the years 2015-2020 as his baseline period, but in 2015-2020 the number of deaths fell unusually close to a line, which made the increase in deaths since 2021 seem fairly impressive in comparison. But during earlier years the deaths didn't follow such a neat trend, and for example there was a big drop in the number of deaths between 2014 and 2015. The data for 2015 was published in the report for 2016, but I didn't find any explanation for the drop in the report, I don't know if it there was a genuine decrease in deaths, or if there was some kind of a change in reporting practices, or if for example before 2015 the King County EMS used to serve a larger part of the Seattle metropolitan area than earlier.
There was also a fairly big drop in deaths between the years 2005 and 2006, but the PDF report for the year 2007 said that "the decrease in 2006 is due to a modification in case definition": [https://cdn.kingcounty.gov/-/media/king-county/depts/dph/documents/health-safety/health-programs-services/emergency-medical-services/reports/2007-annual-report.pdf]

Hulscher used z-scores to indicate the level of excess deaths, but I think it would've been clearer to just express excess deaths as a percentage of the baseline number of deaths. His z-scores were exaggerated because the deaths fell unusually close to a line during his baseline period. Here when I simply added the year 2014 to my baseline period, my z-score for excess deaths in 2021 fell from about 13 to about 5:
d=data.table(year=2005:2023) d$dead=c(934,819,844,847,866,851,824,882,900,979,893,940,964,1009,1055,1116,1257,1300,1358) d$base1=d[year%in%2015:2020,predict(lm(dead~year),d)] d$base2=d[year%in%2014:2020,predict(lm(dead~year),d)] d[year==2021,dead-base1]/d[year%in%2015:2020,mean(abs(dead-base1))] # 13.24 d[year==2021,dead-base2]/d[year%in%2014:2020,mean(abs(dead-base2))] # 4.662179
Hulscher started the x-axis of his plot from the year 2015, so you couldn't see how the long-term trend in the number of deaths in the EMS data appears to be curved upwards:

library(data.table);library(ggplot2)
d=data.table(x=2005:2023)
d$y=c(934,819,844,847,866,851,824,882,900,979,893,940,964,1009,1055,1116,1257,1300,1358)
d$z=1;d$proj=F
base1=2015:2020;base2=2006:2019
p1=d[,.(x,y=d[x%in%base1,predict(lm(y~x),d)],z=2)][,proj:=!x%in%base1]
p2=d[,.(x,y=d[x%in%base2,predict(lm(y~poly(x,2)),d)],z=3)][,proj:=!x%in%base2]
p=rbind(d,p1,p2)
p[,z:=factor(z,,c("Actual deaths","2015-2020 linear trend","2006-2019 quadratic trend"))]
xstart=min(p$x);xend=max(p$x);ybreak=pretty(c(0,p$y),7)
ggplot(p,aes(x,y))+
geom_point(aes(alpha=z,color=z),stroke=0,size=1.2)+
geom_line(data=p[proj==F],aes(color=z),linewidth=.4)+
geom_line(aes(color=z),linewidth=.4,linetype="11")+
labs(x=NULL,y=NULL,title="Yearly cardiac arrest deaths in King County EMS data")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xstart:xend)+
scale_y_continuous(limits=range(ybreak),breaks=ybreak)+
scale_color_manual(values=c("black",hsv(22/36,1,.8),"#00aa00"))+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(4,"pt"),
axis.ticks.length.x=unit(0,"pt"),
legend.background=element_blank(),
legend.box.background=element_rect(linewidth=.4),
legend.justification=c(0,1),
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(4,5,4,4),
legend.position=c(0,1),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.grid.major=element_blank(),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,face=2,margin=margin(,,4)))
ggsave("1.png",width=5,height=3.5,dpi=300*4)
system("mogrify -resize 25% -colors 256 1.png")
The next plot shows that the long-term trend in all-cause deaths in King County is similarly curved upwards:

library(data.table);library(ggplot2)
t=fread("http://sars2.net/f/wonderkingcountyallcause.csv")
p1=t[,.(y=sum(dead),z=1,proj=F),.(x=year)]
base1=2015:2019;base2=1999:2019
p2=p1[,.(x,y=d[x%in%base1,predict(lm(y~x),d)],z=2)][,proj:=!x%in%base1]
p3=p1[,.(x,y=d[x%in%base2,predict(lm(y~poly(x,2)),d)],z=3)][,proj:=!x%in%base2]
p=rbind(p1,p2,p3)
p[,z:=factor(z,,c("Actual deaths","2015-2019 linear trend","1999-2019 quadratic trend"))]
xstart=min(p$x);xend=max(p$x);ybreak=pretty(p$y,7)
ggplot(p,aes(x,y))+
geom_point(aes(alpha=z,color=z),stroke=0,size=1.4)+
geom_line(data=p[proj==F],aes(color=z),linewidth=.5)+
geom_line(aes(color=z),linewidth=.5,linetype="11")+
labs(x=NULL,y=NULL,title="CDC WONDER: Yearly deaths with county of residence\nKing County, Washington")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xstart:xend)+
scale_y_continuous(limits=range(ybreak),breaks=ybreak)+
scale_color_manual(values=c("black",hsv(22/36,1,.8),"#00aa00"))+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(4,"pt"),
axis.ticks.length.x=unit(0,"pt"),
legend.background=element_blank(),
legend.box.background=element_rect(linewidth=.4),
legend.justification=c(0,1),
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(4,5,4,4),
legend.position=c(0,1),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.grid.major=element_blank(),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,face=2,margin=margin(,,4)))
ggsave("1.png",width=5,height=3.5,dpi=300*4)
system("mogrify -resize 25% -colors 256 1.png")
The EMS data included all cardiac arrest deaths regardless of cause, so it's similar to deaths by multiple cause of death at CDC WONDER. So part of the excess deaths in 2021 and 2022 might be due to COVID, because from the next plot which shows monthly cardiac deaths in Washington State, you can see that spikes in MCD cardiac deaths coincided with COVID waves, and the number of excess MCD cardiac deaths got much lower when I subtracted deaths that also had MCD COVID:

library(data.table);library(ggplot2);library(lubridate);library(ggtext)
cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]
t=fread("http://sars2.net/f/wonderwashingtoncardiac.csv")[age>=45]
pop=fread("http://sars2.net/f/uspopdeadmonthly.csv")
t=merge(t,pop[,.(pop=sum(pop)),.(month=date,age=cul(age,seq(45,85,10)))])
t=t[,month:=as.Date(paste0(month,"-1"))]
t[,dead:=dead/days_in_month(month)]
months=sort(unique(t$month))
base=t[!grepl("COVID",cause)&year(month)%in%2011:2019][,dead:=nafill(dead,,0)]
t=merge(base[,.(month=months,base=predict(lm(dead/pop~month),.(month=months))),.(age,cause)],t)
t[,base:=base*pop]
p=t[,.(base=sum(base),dead=sum(dead)),.(date=month,cause)]
and=fread("http://sars2.net/f/wonderwashingtoncardiacandcovid.csv")
and=and[,date:=as.Date(paste0(month,"-1"))][,.(date,andcovid=dead/days_in_month(date))]
p=rbind(p,merge(and,p[cause%like%"Multiple"])[,.(date,base=NA,cause="MCD I00-I99 and not MCD COVID",dead=dead-andcovid)])
p[,cause:=factor(cause,unique(cause)[c(2,1,3)])]
xstart=as.Date("2015-1-1");xend=as.Date("2024-1-1")
p=p[date>=xstart&date<=xend]
xbreak=seq(xstart,xend,"6 month");xlab=c(rbind("",2015:2023),"")
ystart=0;yend=p[,max(base,dead,0,na.rm=T)*1.02];ybreak=pretty(p[,c(base,dead,0)],8)
color=c("black","#ff2222","#ffaaaa")
lab=c("Actual deaths","Baseline");lab=factor(lab,unique(lab))
ggplot(p,aes(x=date+14,y=dead,color=cause))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray85",linewidth=.25)+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_line(linewidth=.3)+
geom_point(stroke=0,size=.6,show.legend=F)+
geom_line(aes(y=base),linetype="42",linewidth=.3)+
labs(title="Washington State, ages 45+: Monthly deaths with cause I00-I99 (diseases of\nthe circulatory system) divided by number of days in month",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
scale_linetype_manual(values=c("solid","42"),labels=lab)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
axis.ticks.x=element_line(color=alpha("black",c(1,0))),
axis.ticks=element_line(linewidth=.25,color="black"),
axis.ticks.length=unit(.2,"lines"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.just="left",
legend.spacing=unit(5,"pt"),
legend.justification=c(0,0),
legend.key=element_blank(),
legend.key.height=unit(9,"pt"),
legend.key.width=unit(17,"pt"),
legend.position=c(0,0),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.box.background=element_rect(fill="white",color="black",linewidth=.3),
legend.margin=margin(4,4,4,4,"pt"),
legend.text=element_text(size=7,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=7.6,face=2,margin=margin(,,4)))
ggsave("1.png",width=4.2,height=2.8,dpi=400*4)
sub="\u00a0 Source: wonder.cdc.gov/mcd.html. Age groups below 45 were excluded because they had some months with less than 10 deaths so the number of deaths was suppressed.
In order to calculate the dashed baseline, first a linear trend was calculated for CMR within each 10-year age group in 2021 to 2019, and then the projected trend was multiplied by the population size of each age group to get the monthly expected deaths for each age group.
Monthly resident population estimates were downloaded from www2.census.gov/programs-
surveys/popest/datasets/2020-2023/national/asrh/nc-est2022-alldata-r-file0{1..8}.csv, and from the corresponding files in the 2010-2020 directory. In order to get rid of a sudden jump in population size after the switch from the 2010-2020 to 2020-2023 estimates, the 2010-2020 estimates were multiplied by a linear slope so that they matched the 2020-2023 estimates at the point where the estimates were merged in April 2020 (see sars2.net/ethical.html#Files_
for_US_population_estimates_by_single_year_of_age)."
system(paste0("f=1.png;magick 1.png -resize 25% 1.png;mar=32;w=`identify -format %w $f`;magick \\( $f -gravity southwest -chop 0x20 \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize 38 caption:'",sub,"' -gravity southwest -splice $[mar]x20 \\) -append 1.png"))
Added later: In the next plot I again looked at monthly cardiac deaths in Washington State, but I included only the ICD codes I21 (Acute myocardial infarction), I22 (Subsequent myocardial infarction), I46 (Cardiac arrest), and I50 (Heart failure). I also included all ages instead of only ages 45 and above and I used a simple linear baseline instead of a baseline that accounts for the change in the population size of age groups. However now the excess MCD deaths after subtracting COVID were even lower. And by 2024 the MCD deaths were clearly below the baseline:

library(data.table);library(ggplot2)
t=fread("http://sars2.net/f/wonderwashingtoncardiac.csv")[code==code[1]]
t=t[,.(x=as.Date(paste(year,month,1,sep="-")),y=dead,type)]
t[,y:=y/lubridate::days_in_month(x)]
p=t[type=="ucd",.(x,y,type=3)]
p=rbind(p,t[type=="mcd"][,type:=1],dcast(t,x~type,value.var="y")[,.(x,type=2,y=mcd-nafill(and,,0))])
base=p[type%in%c(1,3)&year(x)%in%2012:2019,.(x=unique(p$x),y=predict(lm(y~x),.(x=unique(p$x)))),type]
p=rbind(p[,linetype:=1],base[,linetype:=2])
p=p[!(type==2&x<"2020-3-1")]
p[,type:=factor(type,,c("MCD with MCD COVID not subtracted","MCD with MCD COVID subtracted","UCD"))]
p[,linetype:=factor(linetype,,c("Deaths divided by number of days in month","2012-2019 linear trend"))]
xstart=as.Date("1999-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ybreak=pretty(p$y,6);ystart=0;yend=max(p$y)
ggplot(p,aes(x+15,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.25)+
geom_hline(yintercept=c(ystart,0,yend),linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_line(aes(y=ifelse(y<0,NA,y),color=type,linetype=linetype),linewidth=.3)+
labs(title="Washington State: Monthly deaths divided by number of days in month",subtitle="Source CDC WONDER. Includes causes I21 (Acute myocardial infarction), I22\n(Subsequent myocardial infarction), I46 (Cardiac arrest), and I50 (Heart failure)",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#ff5555","#ffbbbb","black"))+
scale_linetype_manual(values=c("solid","42"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),linetype=guide_legend(order=2),alpha=guide_legend(order=2))+
theme(axis.text=element_text(size=7,color="black"),
axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
axis.text.y=element_text(margin=margin(,1)),
axis.ticks=element_line(linewidth=.25,color="black"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(3,"pt"),
legend.background=element_rect(fill=alpha("white",1),color="black",linewidth=.25),
legend.box="vertical",
legend.box.just="left",
legend.box.spacing=unit(0,"pt"),
legend.justification=c(0,1),
legend.key=element_blank(),
legend.margin=margin(2,3,2,2),
legend.key.height=unit(7,"pt"),
legend.key.width=unit(17,"pt"),
legend.position=c(0,1),
legend.spacing.x=unit(0,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=7,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
plot.caption=element_text(size=6,hjust=0,margin=margin(4)),
plot.margin=margin(4,4,4,4),
plot.subtitle=element_text(size=7,margin=margin(,,3)),
plot.title=element_text(size=7,face=2,margin=margin(,,3)))
ggsave("1.png",width=3.8,height=2.8,dpi=380*4)
system("magick 1.png -resize 25% PNG8:1.png")
The paper by Hulscher et al. showed that there was a much higher number of excess deaths in 2021 than 2020. However compared to other US states, Washington State had an unusually low number of COVID deaths in 2020 relative to 2021 and 2022, and the PCR positivity rate in Washington State was also low in 2020:

The plot above is based on these datasets: https://data.cdc.gov/NCHS/Excess-Deaths-Associated-with-COVID-19/xkkf-xrst/about_data, https://data.cdc.gov/Case-Surveillance/Weekly-United-States-COVID-19-Cases-and-Deaths-by-/pwn4-m3yp/about_data, https://healthdata.gov/dataset/COVID-19-Diagnostic-Laboratory-Testing-PCR-Testing/j8mb-icvb/about_data, https://data.cdc.gov/Vaccinations/COVID-19-Vaccination-Trends-in-the-United-States-N/rh2h-3yt2/about_data.
Washington State is one of the states with the highest percentage of UCD COVID deaths in 2021 and 2022 relative to UCD COVID deaths in 2020:
> t=fread("http://sars2.net/f/wonderstatecovidvsall.csv")[cause=="covid"]
> a=merge(t[year==2020,.(dead,state)],t[year%in%2021:2022,sum(dead),state])
> a[,.(state,pct=V1/dead*100,`2021+2022`=V1,`2020`=dead)][order(-pct)][,pct:=round(pct,1)][]|>print(r=F)
state pct 2021+2022 2020
Maine 506.9 2129 420
Alaska 446.5 1027 230
Oregon 388.8 5583 1436
West Virginia 369.0 5476 1484
Vermont 346.5 499 144
Hawaii 331.3 1133 342
Wyoming 285.1 1317 462
Kentucky 279.3 11542 4133
Washington 254.9 8370 3284 # Washington State is 9th highest
Tennessee 253.2 17311 6838
North Carolina 252.0 19888 7892
Florida 242.9 46724 19237
South Carolina 238.6 12590 5277
Idaho 237.9 3231 1358
Utah 236.3 3225 1365
Virginia 235.7 13723 5822
Georgia 227.1 21470 9456
Nevada 226.9 7347 3238
New Hampshire 221.7 1727 779
Oklahoma 220.5 10692 4848
Arizona 205.0 17315 8447
Ohio 203.0 27621 13607
Alabama 199.7 13068 6544
California 198.0 62044 31338
Arkansas 194.6 6854 3523
Texas 191.6 59092 30844
Montana 187.0 2092 1119
New Mexico 181.9 5167 2841
Colorado 175.1 7559 4316
Michigan 172.1 19608 11391
Delaware 171.8 1732 1008
Kansas 169.5 5667 3344
Missouri 169.2 12081 7138
Mississippi 165.3 7383 4467
Pennsylvania 162.1 26916 16609
Indiana 154.1 13142 8529
Wisconsin 149.8 8140 5434
Maryland 139.1 8344 6000
Louisiana 133.0 8691 6534
Minnesota 129.2 6741 5218
Nebraska 120.7 2467 2044
Illinois 118.1 18581 15735
Iowa 111.0 4812 4336
Rhode Island 95.5 1514 1585
New York 91.8 32804 35736
Massachusetts 86.3 8043 9319
District of Columbia 83.0 690 831
South Dakota 82.2 1229 1496
Connecticut 82.0 4744 5782
New Jersey 81.0 13370 16498
North Dakota 80.0 968 1210
state pct 2021+2022 2020
This shows how in the year 2020 deaths with UCD COVID accounted for only about 5% of all deaths in Washington State, which was one of the lowest percentages out of any state:

library(data.table);library(ComplexHeatmap);library(circlize)
t=fread("http://sars2.net/f/wonderstatecovidvsall.csv")[year>=2020][,year:=factor(year,unique(year))]
t=rbind(t[,.(dead=sum(dead),year="Total"),.(cause,state)],t)
t=rbind(t,t[,.(dead=sum(dead),state="Total"),.(cause,year)])
me=merge(t[cause=="covid",.(year,state,covid=dead)],t[cause=="all",.(year,state,dead)])
m=me[,xtabs(covid/dead*100~year+state)]
states=fread("https://github.com/cphalpert/census-regions/raw/master/us%20census%20bureau%20regions%20and%20divisions.csv")
states[,order:=match(Division,strsplit("Total,New England,Middle Atlantic,East North Central,West North Central,South Atlantic,East South Central,West South Central,Mountain,Pacific",",")[[1]])]
states[,Division:=sub("([WE]).* (South Central)","\\1 \\2",Division)]
div=rbind(states[order(order),.(State,Division)],list(State="Total",Division=""))
m=m[,div$State];disp=round(m)
colnames(m)[colnames(m)=="District of Columbia"]="DC"
png("0.png",w=ncol(m)*32+2000,h=nrow(m)*32+1000,res=120)
ht_opt$COLUMN_ANNO_PADDING=unit(0,"mm");ht_opt$ROW_ANNO_PADDING=unit(0,"mm")
Heatmap(m,
column_split=factor(div$Division,unique(div$Division)),
row_split=rep(letters[1:2],c(1,5)),
row_title=NULL,
column_title_gp=gpar(fontsize=16),
column_gap=unit(8,"pt"),
row_gap=unit(8,"pt"),
border="gray60",
width=unit(ncol(m)*32,"pt"),
height=unit(nrow(m)*32,"pt"),
show_column_names=F,
show_row_names=F,
cluster_columns=F,
cluster_rows=F,
show_heatmap_legend=F,
rect_gp=gpar(col="gray80",lwd=0),
top_annotation=columnAnnotation(text=anno_text(gt_render(colnames(m),padding=unit(c(3,3,3,3),"mm")),just="left",rot=90,location=unit(0,"npc"),gp=gpar(fontsize=17,border="gray60",lwd=1))),
left_annotation=rowAnnotation(text=anno_text(gt_render(rownames(m),padding=unit(c(3,3,3,3),"mm")),just="right",location=unit(1,"npc"),gp=gpar(fontsize=17,border="gray60",lwd=1))),
right_annotation=rowAnnotation(text=anno_text(gt_render(rownames(m),padding=unit(c(3,3,3,3),"mm")),just="left",location=unit(0,"npc"),gp=gpar(fontsize=17,border="gray60",lwd=1))),
col=colorRamp2(seq(0,max(m),,256),sapply(seq(1,0,,256),\(i)rgb(i,i,i))),
cell_fun=\(j,i,x,y,w,h,fill)grid.text(round(disp[i,j]),x,y,gp=gpar(fontsize=16,col=ifelse(abs(m[i,j])>=.45*max(m),"white","black"))))
dev.off()
system("mogrify -trim 0.png;magick -gravity north -font Arial-Bold \\( -size `identify -format %w 0.png`x -pointsize 34 caption:'CDC WONDER: Percentage of deaths with underlying cause COVID out of all deaths' \\) \\( 0.png -splice 0x18 \\) -append -trim -bordercolor white -border 20 1.png")
The paper by Hulscher et al. also included this plot which showed that the mid-year resident population estimates of King County decreased by about 0.94% between 2020 and 2021:

Hulscher et al. wrote that they used population estimates published by the US Census Bureau and cited this URL as their source: https://www2.census.gov/programs-surveys/popest/tables/. Uncle John Returns pointed out that the drop in population size between 2020 and 2021 was missing from the Population Interim Estimates (PIE) published by the Washington State Department of Health: [https://x.com/UncleJo46902375/status/1855602491083161778]

From the R code of the Population Interim Estimates, I found that the population estimates for 2020 to 2023 were taken from a dataset published by the Washington State Office of Financial Management (OFM). [https://github.com/PHSKC-APDE/frankenpop_pub/blob/main/rake_and_output%2eR, https://ofm.wa.gov/washington-data-research/population-demographics/population-estimates/estimates-april-1-population-age-sex-race-and-hispanic-origin] The OFM estimates also had a bigger increase in population size between 2022 and 2023 than the Census Bureau estimates:

dlf=\(x,y,...){if(missing(y))y=sub(".*/","",x);for(i in 1:length(x))download.file(x[i],y[i],quiet=T,...)}
dlf("https://www2.census.gov/programs-surveys/popest/tables/2020-2023/counties/totals/co-est2023-pop-53.xlsx")
dlf("https://www2.census.gov/programs-surveys/popest/tables/2010-2020/intercensal/county/co-est2020int-pop-53.xlsx")
dlf("https://www2.census.gov/programs-surveys/popest/tables/2010-2019/counties/totals/co-est2019-annres-53.xlsx")
dlf("https://www2.census.gov/programs-surveys/popest/tables/2000-2010/intercensal/county/co-est00int-01-53.csv")
dlf("https://www2.census.gov/programs-surveys/popest/tables/2000-2009/counties/totals/co-est2009-01-53.csv")
dlf("https://www2.census.gov/programs-surveys/popest/tables/2000-2010/intercensal/county/co-est00int-01-53.csv")
library(data.table);library(ggplot2);library(readxl)
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
kim=\(x)ifelse(x>=1e3,ifelse(x>=1e6,paste0(x/1e6,"M"),paste0(x/1e3,"k")),x)
pop1=fread("co-est2009-01-53.csv",skip=1)
p=pop1[V1==".King County",.(year=2009:2000,pop=as.integer(gsub(",","",.SD)),z="2000-2009"),.SDcols=2:11]
pop2=fread("co-est00int-01-53.csv",skip=1)
p=rbind(p,pop2[V1==".King County",.(year=2000:2010,pop=as.integer(gsub(",","",.SD)),z="2000-2010 intercensal"),.SDcols=c(3:12,14)])
pop3=read_excel("co-est2019-annres-53.xlsx")
p=rbind(p,list(year=2010:2019,pop=as.integer(dplyr::filter(pop3,pop3[[1]]==".King County, Washington")[4:13]),z="2010-2019"))
pop4=read_excel("co-est2020int-pop-53.xlsx")
p=rbind(p,list(year=2010:2019,pop=as.integer(pop4[pop4[[1]]%like%"King",3:12]),z="2010-2020 intercensal"))
pop5=read_excel("co-est2023-pop-53.xlsx")
p=rbind(p,list(year=2020:2023,pop=as.integer(pop5[pop5[[1]]%like%"King",][3:6]),z="2020-2023"))
p=rbind(p,data.table(year=1999:2023,pop=c(1729058,1737034,1754090,1758685,1763440,1775297,1795268,1822967,1847986,1875020,1912012,1931249,1969722,2007440,2044449,2079967,2117125,2149970,2188649,2233163,2252782,2274315,2252305,2266789,2266789),z="CDC WONDER"))
p=rbind(p,data.table(year=2000:2022,pop=c(1737045.79,1755487.08,1777514.01,1788082.03,1800783.04,1814999.24,1845208.98,1871097.95,1891124.97,1909204.99,1931249,1943608.44,1959305.04,1985687.59,2022469.68,2059056.02,2111487.04,2160624.39,2198063.56,2234581.41,2269674.95,2287050.05,2317700.05),z="DoH PIE"))
p=rbind(p,list(year=2020:2023,pop=c(2269675,2287050,2317700,2347800),z="ofm.wa.gov"))
# p=rbind(p,list(year=2015:2022,pop=c(2.127,2.168,2.205,2.228,2.250,2.274,2.252,2.265)*1e6,z="Hulscher et al."))
p[,z:=factor(z,unique(z))]
xstart=2000;xend=2023
p=p[year%in%xstart:xend]
ybreak=pretty(p$pop);ystart=ybreak[1];yend=max(ybreak);ylab=sprintf("%.1fM",ybreak/1e6)
ggplot(p,aes(x=year,y=pop))+
coord_cartesian(clip="off",expand=F)+
geom_vline(xintercept=c(2009.5,2019.5),color="gray80",linewidth=.23)+
geom_line(aes(color=z,alpha=z),linewidth=.3)+
geom_point(aes(color=z,shape=z,size=z),stroke=.3)+
labs(title="Resident population estimates of King County, Washington",subtitle="Sources: www2.census.gov/programs-surveys/popest/tables, CDC WONDER,
phskc-apde.shinyapps.io/PopPIE (Washington State Department of Health
population interim estimates; based on OFM in 2020-2022), ofm.wa.gov/
washington-data-research/population-demographics/population-estimates/
estimates-april-1-population-age-sex-race-and-hispanic-origin. OFM and PIE
are estimates on April 1st but other sources are mid-year estimates.",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart-.5,xend+.5,.5),labels=c(rbind("",xstart:xend),""))+
scale_y_continuous(labels=ylab,breaks=ybreak,limits=c(ystart,yend))+
scale_color_manual(values=c(hsv(12/36,c(.8,1),c(.8,.4)),hsv(22/36,c(.8,1),c(1,.5)),hsv(30/36,.8,1),"black",hsv(4/36,.5,.6),"red"))+
scale_shape_manual(values=c(16,16,16,16,16,4,1,3))+
scale_alpha_manual(values=c(1,1,1,1,1,0,0,0))+
scale_size_manual(values=c(.7,.7,.7,.7,.7,1,1,1))+
guides(color=guide_legend(nrow=3,byrow=F))+
theme(axis.text=element_text(size=7,color="black"),
axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
axis.ticks=element_line(linewidth=.2,color="black"),
axis.ticks.length=unit(3,"pt"),
axis.ticks.length.x=unit(0,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification="left",
legend.key=element_blank(),
legend.key.height=unit(8,"pt"),
legend.key.width=unit(17,"pt"),
legend.margin=margin(,,4),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(1,"pt"),
legend.text=element_text(size=7,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.23),
plot.margin=margin(5,5,5,5),
plot.subtitle=element_text(size=6.8,margin=margin(,,3)),
plot.title=element_text(size=7.3,face=2,,margin=margin(1,,4)))
ggsave("1.png",width=3.8,height=2.9,dpi=350*4)
system("magick 1.png -resize 25% 1.png")
I don't know if the OFM population estimates are more accurate than the Census Bureau's population estimates or not. At first I thought that a large decrease in population size between mid-2020 and mid-2021 wasn't supported by data for births minus deaths plus net migration. On CDC WONDER I got 23,256 births and 14,779 deaths between July 2020 and June 2021 among residents of King County. [https://wonder.cdc.gov/natality-expanded-current.html, https://wonder.cdc.gov/mcd.html]
There's a discontinued Census Bureau dataset for migration by county which includes data up to the year 2020, where King County had an estimated net migration of -6,437 people in the year 2020: [https://fred.stlouisfed.org/series/NETMIGNACS053033]
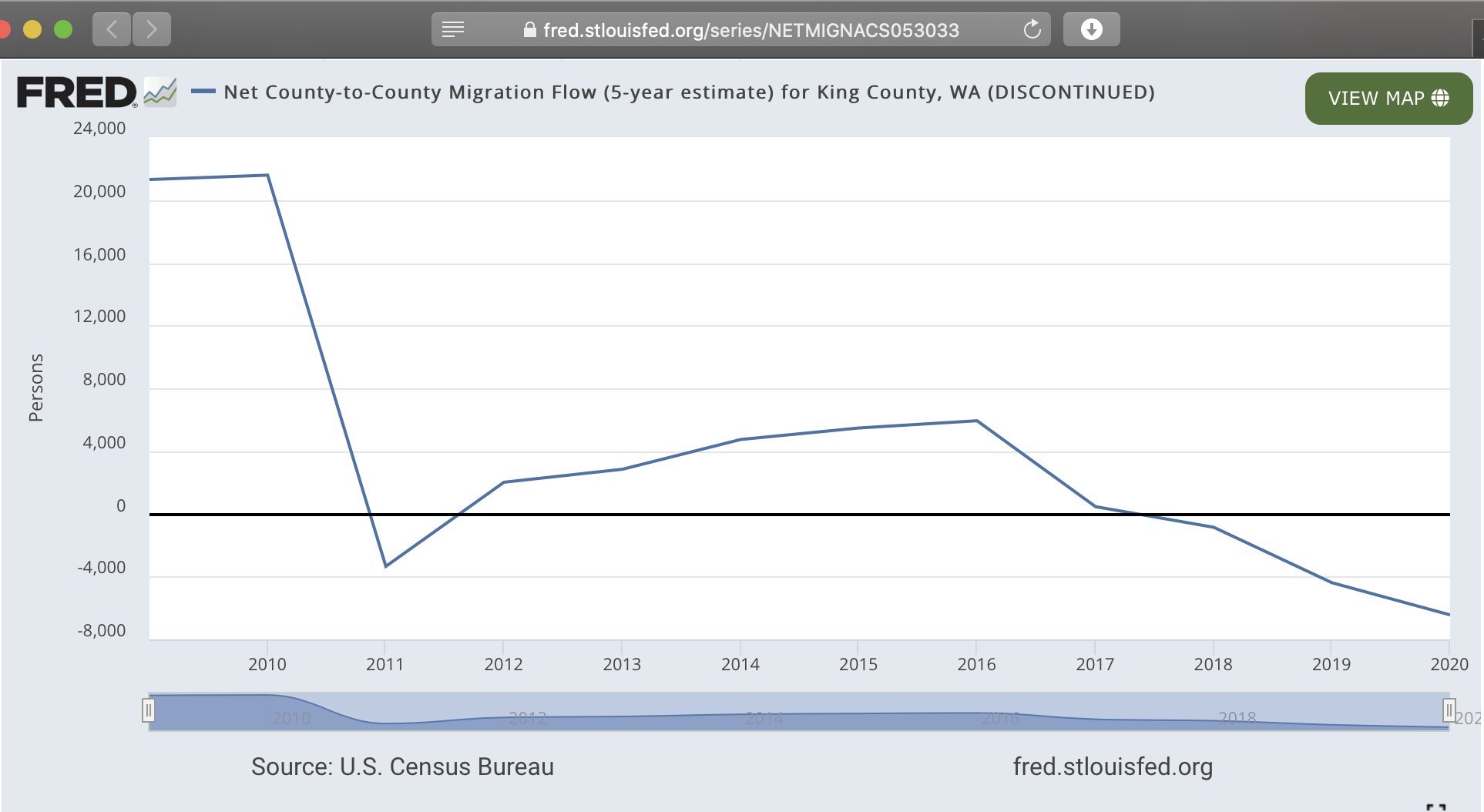
Assuming the same net migration between mid-2020 and mid-2021,
23256-14779-6437 would give 2,040 more people in mid-2021
than mid-2020, which is a much smaller increase than in the OFM
population estimates where there's 17,375 more people in 2021 than 2020.
(The OFM population estimates are for April 1st and not July 1st, but it
shouldn't make much difference when you're comparing the difference
between two adjacent years.)
However later I found that the Census Bureau has published net
migration estimates by county here in the file
co-est2021-comp-53.xlsx:
https://www2.census.gov/programs-surveys/popest/tables/2020-2021/counties/totals/.
In the file King County had a total population change of -20,266 between
July 1st 2020 and July 1st 2021, where there were 23,082 births, 16,444
deaths, and net migration of -26,818. So if the net migration estimate
is accurate, then it would explain a large decrease in population size
between mid-2020 and mid-2021.
Peter McCullough wrote that their paper showed that excess deaths had increased by 1236%: [https://x.com/P_McCulloughMD/status/1857107751756845319]

The paper said: "Excess cardiopulmonary arrest deaths were estimated to have increased by 1,236% from 2020 to 2023, rising from 11 excess deaths (95% CI: -12, 34) in 2020 to 147 excess deaths (95% CI: 123, 170) in 2023." I think it was misleading that McCullough's headline was not even based on actual data but on a projected number of deaths for 2023.
But anyway there were about 11.8% excess deaths in 2023
(1392/1245-1) and about 1.0% excess deaths in 2020
(1121/1110-1). So I guess an increase of 1236% sounds more
exciting than an increase of 10.8 percentage points:

library(data.table);library(ggplot2)
d=data.table(year=2005:2023)
d$dead=c(934,819,844,847,866,851,824,882,900,979,893,940,964,1009,1055,1116,1257,1300,1358)
d$dead2=c(rep(NA,10),891,933,960,1012,1059,1121,1229,1310,1392)
d$base=c(rep(NA,10),884,929,974,1019,1064,1110,1155,1200,1245)
p=d[,.(x=year,y=c(dead,dead2,base),z=rep(c("Original PDFs","McCullough paper","McCullough baseline"),each=.N))]
p[,z:=factor(z,unique(z))]
anno=p[x%in%c(2020,2023)&z!=z[1]]
minus=4
seg=as.matrix(anno[,.(x=x-minus,xend=x,y,yend=y)])
seg=rbind(seg,t(matrix(t(anno[order(x)][,x:=x-minus][,-3]),4))[,c(1,3,2,4)])
lab=cbind(anno[1:2,1:2],base=anno[3:4][[2]])
lab=lab[,.(x,y=(y+base)/2,label=paste0("(",y," - ",base,") / ",base," ≈ ",sprintf("%.1f",(y/base-1)*100),"% excess deaths"))]
note="(1392/1245-1)-(1121/1110-1): increase of about 10.8 percentage points
(1392-1245)/(1121-1110)-1: increase of about 1236% (misleading headline)"
xstart=2005;xend=2023;ybreak=pretty(c(0,p$y),7);ystart=0;yend=max(ybreak)
xbreak=seq(xstart-.5,xend+.5,.5);xlab=ifelse(xbreak%%1==0,xbreak,"")
color=c("black","#ff5555","#ff5555")
cap="Sources: kingcounty.gov/en/dept/dph/health-safety/health-centers-programs-services/emergency-
medical-services/reports-publications, Hulscher et al. 2024, \"Excess Cardiopulmonary Arrest and
Mortality after COVID-19 Vaccination in King County, Washington\"."
sub=str_wrap("The number of deaths in the paper by McCullough foundation is slightly different from the original PDFs because in the paper the number of dead patients was calculated by multiplying the number of treated patients by the rounded percentage of patients who didn't survive, and not by subtracting the number of patients who didn't survive from the number of treated patients. In the paper the number of deaths in 2023 was a linear projection of the number of deaths in 2021 and 2022, but the actual number of deaths in 2023 which was published in September 2024 was slightly lower than the projection. The McCullough paper also erroneously used 18% instead of 16% as the percentage of survived patients in 2021.",80)
ggplot(p,aes(x,y))+
geom_hline(yintercept=c(0,yend),linewidth=.3,lineend="square")+
geom_vline(xintercept=c(xstart-.5,xend+.5),linewidth=.3,lineend="square")+
geom_line(aes(linewidth=z,color=z,linetype=z))+
geom_segment(data=as.data.frame(seg),aes(x=x,xend=xend,y=y,yend=yend),lineend="square",linewidth=.3,color=color[2])+
geom_text(data=lab,aes(x=x-minus-.2,label=label),hjust=1,color=color[2],size=2.4)+
annotate(geom="label",x=2023,y=500,label=note,hjust=1,color=color[2],label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.3,size=2.4)+
annotate(geom="label",x=2023,y=500,label=note,hjust=1,fill="transparent",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=2.4)+
geom_point(aes(color=z,shape=z,alpha=z,size=z),stroke=.4)+
labs(x=NULL,y=NULL,title="Yearly cardiac arrest deaths in King County EMS data",subtitle=sub,caption=cap)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
coord_cartesian(clip="off",expand=F)+
scale_color_manual(values=color)+
scale_linetype_manual(values=c("solid","solid","42"))+
scale_linewidth_manual(values=c(.4,.4,.4))+
scale_shape_manual(values=c(16,16,16))+
scale_size_manual(values=c(.9,.9,1.4))+
scale_alpha_manual(values=c(1,1,0))+
theme(axis.text=element_text(size=7,color="black"),
axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
axis.ticks.length=unit(0,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification=c(1,.5),
legend.key=element_blank(),
legend.key.height=unit(10,"pt"),
legend.key.width=unit(18,"pt"),
legend.margin=margin(1,,4),
legend.position="top",
legend.spacing.x=unit(1.5,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=7),
legend.title=element_blank(),
panel.background=element_blank(),
plot.margin=margin(4,4,4,4),
plot.subtitle=element_text(size=6.5,margin=margin(,,3)),
plot.caption=element_text(size=5.7,margin=margin(4),hjust=0),
plot.title=element_text(size=7.5,face="bold",margin=margin(1,,4)))
ggsave("1.png",width=3.8,height=3.8,dpi=400*4)
system("magick 1.png -resize 25% 1.png")
Even Steve Kirsch misinterpreted the 1236% increase in excess deaths to mean a "13X increase in the rate of sudden deaths": [https://x.com/stkirsch/status/1869642819394277854]
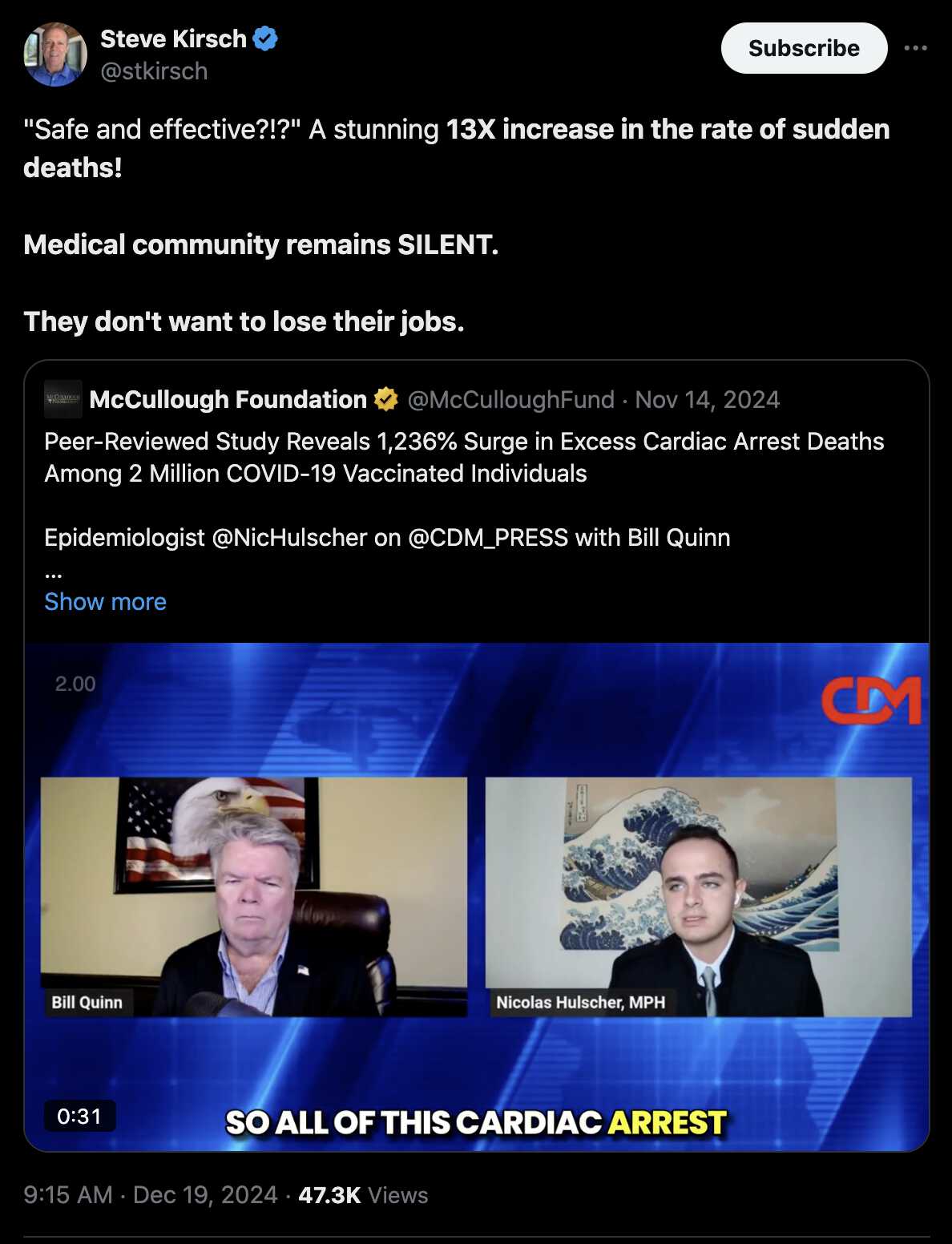
Peter Sweden employed a similar trick in a Substack post where he said that there had been a 1101% increase in excess deaths in children. [https://skeptics.stackexchange.com/questions/53765/has-there-been-a-1101-increase-in-excess-deaths-among-children-aged-0-14-across] And USMortality relied on the same trick in one of his tweets, where he got about 11.2% excess deaths in 2022 and about 4.5% excess deaths in 2020, so he said there had been a 149% increase in excess deaths (because I guess an increase of 6.7 percentage points wouldn't have sounded as dramatic): [https://x.com/USMortality/status/1721410802857730423]

Someone posted this comment to McCullough's Substack: [https://petermcculloughmd.substack.com/p/peer-reviewed-study-reveals-1236/comment/77242096]
It is unlikely that the authors faced any pressure to conform to the mainstream position of being exceedingly avoidant about the possibility of serious harm resulting from the mRNA (Pfizer and Moderna) and adenovirus vector (AstraZeneca and J&J) gene therapy injections falsely marketed and mandated as COVID-19 "vaccines", because this article was not published in a proper peer-reviewed journal.
The same is true of another article, which also likely contains important research, written by Nicholas Hulscher, John Leake and Dr McCullough, on the origins of some bird flu strains: https://petermcculloughmd.substack.com/p/breaking-peer-reviewed-study-finds. See my comment: https://petermcculloughmd.substack.com/p/breaking-peer-reviewed-study-finds/comment/76276072 on how the predatory journal chosen is associated with the well-known predatory publisher Longdom.
A quick search for "Journal of Emergency Medicine: Open Access" finds it is part of the Longdom operation: https://www.longdom.org/emergency-medicine/peer-review-process.html.
If the "Journal of Emergency Medicine: Open Access" was a legitimate, properly peer-reviewed, mainstream journal it would be listed in PubMed, but it is not: https://pmc.ncbi.nlm.nih.gov/journals/. This lists seven journals which have the phrase "Journal of Emergency Medicine" in their titles, but not this one.
The publisher, Opast, is mentioned six times in this recent, mainstream, peer-reviewed journal, report on predatory journals: https://ese.arphahub.com/article/113535/ .
Both Opast and Longdom are listed on Beall's original list of predatory journals: https://beallslist.net and reports like these: https://www.editage.com/insights/my-research-has-been-published-in-a-predatory-journal
https://www.researchgate.net/post/Longdom_Publication_Issue-Is_that_a_Predatory_Publication
https://www.bmj.com/content/384/bmj.q452 (Paywalled, but the PDF is at: http://press.psprings.co.uk/bmj/march/predatoryjournals.pdf)make it clear that Longdom is a predatory publisher. It is a brand of long-established predatory publisher OMICS: https://insights.uksg.org/articles/10.1629/uksg.631.
Hulscher and McCullough also published a paper about H5N1 in a journal called "Poultry, Fisheries & Wildlife Sciences", which is another journal ran by the predatory publisher Longdom. [https://www.longdom.org/open-access/proximal-origin-of-epidemic-highly-pathogenic-avian-influenza-h5n1-clade-2344b-and-spread-by-migratory-1099735.html]
The paper by Hulscher et al. said: "Approximately 98% of the King County population received at least one dose of a COVID-19 vaccine by 2023." The authors took the percentage of vaccinated people from this website: https://data.tennessean.com/covid-19-vaccine-tracker/washing-ton/king-county/53033/. I got an error when I tried to access the website outside of the US, but I was able to access it with a free US VPN server from Proton VPN: https://protonvpn.com. The number of vaccinated people in the dataset seems to be identical to this CDC dataset: https://data.cdc.gov/Vaccinations/COVID-19-Vaccinations-in-the-United-States-County/8xkx-amqh. However the percentage of vaccinated people out of the total population is different. For example on January 4th 2022 the Tennessean dataset has 1,903,416 vaccinated people which matches the CDC data, but it has 87.99% vaccinated people which doesn't match the CDC data:
> t=fread("COVID-19_Vaccinations_in_the_United_States_County_20240227.csv")
> t[Date=="01/04/2022"&FIPS==53033,.(Date,vaxcount=Administered_Dose1_Recip,vaxpoppct=Administered_Dose1_Pop_Pct,pop=Census2019)]
Date vaxcount vaxpoppct pop
1: 01/04/2022 1903416 84.5 2252782 # population is vintage 2019 resident population estimate for mid-2019
I estimated that Tennessean uses a fixed population size of about 2163216 for King County by taking the average value across three different dates for the number of vaccinated people divided by the proportion of vaccinated people:
| Date | Vaccinated people | Vaccinated percent | Estimated population size (from people divided by percent) |
|---|---|---|---|
| 2021-03-22 | 510930 | 23.62 | 2163124 |
| 2022-01-04 | 1903416 | 87.99 | 2163219 |
| 2022-12-07 | 2120471 | 98.02 | 2163304 |
Here you can see how both the Census Bureau and OFM population estimates are higher than the Tennessean population estimate:

library(data.table);library(ggplot2);library(ggtext)
xstart=as.Date("2020-12-1");xend=as.Date("2023-7-1")
t=fread("d/cd/COVID-19_Vaccinations_in_the_United_States_County_20240227.csv.gz")
p=t[FIPS==53033,.(x=as.Date(Date,"%m/%d/%Y"),y=Administered_Dose1_Recip,z="Vaccinated people (CDC)")]
p=rbind(p,t[FIPS==53033,.(x=seq(xstart,xend,1),y=Census2019[1],z="Mid-2019 population (CDC)")])
p=rbind(p,p[,.(x=seq(xstart,xend,1),y=2163216,z="Tennessean population")])
pop=data.table(z="OFM population",x=as.Date(paste0(2020:2023,"-4-1")),y=c(2269675,2287050,2317700,2347800))
pop=rbind(pop,data.table(z="Census Bureau population",x=as.Date(paste0(2020:2023,"-7-1")),y=c(2274282,2252980,2265311,2271380)))
p=rbind(p,pop)
p[,z:=factor(z,unique(z))]
xbreak=seq(as.Date("2021-1-1"),xend,"year");xlab=2021:2023
ystart=0;ybreak=pretty(p$y,10);yend=max(ybreak)
cap="Sources:
data.cdc.gov/Vaccinations/COVID-19-Vaccinations-in-the-United-States-County/8xkx-amqh
data.tennessean.com/covid-19-vaccine-tracker/washing-ton/king-county/53033/
ofm.wa.gov/washington-data-research/population-demographics/population-estimates/
estimates-april-1-population-age-sex-race-and-hispanic-origin
www2.census.gov/programs-surveys/popest/tables/2020-2023/counties/totals/co-est2023-pop-53.xlsx"
ggplot(p,aes(x,y))+
geom_vline(xintercept=seq(as.Date("2021-1-1"),xend,"3 month"),color="gray85",linewidth=.26)+
geom_hline(yintercept=ybreak,linewidth=.26,color="gray85")+
geom_vline(xintercept=seq(as.Date("2021-1-1"),xend,"year"),color="gray65",linewidth=.3)+
geom_vline(xintercept=c(xstart,xend),linewidth=.3,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.3,lineend="square")+
geom_line(aes(color=z,linewidth=z))+
geom_point(aes(color=z,alpha=z,shape=z),stroke=.4,size=1.2)+
labs(title="King County, Washington: Vaccinated people vs population estimates",subtitle=paste0("A CDC dataset for vaccinations by county used mid-2019 resident population estimates for each year, and Tennessean used population estimates from an unknown source. Here they are compared to vintage 2023 population estimates published by the US Census Bureau and 2020-2023 population estimates published by the Washington State Office of Financial Management."),x=NULL,y=NULL,caption=cap)+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x==0,0,sprintf("%.1fM",x/1e6)))+
scale_color_manual(values=c("black",hsv(c(12,23)/36,1,.8),"red",hsv(3/36,1,.7)))+
scale_shape_manual(values=c(1,1,1,4,3))+
scale_alpha_manual(values=c(0,0,0,1,1))+
scale_linewidth_manual(values=c(.4,.4,.4,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
axis.text.x=element_text(hjust=0),
axis.ticks.length=unit(0,"pt"),
legend.background=element_rect(fill="white",color="black",linewidth=.3),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.justification=c(1,.5),
legend.key.height=unit(10,"pt"),
legend.key.width=unit(18,"pt"),
legend.key=element_blank(),
legend.margin=margin(3,5,3,4),
legend.position=c(1,.5),
legend.spacing.x=unit(1.5,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=7),
legend.title=element_blank(),
panel.background=element_blank(),
plot.margin=margin(4,4,4,4),
plot.subtitle=element_textbox_simple(size=6.5,margin=margin(4,,8)),
plot.caption=element_text(size=5.8,margin=margin(2,,1),hjust=0),
plot.title=element_text(size=7.5,face="bold",margin=margin(1,,4)))
ggsave("1.png",width=4,height=3.1,dpi=380*4)
system("magick 1.png -resize 25% 1.png")
The Tennessean dataset only includes data up to December 7th 2022,
when it says there were 98.02% vaccinated people, so Hulscher et
al. used the last value included in the dataset as their figure for the
percentage of vaccinated people in 2023. However the CDC dataset
includes data up to May 10th 2023 when it has 2,150,280 vaccinated
people in King County, which would be about 99.4% of the population size
used by Tennessean (2150280/2163216).
I don't think the percentage of vaccinated people would be as high as 98% anyway, because for example the percentage of vaccinated children under ages 10 is not very high. In the CDC dataset for COVID vaccinations by county state, there's many counties that have more vaccinated people than total people. So I don't know if for example the dataset includes vaccinated people who have died or moved outside the county.
On the website of King County only about 14% of people in ages 0-4 are listed as having completed the primary course: [https://kingcounty.gov/en/dept/dph/health-safety/disease-illness/covid-19/data/vaccination]

Hulscher et al. wrote: "Specifically, the number of cardiopulmonary arrest deaths increased from 891 in 2015 to 1,110 in 2020, representing a 24.6% increase. In 2021, deaths jumped to 1,229 and continued to rise to 1,310 in 2022. The projection for 2023 suggests 1,392 cardiopulmonary arrest deaths in King County, WA, indicating a sharp 25.4% increase since the onset of COVID-19 vaccination campaigns"
However in their Table 1 the number of deaths in 2020 was 1121 and not 1110. But 1110 was the baseline value for 2020, so the authors seem to have accidentally calculated the increase between 2020 and 2023 using the baseline value instead of the number of deaths for 2020.
But the number of deaths actually increased from 1121 in 2020 to 1392
in 2023, so it was an increase of about about 24.2% and not 24.6%. But
the baseline also increased by about 12% from 1110 in 2020 to 1245 in
2023, so the excess deaths only increased by about 10.8 percentage
points: (1392/1245)-(1121/1110).
However the figure for 2023 wasn't even the real number of deaths but
a linear projection of the deaths in 2021 and 2022. And the real number
of deaths in 2023 was 1358, so the excess deaths between 2020 and 2023
increased by only about 8.1 percentage points relative to the baseline:
(1358/1245)-(1121/1110).
But the baseline might have also been too low in 2023 because the long-term trend in deaths seemed to be curved upwards. And the authors also didn't exclude COVID deaths and there were still some COVID deaths in 2023.
Uncle John Returns posted this tweet: [https://x.com/UncleJo46902375/status/1919378805652611419/photo/2]
Hi Andrew
Can you tell me how the authors accounted for the surge in fentanyl deaths in King County?
Ta very much.
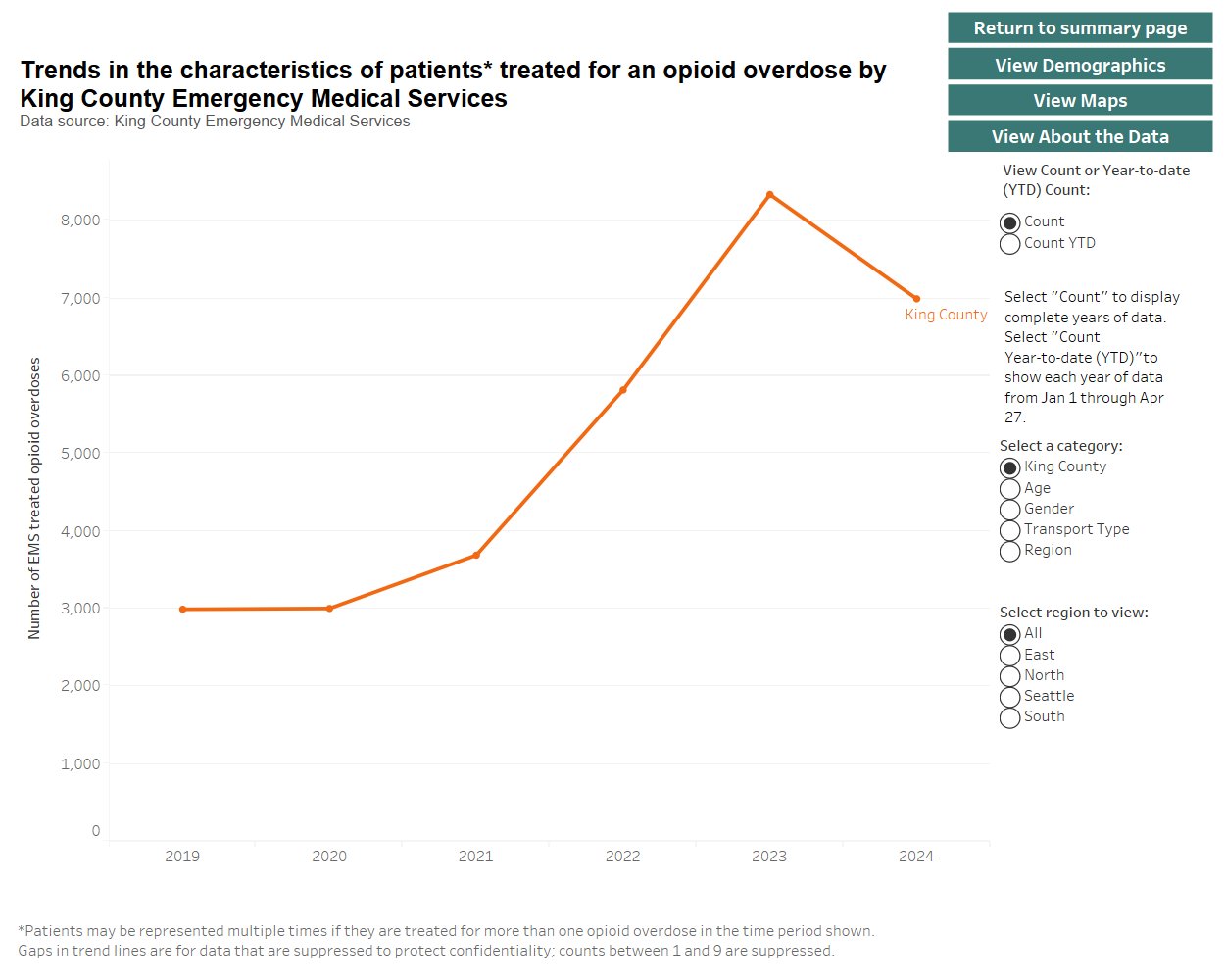
The increase in overdose deaths between 2020 and 2022 was about 3 times higher than the increase in cardiac arrest deaths treated by EMS:
| Measure | 2020 | 2022 | Increase |
|---|---|---|---|
| Overdose deaths | 510 | 1009 | 499 |
| Opioid overdose cases treated by EMS | 3003 | 5819 | 2816 |
| Cardiac deaths with resucitation attempted by EMS | 1116 | 1300 | 184 |
However likely some overdose deaths did not involve EMS, some people had already died of an overdose before EMS arrived, and some people who died of an overdose did not have a cardiac arrest before EMS arrived or while they were treated by EMS.
Uncle John Returns also found an old study which said that even in the year 2000 when the number of opioid deaths was much smaller than in the 2020s, King County EMS responded to 245 cardiac arrest cases caused by a drug overdose, and 234 of them led to a death: "Methods: The study population was composed of death events caused by acute drug poisoning, defined as poisoning deaths and deaths averted (persons successfully resuscitated from out-of-hospital cardiac arrest by EMS) in King County, Washington, during the year 2000. Results: Eleven persons were successfully resuscitated and 234 persons died from cardiac arrest caused by acute drug poisoning, for a total of 245 cardiac events. The EMS responded to 79.6% (195/245), attempted resuscitation in 34.7% (85/245), and successfully resuscitated 4.5% (11/245) of all events." [https://onlinelibrary.wiley.com/doi/abs/10.1197/j.aem.2003.08.014]
There's also a study from 2023 which looked at overdose-related cardiac arrests outside of hospitals in King County, where the rate of overdoses increased by about 2.5-fold between the years 2015 and 2021. [https://jamanetwork.com/journals/jamanetworkopen/fullarticle/2811464]
In my previous plot of NVSS data I included all ICD codes under the chapter for cardiac deaths, but in the next plot I included only ICD codes for cardiac arrest (I46), heart failure (I50), and myocardial infarction (I21 and I22).
When I looked at deaths that included one of the cardiac causes of death but that also included one of 16 ICD codes for overdose from recreational drugs, there was a huge increase from 13 deaths in 2018 to 83 deaths in 2023.
However it seems to be fairly rare for cardiac arrest to be listed as a cause of death for overdose deaths in NVSS, because the EMS datasets have a much higher number of overdose deaths where cardiac resuciation was attempted by EMS.
Another observation you can make from my plot is that there were less cardiac-related deaths in 2023 than 2022, which conflicts with the PDF reports published by King County Emergency Medical Services, where the number of cardiac deaths for which resucitation was attempted increased by about 4% between 2022 and 2023.

t=fread("http://sars2.net/f/seattlecardiac.csv")
t=t[cause!="all"]
p=t[,.(x=year,y=dead,z=cause)]
cause=c(other="All minus drugs minus COVID",drug="Drugs (X40-44, X60-64, Y10-14, and T40)",covid="COVID (U07.1)")
p[,z:=factor(z,names(cause),cause)]
xstart=2010;xend=2024
ystart=0;yend=p[,sum(y),x][,max(V1)*1.1];ybreak=pretty(c(ystart,yend),8)
trend=data.table(x=2010:2024)
trend$y=p[,sum(y),x][x<2020,predict(lm(V1~x),trend)]
trend[,x:=x-xstart+1]
p=p[x%in%xstart:xend]
p[,x:=factor(x)]
lab="2010-2019 linear trend"
ggplot(p)+
geom_bar(aes(x=x,y=y,fill=z),stat="identity",width=.8,position=position_stack(reverse=T))+
geom_line(data=trend,aes(x,y,color=lab,linetype=lab),linewidth=.7)+
labs(title="CDC WONDER: Yearly cardiac deaths in Seattle metropolitan area",x=NULL,y=NULL)+
scale_x_discrete(expand=c(0,.6))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,expand=c(0,0))+
scale_fill_manual(values=c("black",hsv(9/36,1,.8),hsv(27/36,.8,1),"gray60"))+
scale_color_manual(labels=lab,values="gray60")+
scale_linetype_manual(labels=lab,values="42")+
coord_cartesian(clip="off")+
guides(fill=guide_legend(order=1),color=guide_legend(order=2),alpha="none",linetype=guide_legend(order=2))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
axis.ticks.length=unit(0,"pt"),
legend.background=element_rect(fill=alpha("white",1),color="black",linewidth=.4),
legend.box="vertical",
legend.box.just="center",
legend.box.spacing=unit(0,"pt"),
legend.justification=c(.5,.5),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(30,"pt"),
legend.margin=margin(4,5,4,4),
legend.position=c(.5,.3),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid.major.x=element_blank(),
panel.grid.major.y=element_line(linewidth=.4,color="gray70"),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,face=2,margin=margin(1,,4),hjust=1))
ggsave("1.png",width=5.25,height=3.2,dpi=300*4)
sub="\u00a0 Cardiac deaths are deaths with MCD cardiac arrest (I46), heart failure (I50), or myocardial infarction (I21 and I22). The green bar shows deaths that additionally had a drug-related MCD, and the purple bar shows deaths that additionally had MCD COVID.
The included counties of residence are King, Snohomish, and Pierce county. The data was retrieved from CDC WONDER in May 2025, so some drug deaths in 2024 are still missing because of a delay in a cause of death being assigned.
Drug deaths are not included for 2017 because there were less than 10 deaths so the number of deaths was suppressed."
system(paste0("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\''",sub),"' -splice x80 \\) -append -resize 25% -bordercolor white -border 24 -dither none -colors 256 1.png"))
In my plot above I included data for all three counties of the Seattle metropolitan area, because in King County alone there were multiple years when there were less than 10 cardiac deaths that also had a drug-related ICD code, so the number of deaths was suppressed.)
Peter Hegarty, Raphael Lataster, Igor Chudov, and Guyla Nagy have all published a similar analysis where they compared excess mortality across European countries against the percentage of vaccinated people, and they found that the percentage of vaccinated people had a positive correlation with excess mortality in 2023. [https://x.com/PeterHegarty17/status/1700894195362197780, https://okaythennews.substack.com/p/study-shows-european-excess-mortality, https://www.igor-chudov.com/p/2023-excess-mortality-positively, https://forum.index.hu/Article/jumpTree?a=166090420&t=9243202] Chudov took excess mortality data from OECD which used a 2015-2019 average baseline, but the others took excess mortality data from Eurostat which uses a 2016-2019 average baseline.
However a prepandemic average baseline for raw deaths overestimates excess mortality in Western European countries relative to Eastern European countries. And Eastern European countries have a lower percentage of vaccinated people which explains the positive correlation in 2023.
In the years before COVID Western European countries had on average a steeper increase in the number of deaths per year than Eastern European countries. And in Eastern European countries the population size was reduced more by excess deaths in 2020 and 2021, so in the plot below where I calculated the green line for the expected number of deaths by multiplying the pre-COVID trend in deaths for each age by the population estimates for each age, Eastern European countries have a bigger drop in the baseline by 2022:

library(data.table);library(ggplot2)
q=\(...)as.character(substitute(...()))
# sars2.net/stat.html#Eurostat
t=fread("http://sars2.net/f/eurostatpopdead.csv.gz")[year%in%2010:2022]
t=t[location%in%na.omit(t)[,.N,location][N==max(N),location]]
t=t[!location%in%q(DE_TOT,EFTA)]
base=t[year%in%2010:2019,.(year=2010:2022,base=predict(lm(dead/pop~year),.(year=2010:2022))),.(age,location)]
p=merge(t,base)[,.(dead=sum(dead),base=sum(base*pop)),.(year,name)]
p=merge(p,p[year%in%2016:2019,.(ave=mean(dead)),name])
lab=c("Actual deaths","2016-2019 average","2010-2019 trend in CMR by age × population")
p=p[,.(x=year,y=c(dead,ave,base),z=factor(rep(lab,each=.N),lab),group=name)]
west=q(Iceland,Norway,Finland,Sweden,Denmark,Ireland,Netherlands,Belgium,Luxembourg,Germany,Liechtenstein,Switzerland,Austria,France,Portugal,Spain,Italy,Malta,Greece,Cyprus)
east=q(Estonia,Latvia,Poland,Czechia,Slovakia,Hungary,Slovenia,Croatia,Serbia,Romania,Bulgaria)
tot=c("West average","East average")
p=merge(p,p[z==z[1]&x%in%2016:2019,.(base=mean(y)),group])[,y:=y/base*100]
p=rbind(p,p[,.(y=mean(y),base=mean(base)),.(z,x,group=ifelse(group%in%west,tot[1],tot[2]))])
p[,group:=factor(group,c(west,east,tot))]
xstart=2010;xend=2022;p=p[x%in%xstart:xend]
ggplot(p,aes(x,y))+
facet_wrap(~group,ncol=5,dir="v")+
geom_hline(yintercept=0,color="gray60",linewidth=.4)+
geom_line(aes(color=z,linewidth=z,linetype=z))+
geom_point(aes(alpha=z,color=z),stroke=.5,size=1.5,shape=1)+
geom_text(data=p[rowid(group)==1],aes(label=group),color=ifelse(p[rowid(group)==1,group]%in%c(west,tot[1]),"#4444ff","#ff4444"),y=max(p$y),x=xstart,hjust=0,size=3.2,vjust=1.1)+
labs(title="Eurostat: Yearly deaths as percentage of 2016-2019 average",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart+1,xend,2))+
scale_y_continuous(limits=extendrange(p$y,,.03),breaks=pretty,labels=\(x)paste0(x,"%"))+
coord_cartesian(clip="off",expand=F)+
scale_color_manual(values=c("black","black","#00aa00"))+
scale_linewidth_manual(values=c(0,.5,.6))+
scale_linetype_manual(values=c("solid","31","solid"))+
scale_alpha_manual(values=c(1,0,0))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(angle=90,vjust=.5,hjust=),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(3,"pt"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification="right",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(25,"pt"),
legend.margin=margin(,,6),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.spacing.x=unit(0,"pt"),
panel.spacing.y=unit(0,"pt"),
plot.margin=margin(7,7,7,7),
plot.title=element_text(size=11.5,face=2,margin=margin(1,,4)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=7,height=9,dpi=300*4)
system("magick 1.png -resize 25% -colors 256 1.png")
In the plot above I used Eurostat's population estimates on January 1st for each year, so for example in Spain the green line drops between 2020 and 2021 because the excess deaths in 2020 didn't affect the population estimates I used until 2021. If I would've used mid-year population estimates or the average population throughout the year, the green line in Spain would've already dropped in 2020.
I treated Finland, Greece, and Cyprus as Western European even though they are geographically part of Eastern Europe. But they had a higher percentage of vaccinated people than any eastern bloc country in my analysis, and before COVID their yearly number of deaths was also increasing at a steeper slope than in most eastern bloc countries.
Here my correlation between the percentage of vaccinated people and excess mortality in 2022 dropped from about 0.34 to about -0.16 when I switched from the 2016-2019 average baseline to a 2013-2019 linear regression for ASMR:

download.file("https://covid.ourworldindata.org/data/owid-covid-data.csv","owid-covid-data.csv")
library(data.table);library(ggplot2)
o=fread("owid-covid-data.csv")
# sars2.net/stat.html#Eurostat
t=fread("http://sars2.net/f/eurostatpopdead.csv.gz")[year%in%2013:2022]
t=merge(t,t[location=="EU27_2020"&year==2020,.(age,std=pop/sum(pop))])
t=t[location%in%na.omit(t)[,.N,location][N==max(N),location]]
t=t[!location%in%c("DE_TOT")]
a=t[,.(dead=sum(dead),asmr=sum(dead/pop*std)*1e5),.(location,name,year)]
a$base=a[year<2020,predict(lm(asmr~year),.(year=2013:2022)),location]$V1
a$base2=a[year%in%2015:2019,predict(lm(dead~year),.(year=2013:2022)),location]$V1
a=merge(a,a[year%in%2016:2019,.(base3=mean(dead)),location])
p=a[year==2022,.(x=(asmr/base-1)*100,y=(dead/base3-1)*100),name]
p=merge(p,o[year(date)==2022,.(vaxpct=mean(people_vaccinated_per_hundred,na.rm=T)),.(name=location)])
p=na.omit(p)
lab=c("2016-2019 average for raw deaths","2013-2019 linear regression for ASMR")
p=p[,.(name,x=vaxpct,y=c(y,x),facet=factor(rep(lab,each=.N),lab))]
q=\(...)as.character(substitute(...()))
east=q(Bulgaria,Croatia,Cyprus,Czechia,Estonia,Greece,Hungary,Latvia,Poland,Romania,Serbia,Slovenia,Slovakia)
lab=q(Eastern,Western)
p$z=factor(ifelse(p$name%in%east,lab[1],lab[2]),lab)
levels(p$facet)=p[,cor(x,y),facet][,sprintf("Baseline is %s (r ≈ %.2f)",facet,V1)]
xbreak=pretty(p$x,7);ybreak=pretty(p$y,7);ylim=extendrange(p$y,,.02)
ggplot(p,aes(x,y))+
facet_wrap(~facet,dir="v",scales="free_x")+
coord_cartesian(clip="off",expand=F)+
geom_vline(xintercept=0,linewidth=.4,color="gray60")+
geom_hline(yintercept=0,linewidth=.4,color="gray60")+
geom_smooth(method="lm",formula=y~x,linewidth=.5,se=F,color="black",linetype="42")+
geom_label(data=p[rowid(facet)==1],aes(label=stringr::str_wrap(facet,40)),x=xbreak[1],y=ylim[2],lineheight=.9,hjust=0,vjust=1,size=3.7,label.r=unit(0,"pt"),label.padding=unit(6,"pt"),label.size=.4)+
geom_point(aes(color=z),size=.7)+
ggrepel::geom_text_repel(aes(label=name,color=z),size=3,max.overlaps=Inf,segment.size=.3,min.segment.length=.2,box.padding=.07,show.legend=F)+
labs(title="Correlation between percentage of vaccinated people in 2022 and\nexcess mortality percent in 2022",x="Average percentage of vaccinated people throughout 2022 at OWID",y="Excess percentage of deaths in 2022 at Eurostat")+
scale_x_continuous(breaks=xbreak,limits=range(xbreak),labels=\(x)paste0(x,"%"))+
scale_y_continuous(breaks=ybreak,limits=ylim,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("#ff4444","#5555ff"))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(3)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(4,"pt"),
axis.title=element_text(size=11),
axis.title.x=element_text(margin=margin(3)),
axis.title.y=element_text(margin=margin(,2)),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(16,"pt"),
legend.position="top",
legend.justification="right",
legend.spacing.x=unit(2,"pt"),
legend.margin=margin(,,6),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.grid.major=element_blank(),
panel.spacing=unit(4,"pt"),
plot.margin=margin(6,22,5,5),
plot.subtitle=element_text(size=11),
plot.title=element_text(size=11.5,face=2,margin=margin(1,,5)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=6,height=6,dpi=300*4)
sub="Source: covid.ourworldindata.org/data/owid-covid-data.csv and Eurostat datasets demo_magec and demo_pjan. ASMR was calculated by single year of age up to ages 100+ so that the 2020 EU population estimates were used as the standard population. Countries that had deaths or population estimates missing for any combination of age or year in 2013-2022 were omitted. Romania was omitted because it was missing vaccination data at OWID."
system(paste0("mogrify -trim 1.png;w=`identify -format %w 1.png`;magick 1.png \\( -size $[w]x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\'",sub),"' -splice x100 \\) -append -resize 25% -bordercolor white -border 30 -colors 256 1.png"))
Here Western European countries are also more likely to be above the diagonal, which means that the 2016-2019 average baseline likely overestimates their excess mortality in 2022 compared to ASMR:

library(data.table);library(ggplot2)
eu=fread("http://sars2.net/f/eurostatpopdead.csv.gz")[year%in%2013:2022] # sars2.net/stat.html#Eurostat
eu=merge(eu,eu[location=="EU27_2020"&year==2020,.(age,std=pop/sum(pop))])
eu=eu[!location%in%c("DE_TOT","EFTA")]
eu=eu[location%in%na.omit(eu)[,.N,location][N==max(N),location]]
a=eu[,.(dead=sum(dead),asmr=sum(dead/pop*std*1e5)),.(name,year)]
a$base=a[year<2020,predict(lm(asmr~year),.(year=2013:2022)),name]$V1
a=merge(a,a[year%in%2016:2019,.(base2=mean(dead)),name])
p=a[year==2022,.(x=(asmr/base-1)*100,y=(dead/base2-1)*100,name)]
east=c("Bulgaria","Croatia","Czechia","Estonia","Hungary","Latvia","Poland","Romania","Serbia","Slovenia","Slovakia")
lab=c("Western Europe","Eastern Europe")
p[,z:=factor(ifelse(name%in%east,lab[2],lab[1]),lab)]
breaks=p[,pretty(c(x,y),9)];lims=p[,extendrange(range(c(x,y)),,.04)]
ggplot(p,aes(x,y))+
coord_fixed(clip="off",expand=F)+
geom_vline(xintercept=0,linewidth=.4,color="gray60")+
geom_hline(yintercept=0,linewidth=.4,color="gray60")+
geom_abline(linetype="dashed",color="gray60",size=.4)+
geom_point(aes(color=z),size=.6)+
ggrepel::geom_text_repel(aes(label=name,color=z),size=3,max.overlaps=Inf,segment.size=.1,min.segment.length=.2,box.padding=.07,show.legend=F)+
labs(title="Eurostat: Excess ASMR vs excess raw deaths in 2022",x="Excess ASMR in 2022 relative to 2013-2019 linear trend",y="Excess raw deaths in 2022 relative to 2016-2019 average")+
scale_x_continuous(limits=lims,breaks=breaks,labels=\(x)paste0(x,"%"))+
scale_y_continuous(limits=lims,breaks=breaks,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("#5555ff","#ff4444"))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(3)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(-4,"pt"),
axis.title=element_text(size=11),
axis.title.x=element_text(margin=margin(3)),
axis.title.y=element_text(margin=margin(,2)),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.position="top",
legend.justification="left",
legend.spacing.x=unit(2,"pt"),
legend.margin=margin(,,6),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.grid.major=element_blank(),
plot.subtitle=element_text(size=11),
plot.title=element_text(size=11.5,face=2,margin=margin(1,,5)))
ggsave("1.png",width=6,height=6,dpi=300*4)
sub="ASMR was calculated by single year of age up to ages 100+ so that the 2020 EU population estimates were used as the standard population. Deaths and population estimates by single year of age were compiled with this script: sars2.net/stat.html#Compile_a_CSV_file_for_deaths_and_population_estimates_by_single_year_of_age_in_various_countries. Countries that had deaths or population estimates missing for any combination of age or year in 2013-2022 were omitted. Western Europe includes geographically Eastern European countries that were not part of the eastern bloc."
system(paste0("mogrify -trim 1.png;w=`identify -format %w 1.png`;magick 1.png \\( -size $[w]x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\'",sub),"' -splice x100 \\) -append -resize 25% -bordercolor white -border 30 -colors 256 1.png"))
In the previous plots I used the Eurostat dataset demo_magec which has yearly deaths by single year of age: https://ec.europa.eu/eurostat/databrowser/product/page/demo_magec. However it was still missing deaths for 2023 as of December 2024, so in the next plot I looked at the Eurotat dataset for weekly deaths by five-year age groups instead which also has data for 2023 and 2024: https://ec.europa.eu/eurostat/databrowser/product/page/demo_r_mwk_05. In the top panel of the plot below if you look at the black line that includes both Western Europe and Eastern Europe, the average correlation in 2023 is close to zero:

download.file("https://covid.ourworldindata.org/data/owid-covid-data.csv","owid-covid-data.csv")
download.file("https://ec.europa.eu/eurostat/api/dissemination/sdmx/2.1/data/demo_r_mwk_05?format=TSV","demo_r_mwk_05.tsv")
library(data.table);library(ggplot2)
isoweek=\(year,week,weekday=7){d=as.Date(paste0(year,"-1-4"));d-(as.integer(format(d,"%w"))+6)%%7-1+7*(week-1)+weekday}
q=\(...)as.character(substitute(...()))
ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
o=fread("owid-covid-data.csv")
euro=fread("demo_r_mwk_05.tsv")
meta=fread(text=euro[[1]],header=F)
pick=meta[,V2%like%"^Y"&V3=="T"];meta=meta[pick];euro=euro[pick]
meta[,age:=as.integer(sub("\\D+(\\d+).*","\\1",sub("Y_LT5",0,V2)))]
eu=meta[,.(loc=V5,age,date=rep(names(euro)[-1],each=.N),dead=as.integer(sub("\\D+","",unlist(euro[,-1],,F))))]
eu[,year:=as.integer(substr(date,1,4))][,week:=as.integer(substr(date,7,8))]
eu[,date:=isoweek(year,week,4)]
eu=eu[loc%in%eu[year%in%2013:2023,.N,loc][N==max(N),loc]]
eu=eu[year>=2013]
pop=fread("http://sars2.net/f/eurostatpopdead.csv.gz")[year%in%2013:2023] # sars2.net/stat.html#Eurostat
a=pop[,.(pop=sum(pop)),.(location,name,date=as.Date(paste0(year,"-1-1")),age=pmin(age,90)%/%5*5)]
a=a[location%in%na.omit(a)[,.N,location][N==max(N),location]]
a=a[,spline(date,pop,xout=unique(eu$date),method="natural"),.(location,age,name)]
a=merge(eu,a[,.(date=`class<-`(x,"Date"),pop=y,loc=location,name,age)])
a=merge(pop[location=="EU27_2020"&year==2020,.(pop=sum(pop)),.(age=pmin(age,90)%/%5*5)][,.(age,std=pop/sum(pop))],a)
a=a[loc%in%na.omit(a)[year%in%2013:2023,.N,loc][N==max(N),loc]]
a=a[,.(dead=sum(dead),asmr=sum(dead/pop*std/7*365e5)),,.(name,date,year,week)]
slope=a[year%in%2013:2019&week%in%15:35,mean(asmr),.(year,name)]
slope=slope[,{x=.(year=2013:2024,slope=predict(lm(V1~year),.(year=2013:2024)));x$slope=x$slope/x$slope[x$year==2016];x},name]
weekly=a[year%in%2013:2019,.(weekly=mean(asmr)),.(week,name)]
a=merge(slope,merge(weekly,a))
a=merge(a[year%in%2016:2019,.(deadbase=mean(dead)),.(name,week)],a)
p=a[,.(pct=(asmr/(slope*weekly)-1)*100,pct2=(dead/deadbase-1)*100),,.(name,date)]
east=q(Estonia,Latvia,Poland,Czechia,Slovakia,Hungary,Montenegro,Slovenia,Croatia,Serbia,Romania,Bulgaria)
p=merge(p,o[,.(date,vax=nafill(nafill(zoo::na.approx(people_vaccinated_per_hundred,na.rm=F),"locf"),,0)),.(name=location)])
p[,z:=ifelse(name%in%east,"Eastern Europe","Western Europe")]
p=rbind(p,copy(p)[,z:="Total"])
p[,z:=factor(z,unique(z))]
lab=c("Baseline is seasonality-adjusted linear trend for ASMR in 2013-2019","Baseline is average raw deaths on corresponding week number in 2016-2019")
p=na.omit(p)[,.(y=c(cor(pct,vax),cor(pct2,vax)),group=lab),.(x=date,z)]
p[,group:=factor(group,lab)]
p[,y:=ma(y,2),.(z,group)]
xstart=as.Date("2020-12-1");xend=as.Date("2025-1-1")
xbreak=seq(as.Date("2021-1-1"),xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
sub="\u00a0 Weekly excess deaths by 5-year age groups are from the Eurostat dataset demo_r_mwk_05. Weekly population estimates were spline interpolated from population estimates on January 1st from the Eurostat dataset demo_pjan. ASMR was calculated by 5-year age groups up to ages 90+ so that the 2020 EU population was used as the standard population.
The slope of the baseline for ASMR was determined by doing a linear regression for mean ASMR on weeks 15-35 of each year, where winter weeks were excluded due to higher variability in mortality during winters. In order to adjust the baseline for seasonality, each week number has its own intercept.
The variable people_vaccinated_per_hundred at OWID was used for the percentage of vaccinated people. Missing values were interpolated linearly and the percentage was treated as zero before the earliest reported value. The percentage of vaccinated people on each Thursday was used as the percentage for the week.
Andorra, Albania, Germany, Lithuania, and UK were omitted because data for deaths or population estimates was missing.
Western Europe includes Finland, Greece, and Cyprus."
ggplot(p,aes(x,y))+
facet_wrap(~group,ncol=1,dir="v",scales="free_x")+
geom_hline(yintercept=0,color="gray60",linewidth=.4)+
geom_vline(xintercept=seq(as.Date("2021-1-1"),xend,"year"),color="gray60",linewidth=.4)+
geom_line(aes(color=z),linewidth=.6)+
labs(title=paste0("Correlation between excess deaths at Eurostat and vaccinated percent at\nOWID for ",a[,length(unique(name))]," European countries (±2-week moving average)"),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(-1,1),breaks=seq(-1,1,.5))+
scale_color_manual(values=c("#5555ff","#ff5555","black"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(3)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.x=element_line(color=alpha("black",c(1,0))),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification="right",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(25,"pt"),
legend.margin=margin(),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.spacing=unit(0,"pt"),
plot.margin=margin(7,7,7,7),
plot.title=element_text(size=11.5,face=2,margin=margin(1,,5)),
strip.background=element_blank(),
strip.text=element_text(size=11,face=2))
ggsave("1.png",width=6.2,height=4.6,dpi=300*4)
system(paste0("mogrify -trim 1.png;w=`identify -format %w 1.png`;magick 1.png \\( -size $[w]x -font Arial -interline-spacing -3 -pointsize $[46*4] caption:'",gsub("'","'\\\\'",sub),"' -splice x100 \\) -append -resize 25% -bordercolor white -border 30 -colors 256 1.png"))
In the following code I made a model for each country, where at the start of the model each age had the same population size as Eurostat's population estimate for January 1st 2019. Each year I killed the same proportion of people each age that died in 2017-2019, I incremented the age of surviving people by one, and I added the same number of people aged zero as in Eurostat's population estimate for 2019. Then I used the number of deaths produced by the model in 2022 as the expected deaths for each country:
t=fread("http://sars2.net/f/eurostatpopdead.csv.gz")
t=t[year%in%2016:2022]
t=t[location!="DE_TOT"&name!=""]
t=t[location%in%na.omit(t)[,.N,location][N==max(N),location]]
model=\(x){pop=x[year==2019,pop];births=pop[1]
cmr=x[year%in%2017:2019,sum(dead)/sum(pop)]
for(year in 2019:2022){
died=pop*cmr;pop=pop-died
pop=c(births,pop[1:99],sum(pop[100:101]))
}
sum(died)}
a=t[year==2019,.(modeled=model(.SD)),name]
ave=t[year%in%2016:2019,sum(dead),.(year,name)]
a=merge(a,ave[,.(ave=mean(V1)),name])
a[,.(name,ratio=modeled/ave,modeled,ave)][order(-ratio)]
The output shows that when I took the number of deaths produced by the model in 2022 and divided it with the average number of deaths in 2016-2019, the ratio was much higher on average in Western European countries than Eastern European countries, which again shows how Eurostat's 2016-2019 average baseline exaggerates excess deaths in Western European countries relative to Eastern European countries:
name ratio modeled ave
1: Cyprus 1.074 6304 5868
2: Malta 1.037 3705 3572
3: Luxembourg 1.028 4326 4208
4: Ireland 1.024 31520 30771
5: Switzerland 1.023 68214 66701
6: Iceland 1.019 2312 2269
7: France 1.017 616090 605888
8: Greece 1.013 123673 122138
9: Poland 1.013 408750 403692
10: Slovenia 1.012 20558 20318
11: Czechia 1.012 112409 111119
12: Netherlands 1.008 152318 151115
13: Austria 1.007 83408 82825
14: Denmark 1.007 54173 53819
15: Norway 1.006 41018 40756
16: Liechtenstein 1.004 265 264
17: Germany 1.000 934299 934392
18: Slovakia 0.999 53385 53448
19: Belgium 0.998 109051 109310
20: Portugal 0.997 110995 111294
21: Finland 0.995 53766 54030
22: Spain 0.993 414872 417881
23: Italy 0.992 628013 632968
24: Estonia 0.990 15366 15522
25: Romania 0.986 257545 261131
26: Hungary 0.986 128181 130028
27: Sweden 0.984 89490 90976
28: Serbia 0.980 99830 101917
29: Croatia 0.978 51202 52380
30: Bulgaria 0.974 105706 108495
31: Latvia 0.961 27352 28469
32: Lithuania 0.951 37818 39776
name ratio modeled ave
Peter Hegarty also did an analysis of global correlation between excess mortality and vaccination rates at OWID, where he got a positive correlation when he used a 2015-2019 average baseline but a negative correlation when he used a 2015-2019 linear trend (where the 2015-2019 linear trend was probably more accurate, but it would've likely been even better to use ASMR): [https://www.researchgate.net/publication/379815723_EXCESS_MORTALITY_AND_THE_EFFECT_OF_THE_COVID-19_VACCINES_PART_2_GLOBAL_DATA]

Kirsch claimed that Singapore was the country with the highest excess mortality in 2023: [https://x.com/stkirsch/status/1874371023048745288]

However at Mortality Watch Singapore doesn't have as high excess CMR percent in 2023 as Qatar, Macao, and Turkey:
t=fread("https://s3.mortality.watch/data/mortality/world_yearly.csv")
a=t[date==2023&!iso3c%like%"-",.(iso3c,pct=(cmr/cmr_baseline-1)*100)]
na.omit(a)[order(-pct)][1:16]
# iso3c pct
# 1: QAT 40.211640
# 2: MAC 26.718759
# 3: TUR 18.019009
# 4: SGP 16.584036 # Singapore has 4th highest excess CMR percent in 2023
# 5: TWN 13.045924
# 6: GLP 12.944331
# 7: HKG 12.094968
# 8: NOR 11.926244
# 9: THA 10.936049
# 10: AUS 10.927573
# 11: ECU 10.246085
# 12: GBRTENW 10.225523
# 13: IRL 9.575793
# 14: BRB 9.489875
# 15: SMR 9.445180
# 16: FIN 9.440650
Macao has about 260% excess deaths in January 2023 on OWID. The first big COVID wave in China was in December 2022 to January 2023 after the zero COVID policy was dropped.
Singapore had the first big COVID wave in October to November of 2021, so Singapore was still essentially in its second year of COVID for most of 2023. But if the excess deaths were caused by the vaccines then why was there were low excess deaths in the first half of 2021 when most people got vaccinated?

Clare Craig wrote: [https://drclarecraig.substack.com/p/us-mortality-changed-in-2021-and]
So far, so boring. There is no relationship to sequential periods. Even the arrival of covid and lockdowns and the associated mortality did not produce a relationship. However, things change dramatically from this point.
Even if you hate graphs you can easily see that the dots are much less scattered and start to sit really close to the line.
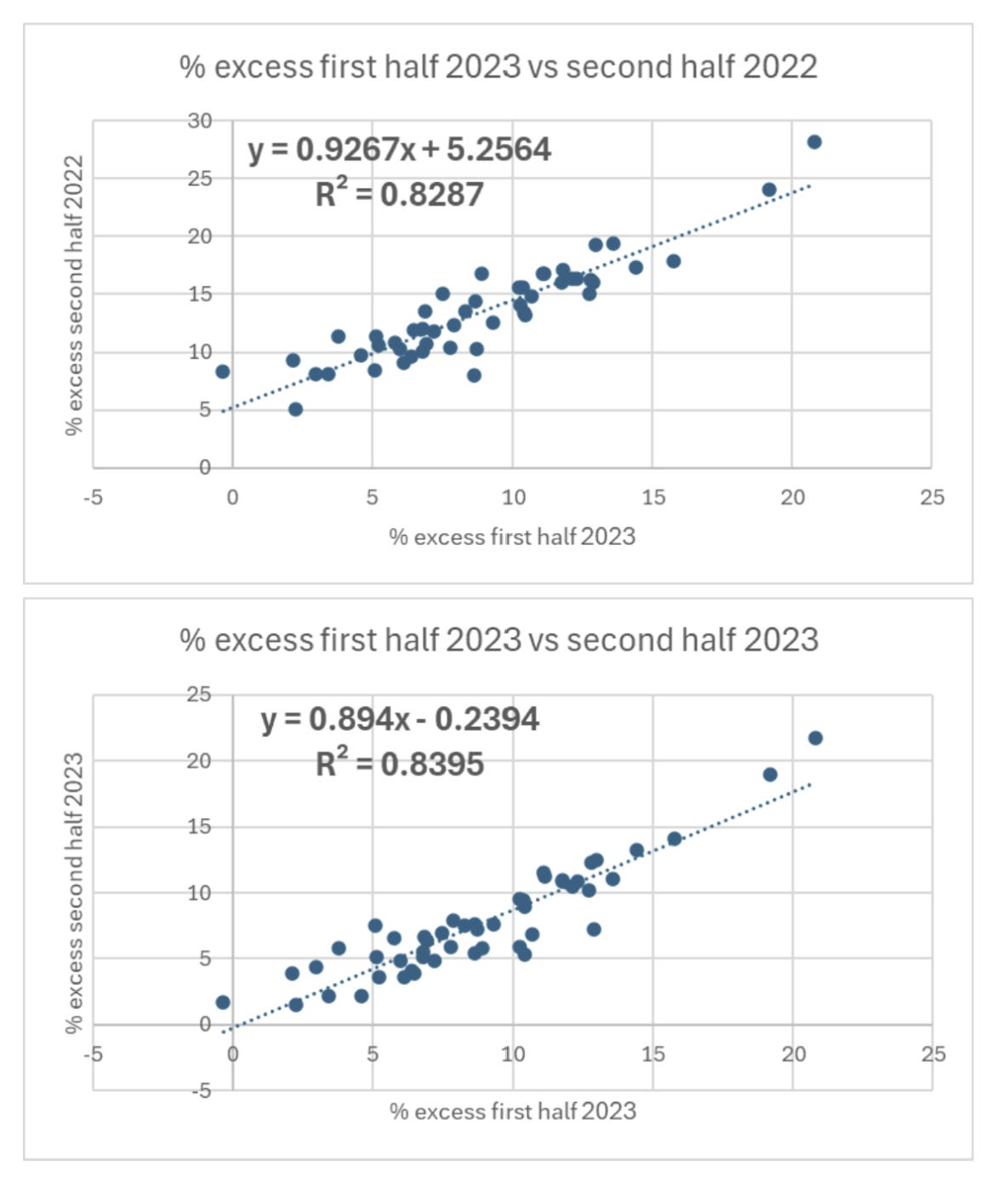
The R2 value is now about as high as they come in biology. If you were trying to predict the percentage excess in the second half of 2023 for each state, knowing the percentage excess in the first half of 2023 would allow you to explain 84% of the differences between states.
Something changed dramatically in 2021. The factors that caused excess mortality prior to 2021 randomly affected the different states and did not remain constant from one 6 month period to the next. However, from 2021 there was a factor that did remain constant over time. Here are the R2 values plotted over time (H1 = first half and H2 = second half).

However Craig fitted her baseline against deaths in 2010-2019, so 2023 was further away from her fitting period than 2021. So by 2023 her baseline was probably further off from the actual long-term trend on average than in 2021.
In the following code I fitted a linear regression against deaths in June of 2010-2019 in each US state and DC. But in the early 00s my baseline was further off than in the late 00s, so my correlation between excess deaths in the first and second half of the year was much higher in the early 00s than the late 00s:
> t=fread("http://sars2.net/f/wonderstatemonthly.csv")[year!=2025]
> t[,date:=as.Date(paste(year,month,1,sep="-"))]
> t=merge(t,t[month==6&year%in%2010:2019,.(date=unique(t$date),base=predict(lm(dead~date),t[rowid(date)==1])),state])
> a=t[,sum(dead)/sum(base),.(year,half=(month-1)%/%6+1,state)]
> print(a[,.(cor=cor(V1[half==1],V1[half==2])),year],r=F)
year cor
1999 0.949
2000 0.971
2001 0.945
2002 0.951
2003 0.940
2004 0.949
2005 0.878
2006 0.845
2007 0.788
2008 0.793
2009 0.892
2010 0.712
2011 0.670
2012 0.256
2013 0.622
2014 0.201
2015 0.437
2016 0.390
2017 0.287
2018 0.410
2019 0.455
2020 -0.323
2021 0.301
2022 0.794
2023 0.916
2024 0.765
year cor
Kirsch posted the image below and wrote: "If the Covid vaccine worked so well, then why wasn't there a divergence in these curves? Palestine was severely under vaccinated compared to Israel, so why does Israel have more Covid deaths per capita than Palestine? They basically tracked each other!!" [https://x.com/stkirsch/status/1887186858326790420]

However in early 2021 there was a big spike in all-cause deaths in Palestine but not Israel, but at the time Israel already had a high percentage of vaccinated people but in Palestine almost no-one was vaccinated:

Also COVID deaths seem to be underreported relative to all-cause excess deaths in Palestine. If you look at excess all-cause deaths per capita instead, Israel is initially above Palestine but after the vaccine rollout Palestine crosses above Israel: [https://ourworldindata.org/grapher/cumulative-excess-deaths-per-million-covid?tab=chart&time=2020-01-25..2021-12-31&country=ISR~PSE]

The plot above is not even adjusted for age but the population of Israel is much older than the population of Palestine. Kirsch's plot for COVID deaths per capita was not adjusted for age either.
The Twitter user Humanspective posted this plot of yearly deaths registered in Western Australia: [https://x.com/Humanspective/status/1888016480010420707]

He cited this website as his source, which had data going back to 1981: https://www.wa.gov.au/organisation/department-of-justice/the-registry-of-births-deaths-and-marriages/statistics-births-deaths-and-marriages-registered. But Humanspective misleadingly started his x-axis from the year 2016 when there was a high number of deaths, so it gave the wrong impression of the trend in mortality before COVID:

p$poly=p[year<2020,predict(lm(dead~poly(year,2)),p)]
p=data.table(year=1981:2024,dead=c(8180,8287,8550,8706,9042,9503,9082,9698,9718,9614,9753,10163,10491,10466,10570,11251,10905,10741,11074,10858,10751,11711,11520,11437,11504,11821,12581,13011,12855,12927,13001,13605,13628,14040,14705,15071,14754,14873,15281,15258,16106,17516,17734,18303))
p$trend=p[year%in%2010:2019,predict(lm(dead~year),p)]
p$trend2=p[year%in%2016:2019,predict(lm(dead~year),p)]
png("1.png",1800,1200,res=300)
par(mar=c(4.9,2.7,1.8,.7),mgp=c(0,.6,0),adj=0,lend="square",tck=-.03)
tit="Yearly deaths registered in Western Australia"
leg=c("Deaths","2010-2019 linear trend","2016-2019 linear trend")
color=c("black","blue","#9999ff")
ybreak=pretty(c(0,p$dead,p$trend));ylim=range(ybreak)
xstart=min(p$year);xend=max(p$year)
xbreak=seq(1982,2024,2)
plot(p$year,p$trend,type="n",main=tit,xlab=NA,ylab=NA,xaxs="i",yaxs="i",xaxt="n",yaxt="n",ylim=ylim,xlim=c(xstart-.5,xend+.5),cex.main=1)
axis(1,at=xbreak,las=2)
axis(2,at=ybreak,las=1,labels=ifelse(ybreak==0,0,paste0(ybreak/1e3,"k")))
lines(p$year,p$dead,lwd=1.5)
points(p$year,p$dead,pch=20,cex=.6)
lines(p$year,p$trend,type="l",lty=2,lwd=1.5,col=color[2])
lines(p$year,p$trend2,type="l",lty=2,lwd=1.5,col=color[3])
legend("topleft",legend=leg,lty=c(1,2,2),lwd=1.5,col=color)
mtext(text="Source: https://www.wa.gov.au/organisation/department-of-justice/the-registry-
of-births-deaths-and-marriages/statistics-births-deaths-and-marriages-registered",side=1,line=3.5,adj=1,col="gray50",cex=.95)
dev.off()
In the plot above my 2010-2019 linear trend might be too low by 2024, because the long-term trend in deaths seems to be curved upwards. There hasn't been any big increase in age-standardized mortality rate in Western Australia: [https://www.abs.gov.au/statistics/people/population/deaths-australia/latest-release]

Jikkyleaks claimed that the weekly data for deaths in the Short Term Mortality Fluctuations dataset is synthetic, because he said the US chart looks too smooth compared to other countries (never mind that the United States has a bigger sample size of deaths than other countries in his plot): [https://x.com/Jikkyleaks/status/1888460292923023454]

And another reason why Jikky claimed STMF's data for the United States was fake was because the deaths in ages 0-14 and 15-64 were not integers: [https://x.com/Jikkyleaks/status/1888460292923023454]

However STMF uses the same set of 5 age groups for each country (0-14, 15-64, 65-74, 75-84, and 85+). So in countries where data using the STMF age groups is not available, the deaths are estimated by modifying the source age groups to match the set of 5 age groups used by STMF: [https://mortality.org/File/GetDocument/Public/STMF/DOC/STMFmetadata.pdf]

In STMF's data for the United States, the "Split" column is set to 1 on weeks before week 2 of 2018, because the deaths in the age groups 0-14 and 15-64 were estimated by splitting the age group 0-24 into two parts: [https://mortality.org/File/GetDocument/Public/STMF/DOC/STMFNote.pdf]

From week 2 of 2018 onwards STMF takes data for United States from CDC WONDER, which has weekly deaths available by single year of age, so the number of deaths in ages 0-14 and 15-64 is an integer:
> t=fread("https://mortality.org/File/GetDocument/Public/STMF/Outputs/USAstmfout.csv")
> t[Year==2018&Week==2&Sex=="b"]
CountryCode Year Week Sex 0-14 15-64 65-74 75-84 85+ Total 0-14
1: USA 2018 2 b 598 15718 12570 15992 22615 67493 0.0005110076
15-64 65-74 75-84 85+ Total Split SplitSex Forecast
1: 0.003826951 0.02147169 0.05414476 0.1949695 0.01075724 0 0 0
In April 2024 Miki Gibo et al. published a paper about cancer ASMR in Japan which eventually got retracted by the journal. [https://www.cureus.com/articles/196275-increased-age-adjusted-cancer-mortality-after-the-third-mrna-lipid-nanoparticle-vaccine-dose-during-the-covid-19-pandemic-in-japan] In February 2025 the authors published an updated version of the paper as a preprint. [https://zenodo.org/records/14847943] The updated version also included data for 2023 which was missing from the original version.
(Edit: Zenodo deleted the new version of the paper, which might be if they don't allow authors to publish a paper as a preprint if the paper has been previously published in a journal and retracted by the journal. But the PDF of the new version of the paper can still be downloaded from here: http://web.archive.org/web/20250212180857/https://zenodo.org/records/14847943/files/Excess%20Cancer%20Mortality%20after%20mRNA-Lipid%20Nanoparticle%20SARS-CoV-2%20Vaccination%20in%20Japan%20Observation%20until%202023.pdf?download=1.)
The paper featured the plot below where cancer ASMR went up between 2020 and 2021. However I found a spreadsheet of yearly cancer ASMR values on a website of the Japanese National Cancer Center: https://ganjoho.jp/reg_stat/statistics/data/dl/index.html (second link, fifth sheet, second row). The spreadsheet includes the ICD codes C00-C97 and it uses the 2015 standard population by 5-year age groups up to ages 95+, so it should match the paper by Gibo et al. in both ways. But the red circles here show that the cancer ASMR in the spreadsheet went down between 2020 and 2021 and not up like in the paper by Gibo et al.:

This plot from the Japanese paper shows that several months that have local maxima in excess cancer deaths coincide with a month that has a local maximum in the number of vaccine doses administered:

In the plot above there's three vaccination waves in 2022, but the yellow line shows that all three of them coincided with a COVID wave. However the plot above only shows COVID cases and not COVID deaths, and CFR was much higher in 2021 than 2022 so the yellow line for cases is very low in 2021, so you can't easily see that a COVID wave also coincided with the period with elevated cancer deaths in August to September 2021:

I wasn't sure if the Japanese paper looked at deaths by underlying cause of death or multiple cause of death. At first I thought the paper might have shown MCD deaths which would have explained why there were spikes in cancer deaths during COVID waves. In the United States there are spikes in MCD cancer deaths during COVID waves, but the spikes disappear if you exclude deaths with MCD COVID, or if you look at deaths with UCD cancer instead of MCD cancer.
However Table 1 of the Japanese paper shows that there were 1,575,936 deaths from all causes in 2023, out of which 382,492 deaths had the cause malignant neoplasms (C00-C97). It's almost the same as the number of deaths in file 2 under volume 2 here: https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00450011&tstat=000001028897&cycle=7&year=20230&month=0&tclass1=000001053058&tclass2=000001053061&tclass3=000001053065&result_back=1&cycle_facet=tclass1&tclass4val=0. The file had 1,576,016 deaths from all natural causes in 2023, but the deaths under all individual 3-letter ICD codes added up to 1,537,930, and the deaths under ICD codes starting with C added up to 382,504. So since the number of deaths under individual codes added together was nearly the same as the total number of deaths, you can tell that the file shows deaths by underlying cause of death and not by multiple cause of death, which means that Table 1 in the Japanese paper also shows UCD deaths.
However it's still possible that there were elevated UCD cancer deaths during COVID waves if COVID contributed to the cancer deaths even though it was not listed as the underlying cause. But cancers normally take time to develop, so unless there were a lot of people who died of a fast-acting turbo cancer soon after vaccination, I don't think vaccines would explain why the peaks in cancer deaths occurred around the same months as peaks in new vaccine doses administered.
The next plot shows monthly cancer ASMR I calculated myself. I took cancer deaths by 5-year age groups from table 6 for each month here: https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00450011&tstat=000001028897&cycle=1&tclass1=000001053058&tclass2=000001053060&cycle_facet=tclass1&tclass3val=0. I took yearly population estimates from here and I interpolated them to monthly population estimates: https://www.e-stat.go.jp/en/stat-search/files?page=1&toukei=00200524&tstat=000000090001 (where I combined annual reports for 2021-2023 with the 2000-2020 time series reports). I used the 2015 Japanese standard population like Gibo et al.: https://www.mhlw.go.jp/content/10700000/000557741.pdf.

library(data.table);library(ggplot2);library(lubridate)
t=fread("http://sars2.net/f/japancancerbyage.csv")
t[,date:=as.Date(paste0(date,"-1"))]
t=t[,.(dead=sum(dead),pop=sum(pop)),.(date,age=pmin(age,95))]
std=data.table(age=0:19*5)
std$std=c(978+4048,5369,5711,6053,6396,6738,7081,7423,7766,8108,8451,8793,9135,9246,7892,6306,4720,3134,1548,423)*1e3
std[,std:=std/sum(std)]
a=merge(t,std)[,.(asmr=sum(dead/pop/days_in_month(date)*std*365e5)),date]
a$base=a[year(date)%in%2010:2019,predict(lm(asmr~date),a)]
a[,month:=month(date)]
a=merge(a,a[year(date)%in%2010:2019,.(monthly=mean(asmr-base)),month])
lab=c("ASMR","2010-2019 linear baseline","Seasonal baseline","Excess ASMR")
facet=c("ASMR","Excess ASMR percent") p=a[,.(x=date,y=c(asmr,base,base+monthly,(asmr/(base+monthly)-1)*100),z=factor(rep(lab,each=.N),lab),facet=factor(rep(facet,c(.N*3,.N)),facet))]
p=rbind(p,p[z==z[1]&x==max(x)][,x:=seq(x,,"month",2)[2]])
xstart=as.Date("2010-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ggplot(p,aes(x=x,y))+
facet_wrap(~facet,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray83",linewidth=.4)+
geom_segment(data=data.table(facet=facet[2]),x=xstart,xend=xend,y=0,yend=0,linewidth=.4,lineend="square")+
geom_step(data=p[z==levels(z)[1]],aes(color=z))+
geom_line(data=p[z%in%levels(z)[2:3]],aes(x=x+14,color=z))+
geom_rect(data=p[z==levels(z)[4]],aes(xmin=x,xmax=x%m+%months(1),ymin=pmin(y,0),ymax=pmax(y,0)),color="gray20",fill="gray50",linewidth=.15)+
geom_text(data=p[,.(y=max(y)),facet],x=pmean(xstart,xend),aes(label=facet),size=3.8,fontface=2,vjust=1.4)+
labs(x=NULL,y=NULL,title="Age-standardized cancer mortality rate per 100,000 person-years in Japan")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab,expand=expansion(0,0))+
scale_y_continuous(breaks=\(x)pretty(x,7),labels=\(x)ifelse(x<10,paste0(x,"%"),x),expand=expansion(.03,0))+
scale_color_manual(values=c("black","#8888ff","blue"))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(3)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(5,"pt"),
legend.background=element_blank(),
legend.box.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="left",
legend.key=element_blank(),
legend.key.height=unit(11,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(,,6,-2),
legend.position="top",
legend.spacing.x=unit(3,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.spacing=unit(2,"pt"),
plot.margin=margin(6,6,1,5),
plot.title=element_text(size=11.5,face=2,margin=margin(2,,4)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=6.3,height=4.8,dpi=300*4)
sub="\u00a0 Cancer deaths are deaths with underlying cause of death malignant neoplasms (C00-C97). Cancer deaths by 5-year age groups were compiled from table 1-6 for each month here: www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00450011&tstat=000001028897
&cycle=1&tclass1=000001053058&tclass2=000001053060&cycle_facet=tclass1&tclass3val=0. Population estimates on October 1st of each year were spline interpolated to monthly population estimates: www.e-stat.go.jp/en/stat-search/files?page=1&toukei=00200524&tstat=000000090001 (annual reports for 2021-2023 combined with 2000-2020 time series reports). The 2015 Japanese standard population was used by 5-year age groups up to ages 95+: www.mhlw.go.jp/content/
10700000/000557741.pdf.
The seasonality-adjusted baseline was calculated by adding the average difference between the linear trend and actual ASMR in January 2010-2019 to the baseline for each January, and similarly for other months."
system(paste0("f=1.png;mar=100;w=`/usr/local/bin/identify -format %w $f`;/usr/local/bin/magick \\( $f \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[42*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x80 \\) -append -resize 25% -dither none -colors 256 1.png"))
The average of my monthly ASMR values was about 273.9 in 2021 and 275.1 in 2020, so I again got lower ASMR in 2021 than 2020 like in the spreadsheet at ganjoho.jp.
In the next plot I overlaid the same monthly excess ASMR values that are shown in the previous plot on top of Gibo et al.'s plot. I don't know if Gibo et al. manually modified their excess ASMR results to get a better correspondence between peaks in excess ASMR and months when vaccines were administered, because the correspondence was not nearly as impressive in my plot:

From the plot above you can also see that Gibo et al. got much lower excess ASMR each February than me, so I don't know if they forgot to adjust their excess ASMR calculation for the difference in the length of months. But maybe that's not the case, because Gibo et al. also got much lower excess ASMR each January than me.
However Gibo et al. also used a different method to calculate the baseline than me, and they only linked a generic page for Japanese vital statistics as the source of their mortality data, so I don't know which specific tables under their link they used to calculate ASMR, or if they used precalculated mortality rates to calculate ASMR or if they combined one dataset for deaths with another dataset for population estimates like me. They should publish the code they used to calculate the baseline and mention which exact tables of data they used.
If the spikes in cancer deaths which coincided with vaccination waves were caused by vaccines, you would expect the spikes to occur earlier in older age groups that got vaccinated earlier and later in younger age groups that got vaccinated later. However such a pattern is not apparent in this plot:

t=fread("http://sars2.net/f/japancancerbyage.csv")
t[,date:=as.Date(paste0(date,"-1"))]
a=t[,.(dead=sum(dead),pop=sum(pop)*days_in_month(date)),.(date,age)]
a[,cmr:=dead/pop]
a=merge(a,a[year(date)%in%2010:2019,.(date=unique(t$date),base=predict(lm(cmr~date),.(date=unique(t$date)))),age])
a[,month:=month(date)]
a=merge(a[year(date)%in%2010:2019,.(monthly=mean(cmr-base)),.(month,age)],a)
a=a[year(date)>=2020,.(dead=sum(dead),base=sum((base+monthly)*pop)),.(age=agecut(age,c(0,40,6:9*10)),date)]
a[,date:=factor(substr(date,1,7))]
a=rbind(a,a[,.(age="Total",dead=sum(dead),base=sum(base)),date])
a=rbind(a,a[,.(date="Total",dead=sum(dead),base=sum(base)),age])
m1=a[,tapply(dead,.(age,date),c)]
m2=a[,tapply(base,.(age,date),c)]
m=(m1-m2)/ifelse(m1>m2,m2,m1)*100
disp=round((m1/m2-1)*100)
exp=.8
maxcolor=max0(m)
pheatmap::pheatmap(abs(m)^exp*sign(m),filename="1.png",display_numbers=disp,gaps_row=nrow(m)-1,
gaps_col=seq(12,ncol(m),12),
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=14,cellheight=14,fontsize=9,fontsize_number=8,
border_color=NA,na_col="gray90",
number_color=ifelse(!is.na(m)&abs(m)^exp>maxcolor^exp*.4,"white","black"),
breaks=seq(-maxcolor^exp,maxcolor^exp,,256),
colorRampPalette(hsv(rep(c(7/12,0),5:4),c(.9,.75,.6,.3,0,.3,.6,.75,.9),c(.4,.65,1,1,1,1,1,.65,.4)))(256))
system("w=`identify -format %w 1.png`;pad=20;magick -pointsize 43 -font Arial-Bold \\( -size $[w-pad] caption:'Monthly percentage of excess cancer deaths in Japan (underlying cause of death malignant neoplasms, C00-C97)' -splice $[pad]x24 \\) -pointsize 40 -font Arial \\( -size $[w-pad*2] caption:'First a seasonality-adjusted linear trend in CMR was calculated by each 5-year age group in 2010-2019, and the projected trend was multiplied by the population size of the age group each month to get monthly expected deaths. The age groups shown here were aggregated from 5-year age groups.' -splice $[pad]x8 \\) 1.png -append -dither none -colors 256 1.png")
In the plot above some age groups have consistently positive excess mortality and others have consistently negative mortality. But it might be because there is some degree of error introduced to the slope of the baseline due to random variation in mortality during the prediction period, or because the long-term trend in mortality was not actually linear, or because I calculated the excess mortality by 5-year age groups and not by single year of age.
My previous plot showed that the peak monthly excess cancer ASMR was about 3.5%. But it's actually fairly small in comparison to the excess all-cause ASMR shown below, which has remained at a sustained level of over 5% each month since February 2022, and which reached above 20% during two months of 2024:

library(data.table);library(ggplot2);library(lubridate)
t=fread("http://sars2.net/f/japanacmbyage.csv")
t[,date:=as.Date(paste0(date,"-1"))]
t=t[,.(dead=sum(dead),pop=sum(pop)),.(date,age=pmin(age,95))]
std=data.table(age=0:19*5)
std$std=c(978+4048,5369,5711,6053,6396,6738,7081,7423,7766,8108,8451,8793,9135,9246,7892,6306,4720,3134,1548,423)*1e3
std[,std:=std/sum(std)]
a=merge(t,std)[,.(asmr=sum(dead/pop/days_in_month(date)*std*365e5)),date]
a$base=a[year(date)%in%2010:2019,predict(lm(asmr~date),a)]
a[,month:=month(date)]
a=merge(a,a[year(date)%in%2010:2019,.(monthly=mean(asmr-base)),month])
lab=c("ASMR","2010-2019 linear baseline","Seasonal baseline","Excess ASMR")
p=a[,.(x=date,y=c(asmr,base,base+monthly,(asmr/(base+monthly)-1)*100),z=factor(rep(lab,each=.N),lab),facet=factor(rep(facet,c(.N*3,.N)),facet))]
p=rbind(p,p[z==z[1]&x==max(x)][,x:=seq(x,,"month",2)[2]])
xstart=as.Date("2010-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ggplot(p,aes(x=x,y))+
facet_wrap(~facet,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray83",linewidth=.4)+
geom_segment(data=data.table(facet=facet[2]),x=xstart,xend=xend,y=0,yend=0,linewidth=.4,lineend="square")+
geom_step(data=p[z==levels(z)[1]],aes(color=z))+
geom_line(data=p[z%in%levels(z)[2:3]],aes(x=x+14,color=z))+
geom_rect(data=p[z==levels(z)[4]],aes(xmin=x,xmax=x%m+%months(1),ymin=pmin(y,0),ymax=pmax(y,0)),color="gray20",fill="gray50",linewidth=.15)+
geom_text(data=p[,.(y=max(y)),facet],x=pmean(xstart,xend),aes(label=facet),size=3.8,fontface=2,vjust=1.4)+
labs(x=NULL,y=NULL,title="All-cause ASMR 100,000 person-years in Japan")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab,expand=expansion(0,0))+
scale_y_continuous(breaks=\(x)pretty(x,7),labels=\(x)ifelse(x<100,paste0(x,"%"),x),expand=expansion(.03,0))+
scale_color_manual(values=c("black","#8888ff","blue"))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(3)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(5,"pt"),
legend.background=element_blank(),
legend.box.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="left",
legend.key=element_blank(),
legend.key.height=unit(11,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(,,6,-2),
legend.position="top",
legend.spacing.x=unit(3,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.spacing=unit(2,"pt"),
plot.margin=margin(6,6,1,5),
plot.title=element_text(size=11.5,face=2,margin=margin(2,,4)),
plot.subtitle=element_text(size=10.5,margin=margin(,,4)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=6.3,height=4.8,dpi=300*4)
sub="\u00a0 The monthly number of deaths from all causes was compiled from table 1-6 here: www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00450011&tstat=
000001028897&cycle=1&tclass1=000001053058&tclass2=000001053060&cycle_facet=tclass1&
tclass3val=0. Population estimates on October 1st of each year were spline interpolated to monthly population estimates: www.e-stat.go.jp/en/stat-search/files?page=1&toukei=00200524&tstat=
000000090001 (annual reports for 2021-2023 combined with 2000-2020 time series reports). The 2015 Japanese standard population was used by 5-year age groups up to ages 95+: www.mhlw.go.jp/content/10700000/000557741.pdf.
The seasonality-adjusted baseline was calculated by adding the average difference between the linear trend and actual ASMR in January 2010-2019 to the baseline for each January, and similarly for other months."
system(paste0("f=1.png;mar=100;w=`/usr/local/bin/identify -format %w $f`;/usr/local/bin/magick \\( $f \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[42*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x80 \\) -append -resize 25% -dither none -colors 256 1.png"))
So cancer deaths in Japan are not even elevated that much compared to deaths from other causes.
This code downloads files for monthly deaths by cause and age group:
curl 'https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00450011&tstat=000001028897&cycle=1&tclass1=000001053058&tclass2=000001053060&cycle_facet=tclass1&tclass3val=0'|grep -Po 'href="\K[^"]*'|grep '^/stat.*year'|sed 's/&/\&/g'>japanmonthurl
for x in `<japanmonthurl`;do curl -Ls "https://www.e-stat.go.jp/$x"|sed '1,/6<\/span/d'|grep fileKind|sed 1q|cut -d\" -f2;done>japanmonthurl2
mkdir japanasmr
paste -d\ <(sed 's/.*year=//;s/0&month=......\(..\).*/-\1/' japanmonthurl) japanmonthurl2|sed 's/0$/& xls/;s/4$/& xlsx/;s/1$/& csv/'|parallel -C\ curl https://www.e-stat.go.jp{2} -Lso japanasmr/{1}.{3}
rename s/xls/xlsx/ japanasmr/{2019-12,2020}*xls
recode shiftjis.. japanasmr/*.csv
I took population estimates from tables 3 here under "Yearly > 2024" and "Time Series 2000 - 2020": https://www.e-stat.go.jp/en/stat-search/files?page=1&toukei=00200524&tstat=000000090001. This code makes a single file for the combined population estimates and deaths:
u="https://www.e-stat.go.jp/en/stat-search/file-download?statInfId="
download.file(paste0(u,"000013168603&fileKind=4"),"jappopold.xlsx")
download.file(paste0(u,"000040268912&fileKind=4"),"jappopnew.xlsx")
g=Sys.glob("japanasmr/*.csv")
new=sapply(g,\(f)fread(f)[V3%like%"総数|全死因"][1,as.integer(unlist(.SD)),.SDcols=12:32])
new=data.table(date=rep(sub(".*/(.*).csv","\\1",g),each=21),age=0:20*5,dead=c(new))
g=Sys.glob("japanasmr/*.xls*")
old=sapply(g,\(f){s1=setDT(read_excel(f,skip=2))
d1=s1[s1[[2]]%like%"全.*死.*因"|s1[[3]]%like%"全.*死.*因"]
d1=d1[1,as.integer(unlist(.SD)),.SDcols=patterns("~")]
s2=setDT(read_excel(f,sheet=2,skip=2))
d2=s2[s2[[2]]%like%"全.*死.*因"|s2[[3]]%like%"全.*死.*因"]
d2=d2[1,as.integer(unlist(.SD)),.SDcols=patterns("~|100歳以上")]
c(d1,d2)})
old=data.table(date=rep(sub(".*/([^.]*).*","\\1",g),each=21),age=0:20*5,dead=c(old))
dead=rbind(new,old)[,date:=as.Date(paste0(date,"-15"))]
pop=unlist(read_excel("jappopold.xlsx",range="C17:R37",col_names=F))
pop=c(pop,unlist(read_excel("jappopold.xlsx",sheet=7,range="D16:G36",col_names=F)))
pop=c(pop,unlist(read_excel("jappopnew.xlsx",range="J20:N40",col_names=F)))
pop=data.table(year=rep(2000:2024,each=21),age=0:20*5,pop)
pop[,date:=as.Date(paste0(year,"-10-1"))]
pop=pop[,spline(date,pop,xout=unique(dead$date)),age]
pop=pop[,.(date=`class<-`(x,"Date"),age,pop=round(y*1000))]
out=merge(dead,pop)[,date:=substr(date,1,7)]
fwrite(out,"japanacmbyage.csv")
The last author of the Japanese cancer paper was Masanori Fukushima, who is a Japanese alt media celebrity who is frequently featured in videos of press conferences that appear similar to Füllmich's press conference larping operations. While I was researching Twitter bots that promote content from the controlled alternative media, I saw many of them posting videos of Fukushima. Videos by the first author Miki Gibo have also been posted by bots that promote Miles Guo. [https://x.com/search?q=miki%20gibo&f=live]
Masanori Fukushima was also the last author of a paper from December 2024 about a Japanese vaccination survey. The paper about the survey was published by Cureus which also published the previous version of the Japanese cancer paper. However the paper about the survey might have been AI-generated: [rootclaim2.html#Japanese_survey_for_self_reported_incidence_of_COVID]
Here's another plot that shows how the months with elevated cancer deaths coincide with COVID waves. Japan followed a similar pattern as southern US states, where there was regularly one COVID wave in the winter and one wave in the summer. New vaccine doses were rolled out about 4-6 months apart, so the first three boosters were all rolled out during months that happened to coincide with a COVID wave:

t=fread("https://sars2.net/f/japancancerbyage.csv")
p1=t[,.(y=sum(dead),z=1),.(x=as.Date(paste0(date,"-1")))]
a=t[,.(dead=sum(dead),pop=sum(pop)),.(date=as.Date(paste0(date,"-1")),age=pmin(age,95))]
std=CJ(age=0:19*5)
std$std=c(978+4048,5369,5711,6053,6396,6738,7081,7423,7766,8108,8451,8793,9135,9246,7892,6306,4720,3134,1548,423)*1e3
std[,std:=std/sum(std)]
a=merge(a,std)[,.(asmr=sum(dead/pop/days_in_month(date)*std*365e5)),date]
a$base=a[year(date)%in%2010:2019,predict(lm(asmr~date),a)]
a[,month:=month(date)]
a=merge(a,a[year(date)%in%2010:2019,.(monthly=mean(asmr-base)),month])
p2=a[,.(y=(asmr/(base+monthly)-1)*100,z=2),.(x=date)]
d20=c(0,10,56,450,336,59,46,275,249,192,401,1392)
d21=c(2669,2159,1139,1554,3090,1669,579,1568,1617,471,151,90)
d22=c(668,6503,4630,1705,1030,566,1941,9293,5216,2319,3977,9787)
d23=c(12713,4511,1868,1011,986,1154,1878,3852,4049,2496,1628,1934)
d24=c(3911,4569,3623,2506,1722,1734,3356,4881,3155,1919,1387,3012)
d25=c(5104,3311)
p3=CJ(x=seq(as.Date("2020-1-1"),as.Date("2025-2-1"),"month"))[,y:=c(d20,d21,d22,d23,d24,d25)][,z:=3]
vax=fread("https://sars2.net/f/japanvax.csv")
p4=vax[,.(vax=rowSums(vax[,2:8]),date=as.Date(date,"%Y/%m/%d"))][,.(y=sum(vax),z=4),.(x=`day<-`(date,1))]
p=rbind(p1,p3,p4)
p[,z:=factor(z,,c("Cancer deaths","COVID deaths","New vaccine doses"))]
p[,x:=x+15]
p[,y:=y/days_in_month(x)]
xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
p=p[x>=xstart&x<=xend]
ylim=p[,{x=as.double(pretty(y));.(min=as.double(x[1]),max=max(x))},z]
ggplot(p)+
facet_wrap(~z,ncol=1,dir="v",scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=min,ymax=max),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_line(aes(x,y),linewidth=.65)+
labs(x=NULL,y=NULL,title="Monthly deaths and vaccine doses in Japan, divided by\nnumber of days in month")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(breaks=pretty,labels=\(x)ifelse(x>=1e5,paste0(x/1e6,"M"),x))+
coord_cartesian(clip="off",expand=F)+
guides(fill=guide_legend(override.aes=list(linewidth=0,keyheight=unit(1,"pt"))))+
theme(axis.text=element_text(size=11,color="gray50"),
axis.ticks.length=unit(0,"pt"),
axis.title=element_text(size=11,margin=margin()),
legend.position="none",
panel.background=element_blank(),
panel.grid.major.x=element_blank(),
panel.grid.major.y=element_line(linewidth=.4,color="gray90"),
panel.spacing=unit(3,"pt"),
plot.subtitle=element_text(hjust=.5,margin=margin(,,2)),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,2)),
strip.background=element_blank(),
strip.text=element_text(size=11,margin=margin(,,1)))
ggsave("1.png",width=4.7,height=4,dpi=300*4)
I took cancer deaths from Table 6 here: https://www.e-stat.go.jp/stat-search/files?page=1&layout=datalist&toukei=00450011&tstat=000001028897&cycle=1&tclass1=000001053058&tclass2=000001053060&cycle_facet=tclass1&tclass3val=0. I took data for COVID deaths from Table 7 here: https://e-stat.go.jp/stat-search/files?layout=datalist&toukei=00450011&tstat=000001028897&cycle=1&tclass1=000001053058&tclass2=000001053060&tclass3val=0. I took data for vaccine doses administered from here: https://www.mhlw.go.jp/stf/seisakunitsuite/bunya/kenkou_iryou/kenkou/kekkaku-kansenshou/yobou-sesshu/syukeihou_00002.html.
The gray line here shows that even after subtracting COVID deaths, there's still clear spikes in deaths during COVID waves. So COVID deaths seem to be undercounted in Japan:

d20=c(0,10,56,450,336,59,46,275,249,192,401,1392)
d21=c(2669,2159,1139,1554,3090,1669,579,1568,1617,471,151,90)
d22=c(668,6503,4630,1705,1030,566,1941,9293,5216,2319,3977,9787)
d23=c(12713,4511,1868,1011,986,1154,1878,3852,4049,2496,1628,1934)
d24=c(3911,4569,3623,2506,1722,1734,3356,4881,3155,1919,1387,3012)
d25=c(5104,3311)
dead=CJ(date=seq(as.Date("2020-1-1"),as.Date("2025-2-1"),"month"))
dead[,coviddead:=c(d20,d21,d22,d23,d24,d25)]
t=fread("https://sars2.net/f/japanacmbyage.csv")
t[,date:=as.Date(paste0(date,"-1"))]
t=t[,.(dead=sum(dead),pop=sum(pop)),.(date,age=pmin(age,95))]
t[,year:=year(date)][,month:=month(date)]
lm=glm(dead~year+factor(age)+factor(month),poisson,t[year%in%2010:2019],offset=log(pop*days_in_month(date)))
t$base=predict(lm,t,type="response")
a=t[,.(dead=sum(dead),base=sum(base)),date]
a=merge(a,dead,all.x=T)
p1=a[,.(x=date,y=c(dead,dead-coviddead,base)/days_in_month(date),z=rep(1:3,each=.N))]
p2=a[,.(x=date,y=c(dead/base-1,(dead-coviddead)/base-1)*100,z=rep(1:2,each=.N))]
p=rbind(p1[,facet:=1],p2[,facet:=2])
p[,z:=factor(z,,c("Deaths","Deaths minus COVID deaths","Baseline"))]
p[,facet:=factor(facet,,c("Deaths divided by days in month","Percentage of excess deaths"))]
xstart=as.Date("2015-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
p=p[x%in%xstart:xend]
ggplot(p)+
facet_wrap(~facet,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_segment(data=p[,.(facet=levels(facet)[2])],x=xstart,xend=xend,y=0,yend=0,linewidth=.4,color="gray75",lineend="square")+
geom_line(aes(x+15,y,color=z))+
geom_label(data=p[,.(y=extendrange(y,,.03)[2]),facet],aes(as.Date("2020-1-1"),y,label=facet),vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4,size=3.87,fill="white",color="gray75")+
geom_label(data=p[,.(y=extendrange(y,,.03)[2]),facet],aes(as.Date("2020-1-1"),y,label=facet),vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=0,size=3.87,fill=NA)+
labs(x=NULL,y=NULL,title="Monthly deaths in Japan divided by number of days in month")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=\(x)extendrange(x,,c(.03,0)),breaks=\(x)pretty(x,7),labels=\(x)ifelse(x<100,paste0(x,"%"),x))+
scale_color_manual(values=c("black","gray60","blue"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
axis.ticks=element_line(linewidth=.4,color="gray75"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="center",
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(23,"pt"),
legend.margin=margin(,,6,-2),
legend.position="top",
legend.spacing.x=unit(3,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4,color="gray75"),
panel.spacing=unit(2,"pt"),
plot.title=element_text(size=11,face=2,margin=margin(,,4),hjust=.5),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.4,height=4,dpi=300*4)
A Swiss article said this in German: "The data show that cancer cases have increased significantly among people under 50. For the analysis, the German Cancer League evaluated over 57,000 tumor cases among 20- to 49-year-olds between 1993 and 2022. The result: According to the annual report, there were 32 percent more cancer cases between 2018 and 2022 than between 1993 and 1997." [https://www.tagblatt.ch/ostschweiz/ressort-ostschweiz/krankheit-erschreckende-zahlen-krebsfaelle-bei-unter-50-jaehrigen-haben-in-der-ostschweiz-stark-zugenommen-ld.2626093]
The article didn't include any time series plot of the incidence over time. The source of the data was given as an annual report by the cancer society of East Switzerland, but it didn't include any time series data either. [https://ostschweiz.krebsliga.ch/ueber-uns-kontakte/jahresberichte]
The article compared the incidence in 2018-2022 against 1993-1997, but it didn't say if there had been a change in the trend of incidence since 2021. The incidence may have even been lower in 2021-2022 than in 2018-2019, like in this plot of Swedish data:

library(data.table);library(ggplot2)
t=fread("http://sars2.net/f/swedencancercases.csv")[age>="20"&age<="45"]
t=t[year%in%1990:2023,.(cases=sum(cases)),.(year,age=as.integer(age))]
pop=fread("https://sars2.net/f/swedenpopdead.csv")
pop=pop[,.(pop=sum(pop)),.(year,age=age%/%5*5)]
t=merge(pop[year==2020,.(age,std=pop/sum(pop))],merge(t,pop))
p=t[,.(y=c(sum(cases),sum(cases)/sum(pop)*1e5,sum(cases/pop*std*1e5)),facet=1:3),.(x=year)]
p[,facet:=factor(facet,,c("Cases","Cases per 100,000 people","Age-standardized cases per 100,000 people"))]
xstart=1990;xend=2023
expand=p[,.(min=min(y),max=max(y)),facet]
rat=expand[,max(max/min)]*1.04
expand=expand[,{x=(rat*min-max)/(1+rat);.(y=c(min-x,max+x),facet)}]
lab=p[,.(pct=(mean(y[x%in%2018:2022])/mean(y[x%in%1993:1997])-1)*100),facet]
ggplot(p)+
facet_wrap(~facet,ncol=1,dir="v",scales="free")+
geom_rect(data=data.table(x1=c(1993,2018),x2=c(1997,2022)),aes(xmin=x1-.5,xmax=x2+.5,ymin=-Inf,ymax=Inf),fill="gray90")+
geom_line(aes(x,y),linewidth=.6)+
geom_point(aes(x,y),stroke=0,size=1.4)+
geom_text(data=merge(rbind(expand,p[,.(y,facet)])[,max(y),facet],lab),aes(y=V1,label=paste0(facet,":\n2018-2022 is about ",round(pct),"% higher than 1993-1997"),x=xstart+.3),lineheight=1,size=3.9,hjust=0,vjust=1.3)+
geom_point(data=expand,aes(x=xstart,y=y),alpha=0)+
labs(title="Cancer cases in Sweden in ages 20-49",subtitle=paste0("Source: sdb.socialstyrelsen.se/if_can/val_eng.aspx. Resident population
estimates are from statistikdatabasen.scb.se/pxweb/en/ssd/START__BE
__BE0101__BE0101A/BefolkningR1860N. The age-standardized rate was
calculated by 5-year age groups so that the 2020 resident population
estimates were used as the standard population."),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart,xend,5))+
scale_y_continuous(breaks=\(x)pretty(x,4))+
coord_cartesian(clip="off",expand=F)+
scale_color_manual(values=c("black","#ff66ff","#ff66ff"))+
scale_alpha_manual(values=c(1,0,0))+
scale_linetype_manual(values=c("solid","solid","11"))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(3)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(-4,"pt"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(24,"pt"),
legend.justification="left",
legend.margin=margin(,,6),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.spacing.y=unit(2,"pt"),
plot.margin=margin(5,5,5,5),
plot.subtitle=element_text(size=11,margin=margin(,,5)),
plot.title=element_text(size=11.5,face=2,margin=margin(2,,4)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.6,height=5.6,dpi=300*4)
system("magick 1.png -resize 25% -colors 256 1.png")
Retsef Levi wrote: "JAMA study re cardiac arrest incidents in US marathons & half marathons, shows significant increase during 2020-2023 compared to 2014-2019 (0.81 vs. 0.54 per 100K participants)." [https://x.com/RetsefL/status/1906492494856028482] And he showed this table from the JAMA study:

The study he linked is behind a paywall on the publisher's website, but it's outside a paywall at ResearchGate: https://www.researchgate.net/publication/390320605_Cardiac_Arrest_During_Long-Distance_Running_Races.
In 2014-2019 there were 90 cardiac arrests per about 14.919 million participants, and in 2020-2023 there were 41 cardiac arrests per about 5.054 million participants. The p-value of the ratios is about 0.14 with a two-sided chi-squared test or about 0.07 with a one-sided test, so neither is significant:
prop.test(c(90,41),c(14919000,5054000))$p.value # 0.1395663 prop.test(c(90,41),c(14919000,5054000),alternative="less")$p.value # 0.06978313
Levi highlighted this sentence from the paper: "Cardiac arrest proportions were stable between 2010-2014 (0.54 per 100 000 [95% CI, 0.41-0.68]) and 2015-2019 (0.58 per 100 000 [95% CI, 0.45-0.73]) but increased significantly in 2020-2023 (0.81 per 100 000 [95% CI, 0.58-1.10])." However the 95% CIs of the ratios overlapped, and the authors didn't specify how they determined if the increase was significant or not, so they may have used the word "significantly" in a colloquial sense of "considerably" rather than in the sense of statistical significance.
There was already an increasing trend in the rate of cardiac arrests before COVID, in order to determine if there has been a significant increase in the rate relative to the pre-COVID trend, you can look at whether the rate crosses above the upper bound of the 95% PI or not. But here relative to a 2000-2019 linear trend, the rate remained below the upper bound of the PI each year between 2000 and 2023:

d=CJ(year=2000:2023)
d$events=c(3,3,4,7,2,2,10,7,6,NA,9,17,9,10,20,19,10,20,12,9,6,8,9,18)
d$participants=c(835,849,904,937,998,1053,1134,1208,1325,NA,2000,2237,2469,2635,2763,2673,2593,2396,2265,2229,685,1029,1578,1762)* 1e3
d[,rate:=events/participants*1e5]
d=cbind(d,predict(lm(rate~year,d[year<2020]),d,interval="prediction",level=.95))
tit="Cardiac arrest incidence per 100,000 participants"
leg=c("Rate per 100,000","2000-2019 linear trend","95% PI")
col=c("black","#0000ff","#8888ff")
p=d[,.(x=year,y=c(rate,fit),z=factor(rep(1:2,each=.N),,c("Rate per 100,000","2000-2019 linear trend with 95% prediction interval")))]
xstart=2000;xend=2023;xbreak=seq(xstart,xend,2)
color=c("black","#3333ff")
ggplot(p)+
geom_ribbon(data=d,aes(x=year,ymin=lwr,ymax=upr),fill="blue",color=color[2],alpha=.2,linewidth=.3)+
geom_line(data=p[!(z==levels(z)[2]&x>2019)],aes(x,y,color=z),linewidth=.6)+
geom_line(data=d,aes(x=year,y=fit),color=color[2],linewidth=.6,linetype="22",show.legend=F)+
geom_point(aes(x,y,color=z,alpha=z),stroke=0,size=1.5)+
labs(title="Cardiac arrests per 100,000 participants in marathon and half-marathon\nraces in the United States",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak)+
scale_y_continuous(breaks=\(x)pretty(x,6))+
coord_cartesian(clip="off",expand=F)+
scale_color_manual(values=color)+
scale_fill_manual(values="#3333ff")+
scale_alpha_manual(values=c(1,0,0))+
theme(axis.text=element_text(size=11,color="black"),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(4,"pt"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(24,"pt"),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.margin=margin(,,5),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,2)))
ggsave("1.png",width=5.85,height=3.7,dpi=300*4)
In the plot above I took data for the years 2000 to 2008 from an earlier version of the JAMA study that was published in 2012: https://www.nejm.org/doi/full/10.1056/NEJMoa1106468.
In the English ONS data, the ASMR of people with n-1 doses shoots up after the nth dose is rolled out. Neil and Fenton hypothesized it was because people who died soon after they got the nth dose were misclassified under dose n-1. But the same n-1 dose phenomenon also occurs in the Czech record-level data and Barry Young's New Zealand data even though they don't employ any Fentonian cheap tricks.
In May 2025 Kenji Fujikawa published a dashboard for Japanese all-cause mortality data by vaccination status, which was based on data received through freedom of information requests: https://x.com/hudikaha/status/1921935565894852619, https://medicalfacts.info/vdeath.rb.
You can download the data as JSON by selecting "Open in Vega Editor" from the triple dot menu and selecting "JSON" under "Export". Then this converts the JSON data to CSV:
jq -r '.data.values[]|select(.yearmonth|strings)|[.area,.age,.dose,.deaths,.persondays,.yearmonth]|@csv' visualization.vl.json|tr -d \"
The Japapanese data only included two age categories, which were all ages and ages 80 and above. But in this plot that shows the crude mortality rate in ages 80 and above, you can see how the mortality rate of people with n-1 doses shoots up when the nth dose is rolled out, but the mortality rate of all vaccinated people combined still remains lower than the mortality rate of unvaccinated people:

t=fread("http://sars2.net/f/japanfoihudikaha.csv")
t=t[location==location[1]&age=="80over"]
t=rbind(t,t[dose!=0][,dose:=1])
a=t[,.(dead=sum(dead),pop=sum(pop)),.(month,dose=pmin(dose,6))]
a[,dose:=factor(dose,,c("Unvaccinated","Vaccinated",paste("Dose",2:5),"Dose 6+"))]
p=a[,.(x=as.Date(paste0(month,"-15")),y=dead/pop*365e5,dose)]
xstart=as.Date("2021-1-1");xend=as.Date("2024-7-1")
xbreak=seq(xstart,xend,"year");xlab=year(xbreak)
ybreak=pretty(c(0,p$y),8);ystart=0;yend=max(p$y,na.rm=T)
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="black")+
geom_line(aes(x,y,color=dose),linewidth=.5)+
geom_point(aes(x,y,color=dose),size=1)+
labs(title="Japanese FOI data, ages 80+, deaths per 100,000 person-years",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black","gray50",hsv(c(6,12,21,28,33)/36,1,.8)))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=2,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(4),hjust=0),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification="center",
legend.key=element_blank(),
legend.margin=margin(,,4),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,face=2,margin=margin(1,,4)))
ggsave("1.png",width=5.5,height=2.8,dpi=300*4)
sub="Source: medicalfacts.info/vdeath.rb via x.com/hudikaha/status/
1921935565894852619. JSON data was downloaded by selecting \"Open in Vega Editor\" from the triple dot menu and selecting \"JSON\" from \"Export\". The JSON data was converted to TSV with `jq -r '.data.values[]|select(.yearmonth|strings)|[
.area,.age,.dose,.deaths,.persondays,.yearmonth]|@tsv' visualization.vl.json`."
system(paste0("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\''",sub),"' -splice x80 \\) -append -resize 25% -bordercolor white -border 24 -dither none -colors 256 1.png"))
So now this Japanese FOI data also shows that it's expected for the all-cause mortality rate of people with n-1 doses to go up when the nth dose is rolled out, so it's yet another nail in the coffin of the cheap tricksters at the Queen Mary University of London.
In June 2025 the Japanese Yuukoku Union and National Coalition to Stop mRNA Vaccines published a website that displayed mortality statistics based on FOI requests that covered a total of about 18 million vaccine doses administered in 35 municipalities of Japan: https://stop-mrna.sakura.ne.jp/db/lot_totalization.php. The original FOI data does not seem to have been published.
Additional plots of the data were presented in a video hosted by Masako Ganaha, including this plot that went viral because it appears to show that vaccinated people had higher mortality than unvaccinated people: [https://x.com/5rHxIhQGQnnRSOe/status/1934472762829222102]

The plot is supposed to use "the person-years method", but I suspect people with multiple doses were not counted multiple times in the denominator for the person-years, since the mortality of vaccinated people is about 5 times higher at the peak than on day 360.
The shape of the curve is similar to this plot, which simply shows raw deaths not adjusted for population size, even though here the peak is only about 4 times higher than the number of deaths on day 365: [https://stop-mrna.sakura.ne.jp/db/lot_totalization.php]

The curve also looks similar to this plot that shows raw deaths split out by dose number: [https://x.com/826santa139270/status/1934620865263816877]

In the plot above the second dose has a peak in deaths later than the third dose. But it's simply because the time interval between the third and fourth doses was shorter than the time interval between the second and third doses. Deaths after the first dose already peaks on the 4th week, because people typically got the second dose 3-6 weeks after the first dose.
People on Japanese Twitter also said that the mortality rates were probably calculated incorrectly because they looked too similar to the raw number of deaths: [https://x.com/donkey1399/status/1934757648702034189]

So basically even if the plot was adjusted for person-years, it might be that deaths were added together for multiple doses like in the top panel here, but people were only counted once in the person-years like in the bottom panel:

t=fread("https://sars2.net/f/czbuckets.csv.gz")[dose>=1][,facet:=1]
t=rbind(t,fread("https://sars2.net/f/czbucketskeep.csv.gz")[,facet:=2][dose==1])
a=t[,.(dead=sum(dead),pop=sum(alive)/365e2),.(week,facet)]
p=a[,.(x=week,y=c(dead,pop),z=rep(1:2,each=.N),facet)]
p[,facet:=factor(facet,,c("Since last dose (all doses)","Since dose 1 (other doses ignored)"))]
p[,z:=factor(z,,c("Deaths","Population (hundreds of person-years)"))]
xstart=0;xend=100;xbreak=0:10*10;ybreak=pretty(p$y);ystart=0;yend=max(ybreak)
ggplot(p,aes(x,y))+
facet_wrap(~facet,ncol=1,scales="free")+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(color=z),linewidth=.6)+
geom_label(data=p[rowid(facet)==1],aes(label=facet),vjust=1,y=yend,x=pmean(xstart,xend),hjust=.5,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4,size=3.8,fill="white",color="gray70")+
geom_label(data=p[rowid(facet)==1],aes(label=facet),vjust=1,y=yend,x=pmean(xstart,xend),hjust=.5,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=0,size=3.8,fill=NA)+
labs(title="Deaths and population by weeks since vaccination in Czechia",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black","#00cc00"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray45"),
axis.ticks.length=unit(0,"pt"),
legend.background=element_blank(),
legend.box="vertical",
legend.box.just="right",
legend.box.margin=margin(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="center",
legend.key.height=unit(13,"pt"),
legend.key.width=unit(21,"pt"),
legend.key=element_rect(fill="white"),
legend.margin=margin(,,4),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray90"),
panel.background=element_blank(),
panel.spacing=unit(2,"pt"),
plot.margin=margin(4,14,4,4),
plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11,face="bold",hjust=.5,margin=margin(1,,2)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.1,height=3.5,dpi=300*4)
When I used the New Zealand data released by Barry Young to plot mortality by weeks since the last vaccine dose, the peak in raw deaths was about 3 times higher than the number of deaths on week 50, but the peak in CMR was only about 1.5 times higher than the CMR on week 50:

t=fread("https://sars2.net/f/buckets.gz")
p=t[dose>0,.(y=sum(dead),z=1),.(x=week)]
p=rbind(p,t[dose>0,.(y=sum(dead)/sum(alive)*365e5,z=2),.(x=week)])
a=t[dose>0,.(dead=sum(dead),alive=sum(alive)),.(week,age=pmin(age,95))]
std=fread("https://sars2.net/f/nzpopdead.csv")[year==2020&age<=95,pop/sum(pop)]
p=rbind(p,a[,.(y=sum(dead/alive*std[age+1])*365e5,z=3),.(x=week)])
p[,z:=factor(z,,c("Raw number of deaths","Crude mortality rate per 100,000 person-years","Age-standardized mortality rate per 100,000 person-years"))]
xstart=0;xend=90;xbreak=0:9*10
p=p[x%in%xstart:xend]
ylim=c(0,max(p$y)*1.02);ybreak=pretty(ylim,7)
ggplot(p,aes(x,y,z))+
geom_line(aes(color=z),linewidth=.6)+
geom_point(aes(color=z),size=1.1)+
labs(x=NULL,y=NULL,title="Mortality by weeks since last vaccine dose in New Zealand",subtitle="Source: github.com/skirsch/NewZealand")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak)+
scale_y_continuous(limits=ylim,breaks=ybreak)+
scale_color_manual(values=c("black",hsv(c(21,30)/36,.7,1)))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="black",margin=margin(2,2,2,2)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(0,"pt"),
legend.background=element_blank(),
legend.box.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.justification="center",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(,,4),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.grid.major=element_line(linewidth=.4,color="gray87"),
plot.margin=margin(5,10,5,5),
plot.subtitle=element_text(margin=margin(,,2),hjust=.5),
plot.title=element_text(size=11.3,face=2,margin=margin(2,,4),hjust=.5))
ggsave("1.png",width=5.7,height=3.7,dpi=300*4)
In the plot above the reason why the CMR peaks around week 20 and later goes down is that the average age of the vaccinated people dropped from about 52 on week 20 to 42 on week 60, because older people got more boosters than younger people, and people who got boosters were likely to have cycled back to week 0 before 40 weeks had passed from their previous dose:
t=fread("https://sars2.net/f/buckets.gz")
print(round(t[week%%10==0,.(age=weighted.mean(age,alive),pyears=sum(alive)/365),week]),r=F)
# week age pyears
# 0 49 80378
# 10 52 64542
# 20 52 54460
# 30 48 41089
# 40 45 35591
# 50 43 31833
# 60 42 29067
# 70 40 25110
# 80 40 22966
# 90 37 10812
# 100 36 5255
# 110 50 324
# 120 51 23
In the next plot that shows the raw number of deaths by weeks since vaccination, it takes until approximately week 70 for the total number of deaths to fall down to one fifth of the peak number of deaths, but even then it's partially because people with 4 doses start to run out of follow-up time around week 57, so there are almost no deaths under the 4th dose on week 70:

nz=fread("https://sars2.net/f/nz_monthly_deaths_by_age.csv")
nz[,date:=as.Date(paste0(year_reg,"-",month_reg,"-15"))]
nz=nz[ethnicity=="Total",.(dead=sum(count)),.(date,age=as.integer(substr(age_group,1,2))%/%5*5)]
nzpop=fread("https://sars2.net/f/nzpopquartermean.csv")
nzpop=nzpop[,.(pop=sum(pop)),.(age=age%/%5*5,date=as.Date(paste(year,q*3-1,15,sep="-")))]
nz=merge(nz,nzpop[,spline(date,pop,xout=unique(nz$date)),age][,.(age,date=x,pop=y)])
nz=nz[,.(date,base=dead/pop/days_in_month(date),age)]
t=fread("https://sars2.net/f/buckets.gz")
t[,age:=pmin(age,95)%/%5*5]
a=t[dose<=4,.(dead=sum(dead),pop=sum(alive)),.(date=ua(date,`day<-`,15),age,week,dose)]
a=merge(a,nz)[,.(dead=sum(dead),base=sum(base*pop)),.(age,week,dose,date)]
a=rbind(a,a[,.(dead=sum(dead),base=sum(base),dose=0),.(age,week,date)])
p=a[,.(y=c(sum(dead),sum(base)),type=1:2),.(x=week,z=dose)]
p[,z:=factor(z,,c("Total",paste("Dose",1:4)))]
p[,type:=factor(type,,c("Deaths","Baseline"))]
xstart=0;xend=100;xstep=10;ystart=0;yend=900;ystep=100
ggplot(p,aes(x,y))+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="black")+
geom_line(aes(color=z,linetype=type),linewidth=.6)+
labs(title="Deaths by weeks since vaccination in New Zealand",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,xstep))+
scale_y_continuous(limits=c(ystart,yend),breaks=seq(ystart,yend,ystep))+
scale_color_manual(values=c("black",hsv(c(21,24,28,32)/36,.6,1)))+
scale_linetype_manual(values=c("solid","11"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),linetype=guide_legend(order=2))+
theme(axis.text=element_text(size=11,color="black"),
axis.ticks.length=unit(0,"pt"),
legend.background=element_rect(fill="white",color="black",linewidth=.4),
legend.box="vertical",
legend.box.just="right",
legend.box.margin=margin(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification=c(1,1),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(21,"pt"),
legend.key=element_rect(fill="white"),
legend.margin=margin(3,5,3,3),
legend.position=c(1,1),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray90"),
panel.background=element_blank(),
plot.margin=margin(4,14,4,4),
plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11.5,face="bold",hjust=.5,margin=margin(2,,4)))
ggsave("1.png",width=5.1,height=3.2,dpi=300*4)
The New Zealand dataset only included data up to October 2023, but a similar Czech dataset published in November 2024 includes data up to October 2024, so the people with four doses who were vaccinated during the main rollout wave only start to run out of follow-up time around week 96 (even though people who got the 4th dose late already run out of follow-up time earlier). But anyway, now there is not such a dramatic drop in deaths between the peak and later weeks as in the plots from Japan and New Zealand, so now even on week 60, the number of deaths is still about half of the peak number of deaths. It seems to be because there were many people who only got the first booster but not the second booster:

b=fread("curl -Ls https://sars2.net/f/nzipbuckets.csv.xz|xz -dc")
d=merge(b[dose%in%1:4],b[,.(base=sum(dead)/sum(pop)),.(obsweek,born)])[,base:=base*pop]
a=d[,.(dead=sum(dead),pop=sum(pop),base=sum(base)),.(born,obsweek,week=obsweek-vaxweek,dose)]
a=rbind(a,a[,.(dead=sum(dead),pop=sum(pop),base=sum(base),dose=0),.(born,obsweek,week)])
p=a[,.(y=sum(dead),base=sum(base)),.(x=week,z=dose)][x>=0]
p[,z:=factor(z,,c("Total",paste("Dose",1:4)))]
p=p[,.(x,y=c(y,base),z,type=factor(rep(1:2,each=.N),,c("Deaths","Baseline")))]
xstart=0;xend=160;xstep=20;ystart=0;yend=6000;ystep=1000
note="The baseline was calculated by multiplying the number of person-days for each combination of 5-year age group and observation month with the mortality rate among all people who are included in the dataset for the same combination of age group and observation month."|>stringr::str_wrap(44)
ggplot(p,aes(x,y))+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="black")+
geom_line(aes(color=z,linetype=type),linewidth=.6)+
labs(title="Deaths by weeks since vaccination in Czech Republic",subtitle="Source: nzip.cz/data/2135-covid-19-prehled-populace",x=NULL,y=NULL)+
annotate(geom="label",label=note,x=57,y=yend*.79,hjust=0,vjust=1,size=3.6,lineheight=.85,label.size=.4,fill="white",label.padding=unit(5,"pt"),color="gray90")+
annotate(geom="label",label=note,x=57,y=yend*.79,hjust=0,vjust=1,size=3.6,lineheight=.85,label.size=0,fill=NA,label.padding=unit(5,"pt"))+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,xstep))+
scale_y_continuous(limits=c(ystart,yend),breaks=seq(ystart,yend,ystep))+
scale_color_manual(values=c("black",hsv(c(21,24,28,32)/36,.6,1)))+
scale_linetype_manual(values=c("solid","11"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),linetype=guide_legend(order=2))+
theme(axis.text=element_text(size=11,color="black"),
axis.ticks.length=unit(0,"pt"),
legend.background=element_rect(fill="white",color="black",linewidth=.4),
legend.box="vertical",
legend.box.just="right",
legend.box.margin=margin(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification=c(1,1),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(21,"pt"),
legend.key=element_rect(fill="white"),
legend.margin=margin(3,5,3,3),
legend.position=c(1,1),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray90"),
panel.background=element_blank(),
plot.margin=margin(4,14,4,4),
plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11.5,face="bold",hjust=.5,margin=margin(2,,4)))
ggsave("1.png",width=5.1,height=3.5,dpi=300*4)
Japan has a very high number of booster doses per capita, but New Zealand also has a much higher number of booster doses than the Czech Republic (at least up to May 2nd 2023, which was the last date with data for all three countries available at OWID):
download.file("https://covid.ourworldindata.org/data/owid-covid-data.csv","owid-covid-data.csv")
o=fread("owid-covid-data.csv")
s=o[location%like%"Czech|Japan|Zea"]
maxdate=s[!is.na(total_boosters_per_hundred),.N,date][N==3,max(date)]
print(s[date==maxdate,.(date,location,total_boosters_per_hundred)],r=F)
# date location total_boosters_per_hundred
# 2023-05-02 Czechia 49.30
# 2023-05-02 Japan 141.71
# 2023-05-02 New Zealand 70.60
In May 2025 Kenji Fujikawa published another analysis of the same FOI data. [https://x.com/hudikaha/status/1921935565894852619, https://medicalfacts.info/vdeath.rb] I downloaded the data from his website as JSON by selecting "Open in Vega Editor" from the triple dot menu and selecting "JSON" under "Export". Then I used JQ to convert the JSON data to CSV:
jq -r '.data.values[]|select(.yearmonth|strings)|[.area,.age,.dose,.deaths,.persondays,.yearmonth]|@csv' visualization.vl.json|tr -d \"
I uploaded the CSV data here: f/japanfoihudikaha.csv.
The earlier data published by Fujikawa does not show the number of deaths grouped by days or weeks since vaccination, but only by calendar month. It also has only two age groups, which are ages 80 and above and all ages.
The data for ages 80 and above shows how new booster doses were rolled out about once every 5 months, and after the nth dose is rolled out, the mortality rate of people with n-1 doses shoots up because of the healthy vaccinee effect:

t=fread("https://sars2.net/f/japanfoihudikaha.csv")
t=t[location==location[1]&age=="80over"]
a=t[,.(dead=sum(dead),pop=sum(pop)),.(month,dose)]
a2=a[dose>0,.(dead=sum(dead),pop=sum(pop),dose=.5),month]
a3=a[,.(dead=sum(dead),pop=sum(pop),dose=.7),month]
a=rbind(a,a2,a3)
a[,x:=as.Date(paste0(month,"-15"))][,people:=pop/days_in_month(x)]
p=a[,.(x,y=c(dead,people,dead/pop*365e5),facet=rep(1:3,each=.N),dose)]
p=p[y>0]
p[,dose:=factor(dose,,c("Unvaccinated","Vaccinated","All people",paste("Dose",1:7)))]
p[,facet:=factor(facet,,c("Deaths divided by days in month","Person-days divided by days in month","Deaths per 100,000 person-years"))]
xstart=as.Date("2021-1-1");xend=as.Date("2024-7-1")
xbreak=seq(xstart,xend,"year");xlab=year(xbreak)
ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray75",linewidth=.4)+
geom_rect(data=p[,max(pretty(y)),facet],aes(ymax=V1),ymin=0,xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray75",linewidth=.4)+
geom_line(aes(x,y,color=dose,linetype=dose))+
geom_point(aes(x,y,color=dose,alpha=dose),shape=16,size=1.3,stroke=0)+
geom_line(data=p[dose%in%levels(dose)[1:2]],aes(x,y,color=dose,linetype=dose))+
labs(title="Japanese FOI data, age 80+ at time of data extraction",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=\(x)range(pretty(x)),breaks=pretty,labels=kim)+
scale_color_manual(values=c("black","gray65","gray35",hsv(c(1,3)/36,c(.5,.5),c(1,.9)),hsv(c(6,12,21,28,33)/36,1,.8)))+
scale_linetype_manual(values=c("solid","solid","11",rep("solid",7)))+
scale_alpha_manual(values=c(1,1,0,rep(0,7)))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=3,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
axis.text.x=element_text(hjust=0),
axis.ticks=element_line(linewidth=.4,color="gray75"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification="center",
legend.key=element_blank(),
legend.margin=margin(,,1),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(23,"pt"),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.spacing=unit(0,"pt"),
plot.margin=margin(4,5,4,5),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(1,,4)),
strip.background=element_blank(),
strip.text=element_text(size=11,margin=margin(3,,3)))
ggsave("1.png",width=4.8,height=4.8,dpi=300*4)
If you look at all ages instead, then the mortality rate of unvaccinated people decreases from about 88 per 100,000 person-years in March 2021 to about 56 a year later. So it roughly matches the plot that went viral, where the mortality rate of unvaccinated people is about 0.010 per person-year on the first week from March 8th 2021, and it gradually falls to about 0.006 a year later:

When a Japanese user on Twitter said the new data was meaningless because it was not standardized by age, Jikkyleaks pointed out that in the ONS dataset for deaths by vaccination status, people with 3 doses had higher ASMR than unvaccinated people: [https://x.com/Jikkyleaks/status/1935225383303135497]

However I pointed out to him that the ASMR of people with 3 but not more doses shoots up when the 4th dose is rolled out, because the healthy vaccinee effect causes people with low mortality risk to move under the 4th dose, so the people who have elevated mortality risk remain under the 3rd dose. The mortality rate of people with 3 or more doses remains stable even after the 4th dose is rolled out: [uk.html#Problems_with_Fenton_and_Neils_n_1_dose_misclassification_hypothesis]

In December 2022 when the ASMR of people with 3 but not more doses peaks, about 60% of all deaths in the ONS dataset were in ages 80 and above. However ages and above had about 16 times more people with 4 or more doses than people with 3 but not more doses. So the small number of people who remained under the 3rd dose were not representative of the overall vaccinated population:
t=fread("https://sars2.net/f/ons.csv")
s=t[ed==9&cause=="All causes"&month=="2022-12"]
a=s[,.(dose3pop=sum(pop[status%like%"Third"]),dose4pop=sum(pop[status%like%"Fourth"])),age]
print(a[,ratio:=round(dose4pop/dose3pop,1)][],r=F)
# age dose3pop dose4pop ratio
# 18-39 538375 72979 0.1
# 40-49 320846 76424 0.2
# 50-59 198558 312930 1.6
# 60-69 101454 356768 3.5
# 70-79 36377 348478 9.6
# 80-89 10938 172366 15.8
# 90+ 2335 36818 15.8
# Total 1224004 1378612 1.1
In the Japanese FOI data in ages 80 and above, the mortality rate of people with 3 but not more doses similarly shoots up when the 4th dose is rolled out, even though the mortality rate of people with 3 or more doses remains stable:

t=fread("https://sars2.net/f/japanfoihudikaha.csv")
t=t[location==location[1]&age=="80over"]
p1=t[dose==0,.(y=sum(dead)/sum(pop),dose=1),month]
p2=t[dose>0,.(y=sum(dead)/sum(pop),dose=2),month]
p3=t[dose==3,.(y=sum(dead)/sum(pop),dose=3),month]
p4=t[dose>=3,.(y=sum(dead)/sum(pop),dose=4),month]
p=rbind(p1,p2,p3,p4)[,.(x=as.Date(paste0(month,"-15")),y=y*365e5,dose)]
p[,dose:=factor(dose,,c("Unvaccinated","Vaccinated","Dose 3 but not more","Dose 3 or more"))]
xstart=as.Date("2021-1-1");xend=as.Date("2024-7-1")
xbreak=seq(xstart,xend,"year");xlab=year(xbreak)
ybreak=pretty(c(0,p$y),8);ystart=0;yend=max(p$y,na.rm=T)
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="black")+
geom_line(aes(x,y,color=dose),linewidth=.5)+
geom_point(aes(x,y,color=dose),size=1)+
labs(title="Japanese FOI data, ages 80+, deaths per 100,000 person-years",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x>=1e3,paste0(x/1e3,"k"),x))+
scale_color_manual(values=c("black","gray50",hsv(21/36,c(1,.5),c(.8,1))))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=2,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(4),hjust=0),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification="center",
legend.key=element_blank(),
legend.margin=margin(,,4),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,face=2,margin=margin(1,,4)))
ggsave("1.png",width=5.5,height=2.8,dpi=300*4)
sub="Source: medicalfacts.info/vdeath.rb via x.com/hudikaha/status/ 1921935565894852619. JSON data was downloaded by selecting \"Open in Vega Editor\" from the triple dot menu and selecting \"JSON\" from \"Export\". The JSON data was converted to TSV with `jq -r '.data.values[]|select(.yearmonth|strings)|[ .area,.age,.dose,.deaths,.persondays,.yearmonth]|@tsv' visualization.vl.json`."
system(paste0("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\''",sub),"' -splice x80 \\) -append -resize 25% -bordercolor white -border 24 -dither none -colors 256 1.png"))
The Japanese FOI data also shows that unvaccinated people have a bigger increase in all-cause mortality during COVID waves than vaccinated people:

download.file("https://srhdpeuwpubsa.blob.core.windows.net/whdh/COVID/WHO-COVID-19-global-daily-data.csv","WHO-COVID-19-global-daily-data.csv")
t=fread("https://sars2.net/f/japanfoihudikaha.csv")
t=t[location==location[1]&age=="80over"]
t=rbind(t,t[,.(dead=sum(dead),pop=sum(pop),dose=-1),.(location,age,month)])
p=t[,.(y=sum(dead)/sum(pop)*365e5),.(x=as.Date(paste0(month,"-15")),z=pmin(dose,1))]
p[,z:=factor(z,,c("Total","Unvaccinated","Vaccinated"))]
dead=fread("WHO-COVID-19-global-daily-data.csv")[Country=="Japan"&year(Date_reported)<=2022]
dead=dead[,.(y=sum(New_deaths)),.(x=as.Date(`day<-`(Date_reported,15)))][y>0]
dead2=c(12713,4511,1868,1011,986,1154,1878,3852,4049,2496,1628,NA,3911,4569,3623,2506,1722,1734,3356,4881,3155,1919,1387)
dead=rbind(dead,list(seq(as.Date("2023-1-15"),as.Date("2024-11-15"),"month"),dead2))
p=rbind(p,dead[,z:="COVID deaths (all ages, not CMR)"])
xstart=as.Date("2020-1-1");xend=as.Date("2024-7-1")
xbreak=seq(xstart,xend,"year");xlab=year(xbreak)
ybreak=pretty(c(0,p$y),8);ystart=0;yend=max(p$y,na.rm=T)
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="black")+
geom_line(aes(x,y,color=z),linewidth=.5)+
geom_point(aes(x,y,color=z),size=1)+
labs(title="Japanese FOI data, ages 80+, deaths per 100,000 person-years",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=kim)+
scale_color_manual(values=c("black","#5555ff","#ff5555","gray50"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=2,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(4),hjust=0),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification="center",
legend.key=element_blank(),
legend.margin=margin(,,4),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,face=2,margin=margin(1,,4)))
ggsave("1.png",width=5.5,height=2.8,dpi=300*4)
In the previous plot if you look at the black line which shows the mortality rate of both vaccinated and unvaccinated people added together, there's a large increase in the mortality rate between 2021 and 2024. It's because the age of each person was determined at the time the data was extracted in 2024 or 2025, so some of the people who were 80 years old at the time the data was extracted may have been only 75 or 76 years old in 2021.
The issue was pointed out in this tweet that I translated from Japanese: [https://x.com/donkey1399/status/1923593814704521298]

Fujikawa later posted a response to the tweet where he wrote: "I checked with the secretariat, and they told me that basically the age is the age at the time of data extraction. In other words, it will be after June 2024. (It varies by municipality, and the later the disclosure, the later the age is thought to be.)" [https://x.com/hudikaha/status/1924666052409229765] The Twitter user donkey1399 also pointed out that the number of deaths in ages 80 and above appears to match the officially reported number of deaths, so the numerator for deaths and denominator for population size employ different definitions of the age groups. [https://x.com/donkey1399/status/1926430257491374410]
Next I came up with a method to match unvaccinated people to vaccinated people based on weeks since vaccination. For each week from vaccination, I counted what proportion of total vaccinated person-days were contributed by each combination of age group and observation month. Then I took a weighted average of unvaccinated mortality rate for each combination of age group and observation month where I used the fractions as the weight. Then when I calculated age-standardized mortality rates for each group, it was not surprising that unvaccinated people had much higher ASMR than vaccinated people.
I did the calculation based on the Czech dataset released in March 2024, which only includes deaths up to the end of 2022, so by week 80 a lot of vaccinated people had already run out of observation time, and vaccinated people had high ASMR because vulnerable groups of people who were priorized for early vaccination were now overrepresented:

t=fread("https://sars2.net/f/czbuckets.csv.gz")[,facet:=1]
t=rbind(t,fread("https://sars2.net/f/czbucketskeep.csv.gz")[,facet:=2][dose<=1])
a=t[,.(dead=sum(dead),pop=sum(alive)),.(week,month,dose,age=pmin(age,95)%/%5*5,facet)]
std=fread("https://sars2.net/f/czcensus2021pop.csv")[,sum(pop),age%/%5*5][,.(age,std=V1/sum(V1))]
vax=a[dose>0,.(dead=sum(dead),pop=sum(pop)),.(week,month,age,facet)]
base=merge(vax,vax[,.(sum=sum(pop)),.(week,facet)])
base=base[,.(frac=pop/sum,month,age,week,facet)]
unvax=a[dose==0,.(dead,pop,age,month,dose,facet)]
unvax=merge(unvax,base)[,.(dead=sum(dead*frac),pop=sum(pop*frac)),.(age,week,dose,facet)]
p=vax[,.(dead=sum(dead),pop=sum(pop),dose=1),.(week,age,facet)]
p=rbind(p,unvax)
p=merge(std,p)[,.(y=ifelse(sum(pop)<365e3,NA_real_,sum(dead/pop*std*365e5))),.(x=week,dose,facet)]
p[,dose:=factor(dose,,c("Unvaccinated","Vaccinated"))]
xstart=0;xend=100;xbreak=0:10*10;ybreak=pretty(p$y);ystart=0;yend=max(ybreak)
p[,facet:=factor(facet,,c("All doses counted","Only first dose counted"))]
ggplot(p,aes(x,y))+
facet_wrap(~facet,ncol=1,scales="free")+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(color=dose),linewidth=.6)+
labs(title="ASMR by weeks since vaccination in Czech Republic",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#5555ff","#ff5555","black"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50"),
axis.ticks.length=unit(0,"pt"),
legend.background=element_blank(),
legend.box="vertical",
legend.box.just="right",
legend.box.margin=margin(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="center",
legend.key.height=unit(13,"pt"),
legend.key.width=unit(21,"pt"),
legend.key=element_rect(fill="white"),
legend.margin=margin(,,2),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray90"),
panel.background=element_blank(),
panel.spacing=unit(2,"pt"),
plot.margin=margin(4,14,4,4),
plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11,face="bold",hjust=.5,margin=margin(1,,3)),
strip.background=element_blank(),
strip.text=element_text(size=11,margin=margin(1,,3)))
ggsave("1.png",width=5.1,height=3.5,dpi=300*4)
The next example demonstrates how the population sizes for each week since vaccination should be calculated correctly. If you have million people followed over 1095 days, you can make a table with 1,095,000,000 rows for each combination of date and person, with one column for days since last dose.
Here are sample rows for two dates and three people from my imaginary table:
date person_id days_since_last_dose 2021-05-01 12345 18 2021-05-01 12446 35 2021-05-01 12447 19 2021-05-02 12345 19 2021-05-02 12346 36 2021-05-02 12447 20
Then to get the number of person-days for each day since vaccination, you can simply count how many times each number of days since last dose appears in the table:
days_since_last_dose count 18 1 19 2 20 1 35 1 36 1
Rows where the date is after a date of death or emigration can be first removed. Rows where the date is earlier than a date of birth or immigration can similarly be removed.
Added in July 2025: Steve Kirsch published Japanese FOI data for the city of Koganei, which includes a total of about 130,000 people and about 4,000 deaths: https://kirschsubstack.com/p/my-2500-challenge-to-the-worlds-epidemiologists/, https://github.com/skirsch/covid/blob/main/japan/jp132101_Koganei-Tokyo_all_doses.xlsx. He obfuscated the data by shifting the ages of people by -4 to 4 years, and by shifting vaccination dates by -1 to 1 days. A few days later Kenji Fujikawa published an unobfuscated version of the same dataset that also included columns for vaccine brand and lot number: https://medicalfacts.info/vdeath.rb, https://fujikawa.org/pub/jp132101_Koganei-Tokyo_all.csv.
I used this script to make "buckets" files of the data, which show the number of deaths and person-days grouped by dose number, sex, age, vaccine brand, weeks since vaccination, observation month, and vaccination month:
download.file("https://fujikawa.org/pub/jp132101_Koganei-Tokyo_all.csv","jp132101_Koganei-Tokyo_all.csv")
library(data.table);library(lubridate)
t=fread("jp132101_Koganei-Tokyo_all.csv",fill=T)
age=\(x,y){class(x)=class(y)=NULL;(y-x-(y-789)%/%1461+(x-789)%/%1461)%/%365}
set.seed(0);t[,born:=as.Date("2025-5-16")-years(age)-sample(0:364,.N,T)]
t[born>date_lot1,born:=date_lot1]
mindate=as.Date("2021-2-1");maxdate=as.Date("2025-3-31")
d=t[,.(id,sex,born,dead=date_death,dose=rep(0:7,each=.N))]
d$date=c(rep(mindate,nrow(t)),t[,unlist(.SD,,F),.SDcols=patterns("date_lot")])
d$brand=c(rep("",nrow(t)),t[,unlist(.SD,,F),.SDcols=patterns("pharma")])
d[,brand:=fcase(brand=="moderna","Moderna",brand=="pfizer","Pfizer",brand=="","",default="Other")]
d=d[!is.na(date)][date<=maxdate][.N:1]
d[,vaxmonth:=substr(date,1,7)]
buck=data.table()
for(day in as.list(seq(mindate,maxdate,1))){
cat(as.character(day),"\n")
sub=d[date<=day&!(day<=dead)%in%F&day>=born]
sub=sub[rowid(id)==1] # remove under earlier doses
# sub=sub[!(dose==0&id%in%id[dose>0])] # keep under earlier doses
sub=sub[,.(week=ifelse(dose==0,0,as.numeric(day-date)%/%7),month=substr(day,1,7),
vaxmonth,age=age(born,day),sex,dose,brand,pop=1,dead=dead==day)]
buck=rbind(buck,sub)[,.(pop=sum(pop),dead=sum(dead,na.rm=T)),.(month,vaxmonth,week,age,sex,dose,brand)]
}
setorder(buck,month,vaxmonth,week,age,sex,dose,brand)
fwrite(buck,"koganeibuckets.csv.gz",quote=F)
I uploaded the output here: f/koganeibuckets.csv.gz. In this version people are kept under earlier doses after a new dose: f/koganeibucketskeep.csv.gz.
Kirsch said that the age of people was calculated in May 2025 but he didn't specify which date it was, so in the code above I generated a random birthday for each person based on their age on the middle day of May 2025.
Fujikawa wrote that "Age categories are based on the data as of the time of disclosure and do not reflect changes due to individuals aging into a new category" and that "The deceased's age is based on the data disclosure date and is thus older than at the time of death". [https://medicalfacts.info/vdeath.rb] In the Koganei data, the average age at death is about 3 years higher for people who died in 2021 than people who died in 2024, and it's implausibly high in 2021 to be the age at death. So I don't know if the age of people who died was determined based on the age at death in Hamamatsu but age in May 2025 in Koganei:
t=fread("jp132101_Koganei-Tokyo_all.csv",fill=T)
t[!is.na(date_death),.(meanage=round(mean(age),2)),,year(date_death)][year<2025]
# year meanage
# 2021 86.69 # about 3.3 years higher than 2024
# 2022 86.10 # about 2.7 years higher than 2024
# 2023 84.56 # about 1.1 years higher than 2024
# 2024 83.43
In the next plot I compared the two versions of the file generated by my script above. In the magenta line people are removed under earlier doses after a new dose, and in the blue line people are kept under earlier doses after a new dose. The plot that went viral looks he most like the magenta line for raw deaths, where the deaths peak around week 10-20, and week 20 has about 3 times more deaths than week 50. The magenta line for CMR is roughly stable from week 20 to week 60, so it doesn't look like the plot that went viral where there were about 5 times more deaths on day 120 than day 360:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
b=fread("https://sars2.net/f/koganeibucketskeep.csv.gz")[,type:=1]
b=rbind(b,fread("https://sars2.net/f/koganeibuckets.csv.gz")[,type:=2])
b[,age:=pmin(age,95)%/%5*5]
d=merge(b,rbind(b[type==1&dose<=1],b[type==2])[,.(base=sum(dead)/sum(pop)),.(month,age,type)])
d[,base:=base*pop]
a=d[dose>0,.(dead=sum(dead),pop=sum(pop),base=sum(base)),.(age,week,type)]
a=merge(a,d[type==1&month=="2022-01",sum(pop),age][,.(age,std=V1/sum(V1))])
p1=a[,.(y=c(sum(dead),sum(dead)/sum(pop)*365e5,sum(dead/pop*std*365e5)),facet=1:3,z=1),.(type,x=week)]
p2=a[,.(y=c(sum(base),sum(base)/sum(pop)*365e5,sum(base/pop*std*365e5)),facet=1:3,z=2),.(type,x=week)]
p=rbind(p1,p2)
p=merge(p,a[,sum(pop),.(week,type)][V1>=1e5,.(x=week,type)])
p[,y:=ma(y,2),.(type,facet,z)]
p[,facet:=factor(facet,,c("Deaths","CMR per 100,000 person-years","ASMR per 100,000 person-years"))]
p[,type:=factor(type,,c("Kept under earlier doses after new dose","Removed under earlier doses after new dose"))]
p[,z:=factor(z,,c("Deaths","Baseline"))]
xstart=0;xend=max(p$x)
ggplot(p)+
facet_wrap(~facet,dir="v",scales="free_y")+
geom_rect(data=p[,max(pretty(c(0,y))),facet],aes(ymax=V1),ymin=0,xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray75",linewidth=.4)+
geom_line(aes(x,y,color=type,alpha=z),linewidth=.6)+
geom_label(data=p[,max(pretty(c(0,y))),facet],aes(y=V1,label=facet),x=pmean(xstart,xend),vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87)+
geom_label(data=p[,max(pretty(c(0,y))),facet],aes(y=V1,label=facet),x=pmean(xstart,xend),vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87)+
labs(x=NULL,y=NULL,title="Mortality by weeks since vaccination in Koganei, Japan",subtitle="All lines are ±2-week moving averages")+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,20))+
scale_y_continuous(limits=\(x)range(pretty(c(0,x))),breaks=\(x)pretty(c(0,x)),labels=\(x)ifelse(x==max(pretty(c(0,x))),"",x))+
scale_color_manual(values=c("#2222ff","#ff22ff"))+
scale_alpha_manual(values=c(1,.4))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),alpha=guide_legend(order=2))+
theme(axis.text=element_text(size=11,color="gray40"),
axis.ticks.length=unit(0,"pt"),
legend.background=element_rect(color="gray75",linewidth=.4),
legend.box="horizontal",
legend.box.just="center",
legend.box.margin=margin(,,3),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(24,"pt"),
legend.margin=margin(3,5,3,3),
legend.position="top",
legend.spacing.x=unit(3,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray90"),
panel.spacing=unit(3,"pt"),
plot.margin=margin(5,15,5,5),
plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(1,,3)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.29,height=4.8,dpi=300*4)
In the next plot the top left panel shows the same data that is shown in the top panel in the previous plot, but the other panels show the results split out by dose number. Regardless of dose number, the deaths remain below the baseline if you look at the blue line. In the magenta line the deaths cross above the baseline after a new dose is rolled out, but it's because the healthy vaccinees move under the new dose, so the stragglers who remain under the previous dose have elevated mortality:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
b=fread("s/f/koganeibuckets.csv.gz")[,type:=1]
b=rbind(b,fread("s/f/koganeibucketskeep.csv.gz")[,type:=2])
b[,age:=pmin(age,95)%/%5*5]
base=rbind(b[type==1],b[type==2&dose<=1])
d=merge(b,base[,.(base=sum(dead)/sum(pop)),.(month,age,type)])[,base:=base*pop]
d=rbind(d[dose>0][,dose:=0],d[dose>0])
a=d[,.(dead=as.double(sum(dead)),base=sum(base)),.(week,dose,type)]
a[,dead:=ma(dead,2),.(dose,type)]
a=merge(a,a[week<=60&type==2,.(mean=mean(base)),dose])
p=a[,.(x=week,y=c(dead,base)/mean*100,z=rep(1:2,each=.N),dose,type)]
p[,z:=factor(z,,c("Deaths","Baseline"))]
p[,type:=factor(type,,c("Removed under earlier doses after new dose","Kept under earlier doses after new dose"))]
p[,dose:=factor(dose,,c("Doses 1-7",1:7))]
xstart=0;xend=max(p$x);xstep=20;ystart=0;yend=max(p$y);ybreak=0:5*25
ggplot(p)+
facet_wrap(~dose,ncol=2,dir="v")+
geom_hline(yintercept=100,color="gray75",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=type,alpha=z),linewidth=.6)+
labs(title="Deaths by weeks since vaccination in Koganei (±2-week moving average)",subtitle="Shown as percentage of average blue baseline value on weeks 0-60",x=NULL,y=NULL)+
geom_label(data=p[rowid(dose)==1],aes(label=dose),x=xend,hjust=1,y=yend,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87)+
geom_label(data=p[rowid(dose)==1],aes(label=dose),x=xend,hjust=1,y=yend,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87)+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,xstep))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#ff22ff","#2222ff"))+
scale_alpha_manual(values=c(1,.4))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),alpha=guide_legend(order=2))+
theme(axis.text=element_text(size=11,color="gray40"),
axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
axis.ticks.length=unit(0,"pt"),
legend.background=element_rect(color="gray75",linewidth=.4),
legend.box="horizontal",
legend.box.just="center",
legend.box.margin=margin(,,3),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(24,"pt"),
legend.margin=margin(3,5,3,3),
legend.position="top",
legend.spacing.x=unit(3,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray91"),
panel.spacing=unit(3,"pt"),
plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11,face=2,hjust=1,margin=margin(1,,4)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.5,height=5.2,dpi=300*4)
In both plots above, I calculated the baseline by multiplying the number of person-days for each combination of age group and observation month with the mortality rate among all people included in the dataset for the same combination of age group and observation month. I calculated the ASMR by 5-year age groups up to ages 95+, so that I used the fraction of person-days for each age group in January 2022 as my standard population.
In the plot that went viral, the mortality rate of unvaccinated people drops from about 0.010 at the start of the x-axis in March 2021 to about 0.006 towards the end of the x-axis. The x-axis starts on March 8th 2021 and ends around 420 days later, which is around May 2nd 2022. But I think there should be a bigger drop in the unvaccinated CMR, because there's a huge drop in the average age of unvaccinated people between the start and end of the x-axis, and the HVE for first doses is also stronger in 2021 than 2022. Here my unvaccinated CMR drops from about 808 in March 2021 to about 226 in May 2022:

t=fread("https://sars2.net/f/koganeibucketskeep.csv.gz")[dose<=1]
ages=c(0,20,30,8:19*5)
t[,agegroup:=ages[findInterval(age,ages)]]
a=t[,.(dead=sum(dead),pop=sum(pop)),.(age,month,dose,agegroup)]
a=rbind(a,a[,.(dead=sum(dead),pop=sum(pop),dose=2),.(age,agegroup,month)])
a=merge(a,a[dose<2,.(base=sum(dead)/sum(pop)),.(agegroup,month)])[,base:=base*pop]
a=merge(a[,sum(pop),agegroup][,.(agegroup,std=V1/sum(V1))],a)
a2=a[,.(dead=sum(dead),pop=sum(pop),base=sum(base)),.(month,agegroup,dose,std)]
p1=a2[,.(y=c(sum(dead),sum(dead)/sum(pop)*365e5,sum(dead/pop*std*365e5)),facet=1:3),.(month,dose)]
p2=a2[,.(y=c(sum(base),sum(base)/sum(pop)*365e5),facet=1:2),.(month,dose)]
p=rbind(p1[,z:=1],p2[,z:=2])
p=rbind(p,a[,.(y=weighted.mean(age,pop),facet=4,z=1),.(month,dose)])
p[,facet:=factor(facet,,c("Deaths","CMR","ASMR","Average age"))]
p[,z:=factor(z,,c("Actual","Baseline"))]
p[,dose:=factor(dose,,c("Unvaccinated","Vaccinated","Total"))]
p[,x:=as.Date(paste0(month,"-15"))]
xstart=as.Date("2021-1-1");xend=as.Date("2025-4-1")
xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ylim=p[,.(y=max(y)*1.02),facet]
ggplot(p)+
facet_wrap(~facet,ncol=2,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymax=y),ymin=0,xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_line(aes(x,y,color=dose,alpha=z),linewidth=.5)+
geom_label(data=ylim,aes(mean(c(xstart,xend)),y,label=facet),vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4,size=3.8,fill="white",color="gray72")+
geom_label(data=ylim,aes(mean(c(xstart,xend)),y,label=facet),vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=0,size=3.8,fill=NA)+
labs(title="Mortality in FOI data for Koganei, Japan",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(0,NA),breaks=\(x)pretty(c(0,x)))+
scale_color_manual(values=c("#5555ff","#ff5555","black"))+
scale_alpha_manual(values=c(1,.4))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50"),
axis.ticks=element_line(linewidth=.4,color="gray72"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(-4,"pt"),
legend.background=element_rect(color="gray72",linewidth=.4),
legend.box="horizontal",
legend.box.just="center",
legend.box.margin=margin(,,3),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(24,"pt"),
legend.margin=margin(3,5,3,2),
legend.position="top",
legend.spacing.x=unit(3,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.background=element_blank(),
panel.spacing=unit(3,"pt"),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,face=2,margin=margin(1,,4),hjust=.5),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.825,height=4.3,dpi=300*4)
I hadn't earlier noticed that the Japanese website about the FOI data has a section for additional information, which says the following in Japanese: [https://stop-mrna.sakura.ne.jp/db/appendix.php]
Depending on the local government, age may be disclosed in 5-year or 10-year increments. In addition, vaccination dates and death dates may only be shown up to the year and month, with no actual dates being disclosed. In such cases, we may negotiate to see if the information can be obtained in a format such as "number of days from vaccination to death," and we may switch from a disclosure request to a "provision of information."
[...]
Regarding age, we basically use the "age at the time of data extraction." If the person has already died, the "age at the time of death" is provided by the local government. In principle, if the date of birth can be obtained, it is possible to calculate the exact "age at the time of vaccination" and the "age category" at that time. However, in reality, the disclosure format differs from local government to local government, and age, date of birth, 10-year increments, 5-year increments, etc. are mixed. Therefore, if the age category is disclosed, that category is used, and if individual ages are obtained, that value is used as is. Since the period during which vaccinations are observed is limited to a maximum of about three years, only a few percent of the cases cross age boundaries (20, 65, 70, etc.). Therefore, considering the balance between accuracy and efficiency, we compile the data in this manner.
[...]
The request for disclosure asks for "information on all residents (including those who have not been vaccinated) from the month the COVID-19 vaccine was administered until the date of this disclosure request." However, in reality, many municipalities do not disclose any information after the end of March 2024, because the operation of the VRS (Vaccination Record System) ended. On the other hand, there are cases where information is stored in some form even after the end of VRS operation, and records of deaths of unvaccinated people up to 2025 have been disclosed.
Here's also a plot of the Koganei data that simply shows deaths by weeks after the first dose, where I calculated the matched baselines using the same method as earlier:

b=fread("https://sars2.net/f/koganeibucketskeep.csv.gz")[dose<=1]
b[,age:=pmin(age,95)%/%5*5]
b=merge(b,b[,.(base=sum(dead)/sum(pop)),.(month,age)])[,base:=base*pop]
b=merge(b,b[dose==0,.(base2=sum(dead)/sum(pop)),.(month,age)])[,base2:=base2*pop]
p=b[dose==1,.(y=c(sum(dead),sum(base2),sum(base)),z=1:3),.(x=week)]
p=rbind(p[,facet:=1],p[,.(y=y/y[3]*100,z,facet=2),x])
p=p[!(facet==2&x%in%b[,sum(pop),week][V1<365e2,week])]
p[,z:=factor(z,,c("Vaccinated","Unvaccinated (matched)","Total (matched)"))]
p[,facet:=factor(facet,,c("Deaths","Deaths as percentage of matched total"))]
xstart=0;xend=max(p$x);xstep=20
ylim=p[,.(y=max(y)),facet]
ggplot(p)+
facet_wrap(~facet,dir="v",scales="free")+
geom_segment(data=ylim[2],y=100,yend=100,x=xstart,xend=xend,linewidth=.4,color="gray75")+
geom_rect(data=ylim,aes(ymax=y),ymin=0,xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_label(data=ylim,aes(mean(c(xstart,xend)),y,label=facet),vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87)+
geom_label(data=ylim,aes(mean(c(xstart,xend)),y,label=facet),vjust=1,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,fill=NA,size=3.87)+
labs(title="Deaths by weeks since first dose in Koganei, Japan",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,xstep))+
scale_y_continuous(limits=c(0,NA),breaks=pretty)+
scale_color_manual(values=c("#ff5555","#5555ff","black"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40"),
axis.ticks.length=unit(0,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.key=element_blank(),
legend.key.height=unit(11,"pt"),
legend.key.width=unit(23,"pt"),
legend.margin=margin(,,5),
legend.position="top",
legend.spacing.x=unit(1.5,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray91"),
panel.spacing=unit(3,"pt"),
plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,3)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5,height=4,dpi=300*4)
Jeffrey Morris posted this tweet about the plot that went viral: [https://x.com/jsm2334/status/1950964408026370492]
As noted earlier, the shape of these curves does not imply that the vaccine is "killing" anyone.
Several artifactual factors can cause death rates to vary by time since last dose, none of which reflect actual vaccine risk.
One well-known example is the healthy vaccinee effect: individuals in poor health are less likely to get vaccinated, resulting in artificially low mortality in the days immediately following vaccination. The observed rise in deaths with time since dose simply reflects a return to baseline risk as this bias wears off.
After enough time passes, some individuals move on to their next dose. Those who remain in a given "days since last dose" group tend to be younger and healthier, producing a strong selection bias. This gradually shifts the age distribution and naturally lowers mortality rates over time, creating a spurious downward trend. This is why age confounding has such a major influence on these curves, and why proper analyses must adjust or stratify by age.
Moreover, the age distribution differs substantially across dose groups, with older individuals more likely to receive higher doses. As a result, the early days since last dose are disproportionately populated by older individuals, especially in higher dose groups, introducing further artifacts into their curve of death rate since last dose that combines information across all doses received.
If that combined analysis does not appropriately count individuals with dose K in the denominator K times, then that introduces another major bias - one that further distorts the shape by inappropriately inflating the death rate at the earlier days.
Finally, in the dose-specific plots, it appears they show raw death counts, which decline over time simply because the size of each dose group shrinks as people move on to their next dose. This creates a purely mathematical artifact. Had they plotted death rates per 100,000 people instead of raw counts, the shapes would have looked very different.
In short, there is no scientific justification for inferring that vaccines cause death based solely on the shapes of these curves.
Steve Kirsch claimed this plot of the Koganei data showed that vaccines were harmful, because the vaccinated line was less straight than the unvaccinated line: [https://kirschsubstack.com/p/the-single-most-convincing-covid]

The reason why his unvaccinated line seems relatively straight is because unvaccinated people have low total deaths. In the next plot the light blue line shows unvaccinated deaths multiplied to match vaccinated deaths at the end of the y-axis. It makes the unvaccinated line rather look less straight than the vaccinated line:

t=fread("jp132101_Koganei-Tokyo_all.csv",fill=T)
t[,dose:=(date_lot1<="2021-09-14")%in%T*1]
p=t[!is.na(date_death),.(y=.N),,.(x=date_death,z=dose)]
p=merge(do.call(CJ,lapply(p[,-3],unique)),p,all=T)[,y:=nafill(y,,0)]
p=p[x>="2021-09-15"]
p[,y:=cumsum(y),z]
p=rbind(p,p[z==0][,y:=y*p[,max(y[z==1])/max(y[z==0])]][,z:=2][])
p=rbind(p,p[,.(x=range(x),y=range(y),z=4)])
p[,z:=factor(z,,c("Unvaccinated","Vaccinated","Unvaccinated (matched total)","Straight reference line"))]
xstart=as.Date("2021-7-1");xend=as.Date("2025-7-1")
xbreak=as.Date(c("2021-10-1",paste0(2022:2024,"-7-1"),"2025-4-1"))
ybreak=pretty(p$y);ystart=0;yend=max(ybreak)
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
geom_vline(xintercept=seq(as.Date("2022-1-1"),xend,"year"),color="gray70",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_line(data=p[rleid(z)<4],aes(x,y,color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Cumulative deaths in Koganei, Japan (fixed cohorts)")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#5555ff","#ff5555","#aaaaff","black"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
axis.ticks.length=unit(0,"pt"),
legend.background=element_rect(color="gray70",linewidth=.4),
legend.box.spacing=unit(0,"pt"),
legend.justification=c(0,1),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(23,"pt"),
legend.margin=margin(3,5,3,3),
legend.position=c(.017,.97),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
plot.subtitle=element_text(hjust=.5,margin=margin(,,3)),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(1,,3)))
ggsave("1.png",width=4.7,height=2.8,dpi=300*4)
In the next plot the red ribbon only shows vaccine doses administered to ages 60 and above, because in the Koganei data about 95% of deaths are in ages 60 or above (based on the value of the age column, which shows the age in May 2025). The 3rd, 5th, 6th, and 7th doses were administered about 1-2 months before a peak in the moving of vaccinated deaths, but all of the peaks coincide with either a peak in COVID deaths or the winter peak in deaths:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
d21=c(2669,2159,1139,1554,3090,1669,579,1568,1617,471,151,90)
d22=c(668,6503,4630,1705,1030,566,1941,9293,5216,2319,3977,9787)
d23=c(12713,4511,1868,1011,986,1154,1878,3852,4049,2496,1628,1934)
d24=c(3911,4569,3623,2506,1722,1734,3356,4881,3155,1919,1387,3012)
d25=c(5104,3311)
dead=CJ(x=seq(as.IDate("2021-1-1"),as.IDate("2025-2-1"),"month"))[,y:=c(d21,d22,d23,d24,d25)]
t=fread("jp132101_Koganei-Tokyo_all.csv",fill=T)
t[,dose:=(date_lot1<="2021-09-14")%in%T*1]
t[,dose:=(!is.na(date_lot1))*1]
p=t[!is.na(date_death),.(y=.N),,.(x=date_death,z=dose)]
p=merge(do.call(CJ,lapply(p[,-3],unique)),p,all=T)[,y:=nafill(y,,0)]
p=p[x>="2021-09-15"]
doses=t[age>=60,.(date=as.IDate(unlist(.SD,,F))),.SDcols=patterns("^date_lot")]
doses=doses[!is.na(date),.(y=.N),.(x=date)]
doses=merge(doses[,.(x=seq(min(x),max(x),1))],doses,all=T)[is.na(y),y:=0]
p=p[,.(x,y=ma(y,30)),z]
p=rbind(p,doses[,.(x,y=ma(y,3),z=2)])
p=rbind(p,dead[,z:=3])
p[,y:=y/max(y)*100,z]
lab=c("Unvaccinated deaths (±30-day MA)","Vaccinated deaths (±30-day MA)","Monthly COVID deaths (whole Japan)","Vaccine doses in ages 60+ (±3-day MA)")
p[,z:=factor(z,,lab)]
xstart=as.Date("2021-1-1");xend=as.Date("2025-7-1");xbreak=seq(xstart,xend,"year")
ystart=0;yend=100;ybreak=0:5*20
ggplot(p)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
geom_vline(xintercept=seq(as.Date("2022-1-1"),xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,lineend="square",fill=NA,color="gray80",linewidth=.4)+
geom_rect(data=p[z==lab[4]],aes(xmin=x,xmax=x%m+%months(1),ymin=0,ymax=y,fill=lab[3]),color="gray50",linewidth=.2)+
geom_line(data=p[z%in%lab[1:2]],aes(x,y,color=z),linewidth=.65)+
geom_area(data=p[z==lab[3]],aes(x,y,fill=lab[4]),size=.2,alpha=.4,color="#ff7777")+
labs(x=NULL,y=NULL,title="Deaths and vaccine doses in Koganei, Japan (fixed cohorts)",subtitle="Displayed as a percentage of maximum value")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("#5555ff","#ff5555","gray50"))+
scale_fill_manual(label=lab[3:4],values=c("gray80","#ffaaaa"))+
coord_cartesian(clip="off",expand=F)+
guides(fill=guide_legend(override.aes=list(linewidth=0,keyheight=unit(1,"pt"))))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
axis.text.x=element_text(hjust=0),
axis.ticks.length=unit(0,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.box="vertical",
legend.box.just="left",
legend.direction="vertical",
legend.key=element_blank(),
legend.key.height=unit(11,"pt"),
legend.key.width=unit(23,"pt"),
legend.margin=margin(2),
legend.position="bottom",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
plot.subtitle=element_text(hjust=.5,margin=margin(,,3)),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,2)))
ggsave("1.png",width=5.5,height=3.4,dpi=300*4)
Unvaccinated people have such a small sample size in the plot above that it's not easy to see spikes in deaths that coincide with COVID waves, even though in the full FOI data for different municipalities combined, the spikes in deaths during COVID waves are clearly bigger in unvaccinated people than vaccinated people.
Here's also an ASMR version of the same data, where this time I didn't use fixed cohorts like Kirsch:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
t=fread("jp132101_Koganei-Tokyo_all.csv",fill=T)
for(i in which(sapply(t,inherits,"IDate")))t[[i]]=as.Date(t[[i]])
set.seed(0);t$born=as.Date("2025-5-16")-years(t$age)-sample(0:364,nrow(t),T)
mindate=as.Date("2021-2-1");maxdate=as.Date("2025-3-31")
d=t[,.(start=pmax(born,mindate,na.rm=T),end=pmin(date_death,maxdate,na.rm=T),born)]
d$dead=t$date_death;d$vax=t$date_lot1
d=d[born<=maxdate]
e=d[,.(age=age(born,start),date=start,dose=0,pop=1)]
vax=d[!is.na(vax)]
e=rbind(e,vax[,.(age=age(born,vax),date=vax,dose=1,pop=1)])
e=rbind(e,vax[born!=vax,.(age=age(born,vax-1),date=vax,dose=0,pop=-1)])
bday=cbind(d,date=c(outer(d$born,2021:2025,`year<-`)))
bday[,age:=age(born,date)][,dose:=(date>=vax)%in%T*1]
bday=bday[!(date==vax%in%T)&date>start&date<=end]
e=rbind(e,bday[,.(age,dose,pop=1,date)],bday[,.(age=age-1,dose,pop=-1,date)])
dead=d[!is.na(dead),.(date=dead,dose=(!vax%in%NA)*1,age=age(born,dead))]
e=rbind(e,dead[,.(date=date+1,dose,age,pop=-1)])
b=e[,.(pop=sum(pop)),.(date,age=pmin(age,100),dose)]
b=merge(b,dead[,.(dead=.N),.(age=pmin(age,100),dose,date)],all=T)
b=rbind(b,b[,.(dead=sum(dead,na.rm=T),pop=sum(pop,na.rm=T),dose=2),.(date,age)])
b=merge(CJ(date=seq(mindate,maxdate,1),age=0:100,dose=0:2),b,all=T)
b[is.na(b)]=0
b[,pop:=cumsum(pop),.(dose,age)]
a=b[,.(dead=sum(dead),pop=sum(pop)),,.(age=pmax(age,0)%/%5*5,date,dose)]
a=merge(do.call(CJ,lapply(a[,1:3],unique)),a,all=T);a[is.na(a)]=0
a$std=a[dose==2,tapply(pop,age,sum)/sum(pop)][factor(a$age)]
a=a[,.(date,dead=ma(dead,30),pop=ma(pop,30)),.(age,dose,std)]
p1=a[pop>0,.(y=sum(dead/pop*std*365e5),facet=1),.(x=date,z=dose)]
d21=c(2669,2159,1139,1554,3090,1669,579,1568,1617,471,151,90)
d22=c(668,6503,4630,1705,1030,566,1941,9293,5216,2319,3977,9787)
d23=c(12713,4511,1868,1011,986,1154,1878,3852,4049,2496,1628,1934)
d24=c(3911,4569,3623,2506,1722,1734,3356,4881,3155,1919,1387,3012)
d25=c(5104,3311)
dead=CJ(x=seq(as.Date("2021-1-1"),as.Date("2025-2-1"),"month"))[,y:=c(d21,d22,d23,d24,d25)]
t=fread("jp132101_Koganei-Tokyo_all.csv",fill=T)
doses=t[age>=60,.(date=as.IDate(unlist(.SD,,F))),.SDcols=patterns("^date_lot")]
doses=doses[!is.na(date),.(y=.N),.(x=date)]
doses=merge(doses[,.(x=seq(min(x),max(x),1))],doses,all=T)[is.na(y),y:=0]
p2=doses[,.(x=as.Date(x),y=ma(y,3),z=3)]
p2=rbind(p2,dead[,z:=4])
p2[,y:=y/max(y)*100,z]
p=rbind(p1,p2[,facet:=2])
lab=c("Unvaccinated","Vaccinated","Total","New vaccine doses in ages 60+ (±3-day MA)","COVID deaths in whole Japan")
color=c("#5555ff","#ff5555","black","#ff9999","gray50")
p[,z:=factor(z,,lab)]
p[,facet:=factor(facet,,c("ASMR per 100,000 person-years (±30-day moving average)","Other variables (percentage of maximium)"))]
xstart=as.Date("2021-1-1");xend=as.Date("2025-4-1");xbreak=seq(xstart,xend,"year")
ystart=0;yend=100;ybreak=0:5*20
ylim=p[,.(max=max(y,na.rm=T)),facet]
leg=cbind(ylim[,.(y=max*seq(.90,,-.14,3)),facet][-6],color,label=lab)
ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free")+
geom_rect(data=ylim,aes(ymax=max),xmin=xstart,xmax=xend,ymin=ystart,lineend="square",linejoin="mitre",fill=NA,color="gray80",linewidth=.4)+
geom_rect(data=p[z==lab[5]],aes(xmin=x,xmax=x%m+%months(1),ymin=0,ymax=y,fill=lab[3]),color="gray50",linewidth=.2)+
geom_line(data=p[z!=lab[5]],aes(x,y,color=z),linewidth=.65)+
geom_text(data=leg,aes(xend-18,y,label=label),color=color,hjust=1,size=3.87)+
labs(x=NULL,y=NULL,title="Age-standardized mortality rate in Koganei, Japan")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(0,NA),breaks=pretty,labels=\(x)if(max(x,na.rm=T)==100)paste0(x,"%")else x)+
scale_color_manual(values=color)+
scale_fill_manual(label=lab[3:4],values=c("gray80","#ffaaaa"))+
coord_cartesian(clip="off",expand=F)+
guides(fill=guide_legend(override.aes=list(linewidth=0,keyheight=unit(1,"pt"))))+
theme(axis.text=element_text(size=11,color="gray50"),
axis.text.x=element_text(hjust=0),
axis.ticks.length=unit(0,"pt"),
legend.position="none",
panel.background=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray90"),
panel.spacing=unit(2,"pt"),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,2)),
strip.background=element_blank(),
strip.text=element_text(size=11,margin=margin(,,2)))
ggsave("1.png",width=5.5,height=3.4,dpi=300*4)
If you look at the aggregate data for different municipalities combined, the spikes in deaths during COVID waves are more pronounced in unvaccinated people than vaccinated people:

t=fread("https://sars2.net/f/japanfoihudikaha.csv")
p1=t[location==location[1]&age=="all",.(y=sum(dead)),.(z=pmin(dose,1),x=as.Date(paste0(month,"-15")))]
p1[,y:=y/days_in_month(x)]
p1[,y:=y/p1[year(x)==2023,tapply(y,z,mean)][z+1]*100]
p1=p1[y<200]
d20=c(0,10,56,450,336,59,46,275,249,192,401,1392)
d21=c(2669,2159,1139,1554,3090,1669,579,1568,1617,471,151,90)
d22=c(668,6503,4630,1705,1030,566,1941,9293,5216,2319,3977,9787)
d23=c(12713,4511,1868,1011,986,1154,1878,3852,4049,2496,1628,1934)
d24=c(3911,4569,3623,2506,1722,1734,3356,4881,3155,1919,1387,3012)
d25=c(5104,3311)
dead=CJ(x=seq(as.Date("2020-1-1"),as.Date("2025-2-1"),"month"))[,y:=c(d20,d21,d22,d23,d24,d25)]
p=rbind(p1,dead[,z:=3])
lab=c("Unvaccinated","Vaccinated","COVID deaths in whole Japan")
color=c("#5555ff","#ff5555","gray50")
p[,z:=factor(z,,lab)]
xstart=as.Date("2020-1-1");xend=as.Date("2025-5-1");xbreak=seq(xstart,xend,"year")
ystart=0;yend=p[z!=lab[3],max(y)];ybreak=pretty(c(ystart,yend))
leg=data.table(y=yend*seq(.93,,-.09,2)[c(1,2,1)],hjust=c(0,0,1),x=rep(c(xstart+30,xend-30),2:1),label=lab,color)
ggplot(p)+
annotate("rect",xmin=xstart,xmax=xend,ymin=0,ymax=yend,lineend="square",linejoin="mitre",fill=NA,color="gray80",linewidth=.4)+
geom_rect(data=p[z==lab[3]],aes(xmin=x,xmax=x%m+%months(1),ymin=0,ymax=y/100),fill="gray80",color="gray50",linewidth=.2)+
geom_line(data=p[z!=lab[3]],aes(x,y,color=z),linewidth=.65)+
geom_text(data=leg,aes(x,y,label=label,hjust=hjust),color=color,size=3.87)+
labs(x=NULL,y=NULL,title="Monthly deaths in Japan FOI data divided by days in month",subtitle="Shown as percentage of average value in 2023")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(0,NA),breaks=pretty,labels=\(x)paste0(x,"%"),sec.axis=sec_axis(trans=~.+0,breaks=ybreak,labels=\(x)ifelse(x>0,paste0(x*100/1e3,"k"),x*100)))+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
guides(fill=guide_legend(override.aes=list(linewidth=0,keyheight=unit(1,"pt"))))+
theme(axis.text=element_text(size=11,color="gray50"),
axis.text.x=element_text(hjust=0),
axis.ticks.length=unit(0,"pt"),
axis.title=element_text(size=11,margin=margin()),
legend.position="none",
panel.background=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray90"),
panel.spacing=unit(2,"pt"),
plot.subtitle=element_text(hjust=.5,margin=margin(,,2)),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,2)))
ggsave("1.png",width=5.1,height=2.7,dpi=300*4)
Japan followed a regular pattern in 2022-2024 with one COVID wave each winter and one wave each summer. Doses 3-7 were rolled out on average about 4-6 month apart, so that odd doses were rolled out before winter waves and even doses were rolled out before summer waves.
Hideki Kakeya was the first author of the Japanese papers which argued that Omicron had a non-natural origin, and he is also a critic of COVID vaccines. However he wrote this in Japanese: "The peak at 120 days post-vaccination can be explained by the healthy vaccinee bias and the transition to the next vaccination, while the low mortality rate among the unvaccinated can be explained by their lower average age." [https://x.com/hkakeya/status/1958500554482532407]

Added in October 2025: There's now record-level FOI data for the cities of Hamamatsu (about 900,000 people) and Matsudo (about 500,000) people. [https://x.com/donkey1399/status/1962650292413178184, https://covid-vaccine-jp.iwmtyss.com/VRS.zip]
The Hamamatsu data has a bigger sample size than the Koganei data, so there's less noise in unvaccinated people, and you can see that the wave pattern is more pronounced in unvaccinated people than vaccinated people:

system("wget covid-vaccine-jp.iwmtyss.com/VRS.zip;unzip VRS.zip")
d21=c(2669,2159,1139,1554,3090,1669,579,1568,1617,471,151,90)
d22=c(668,6503,4630,1705,1030,566,1941,9293,5216,2319,3977,9787)
d23=c(12713,4511,1868,1011,986,1154,1878,3852,4049,2496,1628,1934)
d24=c(3911,4569,3623,2506,1722,1734,3356,4881,3155,1919,1387,3012)
d25=c(5104,3311)
dead=CJ(x=seq(as.Date("2021-1-1"),as.Date("2025-2-1"),"month"))[,y:=c(d21,d22,d23,d24,d25)]
t=fread("sed s,NULL,,g VRS/221309_Hamamatsu/公開文書.csv")
names(t)=q(person,latesthistory,age,sex,dose,lot,manufacturer,vaxdate,deathdate,deathage,moveindate1,moveoutdate1,moveindate2,moveoutdate2,moveindate3,moveoutdate3,moveindate4,moveoutdate4,moveindate5,moveoutdate5)
s=merge(t,t[!is.na(deathdate),.(died=deathdate,person)])
cutoff=as.Date("2021-11-01")
p=s[dose%in%c("","1回目")&died>=cutoff,.(y=.N),.(x=died,z=dose!=""&vaxdate<cutoff)]
p=merge(p[,.(x=seq(min(x),max(x),1),z=c(F,T))],p,all=T)[is.na(y),y:=0]
p[,y:=cumsum(y),z]
p=rbind(p,p[z==z[1],.(x,y=y*p[x==max(x),y[2]/y[1]],z=2)])
p[,z:=factor(z,2:0,c("No first dose by cutoff (matched at end)","First dose by cutoff","No first dose by cutoff"))]
xstart=as.Date("2021-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=pretty(p$y);ystart=0;yend=max(ybreak)
fillab="Monthly COVID deaths in whole Japan"
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_vline(xintercept=cutoff,color="gray80",linetype="42",linewidth=.4)+
geom_rect(data=dead,aes(xmin=x,xmax=x%m+%months(1),ymin=0,ymax=y,fill=fillab),color="gray63",linewidth=.2)+
geom_line(aes(x,y,color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Cumulative deaths in fixed cohorts in Hamamatsu FOI data")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=kim)+
coord_cartesian(clip="off",expand=F)+
scale_color_manual(values=c(hsv(2/3,.4,1),hsv(3:2/3,.8,1)))+
scale_fill_manual(label=fillab,values="gray80")+
guides(color=guide_legend(order=1),fill=guide_legend(order=2,keyheight=unit(10,"pt")))+
theme(axis.text=element_text(size=11,color="gray40"),
axis.text.x=element_text(margin=margin(2)),
axis.text.y=element_text(margin=margin(,1)),
axis.ticks=element_line(linewidth=.4,color="gray75"),
axis.ticks.length=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_rect(color="gray75",fill="white",linewidth=.4),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.justification=c(0,1),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.spacing.x=unit(0,"pt"),
legend.key.spacing.y=unit(0,"pt"),
legend.key.width=unit(24,"pt"),
legend.margin=margin(3,5,3,3),
legend.position=c(0,1),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,margin=margin(,,,2)),
legend.title=element_blank(),
panel.background=element_blank(),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)))
ggsave("1.png",width=5.2,height=2.9,dpi=300*4)
system("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[41*4-2] caption:'The cutoff date was November 1st 2021. Source: covid-vaccine-jp.iwmtyss.com/VRS.zip and e-stat.go.jp/stat-search/files?layout=datalist&toukei=00450011&tstat=000001028897&cycle=1&tclass1=000001053058&tclass2=000001053060&tclass3val=0 (table 7).' -splice x$[16*4] \\) -append -trim -resize 25% -bordercolor white -border 20 -dither none -colors 256 1.png")
In the Hamamatsu data, the difference between unvaccinated and vaccinated mortality is particularly pronounced during the summer 2022 COVID wave (which happened to coincide with the rollout of the 4th dose):

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
t=fread("sed s,NULL,,g c/VRS/221309_Hamamatsu/公開文書.csv")
t=t[,c(1,3,5,8,9)]
names(t)=c("id","age","dose","vax","dead")
t[t,on=.(id),dead:=fcoalesce(dead,i.dead)]
t[,age:=as.integer(sub("\\D.*","",age))]
t[,dose:=match(dose,c("","1回目","2回目","3回目","4回目","5回目","6回目","7回目"))-1]
mindate=as.Date("2021-2-1");maxdate=as.Date("2024-6-30")
d=t[dose<2&!is.na(age)&!(!is.na(vax)&vax<mindate)]
e=d[!is.na(vax),.(dose=1,pop=.N),.(age,date=vax)]
e=rbind(e,d[,.(date=mindate,pop=.N,dose=0),age])
e=merge(e,d[!is.na(dead),.(dead=.N),.(age,dose,date=dead)],all=T)
a=merge(do.call(CJ,lapply(e[,1:3],unique)),e,all=T)
a[is.na(a)]=0
a[dose==0,pop:=pop-a[dose==1,pop]]
a[,pop:=cumsum(pop)-cumsum(dead),.(dose,age)]
a=rbind(a,a[,.(dead=sum(dead),pop=sum(pop),dose=2),.(age,date)])
a[,std:=tapply(pop,age,sum)[factor(age)]/sum(pop)]
a=a[,.(date,dead=ma(dead,15),pop=ma(pop,15)),.(age,dose,std)]
p1=a[pop>0,.(y=sum(dead/pop*std*365e5),facet=1),.(x=date,z=dose)]
d21=c(2669,2159,1139,1554,3090,1669,579,1568,1617,471,151,90)
d22=c(668,6503,4630,1705,1030,566,1941,9293,5216,2319,3977,9787)
d23=c(12713,4511,1868,1011,986,1154,1878,3852,4049,2496,1628,1934)
d24=c(3911,4569,3623,2506,1722,1734,3356,4881,3155,1919,1387,3012)
d25=c(5104,3311)
dead=CJ(x=seq(as.Date("2021-1-1"),as.Date("2025-2-1"),"month"))[,y:=c(d21,d22,d23,d24,d25)]
vax=t[!is.na(vax)&age>=60,.(y=.N),.(x=vax)]
vax=vax[CJ(x=seq(min(x),max(x),1)),on="x",all=T][is.na(y),y:=0]
p2=rbind(vax[,.(x,y=ma(y,3),z=3)],dead[,z:=4])
p2[,y:=y/max(y)*100,z]
p=rbind(p1,p2[,facet:=2])
lab=c("Unvaccinated","Vaccinated","Total","New vaccine doses in ages 60+ (±3-day MA)","COVID deaths in whole Japan")
color=c("#5555ff","#ff5555","black","#ff9999","gray50")
p[,z:=factor(z,,lab)]
p[,facet:=factor(facet,,c("ASMR per 100,000 person-years (±15-day moving average)","Other variables (percentage of maximium)"))]
xstart=as.Date("2021-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart,xend-1,"year")
ystart=0;yend=100;ybreak=0:5*20
ylim=p[,.(max=max(y,na.rm=T)),facet]
leg=cbind(ylim[,.(y=max*seq(.90,,-.14,3)),facet][-6],color,label=lab)
ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free")+
geom_rect(data=ylim,aes(ymax=max),xmin=xstart,xmax=xend,ymin=ystart,lineend="square",linejoin="mitre",fill=NA,color="gray80",linewidth=.4)+
geom_rect(data=p[z==lab[5]],aes(xmin=x,xmax=x%m+%months(1),ymin=0,ymax=y,fill=lab[3]),color="gray50",linewidth=.2)+
geom_line(data=p[z!=lab[5]],aes(x,y,color=z),linewidth=.65)+
geom_text(data=leg,aes(xend-18,y,label=label),color=color,hjust=1,size=3.87)+
labs(x=NULL,y=NULL,title="Age-standardized mortality rate in Hamamatsu, Japan")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(0,NA),breaks=pretty,labels=\(x)if(max(x,na.rm=T)==100)paste0(x,"%")else x)+
scale_color_manual(values=color)+
scale_fill_manual(label=lab[3:4],values=c("gray80","#ffaaaa"))+
coord_cartesian(clip="off",expand=F)+
guides(fill=guide_legend(override.aes=list(linewidth=0,keyheight=unit(1,"pt"))))+
theme(axis.text=element_text(size=11,color="gray50"),
axis.text.x=element_text(hjust=0),
axis.ticks.length=unit(0,"pt"),
legend.position="none",
panel.background=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray90"),
panel.spacing=unit(2,"pt"),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,2)),
strip.background=element_blank(),
strip.text=element_text(size=11,margin=margin(,,4)))
ggsave("1.png",width=5.5,height=3.4,dpi=300*4)
system("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[42*4-2] caption:'Source: covid-vaccine-jp.iwmtyss.com/VRS.zip. ASMR was calculated by 5-year age groups so that the total person-days for each age group during the observation period were used as the standard population. Each person had a fixed age so that aging over time was not accounted for, which causes the ASMR to increase over time. The COVID deaths in whole Japan are from table 7 here: e-stat.go.jp/stat-search/files?layout=datalist&toukei=00450011&tstat=000001028897&cycle=1&tclass1=000001053058&tclass2=000001053060&tclass3val=0.' -splice x$[16*4] \\) -append -trim -resize 25% -bordercolor white -border 20 -dither none -colors 256 1.png")
canceledmouse posted this plot: [https://openvaet.substack.com/p/sweden-births1000-women-and-age-groups]

However if he would've started his x-axis from 2000 instead of 2010, it would've been more clear how the fertility rate has followed a convex curve on the long term. So relative to the long-term curved trend, his 2010-2019 linear baseline might be too high by the 2020s:

download.file("https://ec.europa.eu/eurostat/api/dissemination/sdmx/2.1/data/demo_fordager?format=TSV","demo_fordager.tsv")
download.file("https://ec.europa.eu/eurostat/api/dissemination/sdmx/2.1/data/demo_pjan?format=TSV","demo_pjan.tsv")
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
library(data.table);library(ggplot2)
pop=fread("demo_pjan.tsv",header=T)
meta=fread(text=pop[[1]],header=F)
pick=meta[,V5=="SE"&V4=="F"&V3%like%"Y\\d+$"]
meta=meta[pick];pop=pop[pick,-1]
age=as.integer(sub("^Y","",meta[[3]]))
pop=pop[,.(year=as.integer(names(.SD)[col(.SD)]),age,pop=as.integer(sub("[ :].*","",unlist(.SD,,F))))]
std=pop[age%in%15:49&year==2020,.(age,std=pop/sum(pop))]
pop=merge(pop,pop[,.(year=year-1,prev=pop,age)])[,.(year,age,pop=(pop+prev)/2)]
t=fread("demo_fordager.tsv",header=T)
meta=fread(text=t[[1]],header=F)
pick=meta[,V3%like%"^Y\\d+$"&V4=="TOTAL"&V5=="SE"]
meta=meta[pick];t=t[pick,-1]
age=as.integer(sub(".*?(\\d+).*","\\1",meta[[3]]))
t=t[,.(year=as.integer(names(.SD)[col(.SD)]),age,born=as.integer(sub("[ :].*","",unlist(.SD,,F))))]
a=merge(std,merge(t,pop))
a[,agegroup:=agecut(age,c(15,25,30,35,40,50))]
a=rbind(a,copy(a)[,agegroup:="Total"])
p=a[year>=2000,.(y=sum(born/pop*std*1e3)),.(x=year,agegroup)]
xstart=2000;xend=2023;xbreak=seq(xstart,xend,5)
ylim=p[,{x=range(y);.(min=x[1],max=x[2])},agegroup]
ggplot(p)+
facet_wrap(~agegroup,ncol=2,dir="v",scales="free_y")+
geom_rect(data=ylim,aes(ymin=min,ymax=max),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray75",linewidth=.4)+
geom_line(aes(x,y),linewidth=.6)+
geom_label(data=ylim,aes(mean(c(xstart,xend)),min+(max-min)*.25,label=agegroup),label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,size=3.87,fill="white",color="gray75")+
geom_label(data=ylim,aes(mean(c(xstart,xend)),min+(max-min)*.25,label=agegroup),label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87,fill=NA)+
geom_point(aes(x,y),size=1.1)+
labs(x=NULL,y=NULL,title="Age-standardized fertility rate per 1,000 women in Sweden")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(breaks=\(x)pretty(x,4,3))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
axis.ticks.length=unit(0,"pt"),
panel.background=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray87"),
panel.spacing=unit(4,"pt"),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,5)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5,height=3.7,dpi=300*4)
You would also get a scary drop in the fertility trend in the 90s if you fitted a linear baseline against the 80s, or in the 10s if you fitted a linear baseline against the 00s:

t=fread("https://sars2.net/f/swedenfertility.csv")
t[,std:=t[year==2020,pop/sum(pop)][factor(age)]]
p=t[age%in%15:48,.(y=sum(born/pop*std*1e3),z=1,fit=T),.(x=year)]
xstart=1968;xend=2025;xbreak=seq(1970,xend-1,10)
ystart=0;yend=max(p$y)*1.04;ybreak=pretty(c(0,yend),7)
ggplot(p)+
geom_hline(yintercept=0,color="gray70",linewidth=.4)+
annotate("rect",ymin=ystart,ymax=yend,xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray75",linewidth=.4)+
geom_line(aes(x,y),linewidth=.6)+
geom_point(aes(x,y),shape=16,stroke=.6,size=1.3)+
labs(x=NULL,y=NULL,title="Age-standardized fertility rate in Sweden (births per 1,000\nwomen aged 15-48)")+
scale_x_continuous(breaks=xbreak)+
scale_y_continuous(breaks=ybreak)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray45"),
axis.ticks.length=unit(0,"pt"),
panel.background=element_blank(),
panel.grid.major=element_line(linewidth=.4,color="gray90"),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)))
ggsave("1.png",width=4.6,height=3,dpi=300*4)