Sections about UK statistics have been moved here: uk.html. Sections about papers by Ed Dowd's group Phinance Technologies have been moved here: dowd.html. Further updates are added to part 2: statistic2.html.
Fabian Spieker published a Substack post where he presented the hypothesis that many of the COVID deaths in summer 2021 in the United States were caused by "vaccine-medicated enhanced disease", since in the southeastern states which had a massive wave of COVID deaths in the summer of 2021, many people who had previously not been vaccinated were getting their first vaccine dose around the same time. [https://vigilance.pervaers.com/p/us-summer-deaths-of-2021]
Kirsch posted this tweet: [https://twitter.com/stkirsch/status/1750573957856792983]
However the states where people were still getting first shots in August 2021 tended to have a low percentage of vaccinated people. I got a correlation of about -0.55 when I included all ages and all sexes and I looked at the percentage of vaccinated people in August 2021 and not the percentage of people who got the first shot in August 2021:
In the southeastern states which had the highest number of COVID deaths per capita in August 2021, there was also a spike in PCR positivity rate which slightly preceded the deaths:
In fact the plot above shows that the spike in PCR positivity was short-lived like the spike in excess deaths, so both PCR positivity and excess deaths had fallen back near zero around November 2021, even though the daily number of new vaccine doses remained elevated until around March 2022. So the excess deaths not only rose in sync with PCR positivity rate but they also fell in sync after the PCR positivity rate fell down. And the same thing happened again during the Omicron wave.
In Florida there is only a small peak in vaccine doses around August 2021 when deaths peaked, and new vaccine doses remained around the same level until the end of 2021. But there was a sharp drop in PCR positivity rate which was followed by a sharp drop in excess mortality:
In February 2023 Kirsch published a spreadsheet of data from Medicare, which includes the dates of vaccination and dates of death of about 110,000 vaccinated people who died between December 2020 and January 2023: [https://kirschsubstack.com/i/104943824/the-medicare-data-that-i-received, moar.html#Connecticut_Medicare_data_published_by_Kirsch]
$ curl -Ls sars2.net/f/kirsch_medicare_all_states_subset.csv|head state,date_of_vaccination,date_of_death,age_at_death MI,2020-12-16,2020-12-20,74 WI,2020-12-16,2021-02-16,79 ME,2020-12-16,2021-05-18,77 WI,2020-12-16,2021-10-24,75 MN,2020-12-16,2021-11-24,76 MI,2020-12-16,2021-12-06,77 MI,2020-12-16,2022-01-24,60 IN,2020-12-16,2022-01-28,73 MI,2020-12-16,2022-11-08,71
Compared to the total US population which also includes unvaccinated people, the vaccinated people who are included in the Medicare spreadsheet have reduced mortality during the Omicron wave in January 2022 and the Delta wave in August to September 2021, and in fact the bump in deaths during the Delta wave seems to be almost flat among the vaccinated people:
If you only look at ages 15-44 in Kirsch's Medicare spreadsheet, the sample size is so small that it's diffficult to tell if there's actually an increase in deaths in August 2021 or not:
In the Medicare data there's also a reduced number of deaths in the first weeks following a vaccination. For example in people who were vaccinated in August 2021, there's only 9 deaths during the first week from vaccination and 11 deaths the next week, but during later weeks the average number of deaths is about 25:
> med=read.csv("https://sars2.net/f/kirsch_medicare_all_states_subset.csv")
> med[,2]=as.Date(med[,2]);med[,3]=as.Date(med[,3])
> weeks=with(subset(med,grepl("2021-08",date_of_vaccination)),as.numeric(date_of_death-date_of_vaccination)%/%7)
> weeks=table(factor(weeks,min(weeks):max(weeks)))
> weeks
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
9 11 31 36 19 26 24 26 29 24 39 23 22 24 27 28 28 35 28 28 39 32 22 18 32 30
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
32 27 30 25 23 24 18 24 14 20 21 31 26 28 24 24 21 21 20 17 26 23 23 21 27 17
52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76
24 15 20 23 18 22 29 12 18 21 20 19 19 21 30 25 25 26 21 27 22 15 15 14 4
> mean(weeks[3:54])
[1] 25.30769
And if you only look at the 5 southeastern states that had the highest number of COVID deaths per capita in August 2021, among people who were vaccinated in July to September 2021, there were only 3 deaths on the first week after vaccination and 5 deaths on the second week, even though the average number of deaths per week was later about 11:
> sub=subset(med,date_of_vaccination>="2021-07-01"&date_of_vaccination<="2021-09-30"&state%in%c("AL","AR","FL","LA","MS"))
> weeks=as.numeric(sub$date_of_death-sub$date_of_vaccination)%/%7
> weeks=table(factor(weeks,min(weeks):max(weeks)))
> weeks
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
3 5 12 17 11 8 10 6 9 8 9 9 9 12 15 14 14 13 16 8 13 11 13 18 9 12
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
11 14 10 19 12 12 15 8 10 9 12 8 11 7 10 4 13 11 12 8 9 8 12 9 13 11
52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77
7 10 10 8 11 9 12 9 10 9 5 9 8 11 20 9 8 10 9 8 10 5 4 3 3 3
78 79
2 2
> mean(weeks[3:54])
[1] 10.98077
In the Medicare "all states subset" sheet, if you look at the five southeastern states which had the highest number of COVID deaths per capita in August 2021, there's a low number of all-cause deaths in recently vaccinated people in July and August 2021. Among people who were vaccinated in August, there's only 6 deaths in August even though the average date of vaccination was on August 16th so August consists of roughly half a month, and the average number of deaths on subsequent months was about 17.5 which is almost 3 times higher than 6:
med=read.csv("https://sars2.net/f/kirsch_medicare_all_states_subset.csv")
med[,2]=as.Date(med[,2])
med[,3]=as.Date(med[,3])
med=med[med[,2]>="2021-01-01"&med[,2]<="2022-11-30",]
med=med[med[,3]>="2021-01-01"&med[,3]<="2022-11-30",]
med=med[med[,1]%in%c("AL","AR","FL","LA","MS"),]
m=table(sub("...$","",med$date_of_vaccination),substr(med$date_of_death,1,7))
disp=m
m=m/apply(m,1,max)
pheatmap::pheatmap(m,filename="0.png",display_numbers=disp,
cluster_rows=F,cluster_cols=F,legend=F,border_color=NA,
cellwidth=20,cellheight=20,fontsize=9,fontsize_number=8,na_col="white",
number_color=ifelse(m>.85,"white","black"),
breaks=seq(0,1,,256),
colorRampPalette(colorspace::hex(colorspace::HSV(c(210,210,210,160,110,60,30,0,0,0),c(0,.25,rep(.5,8)),c(rep(1,8),.5,0))))(256))
system("convert 0.png -trim -bordercolor white -gravity northwest -splice x16 -size `identify -format %w 0.png`x -pointsize 45 caption:'US Medicare data, Alabama, Arkansas, Florida, Louisiana, and Mississippi: Number of deaths by month of vaccination (y-axis) and by month of death (x-axis). Source: kirschsubstack.com/p/game-over-medicare-data-shows-the, sheet \"Medicare all states subset\".' +swap -append -trim -border 24 +repage 1.png")
In Guam there was also a spike in COVID deaths and PCR positivity rate in September 2021:
A report about COVID death at Guam said: "Though overall vaccination coverage in Guam is high with 93.5% of the eligible population (age ≥5) vaccinated as of 1/22/2022, among individuals who died of COVID-19 in Guam in 2021 with known vaccination status, over 80% were not fully vaccinated." [https://dphss.guam.gov/wp-content/uploads/2022/02/Guam_covid19_DOA_2021_Report_2_1_2022_FINAL.pdf] According to Table 1 of the report, there were 132 deaths in people with a known vaccination status, but 102 of the people were unvaccinated, which is about 77%:
In July to August 2021 there were also news reports that the demand for vaccines had incresed in southeastern states because of the Delta wave. For example an article about Louisiana published in early August 2021 said: [https://www.nytimes.com/2021/08/05/us/louisiana-vaccines-covid-delta.html]
But when Madeline LeBlanc relented and got her first vaccine dose this week, she was motivated by something entirely different: fear.
After seeing news reports about the Delta variant raging across the state, Ms. LeBlanc, 24, had come to see that without a vaccine, she risked not just her own life but those of others around her. "I don't want to be the one inhibiting someone else's health," said Ms. LeBlanc, who lives in Baton Rouge.
Demand for the shots has nearly quadrupled in recent weeks in Louisiana, a promising glimmer that the deadly reality of the virus might be breaking through a logjam of misunderstanding and misinformation.
The new push for vaccinations has been driven by an explosion in coronavirus cases.
When I tried comparing the daily number of COVID deaths in 2021 to daily new vaccine doses given, I got a negative correlation for most states, and the correlation got even lower when I shifted the dates of death 10 days into the past. However when I compared daily COVID deaths to PCR positivity rate instead, I got a positive correlation for all states, and the correlation increased even further when I shifted the dates of death by 10 days:
And I got similar results when I looked at excess all-cause deaths and not COVID deaths:
library(ggplot2)
download.file("https://data.cdc.gov/api/views/rh2h-3yt2/rows.csv?accessType=DOWNLOAD","statesvax.csv")
download.file("https://data.cdc.gov/api/views/pwn4-m3yp/rows.csv?accessType=DOWNLOAD","statescases.csv")
download.file("https://healthdata.gov/api/views/j8mb-icvb/rows.csv","statespcr.csv")
vax=read.csv("statesvax.csv")|>subset(date_type=="Report")
vax[,1]=as.Date(vax[,1],"%m/%d/%Y")
vax=vax[,c("Date","Location","Administered_Daily")]
colnames(vax)=c("date","state","vax")
pcr=read.csv("statespcr.csv")
pos=pcr[pcr$overall_outcome=="Positive",c(6,1,7)]
neg=pcr[pcr$overall_outcome=="Negative",c(6,1,7)]
pcr=merge(pos,neg,by=c(1,2))
pcr=data.frame(as.Date(pcr[,1],"%Y/%m/%d"),pcr[,2],pcr=pcr[,3]/(pcr[,3]+pcr[,4])*100)
cov=read.csv("statescases.csv")|>subset(state%in%state.abb)
cov=data.frame(date=as.Date(cov$start_date,"%m/%d/%Y")-3,state=cov$state,dead=cov$new_deaths)|>subset(grepl(2021,date))
cov=do.call(rbind,lapply(split(cov,cov$state),\(x){x=rbind(x,data.frame(date=as.Date(setdiff(seq(min(x$date),max(x$date),1),x$date),"1970-1-1"),state=x$state[1],dead=NA));x=x[order(x$date),];x$dead=zoo::na.approx(x$dead,na.rm=F)/7;x}))
# cov[,1]=cov[,1]-10
me=merge(vax,pcr,by=1:2)|>merge(cov,by=1:2)
ma=\(x,b=1,f=b)rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T)
xy=t(split(me,me$state)|>sapply(\(x)c(cor(ma(x$vax,3),ma(x$dead,3),use="complete.obs"),cor(ma(x$pcr,3),ma(x$dead,3),use="complete.obs"))))
xy=as.data.frame(xy)|>"colnames<-"(c("x","y"))
region=read.csv(header=F,text="Northeast,CT,MA,ME,NH,RI,VT,NJ,NY,PA
Midwest,IN,IL,MI,OH,WI,IA,KS,MN,MO,ND,NE,SD
South,DC,DE,FL,GA,MD,NC,SC,VA,WV,KY,MS,TN,AL,AR,LA,OK,TX
West,AZ,CO,MT,NM,NV,UT,WY,ID,AK,CA,HI,OR,WA")
xy$region=setNames(rep(region[,1],ncol(region)-1),unlist(region[,-1]))[rownames(xy)]
xy$region=factor(xy$region,region[,1])
color=c("red","#2050cc","black","#dd6600")
xstart=-.7;xend=.4;ystart=-0;yend=1
xtit=paste0("Correlation between daily COVID deaths and daily vaccine doses")
ytit=paste0("Correlation between daily COVID deaths and daily PCR positivity rate")
ggplot(xy,aes(x=x,y=y,color=region))+
geom_hline(yintercept=c(ystart,0,yend),linewidth=.3,lineend="square")+
geom_vline(xintercept=c(xstart,0,xend),linewidth=.3,lineend="square")+
geom_point(size=.6)+
ggrepel::geom_text_repel(label=state.name[match(rownames(xy),state.abb)],size=2.5,max.overlaps=Inf,segment.size=.2,min.segment.length=.2,box.padding=.07,show.legend=F)+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,xstep),labels=\(x)round(x,1))+
scale_y_continuous(limits=c(ystart,yend),breaks=seq(ystart,yend,ystep),labels=\(x)round(x,1))+
labs(x=xtit,y=ytit,title="2021: daily COVID deaths compared to daily new vaccine doses and daily PCR\npositivity rate",subtitle="Sources: CDC datasets titled \"Weekly United States COVID-19 Cases and Deaths by State\", \"COVID-19 Diagnostic Laboratory Testing (PCR Testing) Time Series
\", and \"COVID-19 Vaccination Trends in the United States, National and Jurisdictional\". Daily deaths were interpolated from weekly data. All time series were converted to 7-day centered moving averages before calculating the correlation."|>stringr::str_wrap(100))+
coord_cartesian(clip="off",expand=F)+
scale_fill_manual(values=color)+
scale_color_manual(values=color)+
theme(axis.text=element_text(size=6,color="black"),
axis.ticks=element_blank(),
axis.ticks.length=unit(.05,"lines"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.just="center",
legend.box.margin=margin(0,.3,0,0,unit="lines"),
legend.box.background=element_rect(color="black"),
legend.direction="vertical",
legend.justification=c(0,0),
legend.key=element_rect(fill=alpha("white",0)),
legend.key.size=unit(.8,"lines"),
legend.position=c(0,0),
legend.spacing.x=unit(0,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=8,vjust=.5),
legend.title=element_blank(),
panel.background=element_rect(fill="white"),
panel.grid.major=element_line(color="gray80",linewidth=.3),
plot.background=element_rect(fill="white"),
plot.margin=margin(.4,.65,.4,.4,"lines"),
plot.subtitle=element_text(size=7.5),
plot.title=element_text(size=9))
ggsave("1.png",width=5.4,height=4.4,dpi=450)
In December 2023 Steve Kirsch published a spreadsheet of data from the Maldives, which appears to include the dates of death for all or almost all of citizens of the Maldives who died in 2021-2022, even though it's missing some deaths in 2020 and 2023. [moar.html#Data_for_deaths_in_2020_2023_in_Maldives] The spreadsheet also includes the dates of vaccination of each person, and it includes a column for cause of death, including whether the death was attributed to COVID. During the peak in COVID deaths in May 2021, over half of all deaths are listed as COVID deaths, which are indicated by a pink background color:
The plot below shows that in May 2021 when there was the highest number of deaths, there were 122 deaths in unvaccinated people and 81 deaths in vaccinated people. And in May 2021 the percentage of unvaccinated people was 41.992% based on the average daily percentage of unvaccinated people at OWID, so based on the calculation (122/41.992)/(81/(100-41.992)), unvaccinated people had about 2.1 times higher mortality than vaccinated people in May 2021. However on months with a lower number of COVID deaths, the ratio between unvaccinated and vaccinated mortality was lower, which seems to indicate that the vaccines prevented COVID deaths (even though it could also be that healthy people were more likely to get vaccinated and healthy people were less likely to die of COVID):
Most deaths are of course in older people, and in most countries older people are more likely to be vaccinated than younger people. So if you took a weighted average of the percentage of vaccinated people in each age group where the weight was the number of people in the age group in Kirsch's spreadsheet, you'd probably get a much lower percentage of unvaccinated people than the percentage in the total population.
This plot also shows that the spike in deaths in May to June 2021 was much higher in unvaccinated people (even though it could partially be because people who had been vaccinated in March 2021 still had reduced mortality in May because of the temporal healthy vaccinee effect):
The heatmap below shows that in southern states in summer 2021, there was a particularly high percentage of COVID deaths in ages 0-54 out of all COVID deaths. It could be because young people were less likely to be vaccinated than old people, but maybe by 2022 young people had natural immunity so the vaccine offered less competitive advantage to older people, or maybe by 2022 more young people had gotten vaccinated (R code):
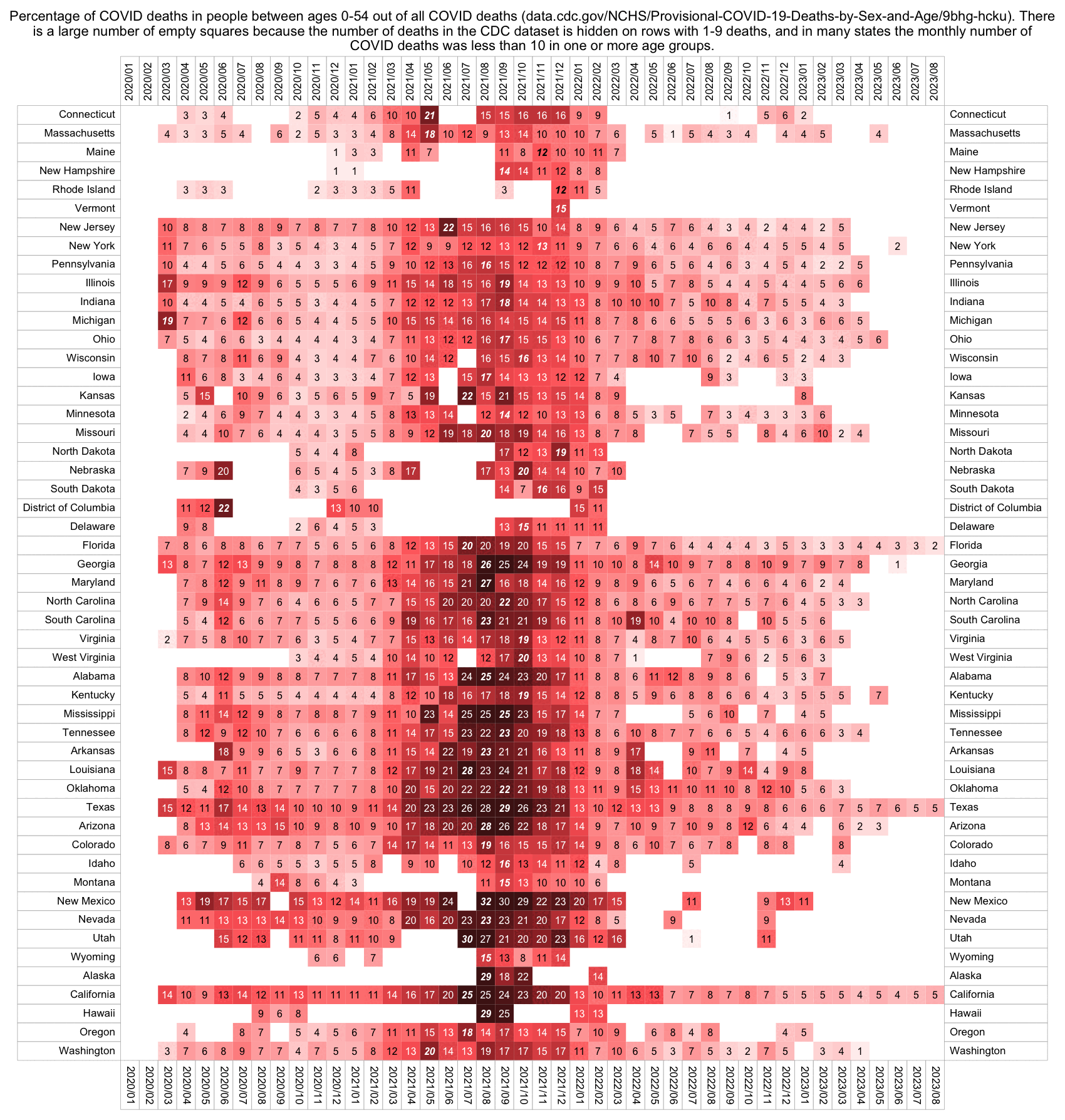
I also tried calculating the percentage of vaccinated people in ages 25-49 as a percentage of the percentage of vaccinated people in ages 65 and above. It was only about 55% in Alabama in August 2021 but it was 90% in Massachusetts, which might explain why Alabama had a higher percentage of COVID deaths in younger age groups than Massachusetts (and in fact in my previous heatmap Massachusetts had the lowest percentage of COVID deaths in ages 0-54):
# install.packages("BiocManager")
# BiocManager::install("ComplexHeatmap")
# install.packages("circlize")
library(data.table);library(ComplexHeatmap)
vax=fread("d/cd/COVID-19_Vaccination_Age_and_Sex_Trends_in_the_United_States__National_and_Jurisdictional_20240131.csv")[grepl("^Age",Demographic_Category)]
abb=setNames(c(state.name,"United States","District of Columbia","American Samoa","Guam","Northern Mariana Islands","Puerto Rico","United States Minor Outlying Islands","Virgin Islands"),c(state.abb,"US","DC","AS","GU","MP","PR","UM","VI"))
vax=vax[,.(pct=mean(Administered_Dose1_pct_agegroup,na.rm=T)),by=.(date=substring(as.Date(vax$Date,"%m/%d/%Y"),1,7),state=Location,age=sub("Ages?_(.*?)_?yrs","\\1",Demographic_Category))]
vax=vax[age=="65+"]|>merge(vax[age=="25-49"],by=c("date","state"))|>transform(pct=pct.y/pct.x*100)
m=xtabs(pct~state+date,vax)
states=read.csv("https://github.com/cphalpert/census-regions/raw/master/us%20census%20bureau%20regions%20and%20divisions.csv")
states=rbind(states,data.frame(State=c("United States","District of Columbia","American Samoa","Guam","Northern Mariana Islands","Puerto Rico","Virgin Islands","FS of Micronesia","Marshall Islands","Palau"),State.Code=c("US","DC","AS","GU","MP","PR","VI","FM","MH","PW"),Region=NA,Division=c("Total",rep("Other",9))))
states$order=match(states$Division,strsplit("Total,New England,Middle Atlantic,East North Central,West North Central,South Atlantic,East South Central,West South Central,Mountain,Pacific,Other",",")[[1]])
states$Division=sub("([WE]).* (South Central)","\\1 \\2",states$Division)
m=m[order(states$ord[match(rownames(m),states$State.Code)]),]
m=m[,-1]
rownames(m)=states$State[match(rownames(m),states$State.Code)]
png("0.png",w=ncol(m)*30+1000,h=nrow(m)*30+1000,res=72)
ht_opt$COLUMN_ANNO_PADDING=unit(0,"mm")
ht_opt$ROW_ANNO_PADDING=unit(0,"mm")
split=states$Division[match(rownames(m),states$State)]
Heatmap(m,
column_split=substring(colnames(m),1,4),
row_split=factor(split,unique(split)),
column_title=NULL,
row_title_gp=gpar(fontsize=16),
column_gap=unit(4,"mm"),
row_gap=unit(4,"mm"),
border="gray60",
width=unit(ncol(m)*30,"pt"),
height=unit(nrow(m)*30,"pt"),
show_column_names=F,
show_row_names=F,
cluster_columns=F,
cluster_rows=F,
show_heatmap_legend=F,
rect_gp=gpar(col="gray80",lwd=0),
top_annotation=columnAnnotation(text=anno_text(gt_render(colnames(m),padding=unit(c(3,3,3,3),"mm")),just="left",rot=90,location=unit(0,"npc"),gp=gpar(fontsize=17,border="gray60",lwd=1))),
bottom_annotation=columnAnnotation(text=anno_text(gt_render(colnames(m),padding=unit(c(3,3,3,3),"mm")),just="left",rot=270,gp=gpar(fontsize=17,border="gray60",lwd=1))),
left_annotation=rowAnnotation(text=anno_text(gt_render(rownames(m),padding=unit(c(3,3,3,3),"mm")),just="right",location=unit(1,"npc"),gp=gpar(fontsize=17,border="gray60",lwd=1))),
right_annotation=rowAnnotation(text=anno_text(gt_render(rownames(m),padding=unit(c(3,3,3,3),"mm")),just="left",location=unit(0,"npc"),gp=gpar(fontsize=17,border="gray60",lwd=1))),
col=colorRamp2(seq(200,0,,11),hex(HSV(c(210,210,210,210,210,0,0,0,0,0,0),c(.9,.8,.6,.4,.2,0,.2,.4,.6,.8,.9),c(.2,.4,.8,1,1,1,1,1,.8,.4,.2)))),
cell_fun=\(j,i,x,y,w,h,fill)grid.text(round(m[i,j]),x,y,gp=gpar(fontsize=16,col=ifelse(abs(m[i,j]-100)>=50,"white","black"))))
dev.off()
system("mogrify -trim 0.png;convert 0.png -gravity northwest -splice x10 -size `identify -format %w 0.png`x -pointsize 25 caption:'Percentage of vaccinated people in ages 25-49 as percentage of the percentage of vaccinated people in ages 65 and above. Source: CDC dataset titled \"COVID-19 Vaccination Age and Sex Trends in the United States, National and Jurisdictional\". The monthly percentages were calculated as the average of daily percentages for males and daily percentages for females. In the CDC dataset percentages above 95% are displayed as 95%, and from late 2021 onwards there are regions where the percentages for both age groups are always 95%, so the ratio between the age groups is always 100%.' +swap -append -trim -bordercolor white -border 24 +repage 1.png")
In the southern states which had a low percentage of vaccinated people in young age groups relative to old age groups, the excess all-cause mortality during the Delta wave was also higher in young age groups:
Younger age groups also had a huge increase in respiratory deaths during the Delta wave: [https://twitter.com/JusDayDa/status/1773804750179639452]
I got monthly COVID deaths by 5-year age groups from CDC WONDER: https://wonder.cdc.gov/mcd-icd10-provisional.html. In section 1 I set "Group Results By" to Month" and "Five-Year Age Groups", in section 6 I selected *U07.1 as the underlying cause of death, and in section 8 I checked "Export Results" and "Show Zero Values".
My heatmap below shows that compared to the winter 2020-2021 wave, the Omicron wave also seems to have killed a disproportionate number of young people, which might be because young people were less likely to be vaccinated than old people.
Each row has its own color scheme where the maximum value is black and zero is white. If you look at the colors of the squares during the summer 2020 wave, ages 60-69 have a higher color than older age groups, even though people were not yet vaccinated in summer 2020. However it could be because seasonal variation in mortality is greater in older age groups, so maybe older age groups also have more COVID deaths in winter relative to summer. But what complicates things further is that during the summer 2022 wave, older age groups again have a higher color than younger age groups.
t=readLines("Provisional Mortality Statistics, 2018 through Last Week.txt")
t=paste(t[1:(which(t=="\"---\"")[1]-1)],collapse="\n")
t=read.table(sep="\t",text=t,header=T)
t=t[t$Month.Code>="2020/02",]
t=t[t$Five.Year.Age.Groups!="Not Stated",]
m=tapply(t$Deaths,t[,c("Five.Year.Age.Groups","Month.Code")],c)
m=m[order(as.numeric(sub("\\W.*","",sub("< 1 year",0,rownames(m))))),]
m=cbind(m,Total=rowSums(m,na.rm=T))
m=rbind(m,Total=colSums(m,na.rm=T))
kimi=\(x){e=floor(log10(ifelse(x==0,1,abs(x))));e2=pmax(e,0)%/%3+1;p=!is.na(x)&x!=0;x[p]=paste0(sprintf(paste0("%.",ifelse(e[p]%%3==0,1,0),"f"),x[p]/1e3^(e2[p]-1)),c("","k","M","B","T")[e2[p]]);x}
disp=kimi(m)
m=m/apply(m[,1:(ncol(m)-1)],1,max,na.rm=T)
pheatmap::pheatmap(m,filename="0.png",display_numbers=disp,
cluster_rows=F,cluster_cols=F,legend=F,border_color=NA,
cellwidth=20,cellheight=20,fontsize=9,fontsize_number=8,na_col="white",
number_color=ifelse(m>.8,"white","black"),
breaks=seq(0,1,,256),
colorRampPalette(colorspace::hex(colorspace::HSV(c(210,210,210,160,110,60,30,0,0,0),c(0,.25,rep(.5,8)),c(rep(1,8),.5,0))))(256))
system("w=`identify -format %w 0.png`;convert 0.png -gravity northwest \\( -splice x20 -size $[$w-60]x -pointsize 40 caption:'CDC WONDER: Monthly deaths with underlying cause of death *U07.1 (COVID-19). CDC WONDER suppresses the number of deaths on rows with 1-9 deaths but not on rows with zero deaths. The total column does not include suppressed deaths. Each row has its own color scale where the maximum value is black and the minimum value is white.' -extent $[w-60]x -gravity center \\) +swap -append +repage 1.png")
Kirsch posted this tweet which showed that 4 out of the 5 biggest counties in Georgia had higher excess mortality in 2021 than 2020: [https://twitter.com/stkirsch/status/1751828835405082658]
However the excess mortality for 2020 includes the period before COVID in January and February (even though Georgia was one of the southern states which already had fairly high excess mortality in March).
The spikes in excess deaths also coincided with spikes in PCR positivity rate, and there was low excess mortality around April 2021 when vaccine doses peaked:
Beaudoin posted this tweet: [https://twitter.com/Coquin_de_Chien/status/1727583296668713020]
Here is 1 of 150 pages of graphs from The CDC Memorandum.
However his plots had a total of 16 deaths so maybe the increase in 2022 could've been due to chance. In the US as a whole in 2022, there's not that many excess deaths with an underlying cause of death C96.9 ("Malignant neoplasm of lymphoid, hematopoietic and related tissue, unspecified"). And actually if I would've used a polynomial baseline here, then the excess deaths would've been close to zero:
Beaudoin also posted this tweet:
Nothing to see here.
Move along.
Don't tell anyone.
Keep it quiet so we can sell more vx's.
However Beaudoin's plot only includes data back to 2015 so it's not that clear that there was an increasing trend in C41 deaths before COVID. When I looked at deaths in the US as a whole and I used a 2015-2019 linear baseline, I got negative excess mortality in 2021-2023 for the underlying cause of death C41 ("Malignant neoplasm of lymphoid, hematopoietic and related tissue, unspecified"):
library(ggplot2)
t=data.frame(year=1999:2023)
t$dead=c(71,85,78,57,47,54,43,47,42,50,45,43,62,59,65,66,74,75,82,88,106,118,126,144,152)
trend=lm(dead~year,t|>subset(year>=2015&year<=2019))
t$trend=predict(trend,t)
t$poly=lm(dead~poly(year,2),t|>subset(year>=1999&year<=2019))|>predict(t)
t$excess=t$dead-t$trend
t$polyexcess=t$dead-t$poly
xy=data.frame(x=t$year,y=t$dead,z="Deaths")
xy=rbind(xy,data.frame(x=t$year,y=t$trend,z="Linear trend (2015-2019)"))
xy=rbind(xy,data.frame(x=t$year,y=t$excess,z="Excess deaths relative to linear trend"))
xy$z=factor(xy$z,unique(xy$z))
xstart=min(xy$x);xend=max(xy$x)
cand=c(sapply(c(1,2,5),\(x)x*10^c(-10:10)))
ystep=cand[which.min(abs(cand-(max(xy$y)-min(xy$y))/6))]
ystart=ystep*floor(min(xy$y,na.rm=T)/ystep)
yend=ystep*ceiling(max(xy$y,na.rm=T)/ystep)
xlab=c(rbind("",unique(xy$x)),"")
xbreak=seq(xstart-.5,xend+.5,.5)
color=c("black","gray50",hcl(225,80,40))
yheight=(yend-ystart)/15
labels=data.frame(x=xstart+.001*(xend-xstart),y=seq(yend-yheight,,-yheight,nlevels(xy$z)),label=levels(xy$z))
tit="Yearly deaths in United States with underlying cause of death C96.9 (\"Malignant neoplasm of lymphoid, hematopoietic and related tissue, unspecified\"). Data from wonder.cdc.gov/mcd.html. The data was downloaded in February 2024 so some deaths in 2023 are still missing because of a registration delay."|>stringr::str_wrap(90)
lab=na.omit(data.frame(xy,label=ifelse(!grepl("Linear",xy$z)&xy$x>=2015,round(xy$y),NA)))
ggplot(xy,aes(x,y,color=z))+
geom_hline(yintercept=c(ystart,0,yend),color="gray65",linewidth=.25)+
geom_vline(xintercept=c(xstart-.5,xend+.5,c(2019.5,2014.5)),color="gray65",linewidth=.25)+
geom_line(aes(color=z),linewidth=.3)+
geom_label(data=lab,aes(color=z,label=label),size=1.8,fill=alpha("white",.7),label.r=unit(0,"lines"),label.padding=unit(.0,"lines"),label.size=0)+
geom_text(data=lab,size=1.8,aes(color=z,label=label))+
geom_label(data=labels,aes(x=x,y=y,label=label),fill=alpha("white",.7),label.r=unit(0,"lines"),label.padding=unit(.04,"lines"),label.size=0,color=color[1:nrow(labels)],size=2.6,hjust=0)+
labs(title=tit,x=NULL,y=NULL)+
coord_cartesian(clip="off",expand=F)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=seq(ystart,yend,ystep))+
scale_color_manual(values=color)+
theme(axis.text=element_text(size=6.5,color="black"),
axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
axis.ticks=element_line(linewidth=.25,color="gray65"),
axis.ticks.x=element_line(color=alpha("gray65",c(1,0))),
axis.ticks.length=unit(.15,"lines"),
axis.title=element_text(size=8),
legend.position="none",
panel.background=element_rect(fill="white"),
panel.grid=element_blank(),
plot.background=element_rect(fill="white"),
plot.margin=margin(.4,.65,.5,.4,"lines"),
plot.caption=element_text(size=6,hjust=0,margin=margin(.6,0,0,0,"lines")),
plot.title=element_text(size=7))
ggsave("1.png",width=4.6,height=3.3)
Tore Aarhus Gulbrandsen posted these tweets: [https://twitter.com/saunasauen/status/1766339791753196004]
It appears that EuroMOMO is now part of the white-washing of excess mortality, perhaps unknowingly.
In mid 2022 the EuroMOMO graph for Finland showed repeatedly high values for the period 2021-06 to 2022-06, with only a few weeks below the zero-line.
Today's graph shows the period as rather normal, with many weeks below the zero-line in the same time frame.
"Oceania had always been at war with Eurasia."
However in a bulletin for week 21 of 2023, EUROMOMO announced that they started including data from spring 2023 onwards in their baseline calculation: [https://www.euromomo.eu/bulletins/2023-21]
After a long period with elevated overall European mortality through the COVID-19 pandemic, the European mortality (both totally for the entire population and in all age groups) is by spring 2023 within the expected level. Therefore, data from spring 2023 and onwards will be included in the estimations of the expected mortality. During the pandemic years, the usual patterns of mortality have been disrupted because of the unexpected and varying excess mortality experienced due to the COVID-19 pandemic. This means that the assumption that there is no elevated mortality in certain weeks in spring (week 16-25) and autumn (week 37-44) did not hold. Therefore, to avoid biasing the estimations of the expected mortality, data from the pandemic years (2020-2022) were excluded from the estimations of the expected mortality. Normally, the estimation of the expected mortality is based on data from a five-year period. However, when data from the three pandemic years are excluded from the estimations, the oldest data currently used is up to 8 years old. This means that until 2028, both data from the pre- and post-COVID-19 pandemic periods will be included in the estimations of the expected mortality.
Clare Craig posted this plot which appears to show that in US counties which had a higher percentage of vaccinated people in 2022, the 2021 mortality rate minus 2020 mortality rate tended to be higher than in counties with a lower percentage of vaccinated people: [https://twitter.com/ClareCraigPath/status/1771230708511449587]
However actually her plot shows the mortality rate in 2020 minus the mortality rate in 2021. With 2021 minus 2020 I got the opposite trend:
In Craig's plot the county which had about 9% vaccinated people was Long County, Georgia, which had a higher mortality rate in 2021 than 2020 on CDC Wonder, so it should've been above zero on the y-axis in her plot. This plot also shows that the county with about 9% vaccinated people had a higher mortality rate in 2021 than 2020: [https://twitter.com/ClareCraigPath/status/1771167720634978639]
Craig also posted this tweet where she used the same CDC dataset for vaccinations by county, but she plotted the Completeness_pct column and not the Administered_Dose1_Pop_Pct column: [https://twitter.com/ClareCraigPath/status/1771154704992465029]
It's not clear why there's such a drastic difference between the two columns (or why the values of the Completeness_pct column seem to fall to a certain fixed set of values where other values in between are omitted):
> vax=fread("COVID-19_Vaccinations_in_the_United_States_County_20240227.csv")
> d=vax[Date=="01/01/2022",]
> table(round(d$Completeness_pct))
0 60 74 81 86 90 91 93 94 95 96 97 98 99
26 160 15 125 4 185 122 122 473 88 305 591 533 528
> table(round(d$Administered_Dose1_Pop_Pct))
0 10 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28
152 1 2 3 6 11 8 5 6 6 9 11 9 9 9 15 6
29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
7 8 7 10 9 12 22 32 26 44 50 59 65 76 56 90 67
46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62
106 75 101 68 108 84 103 83 120 93 93 70 89 75 97 70 68
63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79
56 70 52 52 39 48 32 42 37 36 17 30 25 23 27 28 18
80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95
21 18 22 20 9 18 17 10 12 10 10 2 12 5 7 38
The Completeness_pct column is described like this: "Represents the proportion of people with a completed primary series whose Federal Information Processing Standards (FIPS) code is reported and matches a valid county FIPS code in the jurisdiction." [https://data.cdc.gov/Vaccinations/COVID-19-Vaccinations-in-the-United-States-County/8xkx-amqh/about_data] And the Administered_Dose1_Pop_Pct column is described as the "Percent of Total Pop with at least one Dose by State of Residence".
I posted the Dutch CBS data here: f/dutch_cbs_aukema.csv. I combined the CSV files from sections 3.3.1 to 3.3.8 here: https://www.cbs.nl/nl-nl/longread/rapportages/2024/covid-vaccinatiestatus-en-sterfte/3-resultaten.
I didn't include the confidence intervals, because there's a bug on the website of the CBS where it doesn't include decimal separators for the upper end of the CI, so if for example the upper end of the CI is listed as 149, you can't tell if it's supposed to be 149 or 14.9 or 1.49.
Wouter Aukema also made this spreadsheet where he combined the same CSV files: https://docs.google.com/spreadsheets/d/1PSoPZ2Ugzm9bmhTYIIG1DYopMXbvHtevFeCZ_zPWT0o.
Denis Rancourt posted this tweet: [https://twitter.com/denisrancourt/status/1772434188223824079]
However the spike in December 2022 probably wasn't even caused by COVID, because the Dutch CBS data has a low number of COVID deaths in December 2022:
library(ggplot2)
t=read.csv("http://sars2.net/f/dutch_cbs_aukema.csv")
t=t[!grepl("ully",t$status),]
xy=aggregate(t[,4,drop=F],list(x=as.Date(t$week_ending)-3,z=paste0(t$status,ifelse(t$covid,", COVID",", not COVID"))),sum)
xy$z=factor(xy$z,paste0(rep(c("Unvaccinated","Vaccinated"),2),rep(c(", not COVID",", COVID"),each=2)))
colnames(xy)[3]="y"
xstart=as.Date("2021-1-1");xend=as.Date("2023-1-1")
xbreak=seq(xstart,xend,"2 month")
cand=c(sapply(c(1,2,5),\(x)x*10^c(-10:10)))
ystep=cand[which.min(abs(cand-(max(xy$y,na.rm=T)-min(xy$y,na.rm=T))/6))]
ystart=ystep*floor(min(xy$y,na.rm=T)/ystep)
yend=ystep*ceiling(max(xy$y,na.rm=T)/ystep)
ybreak=seq(ystart,yend,ystep)
color=c(hcl(c(210,0)+15,110,70),hcl(c(210,0)+15,100,30))
ggplot(xy,aes(x=x,y=y))+
geom_vline(xintercept=xbreak,linewidth=.3,lineend="square",color="gray84")+
geom_vline(xintercept=c(xstart,xend),linewidth=.3,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.3,lineend="square")+
geom_line(aes(color=z),linewidth=.4)+
labs(x=NULL,y=NULL)+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,date_labels="%b\n%y")+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
axis.ticks=element_line(linewidth=.3),
axis.ticks.length=unit(.15,"lines"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.background=element_rect(fill=alpha("white",.85),color="black",linewidth=.3),
legend.box.just="center",
legend.direction="vertical",
legend.justification=c(0,1),
legend.key=element_rect(fill=alpha("white",0)),
legend.key.size=unit(.8,"lines"),
legend.margin=margin(.5,.4,.3,.4,"lines"),
legend.position=c(0,1),
legend.spacing.x=unit(.15,"lines"),
legend.spacing.y=unit(-.2,"lines"),
legend.text=element_text(size=7,vjust=.5),
legend.title=element_blank(),
panel.background=element_rect(fill="white"),
panel.grid.major=element_line(linewidth=.3,color="gray88"),
plot.margin=margin(.5,.7,.3,.4,"lines"),
plot.title=element_text(size=7.5,margin=margin(.2,0,.4,0,"lines")))
ggsave("0.png",width=4.3,height=2.8,dpi=400)
system("f=0.png;mogrify -trim $f;w=`identify -format %w $f`;convert -gravity northwest -splice x0 -size $[w]x -pointsize 45 -font /Library/Fonts/Arial\\ Unicode.ttf -interline-spacing -5 caption:'Netherlands mortality statistics by vaccination status: Weekly number of deaths' -pointsize 39 caption:'Source: cbs.nl/nl-nl/longread/rapportages/2024/covid-vaccinatiestatus-en-sterfte/3-resultaten. People are counted as vaccinated from the day of the first vaccination. Weeks are plotted on Thursday.' -gravity south -splice x20 $f -append -trim -bordercolor white -border 30 +repage 1.png")
In winter 2021-2022 COVID deaths peaked on the week ending December 5th 2021, but even then COVID deaths accounted for only about 25% of all deaths in the Dutch CBS data:
> t=read.csv("http://sars2.net/f/dutch_cbs_aukema.csv")
> t=t[!grepl("ully",t$status)&t$week_ending=="2021-12-05",]
> m=tapply(t$deaths,list(ifelse(t$covid,"COVID","not COVID"),t$status),sum)
> m=cbind(m,total=rowSums(m))
> rbind(m,"COVID pct"=round(m[1,]/colSums(m)*100))
Unvaccinated Vaccinated total
COVID 315 765 1080
not COVID 568 2750 3318
COVID pct 36 22 25
The plot below shows that compared to the number of deaths in January 2022, the spike in all-cause deaths in December 2021 was a lot higher in unvaccinated people than vaccinated people. (The unvaccinated population size gets smaller over time as more people get vaccinated, but only a small number of people got their first vaccine dose between the start of December 2021 and the end of January 2022.)
Vaccinated people have lower non-COVID ASMR than unvaccinated people because of the healthy vaccinee effect, but you can adjust for it if you divide COVID ASMR by all-cause ASMR. But even then the ratio in unvaccinated people is much higher during the COVID wave in December 2021:
The Netherlands had a high number of influenza cases in December 2022, which might explain why there was a high number of deaths even though there was a low number of COVID deaths: [https://app.powerbi.com/view?r=eyJrIjoiYWU4YjUyN2YtMDBkOC00MGI1LTlhN2UtZGE5NThjY2E1ZThhIiwidCI6ImY2MTBjMGI3LWJkMjQtNGIzOS04MTBiLTNkYzI4MGFmYjU5MCIsImMiOjh9]
Germany also had a spike in all-cause mortality in December 2022 which coincided with a spike in influenza-like illness even though there was a low number of COVID deaths:
Even though adding together ratios is not correct in many cases, in the case of this dataset the denominators for COVID and non-COVID ASMR are the same, so it's possible to calculate all-cause ASMR by adding together COVID and non-COVID ASMR like in this example:
> stdpop=c(70000,30000) > t=read.table(header=T,text=" + age pop dead_covid dead_non_covid + 0-49 2345 3 28 + 50+ 1234 11 98") > asmr_covid=sum(t$dead_covid/t$pop*stdpop) > asmr_noncovid=sum(t$dead_non_covid/t$pop*stdpop) > asmr_total=sum(rowSums(t[,3:4])/t$pop*stdpop) > asmr_covid+asmr_noncovid [1] 3575.292 > asmr_total [1] 3575.292
So if you calculate all-cause ASMR by adding together COVID and non-COVID ASMR, it's much higher in unvaccinated people than vaccinated people, even though the difference gets smaller over time which is probably because the impact of the temporal healthy vaccinee effect gets weaker:
Netherlands is a bad country for calculating a Rancourtian correlation between all-cause mortality and new vaccine doses given, because the first two doses were rolled out between COVID waves when there was low excess mortality. And the first booster was also given earlier than in other countries where it happened to coincide with the Omicron wave, and for some reason Netherlands had a almost no deaths during the Omicron wave even though the number of cases and PCR positivity were high. So unlike many other countries, Netherlands didn't have a spike in deaths in January 2022 which would've coincided with the rollout of the first booster. Now there's minor bumps in all-cause mortality which coincide with the rollout of the 4th and 5th doses, but if the 4th and 5th doses were killing a bunch of people then why wasn't there also an increase in all-cause mortality when the first three doses were rolled out?
Aukema also posted the plot below which shows that vaccinated people accounted for about 82% of COVID deaths. [https://twitter.com/waukema/status/1763512462412845432] However according to the ECDC's vaccine tracker, about 96% of the Dutch population of ages 60 and above had been vacccinated by December 2021, and after that the percentage remained at 96.3% until 2023. [https://vaccinetracker.ecdc.europa.eu/public/extensions/COVID-19/vaccine-tracker.html#uptake-tab] The percentage might be too high, because in other countries the percentage of vaccinated people in elderly age groups sometimes reaches over 100% (and for example in New Zealand similar statistics were based on the Health Service User population where unvaccinated people are underrepresented, because many people who were not previously included in the population were added to it after they got vaccinated). But anyway, in the elderly age groups which account for most deaths, the percentage of vaccinated people is still probably much higher than 82%.
The heatmap below shows that in February 2021 among people who had not been insured for long-term care, vaccinated people had about twice as high ASMR as unvaccinated people, which might be because vulnerable groups of people were priorized during the early vaccine rollout. However after that unvaccinated people had higher ASMR than unvaccinated people almost every month, regardless of whether you look at COVID deaths or non-COVID deaths or if you look at people in long-term care or not. Among people who had not been insured for long-term care, there were many months when unvaccinated people had over 10 times higher COVID ASMR than vaccinated people. The last row of the bottom heatmap shows that among people in long-term care, vaccinated people initially had over 50% higher non-COVID mortality than unvaccinated people (which was probably because of the healthy vaccinee effect), but the difference had reached close to zero by the end of 2022:
t=read.csv("http://sars2.net/f/dutch_cbs_aukema.csv")
t=t[!grepl("ull",t$status),]
t=t[order(t$long_term_care,!t$covid,t$status),]
g=paste0(ifelse(t$covid,"","Non-"),"COVID deaths, ",ifelse(t$long_term_care,"","not "),"long-term care, ",tolower(t$status))
d=data.frame(x=as.Date(t$week_ending)-3,y=t$asmr/7*365,z=factor(g,unique(g)))
r=do.call(rbind,lapply(split(d,g),\(x){
x=rbind(x,data.frame(x=as.Date(setdiff(min(d$x):max(d$x),d$x),"1970-1-1"),y=NA,z=x$z[1]))
x=x[order(x$x),]
x$y=zoo::na.approx(x$y)
aggregate(x$y,list(x=substr(x$x,1,7),z=x$z),mean)
}))
m=xtabs(r[,3]~r[,2]+r[,1])
disp=ifelse(m>=1e3,sprintf("%.1f",m/1e3),round(m))
m=m^.65
maxcolor=max(m)
pal=colorspace::hex(colorspace::HSV(c(210,210,210,160,110,60,30,0,0,0),c(0,.25,rep(.5,6),.7,.9),c(rep(1,8),.5,0)))
pheatmap::pheatmap(m,filename="i1.png",display_numbers=disp,
gaps_row=seq(2,8,2),
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=19,cellheight=19,fontsize=9,fontsize_number=8,
border_color=NA,na_col="gray90",
number_color=ifelse(abs(m)>maxcolor*.8,"white","black"),
breaks=seq(0,maxcolor,,256),
colorRampPalette(pal)(256))
system("f=i1.png;w=`identify -format %w $f`;convert $f -gravity northwest \\( -splice x16 -size $[w-44]x -pointsize 40 caption:'Netherlands mortality statistics by vaccination status: sex-and-age-standardized mortality rate per 100k person-years. Source: cbs.nl/nl-nl/longread/rapportages/2024/covid-vaccinatiestatus-en-sterfte/3-resultaten (tables 3.3.1 to 3.3.8 compiled to sars2.net/f/dutch_cbs_aukema.cvs). People are counted as vaccinated immediately after the first dose. The monthly rates are somewhat inaccurate because they were calculated by taking the monthly averages of daily rates interpolated from weekly rates.' -extent $[w-44]x -gravity center \\) +swap -append -bordercolor white -border 6 +repage l1.png")
rat=\(x,y)(x-y)/ifelse(x>y,y,x)
m2=rat(m[seq(1,7,2),],m[seq(2,8,2),])*100
rownames(m2)=sub(", unvaccinated","",rownames(m2))
disp2=ifelse(m2>1e4,sprintf("%.1fk",m2/1e3),round(m2))
exp2=.6
m2=abs(m2)^exp2*sign(m2)
maxcolor2=1300^exp2
pal2=colorspace::hex(colorspace::HSV(c(210,210,210,210,0,0,0,0,0),c(1,.8,.6,.3,0,.3,.6,.8,1),c(.3,.65,1,1,1,1,1,.65,.3)))
pheatmap::pheatmap(m2,filename="i2.png",display_numbers=disp2,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=19,cellheight=19,fontsize=9,fontsize_number=8,
border_color=NA,na_col="gray90",
number_color=ifelse(abs(m2)>maxcolor2*.6,"white","black"),
breaks=seq(-maxcolor2,maxcolor2,,256),
colorRampPalette(pal2)(256))
system("f=i2.png;w=`identify -format %w $f`;convert $f -gravity northwest \\( -splice x16 -size $[w-44]x -pointsize 40 caption:'ASMR ratio by vaccination status. 200 means that unvaccinated people have 200% higher ASMR and -50 means that vaccinated people have 50% higher ASMR.' -extent $[w-44]x -gravity center \\) +swap -append -bordercolor white -border 6 +repage l2.png")
system("montage -geometry +0+0 -tile 1x l[12].png 1.png")
In one plot Aukema double-counted deaths, so he had about 5000-7500 deaths per week even though it should've been half of that: [https://twitter.com/UncleJo46902375/status/1763550999916990885]
In the Dutch CBS dataset, there is one set of statistics where people are considered vaccinated immediately after vaccination, and there is another set of statistics where people are only considered as vaccinated after they are fully vaccinated (which generally means that at least two weeks had passed from the second dose): [https://www.cbs.nl/nl-nl/longread/rapportages/2024/covid-vaccinatiestatus-en-sterfte/2-methode]
Vaccination status 'vaccinated' is defined as 'fully vaccinated' (i.e. two weeks after two approved vaccinations, or a positive test at least 56 days for at least one approved vaccination, or four weeks after vaccination where, according to the vaccination certificate, one vaccination counts as fully vaccinated, or when a booster or repeat injection has been given without a known basic series) possible with boosters and repeat injections. Vaccination status 'unvaccinated' is defined as no known vaccination or only one known vaccination without previously reported infection (with the exception of the vaccine where one vaccination counted as fully vaccinated).
The plot below shows that in January and February 2021, unvaccinated people had a spike in deaths which was missing from people who were not fully vaccinated. It might be because vulnerable groups of people were priorized during the earliest part of the rollout (even though based on this data alone, I believe the possibility that some of the deaths were caused by the vaccines cannot be ruled out either):
Actually fully vaccinated people have zero deaths until the week ending February 21st. The recommended minimum duration between the first and second dose was 3 weeks, so there was typically a delay of at least 5 weeks between the first vaccination and the time when a person was considered fully vaccinated.
The plot above also shows that during the first half of 2021 when there was still a fairly high number of new people getting vaccinated, unvaccinated people had much higher ASMR than people who were not fully vaccinated. It might be partially because of the temporal healthy vaccinee effect, where recently vaccinated people have a reduced number of deaths after vaccination, so conversely the people who remain unvaccinated have temporarily elevated mortality during the vaccine rollout. Or it could also be because the people who are not fully vaccinated include the group of people who received only one dose but not the second dose and the group of people who have recently received the second dose. In the ONS dataset for mortality by vaccination status, both of those groups of people had low mortality during the rollout of the first two doses (even though later on they had higher mortality but their population size was also much smaller) (R code):
Igor Chudov wrote: [https://www.igor-chudov.com/p/whites-twice-as-likely-to-die-of]
San Jose Mercury News reports an unusual COVID pattern detected in California.
What is interesting is that despite comprising only 37% of Californians, White people account for 60% of all COVID deaths during the recent period.
The article compares Feb-Aug 2020 (highlighted in blue) vs. Sep 2023 through Feb 2024 (highlighted in red).
The results for 2020 confirm a modest advantage that we would expect from the "white privilege": Whites comprised only 30% of deaths despite being 37% of the population.
[...]
Is it a coincidence that White people are also more vaccinated and boosted against COVID-19?
The more vaccinated and boosted race in California is accounting for GREATER share of Covid deaths compared to their share of the population. Meanwhile, Black and Hispanic Californians, who are less vaccinated, account for fewer deaths than their share of the population would suggest.
However whites of course are older than Hispanics, so I tried calculating ASMR from CDC WONDER: https://wonder.cdc.gov/mcd-icd10-provisional.html. I set "Group Results By" to Year, 6-race categories, and Hispanic status, and I set the underlying cause to U07.1 (COVID). I included the whole US and not just California, because when I only included California, CDC WONDER didn't return population sizes and there were more rows where the number of deaths was suppressed because there were less than 10 deaths. I classified people with Hispanic status under Hispanic and no other race.
In 2022 I got about 7% higher ASMR for Hispanics than whites. The ratio was much higher in 2020, but it was also higher in 2021 even though most people were vaccinated for most of 2021 in the elderly age groups which account for most COVID deaths, so I don't know if the change in the ratio was because of vaccination:
Asians had lower ASMR than whites each year in 2020-2023. Whites had about 5% higher ASMR than Asians in 2020, but it increased to 49% in 2021 and 74% in 2022. But Asians had higher vaccination rates than whites, so it seems to conflict with Chudov's hypothesis that the ratio between whites and Hispanics got lower after 2020 because whites were more likely to be vaccinated. However it could also be that states where Asians lived had more COVID deaths in 2020 relative to 2021-2023.
t=read.csv("http://sars2.net/f/cdc_wonder_ucod_covid_by_race_and_age.csv")
a=rbind(t,cbind(aggregate(t[,4:5],t[,c("year","age")],sum,na.rm=T),race="Total"))
a=rbind(a,cbind(aggregate(a[,4:5],a[,c("race","age")],sum,na.rm=T),year="Total"))
std=with(subset(t,year==2020),tapply(pop,age,sum,na.rm=T))
m=tapply(a$dead/a$pop*std[factor(a$age)]/sum(std)*1e5,list(factor(a$race,unique(a$race)),a$year),sum,na.rm=T)
maxcolor=max(m,na.rm=T)
pal=colorspace::hex(colorspace::HSV(c(210,210,210,160,110,60,30,0,0,0),c(0,.25,rep(.5,8)),c(rep(1,8),.5,0)))
pheatmap::pheatmap(m,filename="0.png",display_numbers=round(m),
gaps_row=nrow(m)-1,gaps_col=ncol(m)-1,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=17,cellheight=17,fontsize=9,fontsize_number=8,
border_color=NA,na_col="gray90",number_color=ifelse(m>maxcolor*.8,"white","black"),
breaks=seq(0,maxcolor,,256),colorRampPalette(pal)(256))
system("f=0.png;w=`identify -format %w $f`;convert -interline-spacing -2 -gravity northwest -splice 18x20 -size $[w-44]x \\( -pointsize 38 caption:'CDC WONDER: ASMR per 100,000 person-years with underlying cause COVID (U07.1). ASMR was calculated by 10-year age groups so that the 2020 US population was used as the standard population. CDC WONDER suppresses the number of deaths on rows with less than 10 deaths, so races with a smaller population size are more likely to have deaths suppressed for young age groups, but it doesn'\\''t have much effect on total ASMR.' \\) 0.png -append 1.png")
Also in the table below which included data up to May 2023, in ages 65-79 in California, Hispanics had about 3 times higher COVID mortality rate than whites ((43/21.8)/(35.2/54)): [https://www.cdph.ca.gov/Programs/CID/DCDC/Pages/COVID-19/Age-Race-Ethnicity.aspx]
In the heatmap below, within five out of six age groups the total UCD COVID CMR in 2020-2023 was much higher among Hispanic people than whites. But in ages 85+ Hispanics had only slightly higher CMR than whites, which might be if whites are overrepresented in the upper end of the 85+ age category relative to Hispanics. However for some reason in the year 2023 Hispanics had lower COVID CMR than whites in all age groups:
Steve Kirsch posted this tweet: [https://x.com/stkirsch/status/1816909730717274405]
A README file for the World Mortality Dataset says that they got data for deaths in the Seychelles through "email correspondence with Seychelles National Bureau of Statistics". [https://github.com/akarlinsky/world_mortality] Based on their data I got only about 3% excess deaths in 2021-2023 when I used the 2015-2019 linear trend as the baseline:
> t=fread("https://github.com/akarlinsky/world_mortality/raw/main/world_mortality.csv")
> t=t[country_name=="Seychelles",.(dead=sum(deaths)),year]
> t$trend=t[year<2020,predict(lm(dead~year),t)]
> t[,excesspct:=(dead/trend-1)*100]
> print(round(t),r=F)
year dead trend excesspct
2015 703 711 -1
2016 747 737 1
2017 748 762 -2
2018 818 788 4
2019 795 813 -2
2020 668 839 -20
2021 925 864 7
2022 941 890 6
2023 879 915 -4
> t[year>2020,(sum(dead)/sum(trend)-1)*100]
[1] 2.843655 # there's only about 3% total excess deaths in 2021-2023
Here's a plot of the same data:
I thought that the Facebook post may have meant 30% excess deaths against a baseline of 2020, because in the code above I got about -20% excess deaths for 2020 but 7% for 2021 and 6% for 2022. And in fact in the Rumble video which was linked in the post, a figure of 38.5% excess deaths in 2021 was calculated relative to a 2020 baseline: [https://rumble.com/v1xv71w-seychelles-excess-deaths.html]
In the image above the figure of 21.4% seems to match a 2015-2019 average baseline: 925/((795+818+748+747+703)/5). But the years 2015 and 2016 were not included in the plot so you couldn't see clearly that there was an increasing trend in the yearly number of deaths before 2020, so the 2015-2019 average baseline exaggerated excess mortality in 2021.
Kirsch also posted this tweet: [https://x.com/stkirsch/status/1818772830026449411]
It looks like Henjin has better data for 2022: 941 deaths.
Seychelles 10 year avg (2011-2020) is 724
941/724=1.2997
which most people would say is a 30% increase above baseline which is what I heard from my friend who lives there.
However according to estimates from the UN's World Population Prospects dataset, the population size of Seychelles also increased by about 32% between 2011 and 2023. So a linear trend makes more sense than an average baseline:
> wpp=fread("https://population.un.org/wpp/Download/Files/1_Indicator%20(Standard)/CSV_FILES/WPP2024_PopulationByAge5GroupSex_Medium.csv.gz")
> wpp[Location=="Seychelles"&Variant=="Medium"&Time%in%2011:2023,.(pop=sum(PopTotal)*1000),.(year=Time)]|>print(r=F)
year pop
2011 97024
2012 99544
2013 102094
2014 104656
2015 107229
2016 109822
2017 112428
2018 115041
2019 117653
2020 120291
2021 122990
2022 125525
2023 127955
The excess deaths were concentrated in two spikes which coincided with spikes in COVID deaths, but there was low excess mortality in the first quarter of 2021 when most vaccine doses listed by OWID were administered (even though I think OWID is missing booster doses):
The Twitter user Camus posted a clip of a video where Pierre Kory said: "If you look at the life insurance data, we have never seen excess deaths amongst young working age Americans that have suddenly risen in one quarter. So in the quarter 3 of 2021, you saw 100% rise in the deaths of people 15 to 44. [...] So you have to ask yourself, what happened in the third quarter of 2021? And here's my answer, that is when mandates proliferated, university, healthcare, government, government contractors, schools." [https://x.com/newstart_2024/status/1823411484380291304]
Howevre if the fairly small number of people who got vaccinated late because of mandates had such high mortality, then why wasn't there also high mortality earlier in 2021 when a much larger number of people got vaccinated?
The plot above also shows that the spike in deaths in the third quarter of 2021 can mostly be acccounted by deaths where the underlying cause was listed as COVID. And the all-cause mortality only increased by about 20% in the third quarter compared to the second quarter. However in the second quarter mortality was already elevated relative to the 2019 average, even though it was partially because there has been a sustained increase in drug deaths since 2020.
Kirsch wrote: [https://kirschsubstack.com/p/covid-vaccinated-kids-are-dying-regularly]
VSRF's Nurse Angela knows of 15 kids, under 20, who died from cardiac arrest. They were all vaccinated with the COVID vaccine.
I did a CDC Wonder search for ICD-10 code I46 which is cardiac arrest.
It shows that those under age 23 don't die from cardiac arrest:
Today, it is the new normal if you've had the COVID shots.
The latest death
An article about the boy in the news story said: "He was born with his heart flipped over on the wrong side of his body, and missing arteries from his heart to his lungs. He had his first open heart surgery at 2 months old and spent the first year of his life at Valley Children's Hospital. He'd have five more heart surgeries in the years after that." [https://abc30.com/post/family-remembers-young-boy-died-after-collapsing-visalias-adventure-park/15237667/]
A cardiac arrest means that the heart stops beating. A heart attack occurs when the flow of blood to the heart is blocked, which can lead to a cardiac arrest, but a cardiac arrest can also occur for other reasons. The news story Kirsch linked said that the boy died of a heart attack, but it might also be possible that he died of a cardiac arrest that was not caused by a heart attack but the journalist who wrote the article was not aware of the distinction.
The boy's GoFundMe page said: [https://www.gofundme.com/f/help-lay-our-angel-richard-to-rest]
"At approximately 5:00pm Visalia PD officers and Visalia Fire personnel were called to Adventure Park on Cypress Avenue for a medical emergency involving a 12-year-old boy who had lost consciousness. The child was taken by ambulance to Kaweah Health" (visaliapd instagram)
...Richard's heart stopped while enjoying time at Adventure Park...he was having fun, running around...and being a normal kid. His first time of death was at 5:58pm. However his last time of death was 9:26pm.
So I don't know if the underlying cause of death would be determined based on the event at the waterpark, the "first death", the "second death", or none of them. So even in the case that he got a heart attack at the water park, the underlying cause of death wouldn't necessarily be listed as a heart attack.
The table by Kirsch only included deaths with the underlying cause I46 (cardiac arrest). But there's also ICD codes for I21 (acute myocardial infarction) and I50 (heart failure). Myocardial infarction is the technical term for a heart attack. A heart failure means that the heart is weakened but not necessarily stopped like in a cardiac arrest.
CDC WONDER suppresses the number of deaths on rows with less than 10 deaths for privacy reasons. If you select ages 0 to 19 but disable grouping the results by age to avoid the suppression, there's about 50 to 80 deaths per year with the underlying cause I46, but the number of deaths is approximately doubled when you also include the underlying causes I21 and I50: [https://wonder.cdc.gov/mcd-icd10-provisional.html]
For some reason there's about 30 times as many deaths with MCD I46 as deaths with UCD I46. At first I thought it might have been because of deaths caused by recreational drugs, but actually there were only about 20 to 30 deaths per year with MCD I46 and a UCD related to recreational drug use.
But anyway, there was an approximately 20% increase in deaths with UCD I46 if the average of 2018 to 2020 is compared against the average of 2021 to 2023. Some of it might be due to COVID or recreational drug use, because there has also been a big increase in opioid deaths since the start of the pandemic.
Kirsch wrote that "VSRF's Nurse Angela knows of 15 kids, under 20, who died from cardiac arrest." So if we assume that the 20% increase could be entirely attributed to vaccines, then in an alternate universe where no kids got a COVID shot, would Nurse Angela know 12.5 kids who died of a cardiac arrest over the same period of time when now there were 15 deaths? (Because 15 divided by 1.2 is 12.5.)
Kirsch didn't specify if Nurse Angela knew the kids personally or if she just heard about them on social media or something. But in the latter case she wouldn't necessarily have heard about them if she wasn't following the news about deaths that might potentially be attributed to vaccines. Or the number could've just been made up by either Kirsch or Nurse Angela.
Clare Craig quoted this plot posted by USMortality that was taken from a paper by Denis Rancourt, and she said that Sweden had incessant excess deaths above the baseline: [https://x.com/ClareCraigPath/status/1836037409940627724]
Rancourt's paper said: "In practice, our reference period is 2015 through 2019, except in the few countries for which the mortality data does not extend as far back as 2015 and may begin in 2017 and 2019, for example. We least-squares fit a straight line to the same week or month in each of the five (or less) reference years as the week or month of interest, where the slope of this fitted line is constrained to always (for every week or month of interest) be equal to the slope of a least-squares fitted line to all of the all-cause mortality data (all weeks or months) in the full 5-year (or less) reference period, for each given country." [https://correlation-canada.org/covid-excess-mortality-125-countries/]
I'm not sure if Rancourt's baseline was calculated based on raw deaths like at OWID or based on CMR. But in either case it's inaccurate for Sweden because of the aging boomer population and because Sweden had an unusually low number of deaths in 2019. In the plot below I calculated the blue baseline based on the trend in CMR in 2015 to 2019. But I think my green baseline is more accurate, and it's a lot higher than the blue line especially in 2023 and 2022. There's still a small number of excess deaths in 2023 even relative to my green baseline, but it's not nearly as much as in Rancourt's plot:
library(data.table);library(ggplot2)
cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]
t=fread("http://sars2.net/f/swedenpopdead.csv")
p=cmr=t[year>=2000,.(y=sum(dead)/sum(pop)*1e5,z="Actual mortality rate"),.(x=year)]
a=t[year>=2000,.(dead=sum(dead),pop=sum(pop)),.(age=cul(age,c(0:10*5,51:100)),year)]
a=merge(a,a[year%in%2010:2019,.(year=2000:2023,base=predict(lm(dead/pop~year),.(year=2000:2023))),age])
p=rbind(p,a[,.(y=sum(base*pop)/sum(pop)*1e5,z="2010-2019 trend in age-specific CMR"),.(x=year)])
p=rbind(p,cmr[x%in%2015:2019,.(x=cmr$x,y=predict(lm(y~x),cmr),z="2015-2019 linear trend")])
p[,z:=factor(z,unique(z))]
cand=c(sapply(c(1,2,5),\(x)x*10^c(-10:10)))
ystep=cand[which.min(abs(cand-(max(p$y)-min(p$y))/6))]
ystart=ystep*floor(min(p$y)/ystep)
yend=ystep*ceiling(max(p$y)/ystep)
ybreak=seq(ystart,yend,ystep)
xstart=min(p$x);xend=max(p$x)
color=c("black","#00aa00",hsv(22/36,1,.8))
ggplot(p,aes(x,y,color=z,linetype=z))+
geom_hline(yintercept=c(ystart,0,yend),linewidth=.3,lineend="square")+
geom_vline(xintercept=c(xstart-.5,xend+.5),linewidth=.3,lineend="square")+
geom_line(linewidth=.3)+
labs(title="Yearly deaths per 100,000 people in Sweden",subtitle="In order to calculate the green baseline, first a linear regression for CMR was done for each age group in 2010-2019, and then the yearly population sizes of each age group were multiplied by the value of the projected trend to get the expected deaths for each age group, and then the results for all ages were added together and divided by the population size of all ages. Five-year age groups were used for ages 0 to 49, single-year ages were used for ages 50 and above, and ages 100 and above were aggregated together. Source: statistikdatabasen.scb.se/pxweb/en/ssd/START__BE / sars2.net/f/swedenpopdead.csv."|>stringr::str_wrap(80),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart,xend,2))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
scale_linetype_manual(values=c(1,2,2))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
axis.ticks=element_line(linewidth=.3,color="black"),
axis.ticks.length=unit(.2,"lines"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.just="left",
legend.justification=c(1,1),
legend.key=element_blank(),
legend.key.height=unit(10,"pt"),
legend.key.width=unit(17,"pt"),
legend.position=c(1,1),
legend.spacing.x=unit(2,"pt"),
legend.box.background=element_rect(fill="white",color="black",linewidth=.3),
legend.margin=margin(-2,5,4,4,"pt"),
legend.text=element_text(size=7,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid.major=element_blank(),
plot.margin=margin(5,5,5,5,"pt"),
plot.subtitle=element_text(size=7,margin=margin(,,4)),
plot.title=element_text(size=8,face=2,margin=margin(1,,5)))
ggsave("1.png",width=4,height=3.5,dpi=400*4)
system("mogrify -resize 25% 1.png")
In September 2024 Aly Cook published a FOI response which included this table for the number of ED presentations for chest pain in ages 0 to 39: [https://x.com/KiwiAly/status/1836636092436746346]
The number of presentations was only 111 in 2018 but about 200 times higher in 2022, so it's clearly not a good proxy of the overall incidence of chest pain in New Zealand. The response said that the earliest approved data was from the year 2018, so it might for example be that hospitals switched to some new system in 2018 but there was a delay until different hospitals adopted the new system.
The same FOI response also included these tables for the number of publicly funded hospital discharges in ages 0 to 39 with a primary diagnosis of myocarditis or pericarditis, where there was no massive increase in the post-vaccine era:
The table of ED presentations was also featured in a PDF by some Ayurvedic guru called Guy Hatchard, but he misleadingly omitted the data for 2018 so you couldn't see as clearly that the early data appeared to be incomplete: [https://x.com/KiwiAly/status/1837645083107328235]
Philipp McMillan from Vejon Health did a video about the data for ED presentations of chest pain, where he showed a plot where the data for 2018 was not omitted, but he didn't mention anything about how the number of presentations was extremely low in 2018. [https://www.youtube.com/watch?v=o0Q8VvBt6Ko&t=4m59s] And he didn't say anything about how the increase in ED presentations did not necessarily reflect a true increase in the incidence of chest pain, which seems to have been the common pattern when the data was covered in alt media.
In the table from Aly Cook's FOI response for presentations of chest pain in ages 0 to 39, there was an approximately 11668% increase in presentations between 2018 and 2021, which is clearly too high to be caused by vaccines. But in this plot for cardiac presentations in Southern Australia in ages 15 to 44, there was an around 35% increase if 2021 is compared to 2018, which seems like it might be realistically caused by the vaccines: [https://x.com/WotsOnInfo/status/1778614447378141449]
However even the 35% increase was for presentations and not admissions, and maybe the increase would be lower if you would look at admissions rather than presentations. Someone from New Zealand wrote: "The health system was on alert for both covid and vax side effects, referring people to EDs for ECGs etc. Hell, I went to the doctor with reflux and as I had a sore chest was sent to ED for an ECG (which was fine). But it's still recorded chest pain. Admissions are what matters". [https://x.com/Thoughtfulnz/status/1838832801875136805] And another person from New Zealand replied: "Can share my personal story. I presented for chest pain a few weeks after vax. They told me to be in the lookout and get checked without hesitation. Turns out I had a pulled muscle. You warn millions of people about chest pain, a ton more are going to turn up. I am in those stats". [https://x.com/CloudyNetwork/status/1838834771776147797] And then the first person replied: "A workmate once cancelled a meeting for a very similar story - taking the warnings seriously they did what they were supposed to and went to the ER - and it was a muscle strain. They would not have gone to the ER with that a decade ago."
Uncle John Returns found the FOIA response that News Whisperer's plot was based on. It also included data for admissions which was omitted from News Whisperer's plot, but the admissions remained roughly flat during the period when there was the increase in presentations: [https://x.com/UncleJo46902375/status/1845842816380936609, https://assets.nationbuilder.com/alexantic/pages/281/attachments/original/1669167781/OCR_FOI2022-00081_%2d_Determination_Redacted.pdf]
Kirsch posted this tweet: [https://x.com/stkirsch/status/1848411122824843478]
However I think unvaccinated people gradually gain natural immunity over time, so vaccinated people end up losing the initial immunization advantage they had in 2021: [czech3.html#Age_standardized_hospitalization_rate_by_vaccination_status]
Jikkyleaks posted this plot: [https://x.com/Jikkyleaks/status/1852894752053887004]
It's weird that the x-axis in the plot starts in 2017 even though the baseline was fitted against data from 2015 to 2020. There was also a low number of cancer deaths in 2020 partially due to reduced screening, so including 2020 in the baseline fitting period artificially pulls the baseline downwards.
In the plot below I took data for yearly deaths by underlying cause of death from here: https://abs.gov.au/statistics/health/causes-death/causes-death-australia/latest-release#data-downloads. However I wasn't able to produce Jikky's plot because I got lower deaths in 2020 than 2019, and I got 52,348 deaths in 2023 even though in Jikky's plot it's about 51,100. My plot also demonstrates how a 2014-2019 baseline is much steeper than a 2015-2020 baseline, because there was a low number of deaths in 2014 which further makes the baseline more steep, so the 2014-2019 baseline actually gave me negative excess deaths in 2023:
p=data.table::data.table(year=2014:2023)
p$dead=c(44854,46640,46593,46690,48245,49722,48973,50694,51951,52348)
p$trend=p[year<2020,predict(lm(dead~year),p)]
p$trend2=p[year%in%2015:2020,predict(lm(dead~year),p)]
png("1.png",1600,1000,res=300)
par(mar=c(4.6,2.7,1.8,.7),mgp=c(0,.6,0),adj=0,lend="square")
tit="Deaths with UCD neoplasms (C00-D97) in Australia"
sub="Source: abs.gov.au/statistics/health/causes-death/causes-
death-australia/latest-release#data-downloads, file
\"Underlying causes of death (Australia)\", Table 1.1."
leg=c("Deaths with UCD neoplasms","2015-2019 linear trend","2015-2020 linear trend")
ybreak=pretty(c(p$dead,p$trend,p$trend2));ylim=range(ybreak)
xstart=min(p$year);xend=max(p$year)
xbreak=xstart:xend
plot(p$year,p$trend,type="n",main=tit,xlab=NA,ylab=NA,xaxs="i",yaxs="i",yaxt="n",xaxt="n",ylim=ylim,xlim=c(xstart-.5,xend+.5),cex.main=1)
axis(2,at=ybreak,las=1,labels=paste0(ybreak/1e3,"k"))
mtext(xbreak,side=1,line=.3,at=xbreak,las=1)
lines(p$year,p$dead,lwd=1.5)
points(p$year,p$dead,pch=20,cex=.6)
lines(p$year,p$trend,type="l",lty=2,lwd=1.5)
lines(p$year,p$trend2,type="l",lty=2,col="gray60",lwd=1.5)
legend("topleft",legend=leg,lty=c(1,2,2),col=c("black","black","gray60"),lwd=1.5)
mtext(text=sub,side=1,line=3.3,adj=0,cex=.95)
dev.off()
However then I realized Jikky's plot used data for "doctor-certified" deaths from here: https://www.abs.gov.au/statistics/health/causes-death/provisional-mortality-statistics/jan-dec-2023. For some reason the doctor-certified cancer deaths have had a sustained elevation above the baseline since 2021. Unlike the previous dataset the doctor-certified deaths were also higher in 2020 than 2019:
The dataset for doctor-certified cancer deaths has 49,609 deaths in 2021, and the baseline value in Jikky's plot is about 48,890 in 2021, so his plot has about 1.47% excess deaths in 2021. However I don't know if the baseline in his plot was just drawn by hand, because when I tried doing a linear regression of the deaths in the years 2015 to 2020, I got only about 1.06% excess deaths in 2021:
> p=data.table(year=2015:2023) > p$dead=c(44822,45452,46178,46825,47844,48294,49609,50371,51043) > p$trend=p[year%in%2015:2020,predict(lm(dead~year),p)] > p[year==2021,dead/trend] [1] 1.010625
Jikkyleaks wrote that "There is a 5-10% excess cancer mortality in Australia since 2021." [https://x.com/Jikkyleaks/status/1852462792621928896] I don't know if he calculated excess deaths relative to something like a 2015-2020 average baseline, because the 2015-2020 linear baseline in his plot wouldn't produce nearly such high excess deaths. However an average baseline is not appropriate because an increasing number of cancer deaths per year is expected due to the aging population structure. Cancer ASMR has remained roughly flat in Australia between 2020 and 2022, or it has even slightly decreased: [https://www.aihw.gov.au/reports/cancer/cancer-data-in-australia/contents/overview]
Someone on Twitter was wondering why the ASMR plot above showed there was a decrease in cancer deaths even though Jikky's plot showed there was an increase in deaths. However it's because Jikky's plot showed a raw number of deaths which does not account for changes to the age composition of the population. In the United States there is also a decreasing trend in cancer ASMR but an increasing trend in the raw number of cancer deaths:
library(data.table);library(ggplot2);library(lubridate)
t=fread("http://sars2.net/f/wondercanceryearly.csv")[year<2024&cause%like%"UCD.*Mal"]
t=merge(t,fread("http://sars2.net/f/uspopdead.csv")[year>=2010][,dead:=NULL])
t=merge(t[year==2020,.(age,std=pop/sum(pop))],t)
p=t[,.(y=sum(dead/pop*std*1e5)),year][,group:="ASMR per 100,000 people"]
p=rbind(p,t[,.(y=sum(dead),group="Raw deaths"),year])
p$z="Actual mortality"
p1=p[year%in%2010:2019,.(year=2010:2023,z="2010-2019 linear trend",y=predict(lm(y~year),.(year=2010:2023))),group]
p=rbind(p,p1)
t$base=t[year<2020,predict(lm(dead/pop~year),.(year=2010:2023)),age]$V1
p=rbind(p,t[,.(y=sum(base*pop),z="Expected based on age composition",group="Raw deaths"),year])
p[,z:=factor(z,unique(z))]
xstart=2010;xend=2023;xbreak=seq(xstart-.5,xend+.5,.5);xlab=c(rbind("",xstart:xend),"")
color=c("black","#0022cc","#009900")
ggplot(p,aes(x=year,y=y))+
facet_wrap(~group,ncol=1,dir="v",scales="free")+
geom_text(data=p[,max(y),group],aes(label=group,y=V1),x=(xstart+xend)/2,vjust=1.4,size=grid::convertUnit(unit(7,"pt"),"mm"),fontface=2)+
geom_vline(xintercept=2019.5,linetype=5,linewidth=.25)+
geom_line(aes(color=z),linewidth=.35)+
geom_point(aes(color=z,alpha=z),stroke=0,size=1)+
labs(title="CDC WONDER, underlying cause of death malignant neoplasms (C00-C97)"|>stringr::str_wrap(72),subtitle="The age-standardized mortality rate was calculated by single year of age so that the 2020 resident population estimates were used as the standard population. In the green baseline first a liner trend for CMR in 2010-2019 was calculated for each age, and then the value of the projected trend was multiplied by the population size to get the expected deaths for each age."|>stringr::str_wrap(91),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=xlab,expand=expansion(0))+
scale_y_continuous(labels=\(x)ifelse(x>1e3,paste0(x/1e3,"k"),x),expand=expansion(.04))+
scale_color_manual(values=color)+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=7,color="black"),
axis.text.x=element_text(margin=margin(3)),
axis.text.y=element_text(margin=margin(,1)),
axis.ticks.x=element_line(color=alpha("black",c(1,0))),
axis.ticks=element_line(linewidth=.25,color="black"),
axis.ticks.length=unit(3,"pt"),
axis.ticks.length.x=unit(0,"pt"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="right",
legend.key=element_rect(fill=alpha("white",0)),
legend.key.height=unit(10,"pt"),
legend.key.width=unit(17,"pt"),
legend.margin=margin(,,4),
legend.position="top",
legend.spacing.x=unit(1.5,"pt"),
legend.text=element_text(size=7,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.25),
panel.spacing=unit(3,"pt"),
plot.margin=margin(4,5,4,5),
plot.subtitle=element_text(size=6.8,margin=margin(,,3)),
plot.title=element_text(size=7.4,face=2,margin=margin(1,,4)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=4.4,height=4,dpi=400*4)
system("magick 1.png -resize 25% 1.png")
In Jikky's plot the number of doctor-certified cancer deaths was only about 1.5% above the baseline in 2021, even though it might have seemed like a fairly large increase if you didn't pay attention to the y-axis units, because the years 2015 to 2020 all fell fairly close to the baseline so the deviation from the baseline in 2021 was fairly large relative to the average deviation from the baseline during the fitting period. However in my next plot where I plotted monthly data and I started the y-axis from zero, the increase in deaths in 2021 seems much smaller in comparison, even though I got about 1.1% excess deaths in 2021 so it was similar to Jikky's plot that had about 1.5% excess deaths. However a prepandemic linear trend for raw deaths might also be too low because the actual trend in raw deaths is curved upwards due to the aging population, so in the bottom panel below where I plotted ASMR instead of raw deaths, I got only about 0.2% total excess mortality in 2021:
library(data.table);library(ggplot2);library(lubridate);library(ggtext)
cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]
t=fread("http://sars2.net/f/australiacancerdoctor.csv")
t[,date:=as.Date(paste0(year,"-",month,"-1"))]
t[,dayim:=days_in_month(date)]
p=t[,.(date,month,year,y=c(dead/dayim,asmr/dayim*365),group=rep(c("Monthly deaths divided by number of days in month","ASMR per 100,000 person-years"),each=.N))]
p[,group:=factor(group,unique(group))]
dates=unique(p$date)
p=merge(p,p[year<2020,.(date=dates,base=predict(lm(y~date),.(date=dates))),group])
p=merge(p[year<2020,.(monthly=mean(y-base)),.(month,group)],p)
pct=p[,.(pct=(sum(y)/sum(base)-1)*100),.(date=as.Date(paste0(year,"-7-1")),group)]
lab=c("Actual mortality","2015-2019 linear baseline","Baseline adjusted for seasonality","Difference from seasonality-adjusted baseline")
p=p[,.(x=date,group,y=c(y,base,base+monthly,y-base-monthly),z=factor(rep(lab,each=.N),unique(lab)))]
pct=merge(p[,.(y=min(y)),group],pct)
xstart=as.Date("2015-1-1");xend=as.Date("2024-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=c(rbind("",2015:2023),"")
ggplot(p,aes(x=x+14,y))+
facet_wrap(~group,ncol=1,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray85",linewidth=.25)+
geom_vline(xintercept=as.Date("2020-1-1"),linetype="44",linewidth=.3)+
geom_line(data=p[z!=lab[4]],aes(linetype=z,color=z),linewidth=.3)+
geom_line(data=p[z==z[1]],aes(linetype=z,color=z),linewidth=.3)+
geom_point(aes(alpha=z),stroke=0,size=.6)+
geom_rect(data=p[z==lab[4]],aes(xmin=x,xmax=x%m+%months(1),ymin=pmin(0,y),ymax=pmax(0,y),fill=z),linewidth=.1,color="gray40")+
geom_text(data=pct,aes(x=date,y=y,label=paste0(ifelse(pct>0,"+",""),sprintf("%.1f",pct),"%")),vjust=1,size=2.4)+
labs(title="Doctor-certified cancer deaths in Australia",subtitle="Source: abs.gov.au/statistics/health/causes-death/provisional-mortality-statistics/jan-dec-2023.\nThe data is by date of occurrence. The numbers show the yearly excess mortality percentage.",x=NULL,y=NULL)+
scale_x_continuous(expand=c(0,0),limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(expand=c(.08,0,.03,0),breaks=\(x)pretty(x,6))+
scale_color_manual(values=c("black","gray60","gray60","gray40"))+
scale_fill_manual(values=rep("gray60",4))+
scale_linetype_manual(values=c("solid","42","solid","solid"))+
scale_alpha_manual(values=c(1,0,0,0),guide="none")+
guides(fill=guide_legend(order=3,keyheight=unit(1,"pt")),color=guide_legend(order=1),linetype=guide_legend(order=1))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=7,color="black"),
axis.ticks.x=element_line(color=alpha("black",c(1,0))),
axis.ticks=element_line(linewidth=.3,color="black"),
axis.ticks.length=unit(3,"pt"),
axis.ticks.length.x=unit(0,"pt"),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.key=element_blank(),
legend.key.height=unit(2,"pt"),
legend.key.width=unit(17,"pt"),
legend.position="bottom",
legend.justification="right",
legend.spacing.x=unit(2,"pt"),
legend.box.margin=margin(),
legend.spacing.y=unit(0,"pt"),
legend.margin=margin(3),
legend.text=element_text(size=7,vjust=.5),
legend.title=element_blank(),
legend.direction="vertical",
legend.box="horizontal",
legend.box.spacing=unit(0,"pt"),
legend.spacing=unit(0,"pt"),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.3),
panel.spacing.y=unit(2,"pt"),
plot.margin=margin(5,5,5,5),
plot.subtitle=element_text(size=6.5,margin=margin(,,4)),
plot.title=element_text(size=7.4,face=2,margin=margin(1,,3)),
strip.background=element_blank(),
strip.text=element_text(size=7,face=2,margin=margin(,,2)))
ggsave("1.png",width=4.2,height=4.4,dpi=400*4)
system("magick 1.png -resize 25% 1.png")