Rootclaim vaccine debate between Steve Kirsch and Saar Wilf (part 5)

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
t[Umrti!=""&DatumUmrtiLPZ=="",DatumUmrtiLPZ:=Umrti]
t=t[DatumUmrtiLPZ!=""]
t=t[DatumUmrtiLPZ>=pmax(Datum_Prvni_davka,Datum_Druha_davka,Datum_Treti_davka)]

t[,dose:=0]
t[Datum_Prvni_davka!=""&Datum_Prvni_davka<="2021-24",dose:=1]
t[Datum_Druha_davka!=""&Datum_Druha_davka<="2021-24",dose:=2]

t2=t[Infekce%in%c(NA,1)]

a=t[,.(coviddead=.N),.(dose,week=Umrti)]
a=merge(t2[,.(dead=.N),.(dose,week=DatumUmrtiLPZ)],a,all=T)
a[is.na(a)]=0

weeks=data.table(date=as.Date("2019-1-1")+(0:3e3))[,week:=format(date,"%G-%V")][rowid(week)==4,setNames(date,week)]

p=a[week!="",.(x=weeks[week],y=c(dead,pmax(0,dead-coviddead)),z=rep(1:2,each=.N),dose)]
p[,z:=factor(z,,c("All causes","Not COVID"))]
p[,dose:=factor(dose,,c("Unvaccinated","Dose 1","Dose 2"))]

p[y==0,y:=NA]

xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ystart=0;yend=max(p$y,na.rm=T);ybreak=pretty(p$y,6)

ggplot(p)+
geom_hline(yintercept=c(ybreak[ybreak<yend],yend),color="gray87",linewidth=.4,lineend="square")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray87",linewidth=.4,lineend="square")+
geom_vline(xintercept=weeks["2021-24"],linewidth=.4,linetype="22")+
geom_line(aes(x,y,color=dose,alpha=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Weekly deaths in Czech Republic")+
annotate(geom="text",x=weeks["2021-27"],label="Week 24 of 2021 (vaccine doses\nadministered on later weeks are ignored)",y=yend*.9,hjust=0,vjust=1,size=3.87,lineheight=.85)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x==0,0,paste0(x/1e3,"k")))+
scale_color_manual(values=c("#EB3727","#DA7842","#67A442","#499CCF"))+
scale_alpha_manual(values=c(1,.4))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),alpha=guide_legend(order=2))+
theme(axis.text=element_text(size=11,color="gray50"),
  axis.text.x=element_text(margin=margin(3)),
  axis.text.y=element_text(margin=margin(,3)),
  axis.ticks.length=unit(0,"pt"),
  legend.box="vertical",
  legend.box.background=element_blank(),
  legend.box.just="center",
  legend.box.margin=margin(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="center",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(23,"pt"),
  legend.background=element_rect(color="gray87",linewidth=.4),
  legend.margin=margin(2,5,2,2),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  panel.spacing=unit(4,"pt"),
  plot.margin=margin(5,4,5,5),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(1,,3)),
  plot.subtitle=element_text(hjust=.5,margin=margin(,,3)))
ggsave("1.png",width=4.9,height=3.3,dpi=300*4)

In order to get fixed cohorts of people by dose number, Kirsch determined the vaccination status at the end of week 24 of 2021. Therefore he didn't have to adjust the deaths for population size since the population sizes remained roughly constant from week 25 of 2021 onwards, apart from depletion due to deaths and change due to migration.

However the period when people with only one dose had the lowest mortality due to HVE was before week 25 of 2021. In Kirsch's plot the number of deaths in people with only one dose remained around the same level between weeks 11 and 24 of 2021. But if you look at ages 60 and above which accounted for about 90% of total deaths in the Czech Republic in 2021, the population size of people with only one dose tripled from about 400,000 on week 11 to about 1,200,000 on week 20, and by week 25 it had falled back down to about 400,000 after people had moved under the second dose. By week 25 of 2021, ages 60 and above had about 4 times as many people with two or more doses as people with only one dose:

The ASMR of people with 1 but not more doses was about 598 per 100,000 person-years on week 18, but by week 25 the ASMR had more than doubled to about 1266, because many of the healthy vaccinees had moved under the second dose:

In the next plot the ASMR of people with 1 but not more doses almost doubled between week 18 and week 24 of 2021. The results are slightly different from the previous code, because I used the November 2024 NZIP data instead of the March 2024 FOI data, and I also calculated the ASMR by year of birth and not by age:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")

t=t[Infekce%in%c(NA,1)][RokNarozeni!="-"]
t[,born:=pmin(2000,pmax(1925,as.integer(substr(RokNarozeni,1,4))))]

t[,dose1:=Datum_Prvni_davka][,dose2:=Datum_Druha_davka]
t=t[!(DatumUmrtiLPZ!=""&pmax(dose1,dose2)>DatumUmrtiLPZ)]

t=rbind(copy(t)[dose1>"2021-24",dose1:=""][dose2>"2021-24",dose2:=""][,facet:=1],t[,facet:=2])
t[,dose:=0][dose1!="",dose:=1][dose2!="",dose:=2]

a=t[,.(week=c(rep("2020-10",.N),dose1,dose2),dose=rep(0:2,each=.N),born,facet)]
a=a[,.(vax=.N),.(week,dose,born,facet)]
a=merge(a,t[,.(dead=.N),.(week=DatumUmrtiLPZ,born,dose,facet)],all=T)[week!=""]
a=merge(do.call(CJ,lapply(a[,1:4],unique)),a,all=T);a[is.na(a)]=0

a[,cumvax:=cumsum(vax),.(born,dose,facet)][,pop:=cumvax-cumsum(dead),.(born,dose,facet)]
a[dose==0,pop:=pop-a[dose==1,cumvax]][dose==1,pop:=pop-a[dose==2,cumvax]]

a=merge(a[week=="2022-01",sum(pop),born][,.(std=V1/sum(V1),born)],a)

iso=`class<-`(0:1e4*7,"Date");names(iso)=format(iso,"%G-%V")
p=a[,.(y=ifelse(sum(pop)*7<365e3,NA_real_,sum(dead/pop/7*365e5*std,na.rm=T))),.(dose,x=iso[week],facet)]
p[,dose:=factor(dose,,c("Unvaccinated","Dose 1","Dose 2 or more"))]
p[,facet:=factor(facet,,paste("Doses admin-\nistered after cutoff\ndate",c("ignored","not ignored")))]

xstart=as.Date("2021-1-1");xend=as.Date("2024-1-1");xbreak=seq(xstart+182,xend,"year")
ystart=0;ybreak=pretty(p$y,6);yend=max(ybreak)

ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free")+
geom_hline(yintercept=c(ybreak[ybreak<yend],yend),color="gray90",linewidth=.4,lineend="square")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4,lineend="square")+
annotate("rect",xmin=xstart,xmax=xend,ymin=0,ymax=yend,color="gray75",linewidth=.4,lineend="square",linejoin="mitre",fill=NA)+
geom_line(aes(x,y,color=dose),linewidth=.6)+
geom_vline(xintercept=iso["2021-24"],linewidth=.4,linetype="22")+
geom_label(data=p[rowid(facet)==1],aes(label=facet),y=yend,x=xend,hjust=1,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87,lineheight=.8)+
geom_label(data=p[rowid(facet)==1],aes(label=facet),y=yend,x=xend,hjust=1,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87,lineheight=.8)+
labs(x=NULL,y=NULL,title="Weekly ASMR per 100,000 person-years in Czech Republic")+
annotate(geom="text",x=iso["2021-25"],label="Vaccination cutoff date (week 24)",y=4250,hjust=0,vjust=.5,size=3.87)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#EB3727","#DA7842","#67A442"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.background=element_rect(color="gray75",linewidth=.4),
  legend.margin=margin(2,5,2,2),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(4,5,4,5),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(1,,3)),
  plot.subtitle=element_text(hjust=.5,margin=margin(,,3)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5,height=4.7,dpi=300*4)

Comment by AI about ratio of all-cause mortality between unvaccinated and vaccinated people

Kirsch's AI seems to have copied his mistaken understanding of what a time series means. Kirsch says that a plot where the x-axis shows time since vaccination and the y-axis shows deaths is a "time series" plot, even though in reality a plot where the x-axis shows calendar time is also a time series plot. In his Substack Kirsch wrote: "But did you know that none of the papers in the peer reviewed scientific literature will show you a time series plot for the COVID vaccine? I couldn't find a single one!" [https://kirschsubstack.com/p/covid-time-series-graphs-show-clearly] So I guess under his definition of a time series plot, he didn't even count survival analysis plots where the x-axis shows days since since-vaccination and the y-axis shows probability of survival, because during the debate he has referred to several survival analysis plots that were published in peer-reviewed papers.

But anyway, the HVE does in fact appear in plots that show mortality by calendar date. In the English ONS data, Dutch CBS data, and Japanese FOI data released by Kenji Fujikawa, there ratio between unvaccinated and vaccinated ASMR reaches above 4 during the vaccine rollout: [rootclaim4.html#Comparison_to_other_datasets]

There are also many studies which have shown more than a 3-fold difference in all-cause mortality between unvaccinated and vacinated people. In the same PDF file Kirsch wrote about a Norwegian study which looked at all-cause mortality in people aged 70 and above during the first three weeks after vaccination. Even though the cohorts were matched for variables like 5-year age group and comorbidity index, the vaccinated group had a mortality HR of only about 0.28 relative to the unvaccinated group, with a 95% CI of about 0.24-0.31. [https://pmc.ncbi.nlm.nih.gov/articles/PMC9637531/]

But my previous plot shows that the monthly ratio between unvaccinated and vaccinated ASMR peaks at over 5 in the ONS data, and at over 3 in the Czech data.

And anyway if it's impossible for unvaccinated people to have 3 times higher mortality than vaccinated people because of the HVE, then why did Kirsch assume in his KCOR analysis that unvaccinated people would've continued to have about 3.2 times higher mortality rate than vaccinated people indefinitely? And then later when the ratio dropped to only about 2.6, why did Kirsch assume it meant that vaccines were killing 23% extra people?

Comparison to Norwegian study of adverse event reports involving death in nursing homes

Kirsch wrote: "The Levi result, which showed vaccine harm, shouldn't be very surprising as it matches what an expert group appointed by the Norwegian Medicines Agency found when it looked at the cause of death of 100 people who died after vaccination and found that 36% of the deaths may have been vaccine mediated ('likely' to 'possible'). After they found that result, they decided that further confirmation was unwise. Nor did they warn the people of Norway; they suppressed the result. They did not publish their findings in the peer-reviewed literature. They did not publicly report the findings through standard scientific channels. Sadly, this is how 'science' works today: if you find something that goes against the narrative, you bury it."

The paper Kirsch talked about was published in Norway's primary peer-reviewed medical journal. [https://tidsskriftet.no/en/2021/05/originalartikkel/nursing-home-deaths-after-covid-19-vaccination] The Wikipedia page about the journal says: "The Journal of the Norwegian Medical Association (Norwegian: Tidsskrift for Den norske legeforening) is a biweekly peer-reviewed medical journal published by the Norwegian Medical Association and established in 1881. It includes research and review articles, news stories, and debates about professional issues and education, as well as discussion of medical education. The journal has been indexed by Index Medicus, MEDLINE, and PubMed since 1965." [https://en.wikipedia.org/wiki/Journal_of_the_Norwegian_Medical_Association] Perhaps Kirsch was confused by the design of the journal's website, which looks more like an informal magazine site than a medical journal, or he was confused by how the website publishes both formal scholarly articles and more informal content.

The Norwegian paper said: "In the period 27 December 2020 to 15 February 2021, about 29 400 of Norway's roughly 35 000 nursing home patients were vaccinated with the mRNA vaccine BNT162b2. During the same period, the Norwegian Medicines Agency received 100 reports of suspected fatal adverse reactions to the vaccine." The paper also said: "The mean age of the patients was 87.7 years (range 61-103 years). Among 100 reported deaths, a causal link to the vaccine was considered probable in 10 cases, possible in 26 and unlikely in 59."

So among approximately the 29,400 first vaccinated people in nursing homes, a causal connection between vaccination and death was considered probable or possible in the case of 36 people, which is a rate of about 0.1% and not 36%. In the case of some reports, the vaccination may have only been a minor contribution to the death of someone who was about to die soon anyway. If it was possible to determine definitively how many of the 100 people died primarily due to vaccination, it would probably be less than 36 people, even though there might of course be additional vaccine-induced deaths with no adverse event report filed.

But anyway, the results of a study are not applicable to the general population, because the proportion of adverse event reports that involve death out of all adverse event reports is higher in older people than younger people. And elderly people who live in nursing homes have even higher mortality rates than age-matched elderly people who live on their own.

Adjusted odds ratios of matched and unmatched cohorts in Levi et al.

Kirsch wrote: "The effect was observed in the full cohort of over 9 million individuals, and after 1:1 matching on 7 key factors to create a 1.5 million person matched cohort, the NCACM odds ratio differed by less than 1%. This strongly suggests that the Pfizer-Moderna mortality gap was not due to confounding from unmatched variables, since such aggressive matching would have materially shifted the result if residual confounding were the primary cause."

By a difference of less than 1%, he probably referred to how the adjusted odds ratio for non-COVID mortality was about 1.356 in the matched cohorts and 1.361 in the unmatched cohorts: [https://www.medrxiv.org/content/10.1101/2025.04.25.25326460v1]

However the odds ratios were adjusted for a similar set of variables that was used to do the matching. The cohorts were matched by age, sex, race, ethnicity, vaccination site, month of second dose, and census tract. The adjusted odds ratios were adjusted for all the same variables except month of second dose, and the adjustment for census tract was done in a different way, and they were additionally adjusted for mortality at the ZIP code level.

So even though both methods produced an odds ratio of about 1.36, in both cases it might be due to confounders that were not adjusted for using either method.

Lack of systematic bias in distribution of vaccines in Florida

Kirsch wrote: "Furthermore, there was no systematic nor systemic bias in the distribution of vaccines in Florida."

Howveer if you look at the full unmatched cohorts in Table 1 of Levi's study, the median age was 54 for Pfizer but 62 for Moderna. The median social vulnerability index score was about 47 for Pfizer but 41 for Moderna.

The unadjusted all-cause mortality odds ratio was about 0.853 between the unmatched cohorts but 1.374 between the matched cohorts.

Kirsch also wrote that there is no "evidence anywhere of a systematic bias that could cause a vaccine preference within a facility". Among Levi's full cohorts, the percentage of vaccine doses where the site type was doctor's clinic was about 21% for Pfizer and 11% for Moderna. But the percentage for hospital ER was about 0.7% for Pfizer and 1.9% for Moderna, and "other pharmacies" was about 2% for Pfizer and 11% for Moderna:

The Czech Ministry of Health has also published a CSV file which shows the number of vaccine doses administered by vaccinator name. When I calculated an age-normalized proportion of doses administered by senior homes, it was much higher for Moderna than Pfizer. [czech3.html#Vaccinator_types]

Kirsch wrote: "The time series plots for Pfizer and Moderna using the Czech data show that both vaccines increase mortality shortly after the shots were given." By the "time series plots", he meant his plots where the x-axis showed times since vaccination and the y-axis showed deaths. However just because there is a low number of deaths in the first few weeks after vaccination, it doesn't mean that

However glass half full perspective, you might just as well say that both vaccines reduce mortality more in the days after vaccination than later on.

13.47% reduction in all-cause mortality during a COVID period

But anyway the HVE was stronger in his baseline period than his COVID period. His COVID period was fairly long because it lasted for 26 weeks, and there wasn't even very high COVID mortality for the first 5 weeks of his COVID period:

library(data.table);library(ggplot2)

ages=c(0,3:19*5)
cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]

nzip=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
nzip=nzip[!(Umrti!=""&Datum_Prvni_davka>Umrti)]
covid=nzip[Umrti!=""&RokNarozeni!="-",.N,.(Umrti,RokNarozeni,vax=Datum_Prvni_davka!=""&Datum_Prvni_davka<=Umrti)]
covid=covid[,.(coviddead=sum(N)),.(dose=ifelse(vax,2,3),age=cul(2020-as.integer(substr(RokNarozeni,1,4)),ages),week=Umrti)]

t=fread("https://sars2.net/f/czbucketsdaily.csv.gz")
a=t[,.(dead=sum(dead),pop=sum(alive)),.(dose=ifelse(dose==0,3,2),week=format(date,"%G-%V"),age=cul(age,ages))]
a=merge(a,covid,all=T)[week%like%"202[012]"]
a[is.na(a)]=0
a=rbind(a,a[,.(dose=1,dead=sum(dead),pop=sum(pop),coviddead=sum(coviddead)),.(age,week)])

a=merge(fread("https://sars2.net/f/czcensus2021pop.csv")[,std:=pop/sum(pop)][,.(std=sum(std)),.(age=cul(age,ages))],a)

p=a[,.(dead=sum(dead/pop*std*365e5),coviddead=sum(coviddead/pop*std*365e5)),.(week,dose)]

iso=data.table(date=as.Date("2019-1-1")+(0:2e3))[,week:=format(date,"%G-%V")][rowid(week)==4,setNames(date,week)]

p=p[,.(x=iso[week],dose,y=c(dead,dead-coviddead),type=rep(1:2,each=.N),facet=1)]
p[,type:=factor(type,,c("All causes","Not COVID"))]

p[,dose:=factor(dose,,c("All people","Vaccinated","Unvaccinated"))]

p=rbind(p,dcast(p,x+type~dose,value.var="y")[,.(x,type,y=Unvaccinated/Vaccinated,dose="All people",facet=2)])
p[,facet:=factor(facet,,c("Age-standardized mortality rate per 100,000 person-years","Ratio between unvaccinated and vaccinated ASMR"))]

p=p[x>="2021-1-7"]

xstart=as.Date("2021-1-1");xend=as.Date("2023-1-1");xbreak=seq(xstart+182,xend,"year")
p=p[x%in%xstart:xend]
ybreak=pretty(c(0,p$y),7)

hl=data.table(start=iso[c("2021-36","2021-40")]-3.5,end=iso[c("2021-40","2022-13")]+3.5)
hl[,label:=factor(c(1,2),,c("Baseline period","COVID period"))]

ggplot(p)+
facet_wrap(~facet,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"month"),color="gray92",linewidth=.4)+
geom_rect(data=hl,aes(xmin=start,xmax=end,fill=label),ymin=0,ymax=Inf,alpha=.3,linewidth=.15)+
geom_vline(xintercept=as.Date("2022-1-1"),color="gray70",linewidth=.4)+
geom_line(aes(x,y,color=dose,linetype=type),linewidth=.6)+
labs(x=NULL,y=NULL,title="Weekly ASMR in Czech Republic")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=\(x)range(pretty(x,4)),breaks=\(x)pretty(x,4),labels=\(x)ifelse(x<1e3,x,paste0(x/1e3,"k")))+
scale_color_manual(values=c("black","#ff6666","#6666ff"))+
scale_linetype_manual(values=c("solid","11"))+
scale_fill_manual(values=c("#77cc77","#ffaaaa"))+
coord_cartesian(clip="off",expand=F)+
guides(fill=guide_legend(order=3),color=guide_legend(order=1),linetype=guide_legend(order=2))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.box="vertical",
  legend.box.background=element_blank(),
  legend.box.just="center",
  legend.box.margin=margin(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="center",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(25,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.margin=margin(2,5,2,2),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(color="gray70",fill=NA,linewidth=.4),
  panel.grid.major=element_blank(),
  panel.grid.major.y=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(0,"pt"),
  plot.margin=margin(5,4,5,5),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(1,,3)),
  plot.subtitle=element_text(hjust=.5,margin=margin(,,3)),
  strip.background=element_blank(),
  strip.text=element_text(size=11))
ggsave("1.png",width=4.8,height=4.2,dpi=300*4)

Kirsch calculated the ratio between unvaccinated and vaccinated people using the raw number of deaths, so that he treated people who were vaccinated after the end of week 41 of 2021 as unvaccinated. In his spreadsheet the ratio of deaths per week in the COVID period relative to the baseline period was about 1.362 in unvaccinated people and about 1.227 in vaccinated people, so by subtracting the two numbers Kirsch got a figure of about 0.135 for his mortality benefit in vaccinated people.

In the following code I did a similar calculation using ASMR so I didn't have to rely on Kirsch's hack of defining people vaccinated after a given date as unvaccinated. Now the ratio of ASMR in the COVID period divided by ASMR in the baseline period was about 1.478 in unvaccinated people had about 1.236 in vaccinated people, so by subtracting the two numbers I get a figure of about 0.242, which is almost twice as high as Kirsch's figure:

However it would've been more appropriate to calculate the mortality benefit as 1-vax/unvax, and not as unvax-vax like Kirsch. So if the ratio of mortality in the COVID period relative to the baseline period would've been 5 in unvaccinated people and 3 in vaccinated people, then vaccinated people would've had a 40% mortality benefit, and not a 200% mortality benefit.

Mortality in ages 80 and above in Japanese FOI data

However if you look at each semiannual group in Fujikawa's plot, the rightmost bar for the newest vaccine dose is always lower than the leftmost bar for unvaccinated people. Many of the doses in between have such a small population size that they don't have much impact on total vaccinated mortality.

After a large number of people has moved under the nth dose, the mortality rate of dose n-1 shoots up because of the straggler effect. But in the bottom panel here if you compare the gray line here against the black line, you can see that the mortality rate of all vaccinated people combined always remains lower than the mortality rate of unvaccinated people: [statistic2.html#Deaths_by_days_since_vaccination_in_Japan]

In the next plot shows the data but presented in a different way, where I'm plotting excess deaths each month relative to the mortality rate among all people included in the dataset the same month. The row for dose 1+ shows that vaccinated people have negative excess mortality each month, apart from April 2021 when only a very small number of people had been vaccinated. As the healthy vaccinee effect wears off, the excess mortality of vaccinated people gradually drops from about -55% in June 2021 to about -9% in November 2021:

kimi=\(x){na=is.na(x);x[na]=0;e=floor(log10(ifelse(x==0,1,abs(x))));e2=pmax(e,0)%/%3+1;x[]=ifelse(abs(x)<1e3,round(x),paste0(sprintf(paste0("%.",ifelse(e%%3==0,1,0),"f"),x/1e3^(e2-1)),c("","k","M","B","T")[e2]));x[na]="NA";x}

t=fread("https://sars2.net/f/japanfoihudikaha.csv")
t=t[location==location[1]&age=="80over",-(1:2)]

t[,dose:=factor(paste("Dose",dose))]
t=rbind(t,t[dose!="Dose 0",.(dead=sum(dead),pop=sum(pop),dose="Dose 1+"),month])
t=merge(t,t[dose!="Dose 1+",.(base=sum(dead)/sum(pop)),month])[,base:=base*pop]
t=rbind(t,t[,.(dead=sum(dead),pop=sum(pop),base=sum(base),month="Total"),dose])

m=t[,tapply((dead-base)/ifelse(dead>base,base,dead),.(dose,month),c)]
disp=t[,tapply((dead/base-1)*100,.(dose,month),round)]
m2=t[,xtabs(pop/365~dose+month)]

max1=5;max2=max(m2[,-ncol(m2)]);exp1=.6;exp2=.85;exp2=.7
m[m==-Inf]=-max1

pal1=hsv(rep(c(21/36,0),4:5),c(1,.8,.6,.3,0,.3,.6,.8,1),c(.3,.65,1,1,1,1,1,.65,.3))
pal2=sapply(seq(1,0,,256),\(i)rgb(i,i,i))

pheatmap::pheatmap(sign(m)*abs(m)^exp1,filename=paste0("i1.png"),display_numbers=disp,
  gaps_col=ncol(m)-1,
  cluster_rows=F,cluster_cols=F,legend=F,cellwidth=18,cellheight=18,fontsize=9,fontsize_number=8,
  border_color=NA,na_col="gray90",number_color=ifelse(abs(m)^exp1>max1^exp1*.53,"white","black"),
  breaks=seq(-max1^exp1,max1^exp1,,256),colorRampPalette(pal1)(256))

pheatmap::pheatmap(m2^exp2,filename=paste0("i2.png"),display_numbers=ifelse(m2<10,round(m2),kimi(m2)),
  gaps_col=ncol(m)-1,
  cluster_rows=F,cluster_cols=F,legend=F,cellwidth=18,cellheight=18,fontsize=9,fontsize_number=8,
  border_color=NA,na_col="gray90",number_color=ifelse(m2^exp2>max2^exp2*.42,"white","black"),
  breaks=seq(0,max2^exp2,,256),pal2)

In the previous plot if you look at the black line which shows the mortality rate of both vaccinated and unvaccinated people added together, there's a large increase in the mortality rate between 2021 and 2024. It's because the age of each person was determined at the time the data was extracted, so some of the people who were 80 years old at the data was extracted may have been only 75 or 76 years old in early 2021. [https://x.com/donkey1399/status/1923593814704521298, https://x.com/hudikaha/status/1924666052409229765]

This plot of the Japanese FOI data also shows that it takes about 120 days after vaccination for the deaths to reach a peak, which conflicts with Kirsch's claim that the curve for HVE flattens out after 3 weeks: [https://stop-mrna.sakura.ne.jp/db/lot_totalization.php]

In the plot above the reason why the deaths start to fall after day 120 is because people start getting new booster doses so they cycle back to day 0, and also because people who got a booster dose in 2024 start to run out of follow-up time. If people were kept under all previous vaccine doses after a new dose and if people wouldn't run out of follow-up time, the deaths would continue to increase even past day 120.

KCOR ratio of dose 2 compared to dose 1

Kirsch included only vaccine doses administered up to week 24 of 2021, so that he determined the vaccination status at the end of week 24, or equivalently at the start of week 25. The baseline period consisted of weeks 27 to 34 of 2021. The observation period started on week 27 of 2021 and ended on week 52 of 2022. The ratio of vaccinated to unvaccinated deaths during the whole period relative to the baseline period was about 1.10 for dose 1 and 1.21 for dose 2. I reproduced his analysis exactly here, so that I even reproduced Kirsch's error of double counting deaths in people with two COVID cases, and I didn't exclude anomalous rows like rows where a date of vaccination was after a date of death:

My plot should've been a clue to Kirsch why he got lower mortality relative to the baseline period for dose 1 than dose 2. His baseline period lasted from July 5th 2021 until August 29th 2021. My plot above shows that people with 1 but not more doses had high ASMR in July and August 2021, because by then many of the healthy vaccinees had moved under the second dose. So during the baseline period the HVE caused dose 1 to have elevated mortality and dose 2 to have reduced mortality, but over time after the HVE became weaker, the ratio of mortality between dose 1 and dose 2 got lower.

In Kirsch's analysis the effect was not quite as dramatic as in my plot above, because he ignored vaccine doses administered on week 25 of 2021 or later, so he classified a large part of people with two doses under the first dose. It considerably reduced the mortality rate of people with 1 dose, as is shown by the top panel of the next plot. But in the bottom panel where I didn't ignore vaccine doses administered after week 24, the mortality rate of people with only 1 dose has a large increase after week 24:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")

t=t[Infekce%in%c(NA,1)][RokNarozeni!="-"]
t[,born:=pmin(2000,pmax(1925,as.integer(substr(RokNarozeni,1,4))))]

t[,dose1:=Datum_Prvni_davka][,dose2:=Datum_Druha_davka]
t=t[!(DatumUmrtiLPZ!=""&pmax(dose1,dose2)>DatumUmrtiLPZ)]

t=rbind(copy(t)[dose1>"2021-24",dose1:=""][dose2>"2021-24",dose2:=""][,facet:=1],t[,facet:=2])
t[,dose:=0][dose1!="",dose:=1][dose2!="",dose:=2]

a=t[,.(week=c(rep("2020-10",.N),dose1,dose2),dose=rep(0:2,each=.N),born,facet)]
a=a[,.(vax=.N),.(week,dose,born,facet)]
a=merge(a,t[,.(dead=.N),.(week=DatumUmrtiLPZ,born,dose,facet)],all=T)[week!=""]
a=merge(do.call(CJ,lapply(a[,1:4],unique)),a,all=T);a[is.na(a)]=0

a[,cumvax:=cumsum(vax),.(born,dose,facet)][,pop:=cumvax-cumsum(dead),.(born,dose,facet)]
a[dose==0,pop:=pop-a[dose==1,cumvax]][dose==1,pop:=pop-a[dose==2,cumvax]]

a=merge(a[week=="2022-01",sum(pop),born][,.(std=V1/sum(V1),born)],a)

iso=`class<-`(0:1e4*7,"Date");names(iso)=format(iso,"%G-%V")
p=a[,.(y=ifelse(sum(pop)*7<365e3,NA_real_,sum(dead/pop/7*365e5*std,na.rm=T))),.(dose,x=iso[week],facet)]
p[,dose:=factor(dose,,c("Unvaccinated","Dose 1","Dose 2 or more"))]
p[,facet:=factor(facet,,paste("Doses admin-\nistered after\ncutoff",c("ignored","not ignored")))]

xstart=as.Date("2021-1-1");xend=as.Date("2024-1-1");xbreak=seq(xstart+182,xend,"year")
ystart=0;ybreak=pretty(p$y,6);yend=max(ybreak)

ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free")+
geom_hline(yintercept=c(ybreak[ybreak<yend],yend),color="gray90",linewidth=.4,lineend="square")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4,lineend="square")+
annotate("rect",xmin=iso["2021-27"]-3.5,xmax=iso["2021-34"]+3.5,ymin=0,ymax=Inf,fill="green",alpha=.25)+
annotate("rect",xmin=xstart,xmax=xend,ymin=0,ymax=yend,color="gray75",linewidth=.4,lineend="square",linejoin="mitre",fill=NA)+
geom_line(aes(x,y,color=dose),linewidth=.6)+
geom_vline(xintercept=iso["2021-24"],linewidth=.4,linetype="22")+
geom_label(data=p[rowid(facet)==1],aes(label=facet),y=yend,x=xend,hjust=1,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87,lineheight=.8)+
geom_label(data=p[rowid(facet)==1],aes(label=facet),y=yend,x=xend,hjust=1,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87,lineheight=.8)+
labs(x=NULL,y=NULL,title="Weekly ASMR per 100,000 person-years in Czech Republic")+
annotate(geom="text",x=iso["2021-30"],label="Baseline (weeks 27 to 34)",color="#00aa00",y=yend*.86,hjust=0,vjust=1,size=3.87,lineheight=.8)+
annotate(geom="text",x=iso["2021-25"],label="Vaccination cutoff date (week 24)",y=yend*.96,hjust=0,vjust=1,size=3.87,lineheight=.8)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#EB3727","#DA7842","#67A442"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.background=element_rect(color="gray90",linewidth=.4),
  legend.margin=margin(2,5,2,2),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(4,5,4,5),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(1,,3)),
  plot.subtitle=element_text(hjust=.5,margin=margin(,,3)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5,height=4.7,dpi=300*4)

In the top panel of the plot above, if you imagine dividing the line for the first dose with the line for the second dose, the ratio between the lines is higher in the baseline period than the average ratio later on. So that's also why Kirsch got a higher KCOR ratio for the second dose than the first dose.

Cumulative CFR in Czech Republic

Kirsch posted the plot below and wrote: "Below, cumulative CFR all ages. It ONLY drops on Delta and then on Omicron variants. Not before. If the shots reduced the CFR, we'd see a drop. If the shots reduced cases of the vaccinated, we'd only be seeing deaths of the younger unvaccinated and that would drop this population CFR as well. No drop."

However if you look at non-cumulative CFR, there is in fact a clear reduction in CFR in 2021 when people got vaccinated:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")[!is.na(Infekce)]

a=t[,.(case=.N,dead=sum(Umrti!="")),,.(week=DatumPozitivity)]

p=a[,.(x=week,y=c(dead/case,cumsum(dead)/cumsum(case))*100,z=rep(1:2,each=.N))]
p[,z:=factor(z,,c("Not cumulative","Cumulative"))]

weeks=data.table(date=as.Date("2019-1-1")+0:3e3)[,week:=format(date,"%G-%V")][rowid(week)==4,setNames(date,week)]
p[,x:=weeks[x]]

xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=pretty(p$y);ystart=0;yend=max(ybreak)

ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray70",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_point(aes(x,y,color=z),size=1.1)+
labs(x=NULL,y=NULL,title="Weekly ercentage of cases that led to a death in Czech Republic",subtitle="Source: nzip.cz/data/2135-covid-19-prehled-populace")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("black","#ff8888"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(.5,1),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(.5,1),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major.x=element_blank(),
  panel.grid.major.y=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(hjust=.5,margin=margin(,,4)),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(2,,4)))
ggsave("1.png",width=5,height=3,dpi=300*4)

Why were deaths in the United States higher than the low point in 2018?

But anyway there's an increasing trend in the number of deaths per year because of the aging population, so it doesn't make sense to use the number of deaths in 2018 as the baseline. When I calculated the baseline by doing a Poisson regression in 2010-2019, I got negative excess deaths in 2023:

t=fread("https://sars2.net/f/uspopdead.csv")[,.(dead=sum(dead),pop=sum(pop)),.(year,age)]
t=t[year%in%2010:2024]

t$poi=predict(glm(dead~factor(age),poisson,t[year<2020],offset=log(pop)),t,type="response")

t=merge(t,t[year<2020,.(year=2010:2024,base=predict(lm(dead/pop~year),.(year=2010:2024))),age])
a=t[,.(dead=sum(dead),base=sum(base*pop),poi=sum(poi)),year]
a$base2=a[year%in%2010:2019,predict(lm(dead~year),a)]
a$ave=a[year==2018,mean(dead)]

p=a[,.(x=year,y=unlist(.SD[,-1]),z=rep(1:(ncol(.SD)-1),each=.N))]
p[,z:=factor(z,,c("Actual deaths","2010-2019 linear CMR by age","2010-2019 Poisson regression","2010-2019 linear regression","Deaths in 2018"))]

xstart=2010;xend=2024;ybreak=pretty(p$y);ystart=ybreak[1];yend=max(ybreak)

ggplot(p)+
annotate("rect",xmin=xstart-.5,xmax=xend+.5,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray50")+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_line(data=p[z==z[1]],aes(x,y,color=z),linewidth=.6)+
geom_point(aes(x,y,color=z,alpha=z),stroke=0,size=1.5)+
labs(title="Yearly deaths in the United States",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart,xend,2))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=kim)+
scale_color_manual(values=c("black","#00aa00","#ff44ff","blue",hsv(3/36,.9,.6)))+
scale_alpha_manual(values=c(1,0,0,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(0,0,0,0)),
  axis.ticks=element_line(linewidth=.4,color="gray50"),
  axis.ticks.length=unit(4,"pt"),
  legend.background=element_blank(),
  legend.box.background=element_rect(color="gray50",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(0,1),
  legend.spacing.x=unit(1,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(4,5,4,5),
  plot.subtitle=element_text(size=11,margin=margin(,,4)),
  plot.title=element_text(size=11.3,face=2,hjust=.5,margin=margin(1,,4)))
ggsave("1.png",width=5,height=2.9,dpi=300*4)

Ratio between unvaccinated and vaccinated ASMR in English ONS data

The reason why he used November and December as his high-COVID period seems to have been because the Czech Republic deaths during the Delta wave peaked in November to December 2021. But the UK already had a lot of Delta deaths in August, and there was a period with elevated COVID mortality from July 2021 until January 2022.

But the ratio between unvaccinated and vaccinated ASMR dropped in February 2022 after the COVID deaths went down. So Kirsch should've used the period from February 2022 onwards as his low-COVID baseline period, and not the period before November 2021 like in his analysis of the Czech data:

t=fread("https://sars2.net/f/ons.csv")
t=rbind(t[ed==7&month<="2021-03"],t[ed==9])

s=t[status%like%"acci"&age=="Total"&cause!="Deaths involving COVID-19"]
p=s[,.(x=as.Date(paste0(month,"-16")),y=asmr,z=status,cause,facet=1)]

p[,cause:=factor(cause,,c("All causes","Not COVID"))]
p[,z:=factor(z,unique(z),c("Unvaccinated","Vaccinated"))]

p=rbind(p,dcast(p,x+cause~z,value.var="y")[,.(x,y=Unvaccinated/Vaccinated,cause,z="Ratio",facet=2)])

p[,facet:=factor(facet,,c("ASMR","Ratio"))]

xstart=as.Date("2021-1-1");xend=as.Date("2023-6-1");xbreak=seq(xstart,xend,"year")

ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free_y")+
geom_line(aes(x,y,color=z,alpha=cause),linewidth=.6)+
geom_point(aes(x,y,color=z,alpha=cause,shape=cause),stroke=.6,size=1.5)+
geom_text(data=p[,max(pretty(c(0,y))),facet],aes(y=V1,label=facet),vjust=1.7,x=pmean(xstart,xend),hjust=.5,size=3.87,fontface=2)+
labs(x=NULL,y=NULL,title="Monthly ASMR per 100,000 person-years in English ONS data")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=\(x)range(pretty(c(0,x))),breaks=\(x)pretty(c(0,x)))+
scale_color_manual(values=c("#5555ff","#ff5555","gray50"))+
scale_alpha_manual(values=c(1,.5))+
scale_shape_manual(values=c(16,1))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),alpha=guide_legend(order=2),shape=guide_legend(order=2))+
theme(axis.text=element_text(size=11,margin=margin(2,2,2,2),color="gray40"),
  axis.text.x=element_text(hjust=0),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box="vertical",
  legend.box.just="center",
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="center",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(2.5,5.5,2.5,2.5),
  legend.position="top",
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4,color="gray70"),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(10,"pt"),
  plot.margin=margin(5,5,4,5),
  plot.title=element_text(size=11.4,face=2,margin=margin(1,,5),hjust=.5),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.2,height=4.1,dpi=300*4)

When Kirsch said that the "the ASMR for the unvaccinated fluctuates in 30 days", I don't know if he meant the change in ASMR during the first months of 2021 that was due to HVE, or the change in later months that was due to variability in COVID deaths.

But in case he meant the former, Kirsch should recognize by now that the HVE explains why unvaccinated people have high mortality when the first dose is rolled out, since he has identified a similar phenomenon in the Czech data. He linked to a Substack post about the ONS data by Norman Fenton and Martin Neil, who used to claim that the high mortality in unvaccinated people in early 2021 was somehow anomalous, and it was not explained by the HVE.

In 2022 Fenton and Neil also wrote a paper where they claimed that the ONS dataset was "corrupted" because there was a very low number of deaths during the first two weeks from vaccination. But since then several other datasets have been released which have a similarly low number of deaths in the first two weeks after vaccination, including the Medicare and New Zealand datasets that were released by Kirsch. Even Kirsch's own analysis of the various record-level datasets has shown why Fenton and Neil's old preprints about the ONS data were wrong.

Does HVE last for only 21 days for non-COVID vaccines?

Kirsch wrote: "Short term HVE is always around 21 days regardless of location or vaccine."

When I searched for studies that showed deaths by time after vaccination for non-COVID vaccines, I found a paper from 2009, which showed that deaths by weeks after influenza vaccination kept climbing long after 21 days from vaccination had passed (even though it might partially be because of seasonal variation in mortality, because influenza vaccines are often administered before the flu season when mortality peaks in the winter).

The paper featured the following plot with this caption: "Mortality (deaths per 100 person-years) by week after influenza vaccination among higher-risk vaccinees, lower-risk vaccinees, and all vaccinees (1.9 million flu shots), Kaiser Permanente, Northern California, 1996-2005. The flat reference line shows the average monthly mortality during all unvaccinated time in the study population. COPD, chronic obstructive pulmonary disease." [https://pmc.ncbi.nlm.nih.gov/articles/PMC2728831/]

A study from 2024 included the plot below that shows all-cause mortality risk by weeks after flu vaccination, where the mortality risk gradually increases from about 0.19 on weeks 5-8 to 1.05 on weeks 25-28: [https://onlinelibrary.wiley.com/doi/10.1002/jmv.29722]

Kaplan-Meier survival plots of Czech data

Then the document included plots like this for various age groups, where the "tangent" looks like a linear regression of the survival probability around days 10-60 of follow-up:

So even though unvaccinated people had a lower survival probability than vaccinated people, the survival probability was above the tangent for vaccinated people but below the tangent for unvaccinated people, which Kirsch interpreted to mean that vaccinated people somehow did worse than unvaccinated people.

The obvious flaw in his reasoning is that there were still many recently vaccinated people during the period that was used to fit the tangent, so the HVE was stronger in the period than later. But as the HVE got weaker over time, the vaccinated mortality fell below the tangent but the unvaccinated mortality rised above the tangent.

Kirsch wrote: "The Aarstad study (39 countries, 1B total population) showed an R2 =56.6%. Relating vaccination level and excess mortality. There is no study anywhere with a comparable population and R2 that shows a negative correlation."

Aarstad got an r-squared value of abotu 0.57 between excess mortality in 2022 and the percentage of vaccinated people across European countries. But that's because he used the average number of deaths in 2016-2019 as the baseline, which exaggerated excess mortality in Western European countries relative to Eastern European countries for two reasons. Western European countries had a more steeply increasing slope in yearly deaths even before COVID. And also Eastern European countries had a higher percentage of excess deaths in 2020-2022, so the baseline should've been lowered more in Eastern European countries to account for the reduction in population size: [rootclaim.html#Aarstads_correlation_between_excess_deaths_at_Eurostat_in_2022_and_percentage_of_vaccinated_people_4g]

When I used a more accurate 2013-2019 linear trend for ASMR instead, I got a negative correlation between the percentage of vaccinated people in 2022 and excess deaths in 2022: [ibid.]

Kirsch regrets not appreciating the effect of confounders in his analysis of the Czech data

However now in the PDF file for his sixth round of arguments, Kirsch wrote that he regrets not having appreciated the effect of confounders when he compared the mortality of Moderna against Pfizer in the Czech data: [https://www.skirsch.com/covid/KIRSCH_COVID_shot_analysis.pdf]

In 2024 Kirsch kept insisting that Pfizer and Moderna vaccines were distributed randomly and without bias in the Czech Republic, so the difference in mortality between the vaccine brands could not have been due to confounders, even though me and Uncle John Returns and Jeffrey Morris kept telling him otherwise.

Kirsch also cherrypicked sources which showed that Moderna had higher mortality than Pfizer, but he ignored the other sources I showed him where Pfizer had higher mortality than Moderna.

I showed him that the average age of VAERS reports is much higher for Moderna than Pfizer, but he did not account for the difference in age distribution when he declared that Moderna was more deadly than Pfizer based on VAERS data. In the unadjusted model of Levi et al., I believe the main reason why Moderna had a higher mortality risk than Pfizer was that the median age was 62 for Moderna but 54 for Pfizer, so simply adjusting the analysis for age would've probably caused Pfizer to have a higher mortality risk than Moderna.

In his initial analysis of the Czech data, Kirsch even wrote that the Pfizer and Moderna vaccines were distributed so randomly that it "created a perfect real-world randomized clinical trial", so that he didn't have to adjust for any confounders when he compared the mortality of the vaccine brands: "Vaccines were randomly distributed for those wishing to get vaxxed. [...] People were not allowed to select which vaccines they got. [...] The randomization of which vaccine someone got created a perfect real-world randomized clinical trial where we could compute the mortality rates for 1 year after Dose 2 for the two most popular vaccines." [https://github.com/skirsch/Czech/blob/5725ac1b64ede7124e00b72af68892f31736b349/README.md] After I pointed out to Kirsch that the average age at first dose was much higher for Moderna than Pfizer, which showed that the vaccine brands were not distributed randomly, he seems to have toned down his initial claim about how the distribution of the vaccine brands was perfectly randomized, but it was still the original basis of his argument that the Czech data showed that Moderna was more deadly than Pfizer.

During the first round of the Rootclaim debate, Kirsch claimed that Moderna vaccines were more deadly than Pfizer vaccines based on his analysis of the Czech data, but in the sixth round of the argument he now seems to have dropped the claim, because in the Levi-Ladapo paper Pfizer now had higher mortality than Moderna.

But in the same way that in 2024 Kirsch was confident that the distribution of vaccines in the Czech Republic was so random that confounders couldn't have explained why Moderna had higher mortality than Pfizer, he is now confident that Levi's matching procedure was so perfect that confounders cannot explain why Pfizer has higher mortality than Moderna.

Time series plots for deaths by time since vaccination

Kirsch referred to this Substack post, which includes various plots for deaths as a function of time since vaccination: https://kirschsubstack.com/p/covid-time-series-graphs-show-clearly. Most of them were based on Medicare data that Kirsch received from a source at the HHS in 2023.

Kirsch claims that the HVE only lasts for 3 weeks, because in this plot of deaths by weeks since the first dose in the Czech data, there is a sharp turning point in mortality around day 21:

But he pointed out that a similar turning point is more difficult to see for second and third doses:

However the sharp turning point around day 21 for first doses is because many people got the first dose at the tail end of the period with high COVID deaths in early 2021, so there was a sharply decreasing trend in background mortality rate: [czech4.html#Plot_for_raw_deaths_by_weeks_after_vaccination]

Kirsch also posted these plots of Medicare data, where people who got the first COVID vaccine in the first quarter of 2021 have a turning point in deaths around the third week after vaccination, but the curve in deaths is more smooth in people who got the first dose in the second quarter of 2021, but it's because people vaccinated in the first quarter had a more sharply decreasing trend in the background mortality rate than people vaccinated in the second quarter:

Kirsch also published a spreadsheet that shows the number of deaths grouped by month of the first COVID vaccine dose. It only includes data for the first three months of 2021, but it still clearly shows how the effect of the COVID deaths during the first 100 days from vaccination was higher for people vaccinated in January than for people vaccinated in February or March. Even among people vaccinated in March, the increase in deaths between days 50 and 100 is more steep than in people vaccinated in February: [f/COVID_vax_jan_feb_mar_2021_plus_ALL_deaths_in_medicare_per_day.xlsx

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

t=fread("https://sars2.net/f/medicarecovidmonthly.csv")
t[,vaxmonth:=factor(vaxmonth,,paste("Vaccinated",month.name[1:3],2021))]

p=t[,.(x=day,y=ma(dead,3)),.(z=vaxmonth)]

xstart=0;xend=1000;xbreak=0:10*100
p=p[x%in%xstart:xend]
ybreak=p[,pretty(y)];ystart=0;yend=max(ybreak)

ggplot(p)+
annotate("rect",ymin=ystart,ymax=yend,xmin=xstart,xmax=xend,lineend="square",fill=NA,color="gray70",linewidth=.4)+
geom_line(aes(x,y,color=z))+
labs(x=NULL,y=NULL,title="Deaths by days since first COVID vaccine dose in Medicare data")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=hsv(22/36,c(1,.8,.4),c(.7,1,1)))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black",margin=margin(2,2,2,2)),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box="vertical",
  legend.box.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.justification=c(.5,0),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(.5,.15),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major=element_line(linewidth=.4,color="gray87"),
  plot.margin=margin(5,18,5,5),
  plot.title=element_text(size=11.3,face=2,hjust=.5,margin=margin(2,,4)))
ggsave("1.png",width=5.45,height=3.3,dpi=300*4)

Kirsch recognized the problem himself in the sheet "vaxxed in jan 2021" of his spreadsheet, where he included these comments:

Kirsch also showed these plots of flu and pneumonia vaccines administered in the first quarter of 2021:

However his plots have the same problem as the plot for COVID vaccines administered in the first quarter of 2021. The United States had very high excess deaths in January 2021 due to COVID, but by March 2021 the excess deaths had returned close to zero. So in Kirsch's plots the background mortality rate is high at the start of the x-axis but afterwards it gradually drops as the proportion of observation time from January and February drops. So the increasing trend in mortality due to the HVE is counteracted by the decreasing trend in the background mortality rate, so it's difficult to evaluate from his plots how long the HVE lasts.

However if you don't cherrypick vaccine doses administered in the first quarter of 2021, then the period after vaccination when there is reduced mortality lasts much longer than 3 weeks. The next screenshot shows one of the spreadsheets that Kirsch published on his S3 server in December 2023. [https://kirschsubstack.com/p/data-from-us-medicare-and-the-new, f/Medicare-flu-pneu-covid_given_21_or_22.xlsx] It shows that for flu vaccines administered at any time in 2021 or 2022, the deaths take about 100 days to reach the peak. The peak is probably due to elevated mortality in the winter combined with the effect of COVID waves, because flu vaccines are often administered before the flu season. But anyway, now the increase in deaths over the first 100 days is more smooth than in the plot for vaccine doses administered in the first quarter of 2021, because the vaccine doses are distributed more evenly across time so there is not a sharp decrease in the background mortality rate at the start of the x-axis:

The plot above actually looks like what would expect from an unsafe vaccine, because there is a high number of deaths on day 0 which refers to the day of vaccination. Deaths caused by vaccines are likely to be heavily concentrated on the day of vaccination and the next few days. So if deaths as a function of time since vaccination go down during the first few days from vaccination, it's a sign that there might be some deaths caused by the vaccination. But Kirsch has developed a counterintuitive line of reasoning, where he claims that if deaths as a function of time since vaccination go up over time, it means that vaccines are killing more people over time.

This plot for shingles vaccines also shows that it takes much longer than 21 days for the HVE to wear off so that deaths reach a stable level:

In the next plot I combined data for deaths by days since vaccination from various spreadsheets on Kirsch's S3 server. I excluded the day of vaccination because it stretched the y-axis too much for pneumonia vaccines. You can see that COVID vaccine administered in 2021 look atypical because they have the notch around day 20-30. But across all vaccine types and all years of vaccination, a more typical curve looks more smooth so that it takes about 100 days to reach a somewhat stable level:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

t=fread("https://sars2.net/f/medicarevaxtypes.csv")
t[,type:=factor(type,unique(type))]

sub=setDT(read_excel("https://sars2.net/f/Medicare-2-1-23_all_states_subset_plus_CT.xlsx"))
sub=sub[,.(dead=.N),,.(year=year(`First Vaccination Date`),day=DTD)][year%in%2021:2022]
t=rbind(t,sub[,type:="COVID (all states subset)"])

p=t[day>0,.(x=day,y=ma(dead,3)),.(facet=type,year)]

xstart=0;xend=1000;xbreak=0:10*100
p=p[x%in%xstart:xend]

ggplot(p)+
geom_rect(data=p[,max(as.integer(pretty(c(0,y)))),facet],aes(ymax=V1),ymin=0,xmin=xstart,xmax=xend,lineend="square",fill=NA,color="gray70",linewidth=.4)+
facet_wrap(~facet,ncol=1,scales="free_y")+
geom_line(aes(x,y,color=year))+
geom_label(data=p[,.(y=max(pretty(c(y,0)))),facet],aes(label=facet,y=y),x=xend,hjust=1,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray70",size=3.87)+
geom_label(data=p[,.(y=max(pretty(c(y,0)))),facet],aes(label=facet,y=y),x=xend,hjust=1,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,color="black",size=3.87)+
labs(x=NULL,y=NULL,title="Deaths by days since vaccination in Medicare data",subtitle="7-day moving average (±3-day window), day 0 excluded.\nThe color of lines shows the year of administration.")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(limits=\(x)range(pretty(c(0,x))),breaks=\(x)pretty(c(0,x)),labels=\(x)ifelse(x==max(pretty(c(0,x))),"",x))+
scale_color_manual(values=c(hcl(c(0,6,12,21,27,32)*10+15,100,60),"black"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=1,byrow=F))+
theme(axis.text=element_text(size=11,color="black",margin=margin(2,2,2,2)),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box="vertical",
  legend.box.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="center",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(16,"pt"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(1,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major=element_line(linewidth=.4,color="gray87"),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(5,17,5,5),
  plot.subtitle=element_text(hjust=.5,margin=margin(,,2)),
  plot.title=element_text(size=11.3,face=2,hjust=.5,margin=margin(1,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5,height=5,dpi=300*4)

Does short-term HVE last for 3 weeks in the Czech FOI data?

Kirsch wrote: "Short term HVE was measured to be 21 days from the Czechia FOIA data which has per day time resolution (source) with a half life of around 5 days."

In the next plot I calculated excess mortality in the Czech dataset that was adjusted for age and the background mortality rate. For each combination of age group and observation month, I used the mortality rate of all people included in the dataset as the baseline. Then for each dose number and week after vaccination, I multiplied the person-days for each combination of age group and observation month with the baseline mortality rate to get the expected number of deaths, and I calculated the percentage of excess deaths by dividing the actual deaths by expected deaths and subtracting 1. It takes about 20 weeks for the excess mortality to stabilize around the level of -25% to -15%, even though it later keeps climbing even closer to 0% [czech2.html#Excess_mortality_by_weeks_after_vaccination]

I also came up with a method to compare vaccinated ASMR by weeks after vaccination against ASMR in a matched cohort of unvaccinated people. When I applied the method to the first 4 doses in the Czech FOI data, for each dose unvaccinated people got over 6 times higher ASMR than vaccinated people during week 0, even though by week 10 the ratio had dropped to about 2.8 for the first dose, 2.5 for the second dose, 3.3 for the third dose, and 2.0 for the fourth dose:

t=fread("https://sars2.net/f/czbucketskeep.csv.gz")[dose<=4]

a=t[,.(dead=sum(dead),pop=sum(alive)),.(week,month,dose,age=pmin(age,95)%/%5*5)]

std=fread("https://sars2.net/f/czcensus2021pop.csv")[,sum(pop),.(age=pmin(age,95)%/%5*5)][,.(age,std=V1/sum(V1))]

vax=a[dose>0,.(dead=sum(dead),pop=sum(pop)),.(week,month,age,dose)]
base=merge(vax,vax[,.(sum=sum(pop)),.(week,dose)])
base=base[,.(frac=pop/sum,month,age,week,dose)]

unvax=a[dose==0,.(dead,pop,age,month)]
unvax=merge(unvax,base)[,.(dead=sum(dead*frac),pop=sum(pop*frac)),.(age,week,dose)]

vax=vax[,.(dead=sum(dead),pop=sum(pop)),.(week,age,dose)]

p=rbind(vax[,z:=2],unvax[,z:=1])
p=merge(std,p)[,.(y=sum(dead/pop*std*365e5)),.(x=week,dose,z)]

p=merge(vax[,sum(pop),.(week,dose)][V1>=365e2,.(x=week,dose)],p)

xstart=0;xend=100;xbreak=0:10*10;ystart=0;yend=4000;ybreak=1:3*1e3

p[,z:=factor(z,,c("Unvaccinated","Vaccinated"))]
p[,dose:=factor(paste("Dose",dose))]

p=rbind(p,dcast(p,x+dose~z,value.var="y")[,.(x,dose,y=Unvaccinated/Vaccinated,z="Ratio (right axis)")])
yend2=8;secmult=yend/yend2

ggplot(p,aes(x,y))+
facet_wrap(~dose,ncol=1,scales="free_y")+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(color=z,y=ifelse(z==levels(z)[3],y*secmult,y)),linewidth=.6)+
geom_label(data=p[rowid(dose)==1],aes(label=dose),y=yend,x=pmean(xstart,xend),vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray70",size=3.87)+
geom_label(data=p[rowid(dose)==1],aes(label=dose),y=yend,x=pmean(xstart,xend),vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87)+
labs(title="ASMR by weeks since vaccination in Czech Republic",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,sec.axis=sec_axis(trans=~./secmult,breaks=1:3*2))+
scale_color_manual(values=c("#5555ff","#ff5555","gray"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray45"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box="vertical",
  legend.box.just="right",
  legend.box.margin=margin(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="center",
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.key=element_rect(fill="white"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  panel.background=element_blank(),
  panel.spacing=unit(0,"pt"),
  plot.margin=margin(4,14,4,4),
  plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
  plot.title=element_text(size=11,face="bold",hjust=.5,margin=margin(1,,3)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.6,height=4,dpi=300*4)

In the next plot I split people into three groups depending on the month when they got the first vaccine dose. Week 0 consists of the day of vaccination and the next 6 days. People vaccinated in January or February have a peak in deaths on week 2, and people vaccinated in March or April have a peak in deaths on week 3, but the early peak is missing in people vaccinated in May or June. However the baseline also has a much bigger drop during the first 10 weeks for the first two groups and a smaller drop for the third group. However once you plot the deaths as a proportion of the baseline, in all three groups the proportion reaches a plateau around week 20:

t=fread("https://sars2.net/f/czbucketskeep.csv.gz")[dose<=1]
t[,age:=pmin(age,95)%/%5*5]
a=t[dose==1,.(dead=sum(dead),pop=sum(alive)),.(week,month,age,vaxmonth)]
a=merge(a,t[,.(base=sum(dead)/sum(alive)),.(age,month)])
a=a[vaxmonth%like%"2021-0[1-6]"]

group=paste0("Vaccinated\n",apply(matrix(month.abb[1:6],2),2,paste,collapse="+"))
a[,vaxmonth:=rep(group,each=2)[factor(vaxmonth)]]
a=a[,.(dead=sum(dead),base=sum(base*pop)),.(week,vaxmonth)]

p=a[,.(x=week,y=c(dead,base),z=factor(rep(1:2,each=.N),,c("Deaths","Baseline")),vaxmonth)]
xstart=0;xend=50;xbreak=0:5*10
p=p[x%in%xstart:xend]
p[,y:=y/p[z=="Baseline",tapply(y,vaxmonth,mean)][factor(vaxmonth)]*100]

p=rbind(p[,facet:=1],a[,.(x=week,vaxmonth,y=dead/base*100,z="Ratio",facet=2)])
p[,facet:=factor(facet,,c("Deaths and baseline (100%\nis average baseline value)","Deaths as percentage of\nbaseline"))]

ybreak=pretty(p$y,4);ystart=0;yend=max(ybreak)

ggplot(p,aes(x,y))+
facet_grid(vaxmonth~facet)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray80")+
geom_line(aes(color=z,linewidth=z))+
geom_point(aes(color=z,alpha=z),size=1.2,stroke=0)+
labs(x=NULL,y=NULL,title="Czech FOI data: Deaths by weeks after first dose")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=ifelse(xbreak==max(xbreak),"",xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x==max(ybreak),"",paste0(x,"%")))+
scale_color_manual(values=c("#dd0000","#ffaaaa","gray60"))+
scale_linewidth_manual(values=c(0,0,.5))+
scale_alpha_manual(values=c(1,1,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(20,"pt"),
  legend.margin=margin(,,0),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(3,"pt"),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(margin=margin(,,2),hjust=1),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(1,,3)),
  strip.background=element_blank(),
  strip.text=element_text(size=10.4,margin=margin(2,2,2,2)))
ggsave("1.png",width=4.5,height=3.8,dpi=300*4)

Ratio of mortality rates by age group in Czech data

When Kirsch first published his KCOR analysis of the Czech data, I told him he should've done the analysis based on mortality rates instead of the raw number of deaths, and he shouldn't have shown simply the ratio between the adjusted unvaccinated and vaccinated mortality, but he should've made a series of plots that first showed what the unvaccinated and vaccinated mortality rates were each week, then what their ratio was, and then what their ratio relative to the baseline period was.

For example among people born in 1950-1954 which Kirsch selected for his initial KCOR analysis, the ratio between unvaccinated and vaccinated mortality rate was about 3.2 in the baseline period but about 2.6 times higher during the whole observation period, so Kirsch said it meant that vaccines had killed about 23% extra people, because he assumed that the ratio between unvaccinated and vaccinated mortality should've remained at a level of about 3.2 indefinitely, but if the ratio later fell lower, it meant that vaccines were killing people. But his analysis was not very transparent because he didn't show the mortality rates anywhere but only the raw number of deaths, so most of his followers probably didn't realize what his claim that vaccines were killing people was based on.

Now he actually fulfilled my request and he did a similar analysis using crude mortality rates:

If you look at the row for people born in 1950-1954 in the table above, you can see that the ratio between unvaccinated and vaccinated mortality was about 3.30 in the baseline period but about 2.66 during the whole observation period. So by dividing 3.30 with 2.66, Kirsch got a ratio of 1.24, which he interpreted to mean that vaccines were killing 24% extra people.

His logic is similar to his earlier KCOR analysis, but this time the steps he took to calculate his supposed vaccine harm are more transparent, so it's easier to see how shaky the foundation of his reasoning is.

In the PDF file Kirsch also wrote that the so-called traditional method of using mortality rates is "much less accurate" than KCOR "because the cohorts change in composition over time". But the vaccinated and unvaccinated cohorts do change in reality as well as more people get vaccinated over time. So is it not inaccurate how with the KCOR method he has to misclassify a part of vaccinated people as unvaccinated? It actually results in a fairly large reduction in unvaccinated mortality during the Delta wave, since the vaccinated people who are misclassified as unvaccinated have lower mortality than real unvaccinated people. And another way in which his KCOR method is less accurate than using mortality rates is that KCOR is not adjusted for a higher rate of depletion in the unvaccinated cohort over time due to a higher mortality rate in unvaccinated people.

Did Arbel et al. show that unvaccinated people were 10 times more likely to die from COVID?

Kirsch wrote: "What's even worse is that the Arbel study showed the unvaccinated were 10 times more likely to die from COVID, but this was likely due to selection bias - not vaccine protection. In other words, the people who got vaccinated were already much healthier and less likely to die from COVID. So even if the vaccine were 100% effective at preventing COVID death, it was given to the population that was already 10x less likely to die. That means, even with a perfect vaccine, the vaccine could have reduced COVID deaths by just 10%. Since COVID deaths accounted for only about 12% of all-cause mortality (ACM), this implies that - even under perfect conditions - the vaccine could only have reduced the absolute ACM of those who got vaccinated by about 1.2%/yr. That is a negligible benefit."

The paper by Arbel et al. didn't compare vaccinated people against unvaccinated people, but people with 3 doses against people with 2 doses.

Arbel's odds ratio was adjusted for medical comorbidities, but still Arbel got odds ratio of about 0.23 for non-COVID mortality, which suggests that the adjustment for medical comorbidities was not sufficient to eliminate confounding by HVE.

But did the HVE disproportionately affect risk of COVID deaths so that the odds ratio of 0.10 could be entirely attributed to the HVE? I don't think that's the case, but there is in fact a mechanism of how HVE could disproportionately affect the risk of death from COVID.

People who had a currently documented case of COVID or who were hospitalized with COVID usually did not get an additional vaccine dose until they had recovered. So a common reason why the subjects in Arbel's study remained under the second dose may have been that they were currently infected with COVID, which might partially explain why people with 2 doses had higher COVID mortality than people with 3 doses.

The study included only people aged 60 and above, and it lasted from August 6th 2021 until September 29th 2021, which was the period when the majority of people aged 60 and above got the first booster dose in Israel, but the period of the study also coincided with the weeks when Israel had the highest number of COVID deaths during the Delta wave:

If a similar study would've been done in another country where the booster dose was rolled out in August to September and there was a COVID wave in October to November, and the study lasted from August to November so that most COVID deaths would've occurred after people already had the opportunity to choose whether they got a booster dose or not, it might have reduced a bias where the COVID mortality of people with 2 doses was elevated because people who were currently infected with COVID decided to not get a booster dose.

But anyway, another possible problem with Arbel's study was that the odds ratio was not adjusted for the proportion of observation time at different parts of the observation period. The number of COVID deaths peaked around the middle of the study, and it was higher at the end of the study than the beginning of the study. All subjects in the study started in the group with 2 dose, and people were only added to the 3-dose group after 7 days from the third dose. So people with 2 doses had more observation time in the first half of the study than the second half, and people with 3 doses had more observation time in the second half than the first half.

In the following code I used the English ONS data to calculate an odds ratio for COVID deaths, where I adjusted the ratio for age by including the age group as a categorical variable, and I adjusted the odds ratio for the amount of observation time from different months by including the age as a categorical variable. I included only people aged 50 and above to be consistent with Arbel's study, but I looked at the last 4 months of 2021 instead of only August and September of 2021, because England took longer than Israel to reach a high booster coverage. Now the odds ratio of people with 3 doses relative to people with 2 doses was about 0.08, which was even lower than the ratio of 0.10 in Arbel's study:

When I looked at the odds ratios for each month individually, I noticed that the odds ratio for COVID mortality was very low during the booster rollout in October 2021 to December 2022, but it increased dramatically after January 2022. But I don't know if it's because the booster rollout was over or the COVID wave in the winter was over or both:

I'll repeat what Kirsch wrote so I can address the error in his arithmetic: "What's even worse is that the Arbel study showed the unvaccinated were 10 times more likely to die from COVID, but this was likely due to selection bias - not vaccine protection. In other words, the people who got vaccinated were already much healthier and less likely to die from COVID. So even if the vaccine were 100% effective at preventing COVID death, it was given to the population that was already 10x less likely to die. That means, even with a perfect vaccine, the vaccine could have reduced COVID deaths by just 10%. Since COVID deaths accounted for only about 12% of all-cause mortality (ACM), this implies that - even under perfect conditions - the vaccine could only have reduced the absolute ACM of those who got vaccinated by about 1.2%/yr. That is a negligible benefit."

Let's suppose there is a country that consists of 9 million healthy people and 1 million unhealthy people. Relative to the healthy people, the unhealthy people have 10 times higher COVID mortality rate and 4 times higher mortality rate from other causes. COVID deaths account for 12% of all deaths in the country, and the country has 100,000 total deaths in a year, so there are 12,000 COVID deaths and 88,000 non-COVID deaths in a year.

By solving the equation x*9e6+10x*1e6=12000 where x is the yearly COVID mortality rate in healthy people, x is 12000/19e6, which is about 0.063%. Similarly the non-COVID mortality rate in healthy people is 88000/13e6, which is about 0.677%.

So therefore if vaccination was 100% effective in eliminating all COVID deaths, it would reduce all-cause mortality in healthy people by about 9%:

And vaccination would reduce all-cause mortality in the whole population by about 6%:

The flaw in Kirsch's reasoning was that he assumed that if healthy people had 10% the COVID mortality risk of unhealthy people, then healthy people would account for 10% of all COVID deaths. But actually the proportion of COVID deaths in healthy people depends on what fraction of the population is healthy.

Cumulative deaths in people under the age of 80 in Czech Republic

Kirsch wrote: "When COVID starts, the unvaxxed die at a LOWER rate than the vaxxed." But his plot showed raw deaths and not mortality rates, so it's confusing how he spoke of rates, unless he meant the rate of deaths per week.

Vaccinated people also happened to have a higher crude mortality rate than unvaccinated people, because the unvaccinated cohort was bigger than the vaccinated cohort, because Kirsch treated people who were vaccinated on week 25 or later as unvaccinated. But neither raw mortality rates or crude mortality rates are too meaningful if you're looking at cohorts with a vastly different age distribution.

The next plot shows that from the start of the observation period on week 24 of 2021 until the end of available data, the ratio of unvaccinated to vaccinated ASMR remains above 1 each week. The ratio is elevated in summer and fall of 2021 because the HVE is still strong because there are many recently vaccinated people, and the ratio is elevated in the winter of 2021-2022 because unvaccinated people have high COVID mortality. But once the COVID deaths go down and the HVE has become weaker, the ratio between unvaccinated and vaccinated ASMR also starts to fall:

library(data.table);library(ggplot2)

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
t=t[RokNarozeni>="1940"]
t[Umrti!=""&DatumUmrtiLPZ=="",DatumUmrtiLPZ:=Umrti]
t[Umrti!=""&DatumUmrtiLPZ!=Umrti,Umrti:=DatumUmrtiLPZ]
t=t[!(DatumUmrtiLPZ!=""&Datum_Prvni_davka>DatumUmrtiLPZ)]
t[,vax:=Datum_Prvni_davka!=""&Datum_Prvni_davka<"2021-24"]
t[,born:=ifelse(RokNarozeni>="2000","2000+",RokNarozeni)]
t[Datum_Prvni_davka>="2021-24",Datum_Prvni_davka:=""]

t2=t[Infekce%in%c(NA,1)]
dead=t2[,.(unvaxdead=sum(!vax),vaxdead=sum(vax)),.(week=DatumUmrtiLPZ,born)]
coviddead=t[,.(unvaxcoviddead=sum(!vax),vaxcoviddead=sum(vax)),.(week=Umrti,born)]
vax=t2[,.(newvax=.N),.(week=Datum_Prvni_davka,born)]

a=merge(dead,merge(coviddead,vax,all=T),all=T)[week!=""]
a=merge(do.call(CJ,lapply(a[,1:2],unique)),a,all=T);a[is.na(a)]=0

a=merge(t2[,.(startpop=.N),born],a)
a[,unvaxpop:=startpop-cumsum(unvaxdead)-cumsum(newvax),born]
a[,vaxpop:=cumsum(newvax)-cumsum(vaxdead),born]

l=a[,.(week,dead=c(unvaxdead,vaxdead),covid=c(unvaxcoviddead,vaxcoviddead),pop=c(unvaxpop,vaxpop),dose=rep(1:2,each=.N),born)]
l=rbind(l,l[,.(dead=sum(dead),pop=sum(pop),covid=sum(covid),dose=0),.(born,week)])
l=l[week>="2021-24"]

l=merge(l,l[week=="2022-01",sum(pop),born][,.(std=V1/sum(V1),born)])

l2=l[,.(dead=sum(dead),covid=sum(covid),pop=sum(pop)),.(week,dose)]
p1=l2[,.(y=c(dead,dead-covid),type=1:2,facet=1),.(week,dose)]
p2=l2[,.(y=c(dead,dead-covid)/pop/7*365e5,type=1:2,facet=2),.(week,dose)]
p3=l[,.(y=c(sum(dead/pop*std),sum((dead-covid)/pop*std))/7*365e5,type=1:2,facet=3),.(week,dose)]

cum=l[,.(dead=cumsum(dead),covid=cumsum(covid),pop=cumsum(pop),week),.(born,dose,std)]
c1=cum[,.(y=c(sum(dead),sum(dead-covid)),type=1:2,facet=1),.(week,dose)]
c2=cum[,.(y=c(sum(dead),sum(dead-covid))/sum(pop)/7*365e5,type=1:2,facet=2),.(week,dose)]
c3=cum[,.(y=c(sum(dead/pop*std/7*365e5),sum((dead-covid)/pop*std/7*365e5)),type=1:2,facet=3),.(week,dose)]

p=rbind(rbind(c1,c2,c3)[,cum:=2],rbind(p1,p2,p3)[,cum:=1])

p[,dose:=factor(dose,,c("Total","Unvaccinated","Vaccinated"))]
p[,type:=factor(type,,c("All causes","Not COVID"))]
p[,facet:=factor(facet,,c("Deaths","CMR","ASMR"))]
p[,cum:=factor(cum,,c("Not cumulative","Cumulative"))]

iso=as.Date(0:1e4*7,"1970-1-1");names(iso)=format(iso,"%G-%V")
p[,x:=iso[week]]

xstart=as.Date("2021-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ybreak=pretty(c(0,p$y),7);yend=max(ybreak)

ggplot(p)+
facet_grid(facet~cum,scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray87",linewidth=.4,lineend="square")+
geom_vline(xintercept=iso["2021-24"]-3.5,color="gray87",linewidth=.4,linetype="22")+
geom_line(aes(x,y,color=dose,alpha=type),linewidth=.6)+
labs(x=NULL,y=NULL,title="Czech Republic, people born in 1940 or later")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=\(x)range(pretty(c(0,x),4)),breaks=\(x)pretty(c(0,x),4),labels=\(x)ifelse(x==max(x),"",ifelse(x>=1e3,paste0(x/1e3,"k"),x)))+
scale_color_manual(values=c("black","#6666ff","#ff6666"))+
scale_alpha_manual(values=c(1,.4))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray87",linewidth=.4),
  legend.box="vertical",
  legend.box.just="center",
  legend.box.margin=margin(,,1),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(2.5,5.5,2.5,2.5),
  legend.position="top",
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major.x=element_blank(),
  panel.grid.major.y=element_line(linewidth=.4,color="gray87"),
  panel.spacing=unit(2,"pt"),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(1,,4)),
  strip.background=element_blank(),
  strip.text=element_text(size=11,margin=margin(3,3,3,3)))
ggsave("1.png",width=5,height=4,dpi=300*4)
sub="The observation period starts on week 24 of 2021. People who received a first dose on week 24 of 2021 or later are counted as unvaccinated. The CMR and ASMR values are deaths per 100,000 person-years. The ASMR was calculated by 5-year groups for other years of birth but people born in the 2000s were combined into a single group. The population included in the dataset on week 1 of 2022 was used as the standard population."
system(paste0("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\''",sub),"' -splice x80 \\) -append -resize 25% -bordercolor white -border 24 -dither none -colors 256 1.png"))

Kirsch says that if the ratio between vaccinated and unvaccinated mortality is higher in 2022 than 2021, it means that unvaccinated people did worse than vaccinated people in 2022. But in reality it could also be that unvaccinated people did worse in both 2022 and 2021, but they did even more worse in 2021.

Kirsch wrote: "We started the counters on 6/14/21 when we define the two cohorts based on their vaccination status on that date". June 14th 2021 is the first day of week 24 2021. But Kirsch actually defined the vaccination status at the end of week 24, or on June 20th, because he included vaccine doses administered up to week 24 inclusive of week 24.

Kirsch said that his cohorts were "naturally matched", because they had a similar number of raw deaths during the early part of his observation period. But the cohorts were not matched by population size or age.

In the plot above I didn't reproduce Kirsch's analysis exactly, because I defined the vaccination status at the start of week 24 instead of the end of week 24, I didn't count people with multiple cases multiple times like Kirsch, I excluded people with a year of birth missing, I excluded people with a date of vaccination after a date of death, and I treated the week of COVID death as the week of death for a few people who had a date of death from all causes missing.

Kirsch included his analysis in the sheet "Matched slopes 80 and younger" of the file KCOR_czech.xlsx. [https://github.com/skirsch/Czech/blob/2bbf02131796e8539a8eb821686452f4cec615a2/analysis/KCOR_czech.xlsx] His sheet has a total of 154,543 deaths in vaccinated people. I was able to reproduce the figure when I didn't exclude rows for duplicate cases, I didn't exclude people with a year of birth missing, and I counted vaccine doses administered up to week 24 of 2021 inclusive of week 24:

In the following code I reproduced Kirsch's analysis exactly so that I also reproduced his errors. I calculated the ASMR by the 5-year groups for year of birth so that I used the people included in the dataset on week 1 of 2022 as the standard population (or strictly speaking I counted people with two cases twice in the standard population, but it doesn't make much difference here). But anyway, on week 24 of 2021, unvaccinated people had about 3.8 times higher ASMR than vaccinated people:

Across all ISO weeks of each year, the ratio between unvaccinated and vaccinated ASMR was about 2.7 in 2021, 2.0 in 2022, 1.6 in 2023, and 1.5 in 2024:

If the ratio is lower in 2022 than 2021, Kirsch interprets it to mean that vaccinated people are doing worse than unvaccinated people in 2022. But he could just as well use the ratio in 2023 as the baseline, and then because the ratio is higher in 2022 than 2023, he could say that unvaccinated people are doing worse than vaccinated people in 2022.

Mortality rate by weeks after third dose in New Zealand

Kirsch posted this plot that shows deaths per 100,000 person-years by weeks since third dose in Barry Young's New Zealand dataset, and he claimed it showed that vaccines were killing people because the mortality rate was not flat over time:

His plot only included ages 60 and above. The reason why the mortality rate increased between week 0 and 30 was because the healthy vaccinee effect got weaker over time, and also because the rollout of the first booster to ages 60 and above peaked in January to February 2022, but New Zealand had the first big wave of COVID deaths in March 2022.

The reason why the mortality rate started going down after week 27 was because people were removed from the population size after they got a fourth dose, people at the lower end of ages 60 and above were less likely to get a second booster than older people, so the average age of people with only three doses went down after the second booster was rolled out.

The mortality rate of people with 3 doses remains above the baseline mortality rate from week 24 onwards, but it's because the healthy vaccinees moved under the 4th dose, so the people who remained under the 4th dose had elevated mortality because of the straggler effect:

ua=\(x,y,...){u=unique(x);y(u,...)[match(x,u)]}

t=fread("https://sars2.net/f/buckets.gz")[dose==3&age>=60]
a=t[,.(dead=sum(dead),pop=sum(alive)),.(week,age=pmin(age,95)%/%5*5,month=ua(date,substr,1,7))]

nz=fread("https://sars2.net/f/nz_monthly_deaths_by_age.csv")
nz[,date:=as.Date(paste0(year_reg,"-",month_reg,"-15"))]
nz=nz[ethnicity=="Total",.(dead=sum(count)),.(date,age=as.integer(substr(age_group,1,2))%/%5*5)]
nzpop=fread("https://sars2.net/f/nzpopquartermean.csv")
nzpop=nzpop[,.(pop=sum(pop)),.(age=age%/%5*5,date=as.Date(paste(year,q*3-1,15,sep="-")))]
nz=merge(nz,nzpop[,spline(date,pop,xout=unique(nz$date)),age][,.(age,date=x,pop=y)])
nz=nz[,.(month=substr(date,1,7),base=dead/pop/days_in_month(date),age)]

a=merge(a,nz)
p1=a[,.(y=`if`(sum(pop)<=365e2,NA_real_,sum(dead)/sum(pop)*365e5),z="Mortality rate per 100,000 person-years"),week]
p2=a[,.(y=sum(base*pop)/sum(pop)*365e5,z="Baseline mortality rate"),week]
p3=t[,.(y=weighted.mean(age,alive),z="Average age"),week]
p4=a[,.(y=sum(pop)/365e2,z="Hundreds of person-years"),week]
p=rbind(p1,p2,p3,p4)[,z:=factor(z,unique(z))]

yend=5000;ybreak=0:5*1000;yend2=100;ybreak2=0:5*20;secmult=yend/yend2
xstart=0;xend=100;xbreak=0:10*10

leg=p[,.(label=levels(z),hjust=c(0,0,1,1),x=c(2,2,98,98),y=yend*c(.16,.07))]
color=c("black","gray60","#bbbb00","#00bb00")

p[,ymult:=ifelse(z%in%levels(z)[1:2],y,y*secmult)]

ggplot(p)+
annotate("rect",xmin=xstart,xmax=xend,ymin=0,ymax=yend,color="gray70",linewidth=.4,lineend="square",linejoin="mitre",fill=NA)+
geom_line(aes(week,ymult,color=z),linewidth=.6)+
geom_point(aes(week,ymult,color=z),stroke=0,size=1.2)+
geom_label(data=leg,aes(x,y,hjust=hjust,label=label),size=3.87,color=color,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.3,fill=alpha("white",.8))+
labs(x=NULL,y=NULL,title="Mortality rate by weeks since third dose in New Zealand, ages 60+")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,sec.axis=sec_axis(trans=~./secmult,breaks=ybreak2))+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.ticks=element_line(linewidth=.4,color="gray70"),
  axis.ticks.length=unit(4,"pt"),
  legend.position="none",
  panel.background=element_blank(),
  plot.title=element_text(size=11.3,hjust=.5,face="bold",margin=margin(1,,6)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.4,height=3.5,dpi=300*4)

COVID and all-cause mortality rates by age

However instead of relying on estimates of IFR, he could've looked up how COVID mortality by age group compares to all-cause mortality. In the United States in 2020-2023, the COVID mortality rate as a percentage of all-cause mortality rate was about 8-9% in all 10-year age groups between 40-49 and 80-89. In ages 30-39 it was only about 5%, and in ages 20-29 it was only about 2%. However younger age groups have a low percentage of deaths from natural causes in general and not only a low percentage of COVID deaths, so the percentage of deaths from natural causes was about 96% in ages 80-89 but only about 24% in ages 20-29:

(In the code above I defined deaths from natural causes as deaths with the underlying cause A-Q or COVID, even though there's also some deaths from natural causes that have an R or U code listed as the underlying cause.)

In the United States in 2020-2023, people aged 60 had only about 11 times higher mortality rate than people aged 20, which is close to Kirsch's estimate of a 10-fold difference, but it's because young people in the United States have a lot of deaths from drug overdoses and other external causes. But for example in the Czech Republic in 2020-2023, people aged 60 had about 21 times higher mortality rate than people aged 20:

However even in the Czech Republic, COVID deaths accounted for only about 2% of all deaths in people in their 20s in 2020-2023:

But again, it's expected for younger age groups to have a low mortality rate for deaths from natural causes relative to the overall mortality rate of the age group. That doesn't mean that within an age group the most frail people would have a disproportionately high risk of dying from COVID relative to dying from other causes. And it doesn't mean that the HVE would explain why unvaccinated people would have a 10 times higher COVID ASMR than vaccinated people but only 3 times higher all-cause ASMR.

In many datasets there isn't even too much difference between age groups in the COVID mortality rate relative to the all-cause mortality rate. For example in the latest version of the English ONS data, the percentage of COVID deaths out of all deaths ranges from about 4.1% in ages 18-39 to about 5.6% in ages 80-89:

Did Levi-Ladapo show that Pfizer vaccines caused a 22% increase in all-cause mortality in the US?

He linked to a spreadsheet where he digitized a plot from Figure 2 of the Levi-Ladapo paper, so he could calculate the ratio between the cumulative Pfizer risk and Moderna risk. The ratio during the early days doesn't seem reliable because of error introduced by the digitization, because Moderna had negative deaths on days 0 to 7, and the ratio was about -12 on day 7 but about 26 on day 8, so Kirsch omitted the first 15 days from his plot. However later on you can see that the ratio remains at a stable level of about 1.4 (even though the ratio of non-cumulative mortality would of course be less stable):

Levi et al. should've extended their analysis further than 1 year. If the ratio between Pfizer and Moderna mortality risk would've continued to be elevated even in 2023 or 2024, it is not compatible with Kirsch's calculation that Pfizer vaccines increased mortality among the entire US population by 22%, because the United States had close to 0% excess mortality in 2023 and 2024:

t=fread("https://sars2.net/f/uspopdeadmonthly.csv")
t=t[year%in%2011:2025][!(year==2025&month>=4)]

lm=glm(dead~year+factor(age)+factor(month),poisson,t[year%in%2011:2019],offset=log(persondays))
t$base=predict(lm,t,type="response")
a=t[,.(dead=sum(dead),base=sum(base)),date]

a=merge(a,dcast(fread("https://sars2.net/f/wondercovidmonthly.csv"),date~type),all=T)
a[,date:=as.Date(paste0(date,"-16"))]

p=a[,.(x=date,y=c(dead,dead-ucd,dead-mcd,base)/days_in_month(date),z=rep(1:4,each=.N),facet=1)]
p=rbind(p,a[,.(x=date,y=(c(dead,dead-ucd,dead-mcd)/base-1)*100,z=rep(1:3,each=.N),facet=2)])

p[,facet:=factor(facet,,c("Deaths divided by\ndays in month","Excess percen-\ntage of deaths"))]
p[,z:=factor(z,,c("Deaths","Not UCD COVID","Not MCD COVID","2011-2019 Poisson regression"))]

xstart=as.Date("2018-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
p=p[x>=xstart&x<=xend]

pct=t[,.(pct=(sum(dead)/sum(base)-1)*100),.(x=as.Date(paste0(year,"-7-1")))]
pct=cbind(pct,p[facet==levels(facet)[2],.(y=extendrange(y)[1]),facet])

ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray92",linewidth=.4)+
geom_segment(data=p[,.(facet=levels(facet)[2])],x=xstart,xend=xend,y=0,yend=0,linewidth=.4,color="gray75")+
geom_point(aes(x,y,color=z,alpha=z),stroke=0,size=1.4)+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_label(data=p[,extendrange(y)[2],facet],aes(label=facet,y=V1),x=xend,hjust=1,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87,lineheight=.85)+
geom_label(data=p[,extendrange(y)[2],facet],aes(label=facet,y=V1),x=xend,hjust=1,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.0,size=3.87,lineheight=.85)+
geom_text(data=pct,aes(x,y,label=paste0(ifelse(pct>0,"+",""),sprintf("%.1f",pct),"%")),vjust=.2,size=3.7,color="gray50")+
labs(title="Monthly deaths in United States divided by days in month",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=\(x)extendrange(x,,c(.05,0)),breaks=\(x)pretty(x),labels=\(x)ifelse(x<1e3,paste0(x,"%"),x))+
scale_color_manual(values=c("black","gray50","gray80","#3333ff"))+
scale_alpha_manual(values=c(1,1,1,0))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=2,byrow=F))+
theme(axis.text=element_text(size=11,color="black",margin=margin(2,2,2,2)),
  axis.ticks=element_line(linewidth=.4,color="gray75"),
  axis.ticks.length=unit(0,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="center",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4,color="gray75"),
  panel.grid.major=element_blank(),
  panel.grid.major.y=element_line(linewidth=.4,color="gray92"),
  panel.spacing.y=unit(5,"pt"),
  plot.margin=margin(4,5,3,4),
  plot.title=element_text(size=11.3,face=2,margin=margin(1,,3),hjust=.5),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.4,height=3.4,dpi=300*4)

Also in my plot above there was a total of only about 17% excess deaths in 2021 and 9% in 2022, and most of it was accounted by deaths with the underlying cause COVID, so there doesn't seem to be room for 22% excess deaths caused by Pfizer vaccines.

Kirsch even calculated the percentage of 22% wrong, because he multiplied 36% with the percentage of vaccinated people who got a Pfizer vaccine, even though he should've multiplied 36% with the percentage of total US population that got a Pfizer vaccine (or a percentage by age group weighted by deaths within each age group).

Further comments to Kirsch

Duration of short-term HVE in light of Japanese Koganei data

t=fread("https://sars2.net/f/jpbuckets.csv.gz")
ages=c(0,3:4*10,10:19*5)
t[,age:=ages[findInterval(pmax(age,0),ages)]]

doses=c("Unvaccinated",paste("Dose",1:7))
a=t[,.(dead=sum(dead),pop=sum(pop)),.(dose=factor(dose,,doses),age,month)]
a=rbind(a,a[dose!="Unvaccinated",.(dead=sum(dead),pop=sum(pop),dose="Vaccinated"),.(age,month)])
a=rbind(a,a[dose%like%"accin",.(dead=sum(dead),pop=sum(pop),dose="All people"),.(age,month)])
a=merge(a,t[month=="2022-01",sum(pop),age][,.(std=V1/sum(V1),age)])

p=a[,.(pop=sum(pop),y=sum(dead/pop*std*365e5)),.(x=as.Date(paste0(month,"-1")),z=dose)]
p[pop/365<1e3,y:=NA]
p[y>=5e3,y:=NA]
frac=p[!z%in%c("Vaccinated","All people"),.(frac=pop/sum(pop),z),x]

ybreak=pretty(p$y,8);ystart=0;yend=max(ybreak);xstart=min(p$x);xend=max(p$x)

pal=c("gray50",hcl(c(23,17,11,7,3,0,33)*10+15,90,70),"black","gray50")

ggplot(p,aes(x,y,color=z))+
geom_area(data=frac,aes(y=frac*yend*.9999,fill=z),linewidth=.15,show.legend=F,alpha=.3)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="black")+
geom_line(aes(linetype=z,linewidth=z))+
geom_point(aes(alpha=z),size=1)+
annotate("label",x=xstart,y=yend,hjust=0,vjust=1,size=3.8,label="ASMR per 100,000 person-years",label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4)+
annotate("label",x=xend,y=yend,hjust=1,vjust=1,size=3.8,label="Percentage of group",label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4)+
scale_x_date(breaks=unique(p$x)[c(F,F,T)],date_labels="%b\n%y")+
scale_y_continuous(limits=c(ystart,yend),breaks=seq(0,yend,1000),labels=\(i)ifelse(i<1000,i,paste0(i/1e3,"k")),sec.axis=sec_axis(trans=~./yend*100,labels=\(x)paste0(x,"%")))+
labs(x=NULL,y=NULL)+
ggtitle("Age-standardized mortality rate in Japanese dataset")+
scale_color_manual(values=pal)+
scale_linetype_manual(values=rep(c("solid","42"),c(9,1)))+
scale_linewidth_manual(values=rep(c(.4,.6),c(9,1)))+
scale_alpha_manual(values=rep(1:0,c(9,1)))+
scale_fill_manual(values=pal)+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=2))+
theme(axis.text=element_text(size=10,color="black"),
  axis.ticks=element_line(linewidth=.4),
  axis.ticks.length=unit(3,"pt"),
  axis.title=element_text(size=11),
  legend.background=element_blank(),
  legend.box.background=element_blank(),
  legend.box.just="center",
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_rect(fill="white"),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.justification="center",
  legend.margin=margin(,,3),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=10.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(5,5,4,5),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,2)))
ggsave("1.png",width=5.6,height=3.7,dpi=300*4)

And I asked him that if the short-term HVE lasts for only 3 weeks like he claims, then why do unvaccinated people in the Koganei data have higher mortality in the last 3 months of 2021 than in 2022-2024? If you look at only ages 60+ which account for about 95% of all deaths in the dataset, then in the last 3 months of 2021 there are no longer many people who had received the first dose less than 21 days ago, so if the short-term HVE only lasts for 3 weeks, it should no longer have elevated the mortality of unvaccinated people by too much:

But in the last 3 months of 2021, unvaccinated people have about 3.4 times higher ASMR than vaccinated people:

In the next plot I calculated the baseline by multiplying the number of person-days for each combination of age group and observation month with the mortality rate among all people included in the dataset for the same combination of age group and observation month. You can see that it takes much longer than 3 weeks after vaccination for the deaths to reach close to the baseline:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

b=fread("https://sars2.net/f/jpbucketskeep.csv.gz")
b[,age:=pmin(age,95)%/%5*5]

d=merge(b,b[dose<=1,.(base=sum(dead)/sum(pop)),.(month,age)])[,base:=base*pop]
d=rbind(d[dose>0][,dose:=0],d[dose>0])
a=d[,.(dead=as.double(sum(dead)),base=sum(base)),.(week,dose)]

a[,dead:=ma(dead,2),dose]
mean=a[week<=60,.(mean=mean(base)),,dose]
a=merge(a,mean)
p=a[,.(x=week,y=c(dead,base)/mean*100,z=rep(1:2,each=.N),dose)]

p[,z:=factor(z,,c("Deaths","Baseline"))]
p[,dose:=factor(dose,,paste0(c("All doses",paste("Dose",1:7))," (",sprintf("%.1f",mean$mean),")"))]

xstart=0;xend=max(p$x);xstep=20;ystart=0;yend=160;ybreak=0:7*20

ggplot(p)+
facet_wrap(~dose,ncol=2,dir="v")+
geom_hline(yintercept=100,color="gray75",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_label(data=p[rowid(dose)==1],aes(label=dose),x=xstart,y=yend,hjust=0,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87)+
geom_label(data=p[rowid(dose)==1],aes(label=dose),x=xstart,y=yend,hjust=0,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87)+
labs(title="Deaths by weeks since vaccination in Koganei (±2-week moving average)",subtitle="Shown as percentage of average baseline value on weeks 0-60 (in parentheses)",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,xstep))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black","#ff5555"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box="vertical",
  legend.box.just="center",
  legend.box.margin=margin(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(21,"pt"),
  legend.key=element_rect(fill="white"),
  legend.margin=margin(,,5),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(3,"pt"),
  plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,2)),
  plot.title=element_text(size=11.3,face="bold",hjust=.5,margin=margin(1,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=6,height=6,dpi=300*4)

HVE test for KCOR

In the spreadsheet Kirsch considered that if unvaccinated deaths follow an exponential decay plus a constant factor, then the unvaccinated deaths subtracted from the constant factor will be linear on a log scale. And similarly if vaccinated deaths follow a constant factor minus exponential decay, then the vaccinated deaths subtracted from the constant factor will be linear on a log scale. That happens to be true in his simulated data at the top, where the HVE deaths decay exponentially, unvaccinated deaths are 100 plus HVE deaths, and vaccinated deaths are 300 minus HVE deaths.

However the Czech plot at the bottom only includes 4 weeks, which are weeks 24 to 27 of 2021. Kirsch should've included a much longer period in his plot, because different people were vaccinated at different times, and many people were vaccinated long before his observation period started, so there was not a very sharp increase in vaccinated mortality at the start of his observation period. And there's so much week-to-week variation in the deaths that 4 weeks is not long enough to evaluate if the deaths follow an expontential function or not.

And anyway the unvaccinated deaths had not yet reached a plateau on week 27 of 2021, so even if the unvaccinated deaths followed an exponential decay, the deaths on a given week minus deaths on week 27 would not be linear on a log scale. Kirsch should've rather tried to fit a curve of the form a*exp(b*week)+c to the data, like in my next plot.

In the next plot I adjusted deaths for seasonality by dividing deaths by deaths the same week in both unvaccinated and vaccinated people. I also excluded weeks with high COVID deaths in October 2021 to April 2022. After that both vaccinated and unvaccinated deaths roughly followed an exponential function:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")[DatumUmrtiLPZ!=""]
t[,dose:=0]
t[Datum_Prvni_davka!=""&Datum_Prvni_davka<="2021-24",dose:=1]

a=t[,.(dead=.N,coviddead=sum(Umrti!="")),,.(dose,week=DatumUmrtiLPZ)]
a=a[,.(dead=dead/sum(dead)*100,dose),week]

iso=`class<-`(0:1e4*7,"Date");names(iso)=format(iso,"%G-%V")
p=a[week>="2021-24"&week<="2022-52",.(x=iso[week],week,y=dead,z=factor(dose,,c("Unvaccinated","Vaccinated")))]
p[,i:=as.integer(factor(x))]

p2=p[,{sub=.SD[!(week>="2021-41"&week<="2022-15")]
  .(x,i,week,y=predict(nls(y~   c-a*exp(-b*i),sub,sub[,.(a=y[1]-y[.N],b=.08,c=max(y))]),.SD),type=2)},z]

p=rbind(cbind(p,type=1),p2)
p[,type:=factor(type,,c("Deaths","Exponential fitted curve"))]

xstart=as.Date("2021-1-1");xend=as.Date("2023-1-1");xbreak=seq(xstart,xend,"month")
ystart=0;yend=100;ybreak=0:10*10

note="Vaccination status was determined at the end of week 24 of
2021. The dotted weeks were excluded from the fitting period
of the exponential curve (2021 week 41 to 2022 week 15)."

ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray75",linewidth=.4)+
geom_line(data=copy(p)[type==type[1]&week>"2021-41"&week<"2022-15",y:=NA],aes(x,y,color=z,alpha=type),linewidth=.6)+
geom_line(data=p[type==type[1]&week>="2021-41"&week<="2022-15"],aes(x,y,color=z,alpha=type),linetype="11",linewidth=.6,show.legend=F)+
labs(x=NULL,y=NULL,title="NZIP data: Deaths as percentage of weekly total deaths")+
annotate(geom="label",x=pmean(xstart,xend),y=17,label=note,label.r=unit(4,"pt"),label.padding=unit(4,"pt"),label.size=.4,size=3.5,color="gray75",lineheight=.9)+
annotate(geom="label",x=pmean(xstart,xend),y=17,label=note,label.r=unit(4,"pt"),label.padding=unit(4,"pt"),label.size=0,fill=NA,size=3.5,lineheight=.9)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=ifelse(month(xbreak)==7,year(xbreak),""))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("#5555ff","#ff5555"))+
scale_alpha_manual(values=c(1,.4))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks=element_line(linewidth=.4,color="gray75"),
  axis.ticks.length.x=unit(-3,"pt"),
  axis.ticks.length.y=unit(0,"pt"),
  legend.background=element_rect(color="gray75",linewidth=.4),
  legend.box="horizontal",
  legend.box.margin=margin(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(.5,1),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(.5,1),
  legend.spacing.x=unit(0,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,color="gray75",linewidth=.4),
  panel.grid.major.x=element_blank(),
  panel.grid.major.y=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(3,"pt"),
  plot.margin=margin(5,5,3,4),
  plot.subtitle=element_text(margin=margin(,,4),hjust=.5),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(1,,4)))
ggsave("1.png",width=4.6,height=3,dpi=300*4)

The next plot shows excess deaths by weeks after the first dose in the Czech FOI data. The exponential, logistic, and Gompertz functions all produce a fairly good fit to the data, even though they are all too low on week 0. However the logarithmic function produces a much worse fit:

b=fread("https://sars2.net/f/czbucketskeep.csv.gz")
b[,age:=pmin(age,95)%/%5*5]
b=merge(b[dose<=1,.(base=sum(dead)/sum(alive)),.(age,month)],b)
b[,week:=week+1]

p1=b[week<=61&dose==3,.(y=sum(dead)/sum(base*alive),z=1),.(x=week)]
p2=p1[,.(x,y=predict(nls(y~L/(1+exp(-k*(x-x0))),start=list(L=1,k=0.3,x0=10)),p1),z=2)]
p3=p1[,.(x,y=predict(nls(y~a*exp(-b*exp(-c*x)),start=list(a=1,b=5,c=0.3)),p1),z=3)]
p4=p1[,.(x,y=predict(lm(y~log(x),p1),p1),z=4)]
p5=p1[,.(x,y=predict(nls(y~a*exp(-b*x)+c,start=list(a=-.6,b=.1,c=.85)),p1),z=5)]

p=rbind(p1,p2,p3,p4,p5)[,z:=factor(z,,c("Dose 3 ratio to baseline","Logistic","Gompertz","Logarithmic","Exponential"))]
p[,x:=x-1]

xstart=min(p$x);xend=max(p$x);ybreak=pretty(c(0,p$y),7);ystart=min(ybreak);yend=max(ybreak)

ggplot(p)+
geom_hline(yintercept=1,color="gray75",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Czech FOI: Deaths relative to baseline by weeks after dose 3")+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,5))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black",hsv(c(22,30,12)/36,.6,1),"#cccc00"))+
scale_alpha_manual(values=c(1,0,0,0,0))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray75",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(.5,0),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(.5,.05),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  plot.margin=margin(5,12,5,5),
  plot.subtitle=element_text(margin=margin(,,4),hjust=.5),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(2,,4)))
ggsave("1.png",width=4.9,height=3,dpi=300*4)

In the Japanese FOI data for the city of Koganei, there's such a small sample size that individual doses have a high level of noise, so in the next plot I looked at all doses added together. Now the exponential, logistic, and Gompertz curves again produce a fairly good fit, even though all of them are too high on week 0. All of them reach a plateau around week 40:

b=fread("https://sars2.net/f/jpbucketskeep.csv.gz")
b[,age:=pmin(age,95)%/%5*5]
b=merge(b[dose<=1,.(base=sum(dead)/sum(pop)),.(age,month)],b)
b=b[week<=170]
b[,week:=week+1]

p1=b[dose>0,.(y=sum(dead)/sum(base*pop),z=1),.(x=week)]
p2=p1[,.(x,y=predict(nls(y~L/(1+exp(-k*(x-x0))),start=list(L=1,k=0.3,x0=10),p1),p1),z=2)]
p3=p1[,.(x,y=predict(nls(y~a*exp(-b*exp(-c*x)),start=list(a=1,b=5,c=0.3),p1),p1),z=3)]
p4=p1[,.(x,y=predict(lm(y~log(x),p1),p1),z=4)]
p5=p1[,.(x,y=predict(nls(y~a*exp(-b*x)+c,start=list(a=-.6,b=.1,c=.85)),p1),z=5)]

p=rbind(p1,p2,p3,p4,p5)
p[,z:=factor(z,,c("Deaths ratio to baseline","Logistic","Gompertz","Logarithmic","Exponential"))]
p[,x:=x-1]

xstart=min(p$x);xend=max(p$x);ybreak=pretty(c(0,p$y));ystart=min(ybreak);yend=max(ybreak)

ggplot(p)+
geom_hline(yintercept=1,color="gray75",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Deaths relative to baseline by weeks after vaccination in\nKoganei, Japan (all doses added together)")+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,20))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black",hsv(c(22,30,12)/36,.6,1),"#cccc00"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray75",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(.5,0),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(.5,.05),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  plot.subtitle=element_text(margin=margin(,,4),hjust=.5),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(1,,4)))
ggsave("1.png",width=5,height=3,dpi=300*4)

Pfizer-Moderna mortality ratio in Japanese Koganei data

A few days after Steve Kirsch published a spreadsheet of the record-level data from Koganei in Japan, Kenji Fujikawa posted a CSV version of the data that also includes vaccine brands: https://medicalfacts.info/vdeath.rb.

I used the CSV file to do a Poisson regression for mortality by vaccine brand, which I adjusted for age group, sex, observation month, and vaccination month. The mortality rate ratio of Pfizer relative to Moderna was about 2.0 for first doses, 2.2 for second doses, 0.8 for third doses, 0.7 for 4th doses, and 0.4 for 5th doses, and 0.5 for 6th doses. So Pfizer had higher mortality for primary course doses but Moderna had higher mortality for booster doses:

The third and fourth doses had the most deaths for Moderna so they had the narrowest confidence intervals. I kept people included under earlier doses after a new dose, so if someone died after getting a Moderna vaccine for the third dose and a Pfizer vaccine for the fourth dose, I counted their death both under Moderna for the third dose and under Pfizer for the fourth dose.

Here's a plot of the same data, where you can see how dose 3 has a much narrower CI than dose 4 on a log scale, even though the CIs have similar width without log transformation:

The Levi-Ladapo study included only primary course doses, but it would be interesting to see if their results would change if they looked at third or fourth doses instead.

The next plot shows a monthly excess percentage of deaths that was only adjusted for age but not other variables. Moderna doesn't have a big enough sample size to calculate monthly mortality rates reliably. But you can still roughly see how Pfizer has higher mortality for doses 1 and 2, Moderna for doses 4-6, and doses 3 and 7 are closest to a draw:

t=fread("https://sars2.net/f/koganeibucketskeep.csv.gz")
t[,age:=pmin(age,95)%/%5*5]

t=merge(t,t[dose<=1,.(base=sum(dead)/sum(pop)),.(month,age)])[,base:=base*pop]
t=rbind(t[dose>0],t[dose>0][,dose:=0])

a=t[,.(dead=sum(dead),base=sum(base),pop=sum(pop)),.(month,brand,age,dose)]
p=a[,.(y=(sum(dead)/sum(base)-1)*100),.(month,brand,dose)]

p=p[brand%like%"Mod|Pfi",.(x=as.Date(paste0(month,"-16")),y,dose,brand)]
p[,dose:=factor(dose,,c("Dose 1-7 total",paste("Dose",1:7)))]
p[,brand:=relevel(factor(brand),"Pfizer")]

xstart=as.Date("2021-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ystart=-100;yend=200;ybreak=-2:3*50

ggplot(p)+
facet_wrap(~dose,ncol=2,dir="v")+
geom_hline(yintercept=ybreak,linewidth=.4,color="gray90")+
geom_vline(xintercept=seq(xstart,xend,"year"),linewidth=.4,color="gray90")+
geom_hline(yintercept=0,linetype="42",linewidth=.4,color="gray75")+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=brand),linewidth=.6)+
labs(title="Monthly excess percentage of deaths in Koganei, Japan",x=NULL,y=NULL)+
geom_label(data=p[rowid(dose)==1],aes(label=dose),x=xstart,hjust=0,y=yend,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87)+
geom_label(data=p[rowid(dose)==1],aes(label=dose),x=xstart,hjust=0,y=yend,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c(hsv(c(240,355)/360,c(.94,.75),c(.76,.82))))+
coord_cartesian(ylim=c(ystart,yend),clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray75",linewidth=.4),
  legend.box="horizontal",
  legend.box.just="center",
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(3,"pt"),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(1,,3)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5,height=4.5,dpi=300*4)

Ratio of COVID deaths to all-cause deaths in Levi study relative to general population of Florida

Levi et al. wrote: "Deaths were attributed to COVID-19 if a corresponding ICD-10 code was listed either as the primary or underlying cause of death on the death certificate." [https://www.medrxiv.org/content/10.1101/2025.04.25.25326460v2.full.pdf] By the primary cause of death, they probably meant that the cause appears on the first line of the first part of the death certificate, which is what the CDC calls the "immediate cause of death". [https://www.cdc.gov/nchs/data/nvss/vsrg/vsrg03-508.pdf] It's not clear if they meant the first item on the first line or any item on the first line, because usually there's only one item on the first line but sometimes there's multiple items. But in any case, CDC WONDER doesn't support retrieving deaths by immediate cause of death, so it's not possible to retrieve data from CDC WONDER using the same definition of COVID death that was used in Levi's paper.

In the fixed-width files for the NVSS data, each multiple cause of death has a field that is 6 characters wide, where the first character shows the part and line of the death certificate, and the last 4 characters show the ICD code. [https://ftp.cdc.gov/pub/Health_Statistics/NCHS/Dataset_Documentation/DVS/mortality/Multiple-Cause-Record-Layout-2021.pdf] Depending on which definition of immediate cause of death you use, you can either select causes that appear at any position of the first line of part I, or causes that appear as the first item on the first line of part I. I used the latter definition here:

The output shows the number of COVID deaths by underlying cause, multiple cause, immediate cause, and immediate or underlying cause:

The number of deaths by immediate or underlying cause is nearly the same as the number of deaths by underlying cause alone. So it won't make much difference if you only retrieve deaths with underlying cause COVID at CDC WONDER but you don't additionally include deaths with immediate cause COVID.

levi=CJ(age=c(18,4:8*10))
levi$all=c(2141,2804,7829,18477,30254,52760)
levi$covid=c(98,176,533,1280,2314,4054)

t=fread("https://sars2.net/f/wonderfloridalevi.csv")
t=t[,x:=.GRP,.(year,month)][,cbind(.SD,i=rep(1:8,each=.N))]

a=t[x>=i&x<i+12,.(flo=sum(covid)/sum(all)),.(age,i)]
a=merge(a,levi[,.(age,levi=covid/all)])

p=a[,.(age,x=i,y=c(c(flo,levi)*100),z=rep(1:2,each=.N))]

p[,z:=factor(z,,c("CDC WONDER (vaccinated and unvaccinated)","Levi study (vaccinated)"))]
p[,age:=factor(age,,levi[,paste0(age,c(paste0("-",age[-1]-1),"+"))])]

lab=format(seq(as.Date("2021-1-1"),,"month",8),"%b %y")
lab=paste0(lab,"-",format(seq(as.Date("2021-12-1"),,"month",8),"%b %y"))

xstart=1;xend=8;ybreak=0:5*5;yend=25

ggplot(p)+
facet_wrap(~age,ncol=2,dir="v")+
geom_rect(data=p[rowid(age)==1],ymin=0,ymax=yend,xmin=xstart-.5,xmax=xend+.5,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_point(aes(x,y,color=z),stroke=0,size=1.5)+
geom_text(data=p[rowid(age)==1],aes(xend+.35,22.5,label=age),hjust=1,size=3.87)+
labs(title="Percentage of COVID deaths out of all deaths in Florida",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xstart:xend,labels=month.abb[1:8])+
scale_y_continuous(limits=c(0,yend),breaks=ybreak,labels=ifelse(ybreak==yend,"",paste0(ybreak,"%")))+
scale_color_manual(values=c("black","#ff5555"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(23,"pt"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(color="gray80",fill=NA,linewidth=.4),
  panel.grid=element_blank(),
  panel.grid.major.y=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(3,"pt"),
  plot.title=element_text(size=11,hjust=.5,face="bold",margin=margin(,,2)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.5,height=3.6,dpi=300*4)

Assumption of 75% efficacy before Omicron and 50% after Omicron by Ioannides

In July 2025 John Ioannides et al. published a paper where they estimated that about 2.5 million deaths were averted by COVID vaccination in 2020-2024. They wrote: "We assume VE equals 75% (sensitivity range, 40%-85%) before Omicron and 50% (sensitivity range, 30%-70%) during Omicron." [https://jamanetwork.com/journals/jama-health-forum/fullarticle/2836434]

Their assumption was criticized by Raphael Lataster, who wrote: "So, first big issue, COVID-19 vaccine effectiveness for death (VE). They claim VE of 75% then 50% post-omicron. Citing 2 sources. The first is a non-gold-standard study of very limited scope, and which did not control for the healthy vaccinee bias (ironically something Ioannidis has done research on)." [https://okaythennews.substack.com/p/debunked-landmark-covid-vaccine-study] He also wrote: "Moving on to another critical issue, VE waning. They say they've already factored waning in their 75%/50% figures which just sounds like a complete cop-out, especially when there's no transparency."

In order to estimate vaccine efficacy against death while simultaneously adjusting for HVE, waning efficacy over time, and unvaccinated people acquiring natural immunity over time, you can look the ratio of (unvaccinated COVID ASMR / vaccinated COVID ASMR) / (unvaccinated non-COVID ASMR / vaccinated non-COVID ASMR). In the ONS dataset the ratio is close to 4 on average in 2021 and 2 in 2022, which corresponds to 75% efficacy before Omicron and 50% efficacy after Omicron:

t=fread("https://sars2.net/f/ons.csv")
t=rbind(t[ed==7&month<="2021-03"],t[ed==9])

s=t[status%like%"acci"&age=="Total"&cause!="All causes"]
p=s[,.(x=as.Date(paste0(month,"-16")),y=asmr,z=(status!="Unvaccinated")*1+1,cause=ifelse(cause%like%"involving",1,2),facet=1)]

ratio=dcast(p,x+cause~z,value.var="y")[,.(x,y=`1`/`2`,cause,z=3,facet=2)]
ratio2=ratio[,.(y=y[1]/y[2],facet=3,z=3,cause=1),x]
p=rbind(p,ratio,ratio2)

p[,z:=factor(z,unique(z),c("Unvaccinated","Vaccinated","Ratio"))]
p[,cause:=factor(cause,,c("COVID","Non-COVID"))]
p[,facet:=factor(facet,,c("ASMR","Unvaccinated-vaccinated ratio","COVID-non-COVID\nratio of UV-V ratios"))]

xstart=as.Date("2021-1-1");xend=as.Date("2023-6-1");xbreak=seq(xstart,xend,"year")
ylim=p[,.(max=max(y)),facet]

ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free_y")+
geom_rect(data=ylim,aes(ymin=0,ymax=max),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray70",linewidth=.4)+
geom_line(aes(x,y,color=z,alpha=cause),linewidth=.6)+
geom_point(aes(x,y,color=z,alpha=cause,shape=cause),stroke=.6,size=1.5)+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4,color="gray72",size=3.87,lineheight=.8)+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=0,size=3.87,fill=NA,lineheight=.8)+
labs(x=NULL,y=NULL,title="ASMR per 100,000 person-years in English ONS data")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(breaks=\(x)pretty(c(0,x)))+
scale_color_manual(values=c("#5555ff","#ff5555","black"))+
scale_alpha_manual(values=c(1,.5))+
scale_shape_manual(values=c(16,1))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),alpha=guide_legend(order=2),shape=guide_legend(order=2))+
theme(axis.text=element_text(size=11,margin=margin(2,2,2,2),color="gray40"),
  axis.text.x=element_text(hjust=0),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box="vertical",
  legend.box.just="center",
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(2.5,5.5,2.5,2.5),
  legend.position="top",
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(3,"pt"),
  plot.title=element_text(size=11.4,face=2,margin=margin(,,4),hjust=.5),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.6,height=4,dpi=300*4)

I also tried using the Czech NZIP data to calculate a ratio of (unvaccinated COVID ASMR / vaccinated COVID ASMR) / (unvaccinated non-COVID ASMR / vaccinated non-COVID ASMR). The ratio was lower than 4 on average in 2021, but it's partially because unvaccinated people are missing a lot of deaths in early 2021. And it's also because COVID deaths are undercounted in the NZIP data, which you can see from how unvaccinated people have a big spike in non-COVID ASMR during the Delta wave:

t=fread("xz -dc https://sars2.net/f/nzipbuckets.csv.xz")
t[,born:=pmin(1990,pmax(1925,born))]

a=t[,.(dead=c(sum(coviddead),sum(dead)-sum(coviddead)),pop=sum(pop),cause=1:2),.(obsweek,born,dose=pmin(dose,1))]
a=merge(a,do.call(CJ,lapply(a[,.(born,obsweek,dose,cause)],unique)),all=T);a[is.na(a)]=0

a=a[,.(dead=ma(dead,2),pop=ma(pop,2),obsweek),.(born,dose,cause)]

a[,date:=as.Date("2020-03-05")+(obsweek-1)*7]

a=merge(t[obsweek==106,sum(pop),born][,.(born,std=V1/sum(V1))],a)

p=a[,.(y=sum(dead/pop*std/7*365e5),facet=1),.(cause,x=date,z=dose)]

ratio=p[,.(y=y[z==0]/y[z==1],facet=2,z=3),.(x,cause)]
ratio2=ratio[,.(y=y[1]/y[2],facet=3,z=3,cause=1),x]
p=rbind(p,ratio,ratio2)

p[,z:=factor(z,unique(z),c("Unvaccinated","Vaccinated","Ratio"))]
p[,cause:=factor(cause,,c("COVID","Non-COVID"))]
p[,facet:=factor(facet,,c("ASMR","Unvaccinated-vaccinated ratio","COVID-non-COVID\nratio of U-V ratios"))]

xstart=as.Date("2021-1-1");xend=as.Date("2024-1-1");xbreak=seq(xstart+182,xend,"year")
p=p[x>=xstart&x<=xend]
ylim=p[,.(max=max(pretty(c(0,y)))),facet]

ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=0,ymax=max),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray70",linewidth=.4)+
geom_line(aes(x,y,color=z,alpha=cause),linewidth=.6)+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray72",fill="#ffffffcc",size=3.87,lineheight=.8)+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,fill=NA,size=3.87,lineheight=.8)+
labs(x=NULL,y=NULL,title="ASMR per 100,000 person-years in Czech NZIP data")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(breaks=\(x)pretty(c(0,x)),labels=\(x)ifelse(x==max(x),"",x))+
scale_color_manual(values=c("#5555ff","#ff5555","black"))+
scale_alpha_manual(values=c(1,.4))+
scale_shape_manual(values=c(16,1))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),alpha=guide_legend(order=2),shape=guide_legend(order=2))+
theme(axis.text=element_text(size=11,margin=margin(2,2,2,2),color="gray40"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box="vertical",
  legend.box.just="center",
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="center",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(2.5,5.5,2.5,2.5),
  legend.position="top",
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major.x=element_blank(),
  panel.grid.major.y=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(3,"pt"),
  plot.title=element_text(size=11.4,face=2,margin=margin(,,4),hjust=.5),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.4,height=4,dpi=300*4)

The COVID deaths in the ONS dataset are deaths where COVID was mentioned anywhere on the death certificate, or what is called multiple cause of death in the United States. In my plot for the ONS data, part of the reason why the 4-way ASMR ratio dropped in 2022 might be because the ratio of UCD to MCD COVID deaths went down, or at least that's what happened in the United States after the emergence of Omicron:

v=fread("curl -Ls sars2.net/f/vital.csv.xz|xz -dc")

p=v[cause=="U071",.(y=sum(ucd)/sum(mcd)*100),.(year,month)][,x:=as.Date(paste(year,month,1,sep="-"))]

xstart=as.Date("2020-1-1");xend=as.Date("2024-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ystart=0;yend=100;ybreak=0:10*10

ggplot(p,aes(x+15,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray91",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray91",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(linewidth=.5)+
geom_point(size=1)+
labs(title="NVSS: Percentage of deaths with underlying cause of death\nCOVID out of deaths with multiple cause of death COVID",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x,"%"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.ticks.length=unit(0,"pt"),
  panel.background=element_blank(),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,4)))
ggsave("1.png",width=4.9,height=2.6,dpi=300*4)

Unvaccinated and vaccinated CMR of people born in 1940-1949

When he said the unvaccinated CMR remained flat, he was talking about the CMR at the start of his x-axis before the Delta wave.

The Czech Republic had a high percentage of unvaccinated people compared to other countries like England or Japan, so unvaccinated people didn't have a very large spike in mortality during the rollout of the primary course doses.

But that doesn't mean that the increase in vaccinated mortality in 2021 wouldn't have been due to the HVE. The vaccinated CMR was about 2,000-3,000 per 100,000 in mid-2021. People born in 1940-1949 were 71 to 81 years old in 2021, but the Czech CMR for ages 71-81 was about 3,700 to 4,000 per 100,000 in 2015-2019:

Kirsch started his x-axis from week 24, so you couldn't see that earlier in 2021 unvaccinated people had a spike in deaths, even though it was mostly because of COVID deaths and not the straggler effect:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
t=t[RokNarozeni%in%c("1940-1944","1945-1949")]
t=t[Infekce%in%c(NA,1)]

t[,dose1:=Datum_Prvni_davka]
t=t[!(DatumUmrtiLPZ!=""&dose1>DatumUmrtiLPZ)]

t=rbind(copy(t)[dose1>"2021-24",dose1:=""][,facet:=1],t[,facet:=2])
t[,dose:=0][dose1!="",dose:=1]

a=t[,.(week=c(rep("2020-10",.N),dose1),dose=rep(0:1,each=.N),facet)]
a=a[,.(vax=.N),.(week,dose,facet)]
a=merge(a,t[,.(dead=.N),.(week=DatumUmrtiLPZ,dose,facet)],all=T)[week!=""]
a=merge(do.call(CJ,lapply(a[,1:3],unique)),a,all=T);a[is.na(a)]=0

a=merge(a,t[,.(coviddead=.N),.(week=Umrti,facet,dose)],all=T)[week!=""]

a[,cumvax:=cumsum(vax),.(dose,facet)][,pop:=cumvax-cumsum(dead),.(dose,facet)]
a[dose==0,pop:=pop-a[dose==1,cumvax]]

a=a[,.(dead,pop,week,facet,dose,coviddead)]
a=rbind(a,a[,.(dead=sum(dead),pop=sum(pop,na.rm=T),coviddead=sum(coviddead),dose=2),.(week,facet)])

iso=`class<-`(0:1e4*7,"Date");names(iso)=format(iso,"%G-%V")
p=a[,.(y=(sum(dead)-c(0,sum(coviddead)))/sum(pop)/7*365e5,z=1:2),.(dose,x=iso[week],facet)]
p[,dose:=factor(dose,,c("Unvaccinated","Vaccinated","Total"))]
p[,z:=factor(z,,c("All causes","Not COVID"))]
p[,facet:=factor(facet,,paste("Doses admin-\nistered after cutoff\ndate",c("ignored","not ignored")))]

xstart=as.Date("2021-1-1");xend=as.Date("2024-1-1");xbreak=seq(xstart+182,xend,"year")
p=p[x>=xstart&x<=xend]
ystart=0;ybreak=pretty(p$y,6);yend=max(ybreak)

ggplot(p)+
facet_wrap(~facet,ncol=1,scales="free")+
geom_hline(yintercept=c(ybreak[ybreak<yend],yend),color="gray90",linewidth=.4,lineend="square")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4,lineend="square")+
annotate("rect",xmin=xstart,xmax=xend,ymin=0,ymax=yend,color="gray75",linewidth=.4,lineend="square",linejoin="mitre",fill=NA)+
geom_line(aes(x,y,color=dose,alpha=z),linewidth=.6)+
geom_vline(xintercept=iso["2021-24"],color="#00aa00",linewidth=.4,linetype="22")+
geom_label(data=p[rowid(facet)==1],aes(label=facet),y=yend,x=xend,hjust=1,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87,lineheight=.8)+
geom_label(data=p[rowid(facet)==1],aes(label=facet),y=yend,x=xend,hjust=1,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87,lineheight=.8)+
labs(x=NULL,y=NULL,title="Czech Republic, people born in 1940-1949: Crude\nmortality rate per 100,000 person-years ")+
annotate(geom="text",color="#00aa00",x=iso["2021-25"],label="Vaccination cutoff date (week 24)",y=18700,hjust=0,vjust=.5,size=3.87)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x>0,paste0(x/1e3,"k"),x))+
scale_color_manual(values=c("#5555ff","#ff5555","black"))+
scale_alpha_manual(values=c(1,.4))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50"),
  axis.ticks.length=unit(0,"pt"),
  legend.box="vertical",
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(22,"pt"),
  legend.background=element_rect(color="gray75",linewidth=.4),
  legend.margin=margin(2,4,2,2),
  legend.position="top",
  legend.spacing.x=unit(1,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(4,5,4,5),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(1,,3)),
  plot.subtitle=element_text(hjust=.5,margin=margin(,,3)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5,height=4.4,dpi=300*4)

His use of fixed cohorts also downplayed the magnitude of the Delta spike in unvaccinated people, because on week 48 when deaths during the Delta wave peaked, his unvaccinated cohort actually consisted of about 35% vaccinated people and 65% unvaccinated people.

However the paper he linked said: "With time from vaccination, the differences in ACM between groups with different vaccination statuses dwindled." [https://link.springer.com/article/10.1186/s12889-025-23619-x] It's not reasonable to assume that unvaccinated people would continue to have 3 to 5 times higher mortality than vaccinated people indefinitely.

KCORv3

He demonstrated the problem with this calculation, where both unvaccinated and vaccinated deaths followed an exponential curve of the form b*exp(a*t).

Both curves in his plot are concave, but the vaccinated curve should be convex. After adjusting for seasonal variation and excluding COVID waves, the mortality of vaccinated people roughly follows an exponential decay subtracted from a constant term: [#HVE_test_for_KCOR]

Therefore he should've added a constant term c to his formula: c+b*exp(a*t). So his curves should've looked something like this:

p=CJ(x=0:100)[,.(x,y=55+25*exp(-.05*x),y2=45-25*exp(-.05*x))]

ybreak=0:5*20;ylim=c(0,100)
xstart=0;xend=100;xbreak=0:10*10

tit="Model of deaths as percentage of total deaths"
leg=c("Unvaccinated: 55+25*exp(-.05*x)","Vaccinated: 45-25*exp(-.05*x)")
col=c("#5555ff","#ff5555")

png("1.png",1400,900,res=300)
par(mar=c(2.9,3,1.8,1.1),mgp=c(0,.5,0),lend="square")
plot(rep(p$x,2),c(p$y2,p$y),type="n",main=tit,xlab=NA,ylab=NA,xaxs="i",yaxs="i",yaxt="n",xaxt="n",ylim=ylim,xlim=c(xstart,xend),cex.main=1)
axis(2,at=ybreak,las=1,tck=-.035,labels=paste0(ybreak,"%"))
axis(1,at=xbreak,las=1,tck=-.035,labels=NA)
mtext(xbreak,side=1,line=.35,at=xbreak)
mtext("Week",side=1,font=2,line=1.4)
lines(p$x,p$y,,col=col[1],lwd=1.5)
lines(p$x,p$y2,col=col[2],lwd=1.5)
legend("topright",legend=leg,col=col,lwd=1.5)

The exponential function he fitted to the data looks close to a line. His x-axis started around mid-July 2021, when the curve for unvaccinated ASMR had already dropped a lot from the peak which was in March 2021 (even though it was partially because unvaccinated people had a lot of COVID deaths during the Alpha wave, and the ratio between unvaccinated and vaccinated ASMR only peaked a bit later): [rootclaim4.html#Cumulative_deaths_in_ages_below_80]

Kirsch's plot had a fairly big drop in unvacinated deaths between the low points in 2023 and 2024, but it's because the NZIP data is missing more deaths in 2024 than 2023. Kirsch claimed that the NZIP data was not missing deaths until late 2024, but I showed him that about 5% of deaths are missing from the second quarter of 2024:

download.file("https://mortality.org/File/GetDocument/Public/STMF/Outputs/stmf.csv","stmf.csv")

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
t=t[Infekce%in%c(NA,1)]
t[,date:=Datum_Prvni_davka]
t[,vax:=date!=""&date<="2021-24"]
x=t[vax==F,.N,,.(x=DatumUmrtiLPZ)][x!=""]
x2=t[Datum_Prvni_davka!="",.N,,.(x=DatumUmrtiLPZ)][x!=""]

p=t[,.(y=.N),.(x=DatumUmrtiLPZ,z=vax*1)][x!=""]
p=rbind(p,p[,.(y=sum(y),z=2),x])

d=fread("stmf.csv")[Sex=="b"&CountryCode=="CZE"]
p=rbind(p,d[,.(x=sprintf("%d-%02d",Year,Week),y=DTotal,z=3)])
iso=as.IDate(0:1e4*7);names(iso)=format(iso,"%G-%V")
p[,x:=iso[x]]

p[,z:=factor(z,,c("NZIP (unvaccinated)","NZIP (vaccinated)","NZIP (total)","STMF"))]

xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=pretty(p$y);ystart=0;yend=max(ybreak)

ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray70",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(x,y,color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Weekly deaths in Czech Republic",subtitle="Source: nzip.cz/data/2135-covid-19-prehled-populace and
mortality.org/File/GetDocument/Public/STMF/Outputs/stmf.csv")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#8888ff","#ff8888","black","gray60"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=2,byrow=F))+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(1,1),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(22,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(1,1),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.subtitle=element_text(hjust=.5,margin=margin(,,3)),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(1,,3)))
ggsave("1.png",width=5.1,height=2.8,dpi=300*4)

In the KCORv3 spreadsheet Kirsch wrote: "KCOR can't be showing growing harm if the raw total population deaths aren't growing". In his initial KCOR analysis he found that among people born in 1950-1954, the ratio of vaccinated to unvaccinated deaths was about 1.23 times higher between week 23 of 2021 and week 34 of 2022 than between week 23 of 2021 and week 25 of 2021, so he declared it meant that "the vaccines caused a 23% net mortality increase in the first year". [https://kirschsubstack.com/p/czech-data-clearly-shows-covid-vaccines]

People born in 1950-1954 were 71-75 years old on December 31st 2021, which was close to the middle of Kirsch's observation period. In my buckets file for the Czech FOI data, ages 71-75 have only about 0.5% higher CMR in June-July 2022 than June-July 2021:

In a ChatGPT conversation Kirsch wrote: "NOTE the side benefit that the normalization is that it PROVES statis HVE is static because we can normalize the unvaxxed (with high HVE) to a straight line death slope using a fitted simple exponential." [https://chatgpt.com/share/6897e1f9-3d94-8009-98b1-2dfdbd0a6a56] However a*exp(b*x) ended up being close to a line even in the next plot. That doesn't prove that HVE is static, but it shows that you need to add a constant term to model the unvaccinated curve:

p=CJ(x=0:100)[,.(x,y=55+25*exp(-.05*x),y2=45-25*exp(-.05*x))]

ybreak=0:5*20;ylim=c(0,100);xstart=0;xend=100;xbreak=0:10*10

tit="Model of deaths as percentage of total deaths"
leg=c("Unvaccinated: 55+25*exp(-.05*x)","Vaccinated: 45-25*exp(-.05*x)","`a*exp(b*x)` fitted to unvaccinated")
col=c("#5555ff","#ff5555","#000088")

p$fit=predict(nls(y~a*exp(b*x),p,start=list(a=80,b=-.001)),p)

png("1.png",1500,1100,res=300)
par(mar=c(2.9,3,1.8,1.1),mgp=c(0,.5,0),lend="square")
plot(rep(p$x,2),c(p$y2,p$y),type="n",main=tit,xlab=NA,ylab=NA,xaxs="i",yaxs="i",yaxt="n",xaxt="n",ylim=ylim,xlim=c(xstart,xend),cex.main=1)
axis(2,at=ybreak,las=1,tck=-.035,labels=paste0(ybreak,"%"))
axis(1,at=xbreak,las=1,tck=-.035,labels=NA)
mtext(xbreak,side=1,line=.35,at=xbreak)
mtext("Week",side=1,font=2,line=1.4)
lines(p$x,p$y,,col=col[1],lwd=1.5)
lines(p$x,p$y2,col=col[2],lwd=1.5)
lines(p$x,p$fit,col=col[3],lwd=1.5)
legend("topright",legend=leg,col=col,lwd=1.5)
dev.off()

The green exponential curve Kirsch fitted against his local minima seems to have been missing a constant term. In the blue line here where I included a constant term, my curve was less close to a line than in the green line where I didn't include a constant term:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

s=t[DatumUmrtiLPZ!=""][Infekce%in%c(1,NA)]
a=s[!(Datum_Prvni_davka!=""&Datum_Prvni_davka<="2021-24"),.(dead=.N),,.(week=DatumUmrtiLPZ)]
a[,dead:=ma(dead,4,3)]
a=a[week>="2021-24"&week<="2024-18"]

iso=as.IDate(0:1e4*7);names(iso)=format(iso,"%G-%V")
a[,x:=rleid(week)][,date:=iso[week]]

p=a[,.(x,y=dead,z=1)]

mini=p[y==apply(p[,embed(c(rep(NA,2),y,rep(NA,2)),5)],1,min)][,.(x,y,z=2)]
mini=rbind(mini,p[.N][,z:=2])[!x%in%a[year(date)==2022&month(date)>7,x]]
p=rbind(p,mini)

exp1=predict(nls(y~a*exp(b*x),mini,list(a=900,b=-.001)),p[z==1])
exp2=predict(nls(y~c+a*exp(b*x),mini,list(c=500,a=400,b=-.01)),p[z==1])
p=rbind(p,p[z==1,.(x,y=c(exp1,exp2),z=rep(3:4,each=.N))])

p[,x:=a$date[x]]
p[,z:=factor(z,,c("Deaths (8-week moving average)","Local minima","a*exp(b*x) fitted to local minima","c+a*exp(b*x) fitted to local minima"))]

xstart=as.Date("2021-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=pretty(p$y);ystart=min(ybreak);yend=max(ybreak)

ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray70",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(x,y,color=z,linewidth=z,linetype=z))+
geom_point(aes(x,y,color=z,shape=z),stroke=.5,size=1.7)+
labs(x=NULL,y=NULL,title="Deaths in people not vaccinated by end of week 24 of 2021")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("gray30","red",hsv(c(12,22)/36,1,.8)))+
scale_shape_manual(values=c(NA,4,NA,NA))+
scale_linewidth_manual(values=c(.7,0,.6,.6))+
scale_linetype_manual(values=c("solid",NA,"42","42"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(1,1),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(25,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(1,1),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,3)))
ggsave("1.png",width=5.1,height=2.8,dpi=300*4)

However the fit to the local minima is not a good representation of the exponential decay in deaths due to the HVE. The unvaccinated deaths had already dropped a lot before they reached the minimum in 2021. And mortality displacement explains a part of the drop between the minima in 2021 and 2022, because unvaccinated people had high COVID deaths in the winter of 2021-2022.

In my plot the red cross in 2024 is about 7% lower than the average of the two red crosses in 2023, but most of the decrease is because about 5% of deaths are missing in the second quarter of 2024.

Even when I plotted unvaccinated deaths as a percentage of total deaths, c+a*exp(b*x) still had a poor fit to the curve during the first weeks:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")[Infekce%in%c(1,NA)]

s=t[DatumUmrtiLPZ!=""]
a=s[,.(dead=mean(!(Datum_Prvni_davka!=""&Datum_Prvni_davka<="2021-24"))*100),,.(week=DatumUmrtiLPZ)]
a=merge(a,t[,.(covid=.N),.(week=Umrti)],all=T)[,covid:=nafill(covid,,0)]
a=a[week>="2021-24"&week<="2024-18"]

iso=as.IDate(0:1e4*7);names(iso)=format(iso,"%G-%V")
a[,x:=rleid(week)][,date:=iso[week]]

p=rbind(a[,.(x,y=ifelse(covid<100,dead,NA),z=2)],a[,.(x,y=dead,z=1)])

exp1=predict(nls(y~a*exp(b*x),mini,list(a=80,b=-.005)),na.omit(p[z==1]))
exp2=predict(nls(y~c+a*exp(b*x),mini,list(c=50,a=30,b=-.05)),na.omit(p[z==1]))
p=rbind(p,p[z==1,.(x,y=c(exp1,exp2),z=rep(3:4,each=.N))])

p[,x:=a$date[x]]
p[,z:=factor(z,,c("Deaths (high-COVID weeks)","Deaths (low-COVID weeks)","a*exp(b*x) fitted to low-COVID weeks","c+a*exp(b*x) fitted to low-COVID weeks"))]

xstart=as.Date("2021-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=pretty(p$y);ystart=min(ybreak);yend=max(ybreak)

ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray70",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(x,y,color=z,linewidth=z,linetype=z))+
labs(x=NULL,y=NULL,title="Unvaccinated deaths as percentage of total deaths")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("gray70","black",hsv(c(12,22)/36,1,.8)))+
scale_linewidth_manual(values=c(.7,.7,.6,.6))+
scale_linetype_manual(values=c("solid","solid","42","42"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(1,1),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(25,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(1,1),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,3)))
ggsave("1.png",width=5.1,height=2.8,dpi=300*4)

In the adjustment that Kirsch did for KCORv3, he derived the slope for vaccinated people from the slope for unvaccinated people by assuming that the total deaths in unvaccinated and vaccinated people combined would've remained constant. However if he would've fitted the exponential curve against the local minima in vaccinated people, his curve would've had a completely different slope (even though the curve without a constant term would've still been close to linear):

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

s=t[DatumUmrtiLPZ!=""][Infekce%in%c(1,NA)]
a=s[Datum_Prvni_davka!=""&Datum_Prvni_davka<="2021-24",.(dead=.N),,.(week=DatumUmrtiLPZ)]
a[,dead:=ma(dead,4,3)]
a=a[week>="2021-24"&week<="2024-18"]

iso=as.IDate(0:1e4*7);names(iso)=format(iso,"%G-%V")
a[,x:=rleid(week)][,date:=iso[week]]

p=a[,.(x,y=dead,z=1)]
mini=a[,.SD[which.min(dead)],year(date)][,.(x,y=dead,z=2)]
exp1=predict(nls(y~a*exp(b*x),mini,list(a=900,b=.005)),p)
exp2=predict(nls(y~c+a*exp(b*x),mini,list(c=1300,a=-400,b=-.01)),p)

p=rbind(p,mini,p[,.(x,y=c(exp1,exp2),z=rep(3:4,each=.N))])

p[,x:=a$date[x]]
p[,z:=factor(z,,c("Deaths","Yearly minima","a*exp(b*x) fitted to yearly minima","c+a*exp(b*x) fitted to yearly minima"))]

xstart=as.Date("2021-1-1");xend=as.Date("2024-7-1");xbreak=seq(xstart,xend,"year")
ybreak=pretty(p$y);ystart=min(ybreak);yend=max(ybreak)

ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray70",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(x,y,color=z,linewidth=z,linetype=z))+
geom_point(aes(x,y,color=z,shape=z),stroke=.5,size=1.7)+
labs(x=NULL,y=NULL,title="Deaths in people vaccinated by end of week 24 of 2021")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("gray30","red",hsv(c(12,22)/36,1,.8)))+
scale_shape_manual(values=c(NA,4,NA,NA))+
scale_linewidth_manual(values=c(.7,0,.6,.6))+
scale_linetype_manual(values=c("solid",NA,"42","42"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=2,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.text.x=element_text(hjust=0),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(25,"pt"),
  legend.margin=margin(,,3),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,3)))
ggsave("1.png",width=5.1,height=2.8,dpi=300*4)

The next plot shows that Kirsch's method of adjusting for the slope of unvaccinated deaths is confounded by mortality displacement, because unvaccinated people had such high mortality in the winter of 2021 to 2022 that they have a big drop in expected deaths between mid-2021 and mid-2022:

t=fread("CR_records.csv")

set.seed(0);t$born=as.Date(paste0(t$Rok_narozeni,"-1-1"))+sample(0:364,nrow(t),T)

mindate=as.Date("2020-1-1");maxdate=as.Date("2022-12-31")
d=t[,.(start=pmax(born,mindate,na.rm=T),end=pmin(DatumUmrti,maxdate,na.rm=T),born)]
d$dead=as.Date(t$DatumUmrti)
d[,vax:=as.Date(t$Datum_1)][vax>"2021-06-21",vax:=NA]
d=d[born<=maxdate]

e=d[,.(age=age(born,start),date=start,dose=0,pop=1)]
vax=d[!is.na(vax)]
e=rbind(e,vax[,.(age=age(born,vax),date=vax,dose=1,pop=1)])
e=rbind(e,vax[born!=vax,.(age=age(born,vax-1),date=vax,dose=0,pop=-1)])

bday=cbind(d,date=c(outer(d$born,2020:2022,`year<-`)))
bday[,age:=age(born,date)][,dose:=(date>=vax)%in%T*1]
bday=bday[!(date==vax%in%T)&date>start&date<=end]
e=rbind(e,bday[,.(age,dose,pop=1,date)],bday[,.(age=age-1,dose,pop=-1,date)])

dead=d[!is.na(dead),.(date=dead,dose=(!vax%in%NA)*1,age=age(born,dead))]
e=rbind(e,dead[,.(date=date+1,dose,age,pop=-1)])

b=e[,.(pop=sum(pop)),.(date,age=pmin(age,100),dose)]
b=merge(b,dead[,.(dead=.N),.(age=pmin(age,100),dose,date)],all=T)
b=merge(CJ(date=seq(mindate,maxdate,1),age=0:100,dose=0:1),b,all=T)
b[is.na(b)]=0
b[,pop:=cumsum(pop),.(dose,age)]

b=merge(fread("https://sars2.net/f/czpopdead.csv")[year==2019,.(age,base=dead/pop/365)],b)
p=b[,.(y=sum(pop*base)),.(x=date,z=dose)]
p=p[x>="2021-6-14"&x<="2022-12-31"]

p[,y:=y/mean(y)*100,z]

p[,z:=factor(z,,c("Unvaccinated","Vaccinated"))]

xstart=as.Date("2021-1-1");xend=as.Date("2023-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=pretty(p$y);ystart=min(ybreak);yend=max(ybreak)

ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
geom_hline(yintercept=100,color="gray70",linewidth=.4)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray70",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(x,y,color=z))+
labs(x=NULL,y=NULL,title="Expected deaths in fixed cohorts assuming 2019 mortality rates",subtitle="Shown as percentage of average daily deaths")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("#5555ff","#ff5555"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(.5,1),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(.5,.97),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,2)))
ggsave("1.png",width=5.2,height=3,dpi=300*4)

In the plot above the jump during the first week is because the cohorts are defined at the end of week 24 but the observation period starts on the first day of week 24.

Kirsch fooled himself with his dose 3 vs dose 2 plot

Kirsch posted this plot, where he showed that the ratio mortality rate for people with three doses relative to people with two but not more doses increased by a factor of about 2.5 between early 2022 and early 2023, where the way he expected people to interpret the plot is that dose 3 was killing more people over time, which would've explained the increase in the ratio: [https://x.com/stkirsch/status/1953345748348588424]

The spreadsheet in his GitHub repository shows why he said there was nothing to see in his plot, because in fact the number of deaths under doses 2 and 3 combined remained stable over time, but if the reason why the ratio went up was that dose 3 was killing more people over time, you'd expect the number of deaths under doses 2 and 3 combined to also go up over time: [https://github.com/skirsch/Czech/blob/main/analysis/fixed_cohort_HR.xlsx]

Kirsch tried to fool his followers, but I told Kirsch that he was fooling himself. He says that "dynamic HVE" or short-term HVE or HVE proper lasts only 3 weeks, but after there remains "static HVE" which he also calls the "selection bias", which he says has a roughly constant magnitude over time. However his plot shows that the ratio between dose 3 and dose 2 follows a curve that takes several months to flatten out. So how can that be "static HVE"?

I guess the increase here is also because of dynamic HVE on weeks 0-2 but static HVE from week 3 onwards: [#HVE_test_for_KCOR]

Also it's not correct to say that the ratio of CMR for dose 3 divided by dose 2 is a hazard ratio, but it's rather a rate ratio:

COVID ASMR by vaccine brand in Czech data

Kirsch claimed that Moderna vaccines had no benefit on all-cause mortality based on the clinical trial, where both the vaccine group and placebo group had 16 deaths: [https://x.com/stkirsch/status/1958236828420772340]

However the trial was not powered to detect a difference in all-cause mortality.

The Czech NZIP data shows that during the Delta peak in December 2021, COVID ASMR as a percentage of total ASMR was the lowest for Moderna, and it was the highest for the two non-mRNA vaccine brands:

agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
t=t[RokNarozeni!="-"]
t[Umrti!=""&DatumUmrtiLPZ=="",DatumUmrtiLPZ:=Umrti]
t[Umrti!=""&DatumUmrtiLPZ!=Umrti,Umrti:=DatumUmrtiLPZ]
t=t[!(DatumUmrtiLPZ!=""&Datum_Prvni_davka>DatumUmrtiLPZ)]
t[,vax:=Datum_Prvni_davka!=""]
t[,born:=agecut(as.integer(substr(RokNarozeni,1,4)),seq(1925,1990,5))]

brand=setNames(rep("Other",24),sprintf("CO%02d",1:24))
brand[c(1,8,9,16,20,21,23,24)]="Pfizer"
brand[c(2,12,15)]="Moderna"
brand[3]="AstraZeneca";brand[4]="Janssen"
t$brand=brand[t$OckovaciLatkaKod_Prvni_davka]
t[is.na(brand),brand:=""]

t2=t[Infekce%in%c(1,NA)]
dead=t2[,.(unvaxdead=sum(!vax),vaxdead=sum(vax)),.(week=DatumUmrtiLPZ,born,brand)]
coviddead=t[,.(unvaxcoviddead=sum(!vax),vaxcoviddead=sum(vax)),.(week=Umrti,born,brand)]
vax=t2[,.(newvax=.N),.(week=Datum_Prvni_davka,born,brand)]

a=merge(dead,merge(coviddead,vax,all=T),all=T)[week!=""&!is.na(born)]
a=merge(do.call(CJ,lapply(a[,1:3],unique)),a,all=T)
a[is.na(a)]=0

a2=setDT(aggregate(a[,4:8],a[,1:2],sum))
a2=merge(t2[,.(startpop=.N),born],a2)
a2[,unvaxpop:=startpop-cumsum(unvaxdead)-cumsum(newvax),born]
a2[,vaxpop:=cumsum(newvax)-cumsum(vaxdead),born]

a[,vaxpop:=cumsum(newvax)-cumsum(vaxdead),.(born,brand)]

a3=a[brand!="",.(week,born,brand,pop=vaxpop,dead=vaxdead,covid=vaxcoviddead)]
a4=a2[,.(week,dead=c(unvaxdead,vaxdead),covid=c(unvaxcoviddead,vaxcoviddead),pop=c(unvaxpop,vaxpop),brand=rep(c("Unvaccinated","Vaccinated"),each=.N),born)]
a4=rbind(a4,a4[,.(dead=sum(dead),covid=sum(covid),pop=sum(pop),brand="All people"),.(week,born)])

l=rbind(a3,a4[brand=="Unvaccinated"])
std=l[week=="2022-01",sum(pop),born][,.(std=V1/sum(V1),born)]
l=l[,.(pop=ma(pop,2),dead=ma(dead,2),covid=ma(covid,2),week),.(born,brand)]
l=merge(l,std)

p=na.omit(l)[,.(y=c(sum(dead/pop*std),sum((dead-covid)/pop*std))/7*365e5,type=1:2,facet=1),.(week,brand)]

p=rbind(p,p[,.(y=(y[type==1]-y[type==2])/y[type==1]*100,facet=2,type=1),.(week,brand)])

p=p[brand!="Other"]
p$brand=factor(p$brand,c("Unvaccinated","Pfizer","Moderna","AstraZeneca","Janssen"))
color=c("black",hsv(c(240,355,120,204)/360,c(.94,.75,.9,.67),c(.76,.82,.7,.87)))

p[,type:=factor(type,,c("All causes","Not COVID"))]
p[,facet:=factor(facet,,c("ASMR per 100,000 person-years","COVID ASMR as per-\ncentage of total ASMR"))]

iso=as.IDate(0:1e4*7);names(iso)=format(iso,"%G-%V")
p[,x:=iso[week]]

xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ylim=p[,.(max=max(y,na.rm=T)*1.03),facet]

ggplot(p)+
facet_wrap(~facet,ncol=1,dir="v",scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray87",linewidth=.4,lineend="square")+
geom_rect(data=ylim,aes(ymax=max),ymin=0,xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray87",linewidth=.4)+
geom_line(aes(x,y,color=brand,alpha=type),linewidth=.6)+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(3,"pt"),label.size=.4,size=3.87,color="gray87",lineheight=.8)+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(3,"pt"),label.size=0,size=3.87,lineheight=.8)+
labs(x=NULL,y=NULL,title="Mortality by type of first vaccine dose in Czech Republic")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(breaks=\(x)pretty(x,4),labels=\(x)if(max(x,na.rm=T)<100)paste0(x,"%")else ifelse(x>=1e3,paste0(x/1e3,"k"),x))+
scale_color_manual(values=color)+
scale_alpha_manual(values=c(1,.3))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=3,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(3,3,3,3)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray87",linewidth=.4),
  legend.box="vertical",
  legend.box.just="center",
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(2.5,5.5,2.5,2.5),
  legend.position="top",
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major.x=element_blank(),
  panel.grid.major.y=element_line(linewidth=.4,color="gray87"),
  panel.spacing=unit(3,"pt"),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(2,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.7,height=4,dpi=300*4)

Mortality in Czech data among people with non-zero DCCI

Kirsch made a plot of the Czech data where he selected people whose DCCI comorbidity score was 1 or higher, where starting from the Omicron wave, he got a massive sustained increase in the vaccinated mortality rate. He posted the plots below (where I added the annotations in magenta), and he wrote: [https://kirschsubstack.com/p/the-czech-republic-dataset-provides]

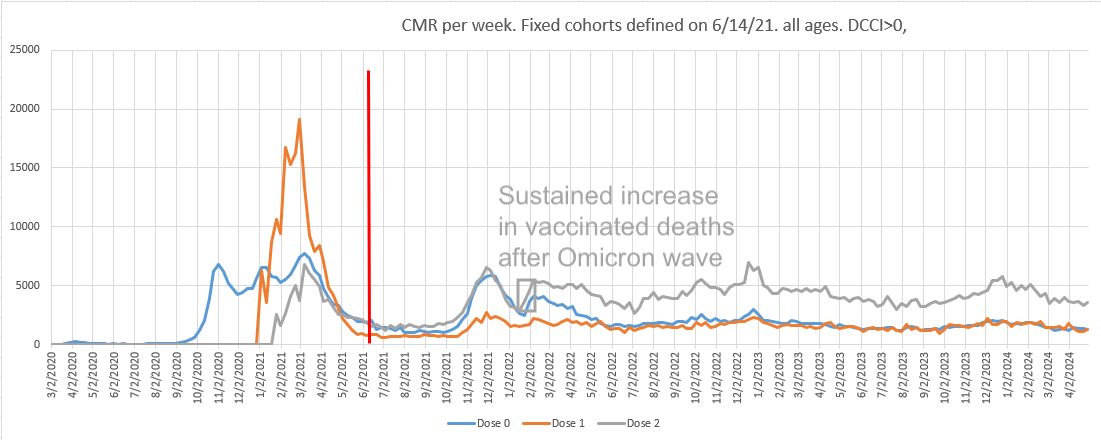
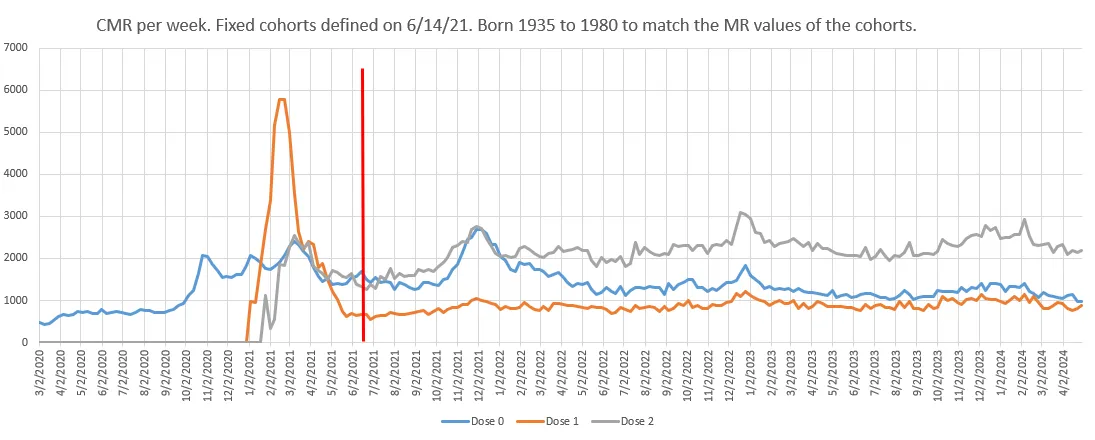
And Kirsch wrote: "Your mortality increased over 6 months then plateaued. If you got vaccinated, your mortality rate increased to a new level over time. If you were unvaccinated, there was no mortality increase. You can see that from the charts above. The mortalities track until after peak COVID. The mortality rate of the unvaccinated return to baseline. The mortality rate of the vaccinated remains elevated. They were matched before and now they are suddenly not matched because the vaccine separated their mortalities."

The DCCI score is only included for people with one or more cases, and there was a massive number of new people with a case added during the Omicron wave, so many people first got a DCCI score assigned during the Omicron wave.

Kirsch ignored vaccine doses given on week 25 of 2021 or later. But the denominator he used to calculate his mortality rate was the number of people who had ever had a case, including people who had not yet had a case but who later ended up getting a case, which is similar to the value of the top right panel at the end of the x-axis in my next plot. He should've instead used the number of people who had so far had a case as the denominator, which is shown by the line in my top right panel. Or he should've excluded all people who didn't have a first case listed before on week 24 of 2021 or earlier, like in my bottom right panel:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
iso=as.IDate(0:1e4*7);names(iso)=format(iso,"%G-%V")

s=t[Infekce==1][,vax:=Datum_Prvni_davka][,case:=DatumPozitivity]
s=rbind(s[,facet:=1],s[case!=""&case<"2021-25"][,facet:=2])
s=rbind(s[,facet2:=1],copy(s)[,facet2:=2][vax>="2021-25",vax:=""])

a=s[,.(y=.N),,.(case=DatumPozitivity,vax,facet,facet2)]

e=a[vax==""|case<vax,.(y=sum(y),z=0),.(x=case,facet,facet2)]
e=rbind(e,a[vax!=""&case>=vax,.(y=sum(y),z=1),.(x=case,facet,facet2)])

e=rbind(e,a[vax>case,.(y=sum(y)),.(x=vax,facet,facet2)][,.(x,y=c(y,-y),z=rep(1:0,each=.N),facet,facet2)])

p=e[,.(y=sum(y)),.(x,z,facet,facet2)]

p=merge(do.call(CJ,lapply(p[,-5],unique)),p,all=T)[,y:=nafill(y,,0)]
p[,y:=cumsum(y),.(z,facet,facet2)]
p[,x:=iso[x]]

p[,z:=factor(z,,c("Unvaccinated","Vaccinated"))]
p[,facet:=factor(facet,,c("Cases not fixed","Cases fixed"))]
p[,facet2:=factor(facet2,,c("Vaccines not fixed","Vaccines fixed"))]

xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=pretty(p$y);ystart=0;yend=max(p$y)

ggplot(p)+
facet_grid(facet~facet2,scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_vline(xintercept=iso["2021-25"]-3.5,linewidth=.4,linetype="22",color="gray75")+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Number of people with a case listed in NZIP data",subtitle="Fixed means cases or vaccines on week 25 of 2021 and later were ignored.")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x>0,paste0(x/1e6,"M"),x))+
coord_cartesian(clip="off",expand=F)+
scale_color_manual(values=hsv(2:3/3,.6,1))+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.text.x=element_text(margin=margin(2)),
  axis.text.y=element_text(margin=margin(,1)),
  axis.ticks=element_line(linewidth=.4,color="gray75"),
  axis.ticks.length=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(-2,,2),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,margin=margin(,,,2)),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(4,"pt"),
  plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)),
  strip.background=element_blank(),
  strip.text=element_text(size=11,margin=margin(2,2,2,2)))
ggsave("1.png",width=5.4,height=3.4,dpi=300*4)
system("mogrify 1.png -resize 25% -dither none -colors 256 1.png")

In the top right panel in the plot above, the population size of both unvaccinated and vaccinated people increases about 50% between week 1 and 20 of 2022. But a large part of the increase is because of younger age groups which account for few deaths. So in the next plot where I included only people born in 1959 and later, vaccinated people clearly have a bigger percentage increase in population size between week 1 and week 20 of 2022:

Observed-to-expected hospitalization rate in Czech data

I showed the plot below to Kirsch and asked him: "If 'NPH' explains why unvaccinated people had a much higher hospitalization rate than vaccinated people in 2021, then why does the line in my bottom panel here remain close to 1 from mid-2022 onwards? Why did the 'NPH' go away after unvaccinated people acquired natural immunity?"

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
t=t[RokNarozeni!="-"]
t[,born:=RokNarozeni][,vax:=Datum_Prvni_davka][,hosp:=min_Hospitalizace]
t2=t[Infekce%in%c(1,NA)]

pop=t2[vax!="",.(pop=.N,dose=1),.(week=vax,born)]
pop=rbind(pop,t2[,.(week="2020-10",pop=.N,dose=0),born])

dead=t2[,.(dead=.N),.(week=DatumUmrtiLPZ,dose=(vax!="")*1,born)]
hosp=t[,.(hosp=.N),.(week=hosp,dose=(vax!=""&vax<=hosp)*1,born)]
a=merge(hosp,merge(dead,pop,all=T),all=T)[week!=""]

a=merge(do.call(CJ,lapply(a[,1:3],unique)),a,all=T);a[is.na(a)]=0
a[dose==0,pop:=pop-a[dose==1,pop]]
a[,pop:=cumsum(pop-dead),.(born,dose)]

a=a[,.(hosp=sum(hosp),pop=sum(pop)),.(week,dose,born)]
a=rbind(a,a[,.(hosp=sum(hosp),pop=sum(pop),dose=2),.(week,born)])

a=merge(a,a[,.(base=sum(hosp)/sum(pop)),born])[,base:=base*pop]

iso=as.IDate(0:1e4*7);names(iso)=format(iso,"%G-%V")
p=a[,.(y=sum(hosp)/sum(base),facet=1),.(x=iso[week],z=dose)]
p=p[!(z==1&year(x)==2020)]
p=rbind(p,p[,.(y=y[z==0]/y[z==1],z=2,facet=2),x])

p[,z:=factor(z,,c("Unvaccinated","Vaccinated","Total"))]
p[,facet:=factor(facet,,c("Observed-expected ratio","Unvaccinated-vaccinated ratio"))]

xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
p=p[x>=xstart&x<=xend]

ylim=p[,.(min=0,max=max(y,na.rm=T)),facet]

ggplot(p)+
facet_wrap(~facet,ncol=1,dir="v",scales="free_y")+
geom_hline(yintercept=1,color="gray75",linewidth=.4)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray75",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=min,ymax=max),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray75",linewidth=.4)+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4,color="gray75",size=3.87)+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=0,fill=NA,size=3.87)+
labs(x=NULL,y=NULL,title="Czech NZIP data: Ratio of observed to expected hospitalizations")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(0,NA),breaks=\(x){y=pretty(x);y[y<max(x)*.96]})+
scale_color_manual(values=c(hsv(2:3/3,.6,1),"black"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50"),
  axis.text.y=element_text(margin=margin(,1.5)),
  axis.ticks=element_line(linewidth=.4,color="gray75"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(11,"pt"),
  legend.key.spacing.x=unit(2,"pt"),
  legend.key.width=unit(22,"pt"),
  legend.margin=margin(,,5),
  legend.position="top",
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,margin=margin(,,,2)),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(4,"pt"),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,2)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.1,height=3.6,dpi=300*4)
system("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[43*4] caption:'In order to calculate the expected number of hospitalizations, the number of people for each 5-year age group was multiplied with the total rate of hospitalizations per person-weeks for the age group during the observation period (week 10 of 2020 to week 41 of 2024).' -splice x$[12*4] \\) -append -trim -resize 25% -bordercolor white -border 20 -dither none -colors 256 1.png")

"NPH" or "non-proportional hazards" is a term that Kirsch has bastardized to mean that unvaccinated people have a higher COVID mortality risk than vaccinated people even after adjusting for HVE, which he invokes to explain why unvaccinated people were dropping like flies during the Delta wave. But in terms of the profile of comorbidities that makes people suspectible to die from COVID or be hospitalized with COVID, the composition of unvaccinated people probably doesn't change too much between the Delta wave and late 2022. So then why is the ratio between unvaccinated and vaccinated hospitalization rate much higher during the Delta wave than in late 2022?

Cumulative deaths in Japanese FOI data

Kirsch posted the plot below and wrote: "Every time you compare the two cohorts, the more vaccinated cohort will have mortality even though they tracked at the start. This is NOT NORMAL. If they track at the start, they should continue to track. If the shots worked, the more vaxxed cohort would exhibit LOWER mortality, not higher mortality." [https://kirschsubstack.com/p/japan-cmrr-data-website-shows-clear]

By "mortality", Kirsch meant the cumulative number of deaths multiplied by a constant factor, where he chose the constant factor so that his two lines were roughly aligned at the start of the x-axis. But if by mortality you mean ASMR instead, then the 4-dose cohort has lower mortality than the 3-dose cohort even at the end of the x-axis.

At the start of the x-axis, people with 4 doses have reduced mortality because of the healthy vaccinee effect, and people with 3 doses have elevated mortality because of the straggler effect. But over time the ASMR of the two cohorts converges.

Kirsch aligned the lines so that they matched at the start of the x-axis, but when the line for dose 4 subsequently rose above the line for dose 3, Kirsch attributed the increase to harm caused by vaccines. But if you align the lines so that they match at the end of the x-axis instead, then it rather looks like dose 3 has high mortality at the start of the x-axis relative to dose 4, which can be explained by the straggler effect: [https://medicalfacts.info/kcor.rb]

Kenji Fujikawa has now published CSV files of FOI data from 7 cities here: https://fujikawa.org/pub/kkcor/. I used his files to make the next plot, which shows that in late 2022 when the 4th dose is rolled out, the mortality of people with 3 but not more doses shoots up because of the straggler effect. But by late 2023 the straggler effect has weakened, so people with 3 but not more doses have almost as low mortality as people with 4 or more doses:

system("wget -rl1 -np -nd -Acsv fujikawa.org/pub/kkcor")

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

t=do.call(rbind,lapply(Sys.glob("jp*WKA.csv"),fread,fill=T))

date1=as.Date("2021-2-21");date2=as.Date("2024-6-30")

d=t[,.(.I,dead=date_death,age,dose=rep(0:4,each=.N),vax=c(rep(date1,.N),as.IDate(unlist(.SD,,F)))),.SDcols=patterns("date_dose[1-4]")]
d=d[!is.na(vax)]
d=d[dose!=2][dose>2,dose:=dose-1]

e=d[,.(pop=.N),.(date=vax,age,dose)]
e=rbind(e,e[dose>0][,.(pop=-pop,dose=dose-1,date,age)])
dead=d[!is.na(dead)][.N:1][rowid(I)==1,.(dead=.N),.(age,dose,date=dead)]
e=rbind(e,dead[,.(age,dose,date=date+7,pop=-dead)])
e=merge(e,dead,all=T)
e=e[date>=date1&date<=date2]
a=merge(do.call(CJ,lapply(e[,1:3],unique)),e,all=T);a[is.na(a)]=0

a[,pop:=cumsum(pop),.(dose,age)]

a[,`:=`(dead=ma(dead,2),pop=ma(pop,2)),.(dose,age)]

a[,base:=pop*a[,sum(dead)/sum(pop),age]$V1[factor(age)]]

a=rbind(a,a[dose>0][,dose:=4],copy(a)[,dose:=5])
a=a[,.(dead=sum(dead),pop=sum(pop),base=sum(base)),.(dose,age,date)]

p=a[,.(y=ifelse(sum(pop)<1e3,NA_real_,sum(dead)/sum(base))),.(x=date-3,z=dose)]

lab=c("Unvaccinated","Dose 1-2","Dose 3","Dose 4+","All vaccinated","All people")
color=c(hsv(c(0,27/36,21/36,1/3),c(.4,.4,.7,.7),c(.9,.9,.7,.7)),"gray60","black")
p[,z:=factor(z,,lab)]

xstart=as.Date("2021-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ystart=0;yend=max(p$y,na.rm=T);ybreak=0:yend
ylim=p[,.(max=max(y,na.rm=T))]

ggplot(p)+
geom_hline(yintercept=ybreak,color="gray91",linewidth=.4)+
geom_rect(data=ylim,aes(ymax=max),xmin=xstart,xmax=xend,ymin=ystart,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_hline(yintercept=1,color="gray72",linewidth=.4)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray72",linewidth=.4)+
geom_line(aes(x,y,color=z),linewidth=.65)+
labs(x=NULL,y=NULL,title="Weekly ratio of observed to expected deaths in Japan FOI data\n(±2-week moving average)")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(0,yend),breaks=ybreak)+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(row=2,byrow=F))+
theme(axis.text=element_text(size=11,color="gray50"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.spacing.x=unit(2,"pt"),
  legend.key.spacing.y=unit(0,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(,,3),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5,margin=margin(,,3)),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_line(),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,3)))
ggsave("1.png",width=5.5,height=3.2,dpi=300*4)

system("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[42*4] caption:'Source: fujikawa.org/pub/kkcor. Includes about 2.3 million people from the cities of Koganei, Sagamihara, Hamamatsu, Makinohara, Kasugai, Toyokawa, and Saiki. The expected number of deaths for each week was calculated by multiplying the number of people for each age group with the total mortality rate of the age group over the observation period (week 7 of 2021 to week 26 of 2024). Weeks with population size below 1,000 people are not shown. People were assigned a fixed 10-year age group so that aging over time was not accounted for, which causes the observed-to-expected ratio to be too high in 2024 relative to 2021.' -splice x$[16*4] \\) -append -trim -resize 25% -bordercolor white -border 20 -dither none -colors 256 1.png")

Mortality that follows a constant minus an exponential decay is consistent with a selection effect

The mortality of vaccinated people as a function of time since vaccination roughly follows a constant minus an exponential decay. The mortality of unvaccinated people peaks during the rollout of the first dose, but afterwards it falls following a curve roughly similar to an exponential decay. In October 2025 Kirsch announced he had discovered a third new type of HVE, which explained the drop in unvaccinated mortality. [https://kirschsubstack.com/p/surprise-there-are-actually-3-types]

Kirsch claims the mortality of vaccinated people increases over time because of harm caused by vaccines. I'd expect vaccine harm as a function of time since vaccination to follow an exponential decay, so that the curve would go down and not up over time, in the same way that a curve for the number of deaths by time since an accident like a car crash might look something like an exponential decay. If vaccination triggered the development of a chronic disease like cancer, where the vaccination resulted in a multiplicative increase in illness that in turn resulted in further illness, the curve of deaths over time might look like an exponential increase.

Out of the following categories, I'd expect harm caused by vaccines to primarily fall under 2, or possibly to a lesser extent 3, but not 1:

When I asked Grok to give more examples of a constant minus exponential decay, it replied:

When I asked ChatGPT to list phenomena in various sciences that follow a function of constant minus exponential decay, and to group them under categories like a return to an equilibrium, diminishing returns over time, or an initial population selection effect, ChatGPT produced this list:

I don't see how harm caused by vaccines could fall under any of the 5 categories listed above.

The healthy vaccinee effect doesn't really fit into any category either, even though it's akin to the inverse of the examples listed under the 4th category of "selective or attritional stabilization". All examples under the 4th category were formulated as a probability of survival after initial attrition, similar to how the survival probability of unvaccinated people increases over time as the straggler effect wears out. But it's not really comparable to HVE, which could rather be characterized as an increasing risk of failure in a population that was initially selected to include members with a low risk of failure, but where over time new members develop a high risk of failure.

5-fold static HVE in Mirror of Erised paper

Jeffrey Morris coined the terms "temporal" and "inherent" HVE, which he later renamed to "time-varying" and "time-invariant" HVE. Kirsch seems to employ the terms "dynamic" and "static" HVE as synonyms for the terms coined by Morris. The inherent/time-invariant/static HVE refers to the plateau level of HVE after the initial temporal/time-varying/dynamic HVE has worn off.

However in the Mirror of Erised paper, the ratio between unvaccinated and vaccinated mortality reached close to 5 only temporarily around April to June 2021, when the first dose was rolled out. So the 5-fold difference was attributable to "dynamic HVE" and not "static HVE": [https://bmcpublichealth.biomedcentral.com/articles/10.1186/s12889-025-23619-x/figures/1]

In the heatmap below if you exclude cells that have a wide confidence interval due to a small sample size, the only cell where the ratio between unvaccinated and vaccinated mortality is above 5 is the cell for ages 60-69 in May 2021. And if you look at the bottom row which shows all ages combined, the highest monthly ratio is about 3.2 in May 2021, and the total ratio in 2021-2022 is about 2.1:

t=fread("https://sars2.net/f/czbuckets.csv.gz")

a=t[,.(dead=sum(dead),pop=sum(alive)),.(month,dose=pmin(dose,1),age)]
a=a[!month%like%2020]
a[,base:=a[,sum(dead)/sum(pop),age]$V1[age+1]*pop]
a=a[,.(pop=sum(pop),dead=sum(dead),base=sum(base)),.(month,dose,age=agecut(age,c(0,2:9*10)))]

a=rbind(a,a[,.(pop=sum(pop),dead=sum(dead),base=sum(base),month="Total"),.(dose,age)])
a=rbind(a,a[,.(pop=sum(pop),dead=sum(dead),base=sum(base),age="Total"),.(dose,month)])

p=a[,.(ratio=dead[dose==0]/base[dose==0]/dead[dose==1]*base[dose==1]),.(age,month)]

m=p[,tapply(ratio,.(age,month),c)]
m[m==Inf]=NA
disp=m;disp[]=sprintf("%.1f",disp)
m=ifelse(m>=1,m-1,-1/m+1)

exp=.8;m=abs(m)^exp*sign(m)
maxcolor=5^exp;m[is.infinite(m)]=-maxcolor

pheatmap::pheatmap(m,filename="i1.png",display_numbers=disp,
  gaps_col=ncol(m)-1,gaps_row=nrow(m)-1,
  cluster_rows=F,cluster_cols=F,legend=F,cellwidth=16,cellheight=14,fontsize=9,fontsize_number=8,
  border_color=NA,na_col="gray90",
  number_color=ifelse((abs(m)>.55*maxcolor)&!is.na(m),"white","black"),
  breaks=seq(-maxcolor,maxcolor,,256),
  colorRampPalette(hsv(rep(c(7/12,0),5:4),c(.9,.75,.6,.3,0,.3,.6,.75,.9),c(.4,.65,1,1,1,1,1,.65,.4)))(256))

system("mogrify -trim i1.png;w=`identify -format %w i1.png`;magick \\( -pointsize 45 -font Arial-Bold -size $[w]x caption:'Czech FOI data: Unvaccinated-vaccinated mortality ratio normalized for age' \\) -interline-spacing -3 -pointsize 38 -font Arial \\( -size $[w]x caption:'The shown ratio was calculated as `(unvaccinated_dead / unvaccinated_expected) / (vaccinated_dead / vaccinated_expected)`, where the expected deaths were calculated by multiplying the number of person-days for each single year of age by the total mortality rate for the age in 2021-2022.' -gravity southwest -splice x10 \\) i1.png -append -trim -bordercolor white -border 16 1.png")

ASMR in Czech Republic up to 2025

Kirsch interprets the results of his Czech KCOR analysis to mean that vaccinated people had sustained high excess mortality since 2021. But about 90% of deaths in the Czech Republic are in ages 60 and above, and based on the FOI data, about 86% of people aged 60 and above were vaccinated at the end of 2022:

So if vaccinated people had something like 30% extra deaths like Kirsch claims, the overall Czech population should also have close to 30% extra deaths.

However the next plot shows that the ASMR was clearly lower in 2023 and 2024 than in the years before COVID, and even relative to the 2010-2019 linear trend, there was still close to 0% excess ASMR in 2023, 2024, and 2025:

isoweek=\(year,week,weekday=7){d=as.Date(paste0(year,"-1-4"));d-(as.integer(format(d,"%w"))+6)%%7-1+7*(week-1)+weekday}

download.file("https://ec.europa.eu/eurostat/api/dissemination/sdmx/2.1/data/demo_r_mwk_05?format=TSV","demo_r_mwk_05.tsv")
w=fread("demo_r_mwk_05.tsv")
meta=fread(text=paste0(w[[1]],collapse="\n"),head=F)
d=cbind(meta,melt(w,id=1))[V3=="T"&V5=="CZ"&V2%like%"^Y"]

d=d[,.(week=variable,dead=as.integer(sub(":| .*","",value)),age=V2)]
d[,age:=ifelse(age=="Y_LT5",0,as.integer(sub("\\D*(\\d*).*","\\1",age)))]
d[,year:=as.integer(substr(week,1,4))]
d[,week:=as.integer(substr(week,7,8))]
d[,date:=isoweek(year,week,7)]
d=d[year(date)>=2010]
d=na.omit(d)

pop=fread("https://sars2.net/f/eurostatpopdead.csv.gz")[location=="CZ"][year%in%2000:2024]
pop[,x:=as.Date(paste0(year,"-1-1"))]
pop=pop[,.(pop=sum(pop)),.(age=pmin(age,90)%/%5*5,x)]
pop=pop[,spline(x,pop,xout=unique(d$date)),age]

d=merge(d,pop[,.(age,date=as.IDate(x),pop=y)])

cov=fread("umrti.csv")
cov=cov[,.(covid=.N),.(date=cut(datum,unique(d$date)),age=pmin(90,vek)%/%5*5)]
d=merge(d,na.omit(cov),all=T)

d[,std:=tapply(pop,age,sum)[factor(age)]/sum(pop)]

a=d[,.(y=sum(dead/pop*std/7*365e5),cov=sum((dead-nafill(covid,,0))/pop*std/7*365e5)),.(x=date,year,week)]
a$base=a[year<2020,predict(lm(y~x),a)]
a[,base:=base+a[year<2020,tapply(y-base,week,mean)][week]]
p=a[,.(x,y=c(y,cov,base),z=rep(1:3,each=.N))]

p=rbind(p[,facet:=1],p[,.(x,y=(y/y[z==3]-1)*100,z,facet=2)][z!=3])

p[,z:=factor(z,,c("All causes","Not COVID","2010-2019 linear regression"))]
p[,facet:=factor(facet,,c("ASMR","Excess ASMR percent"))]

xstart=as.Date("2015-1-1");xend=as.Date("2026-1-1");xbreak=seq(xstart+182,xend,"year")

ylim=p[,{x=extendrange(y);.(ymin=x[1],ymax=x[2])},facet]

ggplot(p)+
facet_wrap(~facet,dir="v",ncol=1,scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=ymin,ymax=ymax),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray75",linewidth=.4)+
geom_segment(data=ylim[2],y=0,yend=0,x=xstart,xend=xend,linewidth=.4,color="gray75")+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_line(data=p[z==z[1]],aes(x,y,color=z),linewidth=.6)+
geom_label(data=ylim,aes(xend,ymax,label=facet),hjust=1,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray75",size=3.87,lineheight=.8)+
geom_label(data=ylim,aes(xend,ymax,label=facet),hjust=1,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87,lineheight=.8)+
labs(x=NULL,y=NULL,title="Weekly ASMR per 100,000 person-years in Czech Republic")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=\(x)year(x))+
scale_y_continuous(breaks=\(x)pretty(x,7),labels=\(x)if(max(x,na.rm=T)>1e3)x else paste0(x,"%"))+
scale_color_manual(values=c("black","gray60",hsv(2/3,.6,1)))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.text.y=element_text(margin=margin(,1.5)),
  axis.ticks=element_line(linewidth=.4,color="gray75"),
  axis.ticks.length=unit(4,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.spacing.x=unit(2,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(-2,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,margin=margin(,,2)),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major=element_blank(),
  panel.spacing=unit(3,"pt"),
  plot.title=element_text(size=11,face=2,margin=margin(,,4),hjust=.5),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.4,height=4.1,dpi=300*4)

system("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[42*4-2] caption:'Source: Eurostat datasets demo_r_mwk_05 and demo_pjan (population estimates on January 1st, spline interpolated to weekly population estimates). The baseline was adjusted for seasonality by adding the average difference between the actual deaths and baseline for each week number to the baseline for the corresponding week number. ASMR was calculated by 5-year age groups up to ages 90+, so that the total person-weeks during the observation period were used as the standard population.' -splice x$[16*4] \\) -append -trim -resize 25% -bordercolor white -border 20 -dither none -colors 256 1.png")

So there is not room for anything like a 30% sustained increase in deaths among vaccinated people.

Deaths by weeks after vaccination in Czech data

He wrote: "AFAIK, this is the first time anyone has done a time series analysis on the Czech data". Kirsch has bastardized the term "time series analysis" to mean an analysis similar to a plot that shows deaths on the y-axis and weeks since vaccination on the x-axis, even though I have told him that a plot that shows calendar date on the x-axis is also a time series plot. So by the normal definition of what a time series plot means, Kirsch has posted many time series plots of the Czech data himself. However even by his bastardized definition of a time series plot, I have made many plots of the Czech data that have shown time since vaccination on the x-axis, and I have shown many of the plots to Kirsch on DM on Twitter, so he should be aware of them.

However among the elderly age groups that account for most deaths, many people got the first dose during the Alpha wave around March 2021, so during the first few weeks from the first dose, the background mortality rate dropped rapidly as the Alpha wave was passing by. But people typically got the second dose within 3-6 weeks of the first dose, so by that time the background mortality rate no longer dropped as sharply, and also there had been sufficient time for an immune response to build up after the first dose, so the risk of death from COVID was reduced: [czech4.html#Plot_for_raw_deaths_by_weeks_after_vaccination]

The reason why Kirsch originally started to claim that the HVE lasted for only 3 weeks is that when he plotted deaths by days after vaccination in his US Medicare data, it took about 3 weeks for the deaths to reach a flat level: [czech.html#Deaths_by_weeks_after_first_dose]

However it's because a lot of people got first doses near the end of the COVID wave in winter 2020-2021, so there was a rapidly falling trend in the background mortality rate during the first few weeks from vaccination. The plot above shows the first known vaccine dose for each person administered in 2021, which was generally but not always the first dose. This plot shows that vaccine doses administered in 2022 take much longer to reach a flat level, and they follow a more smooth curve that is missing the bump in deaths around days 20-30: [ibid.]

But anyway, the main point of Kirsch's post were these plots, where he compared people who got the second dose in February against people who got the second dose in June:

The baseline seems to be roughly halfway between the second and third weeks in the first plot, and halfway between the third and fourth weeks in the second plot, so I don't know why Kirsch didn't determine the baseline the same way in both plots.

But anyway, in the next plot I split people into three groups depending on the month of the first vaccine dose. Week 0 consists of the day of vaccination and the next 6 days. People vaccinated in January or February have a peak in deaths on week 2, and people vaccinated in March or April have a peak in deaths on week 3, but the early peak is missing in people vaccinated in May or June, because at that point there was no longer a decreasing trend in background mortality rate because the COVID wave had already passed by. However the baseline has a much bigger drop during the first 10 weeks for the first two groups and a smaller drop for the third group. So once you plot the deaths as a percentage of the baseline, in all three groups the percentage reaches a plateau around week 20: [rootclaim5.html#Does_short_term_HVE_last_for_3_weeks_in_the_Czech_FOI_data]

Kirsch keeps arbitrarily assuming that the number of deaths 3 weeks after vaccination is the baseline, or sometimes 2.5 weeks or 3.5 weeks or 4 weeks, and any subsequent increase in deaths means that vaccines are killing people.

He should've instead calculated the baseline deaths using the method I employed in the plot above. It's really easy if you use my "buckets" files that show the number of deaths and person-days for each combination of variables like week since vaccination, observation month, and age. [czech.html#Bucket_analysis]

For example this code shows the row from my buckets file for people aged 80, who got a Pfizer vaccine for their first dose in March 2021, and who were 21-26 days from the first dose in April 2021:

In my buckets file people are kept under the first dose even after receiving the second dose, so in order to not count people with multiple doses multiple times, you have to exclude people whose dose number is 2 or higher.

The following code calculates the baseline number of deaths per person-days for each combination of age and observation month:

So basically you get a matrix of baseline mortality rates like this, where each combination of age and month has its own baseline of deaths per person-days:

From the table above, you can see that the baseline mortality rates in ages 80-84 are about twice as high in January 2021 as June 2021.

Then the baseline mortality rate is multiplied by the person-days to get the baseline deaths, and the total baseline deaths for each number of weeks after vaccination are added together:

And finally this code shows the deaths as a percentage of the baseline during the first 30 weeks from the first dose, where you can see that it takes about 15 weeks for the deaths to settle at a level of about 80-90% of baseline deaths:

I have given Kirsch R code similar to the code above multiple times, but I think he has never yet made use of my code. In 2023 when Kirsch released his analysis of Barry Young's New Zealand data, he hired some guy to write a Python script for him that generated "buckets" files similar to the files I have later generated for the Czech data. However I have never seen Kirsch use my buckets files or generate his own buckets files for the Czech data, even though they would make many types of analysis much easier, like for example calculating a baseline for deaths that is adjusted for age and the background mortality rate.

Rootclaim vaccine debate between Steve Kirsch and Saar Wilf (part 5) - sars2.net

2. Should Be Obvious in the Data

Here's why:

HVE tests

1. Relaxation Toward Equilibrium

2. Diminishing Returns or Performance Plateau

3. Saturation Under Physical or Transport Limits

4. Selective or Attritional Stabilization

5. Instrumental and Measurement Settling

The first shot killed people at a higher rate in the first 9 week post shot than the second shot did