
Other parts: rootclaim.html, rootclaim3.html, rootclaim4.html, rootclaim5.html, rootclaim6.html.
In this section I address the third round of arguments by Kirsch: https://kirschsubstack.com/p/the-latest-round-in-the-2m-debate.
Kirsch wrote: "CDC state and county case data: x-axis=vax rate. y-axis=relative # of cases to baseline. Regression shows >1.5X higher cases in 2021, and >2X higher cases in 2022. 95% confidence slope increased in both years over baseline in BOTH all state and all county data. This is dispositive as there is nothing that is more fundamental than this data to resolve the question of cases. More vaccines→ more cases in both years."
He linked to a spreadsheet with these plots (where for some reason on the left he claimed that he got high r2 values even though the values were below 0.1):

At first I thought the plots on the left showed the difference in raw number of cases and not cases in capita, which would have been confounded by population size. However actually the plots on the left do correctly show the difference in cases per capita.
However one bias in Kirsch's analysis is that states with a higher percentage of vaccinated people also tend to have more tests performed per capita. But in states with a low percentage of vaccinated people, there tends to also be a lower number of tests performed per capita which probably makes it less likely that COVID infections are detected as cases:
download.file("https://healthdata.gov/api/views/j8mb-icvb/rows.csv","statespcr.csv")
download.file("https://data.cdc.gov/api/views/rh2h-3yt2/rows.csv","statesvax.csv")
download.file("https://www2.census.gov/programs-surveys/popest/datasets/2020-2023/state/totals/NST-EST2023-ALLDATA.csv","NST-EST2023-ALLDATA.csv")
test=fread("statespcr.csv")
test[,year:=year(as.Date(date,"%Y/%m/%d"))]
test=test[,.(tests=sum(new_results_reported),positive=sum(new_results_reported[overall_outcome=="Positive"])),.(state=state_name,code=state,year)]
pop=fread("NST-EST2023-ALLDATA.csv")
a=merge(test[year==2021],pop[,.(state=NAME,pop=POPESTIMATE2021)])
vax=fread("statesvax.csv")
a=merge(vax[Date=="12/31/2021"&date_type=="Report",.(code=Location,vax=Admin_Dose_1_Cumulative)],a)
a[,.(state,tests,positive,pop,vaxpct=vax/pop*100,testsperpop=tests/pop,positivepct=positive/tests*100)][order(-testsperpop)]
# tests is tests performed in 2021
# positive is tests with positive result in 2021
# pop is mid-2021 resident population estimate
# vaxpct is people with one or more dose at end of 2021 divided by mid-2021 resident population estimate
# testsperpop is tests performed in 2021 divided by mid-2021 resident population estimate
# positivepct is positive/tests*100
a[,.(state,tests,pop,vaxpct=vax/pop*100,testsperpop=tests/pop)][order(-testsperpop)]
state tests positive pop vaxpct testsperpop positivepct
1: District of Columbia 2741963 111520 669037 93.6 4.098 4.07
2: Rhode Island 4165830 148252 1097092 86.2 3.797 3.56
3: Vermont 2329264 79483 647093 86.3 3.600 3.41
4: Massachusetts 24582715 784478 6991951 89.5 3.516 3.19
5: Alaska 2340384 132788 734923 64.8 3.185 5.67
6: New York 48749226 2694052 19854526 82.5 2.455 5.53
7: Connecticut 8106398 372738 3603691 87.9 2.249 4.60
8: Minnesota 12472481 866456 5717968 70.5 2.181 6.95
9: Delaware 2002995 139678 1004881 74.4 1.993 6.97
10: California 76921627 3410337 39145060 83.7 1.965 4.43
11: Illinois 23899042 1121908 12690341 72.1 1.883 4.69
12: Maryland 11472288 925194 6175045 78.9 1.858 8.06
13: New Jersey 15221817 1187286 9269175 80.4 1.642 7.80
14: Maine 2247841 112855 1378787 83.9 1.630 5.02
15: New Hampshire 2215618 133166 1387494 96.9 1.597 6.01
16: Colorado 8780187 635115 5811596 74.0 1.511 7.23
17: West Virginia 2644412 257315 1785249 62.2 1.481 9.73
18: Florida 30568295 3324246 21830708 73.4 1.400 10.87
19: Hawaii 2021761 83129 1446745 86.4 1.397 4.11
20: South Carolina 7247849 629628 5193848 62.3 1.395 8.69
21: New Mexico 2868744 450036 2116950 80.1 1.355 15.69
22: Wisconsin 7932801 599067 5879978 67.7 1.349 7.55
23: Michigan 12379110 1249754 10038117 63.2 1.233 10.10
24: Wyoming 695550 50122 579548 55.9 1.200 7.21
25: Washington 9166186 528703 7741433 74.5 1.184 5.77
26: North Carolina 12266149 1090015 10567100 76.1 1.161 8.89
27: Pennsylvania 14379946 1282627 13013614 77.0 1.105 8.92
28: Kentucky 4916402 517763 4507600 62.0 1.091 10.53
29: North Dakota 837596 48273 777982 61.0 1.077 5.76
30: Arizona 7817275 848050 7272487 67.5 1.075 10.85
31: Louisiana 4786572 349269 4627047 57.8 1.034 7.30
32: Utah 3427578 363276 3339284 64.7 1.026 10.60
33: Missouri 6089925 605957 6170393 62.1 0.987 9.95
34: Nevada 3048542 323186 3146632 68.2 0.969 10.60
35: Oregon 4115224 254855 4256465 73.4 0.967 6.19
36: Indiana 6560258 676954 6813798 57.3 0.963 10.32
37: Ohio 11246047 1074386 11765227 60.2 0.956 9.55
38: Kansas 2718140 245414 2937946 68.8 0.925 9.03
39: Montana 1020546 99165 1106366 60.0 0.922 9.72
40: Virginia 7767854 828465 8657348 78.0 0.897 10.67
41: Texas 26396754 3008760 29561286 65.5 0.893 11.40
42: Idaho 1675952 236285 1904537 49.0 0.880 14.10
43: Iowa 2679250 278373 3197944 64.1 0.838 10.39
44: Georgia 8365941 943862 10790385 60.4 0.775 11.28
45: Arkansas 2126052 174494 3028443 62.5 0.702 8.21
46: Alabama 3367649 443928 5050380 56.9 0.667 13.18
47: Tennessee 4353964 524323 6963709 57.7 0.625 12.04
48: Puerto Rico 1881234 156528 3262693 87.2 0.577 8.32
49: Nebraska 1115678 118021 1964253 65.4 0.568 10.58
50: South Dakota 498453 68883 896299 70.1 0.556 13.82
51: Oklahoma 1830585 300680 3991634 65.6 0.459 16.43
52: Mississippi 1222841 165735 2949582 55.8 0.415 13.55
state tests positive pop vaxpct testsperpop positivepct
My correlation between the percentage of vaccinated people in 2021 and tests per capita in 2021 was about 0.61:
> a[,cor(vax/pop,tests/pop)] [1] 0.61051
But my correlation between the percentage of vaccinated people in 2021 and the proportion of positive tests in 2021 was about -0.60:
> a[,cor(vax/pop,positive/tests)] [1] -0.59976
So since the two previous correlations partially cancel each other out, my correlation between the percentage of vaccinated people in 2021 and positive tests per capita in 2021 was fairly close to zero (where positive tests per capita is similar to the metric of COVID cases per capita that was used by Kirsch):
> a[,cor(positive/pop,vax/pop)] [1] 0.20839
Kirsch wrote: "New Japan study shows more vaccines→more cases as well: 'The odds of contracting COVID-19 increased with the number of vaccine doses: one to two doses (OR: 1.63, 95% CI: 1.08-2.46, p = 0.020), three to four doses (OR: 2.04, 95% CI: 1.35-3.08, p = 0.001), and five to seven doses (OR: 2.21, 95% CI: 1.07-4.56, p = 0.033).' This is consistent with Table 2 in the CC study."
The Japanese study was a survey with only 931 people who responded. Whether the subjects had contracted COVID or not was determined by a self-reported response to the survey.
The percentage of people who reported that they had contracted COVID
was about 42% among unvaccinated people (211/(211+293)) and
about 54% among vaccinated people (222/(222+187)). However
the study didn't differentiate whether people contracted COVID before or
after they were vaccinated, and some vaccinated people might have
contracted COVID before they were vaccinated.
The survey is supposed to have been administered in December 2023, so it's unusual that only 45% of the respondents reported being vaccinated (409 out of 913).
The odds ratios in the study were not adjusted for testing behavior, and part of the reason why unvaccinated people had lower self-reported occurrence of COVID might be if unvaccinated people were less likely to get tested. The authors wrote they collected the following characteristics, which did not include the number of tests performed or whether people had ever been tested or not: "The questionnaire collected information on demographic characteristics (age and gender), COVID-19 infection status, vaccination status (including the number of vaccine doses received), health status before January 2020 (presence of any chronic health conditions), and various preventive behaviors. Preventive behaviors assessed included regular gargling, mask-wearing, bathing frequency, avoiding crowded places, room ventilation, eating habits, sleep patterns, exercise habits, and maintaining humidity in living spaces."
The Japanese paper was published at Cureus which allows readers to post comments about the paper. Someone called Sadao Suzuki posted the following comment: [https://www.cureus.com/articles/313843-behavioral-and-health-outcomes-of-mrna-covid-19-vaccination-a-case-control-study-in-japanese-small-and-medium-sized-enterprises]
First, although the title of the study contains "Case-Control Study," this is not a case-control study. 'The case-control study starts with a group of cases, which are the individuals who have the outcome of interest. The researcher then tries to construct a second group of individuals called the controls, who are similar to the case individuals but do not have the outcome of interest' [1]. In this study, however, the researcher first collects whole study subjects and then divides them into two groups: one with outcome and one without outcome. In this respect, the retrospective cohort approach, which divides the entire subject population by exposure, and examines outcome status by exposure group, is more natural and straightforward. Because the authors chose the framework of a case-control study, Table 1 is divided by outcome information, and an important information of the distribution of potential confounders by exposure status is not known.
Second, the primary outcome of this study was the presence or absence of self-reported COVID-19 infection. However, the time frame of the outcome was not questioned and a longitudinal analysis could not be performed. If a subject was infected with COVID-19 before the first vaccination and then received six additional vaccinations and prevented the infection, then vaccination cannot be the cause of COVID-19 infection. In the study, however, the association would be observed between the vaccination and the infection. Without knowing the time frame of the outcome, a causal relationship cannot be discussed.
Third, the study is inadequate in describing important information. Most importantly, all of the subjects were Yamato project participants and/or employees of SMEs, whose attributes were not described at all. Moreover, the actual questionnaire used is not shown, and the specifics of the questions are not clear. For example, we do not know what "eating habits" refers to. Throughout this paper, such descriptions are severely lacking. In addition, the data set is not publicly available.
Fourth, the studies were derived from two different populations, but were combined without assumption. Here, we would like to point out the possibility of confounding due to the different backgrounds of the two groups, Yamato project participants and employees of SMEs. Confounding could occur if the vaccination or infection status of the two groups differs. Adjustment for the groups or confirmation of the absence of confounding is essential.
Fifth, the study population was described by the authors as "the study team believed that the participants reasonably approximated the broader workforce of SMEs in Japan". However, 504 of the 913 subjects (55.2%) were unvaccinated. Considering that the proportion of unvaccinated persons aged 20 years or older in Japan is 11.6% [2] (as of April 1, 2023), this is a biased population with approximately five times as many unvaccinated persons and is not representative. In this paramount matter, the "reasonable approximation" is completely false. The authors are accountable for the type of population which they chose, why the unvaccinated rate is so high, and with what intent the "reasonable approximation" statement was made.
And last but not least, the validity of the odds ratios is not fully considered. For the odds ratio to be valid, the accuracy of COVID-19 diagnosis must be constant regardless of vaccination status. However, it is conceivable that vaccination is associated with diagnostic diligence for the disease in question, in which case there would be a difference in diagnostic accuracy, resulting in information bias. This bias increases the odds ratio without causality.
References
1) https://pubmed.ncbi.nlm.nih.gov/28846237/
2) https://www.mhlw.go.jp/content/nenreikaikyubetsu-vaccination_data.pdf
A reply to the comment which essentially acknowledged all the errors was posted by Eiji Nakatani who was the first author of the paper. He wrote: "Because our study could not establish whether vaccination preceded infection, causal inference is severely limited. The observed association - more frequent infection reports among vaccinated participants - should not be taken as causal proof of vaccine ineffectiveness or harmful effects. Rather, it points to the need for further exploration, including detailed temporal data and longitudinal designs." He also wrote: "The proportion of unvaccinated individuals in our sample was higher than national averages, indicating possible selection bias and limited generalizability. In retrospect, describing our sample as a 'reasonable approximation' of the broader workforce was inaccurate. We will acknowledge these biases explicitly and refrain from overstating the representativeness of our sample." And he wrote: "Relying on self-reported infections introduces the possibility of information bias. Vaccinated individuals may be more proactive in seeking testing or reporting infections, potentially inflating observed odds ratios."
The response by Eiji Nakatani looks like it was AI-generated:

One comment said that "a GPTZero scan of this document show 100% probability of being AI generated", but comically the first author Eiji Nakatani replied that "the discussion of the potential for AI generation is one interesting aspect regarding this study":

Reference 1 of the Japanese paper says: "Welcome to the Sprinklr DEV portal. (2024). Accessed: October 16, 2024: http://dev.sprinklr.com/." But reference 1 doesn't seem to have anything to do with the sentence it was placed after: "Vaccination campaigns have played a pivotal role in controlling the spread of severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and reducing the severity of COVID-19 [1,2]." Apparently Sprinklr is an AI customer support service which also supports generating various types of documents with AI: [https://www.sprinklr.com/help/articles/sprinklr-ai-powered-article-creation/create-an-article-with-sprinklr-ai/65a94942ab59de79d2a06906/]

Sprinklr also supports using AI to automatically post replies on social media, so I wonder if the replies by Eiji Nakatani were also automated by Sprinklr or another similar service? It wouldn't have made sense for a real person to write "the discussion of the potential for AI generation is one interesting aspect regarding this study". But on the other hand it seems like a fairly niche task to automate posting replies to a comment section in a scientific journal, and setting up automated replies might take more time than simply posting replies manually. So perhaps a more likely scenario would be that Eiji Nakatani generated the reply with AI but he sent it manually, and he was so poor at English that he didn't understand the reply properly or he didn't bother editing the reply manually.
The last author of the Japanese paper was the alt media celebrity Masanori Fukushima. A video from a press conference where he discussed the paper was widely shared on social media, and a version of the video with English subtitles was posted by Aussie17: [https://x.com/_aussie17/status/1880459710115246385]
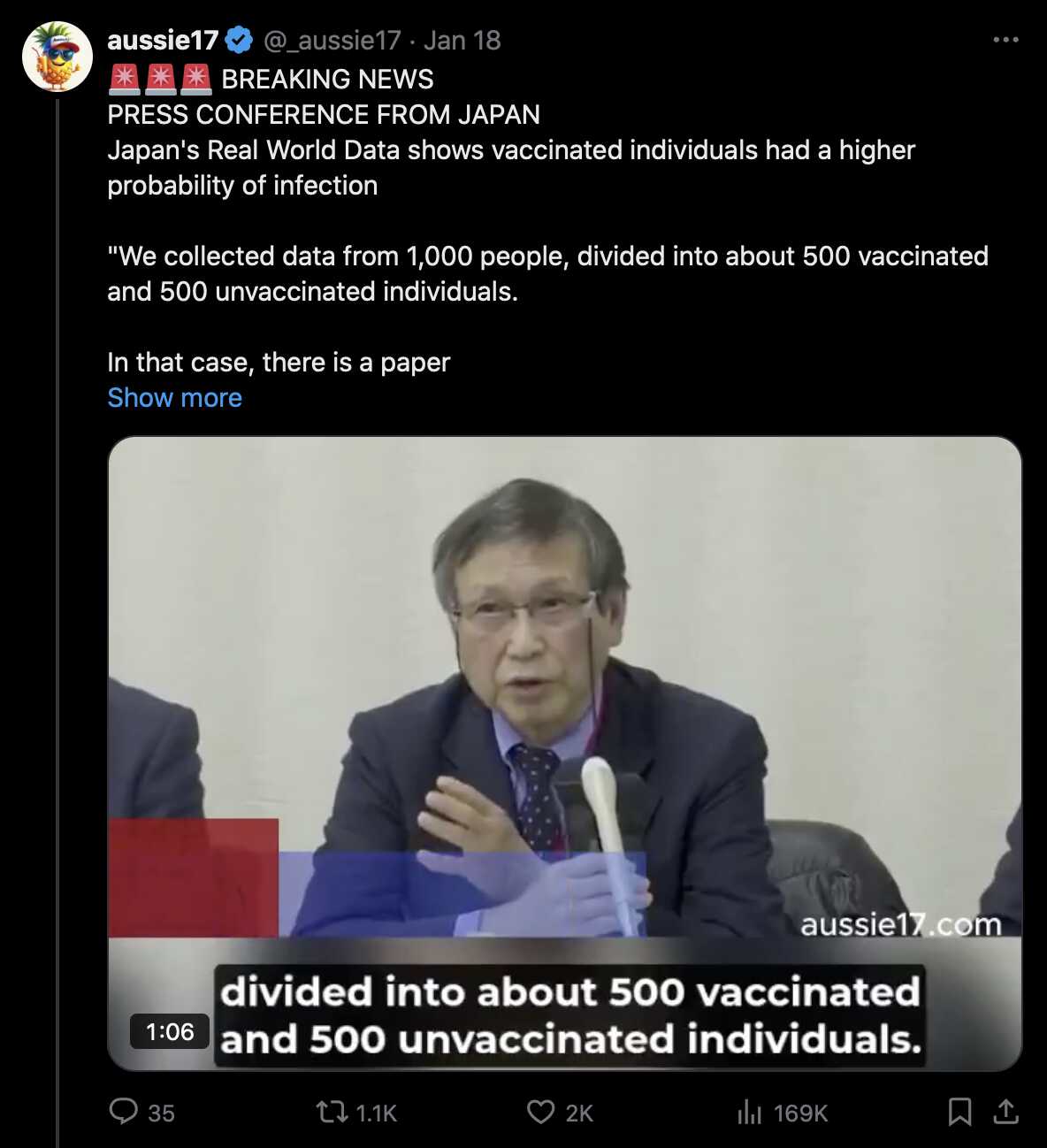
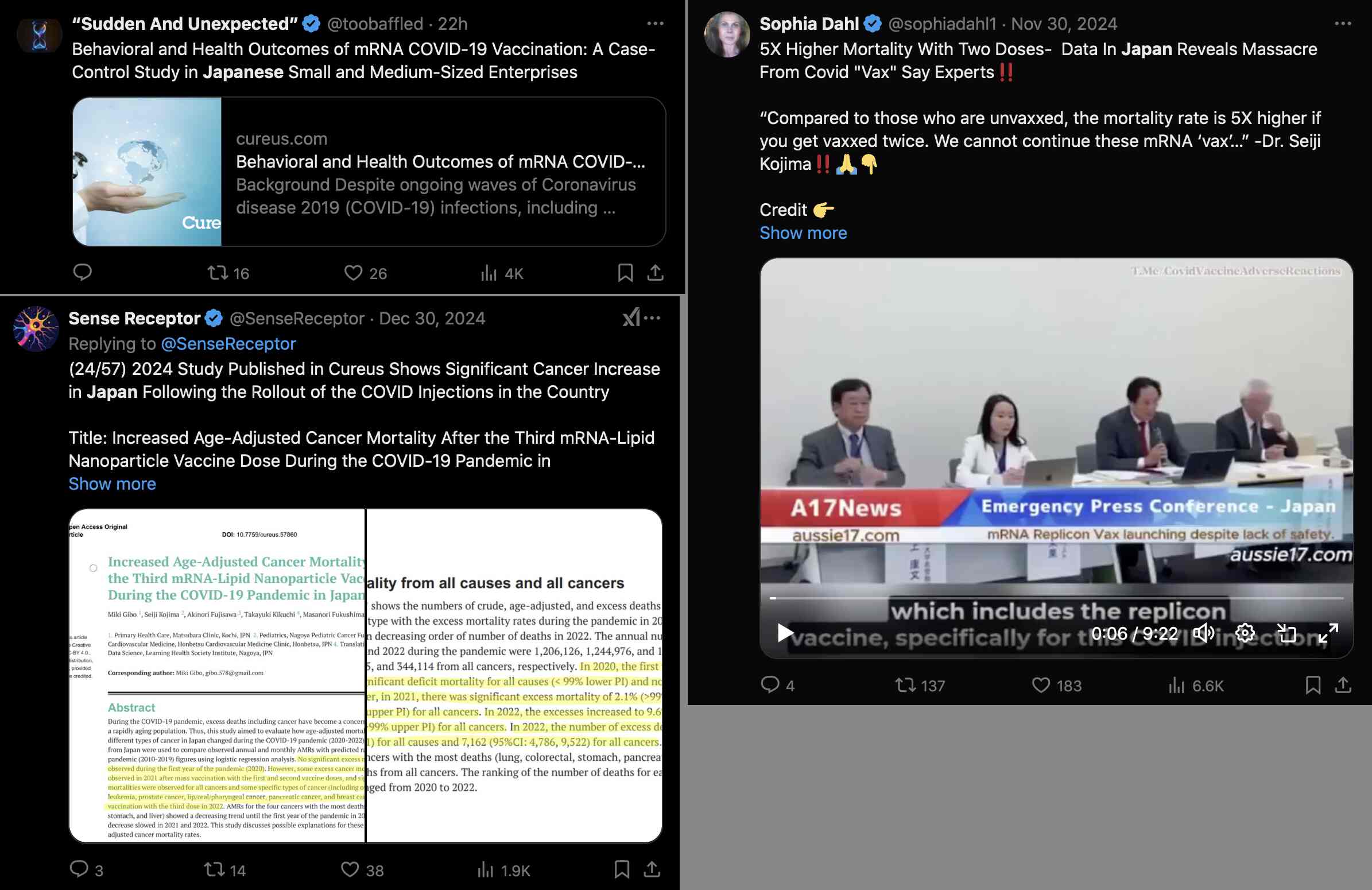
Aussie17 frequently posts subtitled videos produced by the astroturfed anti-vaccine movement in Japan and other Asian countries. His videos are often reposted by bots that promote Miles Guo and other bots that promote content from the fake alternative media. In 2024 I scraped the reposts of about 80 accounts I suspected to be bots that promoted content from controlled alternative media, and I counted how many times they reposted different COVID-related accounts relative the number of followers of each account, but Aussie17 ranked 8th highest. [bot2.html#Reposts_by_bots_compared_to_number_of_followers] The ten highest-ranking accounts also included toobaffled and SenseReceptor which both promoted the Japanese paper, and they included sophiadahl1 who posted another video by Aussie17 of a Japanese press conference:
Kirsch wrote: "CDC/NIH study: The ONLY statistically significant results were: vax increases infection risk, natural infection lowers infection risk. Never in human history does a vax make things risk worse in kids and better in adults. Table 2 confirmed CC findings: prior infection reduces risk; prior vaccination increases risk."
The study was behind a paywall and not at Sci-Hub or Researchgate so I wasn't able to read the study.
However Kirsch didn't mention that the study only included children between the ages of 6 months and 4 years.
In the next plot, the rate of COVID cases per capita was slightly higher in unvaccinated than vaccinated ages between 6 months and 4 years. But in ages 5-11 the rate was higher in unvaccinated people during some periods and in vaccinated people during other periods, but in older age groups the rate was clearly higher in unvaccinated people: [rootclaim.html#CFR_in_the_United_States_2c]

Ages 6 months to 4 years have such a low percentage of vaccinated people that children from various vulnerable subgroups might be overrepresented among vaccinated people.
However if you look at the data for ages 0.5-4 in the CDC dataset for COVID cases and deaths by vaccination status, there's a total of 64 COVID deaths in unvaccinated people but only one death in fully vaccinated people, even though vaccinated people account for only about 3.2% of total person-weeks: [https://data.cdc.gov/Public-Health-Surveillance/Rates-of-COVID-19-Cases-or-Deaths-by-Age-Group-and/54ys-qyzm/about_data]
t=fread("Rates_of_COVID-19_Cases_or_Deaths_by_Age_Group_and_Updated__Bivalent__Booster_Status_20241231.csv")
ages=unique(t$age_group)
t[,age:=factor(age_group,ages[order(as.integer(sub("[-+].*","",ages)))])]
t[,unvaxpop:=nafill(unvaccinated_population,,0)]
t[,vaxpop:=nafill(vaccinated_population,,0)]
o=t[outcome=="death",.(vaxdead=sum(vaccinated_with_outcome,na.rm=T),unvaxdead=sum(unvaccinated_with_outcome,na.rm=T),vaxpoppct=sum(vaxpop,na.rm=T)/(sum(vaxpop,na.rm=T)+sum(unvaxpop,na.rm=T))*100),,age]
o[,.(age,vaxdead,unvaxdead,vaxdeadpct=vaxdead/(vaxdead+unvaxdead)*100,vaxpoppct)]|>print(r=F)
age vaxdead unvaxdead vaxdeadpct vaxpoppct
0.5-4 1 64 1.5 3.2
5-11 3 54 5.3 21.8
12-17 14 174 7.4 41.1
18-29 169 1498 10.1 45.6
30-49 1442 11912 10.8 57.6
50-64 6837 33360 17.0 70.3
65-79 20630 56616 26.7 85.3
80+ 29296 48852 37.5 77.9
all_ages 58374 152238 27.7 62.6
The CDC dataset excluded partially vaccinated people with one dose or a second dose less than 2 weeks ago, so they are also not included in my code above.
Kirsch wrote: "Harvard (Subramanian (2021) was 68 countries. 90% slope CI was [2.83, 25.02] so we are 90% confident that the vaccine INCREASED infections across 68 different nations in September 2021. Data here."
The paper said: "We used COVID-19 data provided by the Our World in Data for cross-country analysis, available as of September 3, 2021 (Supplementary Table 1) [4]. We included 68 countries that met the following criteria: had second dose vaccine data available; had COVID-19 case data available; had population data available; and the last update of data was within 3 days prior to or on September 3, 2021. For the 7 days preceding September 3, 2021 we computed the COVID-19 cases per 1 million people for each country as well as the percentage of population that is fully vaccinated."
However richer countries have a higher percentage of vaccinated people than poorer countries, but richer countries also performed more tests capita which might explain why richer countries had more cases per capita: [rootclaim.html#Why_do_higher_vaccinated_countries_have_more_cases_per_capita_at_OWID_1d]

Kirsch wrote: "Independent survey of 500 Americans on COVID infections done by third party firm PureProfile: More vaccine doses→ higher risk of infection and number of infections."
He linked to a spreadsheet which seems to have been emailed to him by Leonard Murphy from the PureProfile company. Kirsch said the survey was an "independent survey", but I don't know how independent it in fact was, because a year ago Kirsch commissioned Murphy to produce another similar survey, so the new survey may might also been commissioned and paid by Kirsch. There are currently little details available about the new survey, but Kirsch might eventually publish a Substack post about it.
But anyway, the spreadsheet posted by Kirsch included these columns:
However the survey might suffer from a bias where vaccinated people were more likely to get tested than unvaccinated people. It's not possible to adjust for the bias because there's no column that asked people if they had ever been tested for COVID or how many times they got tested.
There was no data for the date when people got the first dose, so it is also not possible to calculate the number of COVID cases per person-weeks.
Kirsh did a simple analysis based on the survey where he didn't even differentiate between people who got COVID after vaccination or before vaccination:

There were 152 vaccinated people who reported a COVID case, but they included 42 people who reported a case before vaccination and 20 people who reported a case both before and after vaccination:
download.file("https://github.com/skirsch/covid/raw/refs/heads/main/debate/US%20infection%20survey%20by%20PureProfile.xlsx","US infection survey by PureProfile.xlsx")
t=setDT(readxl::read_excel("US infection survey by PureProfile.xlsx",sheet=2))
t[,covid:=`Have you EVER tested positive for, and/or been diagnosed with, COVID-19?`]
t[,time:=`When were you diagnosed with COVID-19?`]
t[,.(vax=`num shots`>0,time,covid)]
t[`num shots`>0&covid=="Yes",.(people=N),time]|>print(r=F)
# time people
# After receiving a COVID-19 vaccination 87
# Before receiving a COVID-19 vaccination 42
# Both before and after receiving a COVID-19 vaccination 20
# Unsure 3
There were 107 people who reported a COVID case when they were vaccinated but 109 people who reported a COVID case when they were not vaccinated:
t[`num shots`>0&time%like%"After|Both"&covid=="Yes",.N] # 107 (vaccinated cases) t[(`num shots`==0|(`num shots`>0&time%like%"Before|Both"))&covid=="Yes",.N] # 109 (unvaccinated cases)
About 62% of all people reported being vaccinated:
t[,.(people=.N),.(vaccinated=`num shots`>1)]|>print(r=F) # vaccinated people # TRUE 312 # FALSE 188
The percentage of vaccinated observation time out of total observation time is of course going to be lower than the percentage of vaccinated people. I didn't find any information when the survey was conducted. If for example the survey was conducted in mid-2021 then the rate of COVID cases per observation time would be higher for vaccinated people, but if the survey was conducted in 2024 then the rate would be higher for unvaccinated people. (Even though observation time during the period with low COVID cases after early 2022 would not be very relevant to determining COVID infection risk, so it might be better to do a time-series analysis that compares cases per person-weeks over time, but that is not possible based on Kirsch's survey because it doesn't show the dates of when people were vaccinated or got COVID.)
However I consider it plausible that the entire survey was fake, because Kirsch has a history of publishing fake data like the data from the anonymous military doctor he published in August 2024. [rootclaim.html#Ten_fold_increase_in_deaths_seen_by_NYC_fireman_5g] Kirsch's PureProfile survey is also similar to the Japanese survey by Eiji Nakatani et al. which appears to be fake.
Kirsch's spreadsheet for the PureProfile survey indicates that the data was sent to him by someone called Leonard Murphy:

I found that Kirsch is earlier supposed to have hired Murphy to conduct a poll which surveyed a thousand households that were chosen to be representative of the American population. But the survey seems fake because supposedly 194 households reported a death since 2021, and nearly half of households reported that they thought the death was caused by a COVID vaccine: [https://kirschsubstack.com/p/survey-nearly-half-the-deaths-observed]

Kirsch published his post about Leonard Murphy's earlier survey in January 2024, so the survey would have likely included data up to either January 2024 or some point of 2023. However only about 3% of the US population died between 2021 and 2023. And many of the people who died lived in elderly homes, so they were unlikely to be included in a random sample of US households unless the households also included elderly homes (and even in that case each elderly home included would have contributed only one death to the survey). There is also a survivorship bias where if someone died but they were the lone member of their household, then there was no other member of the household left who could have reported the death.
Kirsch wrote: "13,000 person survey: Consistent with CC study: more vaccines→ more cases."
He linked to this poll he did on Substack in January 2025: [https://kirschsubstack.com/p/did-the-covid-vaccine-reduce-cases]

One problem with his survey is that he asked people how many times they got COVID since January 2021, but there were probably some people got COVID in January 2021 or later but before they were vaccinated. Someone in the comments said: "I answered but there's an issue that you probably need to fix. I got one shot (J&J), and I've had COVID one time since January 2021. But the issue is that I had COVID BEFORE I had the shot."
Kirsch's unvaccinated followers may have been less likely to get tested than his vaccinated followers. Many of his followers even think that viruses are not real or that PCR tests are fake, so that even if they would've tested positive for COVID, they might still answer that they didn't have COVID.
Kirsch might have asked separate questions for how many times his people think they had COVID, how many times they tested positive for COVID, or how many times they had symptoms of a respiratory illness. And he could've also asked how many times people got tested for COVID to see if there's a bias where unvaccinated people were less likely to get tested than vaccinated people.
One person in the comments wrote: "Actually, I said unvaxxed, zero times, but I DID get a bad cold once that could have been COVID. I NEVER took this screamdemic very seriously, never got tested, would not know COVID from regular cold or flu. There must be many others like me and maybe such a phenomenon is the real explanation for your results." Another person wrote: "Since I have not been tested for COVID, its a bit difficult to say whether I contracted it. I HAVE been ill in this period since 2021, but as far as I can tell, its been influenza/cold (but then again: Whats the real difference?!)" A third person wrote: "I supposedly got COVID once, but I'm not sure I had it. The PCR tests are fraudulent. I was told I had COVID, but who knows? I may have simply had a bad cold." A fourth person wrote: "No one has ever had sars-cov-2 covid19, It doesn't exist !" And a fifth person wrote: "The problem is that its impossible to know what illnesses were/are 'covid' and what were/are just plain ordinary illnesses (or poisonings). I never 'tested' when I was ill. And of course the 'testing' was fraudulent."
Another person in the comments seems to have implied that they tested positive for COVID at one point but they still answered that they didn't get COVID: "I'm taking 'got covid' to mean tested positive on one of those OTC AG kits, while having symptoms. That's how I answered. In truth, I never had 'covid' because I never had any novel symptoms, nor do I accept those test kits as revealing anything real about my health (or anyone else's)."
One commenter pointed out: "I also think the opposite is true that the unvaccinated don't want to admit they had covid or they didn't test for it and so they have no idea if an illness was covid. I'm unvaccinated and I think I had it twice but I can't say for sure because I didn't test for it. I just thought the symptoms were different than your average flu."
Another comment said: "Those polls don't work man, for various obvious reasons such as people not getting vaccine in the first place, due to natural immunity, because of being young and healthy, plus people being tied closer to health care measurements, such as vaccines, receicing also more testing. But of course the biggest flaw here is that people don't actually know how many times they got Covid. Such layman polls only prove that the vast majority of people are incompetent to interpret statistics."
Kirsch posted this plot, where he had added annotations to a plot from the website of the California Department of Public Health:

The caption of the original plot by CDPH says that the plot is supposed to show cumulative COVID deaths as a percentage of cumulative cases 30 days earlier: [https://kirschsubstack.com/p/exclusive-the-cdph-is-unable-to-explain]

However I think CDPH might have forgotten to actually shift the cases by 30 days, because the plot by CDPH looks similar to my black line here where I didn't shift the cases and not the red line where I shifted cases forwards by 4 weeks, and in my red line the cumulative CFR actually went down during January and February of 2021:

library(data.table);library(ggplot2)
system("wget https://data.cms.gov/sites/default/files/dataset_zips/ea365a77467a04182b55114c5791c2e3/COVID-19%20Nursing%20Home%20Data.zip;unzip 'COVID-19 Nursing Home Data.zip'")
t=fread("COVID-19 Nursing Home Data/2025-01-05/COVID-19 Nursing Home Data 01.05.2025.csv")
d=rbind(t[,group:="Entire United States"],t[`Provider State`=="CA"][,group:="California only"])
d[,dead:=`Residents Weekly COVID-19 Deaths`]
d[,case:=`Residents Weekly Confirmed COVID-19`]
d[,date:=as.Date(`Week Ending`,"%m/%d/%y")-3]
a=d[,.(dead=sum(dead,na.rm=T),case=sum(case,na.rm=T)),.(group,date)]
a[,shifted:=c(rep(0,4),head(case,-4)),group]
lab=c("Unadjusted","Cases shifted forwards by 4 weeks")
p=a[,.(x=rep(date,2),y=rep(cumsum(dead),2)/c(cumsum(case),cumsum(shifted))*100,z=factor(rep(lab,each=.N),lab)),group]
p=p[is.finite(y)]
xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart+182,xend,"year")
p=p[x%in%xstart:xend]
yend=max(p$y,na.rm=T)
ggplot(p,aes(x,y))+
facet_wrap(~group,dir="v",scales="free_x")+
geom_vline(xintercept=seq(xstart,xend,"year"),linewidth=.4,color="gray88",lineend="square")+
geom_line(aes(color=z),linewidth=.6)+
geom_point(aes(color=z),stroke=0,size=1.1)+
geom_label(data=p[rowid(group)==1],aes(label=sprintf("\n %s \n",group),y=yend),x=xend,lineheight=.5,hjust=1,vjust=1,size=3.6,fill=alpha("white",1),label.r=unit(0,"pt"),label.padding=unit(0,"pt"),label.size=.4)+
labs(x=NULL,y=NULL,title="US nursing home data: Cumulative COVID deaths as percentage of\ncumulative COVID cases",caption="Source: data.cms.gov/covid-19/covid-19-nursing-home-data")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(0,yend),labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("black","#ff6666"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=2,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(4)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(4,"pt"),
axis.ticks.length.x=unit(0,"pt"),
axis.title=element_text(size=11,face=2),
axis.title.x=element_text(margin=margin(3)),
axis.title.y=element_text(margin=margin(,2)),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification="left",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.margin=margin(,,4),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.grid.major=element_blank(),
panel.spacing=unit(3,"pt"),
plot.caption=element_text(size=11,color="gray50"),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,face=2,margin=margin(0,,3)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.5,height=4.5,dpi=300*4)
system("magick 1.png -trim -resize 25% -bordercolor white -border 22 -colors 256 1.png")
In the black line where I didn't shift the cases and in the plot on CDPH's website, there's a dip in CFR during the COVID wave around December 2020 to February 2021, because the CFR went down during the earlier part of the COVID wave because the deaths had not yet caught up to cases, but during the later part of the COVID wave the CFR went up because there was now a surplus of deaths relative to new cases. In the plot below cases peaked on the week ending December 20th 2020 but deaths peaked three weeks later on the week ending January 10th 2021, and the CFR was the lowest in the two weeks in between. There's another similar dip in CFR during the COVID wave in the summer of 2020: [https://www.cdph.ca.gov/Programs/CID/DCDC/Pages/COVID-19/SNFsCOVID_19.aspx]

In the next plot which shows non-cumulative CFR instead of cumulative CFR, the black unadjusted line has a big spike during the tail end of the COVID wave around February 2021, because by February 2021 there were no longer as many people with a new case as during the previous weeks, but people who had acquired a new case during the previous weeks were still dying from COVID. But in the line where I shifted the cases 4 weeks forwards, the CFR now had a big drop between December 2020 and January 2021. But the 4-week shift is too long because the average duration between case onset and death is less than 4 weeks, so when I shifted the cases only 2 weeks forwards instead, the line for the CFR became more flat (even though the CFR still went down during the first weeks of 2021):

Kirsch wrote: "Czech Republic record level data: Moderna recipients had an average >1.3X higher 1 yr mortality than Pfizer during non-COVID months. Setting DCCI=0 for both vaccines didn't change the results so wasn't comorbidity bias. Since Moderna was 40% of US vaccines, a 30% increase in ACM is an annual 12% increase in mortality which is consistent with Skidmore."
In the code below I used the same Czech data to calculate a normalized excess mortality percent within the first 52 weeks from the first vaccine dose. When I calculated the expected baseline number of deaths by multiplying the population size for each age with the mortality rate for the same age among all people included in the Czech dataset, Moderna got only 18 points higher excess mortality percent than Pfizer. But the difference fell to 13 percentage points when I also normalized the baseline mortality rate by comorbidity index in addition to age: [czech4.html#Mortality_rate_within_year_from_vaccination_normalized_by_comorbidity_index_in_new_UZIS_data, https://www.nzip.cz/data/2135-covid-19-prehled-populace]
t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv")
codes=rep("Other",25)
codes[c(1,8,9,16,20,21,23)]="Pfizer"
codes[c(2,15)]="Moderna"
codes[3]="AstraZeneca"
codes[4]="Janssen"
codes[c(7,22)]="Novavax"
names(codes)=sprintf("CO%02d",1:25)
weeks=unique(format(seq(as.Date("2020-1-1"),as.Date("2024-12-31"),1),"%Y-%V"))
d=t[Infekce==1]
d[,case:=match(DatumPozitivity,weeks)]
d[,first:=match(Datum_Prvni_davka,weeks)]
d[,dead:=match(ifelse(DatumUmrtiLPZ=="",Umrti,DatumUmrtiLPZ),weeks)]
d=d[,.(case,first,dead,dcci=DCCI,code=OckovaciLatkaKod_Prvni_davka,born=RokNarozeni)]
d=d[born!="-"&!born%like%"19(05|10)"]
a=d[,.(dead=sum((dead-first)%in%0:51),pop=.N),.(first,name=codes[code],born,dcci)]
a=merge(a,a[,.(base=sum(dead)/sum(pop)),.(first,born,dcci)])
a=merge(a,a[,.(base2=sum(dead)/sum(pop)),.(first,born)])
o=a[,.(dead=sum(dead),pop=sum(pop),`by_age_and_dcci`=(sum(dead)/sum(base*pop)-1)*100,by_age=(sum(dead)/sum(base2*pop)-1)*100),name]
print(mutate_if(o[order(-pop)],is.double,round,1),r=F)
name dead pop by_age_and_dcci by_age
Pfizer 14857 2184868 -5.6 -6.4
Moderna 2729 182299 7.3 11.5
Janssen 1395 152824 13.6 11.8
AstraZeneca 3474 123531 17.7 20.6
Novavax 9 3103 -18.0 -40.8
Other 1 131 -0.1 -1.3
So comorbidities might in fact partially explain why Kirsch got a higher mortality rate for Moderna than Pfizer. In most age groups the percentage of people with the highest value of the comorbidity index was higher for Moderna than Pfizer: [czech4.html#Comorbidity_index_by_age_group_and_vaccine_type_in_new_UZIS_data]

Kirsch listed various sources where people with a Moderna vaccine had a higher mortality risk than people with a Pfizer vaccine:

But Kirsch forgot to mention that in the Medicare data from Connecticut he published in 2024, people who got a Pfizer vaccine for their first dose subsequently had higher ASMR than people who got a Moderna vaccine for their first dose: [connecticut.html#ASMR_by_vaccine_brand_and_month]

In the next plot that is based on VAERS data from European countries, I calculated a ratio of reports involving a death relative to total VAERS reports. When I divided the ratio for Moderna vaccines with the ratio for Pfizer vaccines, the total ratio across all countries and all age groups was about 0.95, which means that Pfizer had a higher ratio of deaths per reports than Moderna. The ratio between Pfizer and Moderna was even bigger in ages 60-79 and 80+, and in certain countries like Germany, Austria, Germany, Belgium, Spain, and Sweden. But on the other hand Moderna got a higher ratio than Pfizer in countries like France, Italy, and Netherlands, which suggests that the differences across countries might be due to different profiles of confounding factors in different countries: [czech4.html#Ratio_of_deaths_per_adverse_event_reports_in_VAERS_calculated_by_Hans_Joachim_Kremer]

I don't think either of my plots above are valid methods to evaluate which vaccine brand is safer, but on his list Kirsch cited similar analyses as evidence that Moderna vaccines were more lethal than Pfizer vaccines. And even though I showed both of the plots above to Kirsch last year, he didn't include them on his list because he cherrypicked sources where Moderna got higher mortality than Pfizer.
Kirsch wrote: "1. Hungary study: Moderna had 18% higher ACM during non-COVID periods than Pfizer. It would have been larger had the groups been evenly distributed, but the paper noted Pfizer got older people with more comorbidities. So 18% excess ACM is a minimum→ 7% annual US mortality increase from Moderna alone (assuming Pfizer is 100% safe) which is 195K excess deaths/yr which is consistent with Skidmore."
Kirsch referred to this table that showed a crude mortality rate that was not adjusted for age or confounders, where Moderna had about 1.18 times higher mortality rate than Pfizer:

However if you look at Table S7 which shows risk ratios that are
adjusted for characteristics like age and comorbidities, Pfizer has only
about 9.6% higher reduction in risk than Moderna (from
(1-0.384)/(1-0.438)):

And in Table S6 which shows risk ratios during the period with high
COVID mortality instead of during the period with low COVID mortality,
then Moderna actually has a greater reduction in risk than Pfizer, even
though the difference is only about 1.2% (from
(1-0.187)/(1-0.197)):

Kirsch wrote: "Embalmers are still finding the novel blood clots in vaccinated cases even now in 2025 suggesting a VERY long kill period for the vaccine.These clots can easily kill people. NEVER SEEN BEFORE COVID VACCINE ROLLOUT. For example, Hirschman has been seeing these clots in over 50% of his cases since 2021 when he first noticed them and only in the last 3 months, has it dipped under 50%. These clots aren't killing everyone who has them, but this is demonstrating a plausible mechanism of action for vaccine deaths happening years after vaccination."
Kirsch linked to a tweet by Richard Hirschman, who I believe was the first embalmer or funeral director who said publicly that they had seen a new type of white blood clots after the vaccine rollout. I haven't found any reference to the clots before January 2022 when Hirschman did his alt media debut on the Jane Ruby Show.
Jane Ruby brags that she broke the news about the clots, but she also brags that she was the first person to break La Quinta Columna's story about graphene oxide in English-language media: [https://x.com/RealDrJaneRuby/status/1619624953036558338, https://x.com/RealDrJaneRuby/status/1604355938881789952]
When Hirschman first appeared on the Jane Ruby Show, the show used to be part of the Stew Peters Network, which is notorious for pushing disinformation stories about strange objects found in vaccines or in the blood of vaccinated people, including hydras, microchips, nanobots, graphene oxide, snake venom, hydrogel, shards of glass, neanderthal DNA, and gorilla feces. I call the stories "Stew ops", because the origin of the stories frequently goes back to the Stew Peters Network or to guests on their network. Stew Peters also says that the earth is flat and viruses are not real.
I believe the FEMA whistleblower Celeste Solum was the first person who started to say that COVID vaccines were going to contain hydrogel, but she has also said that COVID vaccines contain gorilla feces and Neanderthal DNA: [https://gettr.com/post/p2rc1em2ae7]

But anyway if the calamari clots are caused by COVID vaccines, then
why was the story about the calamari clots only breaking news in January
2022? When I searched Twitter for
embalmer clot until:2022-1-27, I didn't find a single
reference to the calamari clots that predated Hirschman's interview with
Jane Ruby.
[https://x.com/search?q=embalmer+clot+until%3A2022-1-27&f=live]
I only found a few tweets which linked to an article from September 2021
titled "'The Clots Were The Size
Of Pancakes' - Texas Embalmer Opens Up About Covid
Horrors". But the article didn't discuss the new type of white
clots that Hirschman is supposed to have found.
Jane Ruby tweeted that she found Richard Hirschman through an unnamed source: "That is my story, that is the story upon which that movie/documentary was made and I was left out. I am that story, I found the Embalmer through a source, I've vetted him over weeks, and I broke the story worldwide in an exclusive Jan 2022". [https://x.com/RealDrJaneRuby/status/1645423764304191492] Mathew Crawford told me that "it was DMED whistleblower Theresa Long who 'found' Hirschman". Crawford used to help out Kirsch with statistical analysis but he broke ties with Kirsch partially because Kirsch was promoting the story about the calamari clots but Crawford thought it was disinformation.
The Died Suddenly film contained about 7 minutes of footage of Steve Kirsch, which is the second most footage of any person featured in the film after Richard Hirschman.
In January 2022 Kirsch was one of the earliest big names in alternative media who started promoting the story about the calamari clots. He posted a link to Hirschman's interview with Jane Ruby soon after the interview was published: [https://kirschsubstack.com/p/worldwide-exclusive-embalmers-find]
I believe Kirsch was the second person in alt media after Jane Ruby who interviewed Hirschman. [https://www.bitchute.com/search/?query=richard%20hirschman] Kirsch has also published two surveys about the calamari clots that were done by Tom Haviland who is a retired Major General in the US Air Force. In the second survey published in 2024, 197 out of the 269 embalmers surveyed are supposed to have answered yes to a question that asked if they had seen the calamari clots in corpses that they embalmed in the year 2023. [https://kirschsubstack.com/p/embalmer-survey-2023-over-75-are] However I suspect the data in the surveys was fake similar to the data by the supposed military doctor that Kirsch released. [rootclaim.html#Ten_fold_increase_in_deaths_seen_by_NYC_fireman_5g]
The Died Suddenly movie featured a long segment about the DMED data by Theresa Long and Pete Chambers, who are both medical officers in the US Air Force. So it's interesting that Kirsch's survey was also done by Haviland who was a Major General in the US Air Force. One of Haviland's surveys was published on Twitter by the Canadian funeral director Laura Jeffery, who said that she was trained in the Air Force Cadets in the 1990s (even though I don't know if it means the Canadian or US Air Force). [https://x.com/LauraJayJayJay/status/1829476769222537242, https://x.com/LauraJayJayJay/status/1898781555314569324] One of the viral videos about DMED data is a video by Pam Long whose bio says that she "served as a medical intelligence officer for NATO Stabilization Forces". [https://x.com/toobaffled/status/1823839301484089807, https://childrenshealthdefense.org/authors/pam-long/] The savvier conspiracy nuts have learned to be wary of whistleblowers who are hyped up in the alt media, especially if the whistleblowers have a background in military or intelligence.
Kirsch has also done videos with the ex-military nurse whistleblower Erin Marie Olszewski. [https://kirschsubstack.com/p/nurse-whistleblowers-tonights-vsrf, https://kirschsubstack.com/p/epic-4-hour-vsrf-episode-what-the] Erin has said that she was "trained at the John F. Kennedy special warfare center in Fort Bragg in psychological operations and civil affairs". [https://gregwyatt.net/did-erin-malone-olszewski-work-undercover-at-hospitals-schools-and-orphanages-in-iraq/] Erin wrote that before she started her anti-vaccine organization in 2019, she worked at an antiterrorism unit at MacDill Air Force Base. [https://books.google.com/books?id=Dn_rDwAAQBAJ&pg=PT91] MacDill is the location of the headquarters of U.S. Special Operations Command, which is responsible for overseeing psychological operations. Reuters reported that in 2020 the Pentagon contracted General Dynamics IT to run a psyop campaign where they posted anti-vaccine content on Twitter and other social media, but the campaign was run out of MacDill Air Force Base. [https://www.reuters.com/investigates/special-report/usa-covid-propaganda/]
Kirsch also did a video with Tom Haviland where they interviewed a couple of people who were said to be either funeral directors or embalmers (even though I don't know if some of them were just actors playing a role). [https://rumble.com/v4c2e79-vsrf-live-113-embalmer-data-revealed.html] Some guy who was presented as an embalmer named Bill said that he started seeing the calamari clots around July or August 2021. He said: "Prior to this - I mean, I've been an embalmer over 30 years - I had never ever seen this - prior to, I'm gonna say July or August of 2021." [time 31:12] Kirsch also asked an embalmer called Lorin Ware "And you started seeing them in mid-2021?" But she answered "Yes sir", and then Kirsch asked: "Was it like a light switch turning on, or did it happen pretty gradually?" And she answered that "It was like a light switch turning on." [time 26:00] But if everyone started suddenly seeing the clots in mid-2021 then how come no-one was speaking out about the clots until January 2022?
If you search for "funeral director" at BitChute and you sort the results by oldest first, you'll find several conspiracy videos posted in 2021 that featured funeral directors. [https://www.bitchute.com/search?query=funeral+director&sort=old] I watched most of the videos but I didn't find any reference to a new type of white clots in the videos.
John O'Looney is a funeral director who was featured in the Died Suddenly film. During an interview in 2024 when O'Looney was asked when he first started seeing the new type of blood clots, he answered: "So, really, in 2021, about halfway through, we started seeing lots and lots of people who were passing away suddenly, who were a lot younger than those that we were used to." [https://www.youtube.com/watch?v=wwdRfbPrGIY&t=10s] And a bit later he said this about the calamari clots: "I've got a BIE-registered embalmer who works for me full time, who's done 22 years, and he's never seen them before, uh, 2021, no." And the interviewer said: "So some people have think they've seen some small ones in 2020, but that's not your experience: it's 2021 they started, midway through 2021." And then O'Looney answered: "Yes, 100%, yeah."
However I didn't find O'Looney mentioning the calamari clots anywhere in 2021. During an interview on September 30th 2021, the only time he mentioned blood clots was when he said: "Children will get cardio issues, inflammation of the heart. There will be blood clots and all the things I'm seeing as a funeral director. Now as a funeral director I'm seeing four main causes of death coming into me now. I'm seeing heart attack and stroke as a result of blood clot." [https://antijantepodden.com/.ajp_enep026.html, 24:59] But he didn't mention anything about a new type of white rubbery clots even though the interview was done on the last day of September so it was already much more than halfway through 2021. And also in a video that O'Looney did in December 2021, he said: "We used to see a blood clot very very rarely, but now I've seen more this year than I have in the previous 14." [https://www.bitchute.com/video/OTvtHkCNzlNE/, time 0:58] But he didn't say anything about a new type of white clots even though he said he has seen a lot of clots. And in another interview of O'Looney dated September 1st 2021, he didn't mention any kind of clots. [https://rumble.com/vlyri3-uk-funeral-director-seeing-alarming-rise-in-deaths.html]
There were 16 tweets which matched the search phrase
from:olooneyjohn until:2021-12-31 clot, but none of them
mentioned anything about a new type of white clots.
[https://x.com/search?q=from%3Aolooneyjohn%20until%3A2021-12-31%20clot&f=live]
But I accidentally found that in July 2021 O'Looney posted a TikTok
video of a guy who was supposed to be a 5G installer, who said that his
job was to install 5G kits which he was told to not crack open. But when
he tried opening one kit, it contained a circuit board which said "COV-19".
[https://x.com/OlooneyJohn/status/1419982639415631873]
Then O'Looney commented "Just imagine having the
ability to induce blood clots and vaccine recipients over
Wi-Fi...":
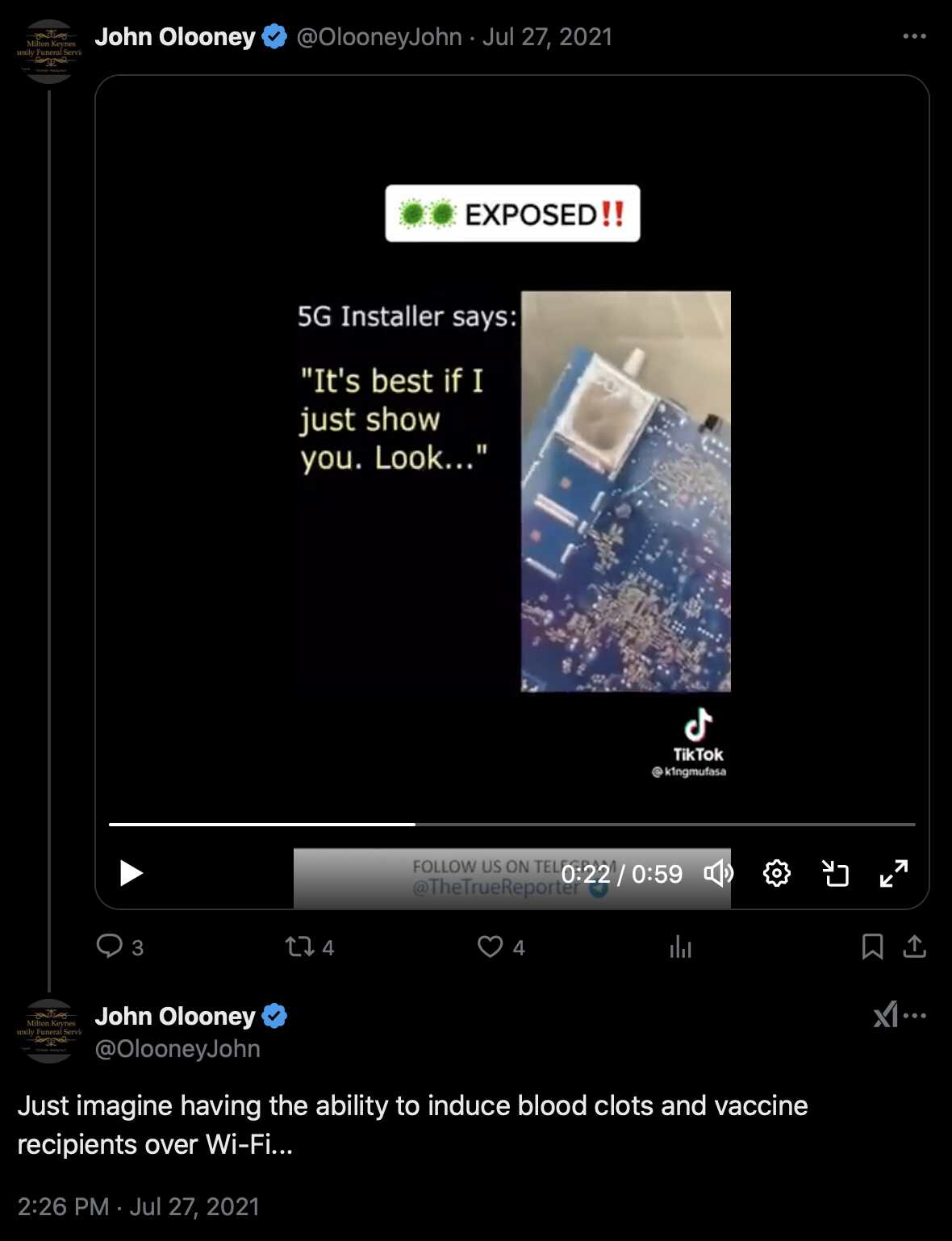
However Reuters said this about the 5G video: "The circuit board was actually taken from a Virgin Media box for cable television - the casing of which can be seen on the bonnet of the van as the camera pans at the end of the footage. Virgin Media confirmed to Reuters it believed the circuit board had been taken from an old TV box, and the 'COV-19' engraving was not authentic." [https://www.reuters.com/article/idUSKBN22R35E/] So it might even be that the people who made the video left the casing of the box visible so the video would be easier to debunk.
Many anti-vaxxers suspect O'Looney of being controlled opposition who is attempting to discredit anti-vaxxers: [https://x.com/Jikkyleaks/status/1804717634270978122]
In 2021 Resistance GB did one interview with John O'Looney and another interview with a British funeral director named Wesley who seems to have later been forgotten (even though I don't know if he was actually a funeral director or if he was just an actor playing a role):

The funeral director Wesley said that there were almost no elderly people dying anymore because they had already died before. [https://www.bitchute.com/video/0QLoXDVmgb3I] But he said that around the time when young people got vaccinated, he had the most funerals he had "ever done in two weeks, and they're all aged 30, 40, no older". However his anecdotal statistics are inconsistent with actual mortality statistics in England, where in May to June 2021 when the highest number of people in ages 30-49 got vaccinated, only about 4% of all deaths were in ages 30-49. [https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/adhocs/1343dailydeathsbydateofoccurrence1stjune2014to31stmay2023bysingleyearofageengland] The funeral director Wesley also said there were about ten times more babies dying than normally, so there was no more room in the fridge for babies so the dead babies had to be placed in an adult fridge. His story was reminiscent of the anecdotes Kirsch has conveyed from various professionals like nurses and funeral directors, because the story was highly emotionally laden and the numeric figures he presented seemed exaggerated and unrealistic.
John O'Looney was one of the funeral directors who were featured in the Died Suddenly film that was produced by the Stew Peters Network. The main star of the film was Richard Hirschman who had earlier done his alt media debut on the Stew Peters Network. The director of the film was Stew Peters, the producer was Lauren Witzke who at the time was Stew's producer, and the editor was Nicholas Stumphauzer who was hired by Witzke and Stew to do their movies. [http://web.archive.org/web/20221122001654/https://stewpeters.com/video/2022/11/live-world-premiere-died-suddenly/] Previously the same team produced a film called "Watch the Water", where Bryan Ardis claimed that COVID was caused by snake venom in tap water (which they said was a "truth satan himself has fought to suppress"): [http://web.archive.org/web/20221105032849/https://stewpeters.com/video/2022/04/world-premiere-watch-the-water/]
The Died Suddenly film includes a video of the basketball player Keyontae Johnson collapsing, but the video is from December 12th 2020. [https://edition.cnn.com/2020/12/15/sport/florida-gators-player-breathing-talking/index.html] At time 47:45, the film features a video of a man falling off a chair but it's from January 2020. [https://kirschsubstack.com/p/answering-the-critics-of-died-suddenly] At time 52:33 the film features a video of a pulmonary embolectomy from 2019: [https://x.com/thereal_truther/status/1596560239247364096]

Jane Ruby claims that she was the first person to break the news about the new white clots in January 2022. Later in 2022 she did an interview with the counterbioterrorism expert Tau Braun, who claimed that COVID vaccines contained nanobots delivered by graphene oxide, and the calamari clots consisted of tissue that was programmed to grow snake venom glands by the nanobots. The description of the interview said: "On today's Dr. Jane Ruby Show, Dr. Jane interviews Counter-bioterrorism expert Dr. Tau Braun who explains that self-replicating nanoparticles in the C19 shots are programmed to grow venom ducts inside the human body. His theory is that the jabbed are growing live venom gland cells and other animal structures. Dr. Jane shows you the DOJ's research using cone snail venom to make huge amounts of deadly synthetic conotoxins. They say that deep ocean cone snail venom is a serious threat to humans who never dive that deep!" [https://stewpeters.com/video/2022/11/the-jabbed-are-growing-animal-venom-glands-and-ducts/] Tau Braun said that people were wondering if COVID vaccines contain snake venom or if they contain graphene oxide, but he said they contain both because the graphene oxide acts as a delivery mechanism for the snake venom. At time 13:18, he said: "How do you get venom into the body and how do you keep it stable? You add graphene oxide." At time 40:33, Tau Braun said that the calamari clots consist of tissue which contains snake venom ducts: "Those monstrous clot-looking things are literally tissue that has grown a duct - and specialized ducts - the closest match I found to these fibrotic clots today is the chameleon tongue - it's the long, very very - extremely - it has what's called the tensile strength, it has elasticity to it. But it's extremely strong. Cause it has to whip out like a whip and it has to come back in, and so it has to have expansion at rapid speed, and it has to be able to go back. So it's like elastic." At time 17:40, Tau Braun said that if there is a species of snake that eats rodents, then the snake won't produce venom which affects amphibians but only venom which affects rodents, and in the same way the snake venom in the COVID vaccines was designed to not affect Aryans because the COVID vaccines are a race-specific bioweapon that was created by the Fourth Reich: "So why are certain people totally fine from this? I'm gonna tell you that this was built by the Fourth Reich, and I'm gonna tell you that Aryans are not having a problem with this vaccine. I'm gonna tell you that you can stick this into an Aryan over and over. And what I mean by Aryan? I mean people that originally came from Viking heritage, Germanic heritage, and that basically you can go and look at those principles of what Nazis believe the superior race to be. And I'm gonna tell you this weapon was not built for them." Tau Braun also said that the Aryans were planning to kill off nine tenths of humanity. Tau Braun's bio says that he is a "U.S. National Counterterrorism & EMS Advisor and Trainer" and that he has been a speaker at a bunch of emergency management conferences. [https://www.drtaubraun.com/about]
Before the story about the new type of white clots was rolled out in January 2022, in 2021 La Quinta Columna were saying that vaccinated women had black period blood that contained black clots (because graphene is black, and at the time La Quinta Columna were primarily famous for their claim that vaccines contained graphene oxide): [https://www.bitchute.com/video/WGjJ2rgw14N9/]

In 2021 La Quinta Columna published videos about how vaccinated parents had "pandemic babies" who appeared to have completely or almost completely black eyes, and the babies were also developing rapidly so that they were able to walk when they were 3 months old or crawl when they were 2 weeks old: [https://www.orwell.city/2021/09/black-eyed-babies.html]

In September 2021 Carrie Madej started to say that COVID vaccines contained eggs of transgenic parasites of the species Hydra vulgaris. In 2021 before the story about the calamari clots had been rolled out, Carrie Madej told Stew Peters that vaccinated people were growing hydra clots: [https://ambassadorlove.blog/2021/11/01/transgenic-hydras-parasites-a-biological-weapons-system-for-rapid-human-cloning/]

Carrie Madej told Stew: "Let's just look at these water parasites. These things have the potential to grow, and be innumerable, right. If you're growing things, it has the potential to clog your arteries, it can clog capillaries, it can clog lymphatics. So we see blood clotting happening, and plus the body's response to having an infection, or a parasitic invasion, right, would be an inflammatory response, would be to have inflammation, which perhaps clotting an area." [https://www.bitchute.com/video/CU7FTZwr54yP/, time 12:12] And then the video cut off to the photo of the clot above, and Madej said: "So, they're pulling clots sometimes out too that's almost as big as my hand, you know, has finger-like extensions coming from let's say the heart."
However the hydra clot was actually a clot from the lungs of a heart failure patient from 2018: [https://empr.com/home/news/heart-failure-patient-coughs-up-bronchial-tree-shaped-blood-clot/]

In an interview with Mary Holland from CHD, Ana Maria Mihalcea claimed that the calamari clots contained spider silk protein. She said: "Clifford Carnicom and I have got the deceased clots from Richard Hirschman, we got a clot from a living vaccine injured person, and from an unvaccinated individual. And what we looked at is clearly this rubber-like material that we know about. And we did by mircoscopy, and we found the same filaments that we see in the blood, absolutely the same stuff, okay. And then we did near-infrared spectroscopy and found that these things have a polyins, which is polyethylene alcohol, polyvinyl alcohol, which is plastic, and polyamide, which is silk, nylon, or Kevlar. And specifically, you know, Kevin Kerningham, Dr. Kerningham [meant McKernan] found the genes of DNA of spidroins of spider silk. That's the strongest military-grade material that they have made. And so we found these in the clots." [https://x.com/ChildrensHD/status/1845970364993798325, time 41:40] However Kevin McKernan did not actually find spidroin in the Pfizer vaccine sequence, but he found a long open reading frame on the reverse strand of the vaccine sequence, and when he searched for the ORF on UniProt BLAST using extremely liberal settings, the closest match happened to be a spidroin sequence by chance (even though it was an extremely distant match that was not actually similar at all to the reverse ORF, and it wouldn't have even been returned as a hit if he would've ran BLAST with normal settings). [https://anandamide.substack.com/p/spider-webs-in-the-pfizer-closet] Later when I repeated the same BLAST search at UniProt, there were now more new sequences that had been added to the database, so the best two matches were a protein from algae and a protein from a cockroach, but the spidroin protein only came on third place. [scripts.html#Search_for_ORFs_on_reverse_strand_in_SARS2_and_Pfizer_vaccine_contigs] Clifford Carnicom is also supposed to have found Morgellons fibers in Hirschman's clots. [http://web.archive.org/web/20230711070359/https://anamihalceamdphd.substack.com/p/blood-clot-analysis-from-living-and] Ana Maria Mihalcea and Carnicom also claim that chemtrails contain both Morgellons fibers and spider silk.
In 2025 Wayne Crouch from Australian National Review published a series of AI-generated documentary videos titled "An Unholy Triad: The Birth of a Plague". One of the three executive producers of the documentaries was Brenton Faithfull, who is an embalmer who was featured in the Died Suddenly film, and the credits of the film also included Richard Hirschman and Greg Harrison who is supposed to have sent Hirschman's clots to Kevin McCairn. The main theme of the documentary series was that Crouch's research team is supposed to have found new mysterious ORFs in the genome of SARS-CoV-2. The first episode of the series said: "Direct evidence, lab records, internal PLA documents, and intercepted communications confirms China engineered three ORFs critical to SARS-CoV-2. ORF11: Documents from the early 2000s detail a gene enhancing viral entry into human cells, tested in bat coronaviruses at WIV to boost infectivity. ORF19: Research logs from 1999 to 2005 describe a sequence amplifying viral replication designed to accelerate spread uncovered in PLA virology studies. ORF29: Military reports from 2003 to 2008 outline a gene modulating host inflammatory responses intended to exacerbate disease severity trace to WIV experiments." [https://rumble.com/v6paaoo-an-unholy-triad-the-birth-of-a-plague-episode-01.html?start=309] But none of the purported "research logs" or "military reports" were actually shown in the documentary. The regular ORFs of SARS-CoV-2 only go up to ORF10, but I don't know if ORF19 and ORF29 were supposed to be a nested ORFs inside the spike protein or something. Later parts of the documentary series claimed that the same ORFs were also included in the vaccines and they were responsible for causing the white clots (even though of course most vaccines only contain the spike protein and not other ORFs from the virus, unless the other ORFs are nested ORFs within the spike protein).
Philip McMillan claimed that Crouch's research team had collected 6,000 pages of documents and that "Within these documents, there is one section that immediately caught my attention - the reference to modified ORFs (Open Reading Frames) 10, 11, and 19 in the SARS-CoV-2 genome." [https://philipmcmillan.substack.com/p/covid-secrets-theyre-hiding-from] So McMillan claims to have seen some of the documents, even though I believe none of the documents have been made public. In March 2025 McMillan published a YouTube video about how Kevin McCairn had supposedly found that Hirschman's clots were fluorescent, but McMillan also promoted Crouch's story about ORF19 in the same video. [https://www.youtube.com/watch?v=ZMFEGLWEXyU] Wayne Crouch is the "head reporter" at Australian National Review, which looks like an Aussie version of the Stew Peters Network, and the front page of their website featured two interviews of Stew Peters when I wrote this. [https://anr.news] Wayne Crouch also posted an infographic about how Kevin McCairn killed a hamster after injecting it with "our amyloid jab clot samples". The graphic said that Kevin McCairn was linked to "Solution of Scientists", which is the group that Crouch and Greg Harrison are part of. Crouch is supposed to be a journalist, but in his infographic he somehow managed to misspell the words "scientist's", "hampsters", and "acess": [https://x.com/WayneC50256258/status/1904696389176803605]

In March 2025 Laura Kasner who works together with Tom Haviland published a document called "Kevin_Mccairn_Findings.pdf" which said "ORF-19 and ORF-11 are now functionally implicated in the induction of prionic seeding" (where the names of ORFs were written with a hyphen like in the documentaries by Wayne Crouch). [https://laurakasner.substack.com/p/a-horrifying-breakthrough-in-the] The document didn't have any authors listed apart from "The Researchers". However the authors probably included Greg Harrison, because in 2024 Laura Kasner posted another similar PDF about the clots, where the cover of the PDF said "authors remain anonymous for safety reasons" even though Kasner wrote that Greg Harrison was one of the authors. [https://laurakasner.substack.com/p/how-the-white-clots-are-formed] Greg Harrison has also posted about ORF19 and ORF29 on Twitter and he writes the names of the ORFs with a hyphen. [https://x.com/search?q=%22orf-19%22&f=live] Wayne Crouch wrote that the mysterious documents which described ORF19 and ORF11 were unearthed by "our chemist", which probably refers to Greg Harrison who is a chemist. [https://puremediaaustralia.org/f/global-conspiracy-exposed-unveiling-the-ultimate-bioweapon] But Greg Harrison is also the person who is supposed to have sent Hirschman's clots to Kevin McCairn and he has done multiple videos with McCairn. In February 2025 Harrison, Haviland, Hirschman, and McCairn also appeared together on an episode of Kirsch's VSRF podcast. [https://rumble.com/v6k0oav-vsrf-live-164-white-clot-roundtable.html]
Kirsch wrote: "Rasmussen, a highly respected national polling company, found 11% of American households lost someone to COVID vs. 10% of American households lost someone to the COVID vaccine. The result was INDEPENDENT of political parties. There are no public polls showing otherwise. I'm claiming only that the vaccines killed 57% of those killed by COVID which is more modest than the 80% ratio (vaccine/covid deaths) found in the Rasmussen poll."
The survey was conducted between March 27th and 29th of 2023. The article about the survey said: "The latest Rasmussen Reports national telephone and online survey finds that 11% of American Adults say a member of their household died from COVID-19, while 86% answer no. Ten percent (10%) say a member of their household has died whose death they think may have been caused by side effects of COVID-19 vaccines, while 85% say there were no such deaths in their household. (To see survey question wording, click here.)" [https://www.rasmussenreports.com/public_content/politics/public_surveys/covid_19_virus_deaths_vs_vaccine_deaths]
The questions asked in the survey were "Has any member of your household died from COVID-19?" and "Has any member of your household died whose death you think may have been caused by side effects of COVID-19 vaccines?"
However the results don't make any sense, because only about 1.0% of the US population died each year in 2020, 2021, and 2022:
> t=fread("http://sars2.net/f/uspopdead.csv")
> t[year>=2018,.(deadpct=sum(dead)/sum(pop)*100),year]
year deadpct
1: 2018 0.86417
2: 2019 0.86454
3: 2020 1.02061
4: 2021 1.04326
5: 2022 0.98411
6: 2023 0.92289
In 2020-2022 there were about 1.13 million MCD COVID covid deaths and 0.95 million UCD COVID deaths, so both are only about 0.3% of the US population.
According to the US Census Bureau's estimates for the year 2021, the average number of people per household was about 2.5, and about 28% of households consisted of 1 person, 35% of 2 people, 15% of 3 people, 13% of 4 people, 6% of 5 people, 2% of 6 people, and so on. [https://www.census.gov/data/tables/time-series/demo/families/households.html]
If someone from a single-person household dies then there is no-one left to report the death in the survey. Many old people also live in elderly homes, but I don't know if the survey included elderly homes as households or not (and if it did then it should've been mentioned somewhere more clearly).
The article by Rasmussen did not include a detailed description of their methodology, but it only linked to a generic methodology article that applied to various surveys by Rasmussen. [https://www.rasmussenreports.com/public_content/about_us/methodology]
Even in ages 18-39, about 17% of people answered yes to the question of "Has any member of your household died from COVID-19?": [https://www.rasmussenreports.com/public_content/politics/public_surveys/crosstabs_2_covid_19_march_27_29_2023]

I don't know who runs the account for Rasmussen Reports on Twitter, but they seem to have posted a lot of anti-vaccine tweets and they seem be a fan of Steve Kirsch: [https://x.com/search?q=from%3Arasmussen_poll+%40stkirsch&f=live]
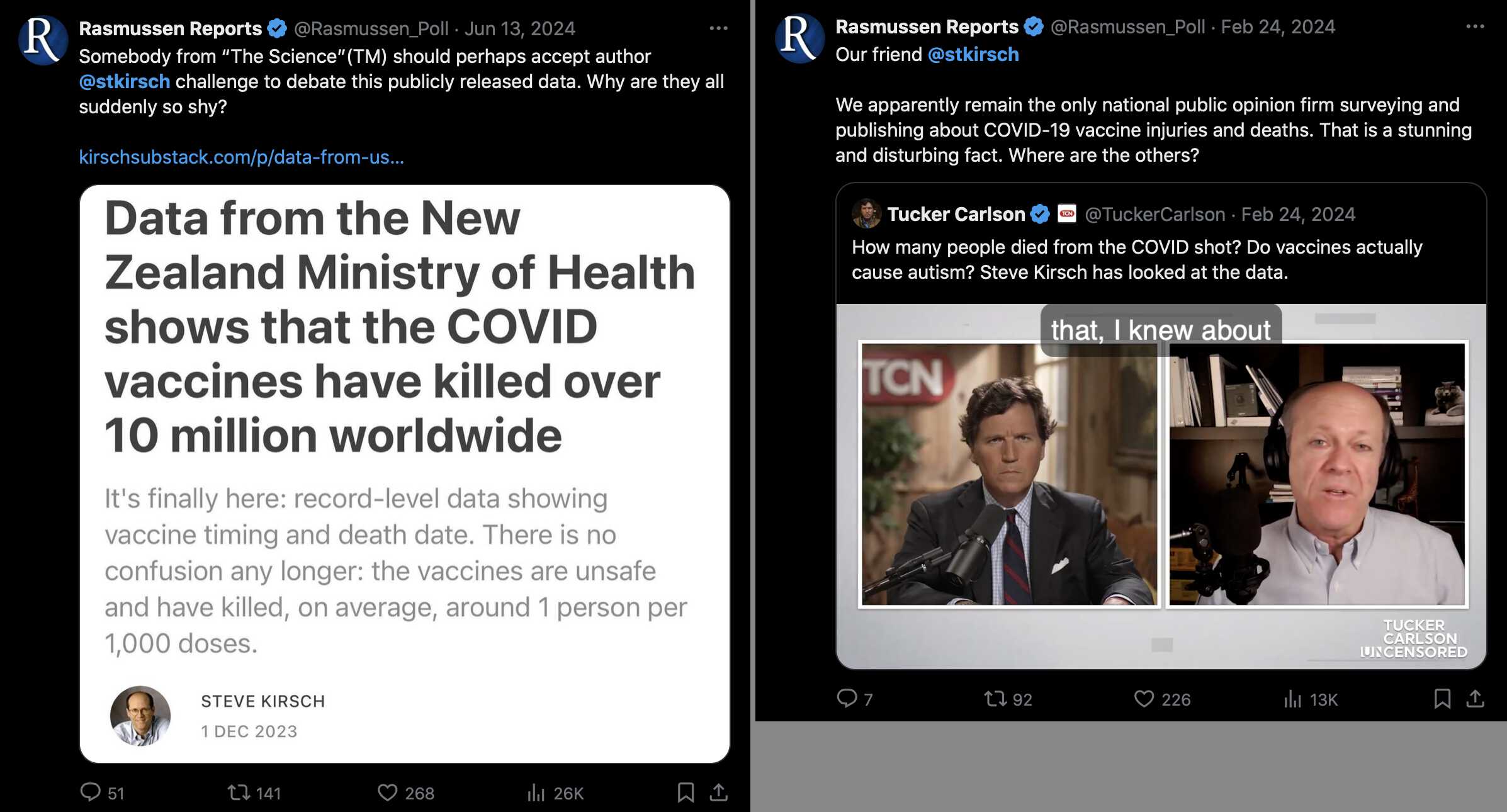
In one tweet where Rasmussen posted screenshots of four surveys which included the two surveys where the participants were asked if any member of their household had died from COVID or vaccines, Rasmusen wrote "The questions were framed by us but suggested by @stkirsch":

Rasmussen's Twitter account might be ran by Mark Mitchell who is the "Lead Pollster" at Rasmussen Reports. He has been a frequent guest on Steve Bannon's War Room show (where one time he talked about a Rasmussen poll where the MyPillow guy Mike Lindell was voted as the most popular candidate for the new chairman of the Republican National Committee):

I don't know if Rasmussen got somehow co-opted by people like Kirsch or Bannon to promote anti-vaccine psyops. Or I guess it's also plausible that they were cooperating with intelligence agencies or other parties to produce fake polls even before COVID. Publishing fake polls with opaque methodology seems like a great way to influence public opinion, because it's difficult for people to verify if the data in the polls is real or not.
Rasmussen seems to have already promoted an anti-vaccine message before COVID. For example in 2019 they published an article by the Fox News commentator Michelle Malkin titled "Fight for the Freedom to Question Vaccines". [https://www.rasmussenreports.com/public_content/political_commentary/commentary_by_michelle_malkin/fight_for_the_freedom_to_question_vaccines]
Or alternatively the reason why so many people in the Rasmussen polls answered that a member of their household died might be due to some bias in the polls. For example some people may have misunderstood the word household to include family members who did not live in the same household, or some people may have intentionally given a wrong answer for the purpose of trolling. But I don't think either bias would've been common enough to explain why about 11% of people answered that a member of their household died of COVID. And if Rasmussen was aware of such biases, they should've explained that the results of their poll might have been inaccurate due to some bias.
Added later: In a video that the Rasmussen's "Lead Pollster" Mark Mitchell did about the survey, he pointed out that the figure 11% of people reporting a COVID death in their household may have been too high "due to people's loose definition of the term 'household'". [https://rumble.com/v2fmz2o-rasmussen-polls-covid-vs.-vaccine.-americans-tell-us-which-is-the-biggest-k.html?start=163] However there was no similar explanation provided in the article about the survey by Rasmussen. The results of the survey were so counterintuitive that Rasmussen should've published a more detailed discussion about possible biases which might have explained the results.
Another addendum: In a German survey there were approximately 31% vaccinated people and 23% unvaccinated people who answered yes to a question that asked in German "Do you know anyone in your immediate family or close family who has been proven to have died from COVID-19?" And approximately 8% of vaccinated people and 17% of unvaccinated people answered yes to a question that asked "Do you know anyone in your immediate family or close family who has almost certainly died from a COVID-19 vaccination?" [https://esmed.org/MRA/mra/article/view/6205/99193548787; original German wording at https://osf.io/y6w8r/] The questions were not restricted to only members of the same household, but the figures still seem too high because Germany hasn't even had very high excess mortality since 2020. The ratio of people who knew someone "proven to have died from COVID" divided by people who knew someone who "almost certainly died from a COVID vaccination" was about 4.0 among vaccinated people but only about 1.3 among unvaccinated people, so there seems to have been a strong bias where unvaccinated people were much more likely to say they knew someone who died from a vaccine relative to someone who died from COVID. So Rasmussen could've also asked their respondents if they were vaccinated or not, and then Rasmussen could've shown the results of the survey separately for vaccinated and unvaccinated respondents. If Rasmussen would've reported what percentage of the respondents were vaccinated, it would've also shown if unvaccinated people were overrepresented among the respondents like in the surveys by Skidmore and Nakatani, which might have biased the results so that vaccine deaths were exaggerated relative to COVID deaths.
Kirsch wrote: "There were just over 1M excess deaths in (2021+2022) vs. 2019 baseline. My vaccine related deaths (415K) are well within this number. This means the vaccines killed nearly as many people as COVID during the period (720K)."
However when I calculated the baseline number of deaths by multiplying the mid-year population estimates for each age with the projected trend in CMR for the age in 2010-2019, I only got about 804,995 excess deaths in 2021 and 2022 combined:
> pop=fread("http://sars2.net/f/uspopdead.csv")
> base=pop[year%in%2010:2019,.(year=2010:2023,base=predict(lm(dead/pop~year),.(year=2010:2023))),age]
> merge(base,pop)[,.(dead=sum(dead),base=sum(base*pop)),year][,excess:=dead-base][]|>print(r=F)
year dead base excess
2010 2468309 2464571 3738
2011 2515324 2509202 6122
2012 2543132 2556832 -13700
2013 2596861 2599336 -2475
2014 2626255 2649724 -23469
2015 2712492 2694306 18186
2016 2744111 2743468 643
2017 2813374 2788658 24716
2018 2839061 2832738 6323
2019 2854691 2878862 -24171
2020 3383613 2913107 470506
2021 3464138 2946844 517294
2022 3279754 2992052 287702
2023 3090884 3056095 34789
When I used the number of deaths in 2019 as the baseline, I got about
1.03 million deaths in 2021 and 2022 combined (from
3279754-2854691+3464138-2854691). However that's not a
valid baseline since the number of deaths increased each year between
2010 and 2019 due to the aging population, and before COVID the yearly
number of deaths was projected to start increasing even more steeply in
the 2020s than the 2010s:
[https://www.census.gov/library/stories/2017/10/aging-boomers-deaths.html]

In this plot the green line was calculated with the same method I used above. But the brown line is similar to Kirsch's baseline which is extremely inaccurate:

library(data.table);library(ggplot2)
t=fread("http://sars2.net/f/uspopdead.csv")[,.(dead=sum(dead),pop=sum(pop)),.(year,age)]
years=2010:2023
t=t[year%in%years]
t=merge(t,t[year<2020,.(year=years,base=predict(lm(dead/pop~year),.(year=years))),age])
t=t[,.(dead=sum(dead),base=sum(base*pop)),year]
t$base2=t[year%in%2013:2019,predict(lm(dead~year),t)]
t$ave=t[year%in%2019,mean(dead)]
p=t[,.(x=year,y=unlist(.SD[,-1]),z=rep(names(.SD)[-1],each=.N))]
lv=c("Actual deaths","2010-2019 linear baseline from CMR by age","2013-2019 linear baseline for raw deaths","Deaths in 2019")
p[,z:=factor(z,unique(z),lv)]
xstart=2010;xend=2023;ybreak=pretty(p$y);ystart=ybreak[1];yend=max(ybreak)
ggplot(p,aes(x,y))+
geom_hline(yintercept=c(ystart,0,yend),color="black",linewidth=.3,lineend="square")+
geom_vline(xintercept=c(xstart-.5,xend+.5),color="black",linewidth=.3,lineend="square")+
geom_line(aes(color=z,linetype=z),linewidth=.4)+
geom_point(aes(color=z,alpha=z),stroke=0,size=1)+
labs(title="Yearly deaths in United States",subtitle="The green baseline was calculated by first doing a linear regression for CMR for each single year of age in 2011-2019, and then the yearly population sizes of each age were multiplied by the value of the projected trend. The 2013-2019 linear trend is based simply on the total number of deaths each year in all ages aggregated together."|>stringr::str_wrap(72),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xstart:xend)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=kim)+
scale_color_manual(values=c("black","#00aa00","blue",hsv(3/36,.9,.5)))+
scale_alpha_manual(values=c(1,0,0,0))+
scale_linetype_manual(values=c(1,1,1,1))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
axis.ticks=element_line(linewidth=.3,),
axis.title=element_text(size=8),
legend.background=element_blank(),
legend.box.just="left",
legend.key=element_rect(fill="white"),
legend.spacing.x=unit(1,"pt"),
legend.key.size=unit(9,"pt"),
legend.key.width=unit(17,"pt"),
legend.position=c(0,1),
legend.justification=c(0,1),
legend.box.background=element_rect(fill=alpha("white",1),color="black",linewidth=.3),
legend.margin=margin(-2,4,4,4),
legend.text=element_text(size=7,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
plot.margin=margin(5,5,5,5),
plot.subtitle=element_text(size=6.9,margin=margin(,,5)),
plot.title=element_text(size=8,face=2,margin=margin(1,,4)))
ggsave("1.png",width=3.8,height=2.6,dpi=400*4)
system("mogrify -resize 25% -colors 256 1.png")
Kirsch said there were about 720K people who died of COVID in 2021-2022, which is closer to the number of MCD deaths than UCD deaths. On NVSS in 2021 and 2022 combined, there's 732,757 deaths with MCD COVID and 603,445 deaths with UCD COVID:
> v=fread("curl -Ls sars2.net/f/vital.csv.xz|xz -dc") # NVSS data used by CDC WONDER
> v[cause=="U071",.(ucd=sum(ucd),mcd=sum(mcd)),.(year,cause)]|>print(r=F)
year cause ucd mcd
2020 U071 350831 397566
2021 U071 416893 478402
2022 U071 186552 254355
So relative to my figure of 804,995 excess deaths in 2021 and 2022 combined, there's only 72,238 deaths remaining after subtracting MCD COVID deaths or 201,550 deaths remaining after subtracting UCD COVID deaths.
But a lot of the remaining excess deaths are due to deaths from external causes. In the following code I calculated the baseline by multiplying the 2010-2019 trend in CMR by age by the population size like earlier. But now I only looked at deaths with an underlying cause under the A-Q ICD codes, which consists of natural causes excluding COVID and U and R codes. It gave me about 111,873 excess deaths in 2021 and 2022 combined, even though it includes deaths where the underlying cause was not listed as COVID even though the deaths were actually due to COVID:
> ua=\(x,y,...){u=unique(x);y(u,...)[match(x,u)]}
> a=v[ua(cause,like,"^[A-Q]"),.(dead=sum(ucd)),.(year,age=pmin(age,100))]
> pop=fread("http://sars2.net/f/uspopdead.csv")
> a=merge(a,pop[,dead:=NULL])
> base=a[year%in%2010:2019,.(year=2010:2023,base=predict(lm(dead/pop~year),.(year=2010:2023))),age]
> merge(base,a)[,.(dead=sum(dead),base=sum(base*pop)),year][,excess:=dead-base][]|>print(r=F)
year dead base excess
2010 2246774 2246816 -42
2011 2285226 2284087 1139
2012 2308241 2324243 -16002
2013 2363528 2359502 4026
2014 2391880 2402194 -10314
2015 2463894 2439264 24630
2016 2475681 2480744 -5063
2017 2533255 2518549 14706
2018 2561481 2555388 6093
2019 2571053 2594283 -23230
2020 2715005 2621852 93153
2021 2700664 2649289 51375
2022 2747657 2687160 60497
Kirsch wrote: "Skidmore (2023): 289,789 (95% CI: 229,319 - 344,319) were killed by the shots in 2021 alone. He didn't look at 2022."
Susan Oliver did a video about Skidmore's paper titled "Is this the worst ANTIVAXXER paper ever?": https://www.youtube.com/watch?v=7WVaWqY87B0.
She pointed out that Skidmore had also published blog posts about how vaccines contained nano-scale graphene razor blades and how vaccinated people were magnetic due to graphene: [https://mark-skidmore.com/2021/12/01/nanoscale-razor-blades-in-vaccine-dr-andreas-noack-europes-leading-carbon-expert/, https://mark-skidmore.com/2021/12/30/imperial-college-london-dr-andrew-goldsworthy-on-vaccin-induced-magnitism/]

Skidmore's paper was originally published by Biomed Central, but after it got retracted by BMC, a revised version of the paper was published in James-Lyons Weiler's journal. [https://bmcinfectdis.biomedcentral.com/articles/10.1186/s12879-023-07998-3, https://publichealthpolicyjournal.com/covid-19-illness-and-vaccination-experiences-in-social-circles-affect-covid-19-vaccination-decisions/] The supplementary materials are only included with the BMC version but not the revised version.
Skidmore's paper said: "Catherine Austin Fitts provided funding to cover the $11,000 cost of the online survey." But under conflicts of interest Skidmore wrote "The author declares no conflict of interest", even though Fitts is an anti-vaxxer.
In her video Susan Oliver said: "I want to point out that the study doesn't even do what it claims in the title: it actually provides no information whatsoever on the role of 'social circle COVID-19 illness and vaccination experiences in COVID-19 vaccination decisions'. Now, they did in fact ask questions about whether or not people they knew had experienced a significant health problem after COVID or the vaccine, and they did show that those people who knew someone who had experienced a health problem after having COVID were more likely to be vaccinated, and those who knew someone who experienced a health problem after vaccination were more likely to be unvaccinated. But they didn't ask whether this actually influenced their decision to get vaccinated or not, or even if it happened before or after they made the decision. It's just as likely that people who have already made the decision not to get vaccinated are more likely to thus notice health problems in people who are vaccinated and attribute them to the vaccine. And as a lot of you probably already know, anti-vaxxers think every person who has died since the vaccines were rolled out who is under the age of 90 died from the vaccine. And likewise people who have made the decision to be vaccinated are more likely to notice social contacts who have done badly after getting COVID, because it affirms that they made the right decision. So basically the paper doesn't even answer what is supposed to be its main objective, even though it would have been easy to add in some questions to the survey to determine this."
Skidmore wrote that the age distribution of his sample of participants was designed to be representative of the US population: "The sample was obtained by Dynata, the world's largest first-party data platform, and is representative for the US American population [7]. The sampling using Dynata is based on opt-in sampling, respondents deliver high quality data, they are diverse and have community norms of honesty and accuracy [8]. The survey was opened to the Dynata panel until the required number of responses was obtained from each category of the stratification variables age, sex, and income, as required for a balanced response set." However he wrote that only 51% of his participants were vaccinated.
I didn't find any direct statement in Skidmore's paper whether the participants of the survey included only adults or also children. But I think children were not included or there was only a small number of children included, because according to Table 2 only about 4% of the participants reported that their education was less than high school. And in Figure 1 which shows the age distribution of the participants, the youngest age group is 20-24 and the oldest age group is 75-84 (even though it might be that people younger or older than the shown age groups were omitted from the figure).
However Skidmore's survey was conducted in December 2021 when over 80% of the US adult population had been vaccinated according to CDC's statistics, which raises a question about how representative his population sample really was: [https://data.cdc.gov/Vaccinations/Archive-COVID-19-Vaccination-and-Case-Trends-by-Ag/gxj9-t96f/about_data]
> t=fread("Archive__COVID-19_Vaccination_and_Case_Trends_by_Age_Group__United_States_20250129.csv")
> t[`Date Administered`%like%"12/20/2021",.(age=AgeGroupVacc,vaxpct=Administered_Dose1_pct_agegroup*100)]|>print(r=F)
age vaxpct
<2 Years 0.0
2 - 4 Years 0.0
5 - 11 Years 23.0
12 - 17 Years 63.3
18 - 24 Years 71.2
25 - 49 Years 77.5
50 - 64 Years 89.3
65+ Years 95.0
Skidmore estimated that 57 respondents reported a vaccine-related
death and 165 respondents reported a COVID-related death. So when he
multiplied the ratio of 57/165 with the number of UCD COVID
deaths at CDC WONDER which was 839,993, he got a figure of 289,789
vaccine deaths. He wrote: "The ratio of COVID-19
vaccine deaths to COVID-19 illness deaths of the people respondents knew
best who had health problems is 57/165=0.345, whereas the ratio of
vaccine-associated fatalities to COVID-19 fatalities from government
sources is 8,023/839,993=0.0096. [...] Assuming the experiences captured
in the survey represent the true ratio, the survey ratio is used to
estimate nationwide COVID-19 vaccine fatalities: Estimated fatalities
are 289,789 (95% CI: 229,319 - 344,319)." However
57/165*839993 is about 290,179 and
0.345*839993 is about 289,998, so neither of them matches
Skidmore's figure of 289,789. But Skidmore wrote that he used
bootstrapping to calculate the 95% CI for his estimate, so the
bootstrapping might have also slightly shifted his average value.
The number of vaccine deaths in the paper was determined based on this question "Of the people you know who experienced a health problem after being vaccinated, think about the one you know BEST. Please describe the health condition experienced by that person." However the wording is ambiguous, because a "health problem after being vaccinated" might be interpreted to mean either a health problem that occurred soon after vaccination and that was related to vaccination, or that occurred long after vaccination and that wasn't even related to the vaccine.
The original version of the paper in BMC included this paragraph that was later removed from the revised version of the paper: "Though a person may report that someone they know experienced a COVID-19 vaccine adverse event, it does not mean that vaccination was the cause of injury. As shown in the Table 4 and Additional file 3, some respondents indicated that a person they know had a heart attack after being vaccinated, though the heart attack could have been unrelated to the inoculation. To address this issue, an estimate of the number of people within respondent social groups who are expected to die regardless of inoculation is calculated and subtracted from reported COVID-19 vaccine fatalities. Three commonly reported vaccine adverse events are heart attacks, strokes and other manifestations of blood clots. The average age of a person in the survey dataset who experienced these conditions after being vaccinated is about 40 years of age, and the average age of death is 48. The incidence of heart attacks (myocardial infarction) for people of age 48 is about 17 per 100,000, and the incidence of strokes and blood clots for this age group is very low, near zero [12]. Heart attacks, strokes and blood clots are also commonly reported causes of COVID-19 vaccine death in VAERS. From the survey, about 51% of respondents reported being vaccinated. It is assumed that same proportion applies to those in respondents' social circles. The estimated total number of people in respondents' social circles is about 28,000. To calculate an estimated number of fatalities that might have occurred regardless of inoculation status, 17 is multiplied by the proportion of people who are vaccinated (0.51) and the proportion of people in social circles out of 100,000 (0.28). The estimated number of fatalities that might have occurred regardless of vaccination status is 17 × 0.51 × 0.28 = 2.43 people."
The questions that were part of the survey were shown in a supplementary Word document. One of the questions asked "Of the people you know who experienced a health problem after being sick from COVID-19 (but not from the vaccine), think about the one you know BEST. Please describe the health condition experienced by that person." And next there was a list where the participant was asked to chose the age of the person, and there was also another similar section for deaths after vaccination rather than COVID. So I guess the average age of people who died of a heart attack is supposed to have been calculated based on those sections:

The answers to the freeform text fields are shown in the supplementary files, where answers that involved a person dying are underlined. There are a total of 55 underlined answers to the question "Of the people you know who experienced a health problem after being vaccinated, think about the one you know BEST. Please describe the health condition experienced by that person." However only the 4 answers I highlighted in red below unambiguously referred to a heart attack as a cause of death (even though the 3 answers I highlighted in orange may have also referred to a heart attack, because one referred to the heart stopping, another referred to a cardiac failure, and in a third answer it was ambiguous if the person who had a heart attack was the person who died or some other person): [https://static-content.springer.com/esm/art%3A10.1186%2Fs12879-023-07998-3/MediaObjects/12879_2023_7998_MOESM3_ESM.docx]
She died don't know the health issues she had from it
Heart attack when he had no heart problems at all before it. He died from the heart attack.
Death
Died
He died from the shot
My grandma's heart stopped 2 days after she got the vaccine. [might refer to cardiac failure and not heart attack]
Cancer retuned in his body spread all over. Died!
They passed away from covid
Death
Died
My friend with no preexisting heart condition died of a heart failure after the second dose. [some people might use the term heart failure to refer to a heart attack, or the cardiac failure might have been accompanied by a heart attack]
One was sick in bed a week delirious and unable to get up eat or anything (90). The other had vaccine and that evening experienced chest pain went to ER died with "stroke" (42)
Death
The shot made it worse. The lose energy and the end result was death. The shot doesn't work if it did then people would not be able to get covid.
They died
Death
A member of my church died from blood clot surgery less than a week after having a covid vaccine in the hospital during recovery
Cousin 47-stroke Cousin- blood clots Friend-death Aunt- death
He died after 5 weeks, he was a diabetic and his kidneys shut down after getting COVID 15 days after vaccine
Got the vaccine shot and it went against the body n he's died
Death
Death from a heart attack after vaccination by a few weeks.
ICU. Then a deceased.
Died
Death
Death
Death
Death
They died
They went into a cardiac arrest and passed away
Never got over covid
The mother of friend she was vaccinated and the next day she died
She lost her baby
Died
One died, one had a heart attack and one had a blood clot [it's not clear if the person who died was the same person who had the heart attack]
Death with organ failure
They died
They died
Death
They died
Horrible they died
Elevated heart issues, high blood pressure, previous conditions come back, death.
Died from covid
Died
They died.
Ended up dying from a reaction to the drug which caused a major heart attack
They got pneumonia after the first shot. They got well and got the second shot and got pneumonia again and died.
Died
One of them lost her life. The other got sick and got over then got sick 2 times after.
Developed covid and died
Died
Heart condition. New conditions never had previous issues. One passed away
Vision and death
Died
My mom passed two weeks after receiving the vaccine. (This event was originally reported under the lasting COVID-19 illness issues.)
Similarly among the answers to the question about health problems after vaccination, I found only one answer which unambiguously mentioned that someone died of a heart attack, which simply said "Died of heart attack". Another answer said "Lungs collapsed and heart gave out", but it might have also referred to a cardiac failure and not a heart attack.
So did Skidmore calculate the average age of people who died from a heart attack based on a sample of only a couple of answers? It might explain why he wrote that the average age of death from a heart attack was only 48 years. In the National Vital Statistics System in 2021-2022, the average age of death with an ICD code for myocardial infarction was about 74 regardless of whether I looked at deaths by multiple cause or underlying cause:
> v=fread("curl -Ls sars2.net/f/vital.csv.xz|xz -dc")
> v[year%in%2021:2022][cause%like%"I21",sum(mcd),age][,weighted.mean(age,V1)]
[1] 73.64
> v[year%in%2021:2022][cause%like%"I21",sum(ucd),age][,weighted.mean(age,V1)]
[1] 73.96
When Skidmore calculated the number of heart attack deaths that might have been expected to occur in the social circle regardless of vaccination, he assumed that the total size of the social circle was 28,000 people, but since there were 2,840 participants, he assumed that the average size of the social circle per participant was about 9.9 people. However he determined the number of heart attack deaths in the social circle based on the questions which asked each participant to describe a health condition in only the single person they knew the best. So the participants may have had other people in their social circle who had a heart attack but they didn't mention it in the survey because it wasn't the person they knew the best.
For non-elderly participants the person they knew the best may have often been their spouse, child, sibling, friend, or coworker, so it might be that elderly people were underrepresented among the set of people who each participant knew the best relative to the set of people who died that were known by the participants.
Skidmore also incorrectly derived the expected number of deaths based on the average age at death instead of the age distribution of the people who died. If the average age of people in the social circle who died of a heart attack was 48 years, then it doesn't mean that you can derive the expected number of heart attack deaths within the social circle by looking at the mortality rate for heart attack in people aged 48.
The age distribution of the participants was supposed to be representative of the overall US age distribution. So if Skidmore would've assumed that the age distribution of the social circle was also representative of the overall US age distribution, he could've simply used the mortality rate for heart attack among the general US population to calculate the expected number of heart attack deaths.
Another anomaly in Skidmore's paper is that when the participants were asked that out of the people they know "who experienced a health problem after being sick from COVID-19 (but not from the vaccine)", 165 out of 2,840 participants are supposed to have answered that the person they knew the best ended up dying, which is about 6%. It seems too high even if it includes people who briefly had some minor health problem after getting COVID and who died a year later for some unrelated reason, because only about 3% of the entire US population died in 2020-2022. Now it's possible that people who were at high risk of dying in the near future had an increased likelihood of getting COVID, or to be sick from COVID as opposed to having an asymptomatic infection, or to experience a health problem after being sick from COVID, and the question only applied to people who got sick from COVID and had some health problem afterwards. But each participant was only allowed to describe a health problem after COVID in the single person they knew the best, which in many cases wouldn't have even been the person they knew who experienced the most severe health problems after COVID, so it seems unlikely that in the case of about 6% of participants the person they knew the best ended up dying.
Kirsch wrote: "99M study: OE for myocarditis in the same age group was 2.8X higher for Moderna. Myocarditis can be fatal. This isn't proof of a mortality ratio, just a confirmation of the other results that Moderna was the more deadly vaccine."
I didn't find observed events for myocarditis by age group anywhere in the paper he linked. But Kirsch told me that he actually referred to this paragraph in the discussion section of the paper: "A large cohort study of 23.1 million residents across four Nordic countries revealed an increased risk of myocarditis among young males aged 16-24 years, based on 4-7 excess events in 28 days per 100,000 vaccinees after a second dose of BNT162b2, and between 9 and 28 per 100,000 vaccinees after a second dose of mRNA-1273 [22]." It referred to a paper by Karlstad et al. titled "SARS-CoV-2 Vaccination and Myocarditis in a Nordic Cohort Study of 23 Million Residents": https://jamanetwork.com/journals/jamacardiology/fullarticle/2791253.
However Kirsch should've mentioned that the confidence intervals in the Nordic paper were so wide that they were barely nonoverlapping. The paper said: "Among males 16 to 24 years of age, adjusted IRRs were 5.31 (95% CI, 3.68-7.68) for a second dose of BNT162b2 and 13.83 (95% CI, 8.08-23.68) for a second dose of mRNA-1273, and numbers of excess events were 5.55 (95% CI, 3.70-7.39) events per 100 000 vaccinees after the second dose of BNT162b2 and 18.39 (9.05-27.72) events per 100 000 vaccinees after the second dose of mRNA-1273. Estimates for pericarditis were similar."
I don't know where Kirsch got the ratio that Moderna was 2.8 times higher than Pfizer, because 18.39/5.55 is about 3.3. He wrote: "OE for myocarditis in the same age group was 2.8X higher for Moderna". But OE means oberved events, and the figures quoted in the 99M study were excess rates of observed events per 100,000 people relative to a baseline adjusted for various parameters.
In the Nordic study in males aged 16-24, the raw number of observed myocarditis events was 37 for two doses of Pfizer and 15 for two doses of Moderna, so the number of OE was about 2.5 time higher for Pfizer. But people with two doses of Pfizer also had about 7 times more observation time than people with two doses of Moderna.
But anyway, it would've been better to calculate the Moderna-Pfizer ratio based on the IRR values instead of the rate of excess events, because ratios of excess rates can be misleadingly high when one of the excess rates is close to zero. For example a paper by McCullough Foundation found that there was about 11.8% excess mortality in 2023 and about 1.0% excess mortality in 2020, but McCullough misleadingly promoted their paper by saying that there was a 1236% increase in excess mortality between 2020 and 2023. [statistic2.html#1236_increase_in_excess_deaths]
Among males aged 16-24, the IRR for myocarditis within 28 days from vaccination was about 5.31 for two doses of Pfizer and about 13.83 for two doses of Moderna, so the ratio between the IRR values is about 2.6:

However if you look at first doses instead of second doses in the table above, the IRR was 2.16 for Pfizer and 2.90 for Moderna, so it was only about 1.3 times higher for Moderna, even though in the case of both Pfizer and Moderna, there was more follow-up time for people with only one vaccine dose than for people with two vaccine doses. I don't know why the difference in the Moderna-Pfizer ratio is between first and second doses is so large. At first I thought it might have been random noise due to a small sample size, because the confidence intervals are very wide. But a similar effect was also found in another study from the UK. [https://www.ahajournals.org/doi/10.1161/CIRCULATIONAHA.122.059970]
My previous screenshot was cropped to show only the section for males aged 16-24 in Table 2. But if you look at the full Table 2, there's a total of 16 combinations of sex, and age, and dose number, but for 3 of them the IRR value is suppressed because the number of myocarditis events was 5 or lower:

For 2 out of 13 combinations of variables where the IRR value was not suppressed, Pfizer had higher IRR than Moderna. They were males aged 25-39 with one vaccine dose, whose Moderna-Pfizer ratio was about 0.78. And they included females aged 12 and above with only one vaccine dose, even though their Moderna-Pfizer ratio was about 0.99 so it was very close to 1. However for males aged 12 and above with only one vaccine dose, the Moderna-Pfizer ratio was also 1.04 so it was also close to 1:
| Sex | Age | Dose | Pfizer IRR | Moderna IRR | Moderna-Pfizer ratio | Comment |
|---|---|---|---|---|---|---|
| male | 12+ | 1 | 1.40 | 1.45 | 1.04 | close to 1 |
| male | 12+ | 2 | 2.04 | 8.55 | 4.19 | |
| male | 16-24 | 1 | 2.16 | 2.90 | 1.34 | |
| male | 16-24 | 2 | 5.31 | 13.83 | 2.60 | |
| male | 25-39 | 1 | 1.62 | 1.27 | 0.78 | below 1 |
| male | 25-39 | 2 | 1.75 | 12.96 | 7.41 | |
| male | 40+ | 1 | 0.93 | 1.89 | 2.03 | |
| male | 40+ | 2 | 1.08 | 3.45 | 3.19 | |
| female | 12+ | 1 | 1.46 | 1.45 | 0.99 | below 1 |
| female | 12+ | 2 | 1.25 | 2.73 | 2.18 | |
| female | 16-24 | 1 | 1.98 | NA | NA | |
| female | 16-24 | 2 | 2.86 | NA | NA | |
| female | 25-39 | 1 | 2.35 | NA | NA | |
| female | 25-39 | 2 | 2.35 | 7.31 | 3.11 | |
| female | 40+ | 1 | 1.37 | 4.68 | 3.42 | |
| female | 40+ | 2 | 1.02 | 3.03 | 2.97 |
The IRR values in Table 2 were adjusted for age, healthcare worker status, nursing home residency, comorbidity variables, and prior COVID infection. However they were not adjusted for country, even though different countries may have had different criteria for diagnosing myocarditis, and Moderna vaccinees were overrepresented in Sweden and Norway relative to Denmark and Finland.
From eTable 3, you can see the number of people under each vaccine brand per country, even though it only shows all sexes combined and not males only. In this table where I compiled the number of people with two doses of the same vaccine type in ages 16-24 from eTable 3, you can see that Moderna vaccinees are overrepresented in Sweden and Norway but underrepresented in Denmark and Finland:
| country | Pfizer | Moderna | ratio |
|---|---|---|---|
| Denmark | 438109 | 19406 | 22.6 |
| Finland | 322345 | 24653 | 13.1 |
| Norway | 185653 | 33685 | 5.5 |
| Sweden | 372483 | 111801 | 3.3 |
eTable 9 shows that among males between the ages of 12 and 39, there were 37 diagnoses of myocarditis in Denmark, 34 in Finland, 53 in Norway, and 54 in Sweden. So there's a high number of diagnoses per capita in Norway, because the population of Sweden is about twice as high as the population of the other three countries:
pop=fread("https://ec.europa.eu/eurostat/api/dissemination/sdmx/2.1/data/demo_pjan?format=TSV",header=T,na.strings=":")
meta=fread(text=pop[[1]],header=F)
pick=meta$V4=="M"&meta$V3%like%"Y1[2-9]|Y[23]"&meta$V5%like%"DK|FI|NO|SE"
a=meta[pick][,pop:=as.integer(pop[pick,`2021`])][,.(pop=sum(pop)),.(country=V5)]
a$myocarditis=c(37,34,53,54)
a[,ratepermil:=myocarditis/pop*1e6]
print(a,r=F)
country pop myocarditis ratepermil
DK 1095355 37 33.8
FI 1011146 34 33.6
NO 1062939 53 49.9
SE 2005240 54 26.9
So if myocarditis was more likely to get diagnosed in Norway than the other three countries, and Moderna vaccinees were overrepresented in Norway, it might partially explain why Moderna got a higher myocarditis IRR than Pfizer. But on the other hand it would be balanced out by how Moderna vaccinees were even more overrepresented in Sweden, and Sweden had the lowest rate of myocarditis diagnoses per million people in my code above. (My code above looked at males of ages 12-39, and my previous table looked at both sexes in ages 16-24, because neither type of data was provided only for males aged 16-24.)
However unlike many of the other papers Kirsch has referred to, the study from the Nordic countries was a serious study published in a proper journal, so it may have well found a genuine signal that Moderna has a higher risk of myocarditis than Pfizer.
A study from British Columbia also found that Moderna had about 2.78 times higher adjusted odds ratio of myocarditis than Pfizer: "The rates of myocarditis and pericarditis per million second doses were higher for mRNA-1273 (n = 31, rate 35.6; 95% CI: 24.1-50.5; and n = 20, rate 22.9; 95% CI: 14.0-35.4, respectively) than BNT162b2 (n = 28, rate 12.6; 95% CI: 8.4-18.2 and n = 21, rate 9.4; 95% CI: 5.8-14.4, respectively). mRNA-1273 vs BNT162b2 had significantly higher odds of myocarditis (adjusted OR [aOR]: 2.78; 95% CI: 1.67-4.62), pericarditis (aOR: 2.42; 95% CI: 1.31-4.46) and myopericarditis (aOR: 2.63; 95% CI: 1.76-3.93)." [https://www.jacc.org/doi/full/10.1016/j.jacc.2022.08.799]
A UK study also found that the IRR for myocarditis within 28 days of
vaccination was about 1.2 times higher for Moderna than Pfizer in the
case of first doses (1.85/1.52) and about 7.5 times higher
in the case of second doses (11.76/1.57), so for some
reason the ratio for second doses was much higher like in the case of
the Nordic study:
[https://www.ahajournals.org/doi/10.1161/CIRCULATIONAHA.122.059970]

Spiro Pantazatos contributed this Substack post to the Rootclaim debate: https://telemimesis.substack.com/p/a-simple-time-series-model-of-pandemic.
He got weekly new COVID cases from OWID, and he got weekly excess deaths from this CDC dataset: https://data.cdc.gov/NCHS/AH-Excess-Deaths-by-Sex-Age-and-Race-and-Hispanic-/m74n-4hbs/about_data. At first when he did a simple linear regression model of excess deaths compared against COVID cases, the COVID cases explained only about 32% of variance in the weekly excess deaths. It increased to about 71.5% when he split the COVID cases into 8 different terms for different COVID waves. And it further increased to about 76.5% when he also added a term for the weekly number of new vaccine doses to his model.
This shows the time periods of the 8 COVID waves in his model:

The reason why his proportion of explained variance increased so much when he added a different term for each COVID wave is that he was using COVID cases as a proxy for COVID deaths, but different COVID waves had vastly different CFR values. For example during the first Omicron wave there was a very high number of cases relative to deaths, but during the spring 2020 wave there was a low number of deaths relative to cases. But if Pantazatos would've directly looked at COVID deaths instead of COVID cases in his model, then he wouldn't even have necessarily needed to split his model into different terms for different COVID waves, because the correlation with excess mortality is much higher for COVID deaths than for COVID cases:

library(data.table);library(ggplot2);library(MMWRweek)
download.file("https://covid.ourworldindata.org/data/owid-covid-data.csv","owid-covid-data.csv")
cdc=fread("AH_Excess_Deaths_by_Sex__Age__and_Race_and_Hispanic_Origin_20250211.csv")
o=owid[,.(date=date-1,cases=new_cases,dead=new_deaths,vax=new_vaccinations)]
o=cbind(o[,-1],setNames(MMWRweek(o$date)[-3],c("year","week")))
o=o[,lapply(.SD,sum,na.rm=T),.(year,week),.SDcols=1:(ncol(o)-2)]
d=cdc[Sex=="All Sexes"&RaceEthnicity=="All Race/Ethnicity Groups"&AgeGroup=="All Ages"]
ex=d[MMWRyear%in%2020:2022,.(excess=`Number above average (unweighted)`,year=MMWRyear,week=MMWRweek)]
me=merge(ex,o,all.r=T)
me[is.na(me)]=0
pop=fread("http://sars2.net/f/uspopdead.csv")
base=merge(pop,pop[year%in%2011:2019,.(year=2011:2023,base=predict(lm(dead/pop~year),.(year=2011:2023))),age])
base=base[,.(base=sum(base*pop)),year]
base=merge(d[,.(year=MMWRyear,week=MMWRweek,dead=`Deaths (unweighted)`)],base)
base[,base:=base/(365+(year%%4==0))*7]
weekly=base[year%in%2015:2019,.(weekly=mean(dead-base)),week]
weekly=rbind(weekly,weekly[week==52,.(week=53,weekly)])
ex2=merge(weekly,base)[year%in%2020:2022,.(excess2=dead-(base+weekly)),,.(year,week)]
me=merge(me,ex2)
lab=strsplit("Excess deaths (CDC's inaccurate baseline; 2015-2019 average)
Excess deaths (my accurate baseline; CMR trend by age × population)
COVID deaths
COVID cases
Vaccine doses","\\n")[[1]]
p=me[,.(x=MMWRweek2Date(year,week,4),y=c(excess,excess2,dead,cases,vax),z=factor(rep(lab,each=.N),lab))]
p=p[,.(x,y=scale(y)[,1]),z]
xstart=as.Date("2020-1-1");xend=as.Date("2023-1-1")
xbreak=seq(xstart+182,xend,"year")
p=p[x%in%xstart:xend]
ggplot(p,aes(x,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),linewidth=.4,color="gray82")+
geom_hline(yintercept=0,linewidth=.4)+
geom_line(aes(color=z),linewidth=.6)+
geom_point(aes(color=z),stroke=0,size=1.1)+
labs(x=NULL,y=NULL,title="United States: z-scores of weekly variables",caption="Sources: OWID, sars2.net/f/uspopdead.csv, and CDC dataset \"AH Excess Deaths by Sex, Age, and Race and Hispanic Origin\"."|>str_wrap(72))+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(breaks=\(x)pretty(x,7))+
scale_color_manual(values=c("gray60","black","#ff0000","#ffaaaa","#bb00bb"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(4)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(5,"pt"),
axis.ticks.length.x=unit(0,"pt"),
axis.title=element_text(size=11,face=2),
axis.title.x=element_text(margin=margin(3)),
axis.title.y=element_text(margin=margin(,2)),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification="left",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.margin=margin(,,5),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.grid.major=element_blank(),
panel.spacing=unit(3,"pt"),
plot.caption=element_text(size=11,color="gray50"),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11.5,face=2,margin=margin(1,,3)))
ggsave("1.png",width=5.7,height=4.5,dpi=300*4)
system("magick 1.png -trim -resize 25% -bordercolor white -border 22 -colors 256 1.png")
In the following code I did a similar model as Pantazatos where I
compared excess deaths in his CDC dataset against weekly new cases at
OWID, but I didn't add separate terms for different COVID waves. My
r^2 value was about 0.38 when I didn't shift the cases,
0.40 when I shifted cases forwards by 1 week, and 0.36 when I shifted
cases forwards by 2 weeks. However my r^2 value increased
to about 0.71 when I compared the excess deaths against COVID deaths
instead of cases, so then my r^2 value was close to the
value Pantazatos got when he split the COVID cases into 8 different
terms for different waves:
library(data.table);library(MMWRweek)
download.file("https://covid.ourworldindata.org/data/owid-covid-data.csv","owid-covid-data.csv")
owid=fread("owid-covid-data.csv")[location=="United States"]
adhoc=fread("AH_Excess_Deaths_by_Sex__Age__and_Race_and_Hispanic_Origin_20250211.csv")
# `date-1` is because new cases during the past week are listed on Sundays but MMWR weeks end on Saturday
o=owid[,.(date=date-1,cases=new_cases,coviddead=new_deaths,vax=new_vaccinations)]
o=merge(owid[,.(date=date-1+7,cases1=new_cases)],o,all=T)
o=merge(owid[,.(date=date-1+14,cases2=new_cases)],o,all=T)
o=cbind(o[,-1],setNames(MMWRweek(o$date)[-3],c("year","week")))
o=o[,lapply(.SD,sum,na.rm=T),.(year,week),.SDcols=1:(ncol(o)-2)]
d=adhoc[Sex=="All Sexes"&RaceEthnicity=="All Race/Ethnicity Groups"&AgeGroup=="All Ages"]
ex=d[MMWRyear%in%2020:2022,.(excess=`Number above average (unweighted)`,year=MMWRyear,week=MMWRweek)]
me=merge(ex,o,all.r=T)
me[is.na(me)]=0
summary(lm(excess~cases,me))$r.squared # 0.379 (weekly number of new cases explains only about 38% of variance in excess deaths)
summary(lm(excess~cases1,me))$r.squared # 0.404 (shifting cases forwards by one week increased explained variance)
summary(lm(excess~cases2,me))$r.squared # 0.359 (shifting cases forwards by two weeks reduced explained variance)
summary(lm(excess~coviddead,me))$r.squared # 0.714 (COVID deaths explain about 71% of variance in excess deaths)
When I added a term for weekly vacine doses administered, my
r^2 value increased only from about 0.379 to 0.384 for
cases and from about 0.714 to 0.735 for deaths. But the plot twist is
that in both models the coefficient for vaccines was negative, which
means that the weekly number of new vaccine doses administered was
inversely associated with weekly excess deaths:
summary(lm(excess~cases+vax,me))$r.squared # 0.384 summary(lm(excess~coviddead+vax,me))$r.squared # 0.735 coef(lm(excess~cases+vax,me)) # (Intercept) cases vax # 8.1779e+03 5.1947e-03 -8.4827e-05 coef(lm(excess~coviddead+vax,me)) # (Intercept) coviddead vax # 4.7433e+03 1.0385e+00 -1.8758e-04
In his Substack post Pantazatos only included a model where he looked at COVID cases split into 8 different waves combined with vaccines. But he didn't include a model where he looked at COVID cases as a single term combined with vaccines, and he also didn't include a model where he looked at COVID deaths combined with vaccines. It might be because in both models he would've gotten a negative coefficient for vaccines. (Edit: He told me he hadn't done a model based on COVID deaths instead of cases.)
In the following code I took data for cases from the same OWID
dataset that Pantazatos used and not from the
owid-covid-data.csv file I used earlier where the number of
cases is slightly different, and I shifted the dates of cases 8 days
forwards like Pantazatos. Pantazatos provided me the starting weeks of
each COVID wave. In his models which had separate terms for each COVID
wave, Pantazatos got an r^2 value of about 0.715 when he
didn't include a term for vaccine and about 0.765 when he did include a
term for vaccines. However I don't understand how my code below was
different from his calculation, because I got an r^2 value
of about 0.780 without the vaccine term and 0.789 with the vaccine
term:
library(data.table);library(MMWRweek)
waves=data.table(year=rep(2020:2022,c(3,3,2)),week=c(1,24,37,10,26,44,14,43))
owid=fread("owid-covid-data.csv")[location=="United States"]
vax=owid[,.(MMWRweek(date),vax=new_vaccinations)][,.(vax=sum(vax,na.rm=T)),.(year=MMWRyear,week=MMWRweek)]
case=fread("daily-new-confirmed-covid-19-cases.csv")[Entity=="United States"]
case=case[,.(MMWRweek(Day+8),cases=.SD[[3]])][,.(cases=sum(cases)),.(year=MMWRyear,week=MMWRweek)]
excess=fread("AH_Excess_Deaths_by_Sex__Age__and_Race_and_Hispanic_Origin_20250211.csv")
excess=excess[Sex=="All Sexes"&RaceEthnicity=="All Race/Ethnicity Groups"&AgeGroup=="All Ages"]
excess=excess[,.(excess=`Number above average (unweighted)`,year=MMWRyear,week=MMWRweek)]
me=merge(merge(excess,case,all=T),vax,all=T)[year%in%2020:2022];me[is.na(me)]=0
me$wave=me[,findInterval(year*100+week,waves[,year*100+week])]
me=cbind(me,`colnames<-`(sapply(1:8,\(i)me[,ifelse(wave==i,cases,0)]),paste0("w",1:8)))
summary(lm(excess~w1+w2+w3+w4+w5+w6+w7+w8,me)) # without vaccine term
# Call:
# lm(formula = excess ~ w1 + w2 + w3 + w4 + w5 + w6 + w7 + w8,
# data = me)
# Residuals:
# Min 1Q Median 3Q Max
# -6891 -1618 -156 1104 12608
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 5.36e+03 4.88e+02 10.99 < 2e-16 ***
# w1 5.66e-02 6.47e-03 8.75 4.4e-15 ***
# w2 1.87e-02 3.02e-03 6.19 5.5e-09 ***
# w3 1.26e-02 7.79e-04 16.15 < 2e-16 ***
# w4 1.05e-03 2.67e-03 0.39 0.695
# w5 1.61e-02 1.19e-03 13.56 < 2e-16 ***
# w6 4.57e-03 3.39e-04 13.49 < 2e-16 ***
# w7 3.40e-03 1.24e-03 2.74 0.007 **
# w8 1.45e-02 3.47e-03 4.19 4.8e-05 ***
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Residual standard error: 3230 on 148 degrees of freedom
# Multiple R-squared: 0.78, Adjusted R-squared: 0.768
# F-statistic: 65.6 on 8 and 148 DF, p-value: <2e-16
summary(lm(excess~w1+w2+w3+w4+w5+w6+w7+w8+vax,me)) # with vaccine term
# Call:
# lm(formula = excess ~ w1 + w2 + w3 + w4 + w5 + w6 + w7 + w8 +
# vax, data = me)
#
# Residuals:
# Min 1Q Median 3Q Max
# -6918 -1641 -24 1277 12805
#
# Coefficients:
# Estimate Std. Error t value Pr(>|t|)
# (Intercept) 4.80e+03 5.33e+02 9.00 1.1e-15 ***
# w1 5.97e-02 6.49e-03 9.20 3.2e-16 ***
# w2 2.03e-02 3.04e-03 6.68 4.7e-10 ***
# w3 1.22e-02 7.81e-04 15.63 < 2e-16 ***
# w4 -6.51e-03 4.05e-03 -1.61 0.1106
# w5 1.54e-02 1.20e-03 12.86 < 2e-16 ***
# w6 4.40e-03 3.41e-04 12.90 < 2e-16 ***
# w7 3.62e-03 1.23e-03 2.95 0.0037 **
# w8 1.48e-02 3.42e-03 4.33 2.8e-05 ***
# vax 2.00e-04 8.20e-05 2.45 0.0156 *
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# Residual standard error: 3180 on 147 degrees of freedom
# Multiple R-squared: 0.789, Adjusted R-squared: 0.776
# F-statistic: 60.9 on 9 and 147 DF, p-value: <2e-16
The next table shows the results of 6 different models out of which 3 included a term for vaccines. I got a negative coefficient for vaccines in 2 of the 3 models, but neither type of model was included in the post by Pantazatos:
| Model |
Included in post by Pantazatos |
Pantazatos r^2 | My r^2 |
Pantazatos vaccine coefficient |
My vaccine coefficient |
|---|---|---|---|---|---|
| cases as single term | yes | 0.321 | 0.379 | NA | NA |
| cases as single term + vaccines | no | NA | 0.384 | NA | negative |
| cases as 8 terms | yes | 0.715 | 0.780 | NA | NA |
| cases as 8 terms + vaccines | yes | 0.765 | 0.789 | positive | positive |
| deaths as single term | no | NA | 0.714 | NA | NA |
| deaths as single term + vaccines | no | NA | 0.735 | NA | negative |
Pantazatos got weekly excess deaths from a CDC dataset titled "AH Excess Deaths by Sex, Age, and Race and Hispanic Origin": https://data.cdc.gov/NCHS/AH-Excess-Deaths-by-Sex-Age-and-Race-and-Hispanic-/m74n-4hbs/about_data. "AH" means "ad hoc", because the CDC dataset was a supplementary dataset that the CDC produced as part of their analysis for excess deaths but that was not updated regularly. [https://www.cdc.gov/nchs/covid19/covid-19-mortality-data-files.htm]
In the primary datasets for excess deaths the CDC published, the CDC used a Poisson regression with a spline trend to calculate the baseline. CDC's website says: "Counts of deaths in the most recent weeks were compared with historical trends (from 2013 to present) to determine whether the number of deaths in recent weeks was significantly higher than expected, using Farrington surveillance algorithms (1). The 'surveillance' package in R (2) was used to implement the Farrington algorithms, which use overdispersed Poisson generalized linear models with spline terms to model trends in counts, accounting for seasonality." [https://www.cdc.gov/nchs/nvss/vsrr/covid19/excess_deaths.htm]
However the ad-hoc dataset used by Pantazatos employed a simple 2015-2019 average baseline which exaggerated excess deaths in 2022 relative to 2020. For example the baseline for MMWR week of 1 of each year was the average of MMWR weeks 1 of 2015-2019, even though in reality there was an increasing trend in deaths so by 2022 the baseline should've been higher than in 2020.
At first I was confused by CDC's ad-hoc dataset because the value of the column "Average number of deaths (unweighted)" was not the same for each year, so I thought the column might have shown the average of the past 5 years and not the average of the years 2015-2019. However then I noticed there was a bug from the year 2020 onwards where the column "Average number of deaths (unweighted)" didn't actually show the baseline but it was instead identical to the column "Deaths (unweighted)" which shows the actual number of deaths. But if you subtract the column "Number above average (unweighted)" from the column "Deaths (unweighted)", the result is always the same as the average number of deaths in 2015-2019, so you can tell that each year does in fact have the same baseline:
adhoc=fread("AH_Excess_Deaths_by_Sex__Age__and_Race_and_Hispanic_Origin_20250211.csv")
adhoc=adhoc[Sex=="All Sexes"&RaceEthnicity=="All Race/Ethnicity Groups"&AgeGroup=="All Ages"]
adhoc[MMWRweek==1,.(MMWRyear,MMWRweek,`Deaths (unweighted)`,`Average number of deaths (unweighted)`,`Number above average (unweighted)`)]|>print(r=F)
# MMWRyear MMWRweek Deaths (unweighted) Average number of deaths (unweighted) Number above average (unweighted)
# 2015 1 61882 60499 NA
# 2016 1 55933 60499 NA
# 2017 1 59898 60499 NA
# 2018 1 66317 60499 NA
# 2019 1 58463 60499 NA
# 2020 1 60176 60176 -323 # the third and fourth
# 2021 1 87073 87073 26574 # columns here are
# 2022 1 79826 79826 19327 # erroneously the
# 2023 1 68841 68841 8342 # same in 2020-2023
adhoc[MMWRweek==1,.(MMWRyear,MMWRweek,deaths_minus_excess=`Deaths (unweighted)`-`Number above average (unweighted)`)]|>print(r=F)
# MMWRyear MMWRweek deaths_minus_excess # deaths minus excess deaths is always
# 2015 1 NA # the same as the 2015-2019 average
# 2016 1 NA
# 2017 1 NA
# 2018 1 NA
# 2019 1 NA
# 2020 1 60499
# 2021 1 60499
# 2022 1 60499
# 2023 1 60499
But anyway since Pantazatos used a 2015-2019 average baseline which exaggerated excess deaths in 2022 and 2021 relative to 2020, in his model where vaccines explained 5% of additional variance in excess mortality beyond COVID cases, it might have partially been because his baseline produced superfluous excess deaths in 2021 and 2022 which happened to partially coincide with periods when vaccine doses were administered. And because his model had a different term for each COVID wave, it allowed the weight of the COVID waves in 2021 and 2022 to be reduced in order to accommodate a higher weight to vaccines.
In this plot by Pantazatos which shows excess deaths in CDC's ad-hoc dataset, after the first few weeks of 2020 there's no week where the excess mortality is even close to zero:

However with a more accurate method of calculating excess mortality, there should be close to zero excess mortality around March to May 2022 and around March 2021. At Mortality Watch if you plot ASMR in the United States with a 2010-2019 linear baseline, there's even a few weeks that get negative excess mortality in March and April of 2022. [https://www.mortality.watch/explorer/?c=USA&ct=weekly&df=2020%2520W01&bm=lin_reg] In CDC's primary dataset for excess deaths which uses a Farrington surveillance algorithm to calculate the baseline, there's also weeks with negative excess deaths in March and April of 2022. [https://www.cdc.gov/nchs/nvss/vsrr/covid19/excess_deaths.htm]
Pantazatos wrote that there were a total of 1,743,770 excess deaths in 2020-2022. I got the same number of total excess deaths in MMWR years 2020-2022 when I looked at the column "Number above average (unweighted)" in the ad-hoc dataset he used. However in CDC's primary dataset for excess deaths which used a Farrington surveillance algorithm to calculate the baseline, there was a total of only about 1.32 million excess deaths on weeks ending in 2020-2022: [https://www.cdc.gov/nchs/nvss/vsrr/covid19/excess_deaths.htm; link "National and State Estimates of Excess Deaths" under downloads]
adhoc=fread("AH_Excess_Deaths_by_Sex__Age__and_Race_and_Hispanic_Origin_20250211.csv")
adhoc=adhoc[MMWRyear%in%2020:2022&Sex=="All Sexes"&RaceEthnicity=="All Race/Ethnicity Groups"&AgeGroup=="All Ages"]
adhoc[,sum(`Number above average (unweighted)`)] # 1743770 (same as Pantazatos)
o=adhoc[,.(cdc_adhoc_excess=sum(`Number above average (unweighted)`)),.(year=MMWRyear)]
# primary analysis where the baseline was calculated using a Farrington surveillance algorithm
main=fread("Excess_Deaths_Associated_with_COVID-19.csv")
main=main[Type=="Predicted (weighted)"&Outcome=="All causes"&State=="United States"]
main=main[,.(cdc_main_excess=sum(`Excess Estimate`)),.(year=Year)]
o=merge(o,main)
o=rbind(o,list("Total",sum(o$cdc_adhoc_excess),sum(o$cdc_main_excess)))
o[,difference:=cdc_adhoc_excess-cdc_main_excess]
print(o,r=F)
# year cdc_adhoc_excess cdc_main_excess difference
# 2020 585409 459421 125988 # difference is smallest in 2020
# 2021 670667 530876 139791
# 2022 487694 331469 156225 # difference is biggest in 2022
# Total 1743770 1321766 422004
In the following code I used my own method to calculate excess deaths where I multiplied the 2011-2019 linear trend in CMR for each age by the mid-year resident population estimates of the age. But I got about about 1.27 million excess deaths in 2020-2022, so it's similar to CDC's main dataset for excess deaths:
pop=fread("http://sars2.net/f/uspopdead.csv")
pop=merge(pop,pop[year%in%2011:2019,.(year=2020:2022,base=predict(lm(dead/pop~year),.(year=2020:2022))),age])
pop=pop[,.(dead=sum(dead),base=sum(base*pop)),year]
my_excess=pop[,dead-base];my_excess=c(my_excess,sum(my_excess))
cbind(o[,-4],my_excess)|>print(r=F)
# year cdc_adhoc_excess cdc_main_excess my_excess
# 2020 585409 459421 468885
# 2021 670667 530876 515125
# 2022 487694 331469 285019
# Total 1743770 1321766 1269029
In the following code I calculated a more accurate weekly baseline adjusted for seasonality. First I multiplied the 2011-2019 linear trend in CMR for each age by the mid-year resident population estimates of the age to get the yearly expected deaths for each age, and I added together the expected deaths for all ages to get the total yearly expected deaths. Then I divided the yearly expected deaths by the number of days in the year and multiplied it by 7 to get the weekly expected deaths for each year. Then I adjusted the baseline for seasonality by calculating the average difference between the actual deaths and weekly expected deaths for each MMWR week number in 2015-2019, and I added the difference to the baseline for the corresponding MMWR week number of each year.
I again did a linear model where I first compared COVID deaths against all-cause deaths, and next I also added a term for weekly new vaccine doses to the model. However regardless of whether I took the excess deaths from CDC's ad-hoc dataset or if I used my own more accurate method of calculating excess deaths, the weekly number of new vaccine doses still got a negative coefficient in the model, which means that vaccines were inversely associated with excess mortality:
# sars2.net/ethical.html#Files_for_US_population_estimates_by_single_year_of_age
pop=fread("https://sars2.net/f/uspopdead.csv")
base=merge(pop,pop[year%in%2011:2019,.(year=2011:2023,base=predict(lm(dead/pop~year),.(year=2011:2023))),age])
base=base[,.(base=sum(base*pop)),year]
base=merge(d[,.(year=MMWRyear,week=MMWRweek,dead=`Deaths (unweighted)`)],base)
base[,base:=base/(365+(year%%4==0))*7]
weekly=base[year%in%2015:2019,.(weekly=mean(dead-base)),week]
weekly=rbind(weekly,weekly[week==52,.(week=53,weekly)])
ex2=merge(weekly,base)[year%in%2020:2022,.(excess2=dead-base-weekly),,.(year,week)]
me=merge(me,ex2)
# inaccurate baseline (CDC's ad-hoc dataset with 2015-2019 average baseline)
summary(lm(excess~coviddead,me))$r.squared # 0.714
summary(lm(excess~coviddead+vax,me))$r.squared # 0.735 (adding vaccines to the model increased r^2 by about 0.021)
coef(lm(excess~coviddead+vax,me))["vax"] # -0.000188 (vaccines have a negative coefficient)
# accurate baseline (my 2011-2019 linear trend in CMR by age multiplied by population size)
summary(lm(excess2~coviddead,me))$r.squared # 0.725
summary(lm(excess2~coviddead+vax,me))$r.squared # 0.754 (adding vaccines to the model increased r^2 by about 0.029)
coef(lm(excess2~coviddead+vax,me))["vax"] # -0.000227 (vaccines have a negative coefficient)
Added later: Spiro Pantazatos posted this reply to me at Substack: "Thanks. When I optimize the fit without a vaccine term I find the model fits best with a 4 day lag on the COVID cases. After adding the vaccine term I then get results consistent with yours (i.e. only a 1.5-2% increase in variance explained). I will update the results in the article to include this improved approach for choosing the lag. Thanks again for your feedback and comments (and excellent idea to apply the lag in days before down-sampling the cases vector)." [https://telemimesis.substack.com/p/a-simple-time-series-model-of-pandemic/comments]
I posted this reply to him:
The reason why vaccines still explain around 1.5-2% of variance might partially be because you have different terms for different COVID waves, so then for example the weight of wave 4 can be reduced in order to accommodate a higher weight to vaccines, because the primary course doses were rolled out during wave 4.
In your models wave 4 had by far the biggest change to the coefficient when you added the term for vaccines, because the coefficient dropped from about 6 to -24.
And anyway why would COVID cases have a negative effect on excess mortality during wave 4 but a positive effect during other waves? Wave 4 was the only wave with a negative coefficient when the term for vaccines was included.
Maybe if you constrained the coefficients of all COVID waves to be nonnegative, then the vaccine coefficient would become negative. (I tried using the
constrOptimfunction in R to do it but I couldn't get it to work.)
The image below shows Spiro's updated models, where now the
r^2 value increased by only about 0.020 on the right side
when he added the term for vaccines, and not by about 0.050 like in his
earlier pair of models. You can see that wave 4 has by far the biggest
change in the weight between the left and right sides, and it's also the
only wave with a negative weight on either side:

In this section I address Kirsch's initial arguments which I didn't cover earlier: https://kirschsubstack.com/p/did-the-covid-vaccine-save-more-people.
Kirsch wrote:
Allen (2024), an Australian study looking at correlation between vaccination and excess deaths, Table 3 summarizes the entire argument: more vaccines → more deaths. If the vaccine worked the coefficients should have been negative.
The *** means highly statistically significant. So excess deaths are related to Booster doses, total # vaccinated, and 'recently vaccinated (RECVAC)':"

However the reason why there was such a high correlation across states between the number of vaccine doses administered and excess deaths is that neither variable was adjusted for population size, so both variables tended to be higher in states with a bigger population size. Peter Hegarty published a review of Allen's paper where he wrote: [https://www.researchgate.net/publication/387207098_Review_of_the_paper_The_correlation_between_Australian_excess_deaths_by_State_and_booster_vaccinations_by_DE_Allen]
In his analysis, Allen deals with numbers of (excess) deaths and vaccinations in the various Australian territories, not with rates of these quantities. This means that the strong correlation that he finds between excess deaths and vaccinations is mostly "explained" by the trivial fact that both correlate with total population. Allen even acknowledges this, for example at the top of Page 6 he writes:
Clearly, State population has a large impact on all the variables used in this cross-sectional regressional analysis.
However, I will be more blunt and assert that his analysis is essentially worthless. Adjusting for State population not only has a "large impact", but makes it impossible to draw any meaningful conclusions, beyond the trivial one that total excess mortality strongly correlates with total population. Moreover, an analysis that did deal with rates of mortality and vaccination is unlikely to have yielded any meaningful conclusion anyway for this particular dataset, because rates of vaccination were very high in all Australian States. I will now elaborate on both points.
We start by focusing on the first three rows of Table 3. These present the least-squares best fits when excess deaths are plotted against three different independent variables: booster doses, total vaccinations, and recently vaccinated (see Table 2), for eight Australian States and Territories. In particular, note the values of the so-called coefficient of determination R2 in the third column: 0.71, 0.71, and 0.69. So these are all slightly above two-thirds, which explains the last sentence in the tweet above. However, there is no doubt that what is being plotted here are absolute numbers of excess deaths and vaccinations, not rates of these. Thus, if we now look at the 5th row of Table 3, we see that R2 is 0.66 when we plot excess deaths against the population of the State or Territory. There is no meaningful difference between an R2-value of 0.66 and the three slightly higher values in the first three rows. Indeed, the last row of Table 3 shows that we have an almost perfect linear relationship (R2=0.99) between total population and number of booster doses - and thus presumably also "total vaccinations" and "recently vaccinated", though these are not shown. Hence, we expect the plots in the first three rows to closely match that in the fifth row. Clearly, the only reasonable course is to admit that we can't say anything meaningful beyond the trivial fact that excess deaths strongly correlate with population size.
I tried to reproduce Allen's analysis, so I took the number of vaccine doses administered per region up to November 2023 from here: https://www.health.gov.au/resources/publications/covid-19-vaccination-vaccination-data-10-november-2023. Allen didn't mention which week's data release he used, but by checking various weeks I found that his figures matched the release for November 10th 2023.
I took expected and excess deaths during the first quarter of 2023 from this page which Allen linked as his source: https://www.abs.gov.au/articles/measuring-australias-excess-mortality-during-covid-19-pandemic-until-first-quarter-2023. I manually copied the expected and actual deaths during the year 2023 from the tables for each state. Northern Territory was missing data for the first quarter of 2023, so like Allen I used data for the whole year of 2022 instead for Northern Territory.
I took resident population estimates on December 31st 2022 from here: https://www.abs.gov.au/statistics/people/population/national-state-and-territory-population/dec-2022.
When I didn't adjust my calculation for population size, my correlation between the number of vaccine doses administered and the excess number of deaths was about 0.97:
t=fread(text=" region expected_deaths actual_deaths excess_deaths total_vaccinations booster_doses population recently_vaccinated unvaccinated NSW 11540 12529 989 21400000 1300000 8238800 584700 136400 VIC 8789 9840 1051 17900000 1100000 6704300 506300 47700 QLD 7550 8141 591 13000000 751800 5378300 341600 208200 SA 3038 3308 270 4800000 325700 1834300 139100 77500 WA 3473 3686 213 7400000 404600 2825200 197400 44600 TAS 931 1092 161 1600000 137200 571600 62900 20400 NT 1122 1241 119 644400 18700 250100 9800 20700 ACT 550 599 49 2200000 131400 460900 49200 9200") t[,cor(total_vaccinations,excess_deaths)] # 0.96581 (not adjusted for population size)
But my correlation fell to about -0.21 when I compared doses per capita against excess deaths per capita instead:
t[,cor(total_vaccinations/population,excess_deaths/population)] # -0.20514 (adjusted for population size)
Allen got an adjusted r-squared value of about 0.71 between excess deaths and vaccine doses. However my adjusted r-squared value was about 0.92:
summary(t[,lm(doses~dead-expecteddead)])$adj.r # 0.91934
In order to find why my r-squared value was different from Allen, I checked if I could reproduce the mean values in Allen's Table 2:

My mean values were off by less than 0.01% from Allen's values for other columns except actual deaths, excess deaths, and population size, but by far the highest percentage difference was for excess deaths which were off by about 34%:
d=data.table(variable=names(t[,-1]),my=colMeans(t[,-1])) d$allen=c(4624.1,5124.1,320.25,8618100,521180,3329200,236380,70588) d[,difference:=my-allen] d[,differencepct:=(my/allen-1)*100] print(d,r=f) # variable my allen difference differencepct # expected_deaths 4624.12 4624.10 0.025 0.00054 # actual_deaths 5054.50 5124.10 -69.600 -1.35829 # excess_deaths 430.38 320.25 110.125 34.38720 # total_vaccinations 8618050.00 8618100.00 -50.000 -0.00058 # booster_doses 521175.00 521180.00 -5.000 -0.00096 # population 3282937.50 3329200.00 -46262.500 -1.38960 # recently_vaccinated 236375.00 236380.00 -5.000 -0.00212 # unvaccinated 70587.50 70588.00 -0.500 -0.00071
Next I tried reproducing Allen's correlation matrix:

I was able to roughly reproduce the correlation coefficients between other pairs of variables, except the correlation coefficients of excess deaths compared to other variables were completely off:
round(cor(t[,-(1:3)]),4) # excess_deaths total_vaccinations booster_doses # excess_deaths 1.0000 0.9648 0.9730 # total_vaccinations 0.9648 1.0000 0.9979 # booster_doses 0.9730 0.9979 1.0000 # population 0.9599 0.9978 0.9942 # recently_vaccinated 0.9733 0.9984 0.9993 # unvaccinated 0.5287 0.6230 0.6055 # population recently_vaccinated unvaccinated # excess_deaths 0.9599 0.9733 0.5287 # total_vaccinations 0.9978 0.9984 0.6230 # booster_doses 0.9942 0.9993 0.6055 # population 1.0000 0.9950 0.6663 # recently_vaccinated 0.9950 1.0000 0.5992 # unvaccinated 0.6663 0.5992 1.0000
In Allen's Table 2 the maximum number of excess deaths was 1051 which matched my table, so I think he calculated the excess deaths for at least one region the same way as me. But his minimum excess deaths were -268 which didn't match my table because I didn't get negative excess deaths for any region. He might have made some error in entering his data or in subtracting actual deaths from expected deaths, because the source dataset didn't have any region that got negative excess deaths in the first quarter of 2023: https://www.abs.gov.au/articles/measuring-australias-excess-mortality-during-covid-19-pandemic-until-first-quarter-2023. I checked multiple times that my actual and expected deaths matched the source data, so I don't think I made any error in copying the data.
As an additional remark on Allen's paper, he wrote: "Most revealing is the insignificant correlation of 0.5 between the unvaccinated and excess deaths." However I don't know what that is supposed to reveal, except that it is notoriously difficult to estimate the number of unvaccinated people, so the relatively low correlation might simply be due to inaccurate estimates for the number of unvaccinated people.
In CDC's vaccination data for the United States, there's some states that have more vaccinated people than the total resident population estimate, but the percentage of vaccinated people is capped at a maximum of 95% because it is not realistic for the percentage to reach much closer to 100%, especially considering that the youngest children are usually not vaccinated. [https://data.cdc.gov/Vaccinations/COVID-19-Vaccinations-in-the-United-States-County/8xkx-amqh] In vaccination data from New Zealand, Hong Kong, and the UK, there are also age groups that have more vaccinated people than total people. [https://github.com/minhealthnz/nz-covid-data/tree/main/vaccine-data/2022-02-16, https://www.coronavirus.gov.hk/eng/index.html, https://www.england.nhs.uk/statistics/wp-content/uploads/sites/2/2021/05/Denominators-for-COVID-19-vaccination-statistics.docx]
In the Australian vaccination data that was used by Allen, the number of unvaccinated people in Victoria is only about 0.7% of Victoria's resident population estimate on December 31st 2022, which is not realistic even if the youngest ages are excluded from the unvaccinated population size:
t[,.(region,unvaxpct=round(unvaccinated/population*100,1))]|>print(r=F) # region unvaxpct # NSW 1.7 # VIC 0.7 # QLD 3.9 # SA 4.2 # WA 1.6 # TAS 3.6 # NT 8.3 # ACT 2.0
In the spreadsheet of vaccination data used by Allen, there's a note which says that the number of unvaccinated people is "based on the total Estimated Resident Population minus individuals who have a dose recorded in the Australian Immunisation Register". [https://www.health.gov.au/resources/publications/covid-19-vaccination-vaccination-data-10-november-2023] However if you look at the rows of the spreadsheet for people whose state of residence is Victoria, the rows for unvaccinated, recently vaccinated, and not recently vaccinated people only add up to 5,154,000, even though the resident population estimate of Victoria on December 31st 2022 was 6,704,300. So I don't know if the youngest ages are excluded from the calculation for the number of unvaccinated people.
Kirsch wrote: "The Czech Republic record-level data obtained under FOIA request from the Czech government showed that people who got the Moderna vaccine were 30% more likely to die within 1 year of the shot than people who got the Pfizer vaccine. The 30% difference appeared in all age groups where there was sufficient data and it happened during NON-COVID time periods. People tried to attack this claiming that it was due to distribution bias, but we showed that was false. The reason this is such an important study is because you cannot compare vaccinated with unvaccinated death rates due to selection bias. But in the Czech Republic, the vaccines were randomly assigned and nobody had any clue which one was safer. So there was no systematic or systemic bias. So how can the death rates be 30% higher in every age group with sufficient data? The only way that can happen is if the Moderna vaccine is more deadly."
In July 2024 when Kirsch had not yet published his analysis of the Czech record-level data, he sent me a link to his GitHub repository which contained a preliminary version of his analysis. At the time the README file of the repository said: "Vaccines were randomly distributed for those wishing to get vaxxed." And the README file said: "People were not allowed to select which vaccines they got." And it said: "The randomization of which vaccine someone got created a perfect real-world randomized clinical trial where we could compute the mortality rates for 1 year after Dose 2 for the two most popular vaccines." [https://github.com/skirsch/Czech/blob/5725ac1b64ede7124e00b72af68892f31736b349/README.md]
I pointed out to Kirsch that people who got a Moderna vaccine for their first dose had much higher average age than people who got a Pfizer vaccine, which meant that the vaccines were not distributed randomly. [czech.html#Were_Pfizer_and_Moderna_vaccines_allocated_randomly] After that Kirsch edited the README file and told me: "i've changed randomly to non-systematically in the github. sorry for the error." And a few days later after Kirsch published his first Substack post about the Czech data, he no longer repeated the claims that people were not allowed to choose which vaccine type they got or that the Czech population essentially participated in a perfect randomized trial.
However in August 2024 when Kirsch went on InfoWars, he resurrected his earlier claims and he said: "The only difference in the Czech Republic between getting a Pfizer shot and a Moderna shot is just pure luck. It was - you weren't allowed to choose, you were just assigned a brand. So it's effectively like the world's largest randomized trial." [czech4.html#Kirschs_resurrected_claim_that_people_were_not_allowed_to_choose_if_they_got_a_Moderna_or_Pfizer_vaccine]
When I called Kirsch out for his comments on InfoWars, he asked me to show evidence that people were allowed to choose which vaccine type they got. But then when I digged through various Czech websites, I found that in an online form for registering a vaccination appointment, there was a dropdown menu where people were allowed to choose their preferred vaccine type: [https://ockodoc.mzcr.cz/wp-content/uploads/2023/07/manual_crs.pdf; translated with Yandex]
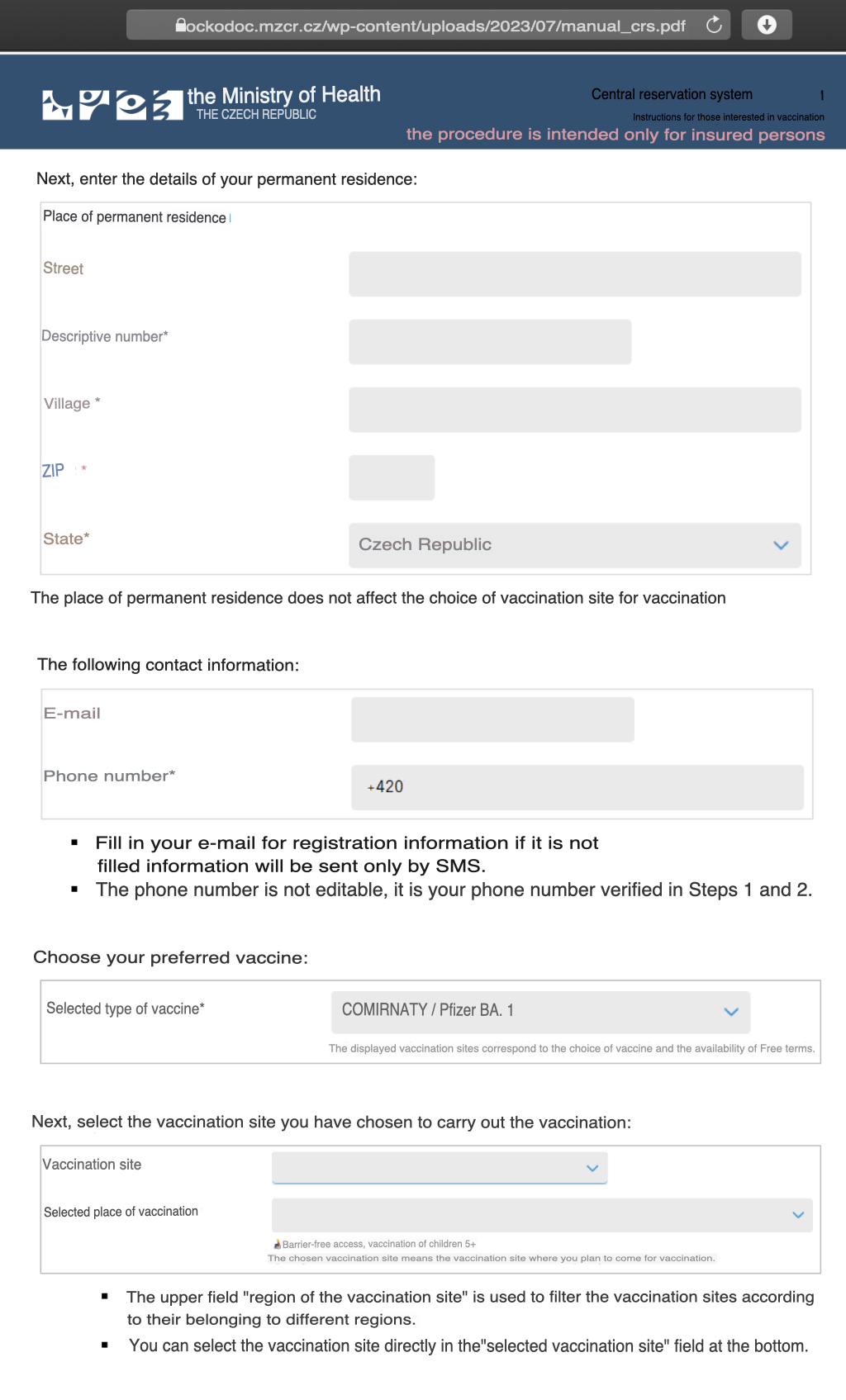
Kirsch's main thesis for why the Czech data showed that vaccines were deadly was that people who got a Moderna vaccine for their first dose had higher age-specific mortality rates than people who got a Pfizer vaccine for their first dose. However Kirsch had already made it into his main thesis in the preliminary version of his analysis at GitHub, even though at the time he was still claiming that the vaccines were distributed randomly and people were not allowed to choose which vaccine type they got. But if the vaccines were not actually distributed randomly then Kirsch's argument becomes much weaker, because then it's possible that the difference in mortality between Moderna and Pfizer can be explained by confounders instead.
For example elderly people who live in a long-term care facility have much higher age-normalized mortality rates than elderly people who live on their own. But compared to people who received a Pfizer vaccine for their first dose, people who received a Moderna vaccine for their first dose had a much higher age-normalized percentage of vaccinators whose name matched Czech terms for senior home. [czech3.html#Vaccinator_types]
In November 2024 a new Czech dataset was published which was similar to the earlier record-level dataset analyzed by Kirsch, but the new dataset also included a column for a comorbidity index. And within most age groups the proportion of people with the highest value of the comorbidity index was higher for Moderna than Pfizer. [czech4.html#Comorbidity_index_by_age_group_and_vaccine_type_in_new_UZIS_data]