
Other parts: ethical.html, ethical2.html, ethical3.html (deaths in ages 0-4).
Ethical Skeptic posted this plot of cancer incidence in England, where he used a hacky method to approximate age-standardized incidence by dividing the number of cases in all ages with the population estimate of ages 65 and above: [https://x.com/EthicalSkeptic/status/1966911244859842912]

His plot has a massive drop in the incidence between the start of 2019 and the end of 2019, but in the dataset he cited as his source, the incidence in 2019 is roughly flat: [https://nhsd-ndrs.shinyapps.io/rcrd/]

In this plot the age-standardized cancer incidence also remained around the same level in 2018 and 2019: [https://researchbriefings.files.parliament.uk/documents/SN06887/SN06887.pdf]

I used WebPlotDigitizer to digitize the data in Ethical Skeptic's plot. The points in his plot have irregular horizontal spacing, so I had to click on each point manually to extract the data correctly: [https://automeris.io/wpd/]

ES seems to have calculated the number of people aged 65 and above through a circuitious method, where he multiplied the yearly population estimates of England with the yearly proportion of people aged 65 and above:

I tried to replicate his methodology, so I took yearly population estimates from a page at Statista titled "Population of England from 1971 to 2023": https://www.statista.com/statistics/975956/population-of-england/. I used 2023 estimates for 2024 and 2025, but I'm not sure if for example ES used a linear projection of the 2022 and 2023 population sizes as the population size for 2024. I multiplied the population estimates by the proportion of people aged 65 and above in England from the website of the ONS (where I used the 2024 proportion for 2025): https://www.ons.gov.uk/explore-local-statistics/indicators/percentage-of-the-population-aged-65-plus ("Line chart > Change areas > Other areas > All countries > England > Download line chart data (CSV)").
The result I got was close to the yearly population estimate of ages 65+ returned by Nomis, apart from the years 2023 and 2024: [https://www.nomisweb.co.uk/datasets/pestsyoala]

Then in order to calculate the yellow line in the next plot, I multiplied the monthly rates in Ethical Skeptic's plot by the yearly number of people aged 65 and above, and I divided the result by 100,000.
I downloaded the rapid cancer registration data from here: https://nhsd-ndrs.shinyapps.io/rcrd/. I used the version of the data adjusted for the number of working days per month, because the unadjusted version gave me a much poorer fit to Ethical Skeptic's plot, so he probably used the adjusted data. Then I took a backwards moving average of the data where the window extended up to 5 months backwards, but for example the window extended only 1 month backwards in February 2018.
I was able to replicate the values in Ethical Skeptic's closely in 2018. But he seems to have manually altered the y-axis values so that he shifted them downwards in 2019 to 2022, and he shifted them upwards in 2024 and 2025. There's a particularly large downwards shift in 2019, so that the yearly average number of diagnoses drops by about 13% between 2018 and 2019, even though in the real data it increases by about 1%:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
rapid=CJ(year=2018:2025,month=1:12)[!(year==2025&month>5)]
diagnoses=c(24265,23485,24346,25994,27661,26373,25833,25212,24953,24540,24564,25231,25169,24844,24873,26294,26401,25994,25037,25043,24770,25236,24966,25444,25128,25621,24809,16910,17246,18362,19806,21826,23169,23614,24274,24592,23870,23534,24370,26499,27741,25785,25686,25425,25493,25801,25927,25658,25752,26316,25826,27370,28176,27371,26549,26517,26984,26615,27285,26179,26944,26909,26700,28151,29276,27220,26845,26652,26579,26473,28109,27843,27733,27699,28826,28654,29560,28914,28213,27783,27948,27807,27565,28289,27863,28261,27960,28428,27754) # adjusted for number of working days
p1=rapid[,.(x=as.Date(paste(year,month,16,sep="-")),y=diagnoses)]
p1[,y:=ma(y,5,0)]
p1$z="Real data (6-month backward moving average)"
es=CJ(year=2018:2025,month=1:12)[1:87]
es$rate=c(239.6,235.7,237.5,242.7,248.6,250.4,253.2,255.5,256.8,254.2,249.6,247.5,239.3,230.8,222.3,218.2,212.1,206.9,206.1,206.4,206.4,204.6,203.1,202.3,206.1,210.5,215.1,206.4,198.9,191.5,184.5,178.6,176.3,185.1,196.1,204.9,212.1,214.6,216.2,220.8,226.2,227.0,230.3,233.1,234.4,233.7,231.3,230.6,230.6,232.1,232.6,236.0,238.5,241.1,242.4,242.4,244.5,243.4,242.1,240.3,242.1,243.9,244.5,248.1,252.4,255.3,254.5,255.0,254.2,251.7,250.1,250.9,253.5,255.5,260.7,266.1,269.4,272.7,273.5,273.5,271.7,269.1,267.3,266.8,268.4,270.9,272.2)
# nomispop=c(10082761,10243221,10332210,10469044,10630852,10787479,10981092) # exact population estimate of ages 65+
espop=c(55924500,56230100,56326000,56554900,57112500,57690300,57690300,57690300) # from Statista
espop=espop*c(.1803,.1822,.1834,.1851,.186,.1862,.1873,.1873) # proportion aged 65 and above from ONS website
p3=es[,.(x=as.Date(paste(year,month,16,sep="-")),y=rate*espop[factor(year)]/1e5)]
p3$z="Ethical Skeptic's rate converted to number of diagnoses"
p=rbind(p1,p3)[,z:=factor(z,unique(z))]
xstart=as.Date("2018-1-1");xend=as.Date("2025-7-1");xbreak=seq(xstart+182,as.Date("2025-1-1"),"year")
ybreak=pretty(c(0,p$y));ystart=0;yend=max(p$y*1.03)
yearly=p[,.(y=mean(y)),.(year=year(x),z)][year%in%c(2018,2019,2021,2024)]
yearly[,x:=as.Date(paste0(year,"-1-1"))]
color=c(hsv(22/36,1,.6),"#aaaa00")
anno1="ES altered his data to get a 13% decrease between 2018 and 2019, even though the real data has a 1% increase"
anno2="ES altered his data to get a 22% increase between 2021 and 2024, even though the real data only has a 12% increase"
anno=data.table(x=c(xstart+50,xend-50),y=14000,label=c(str_wrap(anno1,25),str_wrap(anno2,34)))
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_segment(data=yearly,aes(x,y,xend=x+365,yend=y,color=z),linewidth=.6,linetype="42")+
geom_segment(data=yearly[z!=z[1]],aes(x+182+c(100,-100),14500,xend=x+182,yend=y-500),color=color[2],linewidth=.6,arrow=arrow(type="closed",length=unit(4,"pt")),lineend="butt",linejoin="mitre")+
geom_text(data=anno,aes(x,y,label=label),hjust=c(0,1),vjust=1,size=3.87,color=color[2],lineheight=.8)+
labs(x=NULL,y=NULL,title="Monthly cancer diagnoses in England rapid registration data")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x>=1e3,paste0(x/1e3,"k"),x))+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray40"),
axis.text.y=element_text(margin=margin(,1.5)),
axis.ticks=element_line(linewidth=.4,color="gray75"),
axis.ticks.length=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(24,"pt"),
legend.margin=margin(-2,,4),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.background=element_blank(),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)))
ggsave("1.png",width=5.1,height=3,dpi=300*4)
I'm fairly sure that ES manually falsified the data. He has not documented his methodology precisely enough that other people could reproduce his work exactly, which also makes it difficult for other people to bust him falsifying the data. But the 13% drop between 2018 and 2019 is completely unrealistic, and it's inconsistent with the real data, but it is consistent with Ethical Skeptic's history of falsifying data.
Some points in his plot have irregular horizontal spacing, which might be if he somehow manually moved the points around in a GUI, so that he ended up not only moving the points vertically but also horizontally:

The next plot shows that I found anomalous features next to two pairs of months that had irregular horizontal spacing. It's also weird how there's several segments of months in 2019 and 2020 that look almost like straight lines, but there are sudden discontinuities in slope before or after the line-like segments, which is anomalous for a moving average. In the real data there are only two clear discontinuities in the slope, which are between March and April of 2020 because the incidence dropped dramatically in April, and between September and October of 2020 because April 2020 fell out of the window of the moving average:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
rapid=CJ(year=2018:2025,month=1:12)[!(year==2025&month>5)]
rapid$diagnoses=c(24265,23485,24346,25994,27661,26373,25833,25212,24953,24540,24564,25231,25169,24844,24873,26294,26401,25994,25037,25043,24770,25236,24966,25444,25128,25621,24809,16910,17246,18362,19806,21826,23169,23614,24274,24592,23870,23534,24370,26499,27741,25785,25686,25425,25493,25801,25927,25658,25752,26316,25826,27370,28176,27371,26549,26517,26984,26615,27285,26179,26944,26909,26700,28151,29276,27220,26845,26652,26579,26473,28109,27843,27733,27699,28826,28654,29560,28914,28213,27783,27948,27807,27565,28289,27863,28261,27960,28428,27754) # adjusted for number of working days
espop=c(55924500,56230100,56326000,56554900,57112500,57690300,57690300,57690300) # from Statista
espop=espop*c(.1803,.1822,.1834,.1851,.186,.1862,.1873,.1873) # proportion aged 65 and above from ONS website
rapid[,x:=as.Date(paste(year,month,1,sep="-"))]
p=rapid[,.(x,y=ma(diagnoses/espop[year-2017]*1e5,5,0))]
xstart=as.Date("2018-1-1");xend=as.Date("2025-7-1");xbreak=seq(xstart,xend-10,"6 month")
xlab=ifelse(month(xbreak)==1,paste0(year(xbreak),"\nJan"),"")
ybreak=pretty(c(0,p$y));ystart=0;yend=max(p$y*1.03)
ystart=120;yend=300;ybreak=0:15*20
ggplot(p)+
geom_point(aes(x,y),size=1.4,stroke=0,color=hsv(5/6,1,.4))+
geom_line(aes(x,y),linewidth=.6,color=hsv(5/6,1,.4))+
labs(x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
guides(color=guide_legend(ncol=3,byrow=F))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=9,color="black",lineheight=.8),
axis.ticks=element_line(color="black",linewidth=.3),
axis.ticks.length=unit(3,"pt"),
axis.ticks.x=element_line(color=alpha("black",1:0)),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(23,"pt"),
legend.margin=margin(-2,,14),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=10,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid=element_blank(),
plot.background=element_rect(fill="transparent",color=NA),
plot.title=element_text(size=11,hjust=.5))
ggsave("1.png",width=6,height=3,dpi=300*4)
The next plot also shows how the difference between the pre-2020 and post-2020 slopes is greatly exaggerated by Ethical Skeptic's fake data:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
rapid=CJ(year=2018:2025,month=1:12)[!(year==2025&month>5)]
rapid$cases=c(24265,23485,24346,25994,27661,26373,25833,25212,24953,24540,24564,25231,25169,24844,24873,26294,26401,25994,25037,25043,24770,25236,24966,25444,25128,25621,24809,16910,17246,18362,19806,21826,23169,23614,24274,24592,23870,23534,24370,26499,27741,25785,25686,25425,25493,25801,25927,25658,25752,26316,25826,27370,28176,27371,26549,26517,26984,26615,27285,26179,26944,26909,26700,28151,29276,27220,26845,26652,26579,26473,28109,27843,27733,27699,28826,28654,29560,28914,28213,27783,27948,27807,27565,28289,27863,28261,27960,28428,27754)
p1=rapid[,.(x=as.Date(paste(year,month,16,sep="-")),y=ma(cases,5,0))]
p1$z="Real data (adjusted for working days, 6-month moving average)"
es=CJ(year=2018:2025,month=1:12)[1:87]
es$rate=c(239.6,235.7,237.5,242.7,248.6,250.4,253.2,255.5,256.8,254.2,249.6,247.5,239.3,230.8,222.3,218.2,212.1,206.9,206.1,206.4,206.4,204.6,203.1,202.3,206.1,210.5,215.1,206.4,198.9,191.5,184.5,178.6,176.3,185.1,196.1,204.9,212.1,214.6,216.2,220.8,226.2,227.0,230.3,233.1,234.4,233.7,231.3,230.6,230.6,232.1,232.6,236.0,238.5,241.1,242.4,242.4,244.5,243.4,242.1,240.3,242.1,243.9,244.5,248.1,252.4,255.3,254.5,255.0,254.2,251.7,250.1,250.9,253.5,255.5,260.7,266.1,269.4,272.7,273.5,273.5,271.7,269.1,267.3,266.8,268.4,270.9,272.2)
espop=c(55924500,56230100,56326000,56554900,57112500,57690300,57690300,57690300) # from Statista
espop=espop*c(.1803,.1822,.1834,.1851,.186,.1862,.1873,.1873) # proportion aged 65 and above from ONS website
p2=es[,.(x=as.Date(paste(year,month,16,sep="-")),y=rate*espop[factor(year)]/1e5)]
p2$z="Ethical Skeptic's fake data converted to number of diagnoses"
p=rbind(p1,p2)[,z:=factor(z,unique(z))]
lm=rbind(cbind(p,type=2)[,fit:=year(x)%in%2018:2019],cbind(p,type=3)[,fit:=year(x)%in%2022:2024])
lm=lm[,.(x,y=predict(lm(y~x,.SD[fit==T]),.SD),fit),.(z,type)]
p=rbind(p[,fit:=T][,type:=1],lm)
p[,type:=factor(type,,c("Actual","2018-2019 trend","2022-2024 trend"))]
xstart=as.Date("2018-1-1");xend=as.Date("2025-7-1");xbreak=seq(xstart+182,as.Date("2025-1-1"),"year")
ybreak=pretty(c(0,p$y));ystart=0;yend=max(ybreak)
ggplot(p)+
facet_wrap(~z,ncol=1,dir="v",scales="free_x")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=type),linewidth=.6,linetype="11")+
geom_line(data=p[fit==T],aes(x,y,color=type),linewidth=.6)+
labs(x=NULL,y=NULL,title="Monthly cancer diagnoses in England rapid registration data")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x>=1e3,paste0(x/1e3,"k"),x))+
scale_color_manual(values=c("black",hsv(1/3,1,.7),hsv(0,.7,1)))+
scale_alpha_manual(values=c(1,.4,.4))+
coord_cartesian(clip="off",expand=F)+
guides(alpha="none")+
theme(axis.text=element_text(size=11,color="gray40"),
axis.text.y=element_text(margin=margin(,1.5)),
axis.ticks=element_line(linewidth=.4,color="gray75"),
axis.ticks.length=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(24,"pt"),
legend.margin=margin(-2,,4),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.background=element_blank(),
panel.spacing.y=unit(3,"pt"),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)),
strip.background=element_rect(fill="gray90",color="gray75",linewidth=.4),
strip.text=element_text(size=11,margin=margin(3,,3)))
ggsave("1.png",width=5,height=4,dpi=300*4)
In the next plot I calculated age-standardized incidence rates by downloading age-stratified from here: https://nhsd-ndrs.shinyapps.io/rcrd/ ("Demographic factors > Downloads > Download time trend data for all cancer groups and demographic factors"). I took yearly population estimates by age from Nomis: https://www.nomisweb.co.uk/datasets/pestsyoala. The age-standardized incidence increased by only about 3% between 2022 and 2024. It increased by about 6% between 2021 and 2024, because the number of diagnoses was lower than usual in early 2021:

t=r("Incidence_Treatment_statistics_England.csv.gz")
t=t[`Cancer group`=="All sites combined"]
t=t[Metric=="New cancer diagnoses (working day adjusted)"]
t=t[Breakdown=="Age-group"]
t[,age:=as.integer(sub("\\D.*","",Demographic))]
t=t[,.(year=Year,month=match(Month,month.name),diagnoses=Statistic,age)]
pop=fread("https://sars2.net/f/englandpop.csv")
ages=c(0,5:8*10)
pop=pop[,.(pop=sum(pop)),.(year,age=ages[findInterval(age,ages)])]
pop=rbind(pop,pop[year==2024][,year:=2025])
t=merge(t,pop)
t=merge(pop[year==2020,.(age,std=pop/sum(pop))],t)
p=t[,.(y=sum(diagnoses/pop*std*1e5)),.(x=as.Date(paste(year,month,16,sep="-")))]
xstart=as.Date("2018-1-1");xend=as.Date("2025-7-1");xbreak=seq(xstart+182,as.Date("2025-1-1"),"year")
ybreak=pretty(c(0,p$y));ystart=0;yend=max(p$y*1.03)
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_point(aes(x,y),size=1.3,stroke=0)+
geom_line(aes(x,y),linewidth=.6)+
labs(x=NULL,y=NULL,title="Age-adjusted rate of monthly new cancer diagnoses per\n100,000 people in England rapid registration data")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c(hsv(0,.7,1),"black"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray40"),
axis.text.y=element_text(margin=margin(,1)),
axis.ticks=element_line(linewidth=.4,color="gray75"),
axis.ticks.length=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
panel.background=element_blank(),
plot.subtitle=element_text(hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)))
ggsave("1.png",width=5.2,height=3,dpi=300*4)
Yearly cancer incidence data is available from the NHS publication "Cancer Registration Statistics, England, 2022": https://digital.nhs.uk/data-and-information/publications/statistical/cancer-registration-statistics/england-2022#resources (file "Cancer Registration Statistics, updated to use 2021 census population estimates").
Without any kind of adjustment for population size or age, the yearly number of diagnoses increased by only about 3% between 2019 and 2022. In Ethical Skeptic's plot the rate of new diagnoses per population aged 65 and above increased by about 10% between 2019 and 2022, even though the adjustment for population size should make the percentage smaller and not bigger:
t=fread("https://sars2.net/f/Table_1_machine_readable_updated_June2025.csv.gz")
t=t[stage_at_diagnosis=="All stages"&imd_quintile=="All quintiles"&gender=="Persons"]
# `All` is for breast cancer, empty is for other cancers
t=t[hormone_receptor%in%c("","All")&hormone_receptor_status%in%c("","All")]
t=t[ndrs_detailed_group%like%"^All|ALL"]
t[,.(diagnoses=sum(count)),.(year=diagnosisyear)]
# year diagnoses
# 2013 491633
# 2014 506390
# 2015 521302
# 2016 532723
# 2017 536826
# 2018 554847
# 2019 565363
# 2020 486232
# 2021 551173
# 2022 582160 # about 3% higher than 2019
Here I overlaid the yearly data from the NHS report over the rapid registration data, where you can see that the rapid registration data is missing almost half of all new diagnoses:

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
y=fread("https://sars2.net/f/Table_1_machine_readable_updated_June2025.csv.gz")
y=y[stage_at_diagnosis=="All stages"&imd_quintile=="All quintiles"&gender=="Persons"]
y=y[hormone_receptor%in%c("","All")&hormone_receptor_status%in%c("","All")] # `All` is for breast cancer, empty is for other cancers
y=y[ndrs_detailed_group%like%"^All|ALL"]
p1=y[,.(y=sum(count)),.(x=diagnosisyear)][,.(x=as.Date(paste0(x,"-7-1")),y=y/(365+(x%%4==0)))]
p1$z="Cancer Registration Statistics, England, 2022"
rapid=CJ(year=2018:2025,month=1:12)[!(year==2025&month>5)]
rapid$cases=c(24265,23485,24346,25994,27661,26373,25833,25212,24953,24540,24564,25231,25169,24844,24873,26294,26401,25994,25037,25043,24770,25236,24966,25444,25128,25621,24809,16910,17246,18362,19806,21826,23169,23614,24274,24592,23870,23534,24370,26499,27741,25785,25686,25425,25493,25801,25927,25658,25752,26316,25826,27370,28176,27371,26549,26517,26984,26615,27285,26179,26944,26909,26700,28151,29276,27220,26845,26652,26579,26473,28109,27843,27733,27699,28826,28654,29560,28914,28213,27783,27948,27807,27565,28289,27863,28261,27960,28428,27754) # adjusted for number of working days
p2=rapid[,.(x=as.Date(paste(year,month,16,sep="-")),y=cases)][,y:=y/days_in_month(x)]
p2$z="Rapid registration dashboard"
es=CJ(year=2018:2025,month=1:12)[1:87]
es$rate=c(239.6,235.7,237.5,242.7,248.6,250.4,253.2,255.5,256.8,254.2,249.6,247.5,239.3,230.8,222.3,218.2,212.1,206.9,206.1,206.4,206.4,204.6,203.1,202.3,206.1,210.5,215.1,206.4,198.9,191.5,184.5,178.6,176.3,185.1,196.1,204.9,212.1,214.6,216.2,220.8,226.2,227.0,230.3,233.1,234.4,233.7,231.3,230.6,230.6,232.1,232.6,236.0,238.5,241.1,242.4,242.4,244.5,243.4,242.1,240.3,242.1,243.9,244.5,248.1,252.4,255.3,254.5,255.0,254.2,251.7,250.1,250.9,253.5,255.5,260.7,266.1,269.4,272.7,273.5,273.5,271.7,269.1,267.3,266.8,268.4,270.9,272.2)
espop=c(55924500,56230100,56326000,56554900,57112500,57690300,57690300,57690300) # from Statista
espop=espop*c(.1803,.1822,.1834,.1851,.186,.1862,.1873,.1873) # proportion aged 65 and above from ONS website
p3=es[,.(x=as.Date(paste(year,month,16,sep="-")),y=rate*espop[factor(year)]/1e5)]
p3[,y:=y/ma(days_in_month(x),5,0)]
p3$z="Ethical Skeptic's rate converted to number of diagnoses"
p=rbind(p1,p2,p3)[,z:=factor(z,unique(z))]
xstart=as.Date("2013-1-1");xend=as.Date("2025-7-1");xbreak=seq(xstart+182,as.Date("2025-1-1"),"year")
ybreak=pretty(c(0,p$y),7);ystart=0;yend=max(ybreak)
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_point(aes(x,y,color=z,alpha=z),size=1.4,stroke=0)+
geom_line(aes(x,y,color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="New cancer diagnoses in England (divided by number of\ndays in year or month)")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c(hsv(1/3,1,.6),hsv(22/36,1,.6),"#aaaa00"))+
scale_alpha_manual(values=c(1,0,0,0))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray40"),
axis.text.y=element_text(margin=margin(,1.5)),
axis.ticks=element_line(linewidth=.4,color="gray75"),
axis.ticks.length=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(24,"pt"),
legend.margin=margin(-2,,4),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,margin=margin(,,,1)),
legend.title=element_blank(),
panel.background=element_blank(),
plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)))
ggsave("1.png",width=5.1,height=3.5,dpi=300*4)
The website of the NHS says: "The Rapid Cancer Registration Data contains proxy tumour registrations and some associated events on the cancer patient pathway (e.g. surgery, radiotherapy and systemic anti-cancer therapy data) from January 2018 to the most recently available data on cancer diagnoses. RCRD provides a quicker, indicative source of cancer data compared to the National Cancer Registration Data (NCRD), which is the 'gold-standard' registration data set and which relies on additional data sources, enhanced follow-up with trusts and expert processing by cancer registration officers. Due to the lower quality of RCRD, the data will not match the eventual National Statistics published on the full NCRD." [https://digital.nhs.uk/ndrs/data/data-sets/rcrd]
A document titled "Rapid Cancer Registration Dataset - Data Quality - August 2025" says: [https://digital.nhs.uk/ndrs/data/data-sets/rcrd]
This document outlines the main features of the data to be aware of when interpreting the Rapid Cancer Registration Dataset:
- across all cancer types included approximately 12.1% of cases are missing and 6.0% of cases are included erroneously or with incorrect cancer type or diagnosis date (when compared to 'Gold Standard' registration data for 2018 data)
- these figures vary strongly with cancer site. Broadly, more common cancers (particularly breast and prostate cancer) perform best and less common cancers (particularly bone and soft tissue and cancers of unknown primary) perform worst
- non-melanoma skin cancer (ICD-10 C44) tumours are excluded from the majority of data shown (Figure 3 onwards). Carcinoma of the cervix in-situ (ICD-10 D06) is excluded from all data presented
- there are more missing tumours in those aged over 70 compared to younger age groups
- other factors that reduce data completeness include the patient's route to diagnosis, mortality within 30 days of diagnosis, and the presence of multiple cancers
- usable data is available approximately 4 to 5 months after diagnosis or other clinical activity occurs
- data on cancer stage group at diagnosis is available for a number of common tumour types, although completeness is lower than that for the Gold Standard registration data. Where data is available it generally agrees with the Gold Standard stage group in 80 to 90% of tumours
A presentation about the rapid registration dataset said that the dataset "Covers all malignant cancers (excl. NMSC) and selected non-malignant cancers: Breast, Bladder & Brain (ICD-10 C00-C97 excl. C44, plus D05, D09, D32, D33, D35, D41, D42-D44)". [https://www.ndrs.nhs.uk/wp-content/uploads/2020/10/NDRS-Webinar-Rapid-Registrations-Cancer-Dataset-21.10.2020.pdf]
Ethical Skeptic wrote: [https://theethicalskeptic.com/2025/09/25/the-state-of-things-pandemic/]
All the trolls had to do was wait, and see if my models proved correct. They did prove correct. But when you are spinning deception, you must declare truth early, often, and loudly. This is the heart of Narrative Science. Real credibility is earned by engaging in the meticulous and intensive work entailed in describing a system, not in running stand-alone stats, deceptive linear regression graphs, or academic poseur heuristics.
For instance, making the baseless or linear-extrapolated and lagged claim 'There is no increase in cancer mortality', in a vacuum, and not even knowing what an 'MCoD' or 'Spring Lull' is, constitutes an act of appeal-to-ignorance deception. So much more than pablum is required from these claimants - and no matter how much they scream and insist, they are still wrong (see Excess Cancer Mortality in Charts 5 and 6 below). In the realm of systems analysis, adherence to such a professional standard is paramount, and I make no apologies for upholding it.
Where the third link was linked to this plot:

I immediately thought that the slope of his supposed "2014-2019 regression baseline" didn't look steep enough. ES has a habit of faking these baselines without doing any kind of a real regression of the data. When I tried to reproduce his plot, I confirmed that a real linear regression of the data was in fact much steeper than his baseline:

old=fread("https://sars2.net/f/Weekly_Counts_of_Deaths_by_State_and_Select_Causes__2014-2019.csv.gz")
old=old[`Jurisdiction of Occurrence`=="United States"]
old=old[,.(year=`MMWR Year`,week=`MMWR Week`,dead=`Malignant neoplasms (C00-C97)`)]
t=fread("https://sars2.net/f/wondermalignantweekly.csv")[year>2019,.(year,week,dead)]
t=rbind(old,t)
p=t[,.(x=MMWRweek::MMWRweek2Date(year,week,4),y=dead,z="Actual deaths")]
p=rbind(p,p[,.(x,y=predict(lm(y~x,p[year(x)<2020]),p),z="2014-2019 linear regression")])
p[,z:=factor(z,unique(z))]
xstart=as.Date("2014-1-1");xend=as.Date("2025-7-1");xbreak=seq(xstart,xend-1,"6 month")
ystart=10e3;yend=13e3;ybreak=seq(ystart,yend,500)
ggplot(p)+
geom_line(aes(x,y,color=z,linewidth=z))+
labs(x=NULL,y=NULL)+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=ifelse(month(xbreak)==7,year(xbreak),""))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black","#ff6666"))+
scale_linewidth_manual(values=c(.3,.6))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=9,color="black"),
axis.text.y=element_blank(),
axis.ticks=element_line(color="black",linewidth=.3),
axis.ticks.length=unit(3,"pt"),
axis.ticks.x=element_line(color=alpha("black",1:0)),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification=c(.5,0),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(23,"pt"),
legend.position=c(.5,.86),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=10,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid=element_blank(),
plot.background=element_rect(fill="transparent",color=NA),
plot.title=element_text(size=11,hjust=.5))
ggsave("1.png",width=6,height=3.2,dpi=300*4)
The text in Ethical Skeptic's plot says that "Weekly cancer death rates are up above the 2014 - 2019 regression baseline". The way he appears to have accomplished the feat was to first fake his regression line, and then to manually move points upwards when the points happened to fall below his fake regression line.
In the plot above, my black line otherwise matches Ethical Skeptic's blue line, except there are clusters of weeks in 2022 and 2023 where my line is much lower. I think it's because ES manually shifted points that were below his dashed baseline upwards. His plot has only 4 points in 2022 and 2023 that are below his dashed baseline, but my plot has 12 points.
Ethical Skeptic's blue line is also slightly higher than my black line from 2020 onwards. I took data for 2014-2019 from the same CDC dataset that ES uses in his plots. [https://data.cdc.gov/National-Center-for-Health-Statistics/Weekly-Counts-of-Deaths-by-State-and-Select-Causes/3yf8-kanr] I took data from 2020 onwards from CDC WONDER, but I can't think of any explanation for why my number of deaths from CDC WONDER would be slightly lower than Ethical Skeptic's number of deaths, because I just did a simple query for weekly deaths with underlying cause malignant neoplasms (C00-C97). So ES might have manually applied a slight upwards adjustment to all weeks in 2020-2023.
Ethical Skeptic posted this tweet: [https://x.com/EthicalSkeptic/status/1972021203867951336]

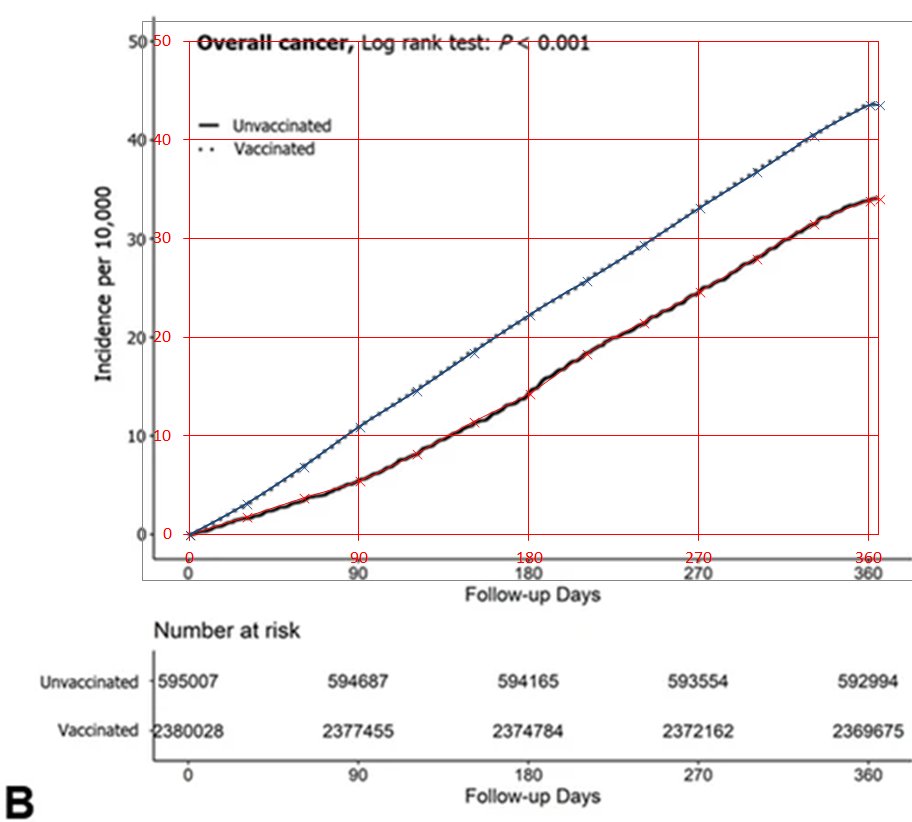
The paper he linked looked at cancer incidence within the first year of vaccination, where vaccinated people had a hazard ratio of about 1.27 for relative to unvaccinated people. [https://biomarkerres.biomedcentral.com/articles/10.1186/s40364-025-00831-w]
The likely explanation for why vaccinated people had a higher incidence of cancer is that vaccinated people are more likely to get screened for cancer than unvaccinated people, because unvaccinated people tend to be more hesitant to interact with medical services, and unvaccinated people tend to have lower health-seeking behavior.
In a Japanese study unvaccinated women were much less likely than vaccinated women to get screening for breast cancer. The authors wrote that when they did a regression adjusted for age, socioeconomic variables, and health-seeking behavior traits, "Individuals who remained unvaccinated due to health concerns (incidence rate ratio (IRR) = 0.47, 95% confidence interval (CI) 0.29-0.77, p = 0.003) and for other unspecified reasons (IRR = 0.73, 95% CI 0.62-0.86, p < 0.001) were significantly less inclined to opt for screening when compared to their fully vaccinated counterparts." [https://www.mdpi.com/2072-6694/16/9/1783]
A Canadian paper from 2024 said: "Unvaccinated respondents were less likely to have received serum cholesterol (aOR 0.69; 95 % CI [0.50-0.70), serum glucose (aOR 0.65; 95 % CI [0.56-0.75]), or blood pressure measurements (aOR 0.47; 95 % CI [0.33-0.66]); and were less likely to have received breast cancer (aOR 0.35; 95 % CI [0.25-0.48]), colorectal cancer (aOR 0.52; 95 % CI [0.46-0.60]) and prostate cancer screening (aOR 0.61; 95 % CI [0.48-0.76])." [https://www.sciencedirect.com/science/article/abs/pii/S0264410X24000070]
A paper about cancer screening behavior in Korea said: "In the city with the highest cancer screening participation rate, factors such as oral health, physical activity, breakfast habits, and past smoking history were all associated with higher participation. This finding aligns with the conclusion of a previous study that identified a correlation between healthy dietary habits, physical activity motivation, and cancer screening participation [35]. A similar trend has been observed in Lithuania, where factors such as the consumption of fresh vegetables, physical activity, and abstinence from alcohol are associated with higher participation in the national breast cancer screening program for women aged 50-69 [36]. In addition, a previous study of cancer screening activity in adults aged 50 years and older in the United States reported that healthy lifestyles, such as physical activity and smoking cessation, are associated with cancer screening behaviors [27]." [https://www.mdpi.com/2227-9032/13/6/664]
Most of the population of South Korea is vaccinated, so if vaccines would've caused a 27% increase in the incidence of cancer in vaccinated people, you'd expect the overall population of Korea to have a major increase in cancer incidence above the pre-COVID trend. However the age-standardized cancer incidence in Korea roughly fell on the pre-COVID trend in 2021 and 2022: [https://e-crt.org/journal/view.php?doi=10.4143/crt.2025.264]
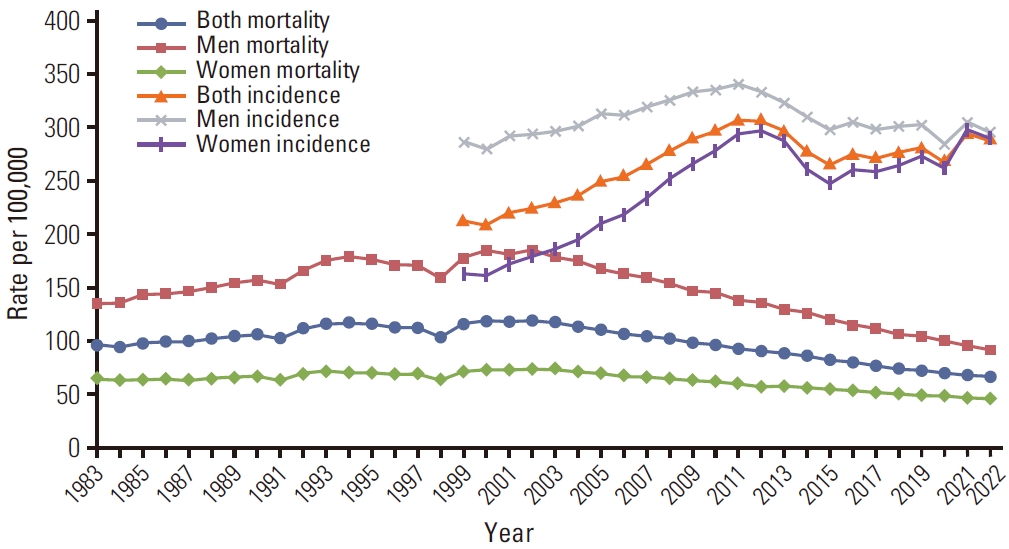
(The rates in the plot above are age-standardized rates calculated using a world standard population, so the rates are much lower than crude mortality rates or age-standardized rates where the Korean population is used as the standard population, because the Korean population has a high percentage of elderly people compared to the world population.)
The Korean paper was also promoted by Kevin McKernan, who says there has been a massive increase in cancer caused by plasmid DNA from mRNA vaccines: [https://x.com/Kevin_McKernan/status/1972004072439140451]

However in the study people who got mRNA vaccines had a lower cancer HR than people who got non-mRNA vaccines. Supplementary file 1 referred to the figure below and said: "For the vaccine type, the highest HR was observed in the cDNA vaccine-only group (1.472; 95% CI, 1.389-1.560), followed by heterologous vaccination (HR, 1.339; 95% CI, 1.208-1.484) and mRNA vaccine-only groups (HR, 1.199; 95% CI, 1.140-1.260; Figure 1C)." [https://static-content.springer.com/esm/art%3A10.1186%2Fs40364-025-00831-w/MediaObjects/40364_2025_831_MOESM1_ESM.docx]

The authors seem to have referred to AstraZeneca and other viral vector vaccines as "cDNA vaccines". Supplementary file 1 says: "Regarding vaccine types between the first and second vaccinations, 1,928,363 individuals (81.02%) were treated with mRNA vaccines only, 333,698 individuals (14.02%) were given cDNA vaccines only, and 117,967 individuals (4.96%) were administered with heterologous vaccinations in the COVID-19 vaccinated cohort (Table S2)."
Normally the term "DNA vaccine" refers to vaccines that deliver DNA in a plasmid, like the Indian ZyCoV-D vaccine, the Korean Genexine vaccine, and the Inovio vaccine. There is no approved DNA vaccine for COVID in Korea, even though there have been clinical trials for the Inovio and Genexine DNA vaccines, but they wouldn't account for 14% of total subjects in the cancer study. AstraZeneca and J&J are normally called viral vector vaccines, where a modified adenovirus is used as a vector to deliver spike DNA to the cell. Adenoviruses are DNA viruses, so the spike gene inside the adenovirus vector is coded as DNA that is complementary to the original RNA, so the term "cDNA vaccine" was likely used in the paper as a nonstandard term for a viral vector vaccine.
A paper about COVID vaccination in Korea said: "As of September 25, 2022, 128,710,064 doses of COVID-19 vaccines were administered: BNT162b2 (62.9%), mRNA-1273 (19.5%), ChAdOx1 (15.8%), Ad26.COV2.S (1.2%), NVX-CoV2373 (0.6%) and GBP510 (< 0.1%)." [https://jkms.kr/DOIx.php?id=10.3346%2Fjkms.2022.37.e351] So if AstraZeneca accounted for about 16% of doses in South Korea, and about 14% of subjects in the cancer study were in the cDNA-only group, then it's likely that the cDNA group included AstraZeneca.
Table S3 has a list of vaccine brands that were administered for booster doses, which includes only three vaccine brands (Pfizer BNT162b2, Moderna mRNA-1273, and AstraZeneca ChAdOx10). There's only a few doses of AstraZeneca listed in the table, because AstraZeneca was generally only administered for primary course doses. The distribution of vaccine brands for primary course doses was not shown anywhere in the paper.
Cancer takes time to develop, but Figure 1B shows that even during the first month of follow-up, vaccinated people already had a much higher incidence of cancer than unvaccinated people:

Supplementary file 2 says that the follow-up period started from the day after the primary series was completed, and not from the day of the first dose. But still, most people got the second dose within a few weeks from the first dose, so if the difference in incidence during the first month of follow-up would be explained by vaccines causing cancer, then the vaccines would have to be causing super fast-acting turbo cancer.
Uncle John Returns posted the images below and wrote: "Why should cancer registration rates among the unvaccinated approximately double in a year? Unless they were undercounted to begin with?" [https://x.com/UncleJo46902375/status/1972676088640757796]

His baseline incidence was the age-standardized incidence rate in 2022 from the website of the Korean National Cancer Center, which was about 522.7 cases per 100,000 person-years, so it's about 4.3 cases per 10,000 people per a 30-day period. [https://www.cancerdata.re.kr/surveillance/en/data?menuId=40]
I didn't find a crude incidence rate anywhere from the website, but in another source the crude incidence rate in 2022 was about 550.2 cases per 100,000 person-years, which is about 4.52 cases per 10,000 people per 30 days. [https://e-crt.org/journal/view.php?doi=10.4143/crt.2025.264]
Supplementary file 2 of the Korean study says that the study only included people aged 20 and above, but about 84.1% of the Korean population was aged 20 and above in the 2022 population estimates, so if you divide 4.52 with 0.841, you get a total incidence of about 5.4 for ages 20 and above. (I didn't exclude cases in children from the numerator, even though they shouldn't make much difference because children account for such a small part of the total incidence. The population included in the cancer study consisted of people from Seoul, but I didn't take into account that the age composition of Seoul might be different from the rest of Korea.)
The authors of the Korean study did propensity score matching to match vaccinated people to unvaccinated people 4-to-1, which ended up skewing the age distribution of the cohorts included in the study, because more than 80% of elderly people were vaccinated, so many vaccinated elderly people had to be discarded. The age distribution of the subjects before the PSM was not shown anywhere, but Table S2 shows the distribution after the PSM, which is compared here to the age distribution of the overall Korean population: [https://x.com/UncleJo46902375/status/1972945872452517945]

I found age-specific cancer incidence from here: https://www.data.go.kr/en/data/3039563/fileData.do. I didn't find annual resident population estimates by age, so as a quick hack, I took population estimates in the 2020 census from here: https://gsis.kwdi.re.kr/statHtml/statHtml.do?orgId=338&tblId=DT_1IN0503.
When I divided the number of new cases in ages 20+ in 2022 with the 2020 population estimate of ages 20+, I got about 5.6 cases per 10,000 people per 30 days:
t=fread("https://sars2.net/f/koreacancerincidence.csv")
names(t)=c("year","sex","icd","type","age","cases","rate")
s=t[icd=="00. All cancers"&age%like%"\\d"&year!="1999-2022"&sex==sex[1]]
s[,age:=as.integer(substr(age,1,2))]
a=s[,.(cases=sum(cases)),.(year=as.integer(year),age))]
pop=c(1684917,2238916,2252113,2422002,3193316,3423231,3032832,3594213,
3758298,4195327,4245683,4091920,3795217,2685773,2009542,1593192,
1115804,801197)
a[,pop:=pop[factor(age)]]
a[age>=20&year==2022,sum(cases)/sum(pop)/365*30*1e4]
# 5.553289
I didn't adjust the incidence for the skewed age distribution produced by the propensity score matching. And of course the PSM ended up skewing other characteristics of the matched cohorts, so that the matched cohorts were not necessarily representative of the overall population of Korea or Seoul.
The Korean study excluded non-melanoma skin cancer (C44), but the dataset for cancer incidence by age didn't have a separate category for C44. In some developed countries non-melanoma skin cancer accounts for about 25-50% of total cancer incidence, but in Korea the percentage appears to be lower.
Supplementary file 2 says that the ICD codes included in the study were "C00 - C96, except for C44". So the authors appear to have also excluded C97, which is "Malignant neoplasms of independent (primary) multiple sites", or perhaps C97 is not used as a diagnosis code in Korea.
At first I didn't understand why Table S2 showed that the subjects were not matched by income level: [https://static-content.springer.com/esm/art%3A10.1186%2Fs40364-025-00831-w/MediaObjects/40364_2025_831_MOESM1_ESM.docx]

But apparently the matching was done based on the insurance level, and the income level was estimated based on the insurance level. Supplementary file 2 says: "The following covariates were considered: age, sex, insurance levels, Charlson comorbidity index (CCI) scores, and prior COVID-19 infection (history of SARS-CoV-2 infection). Insurance levels (recipients of medical aid, grades 1-5, grades 6-10, grades 11-15, and grades 16-20) were defined based on the National Health Insurance premium, which was used as a proxy for income since it is proportional to monthly income and includes both earnings and capital gains." [https://static-content.springer.com/esm/art%3A10.1186%2Fs40364-025-00831-w/MediaObjects/40364_2025_831_MOESM2_ESM.docx]
But anyway, the cohorts were matched by so few variables that there likely remains major residual confounding for the level of health-seeking behavior.
I initially thought that the index dates of the unvaccinated people were determined so that they matched the index dates of the vaccinated people. But supplementary file 2 said that the index date of unvaccinated people was always set as January 1st 2022: "For the unvaccinated group, the index date was set as January 1, 2022; those who had a vaccination history within 1 year based on the index date and those who were deceased were excluded (n = 30,955). A total of 599,124 unvaccinated individuals were included. For the vaccinated group, the index date was set as the day after the vaccination completion date, and those with incomplete vaccination (n = 278,610), unspecified vaccine type (n = 77,674), deceased (n = 33,836), and a prior medical history of overall cancers within 1-year based on index date (n = 499,572) were excluded."
So the reason why unvaccinated people had low incidence during the first 3 months may have been if people avoided getting screening during COVID waves. The first two major COVID waves in Korea were the Delta wave which peaked around December 2021, and the Omicron wave which peaked around March 2022:

kim=\(x)ifelse(x>=1e3,ifelse(x>=1e6,paste0(x/1e6,"M"),paste0(x/1e3,"k")),x)
t=fread("https://srhdpeuwpubsa.blob.core.windows.net/whdh/COVID/WHO-COVID-19-global-data.csv")
p=t[Country_code=="KR"][,.(x=Date_reported,dead=New_deaths,case=New_cases)]
xstart=as.Date("2020-1-1");xend=as.Date("2024-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=0:6*5e5;ystart=0;yend=max(ybreak);ybreak2=ybreak/1e3
secmult=1e3
color=c("black",hsv(0,.5,1))
lab=p[,.(lab=c("Cases","Deaths"),x=c(xstart+50,xend-50),y=yend*.92)]
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_segment(data=CJ(x=seq(xstart,xend,"month")),aes(x,0,xend=x,yend=yend*.015),color="gray75",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,case),linewidth=.6)+
geom_line(aes(x,dead*secmult),color=color[2],linewidth=.6)+
geom_text(data=lab,aes(x,y,label=lab,hjust=0:1),color=color,size=3.87)+
labs(x=NULL,y=NULL,title="South Korea: Weekly COVID cases and deaths by date reported to WHO",subtitle="Source: data.who.int/dashboards/covid19/data")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=range(ybreak),labels=kim,breaks=ybreak,sec.axis=sec_axis(trans=~./secmult,breaks=ybreak2,labels=kim))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40"),
axis.text.y=element_text(margin=margin(,2,,2)),
axis.text.y.left=element_text(color=color[1]),
axis.text.y.right=element_text(color=color[2]),
axis.ticks.length=unit(0,"pt"),
legend.background=element_rect(color="gray70",linewidth=.4),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.justification=c(.5,.5),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(24,"pt"),
legend.margin=margin(3,5,3,3),
legend.position=c(.5,.5),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.background=element_blank(),
plot.subtitle=element_text(hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)))
ggsave("1.png",width=5.5,height=3.2,dpi=300*4)
I only found yearly cancer incidence data for 2022 but not monthly data, so I wasn't able verify if the cancer incidence was low in early 2022 relative to later in 2022.
But for example an article from April 2022 said in Korean: "As the spread of COVID-19 continues, there are many people who are procrastinating the check-up, so please do not delay and actively participate in the early check-up as there is a concern about congestion due to the year-end concentration." [https://blog.naver.com/hdnews9001/222715512561] The Korean cancer screening program targets people born on even years during even years and people born on odd years during odd years. People have until the end of the year to get screening, but it appears that due to COVID some people delayed getting screening until the end of the year.
The deadline for screening in 2021 was extended until June 2022 due to COVID. An article from January 2022 said in Korean: "2021 flew by in the blink of an eye! Many people may have postponed their national health screenings to adhere to quarantine guidelines and then forgot about them. In December 2021, the government announced, 'To ensure access to screenings for those who have postponed or refrained from using them to comply with COVID-19 guidelines, the health screening period will be extended.'" [https://blog.ibk.co.kr/2703]
In 2019-2021, there was a higher number of colonoscopies performed towards the end of the year than the beginning of the year. There was also a big drop in colonoscopies performed during the spring of 2020: [https://www.irjournal.org/journal/view.php?number=1091]

I now found that screening volume was higher than normal in 2021, but much lower than normal in 2022 for breast cancer: [https://www.cancerdata.re.kr/surveillance/en/data?menuId=38]

Ethical Skeptic retrieved the number of deaths with UCD COVID in 2025 by 10-year age groups, and since the median group was 75-84, he said that the median age at death was 79.5, which was the average of the minimum and maximum age within the age group: [https://x.com/EthicalSkeptic/status/1971310148619522151]

He could've calculated the exact median age if he used broad age groups for ages with suppressed deaths and single-year age groups for ages with no suppressed deaths.
When I did a query on September 30th 2025 UTC, there were a total of 10,470 deaths with UCD COVID in 2025. There were 10 or more deaths for each single year of age between 40 and 100+. Ages 0-39 had 141 deaths. The median age of death was 82:
d=data.table(age=c(0,40:100),dead=c(141,11,13,11,10,11,16,11,12,16,23,26,26, 28,21,49,48,40,45,59,56,78,75,77,84,124,126,160,145,151,156,165,203,245, 207,263,240,285,354,372,278,309,372,421,365,353,374,389,383,344,370,370, 291,285,267,228,195,164,165,123,87,154)) median(d[,rep(age,dead)]) # 82
The mean age was about 79.3 if you treat ages 0-39 as age 0, or about 79.9 if you treat ages 0-39 as age 39:
d[,weighted.mean(age,dead)] # 79.32808 d[,weighted.mean(ifelse(age==0,39,age),dead)] # 79.8533
The median age of COVID deaths seems to have gone up over time, because it was 72 in 2021, 77 in 2022, and 81 in 2023. The median age was particularly low in 2021, because in 2021 there were still many unvaccinated people who had not acquired natural immunity, and unvaccinated people are younger than vaccinated people:
v=fread("curl -Ls sars2.net/f/vital.csv.xz|xz -dc")
a=v[cause=="U071"&age!=999,.(dead=sum(ucd)),.(year,age)]
a=rbind(a,a[,.(dead=sum(dead),year="Total"),age])
a[,.(median=as.double(median(rep(age,dead))),mean=round(weighted.mean(age,dead),1)),year]
# year median mean
# 2020 78 76.1
# 2021 72 70.6
# 2022 77 75.0
# 2023 81 79.4
# Total 75 73.8
Ethical Skeptic's image says: "Current U.S. life expectancy for the average 80-year old = 78.4 years". I don't know if he made a typo, because the life expectancy at age 80 should be more than 80. In the 2023 US life table, the remaining life expectancy for age 80 is about 9.3 years. [https://ftp.cdc.gov/pub/Health_Statistics/NCHS/Publications/NVSR/74-06/Table01.xlsx]
When I took the number of deaths in 2023 from CDC WONDER and I took mid-year resident population estimates in 2023 from the vintage 2024 release by the Census Bureau, I also got a remaining life expectancy of about 9.3 years at age 80:
pop=fread("https://sars2.net/f/uspopdead.csv")[year==2023]
age=0:100;n=length(age)
mx=pop[,dead/pop] # cmr
qx=pmin(mx/(1+mx/2),1) # probability of dying (cmr adjusted for exposure time)
px=1-qx # probability of surviving
lx=cumprod(c(1e5,px[-n])) # survivors in a 100,000-person population
dx=lx*qx # deaths
Lx=lx-dx/2 # person-years lived
Tx=rev(cumsum(rev(Lx))) # cumulative person-years remaining
ex=Tx/lx # life expectancy
options(digits=2)
data.table(age,mx,qx,px,lx,dx,Lx,Tx,ex)[age==80]
# age mx qx px lx dx Lx Tx ex
# 80 0.048 0.047 0.95 57918 2694 56571 541332 9.3