Comments to Ethical Skeptic (part 2) - sars2.net

First published 2024-12-01 UTC, last modified 2026-02-25 UTC

Other parts: ethical.html, ethical3.html (deaths in ages 0-4), ethical4.html.

Contents

Is there still excess all-cause mortality in 2024?

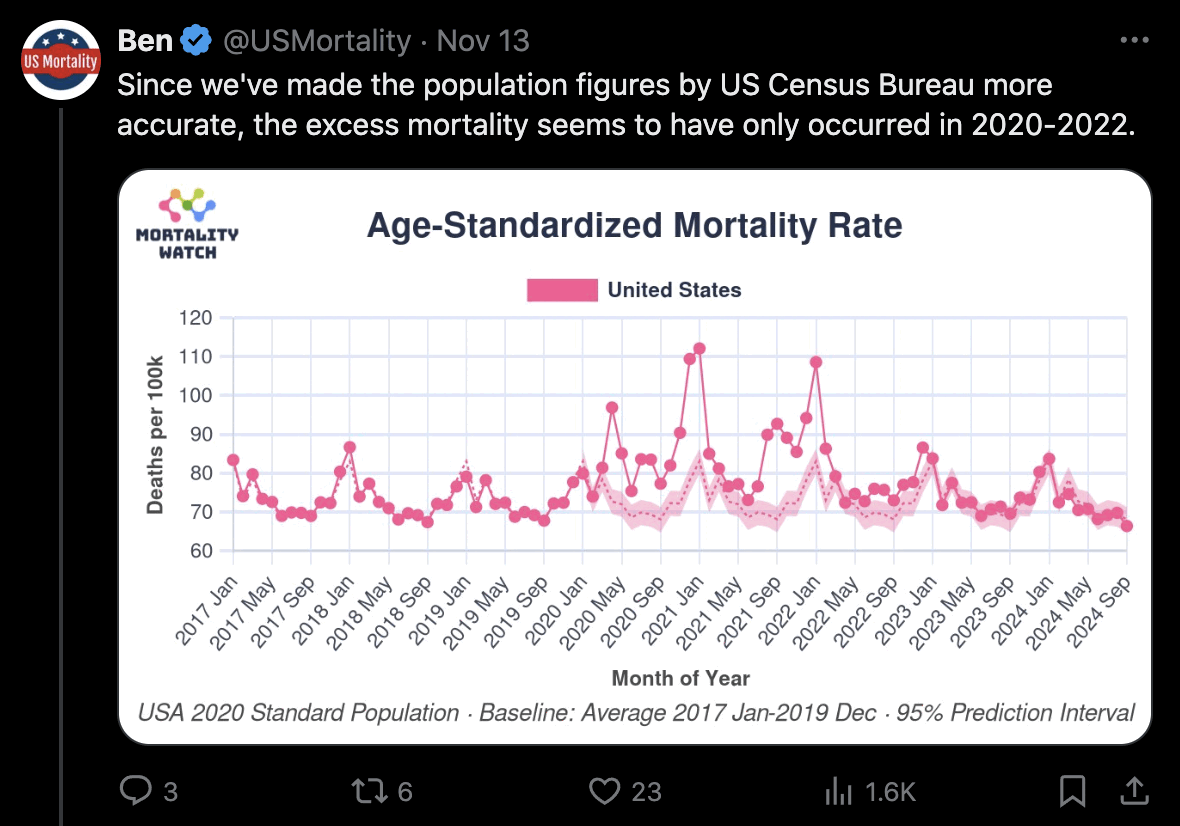
Jeffrey Morris posted this plot by Truth in Numbers where the ASMR in 2024 was below the 2018-2019 average baseline: [https://x.com/jsm2334/status/1859343221677068406]

Ethical Skeptic posted this tweet in response, where he got about 7.1% excess deaths in 2024: [https://x.com/EthicalSkeptic/status/1859361344975159394]

From practitioner experience:

1. Regression is applied to stable troughs, not all data points, which may include volatile isolated surges - otherwise it is Gaussian blindness paltering (using a dishonest baseline).

2. If 1.6 million EXCESS old persons die over a couple years, you must lower the anticipated death rate in subsequent years, or you are doing torfuscation (hiding the dead bodies).

Both are dishonest and/or incompetent.

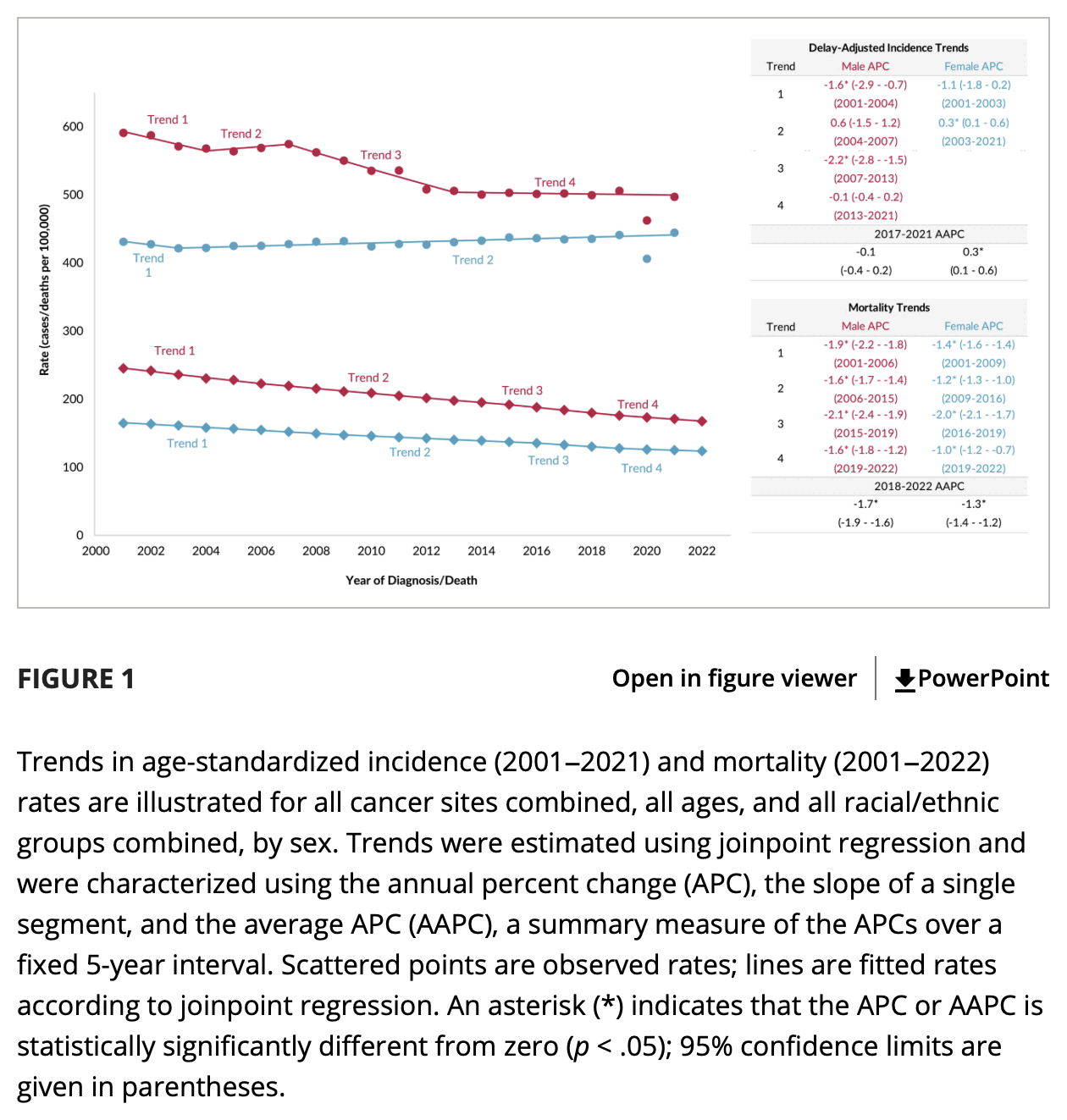
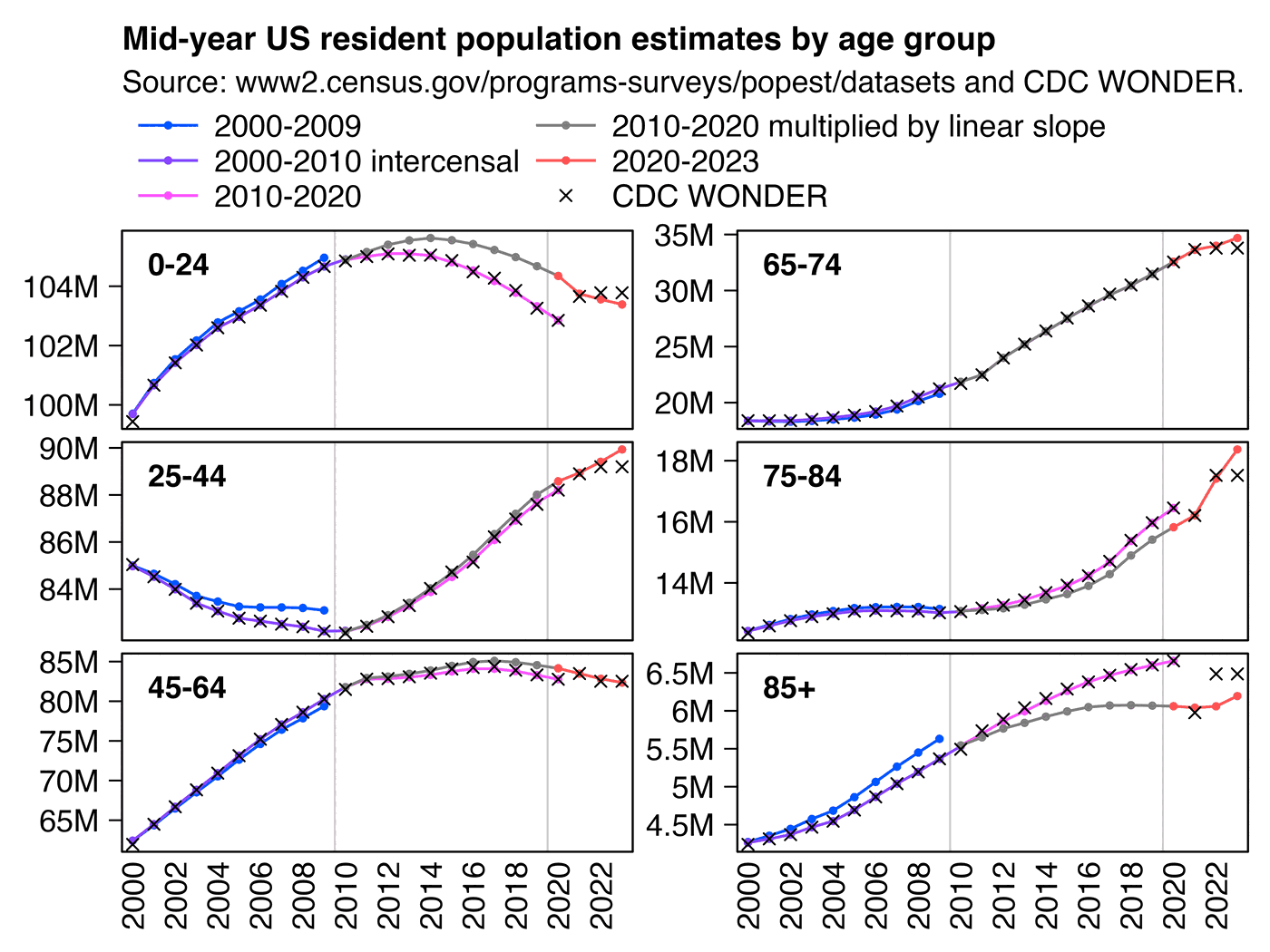
In the plot by Truth in Numbers, the average ASMR on weeks 40 of 2018 and 2019 was drawn as a baseline, but if he would've used a prepandemic linear regression as the baseline then he might have gotten positive excess ASMR in 2024. He used 2010-based population estimates up to 2020 and 2020-based population estimates from 2021 onwards, which exaggerated his ASMR in 2024 relative to 2018 and 2019, because the population sizes of the oldest age groups dropped dramatically between the 2010-based and 2020-based population estimates:

library(data.table);library(ggplot2)

agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)

kim=\(x)ifelse(x>=1e3,ifelse(x>=1e6,paste0(x/1e6,"M"),paste0(x/1e3,"k")),x)

new=fread("https://www2.census.gov/programs-surveys/popest/datasets/2020-2023/national/asrh/nc-est2023-agesex-res.csv")
old=fread("https://www2.census.gov/programs-surveys/popest/datasets/2010-2020/national/asrh/nc-est2020-agesex-res.csv")

old=old[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:4)]),year=rep(2010:2020,each=.N))]
new=new[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:3)]),year=rep(2020:2023,each=.N))]

older=fread("https://www2.census.gov/programs-surveys/popest/tables/2000-2010/intercensal/national/us-est00int-01.csv")
older=older[6:26,c(1,3:12,14)][,.(age=as.numeric(sub("\\D*(\\d+).*","\\1",sub("Under 5",0,V1))),pop=as.numeric(gsub(",","",unlist(.SD[,-1]))),year=rep(2000:2010,each=.N))]

oldest=fread("https://www2.census.gov/programs-surveys/popest/tables/2000-2009/national/asrh/nc-est2009-01.csv")
oldest=oldest[6:26,c(1,2:11)][,.(age=as.numeric(sub("\\D*(\\d+).*","\\1",sub("Under 5",0,V1))),pop=as.numeric(gsub(",","",unlist(.SD[,-1]))),year=rep(2009:2000,each=.N))]

mult=merge(old[year==2020],new[year==2020,.(age,new=pop)])[,.(ratio=new/pop,age)]
mult=merge(old,mult)[,mult:=(year-2010)/10]
mult=mult[,.(age,year,pop=((1-mult)*1+mult*ratio)*pop)]

won=fread("http://sars2.net/f/wondercanceryearlysingle.csv")[age<85,.(year,pop,age)]
won=rbind(won,fread("http://sars2.net/f/wondercanceryearlyten.csv")[cause==cause[1]&age==85,.(year,pop,age)])

p=cbind(oldest,z="2000-2009")
p=rbind(p,cbind(older,z="2000-2010 intercensal"))
p=rbind(p,cbind(old,z="2010-2020"))
p=rbind(p,cbind(mult,z="2010-2020 multiplied by linear slope"))
p=rbind(p,cbind(new,z="2020-2023"))
p=rbind(p,cbind(won,z="CDC WONDER"))

p[,z:=factor(z,unique(z))]

ages=0:4*20
ages=c(0,25,45,65,75,85)

p=p[,.(pop=sum(pop)),.(z,year,age=agecut(age,ages))]

xstart=2000;xend=2023
p=p[year%in%xstart:xend]

ggplot(p,aes(x=year,y=pop))+
coord_cartesian(clip="off")+
facet_wrap(~age,ncol=2,dir="v",scales="free_y")+
geom_vline(xintercept=c(2009.5,2019.5),color="gray80",linewidth=.23)+
geom_line(aes(color=z,alpha=z),linewidth=.3)+
geom_point(aes(color=z,shape=z,size=z),stroke=.3)+
geom_text(fontface=2,data=p[,max(pop),age],aes(label=paste0("\n   ",age,"   \n"),y=V1),x=xstart-.5,lineheight=.4,hjust=0,vjust=1,size=grid::convertUnit(unit(7,"pt"),"mm"))+
labs(title="Mid-year US resident population estimates by age group",subtitle="Source: www2.census.gov/programs-surveys/popest/datasets and CDC WONDER.",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart-.5,xend+.5,.5),labels=c(rbind("",ifelse(xstart:xend%%2==0,xstart:xend,"")),""),expand=expansion(0))+
scale_y_continuous(labels=kim,breaks=\(x)Filter(\(y)y>min(x)+(max(x)-min(x))*.05,pretty(x,4)),expand=expansion(.04))+
scale_color_manual(values=c("#0055ff","#8844ff","#ff55ff","gray50","#ff5555","black"))+
scale_shape_manual(values=c(16,16,16,16,16,4))+
scale_alpha_manual(values=c(1,1,1,1,1,0))+
scale_size_manual(values=c(.7,.7,.7,.7,.7,1))+
guides(color=guide_legend(ncol=2,byrow=F))+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.2,color="black"),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.justification="left",
  legend.key=element_blank(),
  legend.key.height=unit(8,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.margin=margin(-2,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(1,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.23),
  panel.spacing.x=unit(3,"pt"),
  panel.spacing.y=unit(3,"pt"),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=6.9,margin=margin(,,4)),
  plot.title=element_text(size=7.4,face=2,margin=margin(1,,3)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4,height=3,dpi=350*4)
system("magick 1.png -resize 25% 1.png")

In the next plot I adjusted the 2010-2020 population estimates using the same method as in the gray lines in my plot above. It reduced my total excess ASMR in 2024 from about 2.6% to about -3.0%. (The plot was updated in July 2025 to use new resident population estimates instead of population projections for 2024.)

u="https://www2.census.gov/programs-surveys/popest/datasets/"
t1=do.call(rbind,lapply(sprintf("%s2010-2020/national/asrh/NC-EST2020-ALLDATA-R-File%02d.csv",u,1:24),fread))
t2=do.call(rbind,lapply(sprintf("%s2020-2024/national/asrh/nc-est2024-alldata-r-file%02d.csv",u,1:12),fread))

old=t1[YEAR!=2021&MONTH!=4.2&AGE!=999,.(year=YEAR,month=floor(MONTH),age=AGE,pop=TOT_POP)]
new=t2[AGE!=999,.(year=YEAR,month=floor(MONTH),age=AGE,pop=TOT_POP)]

mult=new[year==2020&month==4,pop]/old[year==2020&month==4,pop]
old=old[!(year==2020&month>=4)]
old2=copy(old)[,pop:={x=rleid(year,month);x=(x-1)/max(x);round(pop*(x*mult[age+1]+1-x))}]

a=rbind(rbind(old,new)[,group:=1],rbind(old2,new)[,group:=2])

a=merge(a,fread("https://sars2.net/f/usdeadmonthly.csv"))[!(year==2025&month>5)]

a=merge(new[year==2020&month==7,.(age,std=pop/sum(pop))],a)

a[,group:=factor(group,,c("Original unmodified population estimates","Population estimates based on 2010 census multiplied by linear slope (DIY intercensal)"))]
a[,date:=as.Date(paste(year,month,1,sep="-"))]
a[,pop:=pop*lubridate::days_in_month(date)]

p=a[,.(asmr=sum(dead/pop*std*365e5)),.(date,group)]

p=merge(p[year(date)%in%2011:2019&month(date)%in%4:10,.(date=unique(p$date),base=predict(lm(asmr~date),.(date=unique(p$date)))),group],p)
p[,month:=month(date)]
p=merge(p[year(date)%in%2011:2019,.(monthly=mean(asmr-base)),month],p)

yearly=a[,.(pop=sum(pop),dead=sum(dead)),.(age,std,group,year=year(date))]
yearly=yearly[,.(asmr=sum(dead/pop*std*365e5)),.(year,group)]
yearly=merge(yearly[year%in%2011:2019,.(year=2011:2024,base=predict(lm(asmr~year),.(year=2011:2024))),group],yearly)

lab=c("Actual ASMR","2011-2019 linear baseline","Baseline adjusted for seasonality","Difference from seasonality-adjusted baseline")
p=p[,.(x=date,y=c(asmr,base,base+monthly,asmr-base-monthly),z=factor(rep(lab,each=.N),lab),group)]

pct=yearly[,.(pct=(sum(asmr)/sum(base)-1)*100),.(year,group)][,x:=as.Date(paste0(year,"-7-1"))]
pct=merge(p[,.(y=min(y)),group],pct)

xstart=as.Date("2017-1-1");xend=as.Date("2026-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")

ggplot(p,aes(x=x+14,y))+
facet_wrap(~group,ncol=1,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray85",linewidth=.25)+
geom_vline(xintercept=as.Date("2020-1-1"),linetype="44",linewidth=.3)+
geom_line(data=p[z!=lab[4]],aes(linetype=z,color=z),linewidth=.3)+
geom_line(data=p[z==z[1]],aes(linetype=z,color=z),linewidth=.3)+
geom_point(aes(alpha=z),stroke=0,size=.6)+
geom_rect(data=p[z==lab[4]],aes(xmin=x,xmax=x%m+%months(1),ymin=pmin(0,y),ymax=pmax(0,y),fill=z),linewidth=.1,color="gray40")+
geom_text(data=pct,aes(x,y=y,label=paste0(ifelse(pct>0,"+",""),sprintf("%.1f",pct),"%")),vjust=.8,size=2.4)+
labs(title="Age-standardized mortality rate per 100,000 person-years in United States",x=NULL,y=NULL)+
scale_x_continuous(expand=c(0,0),limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(expand=c(.06,0,.03,0),breaks=\(x)pretty(x,6))+
scale_color_manual(values=c("black","gray60","gray60","gray40"))+
scale_fill_manual(values=rep("gray60",4))+
scale_linetype_manual(values=c("solid","42","solid","solid"))+
scale_alpha_manual(values=c(1,0,0,0),guide="none")+
guides(fill=guide_legend(order=3,keyheight=unit(1,"pt")),color=guide_legend(order=1),linetype=guide_legend(order=1))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.y=element_text(margin=margin(,1.5)),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.ticks=element_line(linewidth=.3,color="black"),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.key=element_blank(),
  legend.key.height=unit(9,"pt"),
  legend.key.width=unit(19,"pt"),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.box.margin=margin(),
  legend.spacing.y=unit(0,"pt"),
  legend.margin=margin(,,2),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  legend.direction="vertical",
  legend.box="horizontal",
  legend.box.spacing=unit(0,"pt"),
  legend.spacing=unit(0,"pt"),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3),
  panel.spacing.y=unit(2,"pt"),
  plot.margin=margin(4,4,2,4),
  plot.title=element_text(size=7.4,hjust=.5,face=2,margin=margin(1,,3)),
  strip.background=element_blank(),
  strip.text=element_text(size=7,face=2,margin=margin(,,2)))
ggsave("1.png",width=4.7,height=3.9,dpi=400*4)

sub="\u00a0     The yearly total excess mortality percentage is shown above the year.
      The data for deaths was retrieved from CDC WONDER in July 2025 UTC.
      ASMR was calculated by single year of age so that the vintage 2024 resident population estimates for July 2020 were used as the standard population.
      The baseline was calculated by doing a linear regression for monthly data in 2011 to 2019. Only April to October were included in the linear regression. In order to calculate the seasonality-adjusted baseline, the average difference between the actual ASMR and baseline during each January of 2011 to 2019 was added to the baseline for each January, and similarly for other months.
      Monthly resident population estimates by single year of age were downloaded from www2.census.
gov/programs-surveys/popest/datasets/2020-2024/national/asrh/nc-est2024-alldata-r-file{01..12}.csv, and from the corresponding files in the 2010-2020 directory.
      Vintage 2024 population estimates based on the 2020 census are used for April 2020 to December 2024, and vintage 2020 population estimates based on the 2010 census are used for January 2011 to March 2020. In the bottom panel the 2010-based estimates were multiplied by a linear slope so that they were equal to the 2020-based estimates in April 2020 when the two sets of estimates were merged. The 2010-based estimates cover a total of 121 months from April 2010 until April 2020, and for example for the age 80 the ratio between the 2020-based and 2010-based estimates was about 0.946 in April 2020, so the population estimate for age 80 was multiplied by about 1/121*0.946+120/121 in May 2010, by about 2/121*0.946+119/121 in June 2010, and so on. A similar adjustment is incorporated in the Census Bureau's intercensal population estimates, but the intercensal estimates for 2010-2020 are only scheduled to be published in 2025."

system(paste0("mar=120;w=`identify -format %w 1.png`;magick 1.png \\( -size $[w-mar*2]x -font Arial -interline-spacing -4 -pointsize 152 caption:'",gsub("'","'\\\\''",sub),"' -gravity southwest -splice $[mar]x70 \\) -append -resize 25% -colorspace gray -colors 16 1.png"))

Ethical Skeptic would probably complain that in the plot above I didn't adjust my baseline for PFE. But I used ASMR which accounts for the reduction in population size due to COVID deaths. And Ethical Skeptic should not only adjust his baseline downwards to account for mortality displacement, but he should also adjust his baseline upwards to account for the changing age structure of the population. Ethical Skeptic seems to apply some kind of subjective judgment to determine the shape and magnitude of his so-called PFE arrival function, and I believe he hasn't published any code or methodology that would allow other people to reproduce his PFE-adjusted baseline exactly. But in contrast ASMR is easy to calculate objectively in a way that different authors end up getting identical results.

USMortality implemented the same method I used above to adjust the 2010-based population estimates at Mortality Watch, after which he now also gets negative excess mortality for the United States in 2024: [https://x.com/USMortality/status/1856489943519920218]

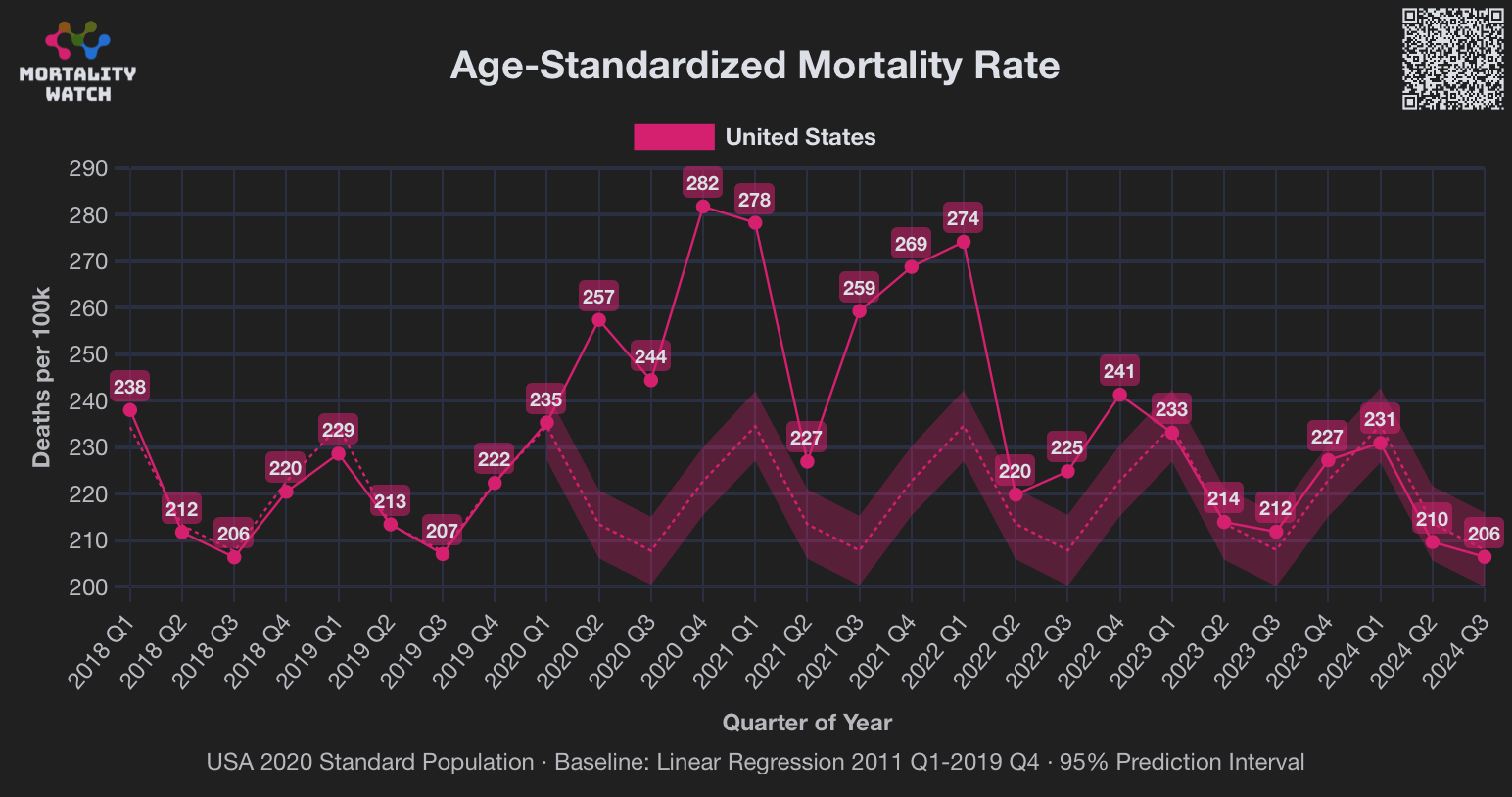
In the plot above USMortality used a 2017-2019 average baseline, but even when I changed the baseline to a 2011-2019 linear regression, I still got negative excess ASMR during each of the first three quarters of 2024: [https://www.mortality.watch/explorer/?c=USA&ct=quarterly&df=2018%2520Q1&bf=2011%2520Q1&bm=lin_reg]

Should the PFE adjustment last for only 6.6 years?

Ethical Skeptic wrote: "The function we currently use for PFE is described by 6.6 years (345 weeks - April 2021 - Oct 2027) of Chi-squared arrival, with an anticipated x_mode (function peak) of mid-late 2023 at 6.02% of Excess Non-Covid Natural Cause Mortality." [https://theethicalskeptic.com/2024/11/20/the-state-of-things-pandemic/] And he linked this image:

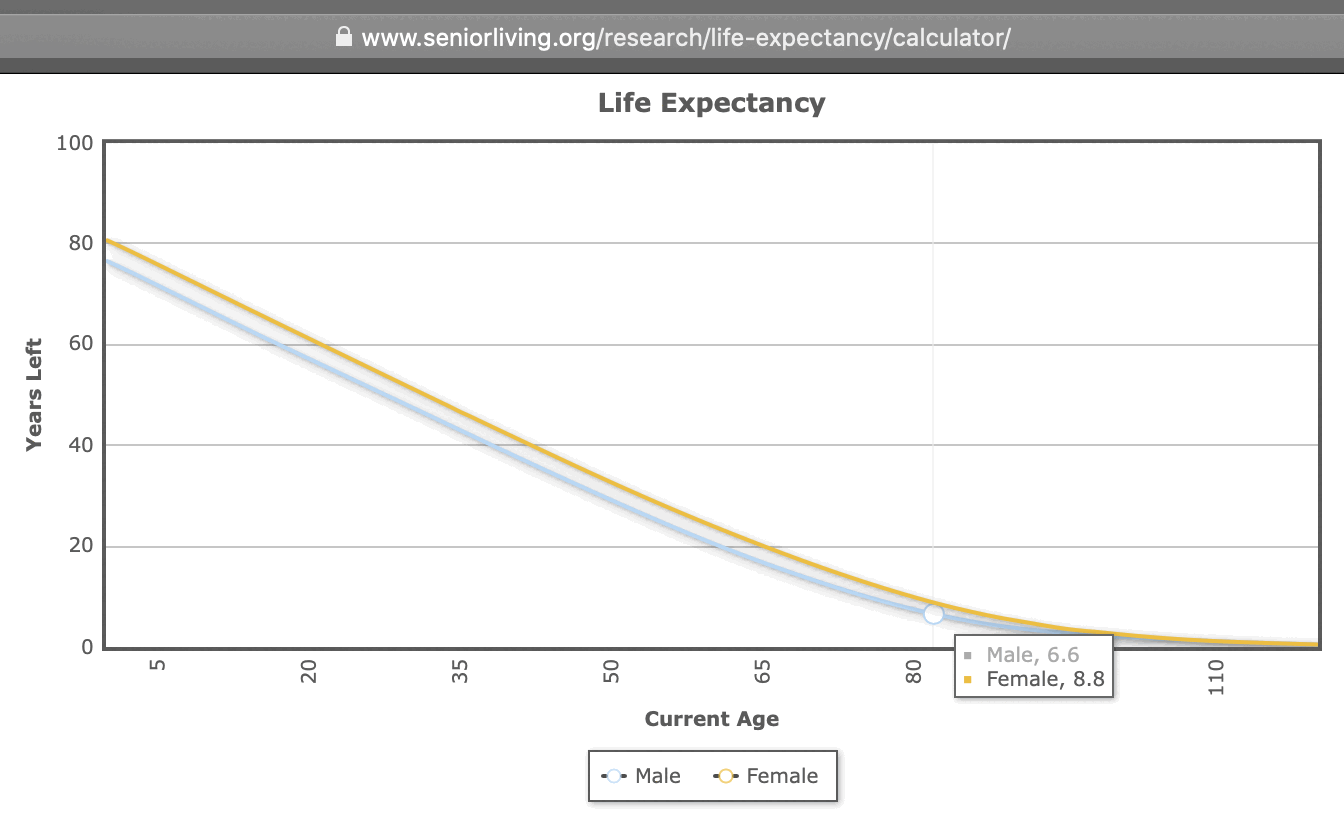
Ethical Skeptic came up with the figure of 6.6 years because he said the average age of COVID deaths in Florida was 82, and he got a life expectancy of 6.6 years for age 82: [https://theethicalskeptic.com/2024/11/20/the-state-of-things-pandemic/]

He got the life expectancy of 6.6 years based on the life expectancy for males listed at seniorliving.com (even though the life expectancy for females of age 82 was listed as 8.8 on the same website so I don't know why he didn't even take the average value of both sexes, and in the 2019 US life table the life expectancy for both sexes combined is about 8.2 years at age 82): [https://www.seniorliving.org/research/life-expectancy/calculator/]

At CDC WONDER the average age of UCD COVID deaths was 73.8 in Florida and about 73.9 in the whole US. And in the 2019 life table the life expectancy for age 74 is about 13.1 years, so it's about twice as high as Ethical Skeptic's figure of 6.6 years. And when I calculated the average of life expectancies for each age weighted by the number of COVID deaths for each age, it was about 14.5 years:

# life expectancy for both sexes combined from 2019 life table
u="https://ftp.cdc.gov/pub/Health_Statistics/NCHS/Publications/NVSR/70-19/Table01.xlsx"
download.file(u,"Table01.xlsx")
ex=read_excel("Table01.xlsx",skip=2,n_max=101)$ex

# UCD COVID deaths by single year of age from CDC WONDER (last value is ages 100+)
coviddead=c(363,116,46,41,39,30,38,32,33,47,40,35,41,56,51,97,88,130,162,210,255,
  288,367,407,499,530,620,707,819,979,1112,1255,1329,1441,1607,1703,1850,2066,2237,
  2502,2713,2987,3253,3486,3942,4197,4610,4912,5686,6278,7075,7365,8017,8227,8942,
  9822,11084,11748,12866,14070,15174,16061,17259,18347,19229,20037,20443,20874,22012,
  22623,23586,24446,25783,27417,27760,26024,26237,27531,28188,27690,27437,27093,
  27200,27223,26753,26849,26190,25121,24827,24104,22756,21336,19309,17787,15069,
  12656,10416,8337,6321,4626,8773)

weighted.mean(ex,coviddead) # 14.50457

The following code shows the average life expectancy by month of death for deaths with UCD COVID. I now calculated the life expectancy separately for males and females even though it didn't make much difference. CDC WONDER suppresses the number of deaths on rows with less than 10 deaths, so I got the number of COVID deaths from the fixed-width files for the NVSS data instead: stat.html#Download_fixed_width_and_CSV_files_for_the_NVSS_data_used_at_CDC_WONDER. The life expectancy was unsurprisingly much higher in 2021 than 2020 (which is because the percentage of COVID deaths in 2021 relative to 2020 is much higher in working-age people than in elderly people, which might be because in 2021 working-age people were less likely to be vaccinated than elderly people):

dlf=\(x,y=sub(".*/","",x),...)for(i in 1:length(x))download.file(x[i],y[i],quiet=T,...)
dlf(paste0("https://ftp.cdc.gov/pub/Health_Statistics/NCHS/Publications/NVSR/70-19/Table0",2:3,".xlsx"))

ex=data.table(age=0:100,sex=rep(c("M","F"),each=101))
ex$ex=c(sapply(2:3,\(i)read_excel(paste0("Table0",i,".xlsx"),skip=2,n_max=101)$ex))

t=do.call(rbind,lapply(2020:2022,\(x)fread(paste0(x,".csv.gz"))))
a=t[restatus!=4&age!=9999&ucod=="U071",.N,.(year,month=monthdth,sex,age=pmin(100,ifelse(age<2000,age-1000,0)))]

merge(ex,a)[,weighted.mean(ex,N),.(year,month)][,xtabs(round(V1)~year+month)]
#       month
# year    1  2  3  4  5  6  7  8  9 10 11 12
#   2020 18 19 15 13 12 14 15 14 13 12 12 12
#   2021 13 14 15 17 18 18 19 19 19 18 17 17
#   2022 15 14 14 14 12 12 12 12 11 11 11 11

In the next plot I simulated two scenarios, where in both scenarios the population started out as one tenth of the mid-2018 US resident population estimates. In both scenarios I calculated the monthly mortality rates for each age by doing a projection of the linear trend in the mortality rate in 2011-2019, except in the red scenario I emulated the pattern of COVID deaths in 2020-2021 by multiplying the mortality rate for each combination of age and month by the ratio between the actual and seasonality-adjusted projection of the mortality rate for the same combination of age and month. I didn't emulate seasonality to make the difference between the two scenarios easier to see. But the COVID scenario got only about 1.5% less deaths in 2023-2024 than the scenario without the COVID event:

library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/uspopdeadmonthly.csv")[year%in%2011:2024]
t[,date:=as.integer(factor(date))-84][,cmr:=dead/persondays]
t=merge(t,t[year<2020,.(date=unique(t$date),base=predict(lm(cmr~date),.(date=unique(t$date)))),age])
t=merge(t[year<2020,.(monthly=mean(cmr/base)),.(month,age)],t)
rate=t[date>0,.(base=base*365/12,mult=ifelse(date%in%25:48,cmr/(base*monthly),1)),,.(date,age)]

set.seed(0)
pop=fread("http://sars2.net/f/uspopdead.csv")[year==2020]
people=pop[age>0,rep(age,pop/10)];people=people2=people+runif(length(people))
sim=data.table(month=1:84,dead=0,dead2=0)

set.seed(0)
for(i in 1:nrow(sim)){
  died=runif(length(people))<rate[date==i,base*mult][people]
  people=pmin(100,people[!died]+1/12)
  sim$dead[i]=sum(died)
  print(i)
}

set.seed(0)
for(i in 1:nrow(sim)){
  died=runif(length(people2))<rate[date==i,base][people2]
  people2=pmin(100,people2[!died]+1/12)
  sim$dead2[i]=sum(died)
  print(i)
}

sim$base=sim[month<25,predict(lm(dead~month),sim)]
lab=c("With elevated mortality in 2020-2021","No elevated mortality in 2020-2021","2018-2019 linear trend")
p=melt(sim,id=1)[,.(x=month,y=value,z=`levels<-`(variable,lab))]

sum=sim[month%in%25:48,colSums(.SD)];sum2=sim[month>48,colSums(.SD)]
note=stringr::str_wrap(sprintf("The scenario with elevated mortality in 2020-2021 has %.1f%% more deaths in 2020-2021 and %.1f%% less deaths in 2022-2024.",(sum[2]/sum[3]-1)*100,(sum2[3]/sum2[2]-1)*100),32)

xstart=1;xend=nrow(sim)+1;xbreak=seq(xstart,xend,6);xlab=c(rbind("",2018:2024),"")
ybreak=pretty(c(0,p$y),8);ystart=0;yend=max(p$y)+.02

ggplot(p,aes(x+.5,y))+
geom_vline(xintercept=seq(xstart,xend,12),linewidth=.3,color="gray83",lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.3,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.3,lineend="square")+
geom_line(aes(color=z,linetype=z),linewidth=.35)+
geom_point(aes(color=z,alpha=z),stroke=0,size=.7)+
labs(title="Simulation for deaths per month in one tenth of US population",x=NULL,y=NULL)+
annotate(geom="label",x=42,y=yend*.48,label=note,hjust=0,label.r=unit(2,"pt"),label.padding=unit(3,"pt"),label.size=.2,size=2.4,lineheight=.9)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#ff6666","black","gray60"))+
scale_alpha_manual(values=c(1,1,0))+
scale_linetype_manual(values=c("solid","solid","42"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks=element_line(linewidth=.3),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(0,0),
  legend.key=element_blank(),
  legend.key.height=unit(9,"pt"),
  legend.key.width=unit(20,"pt"),
  legend.background=element_rect(color="black",linewidth=.3),
  legend.margin=margin(3,3,3,3),
  legend.position=c(0,0),
  legend.spacing.x=unit(1.5,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=7),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(4,4,2,4),
  plot.title=element_text(size=7.5,face="bold",margin=margin(1,,3)))
ggsave("1.png",width=3.7,height=2,dpi=380*4)
sub=paste0("The initial population for each age was one tenth of the mid-2018 US resident population estimates except infants of age zero were excluded, so the total initial population size was about 32 million people. The projection of a linear trend for CMR in 2011-2019 was used for each age throughout the simulation, except in the red scenario the mortality rate for each combination of month and age in 2020-2021 was multiplied by the ratio between the actual CMR for the age during the month and a seasonality-adjusted trend for CMR during the same month.")
sub=paste0(sub," The length of each month is 1/12 years. Births are not simulated. Seasonal variation in mortality or differences in the health of people were not simulated. The same seed was used for both scenarios so the scenarios are identical in 2018 and 2019.")
system(paste0("mar=120;w=`identify -format %w 1.png`;magick 1.png \\( -size $[w-mar*2]x -font Arial -interline-spacing -4 -pointsize 146 caption:'",gsub("'","'\\'",sub),"' -gravity southwest -splice $[mar]x70 \\) -append -resize 25% -colors 256 1.png"))

In the red scenario in the plot above, the number of deaths in 2024 was about 0.2% higher than the gray 2018-2019 baseline in 2024. In many of his plots Ethical Skeptic fits his baseline against deaths from 2018 and 2019 only, but the long-term trend in the raw number of deaths is curved upwards due to the aging population, so in addition to adjusting his baseline downwards to account for the PFE, he should also adjust the baseline upwards to account for the change to the age structure. But by 2024 the two adjustments should roughly cancel each other out based on my simulation above (even though Ethical Skeptic assumes that people with poor health relative to their age have been overrepresented among the people who have died in excess since 2020, which might justify an additional downwards shift of the baseline that was not considered in my simulation).

PFE arrival function determined from monthly deaths by age

In the next plot I calculated a PFE adjustment factor based on the number of UCD COVID deaths in 2020-2022. I got the number of deaths with UCD COVID by age and month from the fixed-width files for the NVSS data to avoid the suppression of deaths at CDC WONDER: stat.html#Download_fixed_width_and_CSV_files_for_the_NVSS_data_used_at_CDC_WONDER.

I converted the age in years at the time of death to an age in months by multiplying the age by 12 and adding 6. For the sake of simplicity each month had a duration of one twelfth of a year. I converted the yearly crude mortality rate for each age in 2019 to a risk of dying per month with the formula 1-(1-cmr)^(1/12). I extrapolated mortality risk for ages 100 to 120 on a log scale from the mortality risk for ages 90 to 99. Each month I determined the number of people who died by multiplying the number of people for each age in months with the mortality risk for the age in months. I also calculated a baseline model of how many people would've died each month in a population which started out as the mid-2019 resident population estimates for each age. And then I calculated the PFE adjustment percent as -monthly_deaths/baseline_deaths*100.

I also applied a similar model to all-cause excess deaths relative to a seasonality-adjusted linear baseline for each age in 2011-2019.

The maximum reduction to the baseline was only about 1.8% based on COVID deaths and about 2.2% based on all-cause deaths, so both were around one third of 6.02% which is the maximum reduction in a PFE adjustment curve that Ethical Skeptic posted on his blog:

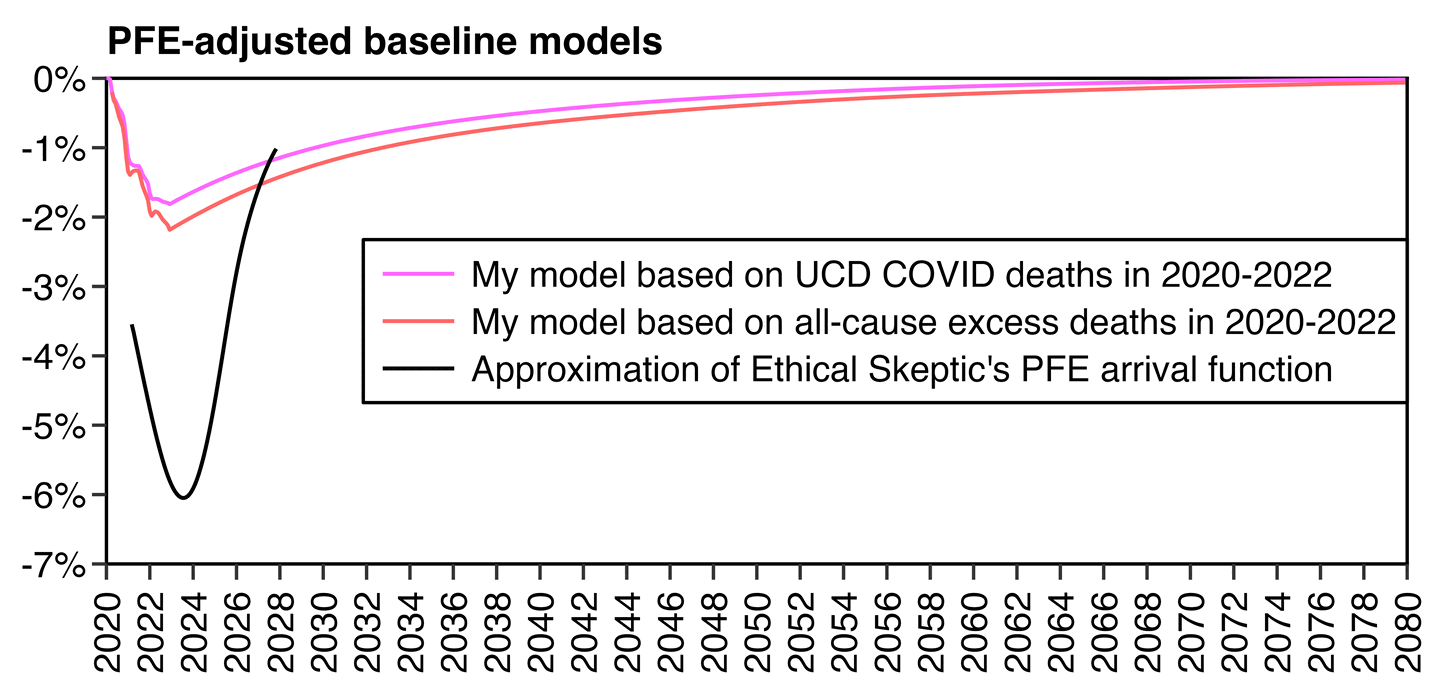
library(data.table);library(ggplot2)

months=12*60;minage=0;maxage=Inf

covid=do.call(rbind,lapply(2020:2022,\(i)fread(paste0(i,".csv.gz"))[ucod=="U071"&restatus!=4,.(age,month=(year-2020)*12+monthdth)]))
covid=covid[age!=9999][,age:=ifelse(age<2000,age%%1000,0)][age>=minage&age<=maxage,.(pop=.N),.(month,age=age*12+6)]

pop=fread("http://sars2.net/f/uspopdead.csv")[year==2019]
risk=pop[age<100,.(age,risk=1-(1-dead/pop)^(1/12))]
risk=c(risk$risk,risk[age>=90,exp(predict(lm(log(risk)~age),.(age=100:120)))])
risk=spline(seq(6,,12,121),risk,xout=0:(121*12-1))$y

all=fread("http://sars2.net/f/uspopdeadmonthly.csv")[year%in%2011:2022]
all[,date:=(year-2020)*12+month][,cmr:=dead/persondays]
all=merge(all,all[year<2020,.(date=unique(all$date),base=predict(lm(cmr~date),.(date=unique(all$date)))),age])
all=merge(all[year<2020,.(monthly=mean(cmr/base)),.(month,age)],all)
allcause=all[age>=minage&age<=maxage&date%in%1:36,.(pop=sum(dead)-sum(base*persondays*monthly)),,.(age=age*12+6,month=date)]

dead0=double();cur=pop[age>=minage&age<=maxage,.(age=age*12+6,pop,month=1)]
for(i in 1:months){
  died=cur[,risk[pmin(age+1,length(risk))]*pop]
  dead0[i]=sum(died)
  cur=cur[,.(month=i+1,age=age+1,pop=pop-died)][,.(pop=sum(pop)),.(month,age)]
}

dead1=double();prev=NULL
for(i in 1:months){
  cur=rbind(prev,covid[month==i])[,.(pop=sum(pop)),.(month,age)]
  died=cur[,risk[pmin(age+1,length(risk))]*pop]
  dead1[i]=sum(died)
  prev=cur[,.(month=i+1,age=age+1,pop=pop-died)]
}

dead2=double();prev=NULL
for(i in 1:months){
  cur=rbind(prev,allcause[month==i])[,.(pop=sum(pop)),.(month,age)]
  died=cur[,risk[pmin(age+1,length(risk))]*pop]
  dead2[i]=sum(died)
  prev=cur[,.(month=i+1,age=age+1,pop=pop-died)]
}

pfe=c(-3.5,-4.9,-5.9,-5.9,-4.7,-2.9,-1.7,-1)
pfe=spline(seq(1,351,50),pfe,xout=seq(1,351,1/7))
pfe=setDT(pfe)[,.(y=mean(y)),.(x=(x*7)%/%(365.25/12)+15)]

lab="My model based on UCD COVID deaths in 2020-2022"
lab=c(lab,"My model based on all-cause excess deaths in 2020-2022")
lab=c(lab,"Approximation of Ethical Skeptic's PFE arrival function")

p=data.table(x=1:months,y=-c(dead1,dead2)/dead0*100)
p[,z:=factor(rep(lab[1:2],each=.N/2),lab[1:2])]
p=rbind(p,pfe[,z:=lab[3]])

xstart=1;xend=months+1;xbreak=seq(xstart,xend,12*2);xlab=seq(2020,,2,length(xbreak))
ystart=floor(min(p$y));yend=0;ybreak=ystart:yend

ggplot(p,aes(x,y))+
geom_hline(yintercept=c(ystart,yend),linewidth=.3,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.3,lineend="square")+
geom_line(aes(color=z),linewidth=.35)+
labs(title="PFE-adjusted baseline models",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x,"%"))+
coord_cartesian(ylim=c(ystart,yend),clip="off",expand=F)+
scale_color_manual(values=c("#ff66ff","#ff6666","black"))+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.text.y=element_text(margin=margin(,1)),
  axis.ticks=element_line(linewidth=.3),
  axis.ticks.length.x=unit(3,"pt"),
  legend.direction="vertical",
  legend.justification=c(1,.5),
  legend.key=element_blank(),
  legend.key.height=unit(9,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.background=element_rect(color="black",linewidth=.3),
  legend.margin=margin(2,2,2,2),
  legend.position=c(1,.5),
  legend.spacing.x=unit(1.5,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=6.8),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(4,7,2,4),
  plot.title=element_text(size=7.3,face="bold",margin=margin(1,,3)))
ggsave("1.png",width=3.8,height=1.8,dpi=380*4)
system("magick 1.png -resize 25% -colors 256 1.png")

Here's a simplified version of my code that only calculates the red model that is based on all-cause deaths:

# monthly mortality risk by age in months for ages 0 to 120 (age 0 to 121*12-1 months)
# risk for ages 100-120 is extrapolated on a log scale from risk for ages 90-99
pop=fread("http://sars2.net/f/uspopdead.csv")[year==2019]
risk=pop[age<100,.(age,risk=1-(1-dead/pop)^(1/12))]
risk=c(risk$risk,risk[age>=90,exp(predict(lm(log(risk)~age),.(age=100:120)))])
risk=spline(seq(6,,12,121),risk,xout=0:(121*12-1))$y

# excess number of all-cause deaths by age and month in 2020-2022
# a seasonality-adjusted linear baseline for CMR in 2011-2019 is used for each age
# date 1 is January 2020 and date 36 is December 2022
all=fread("http://sars2.net/f/uspopdeadmonthly.csv")[year%in%2011:2022]
all[,date:=(year-2020)*12+month][,cmr:=dead/persondays]
dates=unique(all$date)
all=merge(all,all[year<2020,.(date=dates,base=predict(lm(cmr~date),.(date=dates))),age])
all=merge(all[year<2020,.(monthly=mean(cmr/base)),.(month,age)],all)
allcause=all[date%in%1:36,.(pop=sum(dead)-sum(base*persondays*monthly)),.(age,month=date)]

# baseline model
months=12*60
dead0=double();cur=pop[,.(age=age*12+6,pop,month=1)]
for(i in 1:months){
  died=cur[,risk[pmin(age+1,length(risk))]*pop]
  dead0[i]=sum(died)
  cur=cur[,.(month=i+1,age=age+1,pop=pop-died)][,.(pop=sum(pop)),.(month,age)]
}

# model based on all-cause excess deaths
dead2=double();prev=NULL
for(i in 1:months){
  cur=rbind(prev,allcause[month==i])[,.(pop=sum(pop)),.(month,age)]
  died=cur[,risk[pmin(age+1,length(risk))]*pop]
  dead2[i]=sum(died)
  prev=cur[,.(month=i+1,age=age+1,pop=pop-died)]
}

# baseline reduction percent for PFE-adjusted baseline (month 1 is January 2020)
data.table(month=1:months,reductionpct=-dead2/dead0*100)

In November 2024 Ethical Skeptic said that he currently subtracts a total of 668,592 deaths from his PFE-adjusted baseline, even though my approximation of his PFE arrival function was based on this old plot where he only subtracted 587,000 deaths:

Ethical Skeptic's PFE adjustment is fully "expired" by October 2027 which means that after that point he will no longer subtract further deaths. But he said that in November 2024 his baseline was approximately 69% expired, which means that at that point he would've already subtracted about 69% of 668,592 deaths, which is about 460,000. However in the red line in my plot above I had only subtracted a total of only about 238,000 deaths by the end of November 2024, which is only about half of his figure.

Ethical Skeptic often applies heavy adjustment for the PFE even in plots for young age groups like 0-54. But in my plot below for ages 0-54, the maximum reduction to the baseline up to the end of 2024 was only about 0.013% in the model based on COVID deaths and about 0.028% in the model based on all-cause deaths:

Deaths with secondary thrombocytopenia

Ethical Skeptic posted this tweet: [https://x.com/EthicalSkeptic/status/1862983630462554150]

USA Secondary Thrombocytopenia D69.5 MCoD All Ages

This leaves NO DOUBT as to cause. It was not Covid-19.

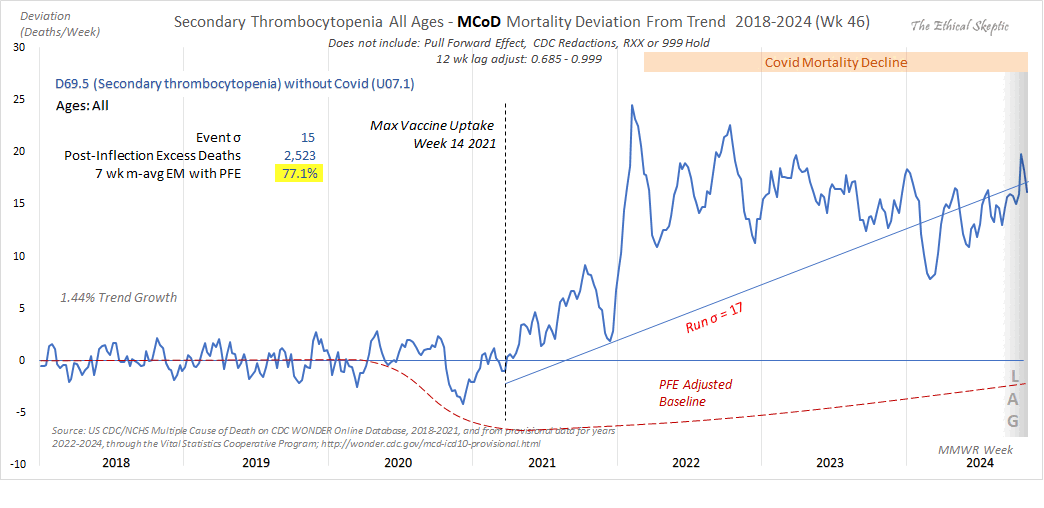
Thrombocytopenia means an abnormally low level of platelets in the blood. Primary thrombocytopenia can be caused by genetic disorders like Wiskott-Aldrich syndrome or by autoimmune disorders which destroy platelets, like idiopathic thrombocytopenic purpura (ITP). Secondary thrombocytopenia can be cause by viral or bacterial infections, chemotherapy, medications like heaprin, diseases like lupus, or bone marrow disorders like leukemia or aplastic anemia.

When I looked at UCD deaths instead of MCD deaths with MCD COVID subtracted, secondary thrombocytopenia didn't have a very clear increase in 2020 either, but there was a clear increase in 2020 for the related ICD codes D69.6 (thrombocytopenia, unspecified) and D68.9 (coagulation defect, unspecified):

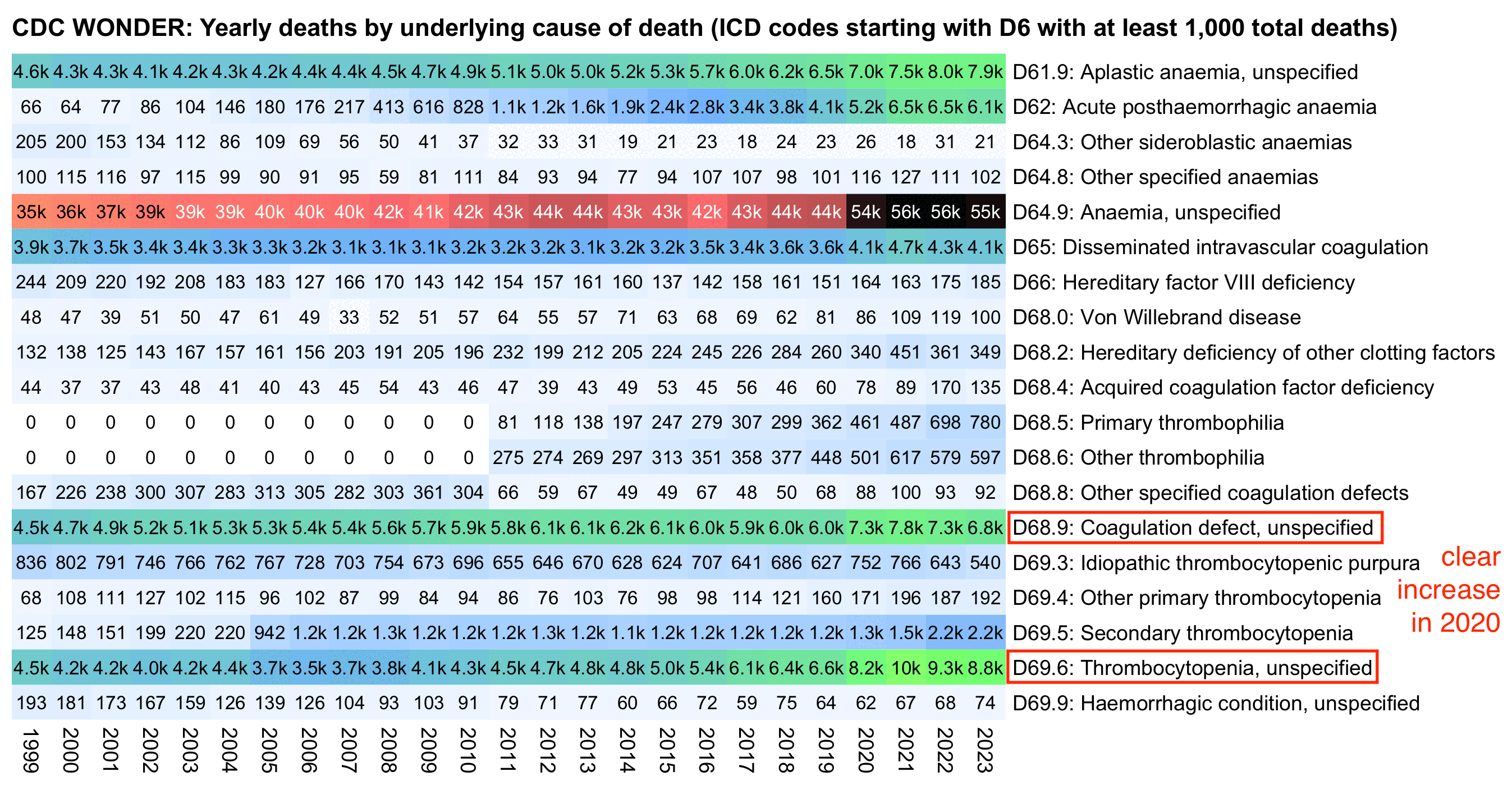
library(data.table)

kimi=\(x){na=is.na(x);x[na]=0;e=floor(log10(ifelse(x==0,1,abs(x))));e2=pmax(e,0)%/%3+1;x[]=ifelse(abs(x)<1e3,round(x),paste0(sprintf(paste0("%.",ifelse(e%%3==0,1,0),"f"),x/1e3^(e2-1)),c("","k","M","B","T")[e2]));x[na]="NA";x}

t=fread("http://sars2.net/f/wonderbyicd.csv.gz")[type=="MCD"&year!=2024&code%like%"D6"]
t=t[code%in%t[,sum(dead),code][V1>=1000,code]]
t=t[order(code)]
t=t[,label:=paste0(code,": ",sub(" \\[.*","",cause))][,label:=factor(label,unique(label))]

m=t[,xtabs(dead~label+year)]
maxcolor=max(m);exp=.6
pal=hsv(c(21,21,12,6,3,0,0)/36,c(0,.5,.5,.5,.5,.5,0),rep(1:0,c(6,1)))

pheatmap::pheatmap(m^exp,filename="1.png",
  display_numbers=ifelse(m<10,m,kimi(m)),
  cluster_rows=F,cluster_cols=F,legend=F,cellwidth=17,cellheight=15,fontsize=9,fontsize_number=8,
  border_color=NA,na_col="gray90",
  number_color=ifelse(abs(m^exp)>maxcolor^exp*.8,"white","black"),
  breaks=seq(0,maxcolor^exp,,256),
  colorRampPalette(pal)(256))

system("w=`identify -format %w 1.png`;pad=20;magick -pointsize 44 -font Arial-Bold \\( -size $[w-pad] caption:'CDC WONDER: Yearly deaths by underlying cause of death (ICD codes starting with D6 with at least 1,000 total deaths)' -splice $[pad]x24 \\) 1.png -append 1.png")

However the plot above also shows that the number of D69.5 deaths increased about 5-fold between 2004 and 2005, so that there were about 100-200 deaths each year in 1999-2004, but from 2005 onwards there were about 1,000 deaths each year. So the increase between 2004 and 2005 was probably due to some change in coding practices, which might also explain the increase between 2021 and 2022.

The next plot shows that in the sharp increase in secondary thrombocytopenia in 2005 coincided with a sudden decrease in unspecified thrombocytopenia (D69.6):

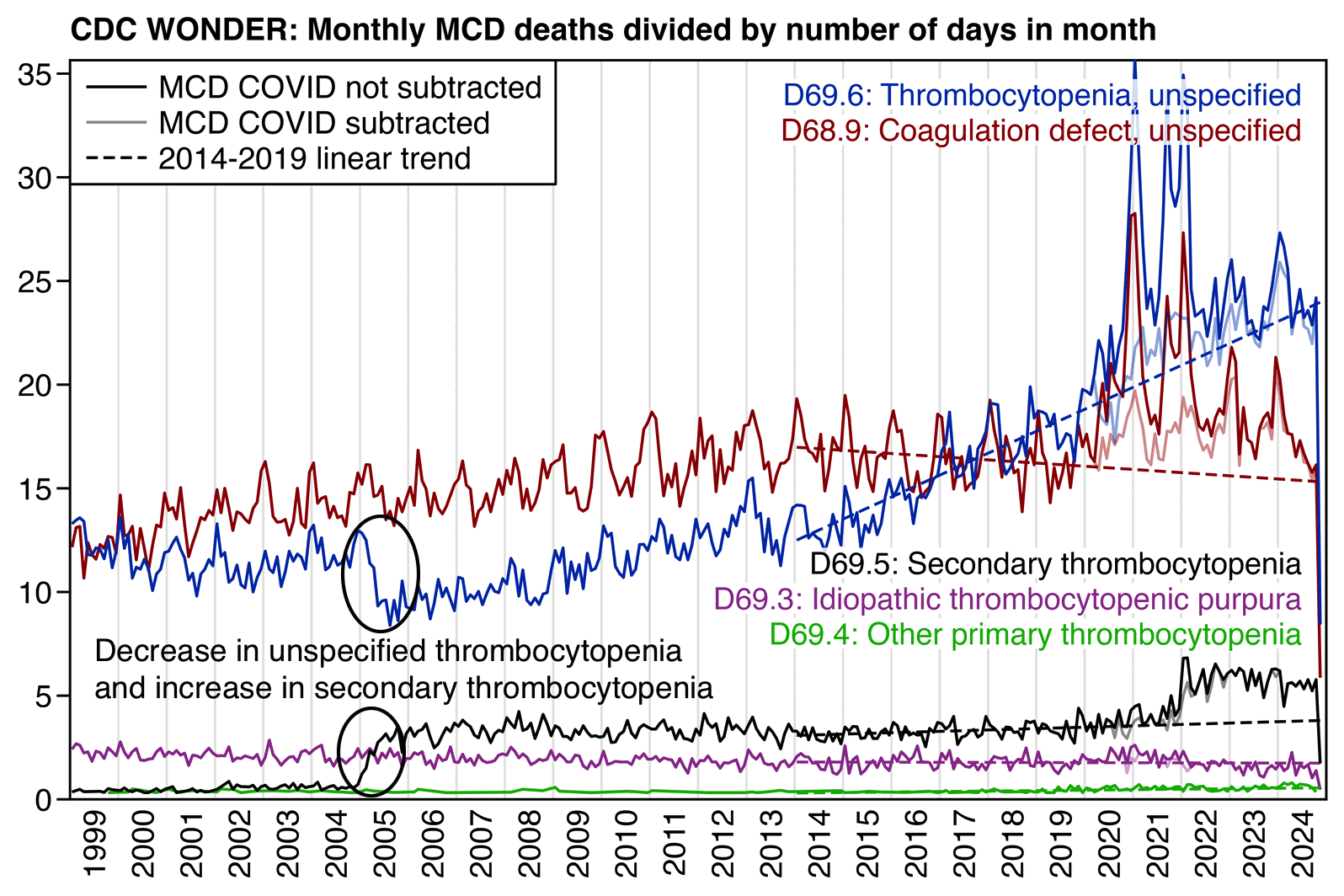
library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wonderthrombocytopenia.csv")
t=t[,.(x=as.Date(paste(year,month,1,sep="-")),y=dead,z=factor(cause,unique(cause)),type)]
t[,y:=y/lubridate::days_in_month(x)]

p=rbind(t[type=="mcd"][,type:=1],dcast(t,z+x~type,value.var="y")[,.(z,x,type=2,y=mcd-nafill(and,,0))])

p=rbind(p,p[type==1&year(x)%in%2014:2019,{i=p[year(x)>=2014,x];.(x=i,y=predict(lm(y~x),.(x=i)),type=3)},z])
p[,type:=factor(type,,c("MCD COVID not subtracted","MCD COVID subtracted","2014-2019 linear trend"))]

xstart=as.Date("1999-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ybreak=pretty(p$y,6);ystart=0;yend=max(p$y)

lab=p[rowid(z)==1][order(z),.(z,x=xend-150,y=c(32.3,9.7,8,11.4,34))]

ggplot(p,aes(x+15,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.25)+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_line(aes(y=ifelse(y<0,NA,y),color=z,alpha=type,linetype=type),linewidth=.3)+
geom_label(data=lab,aes(label=z,color=z,x=x),size=2.4,hjust=1,fill=alpha("white",.85),label.r=unit(0,"pt"),label.padding=unit(1,"pt"),label.size=0,show.legend=F)+
labs(title="CDC WONDER: Monthly MCD deaths divided by number of days in month",,x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(guide="none",values=c(hsv(0,1,.6),hsv(30/36,.6,.6),hsv(12/36,1,.7),"black",hsv(22/36,1,.7)))+
scale_alpha_manual(values=c(1,.4,1))+
scale_linetype_manual(values=c("solid","solid","42"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.text.y=element_text(margin=margin(,1)),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(3,"pt"),
  legend.background=element_rect(fill=alpha("white",1),color="black",linewidth=.25),
  legend.box="vertical",
  legend.box.just="left",
  legend.box.spacing=unit(0,"pt"),
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.margin=margin(2,3,2,2),
  legend.key.height=unit(8,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.position=c(0,1),
  legend.spacing.x=unit(1,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(4,4,4,4),
  plot.title=element_text(size=7,face=2,margin=margin(,,3)))
ggsave("1.png",width=4.2,height=2.8,dpi=380*4)
system("magick 1.png -resize 25% -colors 256 1.png")

And anyway if the increase in MCD secondary thrombocytopenia would've been caused by vaccines, then why was there only a small increase in 2021 but a sudden increase at the start of 2022? And why were the excess deaths higher in 2024 when few people were getting vaccinated than in 2021?

In the case that the increase in deaths with secondary thrombocytopenia would've been due to a change in coding practices, I thought the change might have occurred in some states but not others, or it might have been implemented earlier in some states and later in other states. However there seems to be a fairly uniform pattern across states where there was a clear increase in deaths between 2021 and 2022:

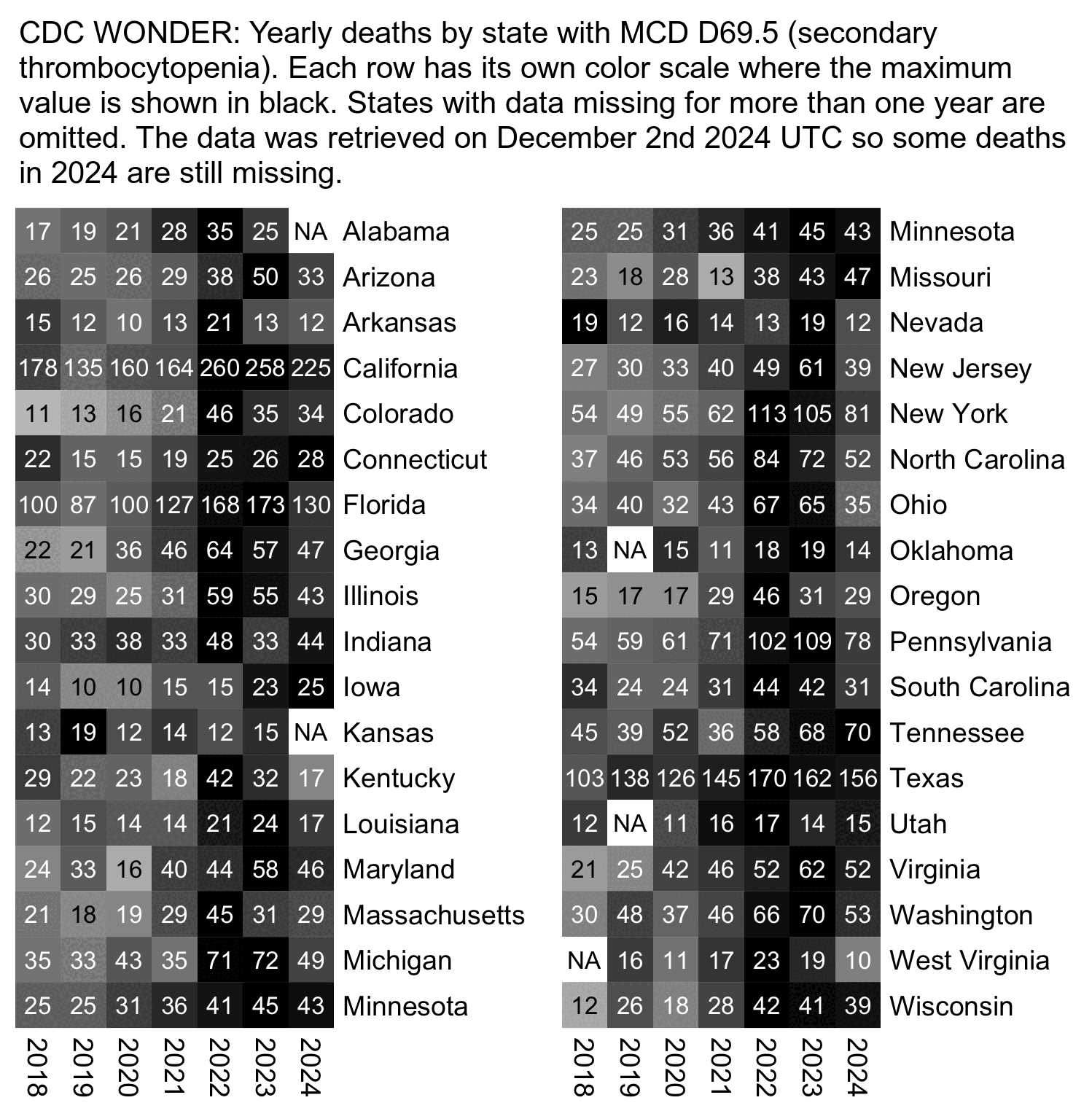
t=fread("http://sars2.net/f/wonderthrombostate.csv")

disp=t[,tapply(dead,.(state,year),c)]
disp=disp[rowSums(is.na(disp))<2,]
m=disp/apply(disp,1,max,na.rm=T)

pal=sapply(255:0,\(i)rgb(i,i,i,maxColorValue=255))

step=ceiling(nrow(m)/2)
for(i in 1:2){
  rows=((i-1)*step):min(nrow(m),i*step)
  pheatmap::pheatmap(m[rows,],filename=paste0("i",i,".png"),display_numbers=disp[rows,],
    cluster_rows=F,cluster_cols=F,legend=F,cellwidth=15,cellheight=15,fontsize=9,fontsize_number=8,
    border_color=NA,na_col="white",
    number_color=ifelse(!is.na(m[rows,])&m[rows,]>.4,"white","black"),
    breaks=seq(0,1,,256),
    colorRampPalette(pal)(256))
}

system("magick i[12].png +append 1.png;w=`identify -format %w 1.png`;pad=26;magick -pointsize 42 -font Arial \\( -size $[w-pad*2] caption:'CDC WONDER: Yearly deaths by state with MCD D69.5 (secondary thrombocytopenia). Each row has its own color scale where the maximum value is shown in black. States with data missing for more than one year are omitted. The data was retrieved on December 2nd 2024 UTC so some deaths in 2024 are still missing.' -splice $[pad]x20 \\) 1.png -append 1.png")

Deaths from natural causes in ages 2-17

Ethical Skeptic posted this tweet: [https://x.com/EthicalSkeptic/status/1864371228309340602]

This is the pièce de résistance.

Ages 2-17 Covid Deaths = 280 (270 post-vaccine) Ages 2-17 Post Inflection Excess Deaths = 5,478

The worst part: this 22-sigma event has not ended.

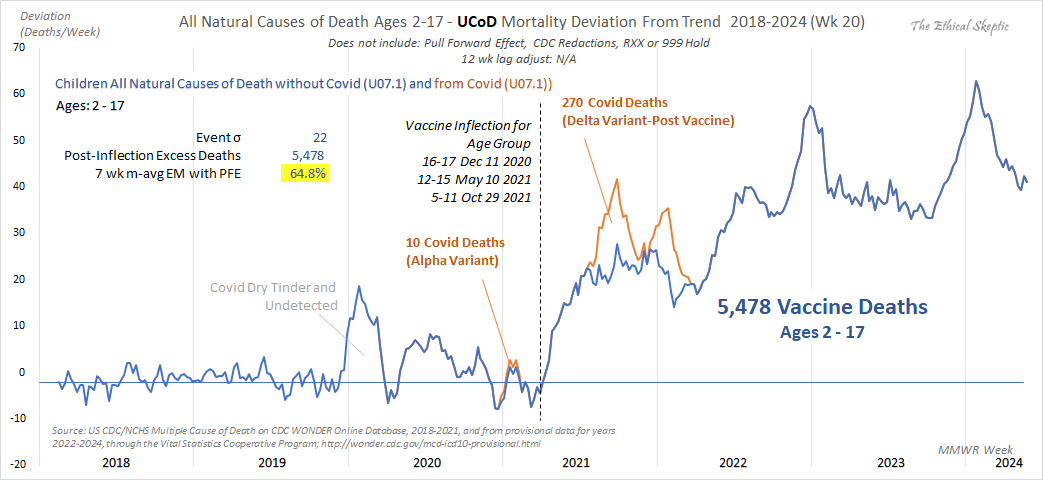
In the replies someone asked: "The 'from Covid (U07.1)' line ends after Q1 2022 because...it goes to zero? Or are we missing data since then?" [https://x.com/41Adanac/status/1864418767444562232] But Ethical Skeptic replied: "No, just no death certificates with Covid as UCoD since then reported by the states." However actually most weeks had less than 10 deaths so the number of deaths was suppressed by CDC WONDER. There's a bunch of deaths with UCD COVID if you look at the fixed-width NVSS files where the deaths are not suppressed, even though the files only include monthly data but not weekly data.

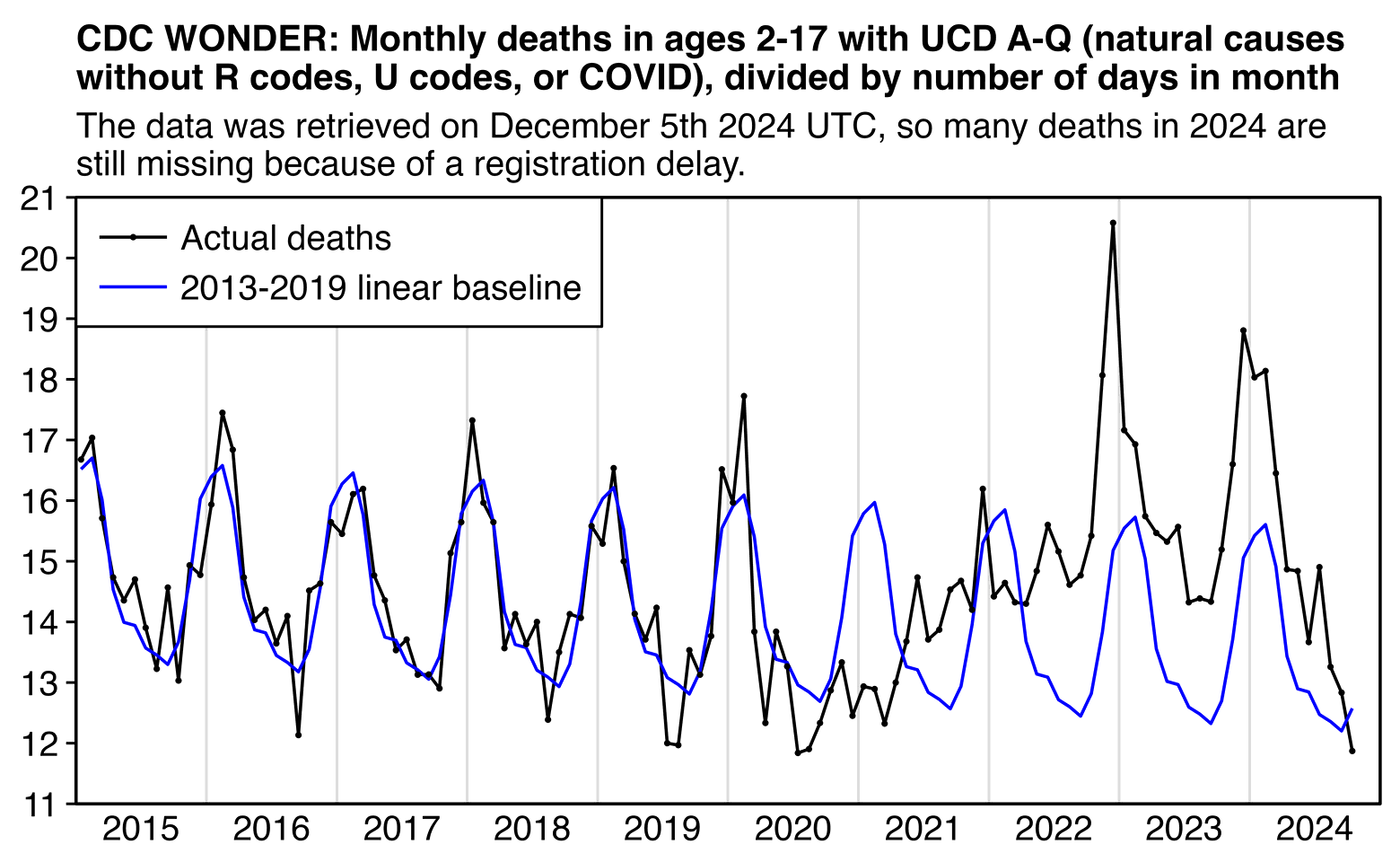
But anyway, when I did a query for deaths with UCD A-Q in ages 2-17, I also got a sustained elevation in deaths above the baseline since around May 2022, but I don't know how to explain it. So this looks like one case where Ethical Skeptic has found a genuine increase in deaths without having to rely on any of his tricks or adjustments:

library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wondernaturalsingle.csv")
t=t[age%in%2:17&date!="2024-11",.(dead=sum(dead)),date]

d=t[,.(x=as.Date(paste0(date,"-1")),dead)]
d[,dead:=dead/lubridate::days_in_month(x)]
d$base=d[year(x)%in%2013:2019,predict(lm(dead~x),d)]
d$base=d$base+d[year(x)%in%2013:2019,mean(dead-base),.(month=month(x))]$V1[month(d$x)]
p=melt(d,id=1,,"z","y")
p[,z:=factor(z,unique(z),c("Actual deaths","2013-2019 linear baseline"))]

xstart=as.Date("2015-1-1");xend=as.Date("2025-1-1")
p=p[x>=xstart&x<=xend]
xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ybreak=pretty(p$y,7);ystart=ybreak[1];yend=max(ybreak)

ggplot(p,aes(x=x+14,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray83",linewidth=.25)+
geom_line(aes(color=z),linewidth=.3)+
geom_point(aes(alpha=z,color=z),stroke=0,size=.6)+
labs(x=NULL,y=NULL,title="CDC WONDER: Monthly deaths in ages 2-17 with UCD A-Q (natural causes\nwithout R codes, U codes, or COVID), divided by number of days in month",subtitle="The data was retrieved on December 5th 2024 UTC, so many deaths in 2024 are
still missing because of a registration delay.")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black","blue"))+
scale_alpha_manual(values=c(1,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.y=element_text(margin=margin(,1.5)),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(2,"pt"),
  legend.background=element_blank(),
  legend.box.background=element_rect(color="black",linewidth=.25),
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.position=c(0,1),
  legend.spacing.x=unit(1,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.margin=margin(3,4,3,3),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3),
  plot.margin=margin(4,4,3,4),
  plot.subtitle=element_text(size=7,margin=margin(,,3)),
  plot.title=element_text(size=7.2,face=2,margin=margin(1,,3)))
ggsave("1.png",width=3.9,height=2.4,dpi=400*4)
system("magick 1.png -resize 25% PNG8:1.png")

Ethical Skeptic's plot says "5,478 Vaccine Deaths Ages 2-17", but I don't know if it's supposed to mean total excess deaths from all natural causes since 2021. However in my plot above I got only about 1,806 excess deaths in 2021-2024. I also got a long period with massive negative excess deaths in December 2020 to March 2021 which seems to be missing from Ethical Skeptic's plot. So did he manually remove it because it didn't jibe with his vaccine inflection?

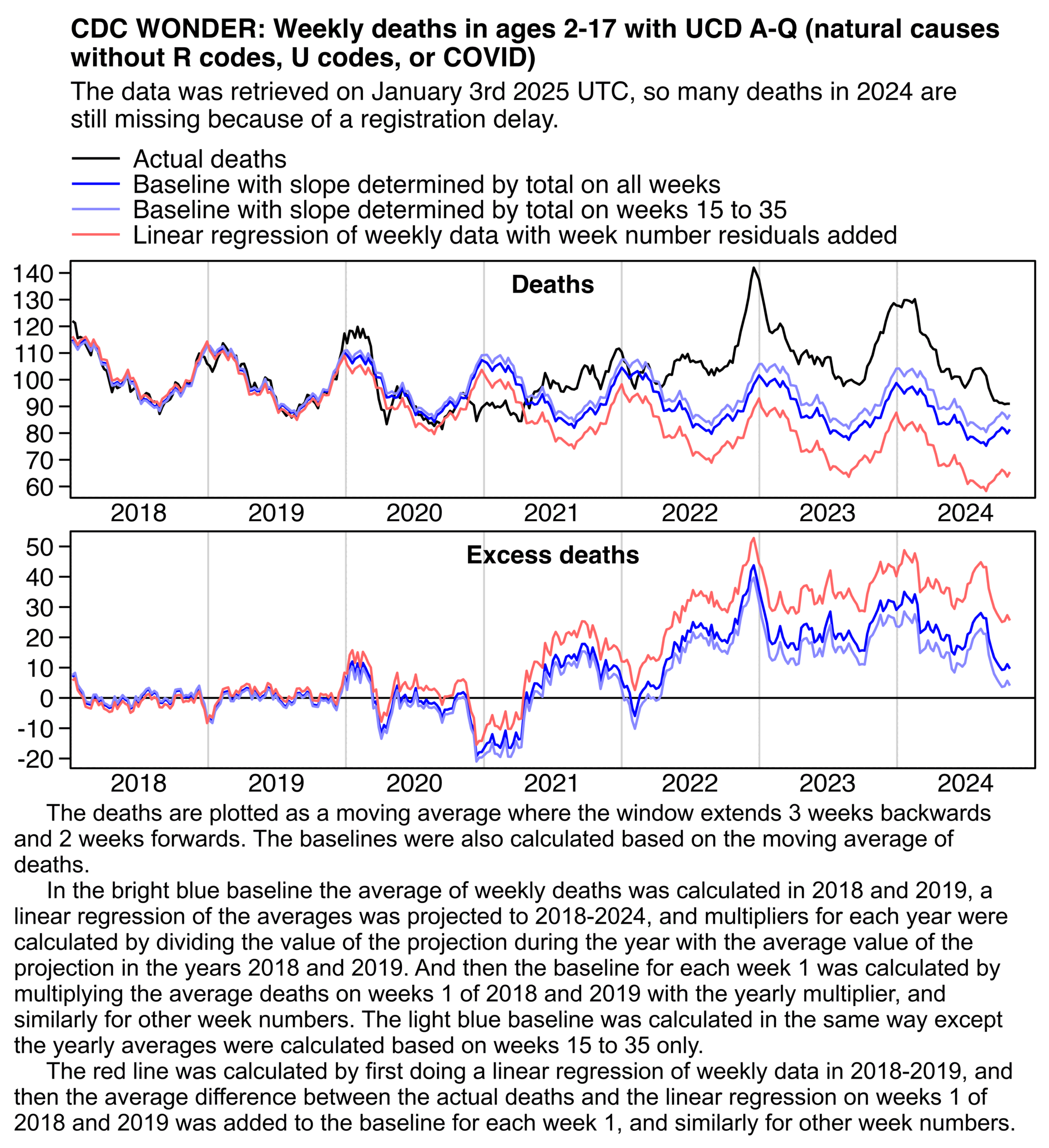
Ethical Skeptic's plot has an average of about 40 excess deaths per week in 2023. But here my weekly average in 2023 was only about 18, 22, and 35 with the different baselines (but my red baseline is too steep because there were high deaths in early 2018 and low deaths in late 2019, and Ethical Skeptic is supposed to fit his baseline using the "summer troughs" only):

library(data.table);library(ggplot2)

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

t=fread("http://sars2.net/f/wonder217naturalweekly.csv")[date<="2024-11-1"]
t[,dead:=ma(dead,3,2)]

t=merge(t,t[year<2020,.(base=mean(dead),base2=mean(dead)),week])
slope=t[year<2020,mean(dead),year][,predict(lm(V1~year),.(year=2018:2024))]
slope2=t[year<2020&week%in%15:35,mean(dead),year][,predict(lm(V1~year),.(year=2018:2024))]
t[,base:=base*(slope/mean(slope[1:2]))[factor(t$year)]]
t[,base2:=base2*(slope2/mean(slope2[1:2]))[factor(t$year)]]

t$base3=t[year<2020,predict(lm(dead~date),t)]
t$base3=t$base3+t[year<2020,mean(dead-base3),week]$V1[t$week]

lab=c("Actual deaths","Baseline with slope determined by total on all weeks","Baseline with slope determined by total on weeks 15 to 35","Linear regression of weekly data with week number residuals added")
p=t[,.(x=date,y=c(dead,base,base2,base3),z=factor(rep(lab,each=.N),lab))]

p$facet="Deaths"
p=rbind(p,merge(p[z!=z[1]],p[z==z[1],.(x,actual=y)])[,.(x,y=actual-y,z,facet="Excess deaths")])
p[,facet:=factor(facet,unique(facet))]

xstart=as.Date("2018-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")

ggplot(p,aes(x=x,y))+
facet_wrap(~facet,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray83",linewidth=.4)+
geom_segment(data=tail(p,1),x=xstart,xend=xend,y=0,yend=0,linewidth=.4)+
geom_line(aes(color=z),linewidth=.5)+
geom_text(data=p[,.(y=max(y)),facet],x=pmean(xstart,xend),aes(label=facet),size=3.8,fontface=2,vjust=1.4)+
labs(x=NULL,y=NULL,title="CDC WONDER: Weekly deaths in ages 2-17 with UCD A-Q (natural causes\nwithout R codes, U codes, or COVID)",subtitle="The data was retrieved on January 3rd 2025 UTC, so many deaths in 2024 are
still missing because of a registration delay.")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab,expand=expansion(0,0))+
scale_y_continuous(breaks=\(x)pretty(x,7),expand=expansion(.03,0))+
scale_color_manual(values=c("black","blue","#8888ff","#ff6666","#ff66ff"))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=11,color="black"),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(5,"pt"),
  legend.background=element_blank(),
  legend.box.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification="left",
  legend.key=element_blank(),
  legend.key.height=unit(11,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(,,6,-2),
  legend.position="top",
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(6,6,1,5),
  plot.title=element_text(size=11.5,face=2,margin=margin(2,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=6.3,height=4.8,dpi=300*4)

sub="\u00a0    The deaths are plotted as a moving average where the window extends 3 weeks backwards and 2 weeks forwards. The baselines were also calculated based on the moving average of deaths.
     In the bright blue baseline the average of weekly deaths was calculated in 2018 and 2019, a linear regression of the averages was projected to 2018-2024, and multipliers for each year were calculated by dividing the value of the projection during the year with the average value of the projection in the years 2018 and 2019. And then the baseline for each week 1 was calculated by multiplying the average deaths on weeks 1 of 2018 and 2019 with the yearly multiplier, and similarly for other week numbers. The light blue baseline was calculated in the same way except the yearly averages were calculated based on weeks 15 to 35 only.
     The red line was calculated by first doing a linear regression of weekly data in 2018-2019, and then the average difference between the actual deaths and the linear regression on weeks 1 of 2018 and 2019 was added to the baseline for each week 1, and similarly for other week numbers.."

system(paste0("f=1.png;mar=100;w=`identify -format %w $f`;magick \\( $f \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[42*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x80 \\) -append -resize 25% -colors 256 1.png"))

I wonder if Ethical Skeptic somehow manually lifts up his excess deaths in these plots that show weekly excess deaths. When I compared two different versions of his plot for weekly excess cancer deaths in ages 0-54, I found that in the newer version he seems to have manually lifted up the excess deaths from around week 9 of 2020 onwards. [ethical.html#Deaths_from_malignant_neoplasms_in_ages_0_to_54] His average weekly number of excess deaths in 2023 was about 175 in the newer version and 150 in the older version, but when I tried to reproduce his plot, I only got an average of about 69, 85, or 105 weekly excess deaths in 2023 depending on the baseline. So his excess deaths were about twice as high as my excess deaths like what again happened here.

I believe Ethical Skeptic has never published the exact methodology he uses to calculate his baseline in these plots for weekly excess deaths, so if other people cannot reproduce his plots then he has plausible deniability because he can just say that other people didn't calculate the baseline correctly. But it also leaves him wiggle room to manually alter his excess deaths.

The next plot shows the causes of death which account for the highest number of excess deaths in 2020-2022 relative to the 2015-2019 linear trend. Many of the top causes seem to have already had a large increase between 2019 and 2020, even though it might be partially on artifact of how I sorted the causes based on the 2020-2022 total so it was biased towards selecting causes which were already elevated in 2020 and not just in 2021-2022. But the top 5 causes also include cancers of brain stem and asthma which didn't have a large increase above the baseline until 2022:

icd=fread("http://sars2.net/f/wonderbyicd.csv.gz")[rowid(code)==1,.(cause,icd=sub("\\.","",code))]

# sars2.net/stat.html#Download_fixed_width_and_CSV_files_for_the_NVSS_data_used_at_CDC_WONDER
t=do.call(rbind,lapply(2013:2022,\(i)fread(paste0(i,".csv.gz"))[age%in%1002:1017,.(ucd=ucod,year)]))

a=t[,.(dead=.N),.(icd=ucd,year)]
a=merge(do.call(CJ,lapply(a[,-3],unique)),a,all.x=T)[is.na(dead),dead:=0]

a=a[a[year%in%2013:2019,.(year=2013:2022,base=predict(lm(dead~year),.(year=2013:2022))),icd],on=names(a)[1:2]]
a=merge(icd,a)

m=a[icd%like%"[A-Q]",tapply(dead-base,.(paste0(icd,": ",cause),year),c)]
m=m[order(-rowSums(m[,ncol(m)-2:0])),][1:40,]

maxcolor=max(abs(m))
exp=.8
pal=hsv(rep(c(21,0)/36,5:4),c(1,.8,.6,.3,0,.3,.6,.8,1),c(.3,.65,1,1,1,1,1,.65,.3))

pheatmap::pheatmap(sign(m)*abs(m)^exp,filename="1.png",display_numbers=kimi(m),
  cluster_rows=F,cluster_cols=F,legend=F,cellwidth=14,cellheight=14,fontsize=9,fontsize_number=8,
  border_color=NA,na_col="gray90",
  number_color=ifelse(!is.na(m)&abs(m)^exp>.7*(maxcolor^exp),"white","black"),
  breaks=seq(-maxcolor^exp,maxcolor^exp,,256),
  colorRampPalette(pal)(256))
system("convert 1.png -extent 2000x 1.png;w=`identify -format %w 1.png`;pad=26;magick -pointsize 44 -font Arial \\( -size $[w-pad] caption:'NVSS, ages 2 to 17: Excess number of deaths by underlying cause of death relative to 2015-2019 linear trend, top 40 causes shown sorted by 2020-2022 total' -splice $[pad]x24 \\) 1.png -append 1.png")

Cancer mortality in ages 0-64 in most-vaccinated and least-vaccinated states

Ethical Skeptic posted this tweet: [https://x.com/EthicalSkeptic/status/1864758742954442778]

Below, we compare Excess Cancer Mortality for the top 17 and bottom 14 states by vaccination percentage, for ages 0-64. Using differential trends and inflection points, we demonstrate the vaccine's impact on cancer mortality.

Vax uptake differentials by state are mild, yet this effect still shows.

Elevated Cancer (same analysis method both cohorts)
🔸Top 17 Vaccinated States = 13.6%
🔸Bottom 14 Vaccinated States = 6.4%

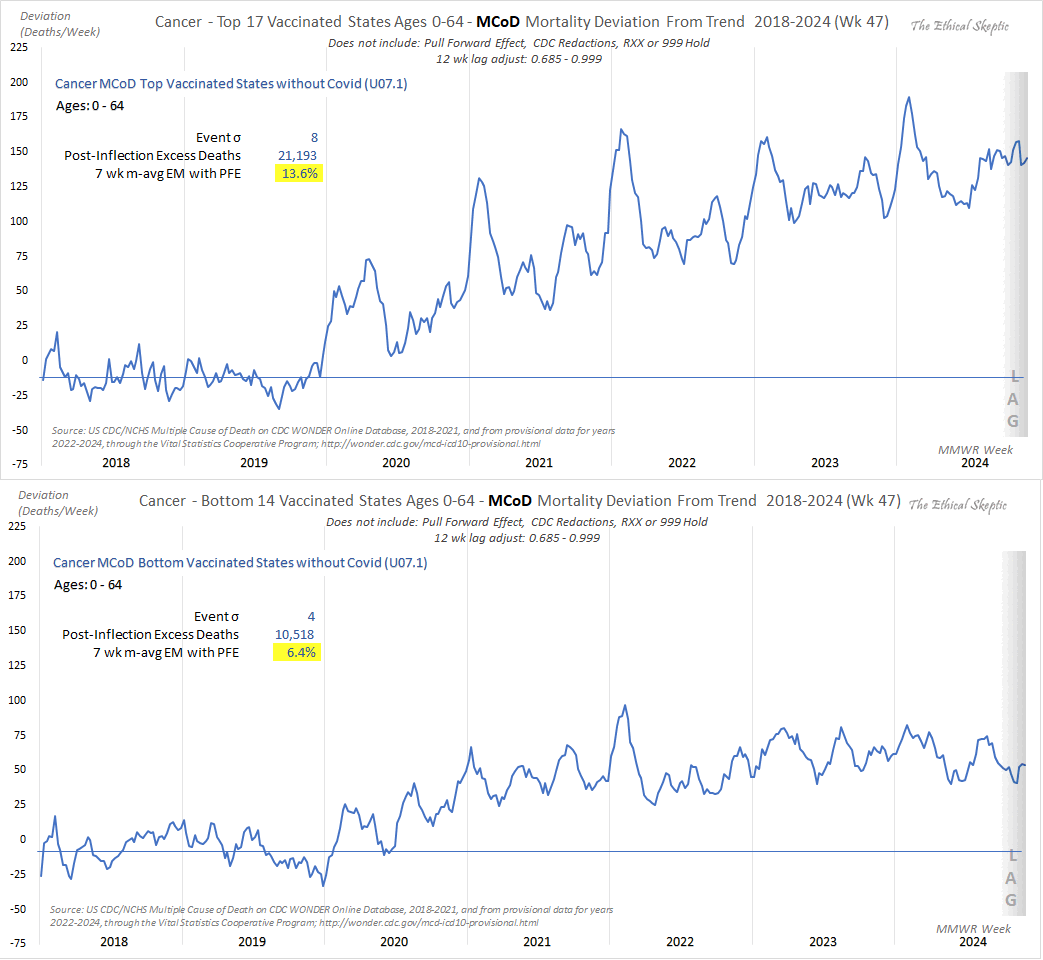
I don't know why he didn't pick the same number of top states and bottom states, or if he cherrypicked the numbers to get a bigger difference between the top states and bottom states. He should've also posted a plot that would've showed the actual deaths and baseline in both groups of states, and ideally he would've used monthly data for the plot so he could've extended it further into the past than 2018. And he could've also included the middle 20 states for comparison, because if the difference in excess mortality between the top and bottom states was primarily explained by a difference in the percentage of vaccinated people, then you'd expect the middle states to have intermediate excess mortality.

In the replies of the tweet he mentioned that he took state vaccination rates from this Statista dataset, so I used the same dataset below: https://statista.com/statistics/1202065/population-with-covid-vaccine-by-state-us/.

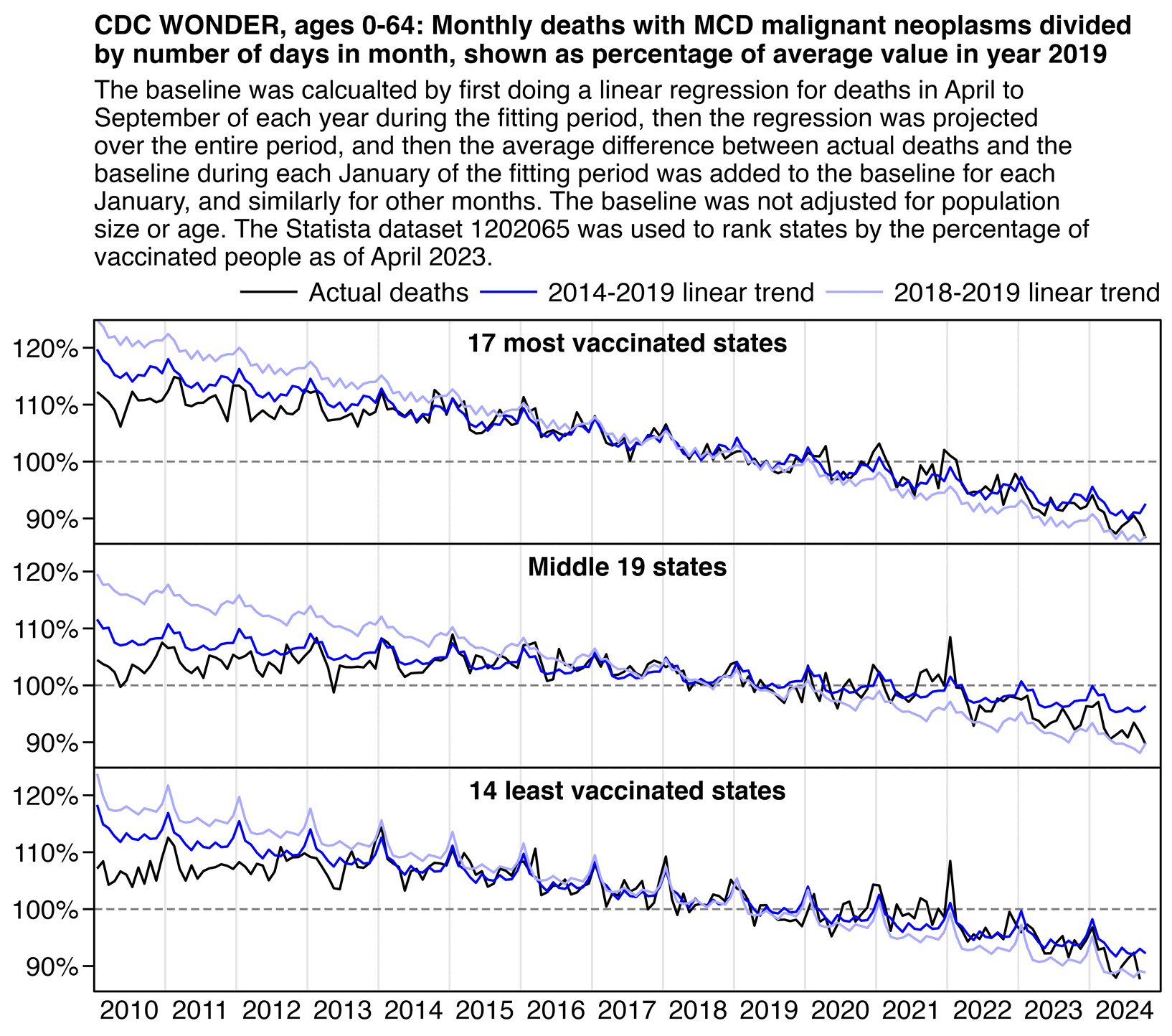
In the plot below I didn't even subtract deaths with MCD COVID, but when I used a 2014-2019 baseline, I still got negative total excess deaths in 2023 and 2024 in both the 17 most vaccinated states and 14 least vaccinated states, even though the 20 states in the middle had even greater negative excess mortality. I didn't adjust the baseline for changes to age composition so that my methodology would be similar to the methodology used by Ethical Skeptic, and I fitted the baseline against only April to September of each year. However the slope of the 2018-2019 baseline seems too steep, so the baseline appears to be too low at the end of the x-axis and too high at the start of the x-axis:

library(data.table);library(ggplot2)

order="RI MA VT ME CT NJ NM NY MD HI VA PA NC NH DE WA CA SD CO FL OR MN IL AZ NV TX KS UT WI OK NE AK SC IA AR MI ND MO KY GA MT WV OH AL TN IN ID LA MS WY"
order=state.name[match(strsplit(order," ")[[1]],state.abb)]

t=fread("http://sars2.net/f/wonderstatemalignant.csv")[!cause%like%"COVID"&age=="0-64"&date!="2024-11"]
g=c("15 most vaccinated states","Middle 20 states","15 least vaccinated states")
t$group=g[2]
t[state%in%order[1:15],group:=g[1]]
t[state%in%tail(order,15),group:=g[3]]
d=t[,.(dead=sum(dead)),,.(group=factor(group,g),date=as.Date(paste0(date,"-1")))]

d[,dead:=dead/lubridate::days_in_month(date)]
d[,month:=month(date)]
d$base=d[year(date)%in%2014:2019&month%in%4:9,predict(lm(dead~date),.(date=unique(d$date))),group]$V1
d$base2=d[year(date)%in%2018:2019&month%in%4:9,predict(lm(dead~date),.(date=unique(d$date))),group]$V1
d=merge(d[year(date)%in%2014:2019,.(monthly=mean(dead-base)),.(group,month)],d)
d=merge(d[year(date)%in%2018:2019,.(monthly2=mean(dead-base2)),.(group,month)],d)
lab=c("Actual deaths","2014-2019 linear trend","2018-2019 linear trend")
p=d[,.(x=date,y=c(dead,base+monthly,base2+monthly2),z=factor(rep(lab,each=.N),lab),group)]

p=merge(p[year(x)==2019,.(base=mean(y)),group],p)[,y:=y/base*100]

xstart=as.Date("2010-1-1");xend=as.Date("2025-1-1")
p=p[x%in%xstart:xend]
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ybreak=pretty(p$y,6);ystart=0;yend=max(p$y)
yend=124.85733
ggplot(p,aes(x+15,y))+
facet_wrap(~group,ncol=1,strip.position="top")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.25)+
geom_hline(yintercept=100,linewidth=.25,linetype="42",color="gray50")+
geom_line(aes(y=ifelse(y<0,NA,y),color=z),linewidth=.3)+
geom_text(data=p[rowid(group)==1],aes(label=group),y=yend,x=pmean(xstart,xend),vjust=1.7,size=2.4,fontface=2)+
labs(title="CDC WONDER, ages 0-64: Monthly deaths with MCD malignant neoplasms divided\nby number of days in month, shown as percentage of average value in year 2019",subtitle=stringr::str_wrap("The baseline was calcualted by first doing a linear regression for deaths in April to September of each year during the fitting period, then the regression was projected over the entire period, and then the average difference between actual deaths and the baseline during each January of the fitting period was added to the baseline for each January, and similarly for other months. The baseline was not adjusted for population size or age. The Statista dataset 1202065 was used to rank states by the percentage of vaccinated people as of April 2023.",88),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(85.54061,124.85733),breaks=pretty,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("black","blue","#aaaaff"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.y=element_text(margin=margin(,1)),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(3,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.justification="right",
  legend.key=element_blank(),
  legend.key.height=unit(7,"pt"),
  legend.key.width=unit(19,"pt"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(1,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.25),
  panel.spacing=unit(0,"pt"),
  plot.margin=margin(3,3,3,3),
  plot.subtitle=element_text(size=6.8,margin=margin(,,2)),
  plot.title=element_text(size=7,face=2,margin=margin(1,,3)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.3,height=3.8,dpi=380*4)
system("magick 1.png -resize 25% -colors 256 1.png")

When I compared the 15 most vaccinated states against the 15 least vaccinated states instead, the excess deaths in 2023-2024 were much lower in both groups of states but the excess deaths were much higher in the middle group. And now also the slope of the 2018-2019 baseline was closer to the 2014-2019 baseline in both the top and bottom groups but further off in the middle group. So I don't know how many different combinations of top and bottom states Ethical Skeptic compared before he arrived at the magic combination of 17 and 14:

In the plot above if you look at the light blue line in the bottom panel, it's a good demonstration of how a 2018-2019 baseline is sensitive to small variations in mortality during the fitting period, because there's a huge change to the slope of the baseline simply depending on whether I included the 14 or 15 least vaccinated states.

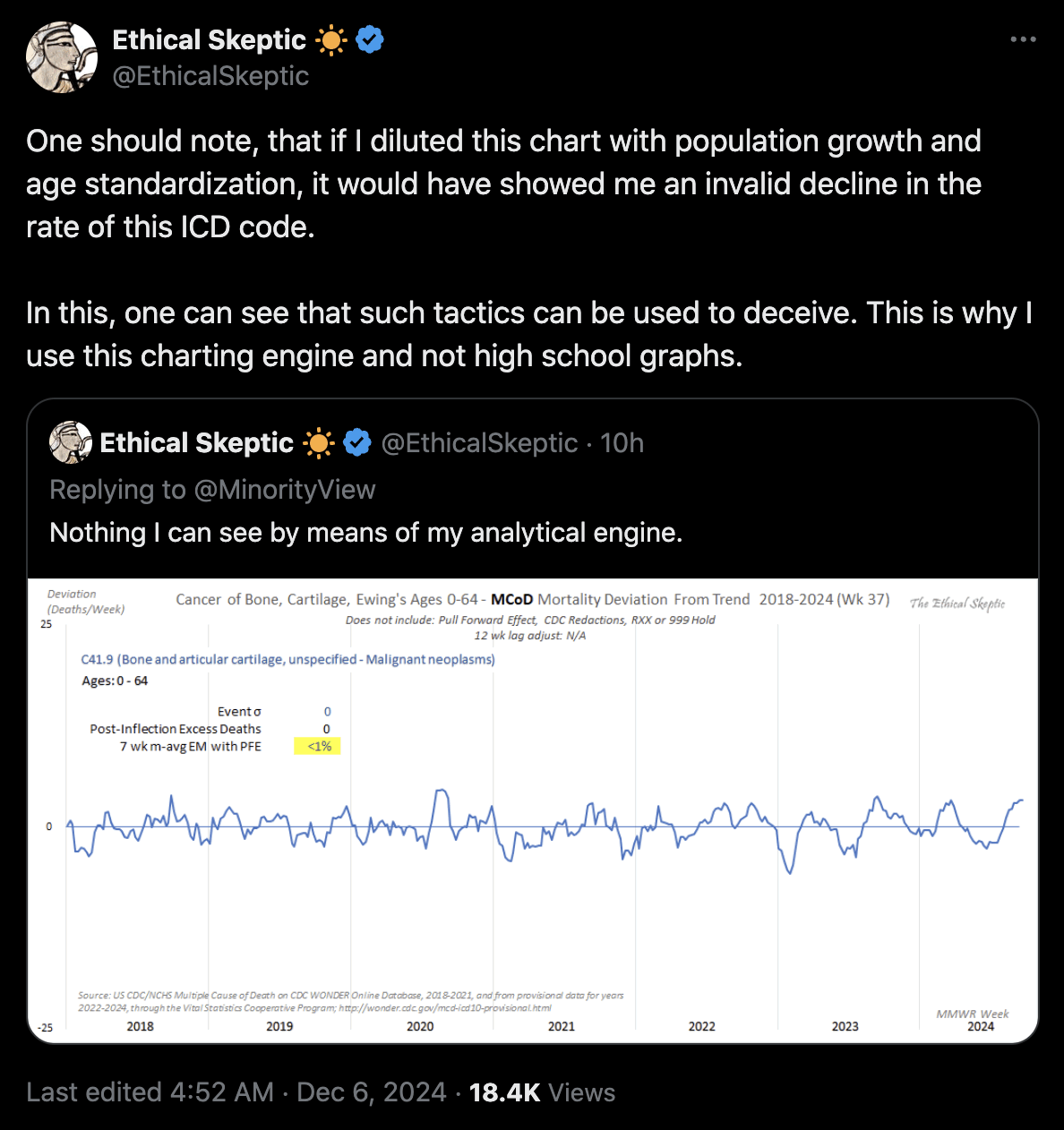
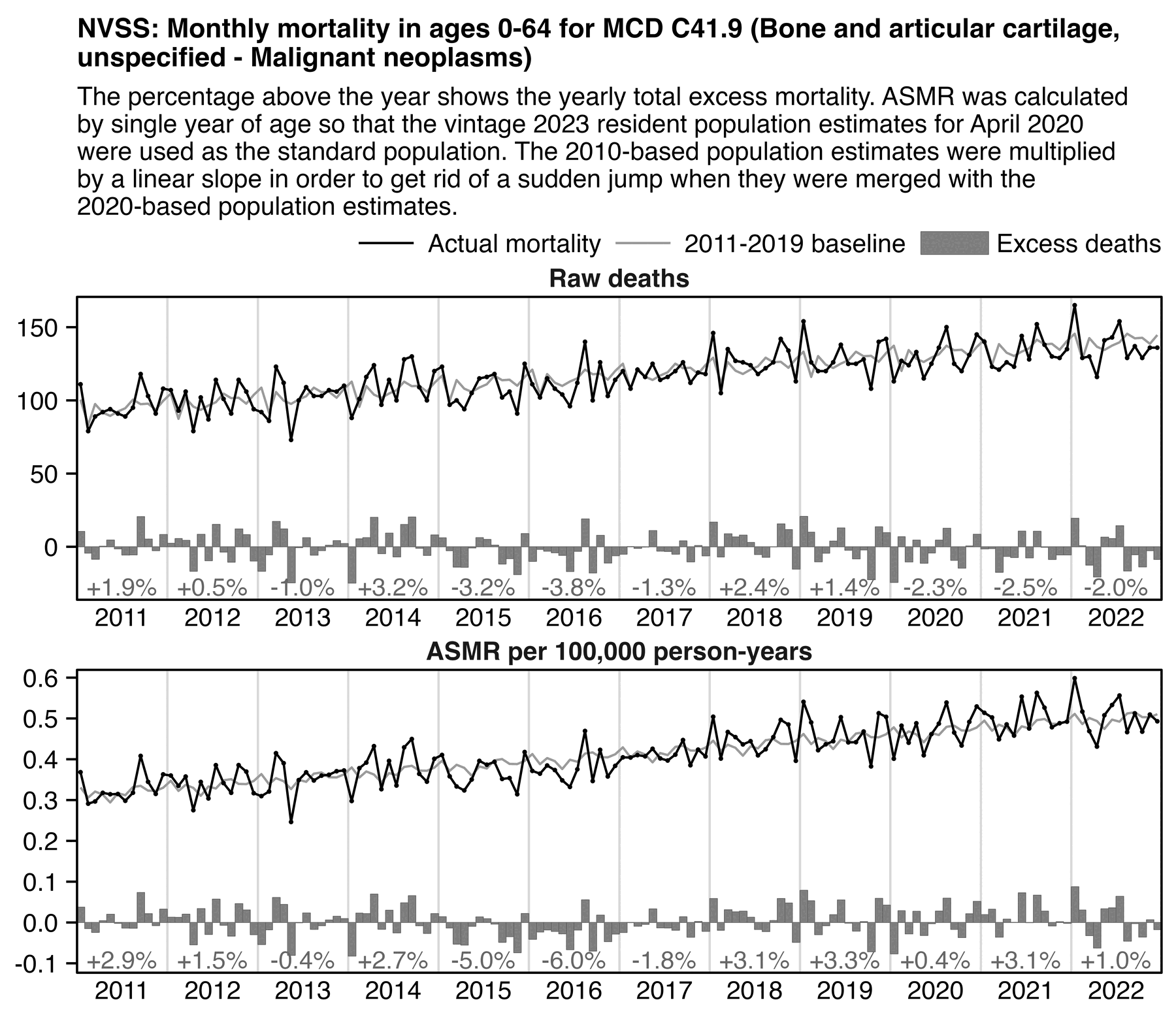
Would using ASMR instead of raw deaths produce an invalid decline in mortality?

Ethical Skeptic keeps coming up with bogus reasons for why he cannot use ASMR in his plots. Here he claimed that if he used ASMR instead of raw deaths to calculate excess deaths for the ICD code for a cancer of cartilage, it would have somehow produced an invalid decline in the rate of the ICD code (even though it's not clear if he meant a decline in excess ASMR or a decline in actual ASMR): [https://x.com/EthicalSkeptic/status/1864865478671245561]

However here my excess deaths in 2020-2022 were negative when I plotted raw deaths but positive when I plotted ASMR, even though in both cases the excess deaths remained close to zero and roughly flat:

library(data.table);library(ggplot2)

# http://sars2.net/stat.html#Download_fixed_width_and_CSV_files_for_the_NVSS_data_used_at_CDC_WONDER
t=do.call(rbind,lapply(2010:2022,\(i)fread(paste0(i,".csv.gz"))[restatus!=4]))

a=t[rowSums(t=="C419",na.rm=T)>0]
a=a[year>=2011&age<65]
a=a[,.(dead=.N),.(age=ifelse(age%%1000%in%c(1,9),age%%1000,0),year,month=monthdth)]

pop=fread("http://sars2.net/f/uspopdeadmonthly.csv")
a=merge(pop[,.(age,year,month,pop=persondays)],a)
a=merge(pop[year==2020&month==4,.(age,std=pop/sum(pop))],a)
a[,x:=as.Date(paste(year,month,1,sep="-"))]

d=a[,.(y=sum(dead),group="Raw deaths"),x]
d=rbind(d,a[,.(y=sum(dead/pop*std*365e5),group="ASMR per 100,000 person-years"),x])
d[,group:=factor(group,unique(group))]

d$base=d[year(x)<2020,predict(lm(y~x),d[rowid(x)==1]),group]$V1
d[,month:=month(x)]
d=merge(d[year(x)<2020,.(monthly=mean(y-base)),.(group,month)],d)

lab=c("Actual mortality","2011-2019 baseline","Excess deaths")
p=d[,.(x=rep(x,3),y=c(y,base+monthly,y-base-monthly),z=factor(rep(lab,each=.N),lab),group)]

xstart=as.Date("2011-1-1");xend=as.Date("2023-1-1")
xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ybreak=pretty(p$y,7);ystart=ybreak[1];yend=max(ybreak)

pct=d[,.(pct=(sum(y)/sum(base+monthly)-1)*100),.(group,year=year(x))]
pct[,x:=as.Date(paste0(year,"-7-1"))]
pct=merge(p[,.(y=min(y)),group],pct)

ggplot(p,aes(x=x+14,y))+
facet_wrap(~group,ncol=1,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray85",linewidth=.25)+
geom_vline(xintercept=as.Date("2020-1-1"),linetype="44",linewidth=.3)+
geom_line(data=p[z!=lab[3]],aes(linetype=z,color=z),linewidth=.3)+
geom_line(data=p[z==z[1]],aes(linetype=z,color=z),linewidth=.3)+
geom_point(aes(alpha=z),stroke=0,size=.6)+
geom_rect(data=p[z==lab[3]],aes(xmin=x,xmax=x%m+%months(1),ymin=pmin(0,y),ymax=pmax(0,y),fill=z),linewidth=.1,color="gray40")+
geom_text(data=pct,aes(x,y=y,label=paste0(ifelse(pct>0,"+",""),sprintf("%.1f",pct),"%")),vjust=.7,size=2.4,color="gray40")+
labs(title="NVSS: Deaths in ages 0-64 with MCD C41.9 (Bone and articular cartilage,
unspecified - Malignant neoplasms)",subtitle="The percentage above the year shows the yearly total excess mortality. ASMR was calculated by single year of age so that the vintage 2023 resident population estimates for April 2020 were used as the standard population. The 2010-based population estimates were multiplied by a linear slope to get rid of a sudden jump when they were merged with the 2020-based population estimates."|>stringr::str_wrap(92),x=NULL,y=NULL)+
scale_x_continuous(expand=c(0,0),limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(expand=c(.06,0,.03,0),breaks=\(x)pretty(x,6))+
scale_color_manual(values=c("black","gray60",NA))+
scale_fill_manual(values=c(NA,NA,"gray60"))+
scale_linetype_manual(values=c("solid","solid",NA))+
scale_alpha_manual(values=c(1,0,0),guide="none")+
guides(color=guide_legend(order=1),linetype=guide_legend(order=1),fill=guide_legend(order=2,keyheight=unit(5,"pt")))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks=element_line(linewidth=.3,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(3,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box="horizontal",
  legend.box.margin=margin(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="right",
  legend.key=element_blank(),
  legend.key.height=unit(5,"pt"),
  legend.key.width=unit(19,"pt"),
  legend.margin=margin(,,3),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3),
  panel.spacing.y=unit(2,"pt"),
  plot.margin=margin(4,4,4,4),
  plot.subtitle=element_text(size=7,margin=margin(1,,3)),
  plot.title=element_text(size=7.4,face=2,margin=margin(1,,3)),
  strip.background=element_blank(),
  strip.text=element_text(size=7,face=2,margin=margin(,,2)))
ggsave("1.png",width=4.5,height=3.9,dpi=400*4)
system("magick 1.png -resize 25% -colorscale gray -colors 16 1.png")

Deaths from lung cancer

Ethical Skeptic tweeted the image below and wrote: "It initially dipped due to its target population being depleted by Covid (PFE). But has since made a strong unfortunate rebound." [https://x.com/EthicalSkeptic/status/1865440856271933538]

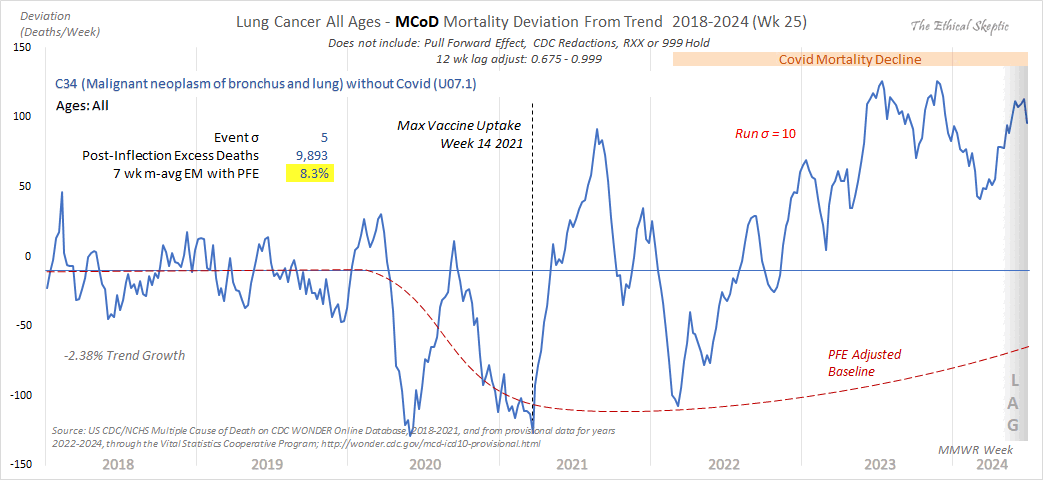
In the next plot I determined the slope of the 2018-2019 baseline based on April to September only so I believe it's similar to Ethical Skeptic's method of fitting the baseline against only "summer troughs". However the 2018-2019 baseline is actually way too high in 2023 and 2024 compared to my dashed baseline which I calculated using a more accurate method.

The reason why there's an increase to my dashed baseline between 2023 and 2024 is because I used population projections for 2024, but there seems to be a discontinuity between the vintage 2023 population estimates for 2023 and the vintage 2023 population projections for 2024.

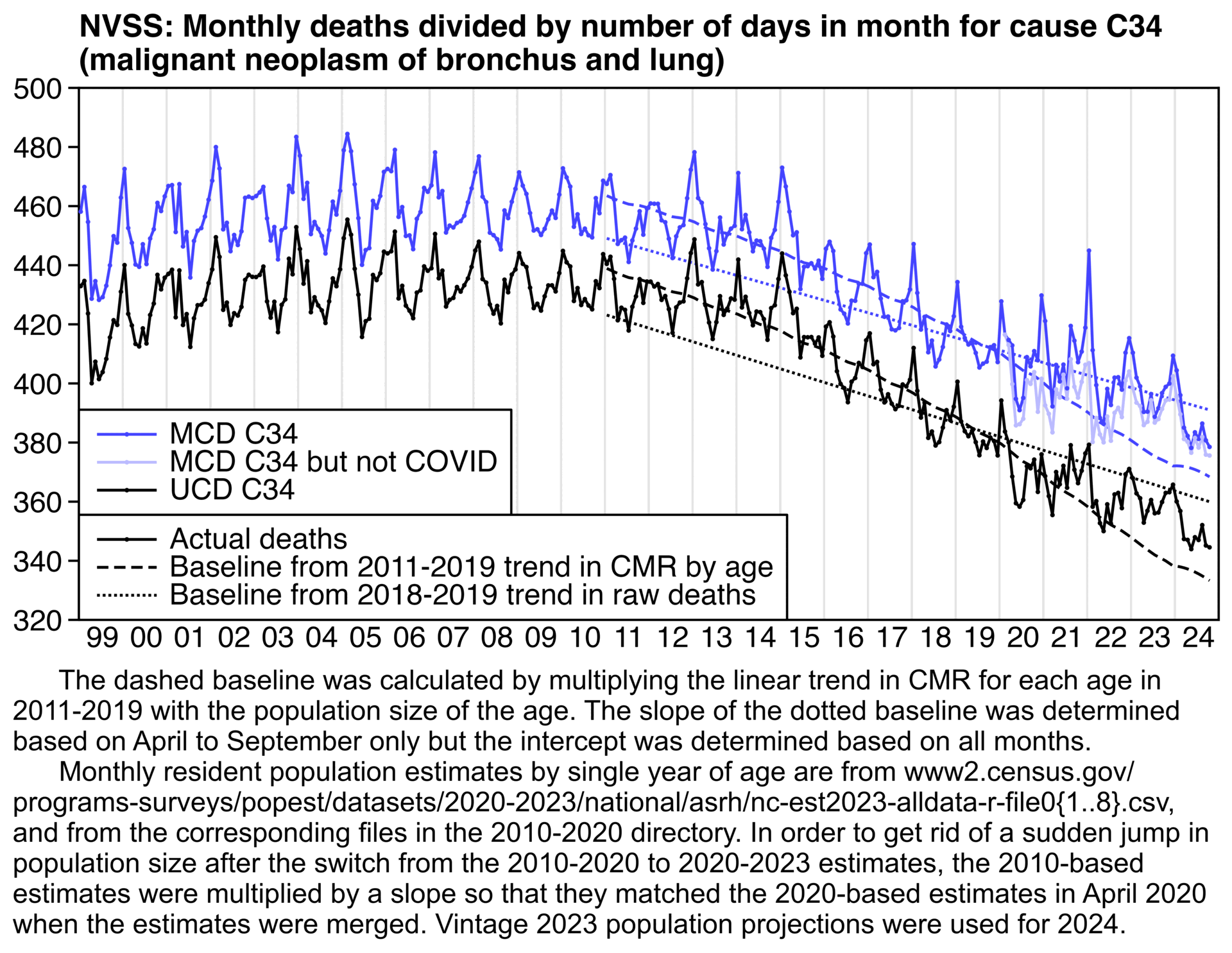
There's also a clear increase above the baseline in 2022-2024 for UCD deaths and not only MCD deaths with COVID subtracted:

library(data.table);library(ggplot2)

v=do.call(rbind,lapply(2011:2019,\(i)fread(paste0(i,".csv.gz"))[restatus!=4,.(.I,year,month=monthdth,age,ucd=ucod,mcd=unlist(.SD,,F)),.SDcols=patterns("enicon_")][mcd%like%"C34"]))
v=v[,age:=pmin(100,ifelse(age%/%1000%in%c(1,9),age%%1000,0))]

a=v[ucd%like%"C34"&rowid(I,year)==1,.(type=3,y=.N),.(age,year,month)]
a=rbind(a,v[mcd%like%"C34"][rowid(I,year)==1,.(type=1,y=.N),.(age,year,month)])
dim=lapply(a[,-5],unique);dim$year=1999:2025
a=merge(do.call(CJ,dim),a,all.x=T)[is.na(y),y:=0]
a=merge(fread("http://sars2.net/f/uspopdeadmonthly.csv"),a)
a[,x:=year*12+month]
a=merge(a[year%in%2011:2019,.(x=unique(a$x),base=predict(lm(y/persondays~x),.(x=unique(a$x)))),.(age,type)],a)

t=fread("http://sars2.net/f/wonderlungcancerallage.csv")[!(year==2024&month>=11)]
p=dcast(t,year+month~type,value.var="dead")
p=p[,.(x=year*12+month,year,month,y=c(mcd,mcd-nafill(and,,0),ucd),type=rep(1:3,each=.N),group=1)]
p=p[!(x&#x3c;t[type=="and",min(year*12+month)]&type==2)]
p[,y:=y/ifelse(month==2,28+(year%%4==0),(31:30)[rep(1:2,,13)[-8]][month])]

base=merge(p,a[year>=2011,.(base=sum(base*pop)),.(x,type)])
base2=p[type!=2&year>=2011]
base2$base=p[year%in%2018:2019&month%in%4:9,predict(lm(y~x),base2[type==3]),type]$V1
base2[,base:=base+.SD[year%in%2018:2019,mean(y)-mean(base)]]
p=rbind(p,rbind(base[,group:=2],base2[,group:=3])[,.(year,month,x,y=base,group,type)])

p[,type:=factor(type,,c("MCD C34","MCD C34 but not COVID","UCD C34"))]
p[,group:=factor(group,,c("Actual deaths","Baseline from 2011-2019 trend in CMR by age","Baseline from 2018-2019 trend in raw deaths"))]

xstart=min(p$x);xend=2025*12;p=p[x%in%xstart:xend]
xbreak=seq(xstart+6,xend,12)
ybreak=pretty(p$y,7);ystart=ybreak[1];yend=max(ybreak)

ggplot(p,aes(x,y))+
geom_vline(xintercept=seq(xstart-.5,xend+.5,12),color="gray90",linewidth=.4)+
geom_hline(yintercept=c(ystart,yend),linewidth=.4,lineend="square")+
geom_vline(xintercept=c(xstart-.5,xend+.5),linewidth=.4,lineend="square")+
geom_line(aes(color=type,linetype=group),linewidth=.5)+
geom_point(aes(color=type,alpha=group),stroke=0,size=.8)+
labs(title="NVSS: Monthly deaths divided by number of days in month for cause C34
(malignant neoplasm of bronchus and lung)",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=substr(xbreak%/%12,3,4))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#4444ff","#bbbbff","black"))+
scale_linetype_manual(values=c("solid","42","11"))+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),linetype=guide_legend(order=2),alpha=guide_legend(order=2))+
theme(axis.text=element_text(color="black",size=11),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_rect(color="black",linewidth=.4),
  legend.justification=c(0,0),
  legend.key=element_blank(),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(28,"pt"),
  legend.position=c(0,0),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.margin=margin(4,5,4,4),
  legend.text=element_text(size=11,vjust=.7),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(5,5,4,5),
  plot.title=element_text(size=11.6,face=2,margin=margin(4,,4),lineheight=.9))
ggsave("1.png",width=6.4,height=3.5,dpi=300*4)
sub="\u00a0     The dashed baseline was calculated by multiplying the linear trend in CMR for each age in 2011-2019 with the population size of the age. The slope of the dotted baseline was determined based on April to September only but the intercept was determined based on all months.
      Monthly resident population estimates by single year of age are from www2.census.gov/
programs-surveys/popest/datasets/2020-2023/national/asrh/nc-est2023-alldata-r-file0{1..8}.csv, and from the corresponding files in the 2010-2020 directory. In order to get rid of a sudden jump in population size after the switch from the 2010-2020 to 2020-2023 estimates, the 2010-based estimates were multiplied by a slope so that they matched the 2020-based estimates in April 2020 when the estimates were merged. Vintage 2023 population projections were used for 2024."
system(paste0("f=1.png;mar=70;w=`identify -format %w $f`;magick \\( $f -chop 0x60 \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[43*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x80 \\) -append -resize 25% -colors 256 1.png"))

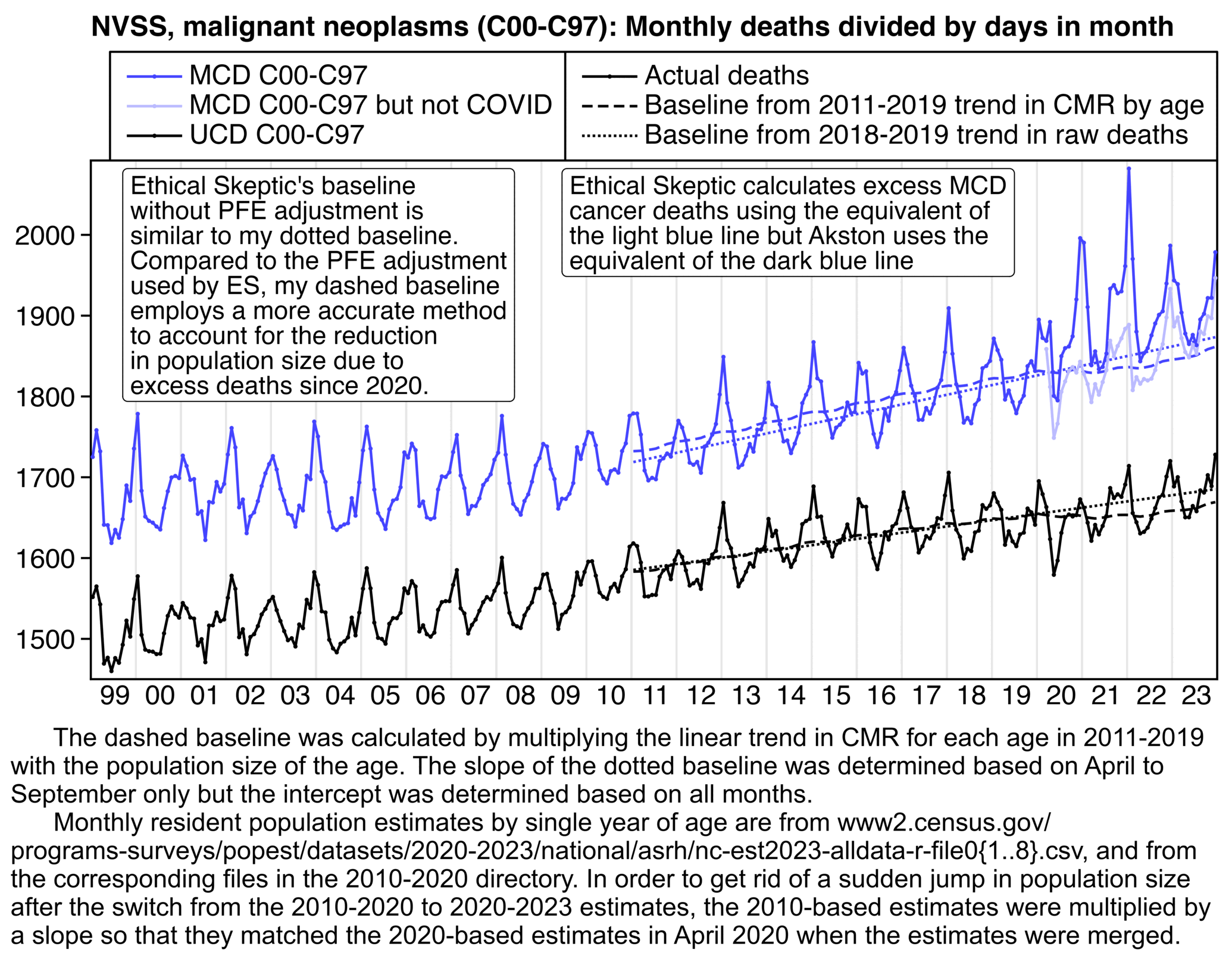
Hugh Akston's corroboration of Ethical Skeptic's plot for cancer mortality

Hugh Akston quoted a plot of cancer mortality by Ethical Skeptic which employed excess MCD normalization and PFE adjustment, and he posted the plot below and wrote: "Using completely different analytical methods, we see the unmistakable signal, similar estimates, and we echo the continue an unabated rise." [https://x.com/ProfessorAkston/status/1861988370190041303]

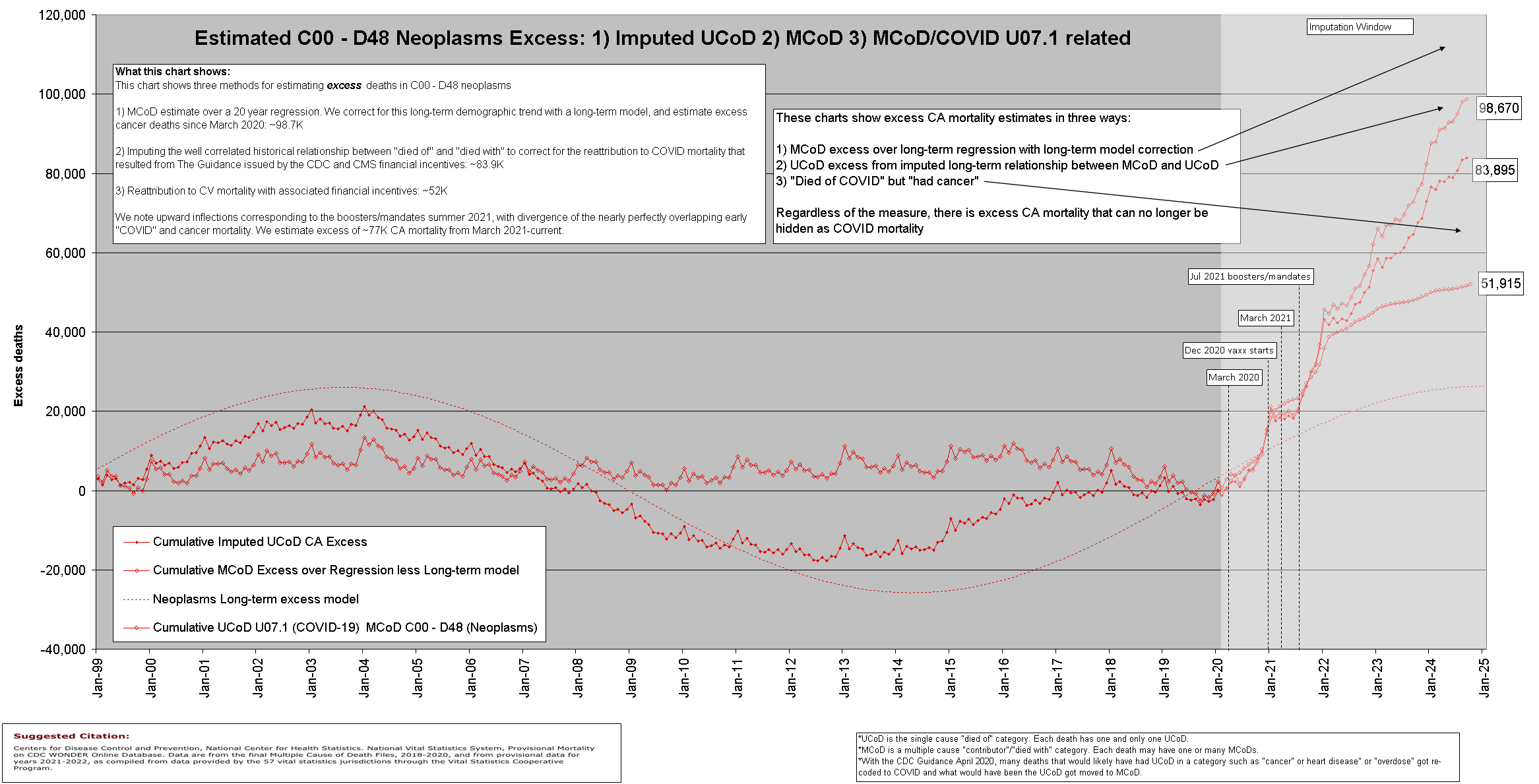
I believe Akston's method of UCD imputation is similar to Ethical Skeptic's method of excess MCD normalization, but Akston's plot doesn't show what the excess deaths would've been without the UCD imputation, so it's difficult to tell what the magnitude of his imputation is or what percentage of his excess deaths are explained by the imputation.

I asked Akston to post a plot which would've had four lines that would've showed unadjusted UCD deaths, UCD deaths with imputation, unadjusted baseline, and baseline with the long-term correction, but he didn't reply to me. I believe he hasn't documented anywhere what exact methodology he used to do the UCD imputation or long-term correction.

Akston claimed that his analytical methods were completely different from Ethical Skeptic, but I think the reason why he gets such high excess UCD cancer deaths is because he applies an adjustment to his plot that is similar to excess MCD normalization, so in that respect his methodology is similar to ES. And his long-term correction also causes the baseline to be too low similar to Ethical Skeptic's PFE adjustment.

Akston's plot includes one line for excess MCD cancer deaths without MCD cancer subtracted and another line for UCD COVID deaths that also have MCD cancer. But both lines went up since 2020, so if people didn't look at the plot too carefully they may have thought it meant that there were two different ways to measure excess deaths which both went up, even though actually it just meant that most excess MCD cancer deaths were explained by deaths that had UCD COVID. And if Akston's plot would've included a line for deaths that had both MCD cancer and MCD COVID, it would've been even higher than the line for deaths that had both MCD cancer and UCD COVID. So if he would've added a line to his plot that showed deaths with MCD cancer but not MCD COVID like my light blue line below, it would've made it more clear how most excess MCD cancer deaths can be explained by COVID:

library(data.table);library(ggplot2)

v=do.call(rbind,lapply(2011:2019,\(i)fread(paste0(i,".csv.gz"))[restatus!=4,.(.I,year,month=monthdth,age,ucd=ucod,mcd=unlist(.SD,,F)),.SDcols=patterns("enicon_")][mcd%like%"C"]))
v=v[,age:=pmin(100,ifelse(age%/%1000%in%c(1,9),age%%1000,0))]

a=v[ucd%like%"C"&rowid(I,year)==1,.(type=3,y=.N),.(age,year,month)]
a=rbind(a,v[mcd%like%"C"][rowid(I,year)==1,.(type=1,y=.N),.(age,year,month)])
dim=lapply(a[,-5],unique);dim$year=1999:2025
a=merge(do.call(CJ,dim),a,all.x=T)[is.na(y),y:=0]
a=merge(fread("http://sars2.net/f/uspopdeadmonthly.csv"),a)
a[,x:=year*12+month]
a=merge(a[year%in%2011:2019,.(x=unique(a$x),base=predict(lm(y/persondays~x),.(x=unique(a$x)))),.(age,type)],a)

t=fread("http://sars2.net/f/wondermalignantallage.csv")[!(year==2024&month>=11)]
p=dcast(t,year+month~type,value.var="dead")
p=p[,.(x=year*12+month,year,month,y=c(mcd,mcd-nafill(and,,0),ucd),type=rep(1:3,each=.N),group=1)]
p=p[!(x&#x3c;t[type=="and",min(year*12+month)]&type==2)]
p[,y:=y/ifelse(month==2,28+(year%%4==0),(31:30)[rep(1:2,,13)[-8]][month])]

base=merge(p,a[year>=2011,.(base=sum(base*pop)),.(x,type)])
base2=p[type!=2&year>=2011]
base2$base=p[year%in%2018:2019&month%in%4:9,predict(lm(y~x),base2[type==3]),type]$V1
base2[,base:=base+.SD[year%in%2018:2019,mean(y)-mean(base)]]
p=rbind(p,rbind(base[,group:=2],base2[,group:=3])[,.(year,month,x,y=base,group,type)])

p[,type:=factor(type,,c("MCD C00-C97","MCD C00-C97 but not COVID","UCD C00-C97"))]
p[,group:=factor(group,,c("Actual deaths","Baseline from 2011-2019 trend in CMR by age","Baseline from 2018-2019 trend in raw deaths"))]

xstart=min(p$x);xend=2024*12;p=p[x%in%xstart:xend]
xbreak=seq(xstart+6,xend,12)
ybreak=pretty(p$y,7);ystart=min(p$y)-10;yend=max(p$y)+10

note="Ethical Skeptic calculates excess MCD cancer deaths using the equivalent of the light blue line but Akston uses the equivalent of the dark blue line"|>stringr::str_wrap(40)

note2="Ethical Skeptic's baseline without PFE adjustment is similar to my dotted baseline. Compared to the PFE adjustment used by ES, my dashed baseline employs a more accurate method to account for the reduction in population size due to excess deaths since 2020."|>stringr::str_wrap(30)

ggplot(p,aes(x,y))+
geom_vline(xintercept=seq(xstart-.5,xend+.5,12),color="gray90",linewidth=.4)+
geom_hline(yintercept=c(ystart,yend),linewidth=.4,lineend="square")+
geom_vline(xintercept=c(xstart-.5,xend+.5),linewidth=.4,lineend="square")+
geom_line(aes(color=type,linetype=group),linewidth=.5)+
geom_point(aes(color=type,alpha=group),stroke=0,size=.8)+
annotate(geom="label",x=2009*12+6,y=yend-10,vjust=1,label=note,label.r=unit(2,"pt"),label.padding=unit(3,"pt"),label.size=.2,size=3.6,lineheight=.82,hjust=0)+
annotate(geom="label",x=1999*12+9,y=yend-10,vjust=1,label=note2,label.r=unit(2,"pt"),label.padding=unit(3,"pt"),label.size=.2,size=3.6,lineheight=.82,hjust=0)+
labs(title="NVSS, malignant neoplasms (C00-C97): Monthly deaths divided by days in month",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=substr(xbreak%/%12,3,4))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#4444ff","#bbbbff","black"))+
scale_linetype_manual(values=c("solid","42","11"))+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),linetype=guide_legend(order=2),alpha=guide_legend(order=2))+
theme(axis.text=element_text(color="black",size=11),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_rect(color="black",linewidth=.4),
  legend.box="horizontal",
  legend.box.just="bottom",
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(1,0),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(28,"pt"),
  legend.margin=margin(4,5,4,4),
  legend.position="top",
  legend.spacing.x=unit(0,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.7),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(6,6,5,6),
  plot.title=element_text(size=11.3,face=2,margin=margin(4,,4),lineheight=.9))
ggsave("1.png",width=6.9,height=4.1,dpi=300*4)
sub="\u00a0     The dashed baseline was calculated by multiplying the linear trend in CMR for each age in 2011-2019 with the population size of the age. The slope of the dotted baseline was determined based on April to September only but the intercept was determined based on all months.
      Monthly resident population estimates by single year of age are from www2.census.gov/
programs-surveys/popest/datasets/2020-2023/national/asrh/nc-est2023-alldata-r-file0{1..8}.csv, and from the corresponding files in the 2010-2020 directory. In order to get rid of a sudden jump in population size after the switch from the 2010-2020 to 2020-2023 estimates, the 2010-based estimates were multiplied by a slope so that they matched the 2020-based estimates in April 2020 when the estimates were merged."
system(paste0("f=1.png;mar=70;w=`identify -format %w $f`;magick \\( $f -chop 0x60 \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[43*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x80 \\) -append -resize 25% -colors 256 1.png"))

Akston later posted the plot below which I think shows the baseline he used to do the UCD imputation. It shows that took the line for the UCD to MCD percentage in 2017-2019 and inserted copies of the line to 2020-2022 and 2023-2025. But it might have been more accurate to do a linear regression of the prepandemic trend in the UCD to MCD percentage instead, because there seems to have been a decreasing trend in the UCD to MCD percentage since around 2015. And it's also misleading how he didn't subtract COVID deaths from his dashed black line which shows the UCD to MCD percentage since 2020, so you can't tell that the reduction in the UCD to MCD percentage is mostly explained by COVID deaths: [https://x.com/ProfessorAkston/status/1868093698871046471]

I believe around half of the excess deaths in Akston's plot can be explained by his method of "long-term model correction". However it's also wrong and it exaggerates excess deaths particularly in 2024 and 2023. Akston assumed that the long-term trend in cumulative excess deaths relative to a linear baseline would follow a sine wave pattern, so his corrected baseline is too low by 2023 and 2024 since by then his sine wave has begun to reach its crest so his adjusted baseline begins to flatten out: [https://x.com/ProfessorAkston/status/1709780661685628998]

In the next plot I tried to reproduce Akston's long-term model. Akston didn't specify which baseline he used to calculate the initial excess deaths that are shown as the solid dark red line, but I calculated them against a 1999-2019 linear baseline which gave me slightly different results than in Akston's plot, so he may have used a different baseline. The dashed dark red line shows a sine wave fitted against the solid dark red line. The lighter red line shows cumulative excess deaths relative to the sine wave model, but in my plot its value is slightly higher than in Akston's plot, which I think is again because he used a different initial baseline. The green line shows excess deaths relative to a more accurate model I calculated myself, but the green line is much lower than the lighter red line particularly in 2024 and 2023, so it shows that Akston's model exaggerates excess deaths particularly in 2024 and 2023 (which should be easy to tell anyway since excess deaths from natural causes have remained close to zero since 2023 when they are measured against a reasonable baseline, but in Akston's plot there's still a sharp increase in cumulative excess deaths from natural causes in 2023):

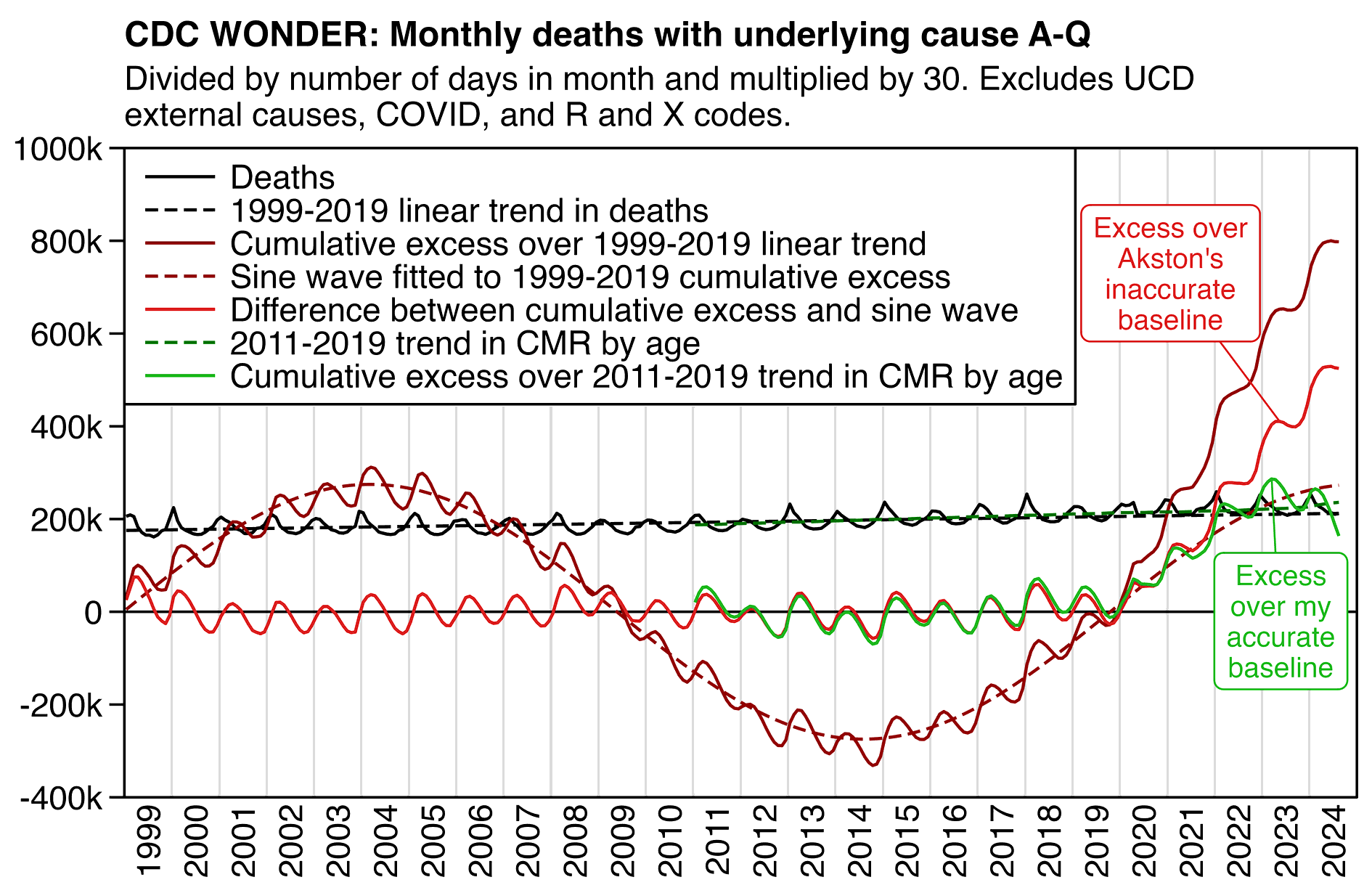
library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wondernatural.csv")[cause=="A-Q"&date<="2024-06"]
p=na.omit(t[,.(dead=sum(dead)),.(x=as.Date(paste0(date,"-1")))])

p[,dead:=dead/days_in_month(x)*30]

p$linear=p[year(x)<2020,predict(lm(dead~x),p)]
p[,excess:=cumsum(dead-linear)]

p2=copy(p)[,x:=as.integer(x)]
fit=nls(excess~A*sin(B*x+C)+D,p2[year(p$x)<2020],
  list(A=(max(p2$excess)-min(p2$excess))/2,B=2*pi/(max(p2$x)-min(p2$x)),C=0,D=mean(p2$excess)),
  nls.control(maxiter=100,tol=1e-6))
p$sine=predict(fit,p2)

p=melt(p,id=1,,"z","y")
p[,z:=factor(z,unique(z),c("Deaths","1999-2019 linear trend in deaths","Cumulative excess relative to linear trend","Sine wave fitted to pre-2020 cumulative excess"))]

xstart=as.Date("1999-1-1");xend=as.Date("2025-1-1")
p=p[x>=xstart&x<=xend]
xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ybreak=pretty(p$y,7);ystart=ybreak[1];yend=max(ybreak)

ggplot(p,aes(x=x+14,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray83",linewidth=.4)+
geom_hline(yintercept=0,linewidth=.4)+
geom_line(aes(color=z),linewidth=.5)+
labs(x=NULL,y=NULL,title="CDC WONDER: Monthly deaths with underlying cause A-Q",subtitle="Divided by number of days in month and multiplied by 30. Excludes UCD external causes, COVID, and R and X codes."|>stringr::str_wrap(74))+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x==0,0,paste0(x/1e3,"k")))+
scale_color_manual(values=c("black","#6666ff","gray60","#ff66ff","#ff8888","#ff66ff"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(5,"pt"),
  legend.background=element_blank(),
  legend.box.background=element_rect(color="black",linewidth=.4),
  legend.direction="vertical",
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(4,4,4,4),
  legend.position=c(0,1),
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3),
  plot.margin=margin(6,6,5,5),
  plot.subtitle=element_text(size=11,margin=margin(,,5)),
  plot.title=element_text(size=11.5,face=2,margin=margin(2,,4)))
ggsave("1.png",width=6.3,height=4,dpi=300*4)
system("magick 1.png -resize 25% PNG8:1.png")

The long-term trend in cumulative excess deaths relative to a 1999-2019 baseline actually has an S shape and not a sine wave shape, because the long-term trend in deaths is curved upwards. So even if COVID never happened, the cumulative excess deaths relative to a 1999-2019 linear baseline would've continued to climb higher and they wouldn't have flattened out in 2020-2024. In the next plot I started a model from 2010 where I used the mid-2010 resident population estimates for each age as the initial population size for the age. Each year I killed the same fraction of people for each age as the 2010 CMR for the age, and I incremented the age of the remaining people by one, and I added the same number of people aged zero as in the mid-2010 resident population estimates. However in my model the deaths didn't flatten out until the 2040s:

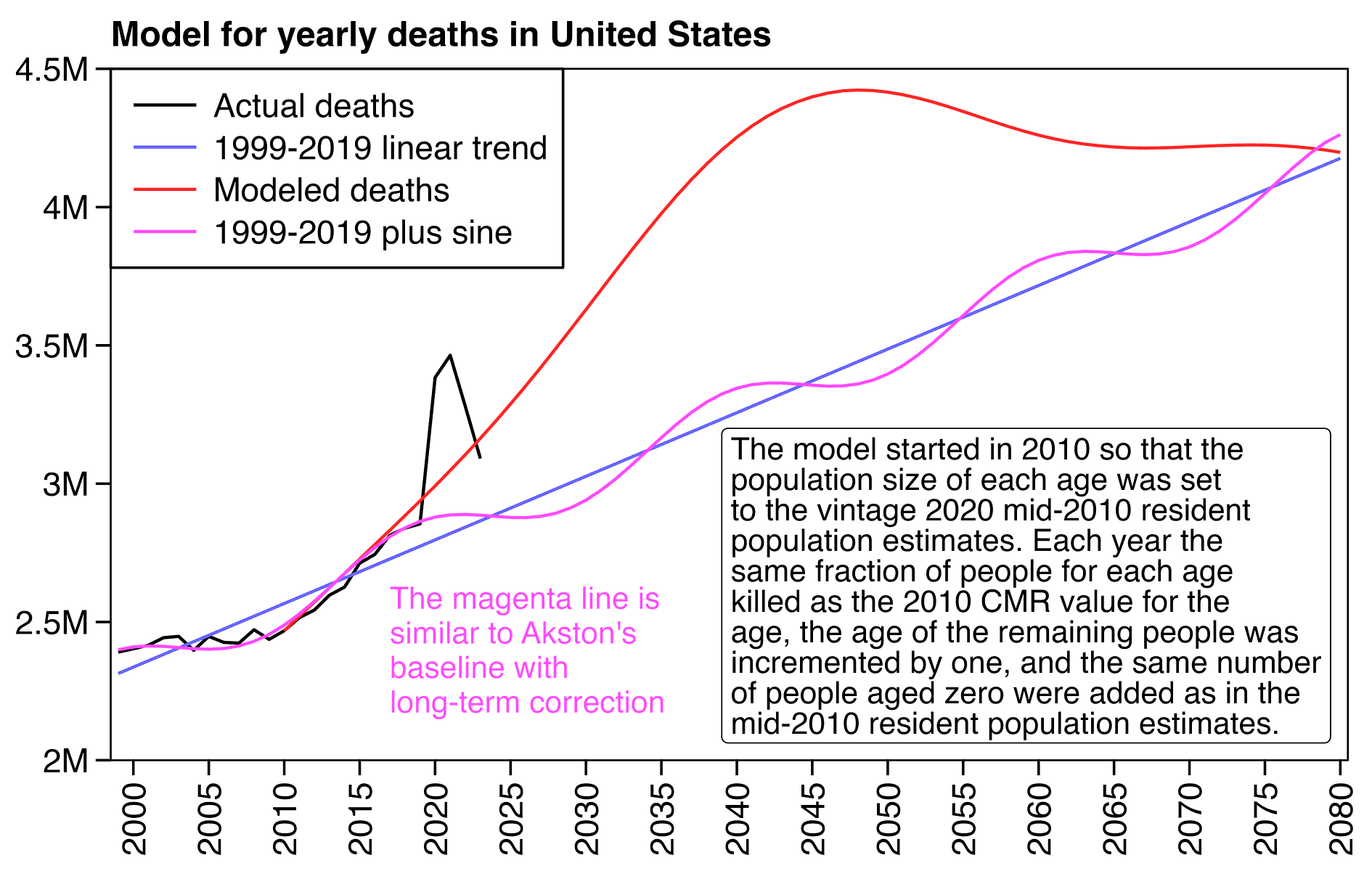
library(data.table);library(ggplot2)

xstart=1999;xend=2080

t=fread("http://sars2.net/f/uspopdead.csv")
p=t[,.(y=sum(dead),z="Actual deaths"),.(x=year)]
cmr=t[year==2010,dead/pop]
pop=t[year==2010,pop]
births=pop[1]
sim=data.table(x=NA,y=NA)
for(year in 2010:xend){
  died=pop*cmr;pop=pop-died
  pop=c(births,pop[1:99],sum(pop[100:101]))
  sim=rbind(sim,list(year,sum(died)))
}

p=rbind(p,p[,.(x=xstart:xend,y=p[x<2020,predict(lm(y~x),.(x=xstart:xend))],z="1999-2019 linear trend")])
p=rbind(p,sim[,z:="Modeled deaths"])
p[,z:=factor(z,unique(z))]

excess=merge(p[z==levels(z)[1]],p[z==levels(z)[2],.(x,y2=y)])[x<2020,.(x,y=cumsum(y-y2))]
fit=nls(y~A*sin(B*x+C)+D,excess,
  list(A=excess[,max(y)-min(y)]/2,B=2*pi/excess[,max(x)-min(x)],C=0,D=mean(excess$y)),
  nls.control(maxiter=100,tol=1e-6))

pred=diff(predict(fit,.(x=1998:2080)))[-1]
p=rbind(p,p[z==levels(z)[2]][,y:=y+pred][,z:="1999-2019 plus sine"])

xbreak=seq(2000,xend,5)
ybreak=pretty(p$y,7);ystart=ybreak[1];yend=max(ybreak)

note=stringr::str_wrap("The model started in 2010 so that the population size of each age was set to the vintage 2020 mid-2010 resident population estimates. Each year the same fraction of people for each age killed as the 2010 CMR value for the age, the age of the remaining people was incremented by one, and the same number of people aged zero were added as in the mid-2010 resident population estimates.",40)

ggplot(p,aes(x=x,y))+
geom_hline(yintercept=0,linewidth=.4)+
geom_line(aes(color=z),linewidth=.5)+
labs(x=NULL,y=NULL,title="Model for yearly deaths in United States")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x/1e6,"M"))+
scale_color_manual(values=c("black","#6666ff","#ff3333","#ff55ff"))+
annotate(geom="label",x=2039,y=32e5,vjust=1,label=note,label.r=unit(2,"pt"),label.padding=unit(3,"pt"),label.size=.2,size=3.6,lineheight=.82,hjust=0)+
annotate(geom="text",x=2017,y=2.4e6,label="The magenta line is\nsimilar to Akston's\nbaseline with\nlong-term correction",hjust=0,size=3.6,lineheight=.93,color="#ff55ff")+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length=unit(5,"pt"),
  legend.background=element_blank(),
  legend.box.background=element_rect(color="black",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.height=unit(14,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.position=c(0,1),
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.margin=margin(5,5,5,5),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3),
  plot.margin=margin(6,8,5,5),
  plot.title=element_text(size=11.5,face=2,margin=margin(1,,5)))
ggsave("1.png",width=6.3,height=4,dpi=300*4)
system("magick 1.png -resize 25% PNG8:1.png")

In the plot above if you compare the red line for my model against the black line for the real number of deaths, my model has a slightly higher number of deaths in the 2010s, but I think it's because in real life elderly age groups had a decreasing trend in age-specific mortality rates in the 2010s but in my model I used 2010 CMR values for each age indefinitely.

The Census Bureau has also published this projection of yearly deaths that is fairly similar to the red line in my previous plot, even though I believe the projection also accounts for migration and it doesn't assume constant CMR values for each age: [https://www.census.gov/library/stories/2017/10/aging-boomers-deaths.html]

This plot also shows how Akston's sine wave baseline is way too low in 2024:

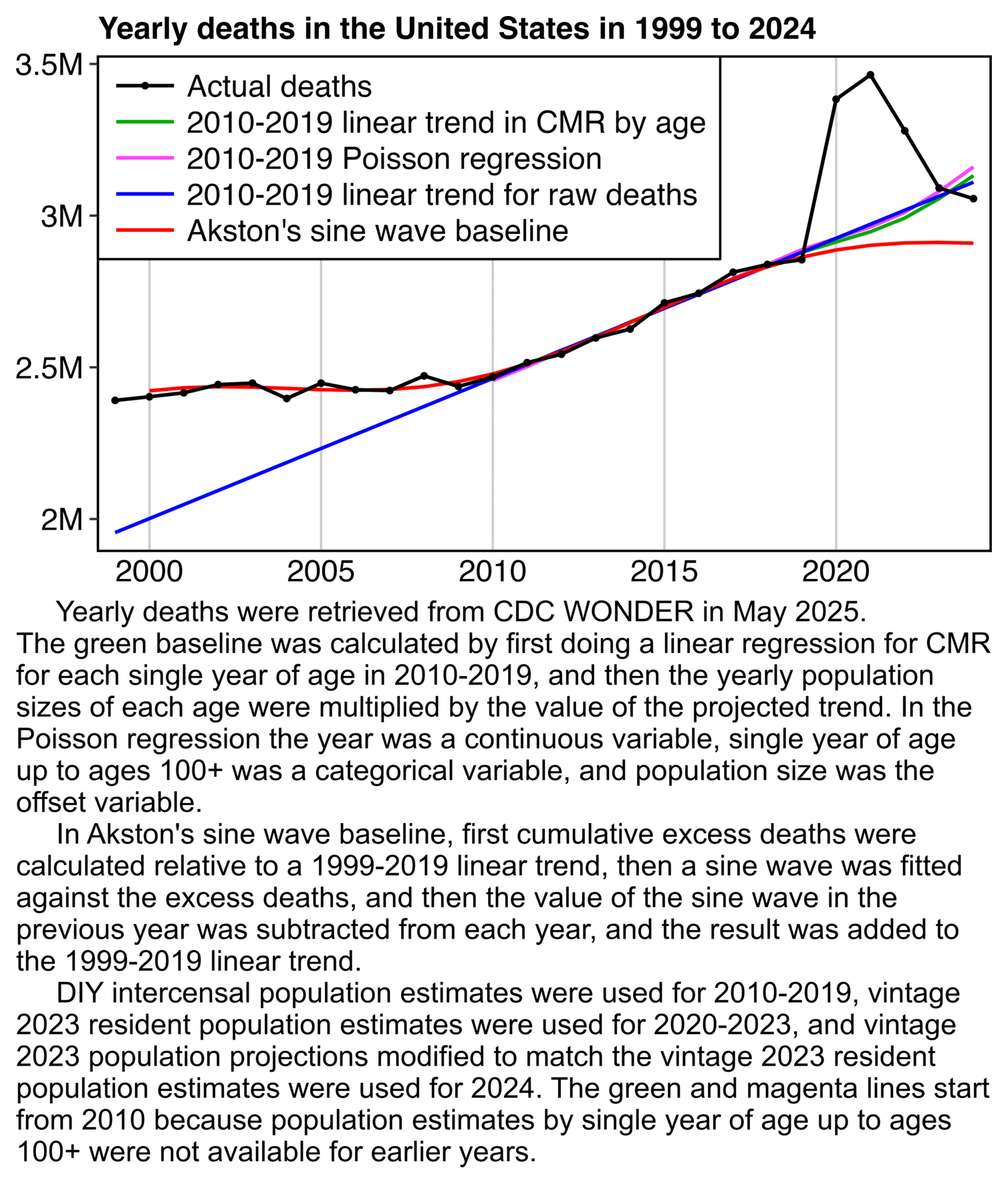
library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/uspopdead.csv")[year<2025]

a=t[,.(dead=sum(dead)),year]
a$base=predict(lm(dead~year,a[year<2020,]),a)
a[,cum:=cumsum(dead-base)]
sub=a[year<2020]
fit=nls(cum~A*sin(B*year+C)+D,sub,
  list(A=sub[,max(cum)-min(cum)]/2,B=2*pi/sub[,max(year)-min(year)],C=0,D=mean(sub$cum)),
  nls.control(maxiter=100,tol=1e-6))
a$sine=diff(c(NA,predict(fit,a)))

t$poi=predict(glm(dead~factor(age),poisson,t[year%in%2010:2019],offset=log(pop)),t,type="response")

t=merge(t,t[year%in%2010:2019,.(year=1999:2024,base=predict(lm(dead/pop~year),.(year=1999:2024))),age])
t=t[,.(dead=sum(dead),base=sum(base*pop),poi=sum(poi)),year]
t$owid=t[year%in%2010:2019,predict(lm(dead~year),t)]
t$akston=a[,base+sine]

p=t[,.(x=year,y=unlist(.SD[,-1]),z=rep(names(.SD)[-1],each=.N))]

lab=c(dead="Actual deaths",base="2010-2019 linear trend in CMR by age",poi="2010-2019 Poisson regression",owid="2010-2019 linear trend for raw deaths",akston="Akston's sine wave baseline")
p[,z:=factor(z,names(lab),lab)]

xstart=1999;xend=2024;ybreak=pretty(p$y);ylim=extendrange(p$y,,.04)

ggplot(p,aes(x,y))+
geom_vline(xintercept=seq(2000,2020,5),color="gray80",linewidth=.4)+
geom_vline(xintercept=c(xstart-.5,xend+.5),color="black",linewidth=.4,lineend="square")+
geom_line(aes(color=z,linetype=z),linewidth=.6)+
geom_line(data=p[z==z[1]],aes(color=z,linetype=z),linewidth=.6)+
geom_point(aes(color=z,alpha=z),stroke=0,size=1.3)+
labs(title="Yearly deaths in the United States in 1999 to 2024",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(2000,xend,5))+
scale_y_continuous(limits=ylim,breaks=ybreak,labels=\(x)ifelse(x>=1e3,paste0(x/1e3,"k"),x))+
scale_color_manual(values=c("black","#00aa00","#ff44ff","blue","red"))+
scale_alpha_manual(values=c(1,0,0,0,0))+
scale_linetype_manual(values=c(1,1,1,1,1))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(margin=margin(3)),
  axis.ticks=element_line(linewidth=.4),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(3,"pt"),
  axis.title=element_text(size=11),
  legend.background=element_blank(),
  legend.box.background=element_rect(fill="white",color="black",linewidth=.4),
  legend.box.just="left",
  legend.justification=c(0,1),
  legend.key=element_rect(fill="white"),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.position=c(0,1),
  legend.margin=margin(4,5,4,4),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  plot.margin=margin(5,5,5,5),
  plot.title=element_text(size=11,face=2,margin=margin(1,,4)))
ggsave("1.png",width=5,height=3,dpi=300*4)
sub="\u00a0    Yearly deaths were retrieved from CDC WONDER in May 2025.
The green baseline was calculated by first doing a linear regression for CMR for each single year of age in 2010-2019, and then the yearly population sizes of each age were multiplied by the value of the projected trend. In the Poisson regression the year was a continuous variable, single year of age up to ages 100+ was a categorical variable, and population size was the offset variable.
     In Akston's sine wave baseline, first cumulative excess deaths were calculated relative to a 1999-2019 linear trend, then a sine wave was fitted against the excess deaths, and then the value of the sine wave in the previous year was subtracted from each year, and the result was added to the 1999-2019 linear trend.
     DIY intercensal population estimates were used for 2010-2019, vintage 2023 resident population estimates were used for 2020-2023, and vintage 2023 population projections modified to match the vintage 2023 resident population estimates were used for 2024. The green and magenta lines start from 2010 because population estimates by single year of age up to ages 100+ were not available for earlier years."
system(paste0("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[43*4] caption:'",gsub("'","'\\\\''",sub),"' -splice x80 \\) -append -resize 25% -bordercolor white -border 24 -dither none -colors 256 1.png"))

When I used Akston's sine wave method to fit a baseline against deaths in 1990-2009, the baseline was way too low by the late 2010s:

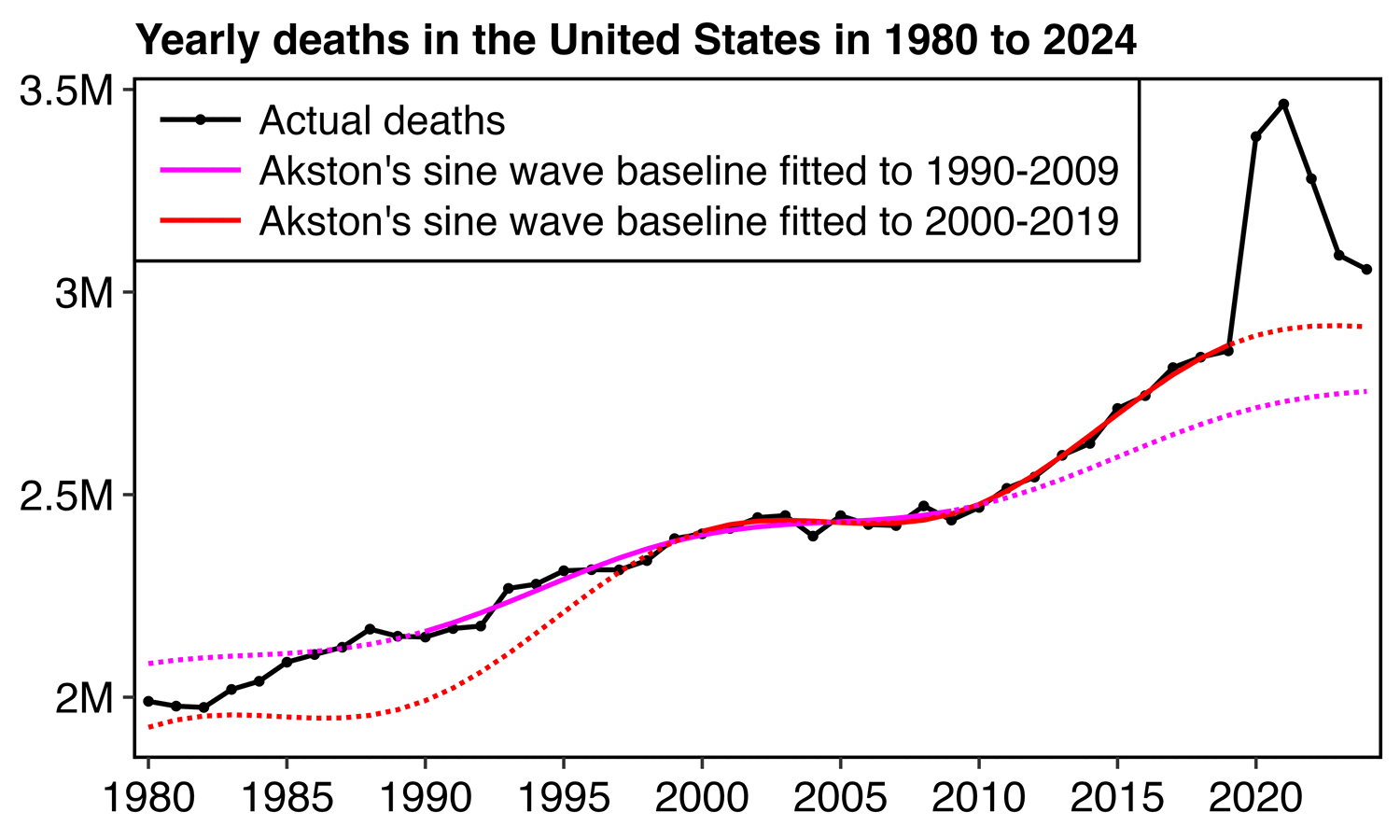
library(data.table);library(ggplot2)

t=data.table(year=1979:2024)
t$dead=c(1913841,1989841,1977981,1974797,2019201,2039369,2086440,2105361,2123323,2167999,2150466,2148463,2169518,2175613,2268553,2278994,2312132,2314690,2314245,2337256,2391399,2403351,2416425,2443387,2448288,2397615,2448017,2426264,2423712,2471984,2437163,2468435,2515458,2543279,2596993,2626418,2712630,2744248,2813503,2839205,2854838,3383729,3464138,3279754,3090884,3055929)

a=copy(t)
a$base=predict(lm(dead~year,a[year%in%1990:2009]),a)
a[,cum:=cumsum(dead-base)]
sub=a[year%in%1990:2009]
fit=nls(cum~A*sin(B*year+C)+D,sub,
  list(A=sub[,max(cum)-min(cum)]/2,B=2*pi/sub[,max(year)-min(year)],C=0,D=mean(sub$cum)),
  nls.control(maxiter=100,tol=1e-6))
t$akston1=diff(c(NA,predict(fit,a)))+a$base

a=copy(t)
a$base=predict(lm(dead~year,a[year%in%2000:2019]),a)
a[,cum:=cumsum(dead-base)]
sub=a[year%in%2000:2019]
fit=nls(cum~A*sin(B*year+C)+D,sub,
  list(A=sub[,max(cum)-min(cum)]/2,B=2*pi/sub[,max(year)-min(year)],C=0,D=mean(sub$cum)),
  nls.control(maxiter=100,tol=1e-6))
t$akston2=diff(c(NA,predict(fit,a)))+a$base

p=t[,.(x=year,y=unlist(.SD[,-1]),z=rep(names(.SD)[-1],each=.N))]

lab=c(dead="Actual deaths",akston1="Akston's sine wave baseline fitted to 1990-2009",akston2="Akston's sine wave baseline fitted to 2000-2019")
p[,z:=factor(z,names(lab),lab)]

xstart=1980;xend=2024;ybreak=pretty(p$y);ylim=extendrange(p$y,,.04)

ggplot(p,aes(x,y))+
geom_vline(xintercept=c(xstart-.5,xend+.5),color="black",linewidth=.4,lineend="square")+
geom_point(aes(color=z,alpha=z),stroke=0,size=1.3)+
geom_line(data=rbind(p[z==levels(z)[1]],p[z==levels(z)[3]&x%in%2000:2019],p[z==levels(z)[2]&x%in%1990:2009]),aes(color=z),linewidth=.6)+
geom_line(data=p[z!=z[1]],aes(color=z),linetype="11",linewidth=.6)+
labs(title="Yearly deaths in the United States in 1980 to 2024",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(1980,xend,5))+
scale_y_continuous(limits=ylim,breaks=ybreak,labels=\(x)paste0(x/1e6,"M"))+
scale_color_manual(values=c("black","magenta","red"))+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(margin=margin(3)),
  axis.ticks=element_line(linewidth=.4),
  axis.ticks.length=unit(3,"pt"),
  axis.title=element_text(size=11),
  legend.background=element_blank(),
  legend.box.background=element_rect(fill="white",color="black",linewidth=.4),
  legend.box.just="left",
  legend.justification=c(0,1),
  legend.key=element_rect(fill="white"),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.position=c(0,1),
  legend.margin=margin(4,5,4,4),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=10.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  plot.margin=margin(5,5,5,5),
  plot.title=element_text(size=11,face=2,margin=margin(1,,4)))
ggsave("1.png",width=5,height=3,dpi=300*4)
system("magick 1.png -resize 25% -dither none -colors 256 1.png")

Added later: Akston claimed that I somehow misunderstood his methodology, even though I don't think I did, but it's more likely that he didn't understand the method I used to convert the cumulative excess deaths back to non-cumulative non-excess deaths. When I asked him to explain his methodology or to post his code, he blocked me. He truly is the poor man's Ethical Skeptic, because he blocks people who ask him to document his methodology: [https://x.com/ProfessorAkston/status/1922015398309830851]

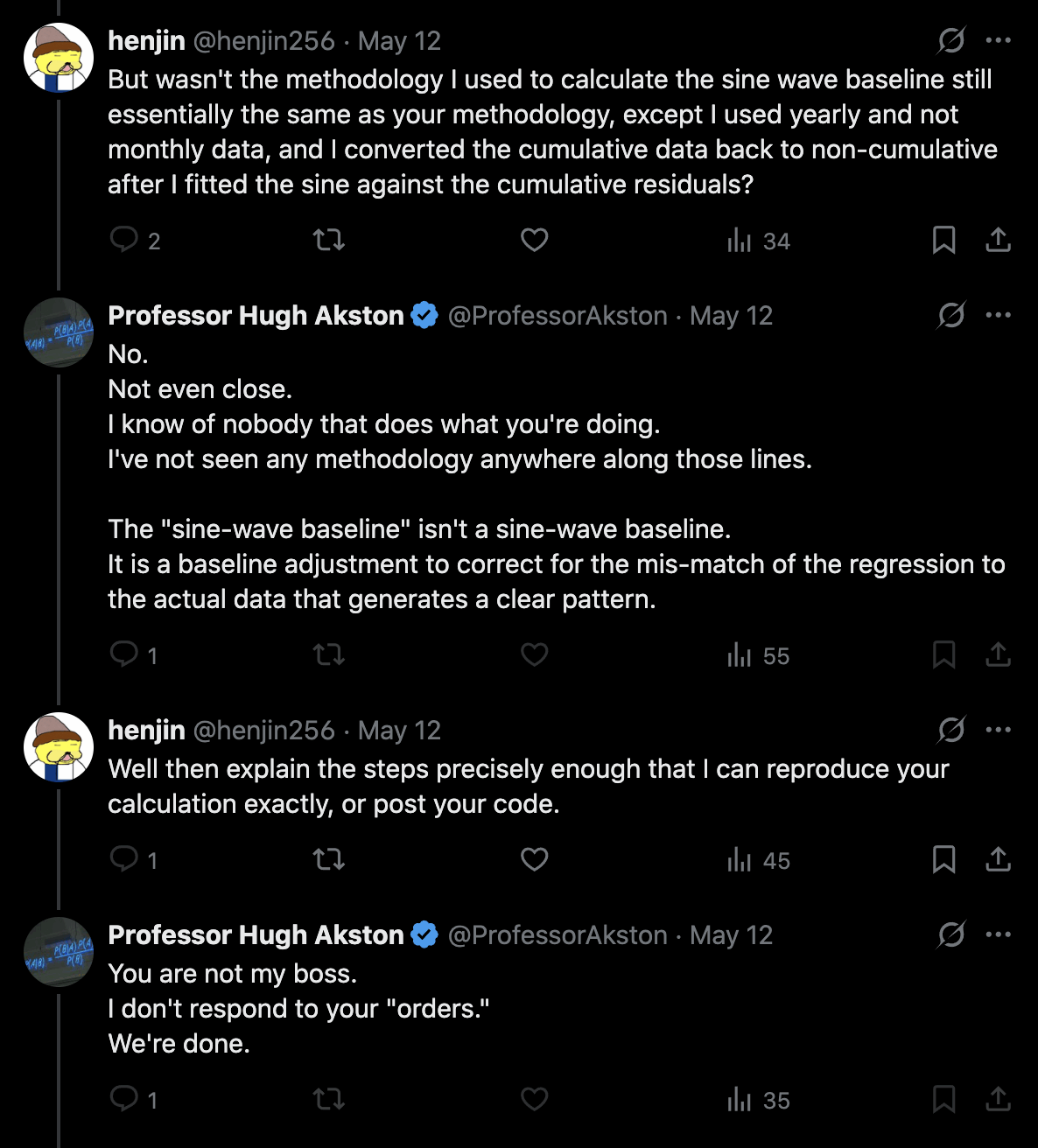
Estimated yearly new cancer cases by American Cancer Society

Ethical Skeptic posted the plot below with this caption: "American Cancer Society Cancer Facts & Figures by Year (with Cancer estimates) - clearly shows a 12.7% excess cancer diagnosis rate, along with a novel 2.7% compounded annualized growth rate. The 2.5-sigma jump in cases immediately following the vaccine rollout is significant. The word 'estimate' here is analytical in context, in that these are not projections, forecasts, nor guesses. They are done objectively and based upon observations in actual inflection and trend." [https://theethicalskeptic.com/2025/06/20/the-state-of-things-pandemic/]

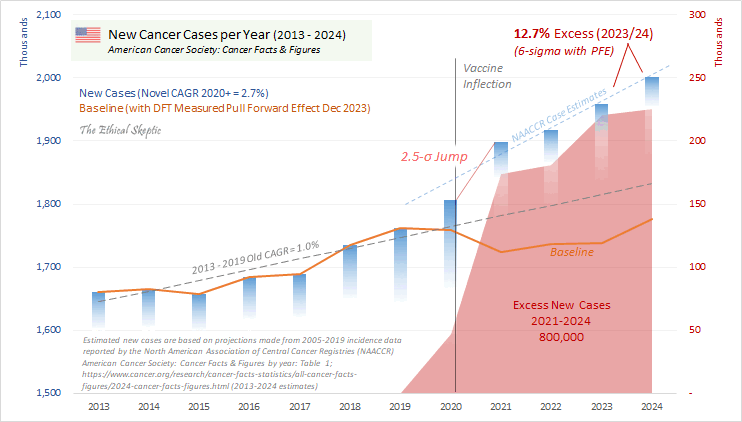
He took the estimated number of new cases in 2024 from a report published by the American Cancer Society titled "Cancer Facts & Figures 2024", the estimate for 2023 from the 2023 report, and so on.

ES blamed the increase in the projected number of cases between 2020 and 2021 on the vaccines. However the estimate for 2021 was based on actual incidence data only up to the year 2017, so it did not take vaccines or even COVID into account: [https://www.cancer.org/research/cancer-facts-statistics/all-cancer-facts-figures/cancer-facts-figures-2021.html]

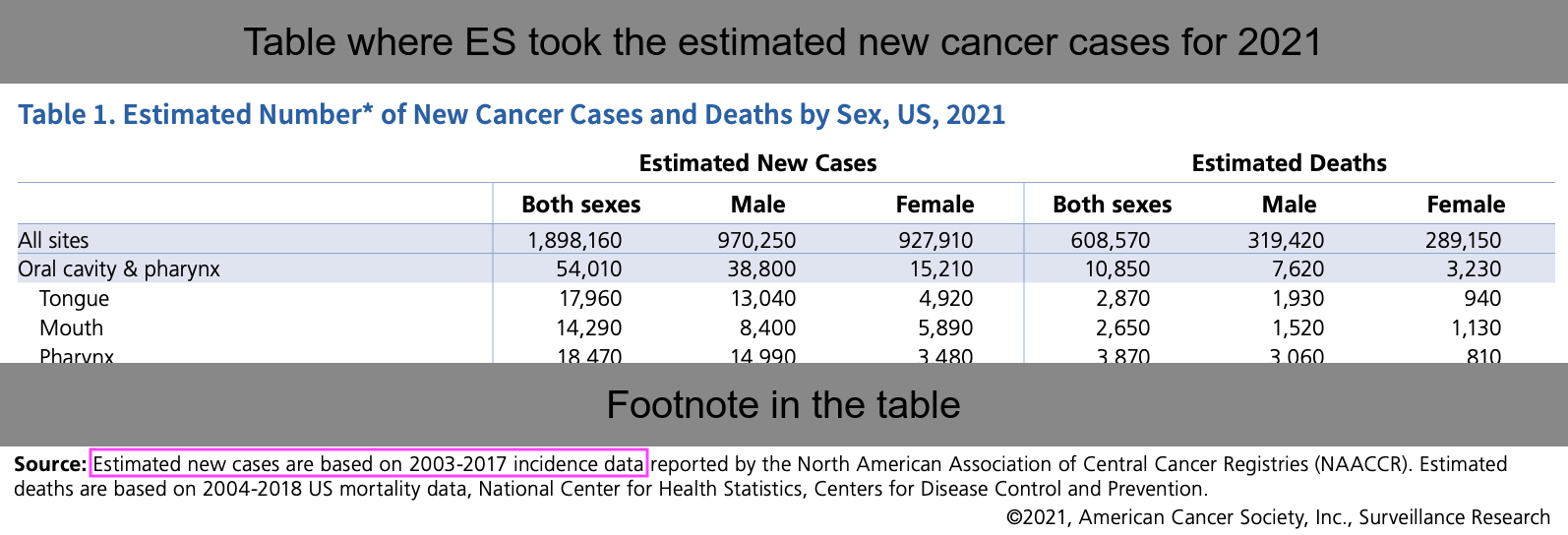
The 2023 report also said: "Importantly, the calculation of these estimates is based on reported cancer incidence and mortality through 2019 and 2020, respectively. Thus, projected cancer cases in 2023 do not account for the impact of the coronavirus disease 2019 (COVID-19) pandemic on cancer diagnoses, and the projected cancer deaths in 2023 only account for the first year." [https://www.cancer.org/research/cancer-facts-statistics/all-cancer-facts-figures/2023-cancer-facts-figures.html]

ES wrote: "The word 'estimate' here is analytical in context, in that these are not projections, forecasts, nor guesses.". However in the paper that the American Cancer Society published about their 2025 estimates, they specifically described their estimates as projections: "The most recent year for which incidence and mortality data are available lags 2-3 years behind the current year because of the time required for data collection, compilation, quality control, and dissemination. Therefore, we project the numbers of new cancer cases and deaths in the United States in 2025 to estimate the contemporary cancer burden using two-step statistical modeling described in detail elsewhere. Briefly, complete cancer diagnoses were estimated for every state from 2007 through 2021 based on high-quality, delay-adjusted incidence data from 50 states and the District of Columbia (99.7% population coverage) and state-level variations in sociodemographic characteristics, lifestyle factors, medical settings, and cancer screening behaviors. Counts were adjusted for the deficit in cases during March through May 2020 because of the COVID-19 pandemic based on the proportion of cases diagnosed in those months in previous years. Modeled state and national counts were then projected 4 years ahead using a novel, data-driven Joinpoint algorithm." [https://acsjournals.onlinelibrary.wiley.com/doi/10.3322/caac.21871]

ES started the x-axis of his plot from 2013, but there was a plateau in the estimated cancer cases around the years 2013-2017, which made the increase since 2020 seem rather impressive in comparison:

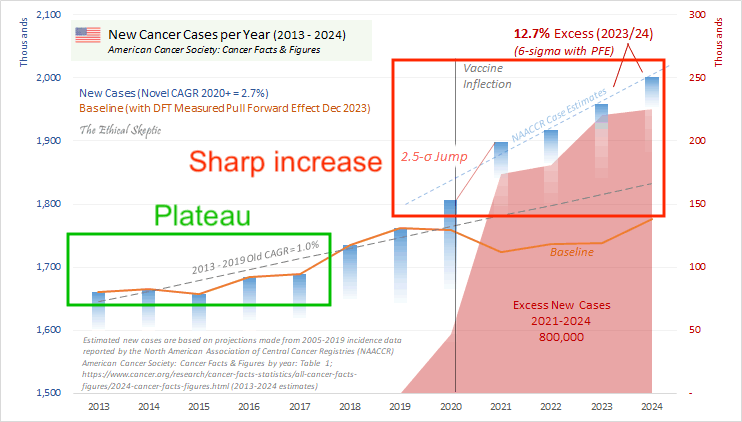
However if he would've extended the x-axis further to the past, people would've seen that the plateau in 2013-2017 was an anomaly relative to the long-term trend, and before the plateau the yearly number of projected new cases increased at a similar rate as in the 2020s:

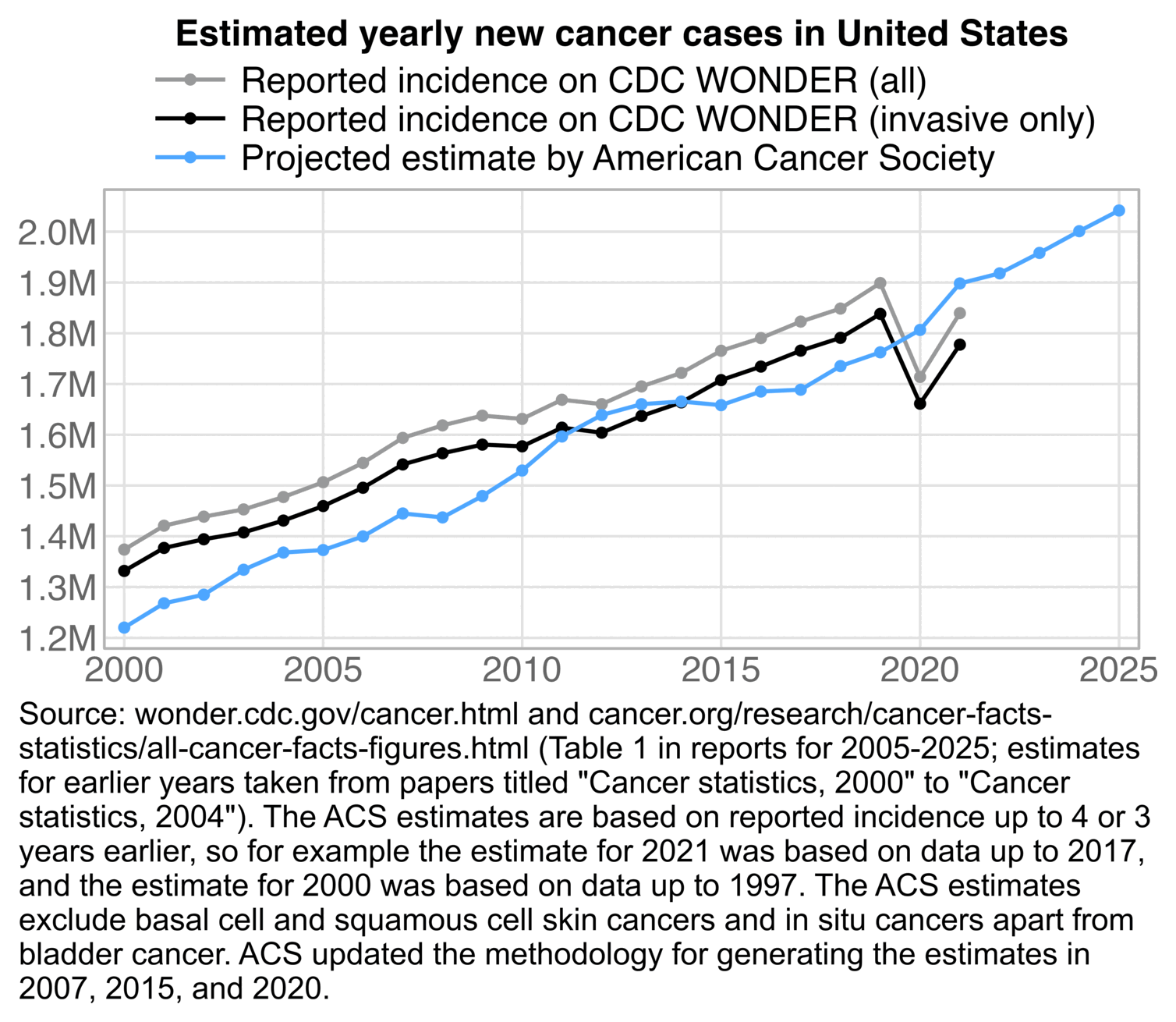
p1=data.table(x=1999:2021,y=c(1344122,1373852,1420906,1438707,1452951,1477359,1506539,1544548,1593851,1618511,1637693,1631299,1668983,1660374,1695256,1721875,1765534,1790526,1822959,1848657,1898978,1713991,1839670),z=1)
p2=data.table(x=2000:2025,y=c(1220100,1268000,1284900,1334100,1368030,1372910,1399760,1444920,1437180,1479350,1529560,1596670,1638910,1660290,1665540,1658370,1685210,1688780,1735350,1762450,1806590,1898160,1918030,1958310,2001140,2041910),z=2)

p=rbind(p1,p2)
p[,z:=factor(z,,c("Reported incidence on CDC WONDER","Projected estimate by American Cancer Society"))]

xstart=2000;xend=2025;xbreak=seq(xstart,xend,5);p=p[x%in%xstart:xend]

ggplot(p)+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_point(aes(x,y,color=z),size=1.1)+
labs(x=NULL,y=NULL,title="Cancer incidence in United States")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak)+
scale_y_continuous(limits=extendrange(p$y),breaks=pretty(p$y,7),labels=\(x)sprintf("%.1fM",x/1e6))+
scale_color_manual(values=c("black",hsv(c(21,30)/36,.7,1)))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.ticks=element_line(linewidth=.4,color="gray70"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4,color="gray70"),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(5,10,5,5),
  plot.title=element_text(size=11.2,face=2,hjust=.5,margin=margin(,,2)))
ggsave("1.png",width=5,height=3,dpi=300*4)

In the plot above one reason for the discrepancy between CDC WONDER and the ACS reports is that the ACS reports exclude "basal cell and squamous cell skin cancers and in situ carcinoma except urinary bladder". [https://www.cancer.org/research/cancer-facts-statistics/all-cancer-facts-figures.html]

A paper by the ACS from 2021 said: "The American Cancer Society (ACS) and the NCI collaborate every 5 to 8 years to update the methods for estimating the numbers of new cancer cases and deaths in the current year". [https://aacrjournals.org/cebp/article-abstract/30/11/1993/670678/Updated-Methodology-for-Projecting-U-S-and-State] So it might explain some of the sudden jumps in the estimates. ChatGPT said the methodology was updated in the years 2007, 2015, and 2020:

2007

2015

2020

The plot by ES was also misleading because it showed a 2013-2019 linear trend for the incidence, but a longer-term linear trend would have been much more steep:

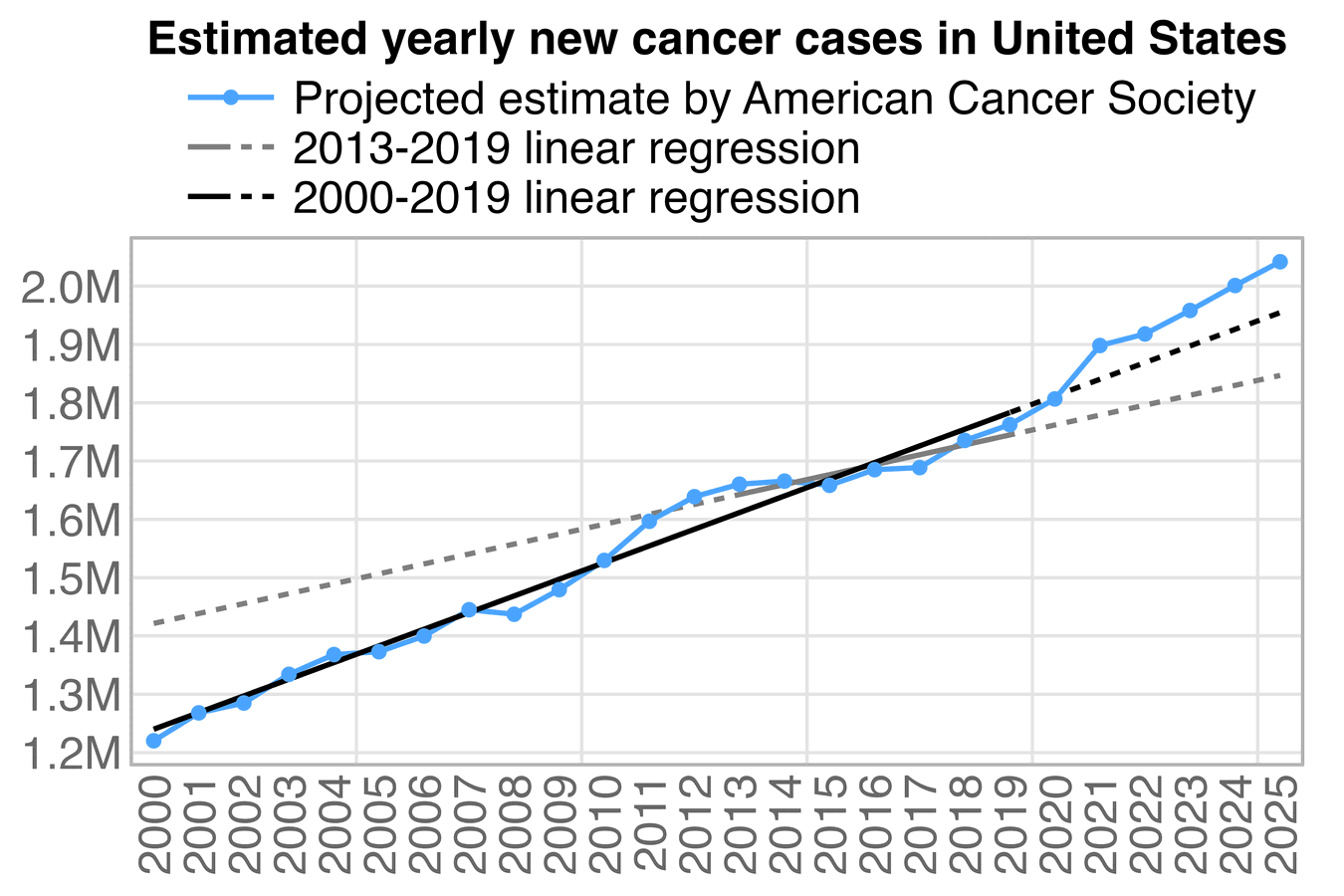
p1=data.table(x=2000:2025,y=c(1220100,1268000,1284900,1334100,1368030,1372910,1399760,1444920,1437180,1479350,1529560,1596670,1638910,1660290,1665540,1658370,1685210,1688780,1735350,1762450,1806590,1898160,1918030,1958310,2001140,2041910),z=1)
p2=p1[,.(x,y=predict(lm(y~x,.SD[x%in%2013:2019]),.SD),z=2)]
p3=p1[,.(x,y=predict(lm(y~x,.SD[x%in%2000:2019]),.SD),z=3)]

p=rbind(p1,p2,p3)
p[,z:=factor(z,,c("Projected estimate by American Cancer Society","2013-2019 linear regression","2000-2019 linear regression"))]

xstart=2000;xend=2025;xbreak=seq(xstart,xend,5);p=p[x%in%xstart:xend]

ggplot(p)+
geom_vline(xintercept=seq(xstart-.5,xend,5),color="gray90",linewidth=.4)+
geom_line(aes(x,y,color=z),linetype="22",linewidth=.6)+
geom_line(data=p[!(z==levels(z)[2]&!x%in%2013:2019)&!(z==levels(z)[3]&x>2019)],aes(x,y,color=z),linewidth=.6)+
geom_point(aes(x,y,color=z,alpha=z),size=1.1)+
labs(x=NULL,y=NULL,title="Estimated yearly new cancer cases in United States")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xstart:xend)+
scale_y_continuous(limits=extendrange(p$y),breaks=pretty(p$y,7),labels=\(x)sprintf("%.1fM",x/1e6))+
scale_color_manual(values=c(hsv(21/36,.7,1),"gray50","black"))+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(override.aes=list(linetype=c("solid","8222","8222"))))+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.4,color="gray70"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4,color="gray70"),
  panel.grid=element_blank(),
  panel.grid.major.y=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(5,10,5,5),
  plot.title=element_text(size=11.2,face=2,hjust=.5,margin=margin(,,2)))
ggsave("1.png",width=4.5,height=3,dpi=300*4)

As of July 2025, the newest year with cancer incidence data available at CDC WONDER is still 2021. [https://wonder.cdc.gov/cancer.html] But in both 2020 and 2021, there was a reduced number of new cancer cases because of reduced screening due to COVID:

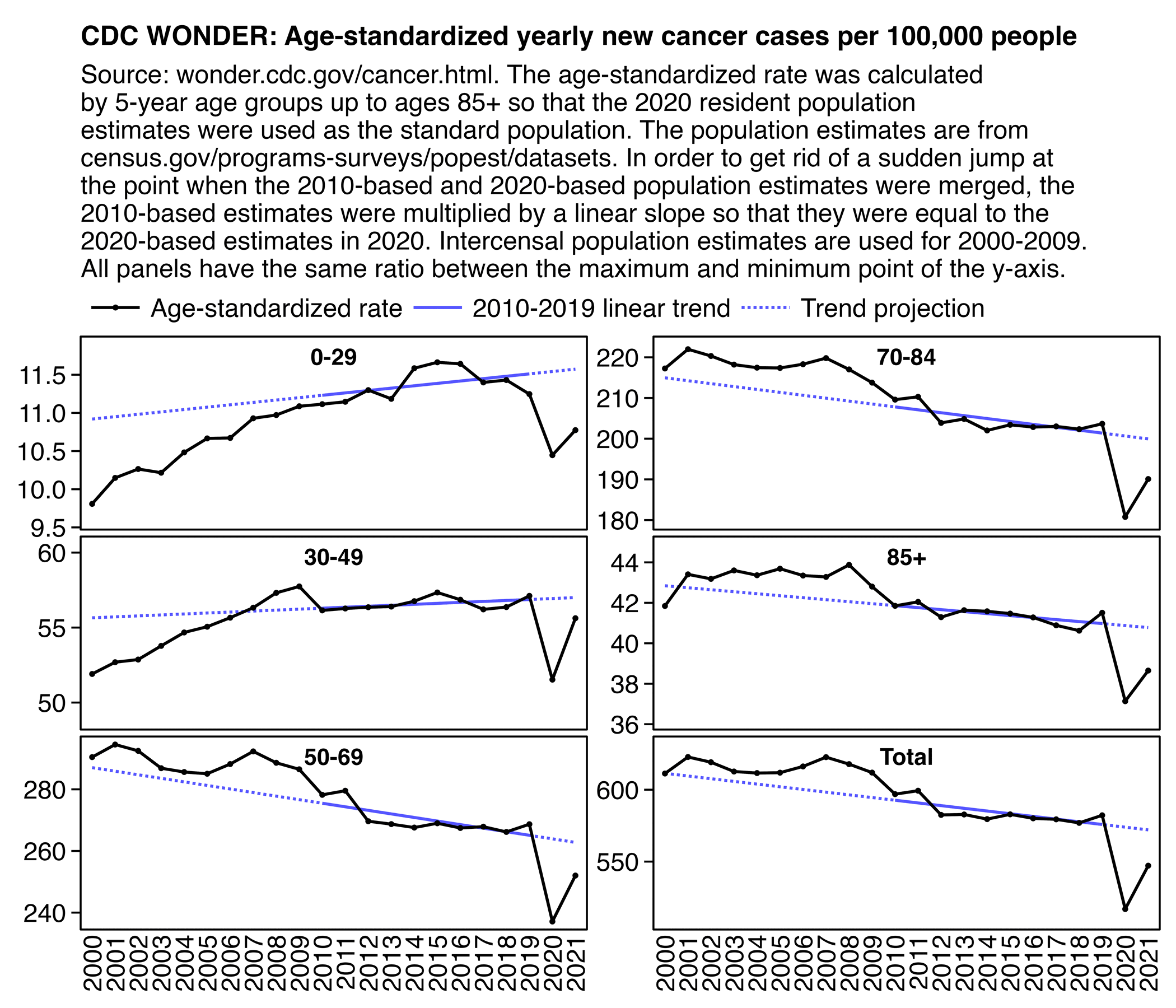
library(data.table);library(ggplot2)

cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)

t=fread("http://sars2.net/f/cancerincidence.csv")

pop=fread("http://sars2.net/f/uspopdead.csv")[year>=2010,.(pop=sum(pop)),.(year,age=cul(age,unique(t$age)))]
pop2=fread("https://www2.census.gov/programs-surveys/popest/datasets/2000-2010/intercensal/national/us-est00int-alldata.csv")
pop=rbind(pop,pop2[MONTH==7&YEAR<2010&AGE!=999,.(pop=sum(TOT_POP)),.(year=YEAR,age=cul(AGE,unique(t$age)))])

t=merge(pop[year==2020,.(age,std=pop/sum(pop))],merge(t,pop))

ages=c(0,30,50,70,85)

p=t[,.(y=sum(cases/pop*std*1e5)),.(x=year,group=agecut(age,ages))]
p=rbind(p,t[,.(y=sum(cases/pop*std*1e5),group="Total"),.(x=year)])

xstart=2000;xend=2021;xbreak=xstart:xend
base=p[x%in%2010:2019,.(x=xbreak,y=predict(lm(y~x),.(x=xbreak))),group]
p$z="Age-standardized rate"
p=rbind(p,base[x%in%2010:2019][,z:="2010-2019 linear trend"],base[,z:="Trend projection"])
p[,z:=factor(z,unique(z))]

expand=p[,.(min=min(y),max=max(y)),group]
rat=expand[,max(max/min)]*1.02
expand=expand[,{x=(rat*min-max)/(1+rat);.(y=c(min-x,max+x),group)}]

ggplot(p,aes(x,y))+
facet_wrap(~group,ncol=2,dir="v",scales="free_y")+
geom_line(aes(linetype=z,color=z),linewidth=.6)+
geom_point(aes(alpha=z),stroke=0,size=1.2)+
geom_line(data=p[z==z[1]],aes(linetype=z,color=z),linewidth=.6)+
geom_text(data=rbind(expand,p[,.(y,group)])[,max(y),group],aes(y=V1,label=group,x=pmean(xstart,xend)),fontface=2,size=3.5,vjust=1.7)+
geom_point(data=expand,x=xstart,alpha=0)+
labs(title="CDC WONDER: Age-standardized yearly new cancer cases per 100,000 people",subtitle=paste0("Source: wonder.cdc.gov/cancer.html. The age-standardized rate was calculated by 5-year age groups up to ages 85+ so that the 2020 resident population estimates were used as the standard population. The population estimates are from census.gov/programs-surveys/popest/datasets. In order to get rid of a sudden jump at the point when the 2010-based and 2020-based population estimates were merged, the 2010-based estimates were multiplied by a linear slope so that they were equal to the 2020-based estimates in 2020. Intercensal population estimates are used for 2000-2009. All panels have the same ratio between the maximum and minimum point of the y-axis.")|>stringr::str_wrap(88),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak)+
scale_y_continuous(breaks=\(x)pretty(x,4))+
coord_cartesian(clip="off",expand=F)+
scale_color_manual(values=c("black","#5555ff","#5555ff"))+
scale_alpha_manual(values=c(1,0,0))+
scale_linetype_manual(values=c("solid","solid","11"))+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length=unit(4,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.position="top",
  legend.justification="left",
  legend.spacing.x=unit(2,"pt"),
  legend.margin=margin(,,6),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  panel.spacing.x=unit(4,"pt"),
  panel.spacing.y=unit(3,"pt"),
  plot.margin=margin(7,7,7,7),
  plot.subtitle=element_text(size=11,margin=margin(,,4)),
  plot.title=element_text(size=11.5,face=2,margin=margin(4,,6)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=7,height=6,dpi=300*4)
system("magick 1.png -resize 25% -colors 256 1.png")

SEER also has incidence data for 2022, but at SEER the age-normalized cancer incidence in 2022 was lower than in 2019: [https://seer.cancer.gov/statistics-network/explorer/application.html]

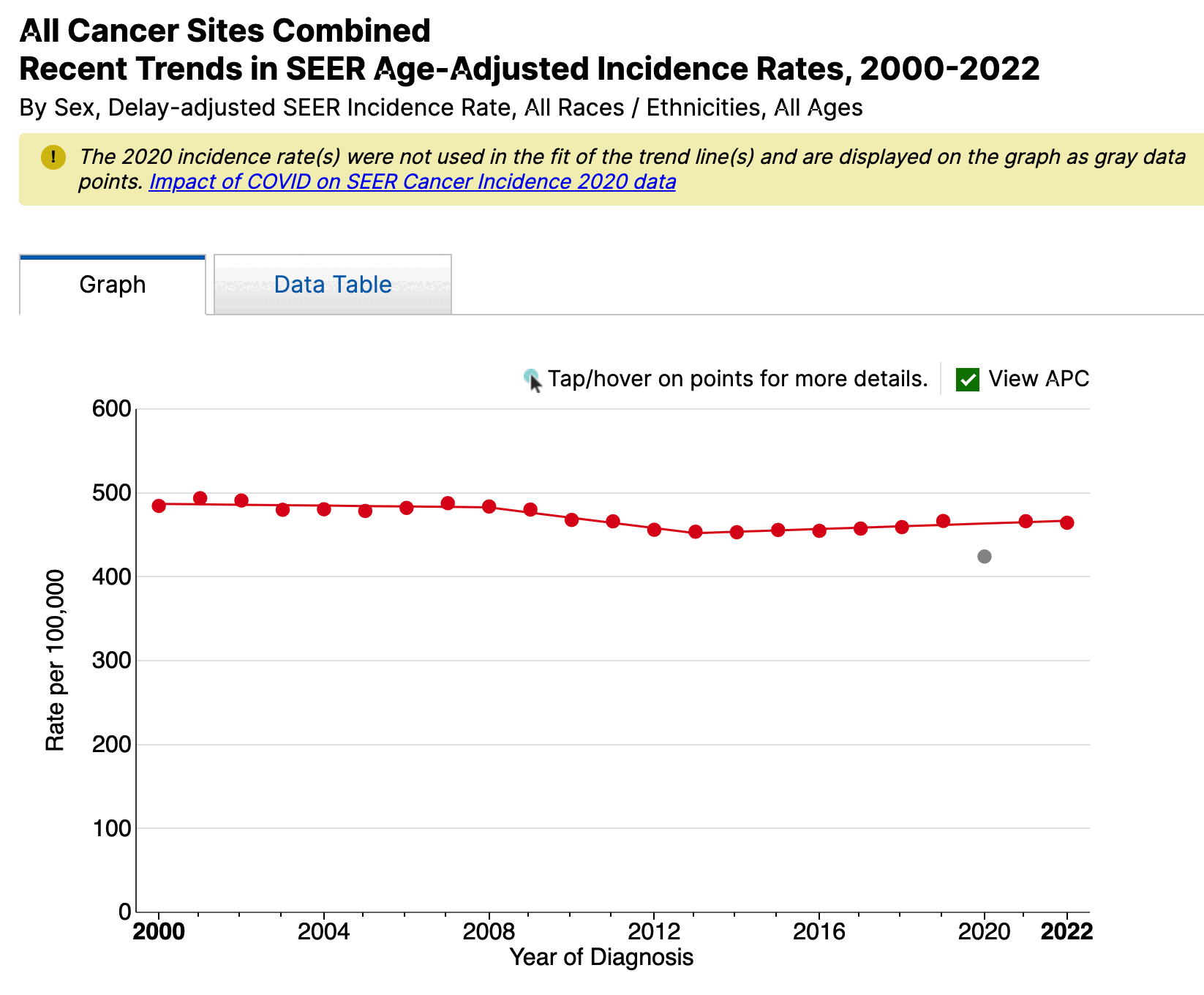
Baseline fitted against summer troughs in 2014-2019

ES posted the plot below and wrote: [https://x.com/EthicalSkeptic/status/1869746508276392017]

How troll-analysts fabricate their disinfo 'graphs':

Paltering the Baseline - fails to detect variation asymmetry in baseline years - Gaussian-blends this bias into their linear regression (creates an unseen future deficit - but looks wonderful now).

Don't possess the real world experience to know to index growth by stable (trough) periods alone.

Fails to employ professional Pull-Forward Effect praxis.

Fail to follow up on their work later, to see if their model was valid (we do this in spades👍).

I can easily replicate their graphs, but could not respect myself or sleep at night if I published them as 'truth'. They do not have the skills to replicate my charts.

However the slope of his yellow-green line doesn't even seem to match the actual summer troughs, because it's above the trough in 2014 but below the trough in 2019.

Here I added four different baselines fitted against the troughs, but all of the baselines were much steeper than the yellow-green line for his "trough regression":

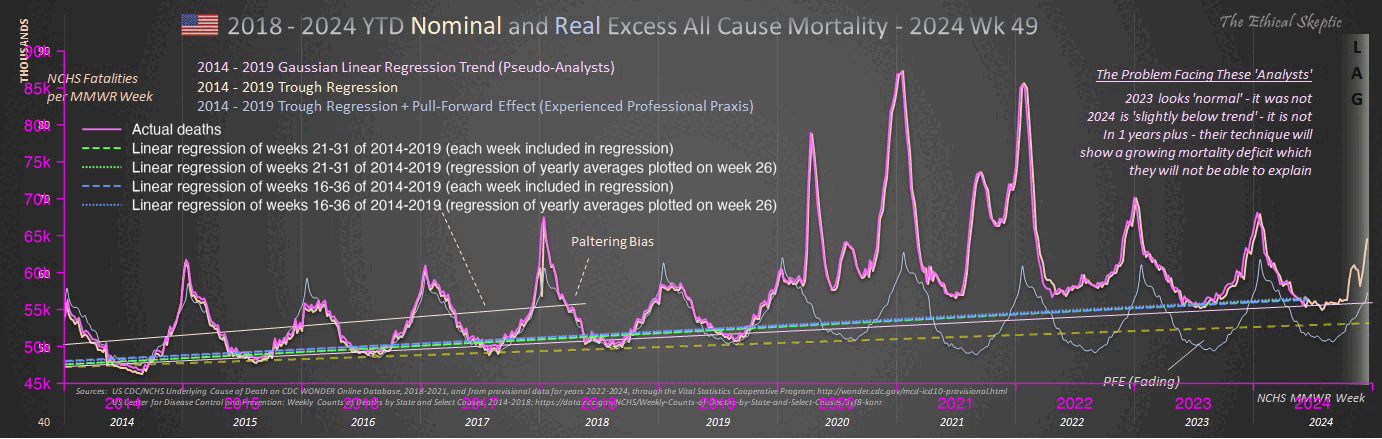
library(data.table);library(ggplot2)

download.file("https://data.cdc.gov/api/views/3yf8-kanr/rows.csv?accessType=DOWNLOAD","Weekly_Counts_of_Deaths_by_State_and_Select_Causes__2014-2019.csv")

t=fread("Weekly_Counts_of_Deaths_by_State_and_Select_Causes__2014-2019.csv")

t=t[t[[1]]=="United States",.(year=`MMWR Year`,week=`MMWR Week`,dead=`All  Cause`,date=as.IDate(`Week Ending Date`,"%m/%d/%Y"))]

t=rbind(t,fread("http://sars2.net/f/wonderdeadweekly.csv")[year>2019&!(year==2024&week>=25)&week!=99])

t$trough=t[year<2020&week%in%21:31,predict(lm(dead~date),t)]
base=merge(t,t[year<2020&week%in%21:31,.(week=26,base=mean(dead)),year])
t$trough2=predict(lm(base~date,base),t)

t$trough3=t[year<2020&week%in%16:36,predict(lm(dead~date),t)]
base2=merge(t,t[year<2020&week%in%16:36,.(week=26,base=mean(dead)),year])
t$trough4=predict(lm(base~date,base2),t)

lab=c("Actual deaths","Linear regression of weeks 21-31 of 2014-2019 (each week included in regression)","Linear regression of weeks 21-31 of 2014-2019 (regression of yearly averages plotted on week 26)","Linear regression of weeks 16-36 of 2014-2019 (each week included in regression)","Linear regression of weeks 16-36 of 2014-2019 (regression of yearly averages plotted on week 26)")
p=t[,.(x=date,y=c(dead,trough,trough2,trough3,trough4),z=factor(rep(lab,each=.N),lab))]

xstart=as.Date("2014-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ybreak=pretty(p$y,7);ystart=ybreak[1];yend=max(ybreak)

ggplot(p,aes(x,y))+
geom_vline(xintercept=c(xstart),color="magenta",linewidth=.2,lineend="square")+
geom_hline(yintercept=c(ystart),color="magenta",linewidth=.2,lineend="square")+
geom_line(aes(color=z,linetype=z),linewidth=.3)+
labs(x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.2,xend+.5),breaks=xbreak,labels=xlab)+
scale_y_continuous(breaks=ybreak,labels=\(x)paste0(x/1e3,"k"))+
scale_color_manual(values=hsv(c(30,12,12,22,22)/36,.6,1))+
scale_linetype_manual(values=c("solid","42","11","42","11"))+
coord_cartesian(ylim=c(ystart,yend),clip="off",expand=F)+
theme(axis.text=element_text(size=6,color="magenta"),
  axis.ticks=element_line(linewidth=.2,color="magenta"),
  axis.ticks.x=element_line(color=alpha("magenta",c(1,0))),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(7,"pt"),
  legend.key.width=unit(18,"pt"),
  legend.position=c(.01,.46),
  legend.justification=c(0,0),
  legend.spacing.x=unit(2,"pt"),
  legend.margin=margin(,,6),
  legend.text=element_text(color="white",size=5.4,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.background=element_rect(fill="transparent",color=NA))
ggsave("1.png",width=7,height=2,dpi=400)

Next I noticed that the State of Things Pandemic article included this explanation of how he calculated the trough baseline: [https://theethicalskeptic.com/2024/12/18/the-state-of-things-pandemic/]

Referencing growth from the least volatile context - specifically, the summer mid-trough months, weighting increasingly more recent years, and avoiding anomalous one year surges or depressions - on a weekly basis offers a superior method for accurate analysis. Academic approaches such as annualized figures, per-capita dilutions, monthly averages, and full-year, monthly, or Gaussian least squares/linear regressions (the fuchsia line in Exhibit 3 above) will serve to palter (distort) the baseline and yield inaccurate progressions in excess mortality. These methods often overweight anomalies in the data, such as remote-in-time depressions (Summer 2014) or surge asymmetry (Winter 2017/18), which are frequently misinterpreted as trend data by less competent analysts. Such anomalies should not be considered part of the background rate, and conflating them with broader trends can lead to erroneous conclusions.

The calculations and method used to establish a salient All Cause Mortality growth rate (1.14% from Chart 1 and Exhibit 3 above) can be seen by clicking on this extract from our 2014 - 2019 baseline module for Chart 1.

The image he linked shows what weights he applied for each year, except the list of weights in orange text is slightly different from the weights shown in black text in the middle of the years. The growth rate is missing for 2019, so I think for example the year 2018 refers to the increase between 2018 and 2019:

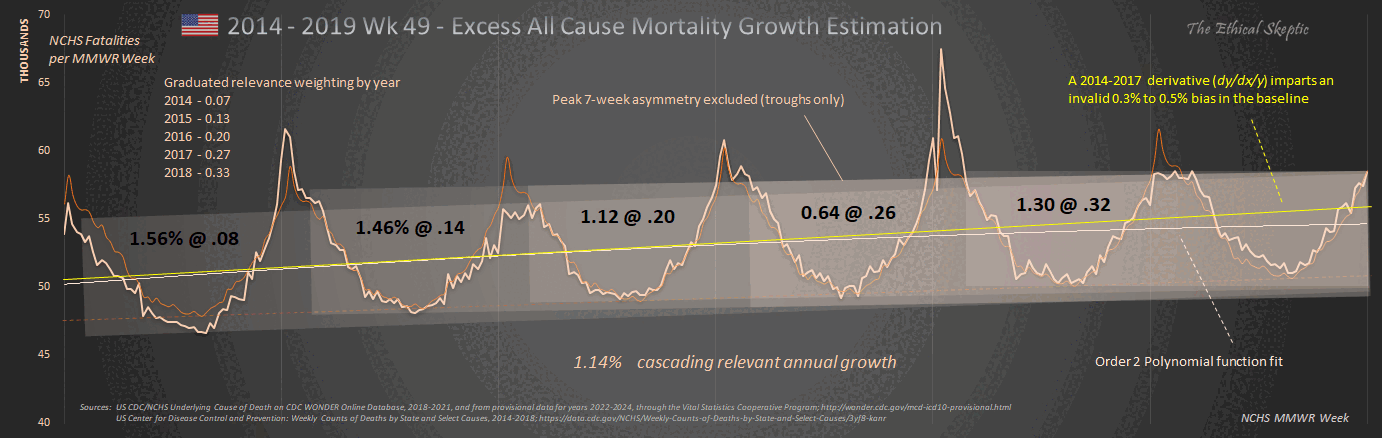
He seems to have calculated the total annual growth rate of about 1.14% by adding together the yearly growth percentages multiplied by the weights shown in the image above (1.56*.08+1.46*.14+1.12*.20+0.64*.26+1.30*.32). However when I used the same weights to calculate a weighted average of yearly growth in deaths on weeks 21 to 31 of 2014-2019, I got an average growth rate of about 1.65%:

f="Weekly_Counts_of_Deaths_by_State_and_Select_Causes__2014-2019.csv"
download.file("https://data.cdc.gov/api/views/3yf8-kanr/rows.csv?accessType=DOWNLOAD",f)
t=fread(f)

a=t[`Jurisdiction of Occurrence`=="United States"&`MMWR Week`%in%16:36,.(dead=sum(`All  Cause`)),.(year=`MMWR Year`)]
a$growthpct=c((a$dead[-1]/head(a$dead,-1)-1)*100,NA)

print(a,r=F)
# year    dead growthpct
# 2014 1008053 2.9655187
# 2015 1037947 1.4521936
# 2016 1053020 1.8066134
# 2017 1072044 0.6089302
# 2018 1078572 2.1455220
# 2019 1101713        NA

weighted.mean(head(a$growthpct,-1),c(8,14,20,26,32))
# 1.64676

My weighted growth rate increased to about 1.80% when I calculated it based on weeks 15-35 instead of weeks 21 to 31. So this method seems to be fairly volatile depending on how many weeks during the summer troughs you include, so Ethical Skeptic should also mention what range of weeks he uses to calculate the baseline. His plot above says "Peak 7-week asymmetry excluded (troughs only)", so I don't know if it means that he fits the baseline by taking 45 weeks from each year (or possibly 46 weeks during years with 53 weeks). But in that case it would be more clear if he wrote that he excludes weeks of peak mortality from the winters instead of saying that he only includes weeks during summer troughs.

When I included only weeks 7 to 51 in my code, I got an average growth rate of about 1.57%, so it was still much higher than the rate of 1.14% shown in the plot by ES. But in case he only excludes 7 weeks from each winter, it's not clear if he excludes a fixed range of weeks from each winter, or if he excludes a different range of 7 weeks from each winter.

But anyway if the deaths would grow by the same percentage each year, then the baseline would be exponential and not linear. So it seems like a hacky solution to determine the slope of a linear baseline based on the average yearly percentage of growth. And I don't even understand how Ethical Skeptic derives the slope of his baseline from a weighted average of the yearly percentage increase.

If yearly deaths increase following a perfectly linear trend, the percentage increase during later years is lower than the percentage increase during earlier years, but Ethical Skeptic gives more weight to later years which might result in a bias to his calculation. In the example below there's 100 deaths the first year, 200 deaths the second year, and so on up to 600 deaths the sixth year. So the deaths increased 100% between the first and second year but only 20% between the fifth and sixth year. But when I took a weighted average of the percentages using Ethical Skeptic's weights, it gave more weight to the later years so the overall percentage increase was about 34.6%, even though the unweighed CAGR for the same range of years would've been about 43%:

deaths=c(100,200,300,400,500,600)
increasepercent=(deaths[2:6]/deaths[1:5]-1)*100 # 100.00 50.00 33.33 25.00 20.00
weights=c(8,14,20,26,32)/100 # taken from plot by ES

sum(increasepercent*weights) # 34.57 (weighted average of growth percentages)
((600/100)^(1/5)-1)*100 # 43.10 (unweighed compound annual growth rate)

Ethical Skeptic wrote that when he fits the baseline, he avoids "anomalous one year surges or depressions", and he gave the summer of 2014 as an example of an anomalous year, but it's not clear if he omits 2014 entirely from his baseline calculation period or if he simply assigns a reduced weight to 2014. And then in order to reproduce his methodology, what criteria should I use to determine which years are anomalous and how much their weights should be reduced or if the years should be excluded entirely? It's also not clear if he applies the same yearly weights for all causes of death or all age groups. So if for example there was an unusually high number of cancer deaths in 2018, then does he reduce the weight for 2018 when he calculates a baseline for cancer deaths?

But in any case his methodology doesn't seem to produce a steep enough baseline in his plot for deaths from all causes since 2014. In US population projections published before COVID, the deaths were projected to start increasing more steeply in the 2020s than the 2010s because of the aging population, so ES should also take it into account when he calculates his initial baseline that has not yet been adjusted for PFE. The long-term trend in raw deaths is also curved upwards if you simply take the prepandemic linear trend in CMR by age and multiply it by the population size of each age, like in the green line in my next plot.

In the next plot I calculated the green baseline by first calculating the total number of deaths for each age in June to September of each year, and then I divided it by 30+31+31+30 and multiplied it by 7, and I plotted the result on August 1st of each year. Then I divided the deaths by the population size of each age in June to September based on monthly population estimates published by the Census Bureau, where I used DIY intercensal estimates for 2010-2019. And then I calculated a linear regression of the CMR values for each age in 2014-2019 and I multiplied the projected regression by the population size to get the expected deaths.

However my green baseline was much higher in 2023 than Ethical Skeptic's yellow-green baseline, even though my baseline accounted for the reduction in population size due to excess deaths since 2020 but the baseline by ES did not:

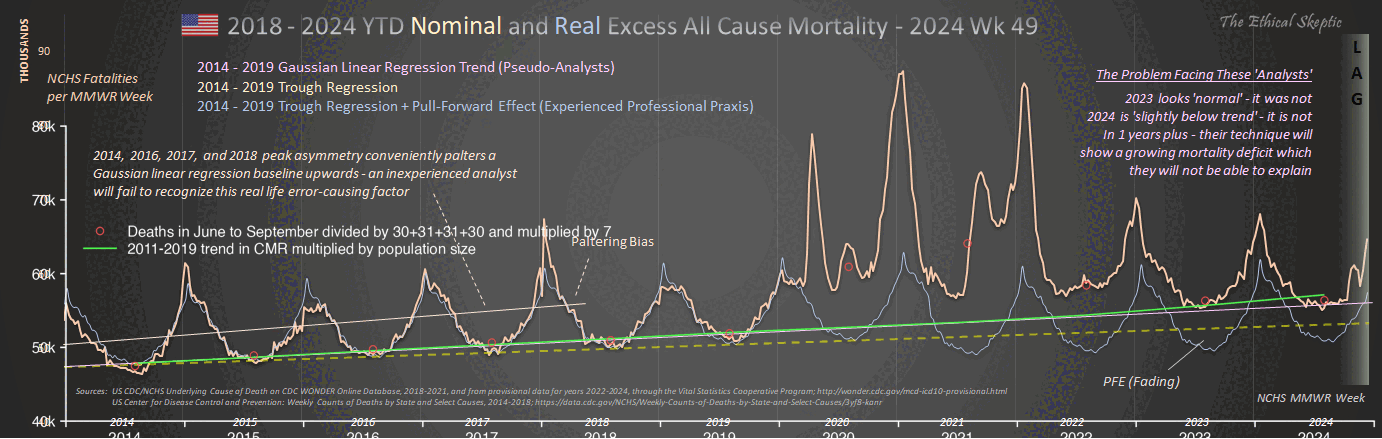
t=fread("http://sars2.net/f/uspopdeadmonthly.csv")
mult=7/(31+30+31+31)
t=t[month%in%5:8,.(dead=sum(dead)*mult,pop=sum(persondays)*mult),.(year,age)]
t=merge(t[year%in%2014:2019,.(year=1999:2024,base=predict(lm(dead/pop~year),.(year=1999:2024))),age],t)
lab=c("Deaths in May to August divided by 31+30+31+31 and multiplied by 7","2014-2019 trend in CMR by age multiplied by population size (May to August only)")
p=t[,.(y=c(sum(dead),sum(base*pop)),z=lab),.(x=as.Date(paste0(year,"-7-1")))]
p[,z:=factor(z,lab)]

xstart=as.Date("2014-1-1");xend=as.Date("2024-1-1")
p=p[x%in%xstart:xend]
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ybreak=4:8*1e4;ystart=4e4;yend=8e4

ggplot(p,aes(x,y))+
geom_line(aes(linewidth=z,color=z,linetype=z))+
geom_point(aes(color=z,alpha=z),size=1.4,stroke=.3,shape=1)+
labs(x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x/1e3,"k"))+
scale_color_manual(values=c("#ff6666",hsv(12/36,.6,1)))+
scale_linetype_manual(values=c("solid","solid"))+
scale_linewidth_manual(values=c(0,.3))+
scale_alpha_manual(values=c(1,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.line=element_line(linewidth=.3,color="white",lineend="square"),
  axis.text=element_text(size=6,color="white"),
  axis.ticks=element_line(linewidth=.2,color="white"),
  axis.ticks.x=element_line(color=alpha("white",c(1,0))),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(7,"pt"),
  legend.key.width=unit(18,"pt"),
  legend.position=c(.01,.6),
  legend.justification=c(0,0),
  legend.spacing.x=unit(2,"pt"),
  legend.margin=margin(,,6),
  legend.text=element_text(color="white",size=5.4,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.background=element_rect(fill="transparent",color=NA))
ggsave("1.png",width=7,height=2.05,dpi=400)

This shows how I calculated the green baseline for 2023:

t=fread("http://sars2.net/f/uspopdeadmonthly.csv")
mult=7/(31+30+31+31)
t=t[month%in%5:8,.(dead=sum(dead)*mult,pop=sum(persondays)*mult),.(year,age)]
t=merge(t[year%in%2014:2019,.(year=1999:2024,base=predict(lm(dead/pop~year),.(year=1999:2024))),age],t)
t[year==2023,sum(base*pop)] # 55537.03

Next I tried doing a simple linear regression of deaths in June to September of each year. But regardless of whether I excluded 2014 from the fitting period or not, my baseline was still much higher in 2023 than Ethical Skeptic's yellow-green baseline:

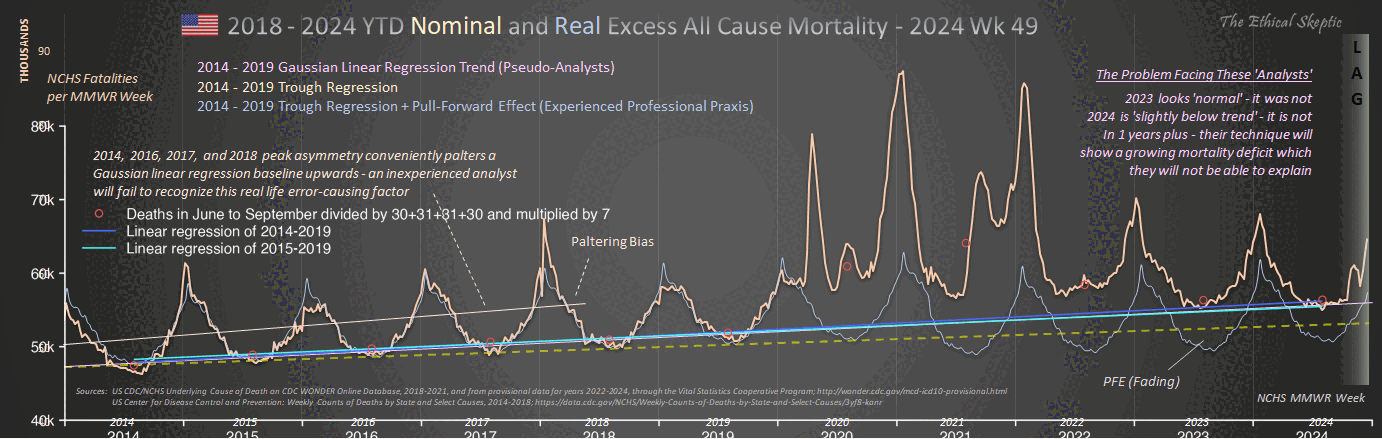
t=fread("https://sars2.net/f/uspopdeadmonthly.csv")[year<2025]

mult=7/(30+31+31+30)
a=t[month%in%6:9,.(dead=sum(dead)*mult),year]

dead2=a[year%in%2014:2019,predict(lm(dead~year),a)]
dead3=a[year%in%2015:2019,predict(lm(dead~year),a)]

p=a[,.(x=year,y=c(dead,dead2,dead3),z=rep(1:3,each=.N))]
p[,z:=factor(z,,c("Deaths in June to September divided by 30+31+31+30 and multiplied by 7","Linear regression of 2014-2019","Linear regression of 2015-2019"))]

p[,x:=as.Date(paste0(x,"-7-1"))]

xstart=as.Date("2014-1-1");xend=as.Date("2025-1-1")
p=p[x%in%xstart:xend]
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ybreak=4:8*1e4;ystart=4e4;yend=8e4

ggplot(p)+
geom_line(aes(x,y,linewidth=z,color=z))+
geom_point(aes(x,y,color=z,alpha=z),size=1.4,stroke=.3,shape=1)+
labs(x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x/1e3,"k"))+
scale_color_manual(values=hsv(c(0,23,18)/36,.7,1))+
scale_linewidth_manual(values=c(0,.3,.3))+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.line=element_line(linewidth=.3,color="white",lineend="square"),
  axis.text=element_text(size=7,color="white"),
  axis.ticks=element_line(linewidth=.3,color="white"),
  axis.ticks.x=element_line(color=alpha("white",c(1,0))),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(8,"pt"),
  legend.key.width=unit(20,"pt"),
  legend.position=c(.01,.52),
  legend.justification=c(0,0),
  legend.spacing.x=unit(3,"pt"),
  legend.margin=margin(,,5),
  legend.text=element_text(color="white",size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.background=element_rect(fill="transparent",color=NA))
ggsave("1.png",width=9,height=2.2,dpi=300)

But I guess the reason why I can't reproduce his baseline is my lack of professional praxis. Ethical Skeptic is a professional taurus coprotor.

Excess deaths compared to percentage of vaccinated people in European countries

Ethical Skeptic posted the plot below with this caption: "Cumulative Excess Mortality (Last 12 Months - Relative to Population) vs Percentage Population Vaccinated - (click on image to expand) - once the noise cleared from national mortality data sets, it became abundantly clear that excess death was non-linearly proportional to the rate of vaccination by European country. The dip in excess mortality below the zero-line of the x-axis (Cumulative Excess Mortality) is Pull-Forward Effect (PFE). The reason the curve flattens near the lower end, is that the nations in this section of the chart are smaller in population, and there is a consequential denominator amplification of the cumulative excess death (relative to population) in the data for smaller nations. The excess mortality in each nation is actually higher than these indices indicate, and the relationship to the vaccine is stark." [https://theethicalskeptic.com/2024/12/18/the-state-of-things-pandemic/]

He listed this file as his source: https://github.com/owid/covid-19-data/tree/master/public/data/excess_mortality. The file has many different columns, so it's not clear if he plotted the value of the cum_excess_per_million_proj_all_ages column which shows excess deaths relative to the 2015-2019 linear projection or some of the other columns that show excess deaths relative to a 2015-2019 average baseline. It's also not clear which period of time his plot shows, but the cum_excess_per_million_proj_all_ages column only includes data up to December 2023, so in the next plot I plotted total excess deaths from December 2022 up to December 2023 so that for both months I picked the last date with data available for each country:

library(data.table);library(ggplot2)

t=fread("https://raw.githubusercontent.com/owid/covid-19-data/refs/heads/master/public/data/excess_mortality/excess_mortality.csv")
o=fread("owid-covid-data.csv")

t2=t[,.(location,date,cum=cum_excess_per_million_proj_all_ages)]
t2=na.omit(t2[location%in%o[continent=="Europe",unique(location)]])
cum=t2[date%like%"2023-12"][rev(order(date))][rowid(location)==1,.(location,cum2=cum)]
cum=merge(cum,t2[date%like%"2022-12"][rev(order(date))][rowid(location)==1,.(location,cum)])

vax=na.omit(o[,.(date,location,vax=people_vaccinated_per_hundred)])[order(-date)][rowid(location)==1]
p=merge(cum,vax)[,.(x=cum2-cum,y=vax,location)]

east=strsplit("Bulgaria,Croatia,Czechia,Estonia,Hungary,Latvia,Poland,Romania,Serbia,Slovenia,Slovakia,Russia,Kosovo,Montenegro,Albania,North Macedonia,Bosnia and Herzegovina",",")[[1]]
lab=c("Not eastern bloc","Eastern bloc")
p[,z:=factor(ifelse(location%in%east,lab[2],lab[1]),lab)]

xbreak=p[,pretty(x,7)];ybreak=p[,pretty(y,7)]

ggplot(p,aes(x,y))+
coord_cartesian(clip="off",expand=F)+
geom_smooth(method="lm",formula=y~x,linewidth=.5,se=F,color="black",linetype="42")+
geom_vline(xintercept=0,linewidth=.4,color="gray60")+
geom_hline(yintercept=0,linewidth=.4,color="gray60")+
geom_point(aes(color=z),size=.6)+
ggrepel::geom_text_repel(aes(label=location,color=z),size=3,max.overlaps=Inf,segment.size=.3,min.segment.length=.2,box.padding=.07,show.legend=F)+
labs(title=sprintf("OWID: Excess deaths in December 2022 to December 2023 vs\npercentage of vaccinated people (r ≈ %.2f)",p[,cor(x,y)]
),x="Excess deaths per million in December 2022 to December 2023",y="Percentage of vaccinated people at OWID")+
scale_x_continuous(limits=range(xbreak),breaks=xbreak)+
scale_y_continuous(limits=range(ybreak),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("#5555ff","#ff4444"))+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(margin=margin(3)),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length=unit(4,"pt"),
  axis.title=element_text(size=11),
  axis.title.x=element_text(margin=margin(3)),
  axis.title.y=element_text(margin=margin(,2)),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.justification="right",
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.margin=margin(,,6),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  panel.grid.major=element_blank(),
  plot.margin=margin(4,18,4,4),
  plot.subtitle=element_text(size=11),
  plot.title=element_text(size=11,face=2,margin=margin(1,,4),hjust=0))
ggsave("1.png",width=6.2,height=4,dpi=300*4)
system("mogrify 1.png -trim -resize 25% -bordercolor white -border 30 -colors 256 1.png")

In Ethical Skeptic's plot the cumulative excess deaths ranged from about -4,500 to 18,000, but in my plot above the cumulative excess deaths per million ranged between about -1,100 and 1,300. I got a similar magnitude of variation when I tried plotting other ranges of 12 months that started in 2022 and ended in 2023. So I don't know if Ethical Skeptic plotted some other variable instead of the cum_excess_per_million_proj_all_ages variable, or if he multiplied the value of the variable by 10 or something.

But in any case both the 2015-2019 linear trend and the 2015-2019 average baseline exaggerate excess deaths in Western European countries relative to Eastern European countries.

In the next plot I calculated excess deaths relative to a 2013-2019 linear trend in ASMR instead. I took data for weekly deaths by 5-year age groups from the Eurostat dataset demo_r_mwk_05: https://ec.europa.eu/eurostat/api/dissemination/sdmx/2.1/data/demo_r_mwk05?format=TSV. I determined the slope of the baseline based on only weeks 15-35 of each year, but I used a different intercept for each ISO week number. I took yearly population estimates on January 1st from the Eurostat dataset demo_pjan and interpolated them into weekly population estimates. Then I divided the total weekly ASMR in 2023 with the total baseline for ASMR in 2023, where I treated weeks whose middle day was in 2023 as part of 2023. I used weekly data because Eurostat's dataset for yearly deaths by age was still missing data for 2023. But anyway, now the correlation between excess mortality and the percentage of vaccinated people dropped to about 0.01:

library(data.table);library(ggplot2)

o=fread("owid-covid-data.csv")

isoweek=\(year,week,weekday=7){d=as.Date(paste0(year,"-1-4"));d-(as.integer(format(d,"%w"))+6)%%7-1+7*(week-1)+weekday}
q=\(...)as.character(substitute(...()))
ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

euro=fread("demo_r_mwk_05.tsv")
meta=fread(text=euro[[1]],header=F)
pick=meta[,V2%like%"^Y"&V3=="T"];meta=meta[pick];euro=euro[pick]
meta[,age:=as.integer(sub("\\D+(\\d+).*","\\1",sub("Y_LT5",0,V2)))]
eu=meta[,.(loc=V5,age,date=rep(names(euro)[-1],each=.N),dead=as.integer(sub("\\D+","",unlist(euro[,-1],,F))))]
eu[,year:=as.integer(substr(date,1,4))][,week:=as.integer(substr(date,7,8))]
eu[,date:=isoweek(year,week,4)]
eu=eu[loc%in%eu[year%in%2013:2023,.N,loc][N==max(N),loc]]
eu=eu[year>=2013]

pop=fread("http://sars2.net/f/eurostatpopdead.csv.gz")[year%in%2013:2023]
a=pop[,.(pop=sum(pop)),.(location,name,date=as.Date(paste0(year,"-1-1")),age=pmin(age,90)%/%5*5)]
a=a[location%in%na.omit(a)[,.N,location][N==max(N),location]]
a=a[,spline(date,pop,xout=unique(eu$date),method="natural"),.(location,age,name)]

a=merge(eu,a[,.(date=`class<-`(x,"Date"),pop=y,loc=location,name,age)])
a=merge(pop[location=="EU27_2020"&year==2020,.(pop=sum(pop)),.(age=pmin(age,90)%/%5*5)][,.(age,std=pop/sum(pop))],a)
a=a[loc%in%na.omit(a)[year%in%2013:2023,.N,loc][N==max(N),loc]]

a=a[,.(dead=sum(dead),asmr=sum(dead/pop*std/7*365e5)),,.(name,date,year,week)]
slope=a[year%in%2013:2019&week%in%15:35,mean(asmr),.(year,name)]
slope=slope[,{x=.(year=2013:2024,slope=predict(lm(V1~year),.(year=2013:2024)));x$slope=x$slope/x$slope[x$year==2016];x},name]
weekly=a[year%in%2013:2019,.(weekly=mean(asmr)),.(week,name)]
a=merge(slope,merge(weekly,a))
a=merge(a[year%in%2016:2019,.(deadbase=mean(dead)),.(name,week)],a)
p=a[year==2023,.(pct2=(sum(asmr)/sum(slope*weekly)-1)*100),name]

vax=o[rev(order(date))][,vax:=people_vaccinated_per_hundred][!is.na(vax)][rowid(location)==1,.(vax,name=location)]
p=na.omit(merge(vax,p))[,.(x=pct2,y=vax,name)]

east=q(Estonia,Latvia,Poland,Czechia,Slovakia,Hungary,Montenegro,Slovenia,Croatia,Serbia,Romania,Bulgaria)
p[,z:=ifelse(name%in%east,"Eastern bloc","Not eastern bloc")]
p[,z:=factor(z,unique(z))]

xbreak=pretty(p$x,8);ybreak=pretty(p$y,8)

ggplot(p,aes(x,y))+
geom_smooth(method="lm",formula=y~x,linewidth=.5,se=F,color="black",linetype="42")+
coord_cartesian(clip="off",expand=F)+
geom_vline(xintercept=0,linewidth=.4,color="gray60")+
geom_hline(yintercept=0,linewidth=.4,color="gray60")+
geom_point(aes(color=z),size=.6)+
ggrepel::geom_text_repel(aes(label=name,color=z),size=3,max.overlaps=Inf,segment.size=.3,min.segment.length=.2,box.padding=.07,show.legend=F)+
labs(title=sprintf("Excess ASMR in 2023 vs percentage of vaccinated people (r ≈ %.2f)",p[,cor(x,y)]
),x="Excess ASMR in 2023 at Eurostat",y="Percentage of vaccinated people at OWID")+
scale_x_continuous(limits=range(xbreak),breaks=xbreak,labels=\(x)paste0(x,"%"))+
scale_y_continuous(limits=range(ybreak),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("#5555ff","#ff4444"))+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(margin=margin(3)),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length=unit(4,"pt"),
  axis.title=element_text(size=11),
  axis.title.x=element_text(margin=margin(3)),
  axis.title.y=element_text(margin=margin(,2)),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.position="top",
  legend.justification="right",
  legend.spacing.x=unit(2,"pt"),
  legend.margin=margin(,,6),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  panel.grid.major=element_blank(),
  plot.margin=margin(4,18,4,4),
  plot.title=element_text(size=11,face=2,margin=margin(1,,4),hjust=1))
ggsave("1.png",width=6.2,height=4,dpi=300*4)
system("mogrify 1.png -trim -resize 25% -bordercolor white -border 30 -colors 256 1.png")

The next plot shows that compared to OWID's 2015-2019 linear baseline, Eurostat's 2016-2019 average baseline overestimates the excess deaths in Western European countries relative to Eastern European countries even more in 2022:

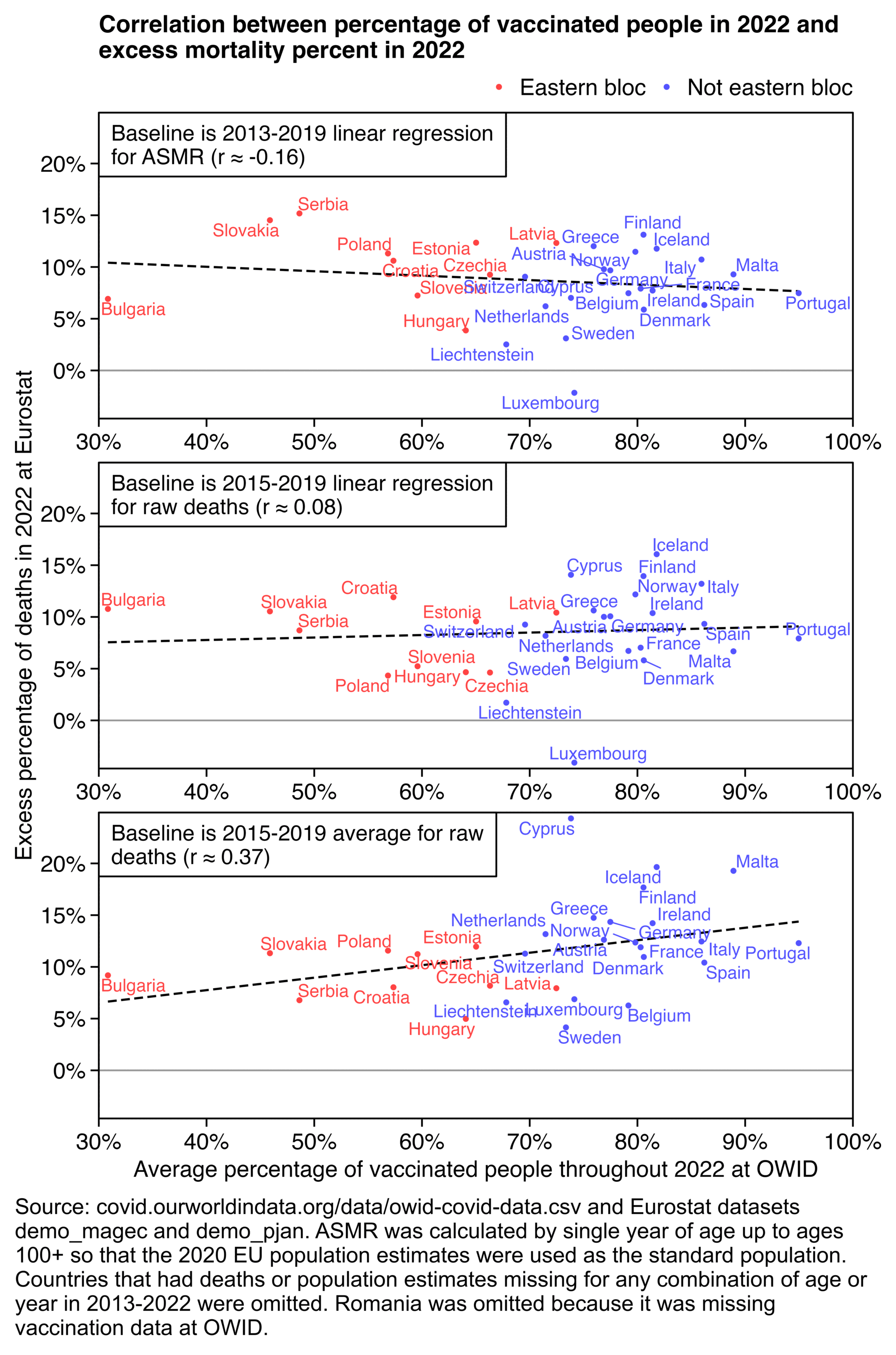
download.file("https://covid.ourworldindata.org/data/owid-covid-data.csv","owid-covid-data.csv")

library(data.table);library(ggplot2)

o=fread("owid-covid-data.csv")

t=fread("http://sars2.net/f/eurostatpopdead.csv.gz")[year%in%2013:2022]
t=merge(t,t[location=="EU27_2020"&year==2020,.(age,std=pop/sum(pop))])
t=t[location%in%na.omit(t)[,.N,location][N==max(N),location]]
t=t[!location%in%c("DE_TOT")]

a=t[,.(dead=sum(dead),asmr=sum(dead/pop*std)*1e5),.(location,name,year)]
a$base=a[year<2020,predict(lm(asmr~year),.(year=2013:2022)),location]$V1
a$base2=a[year%in%2015:2019,predict(lm(dead~year),.(year=2013:2022)),location]$V1
a=merge(a,a[year%in%2015:2019,.(base3=mean(dead)),location])
p=a[year==2022,.(y1=(asmr/base-1)*100,y2=(dead/base2-1)*100,y3=(dead/base3-1)*100),name]

p=merge(p,o[year(date)==2022,.(vaxpct=mean(people_vaccinated_per_hundred,na.rm=T)),.(name=location)])
p=na.omit(p)

lab=c("2013-2019 linear regression for ASMR","2015-2019 linear regression for raw deaths","2015-2019 average for raw deaths")
p=p[,.(name,x=vaxpct,y=c(y1,y2,y3),facet=factor(rep(lab,each=.N),lab))]

q=\(...)as.character(substitute(...()))
east=q(Bulgaria,Croatia,Czechia,Estonia,Hungary,Latvia,Poland,Romania,Serbia,Slovenia,Slovakia)
lab=c("Eastern bloc","Not eastern bloc")
p$z=factor(ifelse(p$name%in%east,lab[1],lab[2]),lab)

levels(p$facet)=p[,cor(x,y),facet][,sprintf("Baseline is %s (r ≈ %.2f)",facet,V1)]

xbreak=pretty(p$x,7);ybreak=pretty(p$y,7);ylim=extendrange(p$y,,.02)

ggplot(p,aes(x,y))+
facet_wrap(~facet,dir="v",scales="free_x")+
coord_cartesian(clip="off",expand=F)+
geom_vline(xintercept=0,linewidth=.4,color="gray60")+
geom_hline(yintercept=0,linewidth=.4,color="gray60")+
geom_smooth(method="lm",formula=y~x,linewidth=.5,se=F,color="black",linetype="42")+
geom_label(data=p[rowid(facet)==1],aes(label=stringr::str_wrap(facet,40)),x=xbreak[1],y=ylim[2],lineheight=.9,hjust=0,vjust=1,size=3.7,label.r=unit(0,"pt"),label.padding=unit(6,"pt"),label.size=.4)+
geom_point(aes(color=z),size=.7)+
ggrepel::geom_text_repel(aes(label=name,color=z),size=3,max.overlaps=Inf,segment.size=.3,min.segment.length=.2,box.padding=.07,show.legend=F)+
labs(title="Correlation between percentage of vaccinated people in 2022 and\nexcess mortality percent in 2022",x="Average percentage of vaccinated people throughout 2022 at OWID",y="Excess percentage of deaths in 2022 at Eurostat")+
scale_x_continuous(breaks=xbreak,limits=range(xbreak),labels=\(x)paste0(x,"%"))+
scale_y_continuous(breaks=ybreak,limits=ylim,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c("#ff4444","#5555ff"))+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(margin=margin(3)),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length=unit(4,"pt"),
  axis.title=element_text(size=11),
  axis.title.x=element_text(margin=margin(3)),
  axis.title.y=element_text(margin=margin(,2)),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(16,"pt"),
  legend.position="top",
  legend.justification="right",
  legend.spacing.x=unit(2,"pt"),
  legend.margin=margin(,,6),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  panel.grid.major=element_blank(),
  panel.spacing=unit(4,"pt"),
  plot.margin=margin(6,22,5,5),
  plot.subtitle=element_text(size=11),
  plot.title=element_text(size=11.5,face=2,margin=margin(1,,5)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=6,height=8,dpi=300*4)

sub="Source: covid.ourworldindata.org/data/owid-covid-data.csv and Eurostat datasets demo_magec and demo_pjan. ASMR was calculated by single year of age up to ages 100+ so that the 2020 EU population estimates were used as the standard population. Countries that had deaths or population estimates missing for any combination of age or year in 2013-2022 were omitted. Romania was omitted because it was missing vaccination data at OWID."
system(paste0("mogrify -trim 1.png;w=`identify -format %w 1.png`;magick 1.png \\( -size $[w]x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\'",sub),"' -splice x100 \\) -append -resize 25% -bordercolor white -border 30 -colors 256 1.png"))

I wrote about the bias introduced by Eurostat's 2016-2019 average baseline in more detail here: statistic2.html#Excess_mortality_in_European_countries_compared_to_percentage_of_vaccinated_people.

Pull-forward effect in Romania

Ethical Skeptic quoted this plot of deaths in Romania: [https://x.com/EthicalSkeptic/status/1875661812336881970, https://x.com/felicittina/status/1875501071579410535]

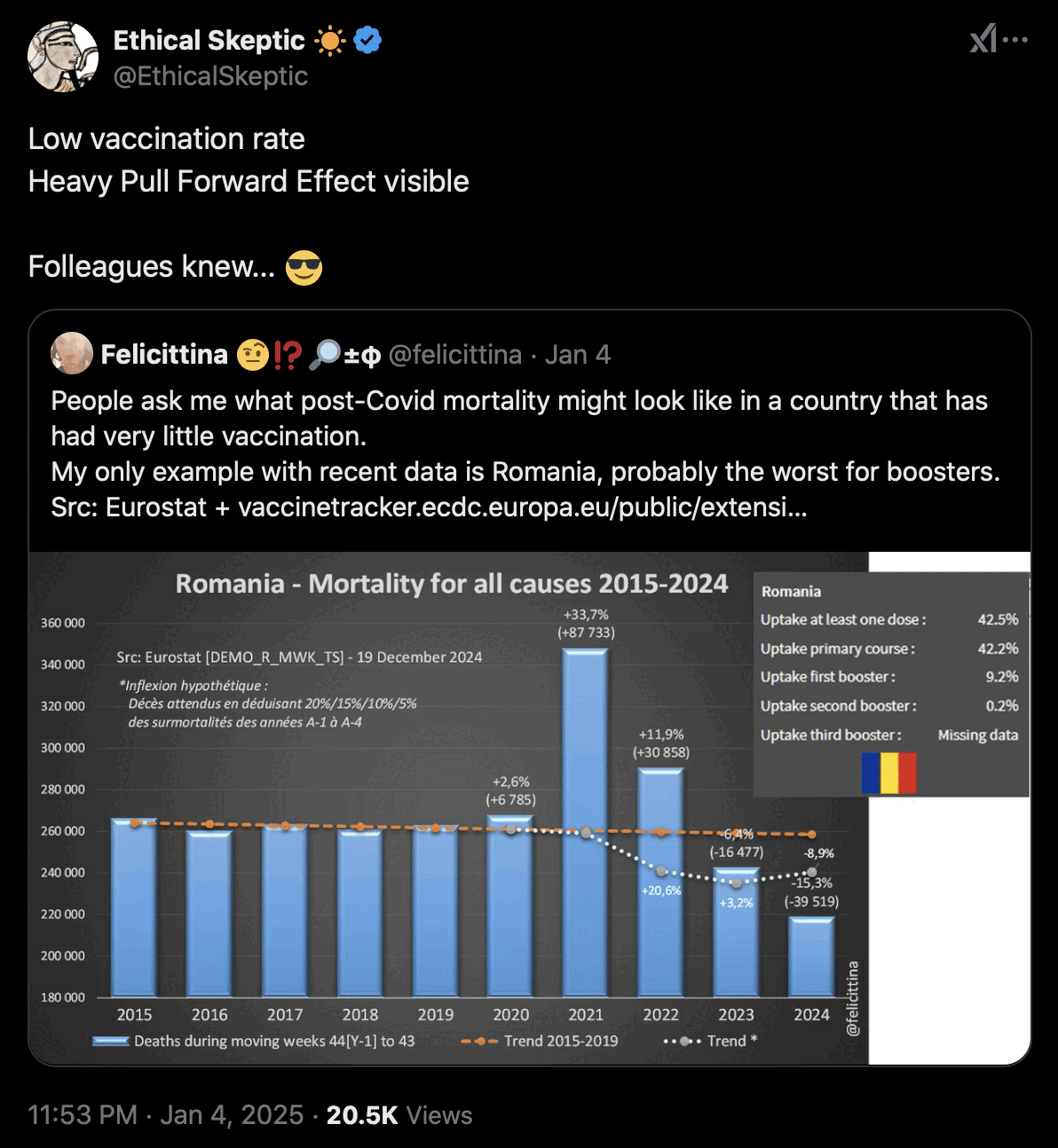
The plot was based on the Eurostat dataset demo_r_mwk_ts, which seems to be missing a part of deaths in Romania in the summer of 2024, because there's only about half the normal number of deaths in July 2024:

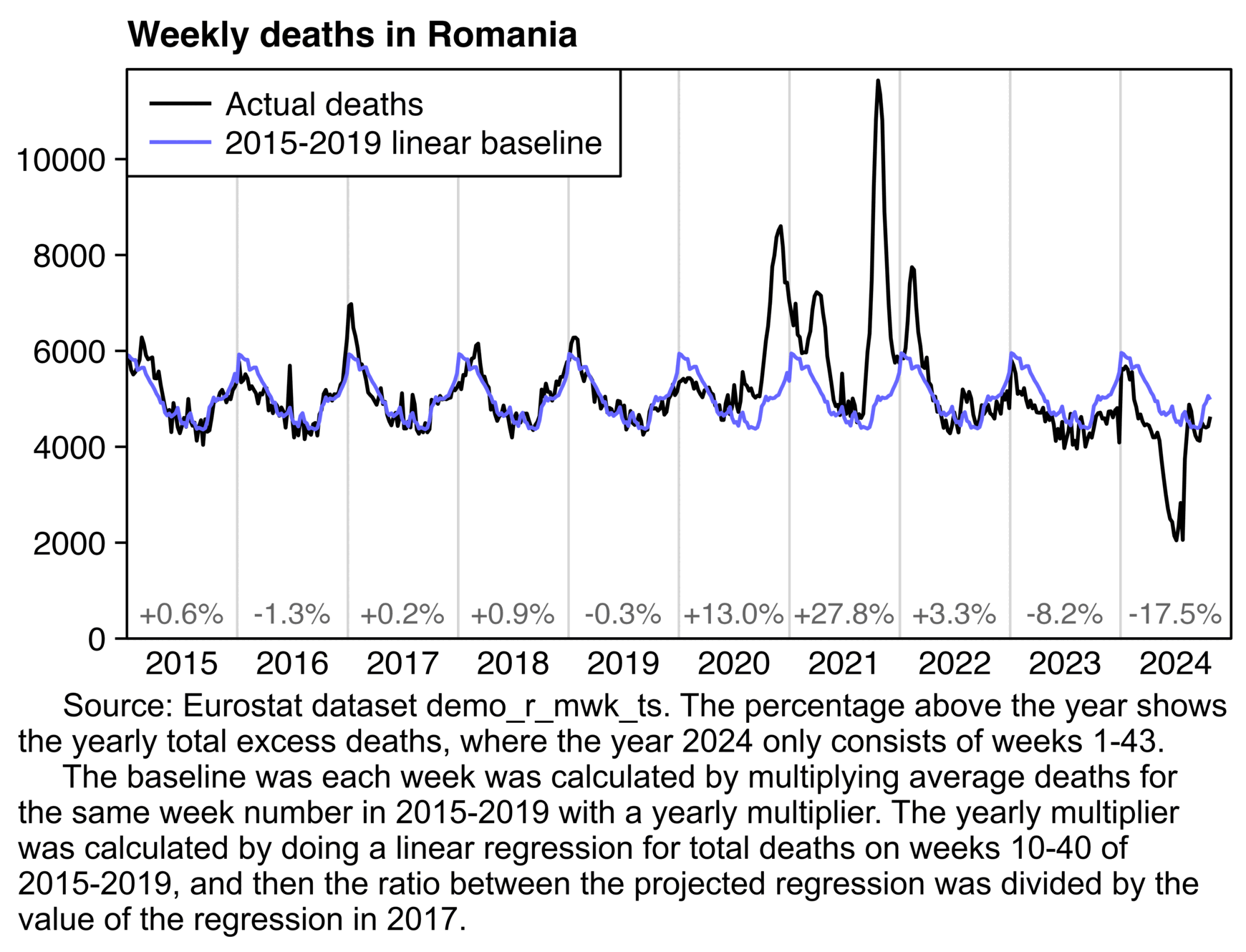
download.file("https://ec.europa.eu/eurostat/api/dissemination/sdmx/2.1/data/demo_r_mwk_ts?format=TSV","demo_r_mwk_ts.tsv")

library(data.table);library(ggplot2)

isoweek=\(year,week,weekday=7){d=as.Date(paste0(year,"-1-4"));d-(as.integer(format(d,"%w"))+6)%%7-1+7*(week-1)+weekday}

euro=fread("demo_r_mwk_ts.tsv")
euro=euro[euro[[1]]%like%"^W,T"]
euro[[1]]=sub(".*,","",euro[[1]])
eu=melt(euro,id=1)
names(eu)=c("iso","date","dead")
eu[,dead:=as.integer(sub("\\D+","",dead))]
eu[,year:=as.integer(substr(date,1,4))]
eu[,week:=as.integer(substr(date,7,8))]

d=na.omit(eu[iso=="RO"][,x:=isoweek(year,week,4)])

yearly=d[,.(year=2015:2024)]
yearly$mult=d[year%in%2015:2019&week%in%10:40,sum(dead),year][,predict(lm(V1~year),yearly)]
yearly[,mult:=mult/mult[year==2017]]
d=merge(d,d[year%in%2015:2019,.(weekly=mean(dead)),week])
d=merge(yearly,d)

p=rbind(d[,.(x,y=dead,z="Actual deaths")],d[,.(x,y=weekly*mult,z="2015-2019 linear baseline")])
p[,z:=factor(z,unique(z))]

xstart=as.Date("2015-1-1");xend=as.Date("2025-1-1")
p=p[x%in%xstart:xend]
ylim=c(0,max(p$y)*1.02);ybreak=pretty(ylim,7)
xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)

pct=d[,.(pct=(sum(dead)/sum(weekly*mult)-1)*100),.(x=as.Date(paste0(year,"-7-1")))]

ggplot(p,aes(x=x,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray84",linewidth=.4)+
geom_hline(yintercept=0,linewidth=.4)+
geom_line(aes(color=z),linewidth=.6)+
geom_text(data=pct,aes(x,y=0,label=paste0(ifelse(pct>0,"+",""),sprintf("%.1f",pct),"%")),vjust=-.7,size=3.5,color="gray40")+
labs(x=NULL,y=NULL,title="Weekly deaths in Romania")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=ylim,breaks=ybreak)+
scale_color_manual(values=c("black","#6666ff"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(margin=margin(4)),
  axis.text.y=element_text(margin=margin(,3)),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_rect(fill="white",color="black",linewidth=.4),
  legend.box.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(5,6,5,5),
  legend.position=c(0,1),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(5,5,2,5),
  plot.subtitle=element_text(margin=margin(,,5)),
  plot.title=element_text(size=12,face=2,margin=margin(2,,5)))
ggsave("1.png",width=5.8,height=3.2,dpi=300*4)

sub="\u00a0    Source: Eurostat dataset demo_r_mwk_ts. The percentage above the year shows the yearly total excess deaths, where the year 2024 only consists of weeks 1-43.
     The baseline was each week was calculated by multiplying average deaths for the same week number in 2015-2019 with a yearly multiplier. The yearly multiplier was calculated by doing a linear regression for total deaths on weeks 10-40 of 2015-2019, and then the ratio between the projected regression was divided by the value of the regression in 2017."
system(paste0("f=1.png;mar=100;w=`identify -format %w $f`;magick \\( $f \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[45*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x80 \\) -append -resize 25% -colors 256 1.png"))

The author of the plot later corrected her plot by using data from a Romanian statistics agency which was not missing deaths like Eurostat: [https://x.com/felicittina/status/1875837395406557285]

Correction: Following an alert from @henjin256 regarding strange values ​​for 2024, I went back to the Eurostat source which is supposed to be @ro_statistics. I found the following values, quite dissimilar from 2020.

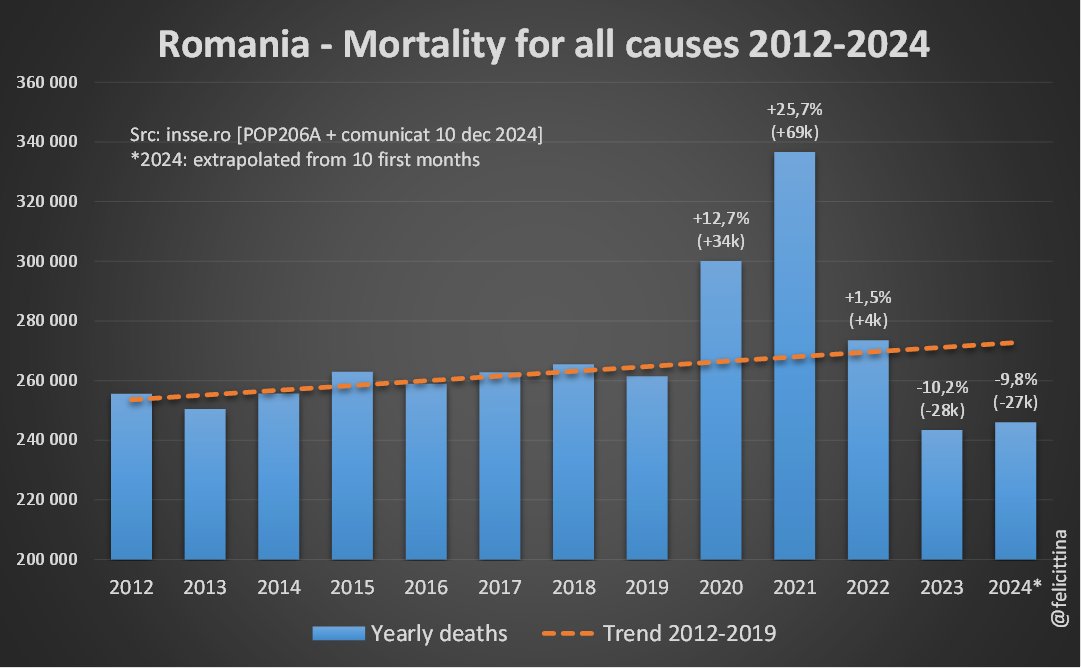
But in the end, excess mortality would have been less severe than announced and the situation would have stabilized in 2022 before starting to compensate for about half of the cumulative excess mortality in 2023 & 2024 (55k of 107k). Sources:

* annual values ​​until 2023 [POP206A]: http://statistici.insse.ro:8077/tempo-online/#/pages/tables/insse-table (I left out values ​​<2012 because of the change of method excluding non-residents from 2012).
* monthly values ​​2024: https://insse.ro/cms/sites/default/files/com_presa/com_pdf/pop10r24.pdf

After a more in-depth comparison, it appears that the differences are minimal (<1%) between the 2 databases until 2023. On the other hand, the 2024 data are incomplete on Eurostat, with a gap of 25k deaths especially between May and July. Probably an update oversight.

The 2024 mortality in the Romanian database is currently slightly higher than that of 2023 but remains well below the 2012-2019 trend.

Apart from this underestimation for 2024, the differences between the 2 graphs are mainly due to a different time window (52 mobiles weeks for the 1st, full years for the 2d) and the replacement of the 2015-2019 trend by 2012-2019 (more realistic)

I don't know how she interpolated the number of deaths in 2024. I tried taking monthly deaths from the spreadsheet linked under her source, and I multiplied the number of deaths in January to October 2024 with the average ratio of deaths in the whole year to deaths in January to October in 2014-2019, but the result was 247,190 which was similar to her plot: https://insse.ro/cms/files/statistici/comunicate/populatie/a24/pop10r24.zip.

What happens when you ask ES questions about his methodology or say you cannot reproduce his plots

Are deaths with UCD COVID but MCD cancer miscoded UCD cancer deaths?

Hugh Akston told me: "You will get the wrong answer with UCoD analysis from WONDER. They recoded nearly 90K deaths (and growing) from UCoD CA to COVID." [https://x.com/ProfessorAkston/status/1885838579945160782]

In the following code I picked 10 random people who died in 2021 with UCD COVID and MCD cancer (where I only included malignant neoplasms but not ICD codes that start with D for non-malignant neoplasms). [https://www.cdc.gov/nchs/data_access/vitalstatsonline.htm#Mortality_Multiple] In US death certificates, part 1 is intended to contain the causes of death which were part of the main cascade of events that led to the death and part 2 is intended to contain contributing conditions. In part 1 the causes are meant to be listed in reverse chronological order so that the underlying cause which initiated the cascade of events is listed on the lowest line, and the immediate causes which directly preceded the death are listed on the first line, even though often the causes of death are not listed in a neat order of causality. [https://www.cdc.gov/nchs/data/nvss/vsrg/vsrg03-508.pdf]

But anyway, cancer was listed in part 2 in 8 out of the 10 people below with UCD COVID and MCD cancer, which means that cancer was recorded as a contributing condition that was not part of the main sequence of events which led to the death. And for 8 out of 10 people the immediate causes of death on line 1a include some respiratory code apart from COVID, like J96.9 (Respiratory failure, unspecified), J18.9 (Pneumonia, unspecified), J80 (Adult respiratory distress syndrome), or R09.0 (Asphyxia). So if the people died primarily of cancer then why did they have a respiratory-related immediate cause of death?

system("wget https://ftp.cdc.gov/pub/Health_Statistics/NCHS/Datasets/DVS/mortality/mort2020us.zip;unzip mort2020us.zip")

icd=setkey(fread("http://sars2.net/f/wonderbyicd.csv.gz")[rowid(code)==1][,code:=sub(".","",code,fixed=T)],"code")

t=setDT(readr::read_fwf("VS20MORT.DUSMCPUB_r20220105",fwf_cols(restatus=c(20,20),age=c(70,73),ucod=c(146,149),
  enicon_1=c(167,170),enicon_2=c(174,177),enicon_3=c(181,184),enicon_4=c(188,191),enicon_5=c(195,198),
  enicon_6=c(202,205),enicon_7=c(209,212),enicon_8=c(216,219),enicon_9=c(223,226),enicon_10=c(230,233),
  enicon_11=c(237,240),enicon_12=c(244,247),enicon_13=c(251,254),enicon_14=c(258,261),enicon_15=c(265,268),
  enicon_16=c(272,275),enicon_17=c(279,282),enicon_18=c(286,289),enicon_19=c(293,296),enicon_20=c(300,303))))

# `restatus!=4` excludes foreign residents like CDC WONDER
d=t[restatus!=4,.(id=.I,pos=rep(0:20,each=.N),age,code=unlist(.SD,,F)),.SDcols=patterns("ucod|enicon")]
d[,age:=ifelse(age%/%1000%in%c(1,9),age%%1000,0)]

l=d[id%in%d[pos==0&code=="U071",id]][!is.na(code)]
l=l[id%in%l[code%like%"C|D[0-4]",id]]
l$cause=icd[l$code,cause]

set.seed(0)
o=l[id%in%l[,sample(id,8)]]
o[,cat(paste0("age ",age[1],", ",paste0(ifelse(pos==0,"UCD ",paste0("MCD ",pos,": ")),code," ",cause,collapse="\n"),"\n\n")),id]
Age 82, UCD U07.1 COVID-19:
1a: U07.1 COVID-19
1a: J18.9 Pneumonia, unspecified
2: C61 Malignant neoplasm of prostate
2: C79.5 Secondary malignant neoplasm of bone and bone m...
2: J44.9 Chronic obstructive pulmonary disease, unspecified
2: I25.1 Atherosclerotic heart disease
2: I10 Essential (primary) hypertension

Age 61, UCD U07.1 COVID-19:
1a: U07.1 COVID-19
1b: C91.0 Acute lymphoblastic leukaemia - Malignant neopl...

Age 82, UCD U07.1 COVID-19:
1a: R63.0 Anorexia
1a: R63.6 Insufficient intake of food and water due to se...
1b: U07.1 COVID-19
2: N13.3 Other and unspecified hydronephrosis
2: C16.9 Stomach, unspecified - Malignant neoplasms
2: E46 Unspecified protein-energy malnutrition

Age 65, UCD U07.1 COVID-19:
1a: R06.4 Hyperventilation
1a: J96.9 Respiratory failure, unspecified
1b: U07.1 COVID-19
2: C61 Malignant neoplasm of prostate
2: I10 Essential (primary) hypertension
2: F17.9 Mental and behavioural disorders due to use of ...

Age 76, UCD U07.1 COVID-19:
1a: U07.1 COVID-19
1a: J18.9 Pneumonia, unspecified
2: N18.9 Chronic renal failure, unspecified
2: J44.9 Chronic obstructive pulmonary disease, unspecified
2: C34.9 Bronchus or lung, unspecified - Malignant neopl...
2: H91.9 Hearing loss, unspecified
2: H93.1 Tinnitus

Age 81, UCD U07.1 COVID-19:
1a: J18.9 Pneumonia, unspecified
1b: U07.1 COVID-19
2: I35.0 Aortic (valve) stenosis
2: I10 Essential (primary) hypertension
2: I25.1 Atherosclerotic heart disease
2: I50.9 Heart failure, unspecified
2: I44.3 Other and unspecified atrioventricular block
2: C61 Malignant neoplasm of prostate

Age 46, UCD U07.1 COVID-19:
1a: U07.1 COVID-19
1a: J18.9 Pneumonia, unspecified
2: C80 Malignant neoplasm without specification of site

Age 77, UCD U07.1 COVID-19:
1a: R09.0 Asphyxia
1b: J96.9 Respiratory failure, unspecified
1c: J12.9 Viral pneumonia, unspecified
1d: U07.1 COVID-19
2: C95.9 Leukaemia, unspecified - Malignant neoplasms
2: J44.9 Chronic obstructive pulmonary disease, unspecified
2: F17.9 Mental and behavioural disorders due to use of ...

Age 79, UCD U07.1 COVID-19:
1a: J80 Adult respiratory distress syndrome
1b: U07.1 COVID-19
1b: J18.9 Pneumonia, unspecified
2: I48 Atrial fibrillation and flutter
2: E14.9 Unspecified diabetes mellitus, without complica...
2: I10 Essential (primary) hypertension
2: C61 Malignant neoplasm of prostate

Age 35, UCD U07.1 COVID-19:
1a: J96.0 Acute respiratory failure
1b: U07.1 COVID-19
1c: J18.1 Lobar pneumonia, unspecified
1d: C54.1 Endometrium - Malignant neoplasms

The code below shows the 20 most common MCDs on line 1a among people with UCD COVID and MCD cancer. They don't even include any ICD code for cancer:

> sub[line==1,.N,.(code,name=icd[code])][,pct:=round(N/sum(N)*100,1)][order(-N)][1:20]|>print(r=F)
  code                                               name    N  pct
 U07.1                                           COVID-19 5688 27.5
 J96.0                          Acute respiratory failure 3603 17.4
 J18.9                             Pneumonia, unspecified 3361 16.3
 J96.9                   Respiratory failure, unspecified 2247 10.9
 I46.9                        Cardiac arrest, unspecified 1386  6.7
   J80                Adult respiratory distress syndrome  857  4.1
 R09.0                                           Asphyxia  614  3.0
 A41.9                           Septicaemia, unspecified  571  2.8
 R09.2                                 Respiratory arrest  290  1.4
 R68.8         Other specified general symptoms and signs  250  1.2
 J96.1                        Chronic respiratory failure  222  1.1
 R06.8   Other and unspecified abnormalities of breathing  104  0.5
 R57.9                                 Shock, unspecified   80  0.4
 J12.9                       Viral pneumonia, unspecified   76  0.4
 I26.9 Pulmonary embolism without mention of acute cor...   67  0.3
 J98.9                  Respiratory disorder, unspecified   64  0.3
   B99          Other and unspecified infectious diseases   53  0.3
 R62.8 Other lack of expected normal physiological dev...   52  0.3
 J69.0                  Pneumonitis due to food and vomit   46  0.2
 N17.9                   Acute renal failure, unspecified   45  0.2

Only about one fourth of people even had cancer listed in part 1 of the death certificate:

> sub[line<6&cause%like%"C",length(unique(id))] # people with cancer listed in part 1
[1] 4257
> sub[,length(unique(id))] # total people with UCD COVID and MCD cancer
[1] 16510

Does Mortality Watch have negative excess ASMR in 2024 because of a lack of PFE adjustment?

The Real Truther posted the plot below where he got negative excess ASMR in 36 out of 37 countries in 2024, and he wrote: "Since 2023 most countries in the world have had no excess mortality. The anti-vaccine narrative is officially dead." [https://x.com/thereal_truther/status/1929248121357320459]

Ethical Skeptic posted the image below and replied: "Yes, the baseline must corrected for pull-forward effect or you get ludicrous results like were in that table." [https://x.com/EthicalSkeptic/status/1929385433600807417]

However ASMR already accounts for the reduction in population size due to excess deaths since 2020, so it incorporates a form of PFE adjustment. The reason why Truther got negative excess mortality in 2024 was because he used a 2017-2019 average baseline, but most countries have a decreasing trend in ASMR.

The default baseline for ASMR at Mortality Watch used to be a linear regression where the fitting period was chosen automatically from the range of 5 to 10 years. But at one point USMortality switched the default baseline for ASMR to a 2017-2019 average. He keeps saying it's a "conservative" baseline. But I think it would be more conservative to assume that the pre-COVID trend in ASMR would've continued into the 2020s, like in the old default baseline. With his new 2017-2019 average baseline, 36 out of 37 countries get negative excess ASMR in 2024.

With a 2010-2019 linear trend, the excess ASMR in 2024 is a lot closer to 0%: [https://www.mortality.watch/ranking?bm=lin_reg&df=2020&dt=2024&t=0]

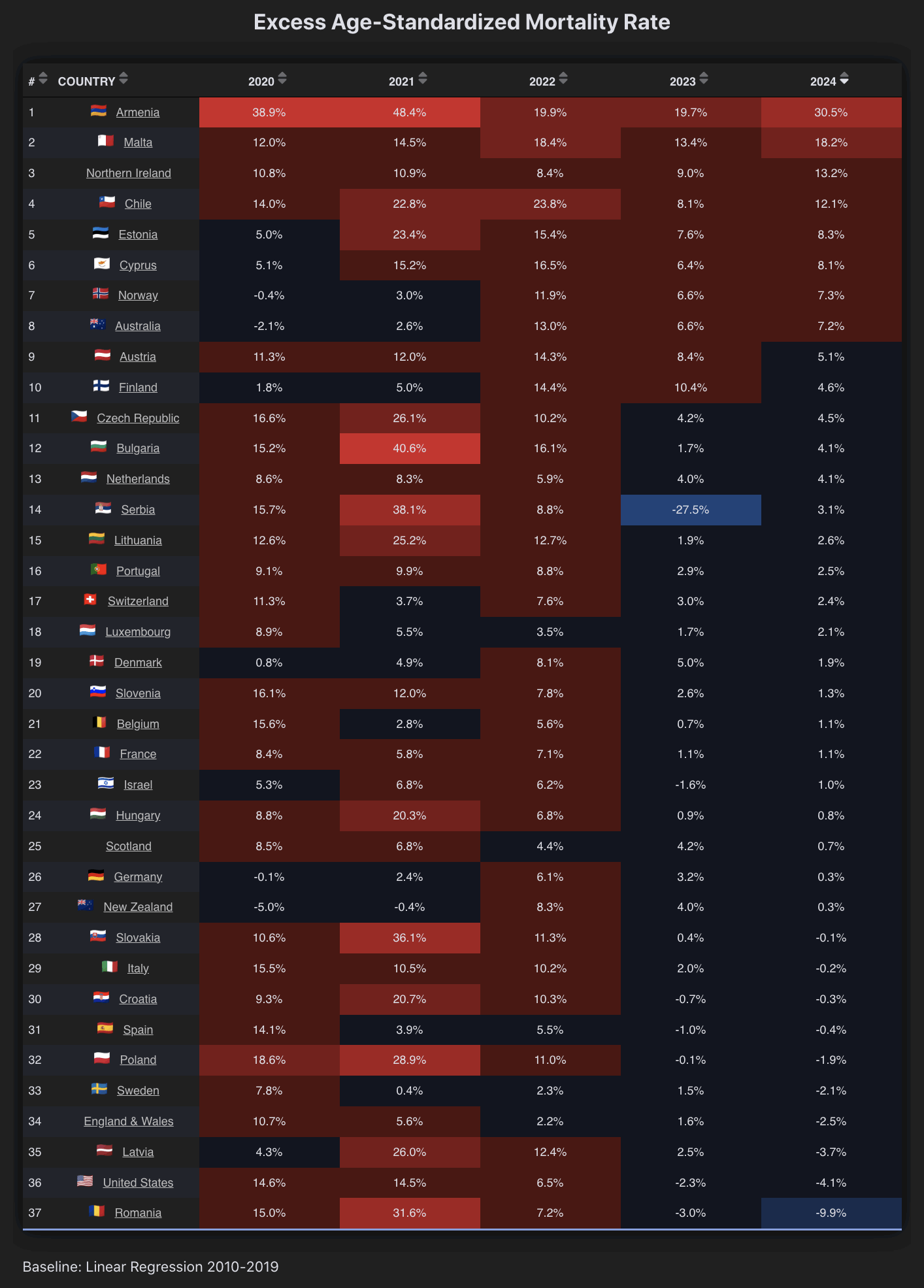
(In the plot above the reason why Serbia has such low excess deaths in 2023 is because Mortality Watch uses data for Serbia from Eurostat, which is missing a lot of deaths for Serbia in mid-2023. Eurostat is also missing deaths for Romania in mid-2024. [https://www.mortality.watch/explorer/?c=SRB&c=ROU&t=asmr&ct=monthly&df=2020%2520Jan&bm=lin_reg&pi=0])

A 2010-2012 average baseline also produced negative excess ASMR for 31 out of 33 countries in 2017: [https://www.mortality.watch/ranking?bm=mean&df=2010&dt=2017&t=0&bf=2010&bt=2012]

But anyway, if ES wants to keep plotting raw deaths instead of ASMR on the y-axis, he can use a method similar to my next plot to calculate a baseline that is adjusted for both the change in age composition and the reduction in population size due to excess deaths. In the plot I did a Poisson regression, where I included the year as a continuous variable, age group and month as categorical variables, and person-days as an offset variable. It gave me about 0.2% excess deaths in 2024:

t=fread("http://sars2.net/f/uspopdeadmonthly.csv")
t=t[year%in%2011:2025][!(year==2025&month>=4)]

lm=glm(dead~year+factor(age)+factor(month),poisson,t[year%in%2011:2019],offset=log(persondays))
t$base=predict(lm,t,type="response")

p=a[,.(x=as.Date(paste0(date,"-1")),y=c(dead,base,dead-base),z=rep(1:3,each=.N))]
p[,y:=y/days_in_month(x)]

pct=t[,.(pct=(sum(dead)/sum(base)-1)*100),.(x=as.Date(paste0(year,"-7-1")))]

p[,z:=factor(z,,c("Deaths divided by number of days in month","2011-2019 Poisson regression","Difference from regression"))]
color=c("black","#3333ff","#3333ff")

xstart=as.Date("2017-1-1");xend=as.Date("2026-1-1")
xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ylim=extendrange(p$y,,c(.07,.03));ybreak=pretty(ylim,6)

ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray70",linewidth=.3)+
geom_point(aes(x+14,y,alpha=z),stroke=0,size=1.2)+
geom_line(data=p[z!=levels(z)[3]],aes(x+14,y,linetype=z,color=z),linewidth=.6)+
geom_line(data=p[z==levels(z)[2]&year(x)<2020],aes(x+14,y),color=color[2],linewidth=.6)+
geom_rect(data=p[z==levels(z)[3]],aes(xmin=x,xmax=x%m+%months(1),ymin=pmin(0,y),ymax=pmax(0,y),fill=z),linewidth=.1,color="gray40")+
geom_text(data=pct,aes(x,label=paste0(ifelse(pct>0,"+",""),sprintf("%.1f",pct),"%")),y=ylim[1],vjust=-.5,size=3.4,color="gray50")+
labs(title="Monthly deaths in the United States divided by number of days in month",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=ylim,breaks=ybreak,labels=\(x)ifelse(x==0,x,paste0(x/1e3,"k")))+
scale_color_manual(values=color)+
scale_fill_manual(values=rep("gray60",3))+
scale_alpha_manual(values=c(1,0,0),guide="none")+
scale_linetype_manual(values=c("solid","11","solid"))+
guides(fill=guide_legend(order=3,keyheight=unit(1,"pt")),color=guide_legend(order=1),linetype=guide_legend(order=1))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=10,color="black"),
  axis.text.x=element_text(margin=margin(3.5)),
  axis.text.y=element_text(margin=margin(,1.5)),
  axis.ticks=element_line(linewidth=.3,color="gray70"),
  axis.ticks.length=unit(4,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box="horizontal",
  legend.box.just="center",
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification="left",
  legend.key=element_blank(),
  legend.key.height=unit(11,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(,18,4,-2),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=10,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3,color="gray70"),
  panel.spacing.y=unit(2,"pt"),
  plot.margin=margin(4,4,2,4),
  plot.subtitle=element_text(size=10,margin=margin(,,4)),
  plot.title=element_text(size=11,face=2,margin=margin(1,,2)))
ggsave("1.png",width=5.66,height=3.3,dpi=300*4)

sub="\u00a0     The yearly total excess mortality percentage is shown above the year.
      The data for deaths was retrieved from CDC WONDER on May 25th 2025 UTC.
      The baseline was calculated by doing a Poisson regression where the year was a continuous variable, month and single year of age up to ages 100+ were categorical variables, and person-days was an offset variable.
      Monthly resident population estimates by single year of age were downloaded from www2.census.gov/programs-surveys/popest/datasets/2020-2024/national/asrh/nc-est2024-alldata-r-file0{1..8}.csv, and from the corresponding files in the 2010-2020 directory.
      Vintage 2023 population estimates based on the 2020 census were used for April 2020 to December 2023, and vintage 2020 population estimates based on the 2010 census were used for January 2011 to March 2020. The 2010-based estimates were multiplied by a linear slope so that they were equal to the 2020-based estimates in April 2020 when the two sets of estimates were merged.
      Monthly population estimates for 2024 were calculated as a spline interpolation of the mid-year population projections for 2023-2025, where the population projections for each age were first multiplied by the ratio of mid-2023 resident population estimates divided by the mid-2023 population projections: www2.census.gov/programs-surveys/popproj/datasets/2023/
2023-popproj/np2023_d1_mid.csv."
system(paste0("mar=120;w=`identify -format %w 1.png`;magick 1.png \\( -size $[w-mar*2]x -font Arial -interline-spacing -4 -pointsize 156 caption:'",gsub("'","'\\\\''",sub),"' -gravity southwest -splice $[mar]x70 \\) -append -resize 25% -dither none -colors 256 1.png"))

I used code like this to do the regression:

t=fread("https://sars2.net/f/uspopdeadmonthly.csv")[year%in%2011:2024]

lm=glm(dead~year+factor(age)+factor(month),poisson,t[year%in%2011:2019],offset=log(persondays))
t$base=predict(lm,t,type="response")
t[,.(dead=sum(dead),base=sum(base)),.(year,month)][1:2]
# year month   dead     base
# 2011     1 233681 235894.1
# 2011     2 211768 206296.8

Why did the population estimate of ages 72 and above increase in 2020-2022 despite COVID deaths?

Ethical Skeptic presented this plot as evidence that the Census Bureau's population estimates were not reliable: [https://x.com/EthicalSkeptic/status/1930015650321240519]

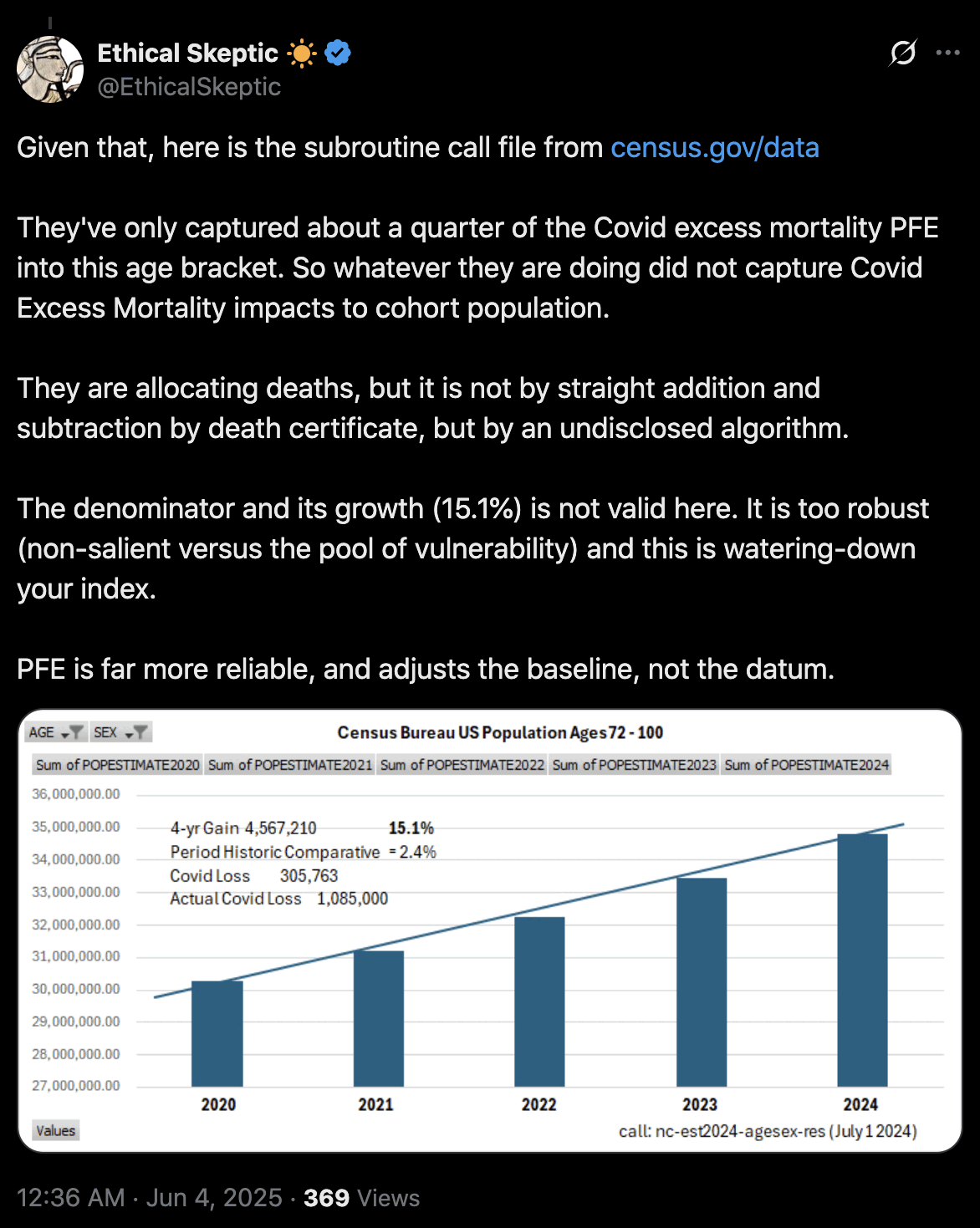
His plot shows that the size of the age group 72 and above increased by about 15.1% between 2020 and 2024, even though the historic baseline increase over a 4-year period was only about 2.4%. But he didn't take baby boomers into account.

The earliest baby boomers were born in mid-1946, so they turned 72 in mid-2018, but there were not yet many baby boomers included in the mid-year population estimate for ages 72 and above until 2019. But in the subsequent years even though there was a large number of COVID deaths, the population size of ages 72 and above still increased by about 1-1.4 million per year:

u="https://www2.census.gov/programs-surveys/popest/datasets/"
old=fread(paste0(u,"2010-2020/national/asrh/nc-est2020-agesex-res.csv"))
new=fread(paste0(u,"2020-2024/national/asrh/nc-est2024-agesex-res.csv"))
old=old[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:4)]),year=rep(2010:2020,each=.N))]
new=new[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:3)]),year=rep(2020:2024,each=.N))]

# ratio between new and old estimates in 2020 for each age
mult=merge(new[year==2020],old[year==2020,.(age,old=pop)])[,pop/old]

# multiply old estimates by linear slope
inter=old[,.(year,age,pop=round(pop*(1-(((year-2010)/10))*(1-mult))))]

a=rbind(inter[year<2020],new)[age>=72,.(pop=sum(pop)),.(age=ifelse(age>89,"90+",age),year)]

m=xtabs(pop/1e6~year+age,a)
rs=rowSums(m)
rownames(m)=sprintf("%s (total %.1fM%s)",rownames(m),rs,c("",sprintf(", diff %.1fM",diff(rs))))
disp=m;disp[]=sprintf("%.1f",m)

pheatmap::pheatmap(m,filename="1.png",display_numbers=disp,
  cluster_rows=F,cluster_cols=F,legend=F,cellwidth=17,cellheight=17,fontsize=9,fontsize_number=8,
  border_color=NA,
  number_color=ifelse(m>max(m)*.45,"white","black"),
  breaks=seq(0,max(m),,256),sapply(seq(1,0,,256),\(i)rgb(i,i,i)))

system("pad=22;w=`identify -format %w 1.png`;magick \\( -size $[w-pad*2]x -font Arial-Bold -pointsize 42 caption:'Mid-year US resident population estimate in millions by age and year' -splice $[pad]x16 \\) \\( -size $[w-pad*2] -font Arial -pointsize 38 caption:'Vintage 2024 population estimates were used for 2020-2024. DIY intercensal estimates were used for 2010-2019, where the 2010-2020 population estimates for each age were multiplied by a linear slope so that they were equal to the 2020-2024 estimates in 2020. Source: www2.census.gov/programs-surveys/popest/datasets, files 2020-2024/national/asrh/nc-est2024-agesex-res.csv and 2010-2020/national/asrh/nc-est2020-agesex-res.csv.' -splice $[pad]x10 \\) 1.png -append -colorspace gray 1.png")

Yearly ASMR in April to September

Ethical Skeptic claims the United States still had about 3,000-5,000 excess deaths per week in 2025, which would be the equivalent of about 7% excess deaths per year: [https://x.com/EmeraldRobinson/status/1937127859698745662]

However I'm getting close to 0% excess deaths in the US since January 2023, and with some methods I'm even getting negative excess deaths in 2024.

The baseline ES used to calculate the excess deaths seemed to be based on his method of "trough regression", where he excludes winter peaks and he calculates a weighted annual growth rate in 2014-2019. [https://x.com/EthicalSkeptic/status/1940487722071666911] His baseline doesn't look steep enough, because it's above the summer trough in 2014 but below the trough in 2019:

Ethical Skeptic gives a low weight to 2014 when he determines the slope of his baseline, because he says the summer of 2014 had an unusually low number of deaths, and because he also gives a lower weight to earlier years than later years:

However in both of his plots above ES started the x-axis from 2014, so it's difficult to tell how the deaths in the summer of 2014 compare to the long-term trend. It would also be easier to see how high the overall deaths in the summer were if he plotted yearly data that showed the deaths on all summer weeks added together, because the number of deaths during the lowest point of the summer is not necessarily representative of deaths during the whole summer.

In order to address both shortcomings, I made the following plot where I calculated ASMR for United States using deaths in April to September only. When I fitted a smoothed spline to the data to approximate the long-term curved trend, the year 2014 was actually not too far from the spline, but the years 2015-2017 were all clearly above the spline:

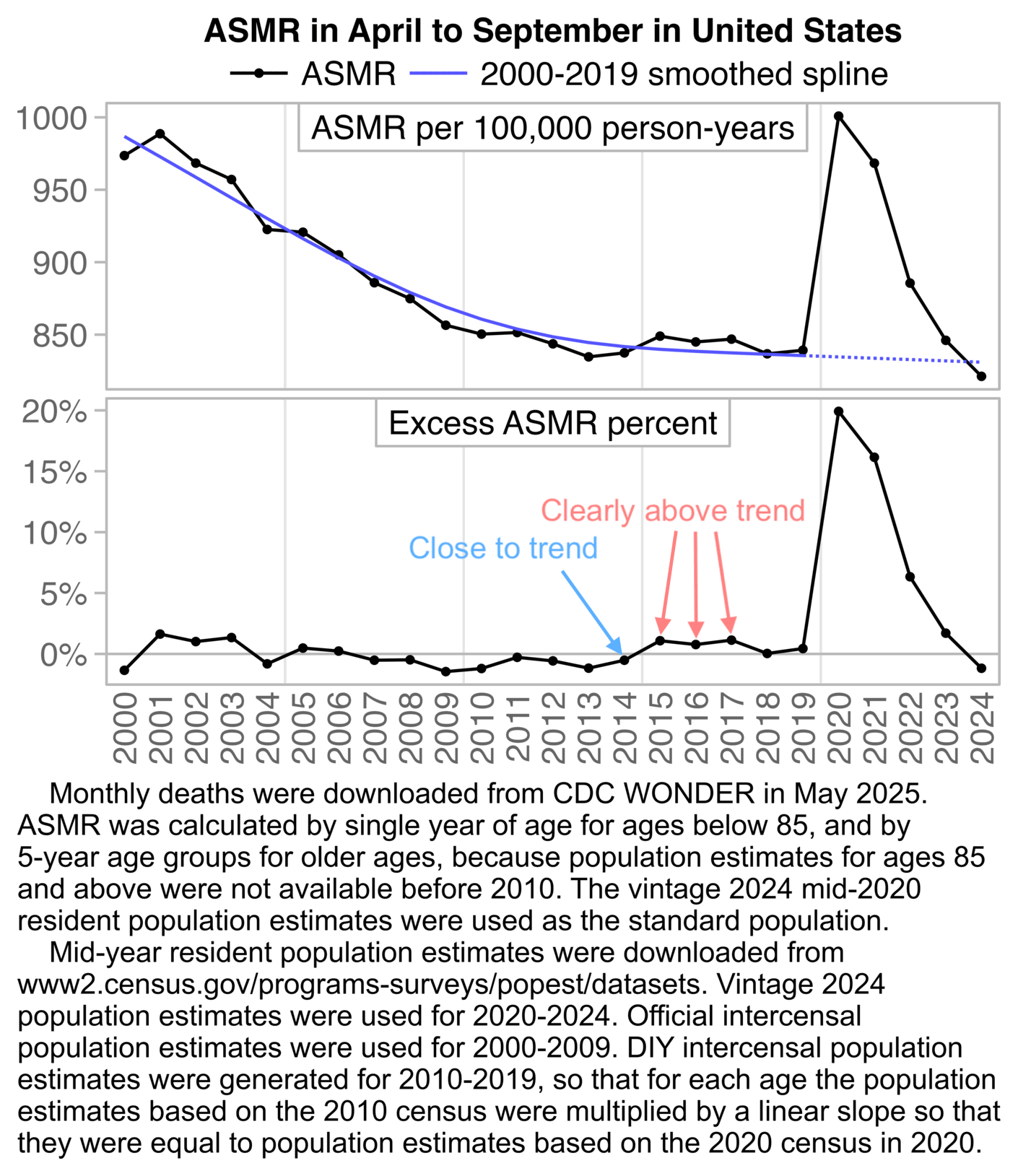
t=fread("https://sars2.net/f/uspopdeadmonthly.csv")[month%in%4:9]
a=t[,.(dead=sum(dead)),.(year,age=ifelse(age>85,age%/%5*5,age))]
pop=fread("https://sars2.net/f/uspopdead.csv")[,.(pop=sum(pop,na.rm=T)),.(age=ifelse(age>85,age%/%5*5,age),year)]
a=merge(a,pop)[year%in%2000:2024]

a=merge(a[year==2020,.(age,std=pop/sum(pop))],a)

p=a[,.(y=sum(dead/pop*std/183*365e5),z=1),.(x=year)]

p=rbind(p,setDT(predict(p[x<2020,smooth.spline(x,y,spar=.7)],p$x))[,z:=2])

p=rbind(p[,facet:=1],p[,.(y=(y[1]/y[2]-1)*100,z=1,facet=2),x])

p[,z:=factor(z,,c("ASMR","2000-2019 smoothed spline"))]
p[,facet:=factor(facet,,c("ASMR per 100,000 person-years","Excess ASMR percent"))]

xstart=1999.5;xend=2024.5;xbreak=seq(2000,xend,1)
ylim=p[,{x=extendrange(y);.(ymin=x[1],ymax=x[2])},facet]

ggplot(p)+
facet_wrap(~facet,dir="v",scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,5),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=ymin,ymax=ymax),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_segment(data=ylim[2],y=0,yend=0,x=xstart,xend=xend,linewidth=.4,color="gray72")+
geom_point(aes(x,y,color=z,alpha=z),stroke=0,size=1.5)+
geom_line(data=p[!(z==levels(z)[2]&x>2019)],aes(x,y,color=z),linewidth=.5)+
geom_line(data=p[z==levels(z)[2]&x>=2019],aes(x,y,color=z),linetype="11",linewidth=.5)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=pmean(xstart,xend),hjust=.5,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray72",size=3.87)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=pmean(xstart,xend),hjust=.5,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87)+
labs(x=NULL,y=NULL,title="ASMR in April to September in United States")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(breaks=pretty,labels=\(x)ifelse(x<100,paste0(x,"%"),x))+
scale_color_manual(values=c("black","#5555ff"))+
scale_alpha_manual(values=1:0)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.4,color="gray72"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.margin=margin(,,4),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(3,"pt"),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,2)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.7,height=3.6,dpi=300*4)

So when ES determines the slope of his baseline, he might just as well give a high weight to 2014 but a low weight to 2015-2017. Here I tried to draw the green line to approximate a linear regression of deaths at the lowest points of 2014, 2018, and 2019, but my green line is much steeper than Ethical Skeptic's yellow-green dashed line:

Increase in raw cancer deaths since 2020

Ethical Skeptic made this plot to show that raw deaths with UCD cancer have increased since 2020: [https://theethicalskeptic.com/2025/06/20/the-state-of-things-pandemic/]

The next plot shows that cancer ASMR has followed a roughly linear trend since 2000, which indicates that cancer mortality has followed a stable trajectory. But because of the uneven age structure of the population, raw number of deaths has followed a wavy pattern, where it has alternated between relatively flat perioads in 2000-2004 and in 2016-2019, and increasing periods in other years. ES started the x-axis of his plot from 2014, so it wasn't clear that before 2014 the yearly number of cancer deaths increasing increased at a similar slope as in 2020-2024:

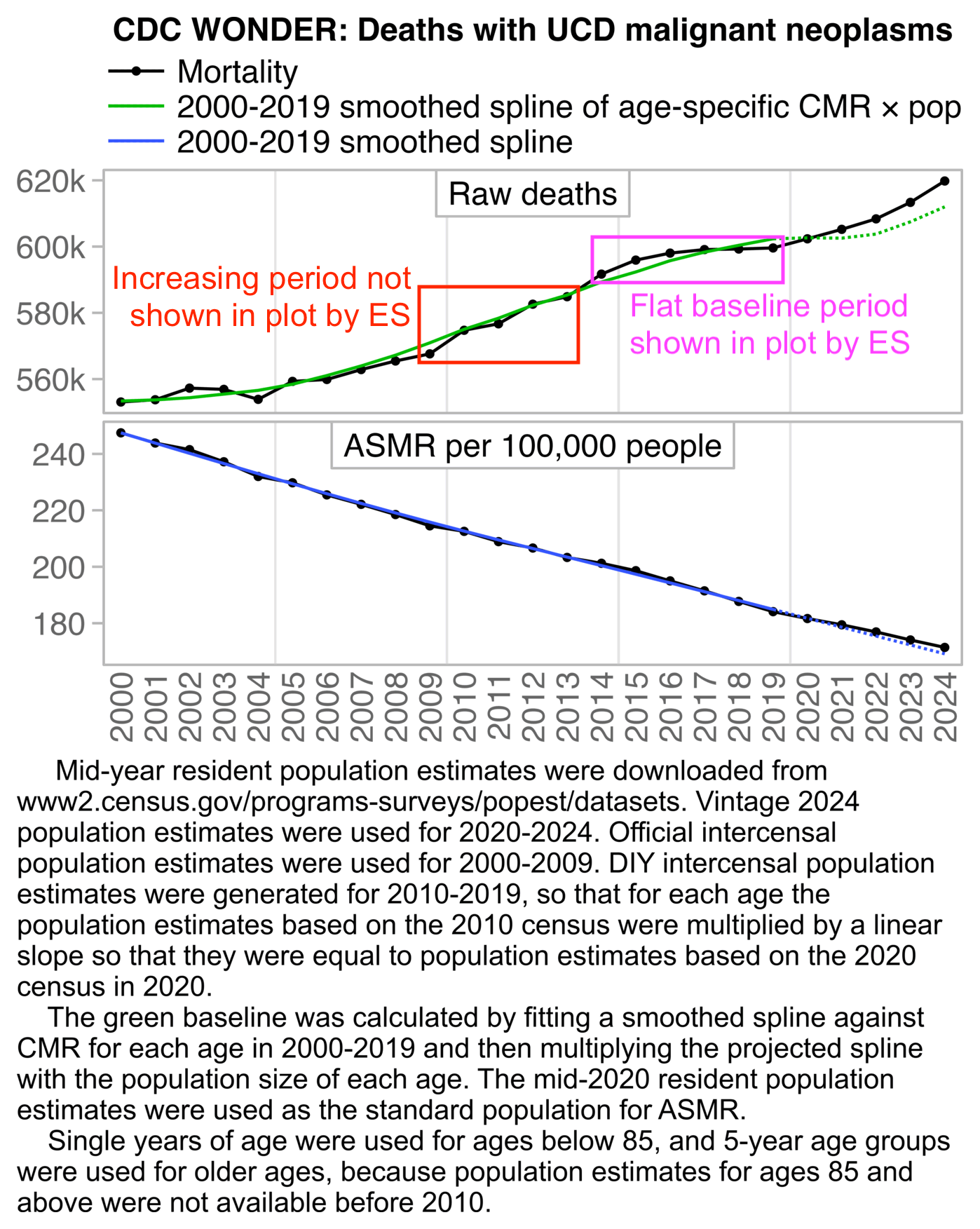
t=fread("https://sars2.net/f/wondermalignantyearly.csv")[cause%like%"UCD"&year%in%2000:2024]
pop=fread("https://sars2.net/f/uspopdead.csv")

d=t[,.(dead=sum(dead)),.(age=ifelse(age>=85,age%/%5*5,age),year)]
d=merge(d,pop[,.(pop=sum(pop,na.rm=T)),.(year,age=ifelse(age>=85,age%/%5*5,age))])
d=merge(d[year==2020,.(age,std=pop/sum(pop))],d)

d$base=d[,predict(.SD[year<2020,smooth.spline(year,dead/pop,spar=.7)],year),age]$y*d$pop

a=d[,.(dead=sum(dead),base=sum(base)),year]
p1=a[,.(x=year,y=c(dead,base),z=rep(1:2,each=.N),facet=1)]

p2=d[,.(y=sum(dead/pop*std*1e5),z=1),.(x=year)]
p2=rbind(p2,setDT(predict(p2[x<2020,smooth.spline(x,y,spar=.7)],p2$x))[,z:=3])
p=rbind(p1,p2[,facet:=2])

p[,z:=factor(z,,c("Mortality","2000-2019 smoothed spline of age-specific CMR × pop","2000-2019 smoothed spline"))]
p[,facet:=factor(facet,,c("Raw deaths","ASMR per 100,000 people"))]

xstart=1999.5;xend=2024.5;xbreak=seq(2000,xend,1)
ylim=p[,{x=extendrange(y);.(ymin=x[1],ymax=x[2])},facet]

ggplot(p)+
facet_wrap(~facet,dir="v",scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,5),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=ymin,ymax=ymax),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_segment(data=ylim[2],y=0,yend=0,x=xstart,xend=xend,linewidth=.4,color="gray72")+
geom_point(aes(x,y,color=z,alpha=z),stroke=0,size=1.5)+
geom_line(data=p[!(z!=z[1]&x>2019)],aes(x,y,color=z),linewidth=.5)+
geom_line(data=p[z!=z[1]&x>=2019],aes(x,y,color=z),linetype="11",linewidth=.5)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=(xstart+xend)/2,hjust=.5,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray72",size=3.87,lineheight=.8)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=(xstart+xend)/2,hjust=.5,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87,lineheight=.8)+
labs(x=NULL,y=NULL,title="CDC WONDER: Deaths with UCD malignant neoplasms")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(breaks=pretty,labels=\(x)ifelse(x>=1e3,paste0(x/1e3,"k"),x))+
scale_color_manual(values=c("black","#00bb00",hsv(23/36,.8,1)))+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.4,color="gray72"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification="right",
  legend.key=element_blank(),
  legend.margin=margin(,,4),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(3,"pt"),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,2)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.65,height=3.6,dpi=300*4)

The plot above also demonstrates how the long-term trend in ASMR tends to be more linear than the long-term trend in raw deaths. If ES plotted ASMR instead of raw deaths, then it would be appropriate to use a simple linear baseline in many cases.

Pre-COVID linear trend in deaths compared to population projections by Census Bureau

In his plots Ethical Skeptic fits a linear baseline to raw deaths in 2014-2019 or 2018-2019. However even before COVID, the yearly number of deaths was projected to start increasing more steeply in the 2020s than the 2010s.

In the next plot I downloaded data for deaths in the 2014 population projections from here: https://www2.census.gov/programs-surveys/popproj/datasets/2014/2014-popproj/np2014_d3.csv. The blue line shows a 2014-2019 linear regression, which is near identical to the actual projected deaths in 2014-2019. However by 2025 the projected deaths are about 1.2% higher than the linear regression:

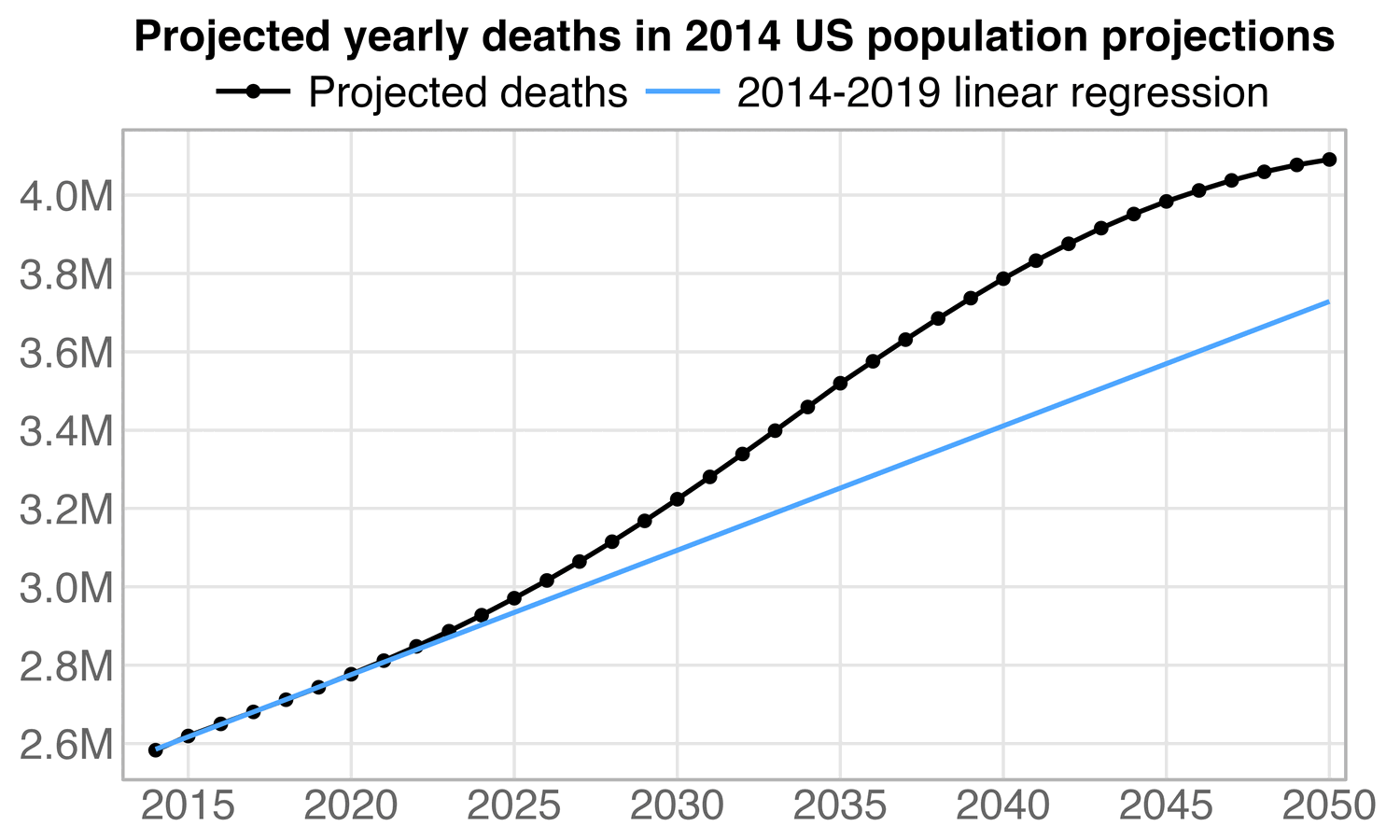
t=fread("https://www2.census.gov/programs-surveys/popproj/datasets/2014/2014-popproj/np2014_d3.csv")

p=t[RACE_HISP==0&SEX==0,.(x=YEAR,y=total_deaths,z=1)]
p=rbind(p,p[,.(x,y=predict(lm(y~x,p[x%in%2014:2019]),p),z=2)])
p[,z:=factor(z,,c("Projected deaths","2014-2019 linear regression"))]

xstart=2013.5;xend=2050;xbreak=seq(2015,xend,5);p=p[x>=xstart&x<=xend]

ggplot(p)+
geom_point(aes(x,y,color=z,alpha=z),size=1.1)+
geom_line(aes(x,y,color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Projected yearly deaths in 2014 US population projections")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak)+
scale_y_continuous(limits=extendrange(p$y),breaks=pretty(p$y,7),labels=\(x)sprintf("%.1fM",x/1e6))+
scale_color_manual(values=c("black",hsv(c(21,30)/36,.7,1)))+
scale_alpha_manual(values=1:0)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.ticks=element_line(linewidth=.4,color="gray70"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4,color="gray70"),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(5,14,3,5),
  plot.title=element_text(size=11.2,face=2,hjust=.5,margin=margin(,,2)))
ggsave("1.png",width=5,height=3,dpi=300*4)

Cancer incidence in ages below 50 in Australia

ES posted this tweet: [https://x.com/EthicalSkeptic/status/1942309005616963722]

The article by ABC he linked said: [https://www.abc.net.au/news/2025-07-07/cancer-diagnosis-rates-under-50s-rising-causes-four-corners/105495620]

Data provided to Four Corners by Cancer Australia, the federal government's cancer agency, paints a concerning picture for young people.

Between 2000 and 2024 - in 30 to 39-year-olds - early onset prostate cancer increased by 500 per cent, pancreatic cancer by 200 per cent, liver cancer by 150 per cent, uterine cancer by 138 per cent and kidney cancer by 85 per cent.

The ABC article was from July 2025. At that time the latest annual report of cancer data by Cancer Australia was published in December 2024. The report only included actual cancer incidence data up to 2020, and the incidence estimates in 2021 to 2024 were projections: [https://www.aihw.gov.au/reports/cancer/cancer-data-in-australia/contents/overview]

The 500% increase in prostate cancer seems to be an increase from 2 cases in 2000 to a projected 11 cases in 2024: [https://www.aihw.gov.au/reports/cancer/cancer-data-in-australia/contents/cancer-incidence-by-age-visualisation]

In the plot above the cancer incidence rates are rounded to the nearest 0.1 per 100,000, so the rounded incidence of prostate cancer only increased from 0.1 per 100,000 in 2000 to 0.3 in 2024. But the numbers reported by ABS might have been based on unrounded rates per capita, and not the raw number of new cases.

The 200% increase in pancreatic cancer seems to be an increase from about 0.5 cases per 100,000 in 2000 to about 1.5 in 2024 (but the raw number of cases increased from 15 to 60, which would be a 300% and not 200% increase):

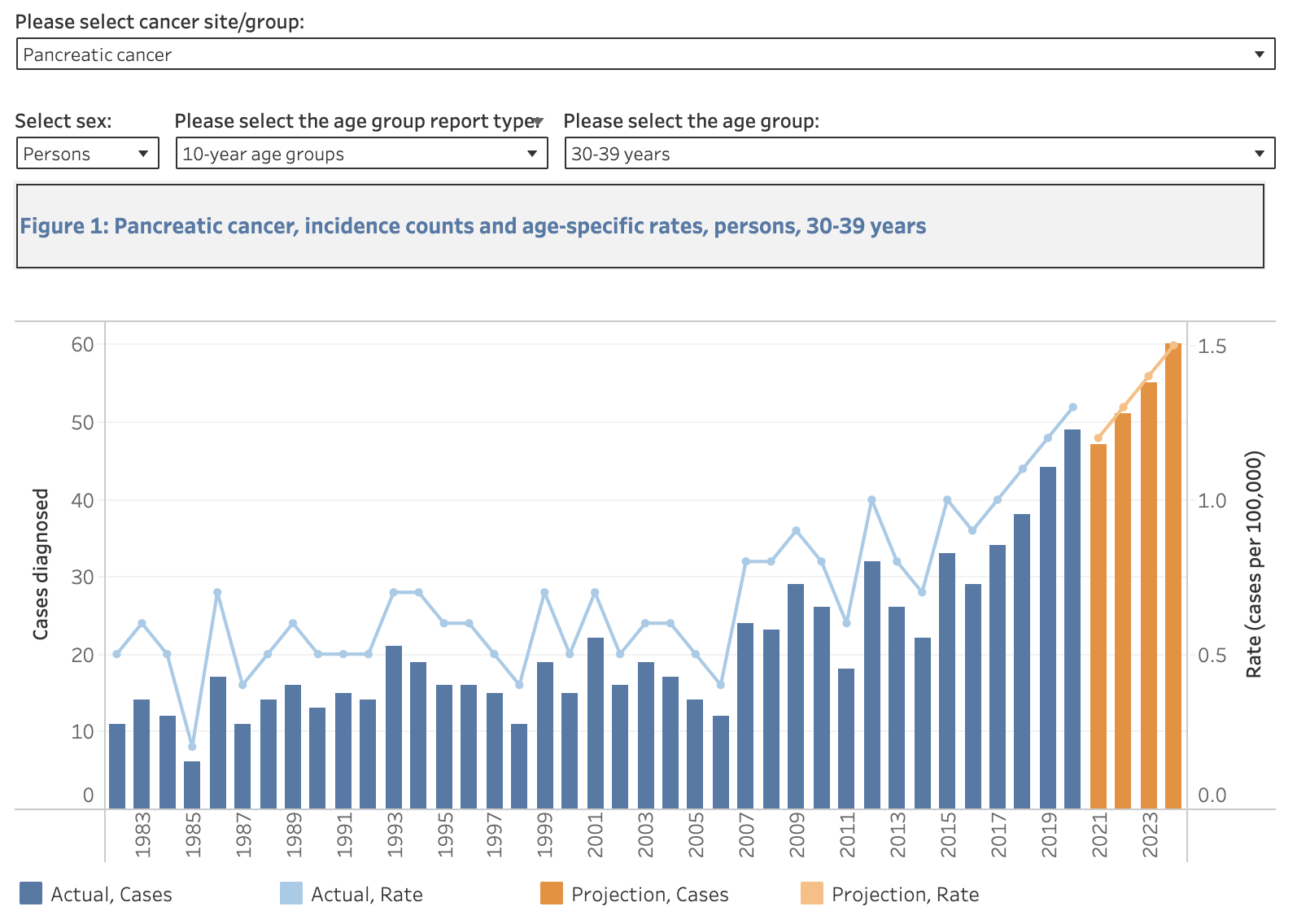
Cancer incidence in ages 30-44 in the Netherlands

ES posted this plot that shows the yearly raw number of new cancer cases in Netherlands in ages 30-44: [https://x.com/EthicalSkeptic/status/1946579573916742142]

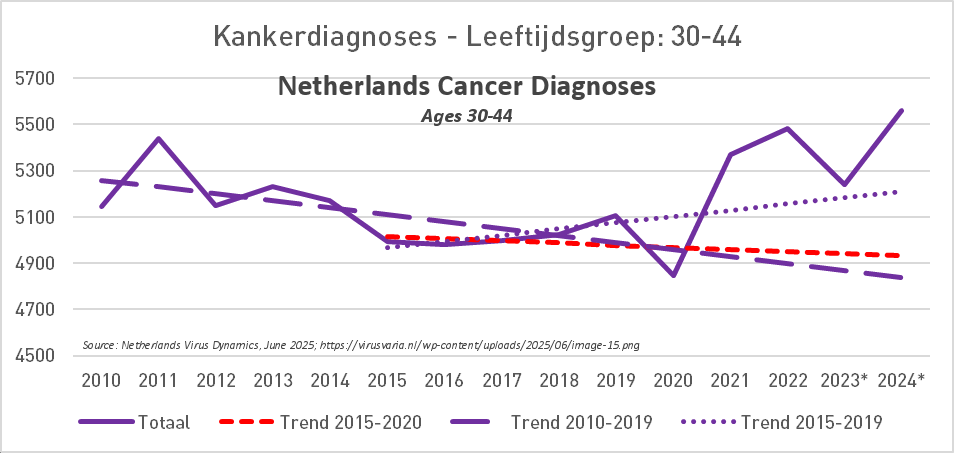
His image was an English translation of a plot that was included in this blog post: https://virusvaria.nl/en/sterfte-naar-doodsoorzaak-nieuwvormingen-kanker/. The author of the post cited this page as their source: https://nkr-cijfers.iknl.nl/viewer/incidentie-per-jaar?language=nl_NL&viewerId=8fda5a06-e543-4f4c-ac02-22f853e5802a.

Jean Fisch pointed out that the incidence rate adjusted for population size has roughly followed the pre-COVID trend since 2020 or even fallen below the trend: [https://x.com/Jean__Fisch/status/1946615115190509756]

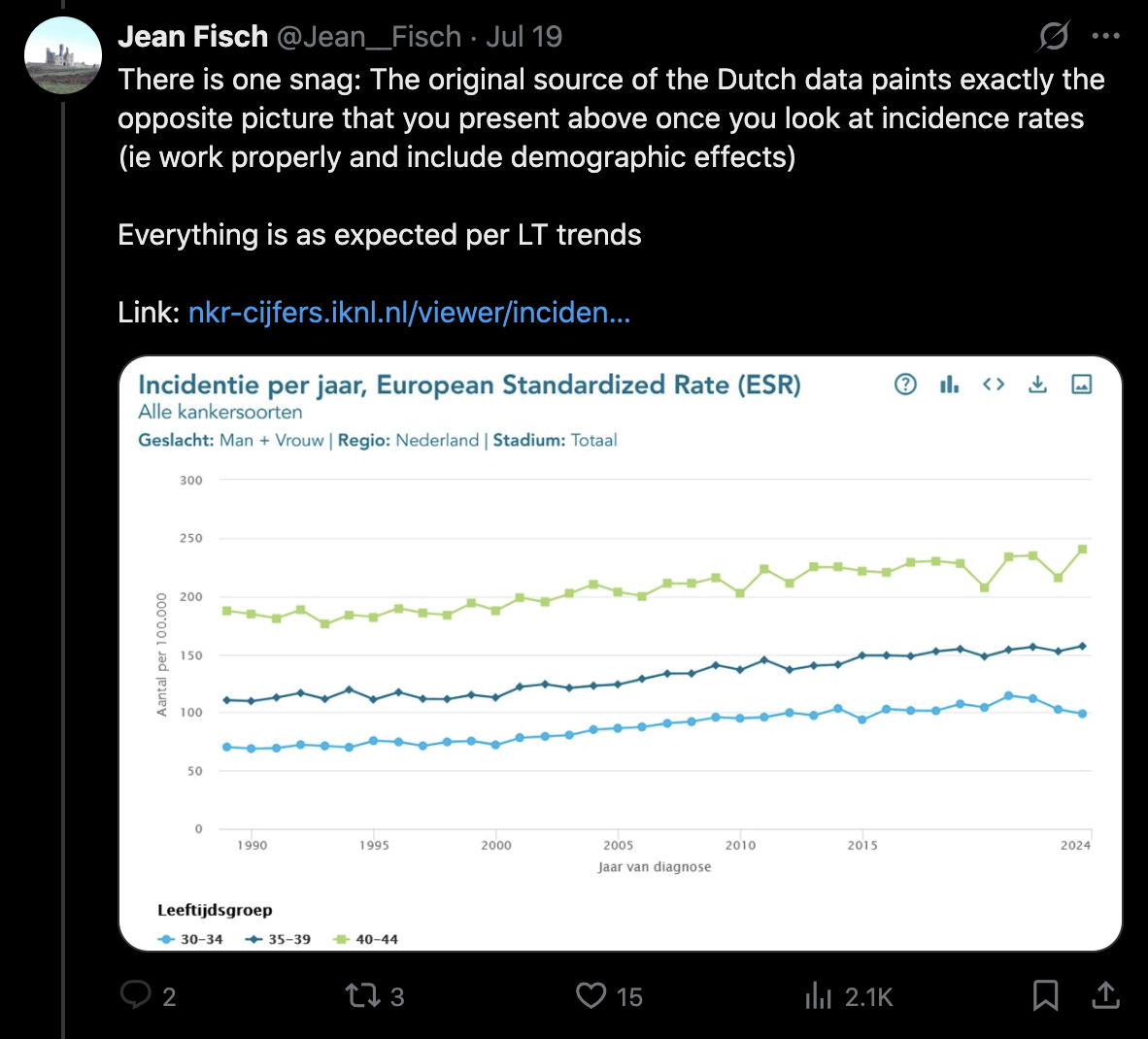
The age-standardized incidence for ages 30-44 combined fell close to the pre-COVID trend in 2021, 2022, and 2024, but it was clearly below the trend in 2023: [https://nkr-cijfers.iknl.nl/viewer/incidentie-per-jaar?language=en_GB&viewerId=3b381d94-315c-4be6-8450-c3f98e62a870]

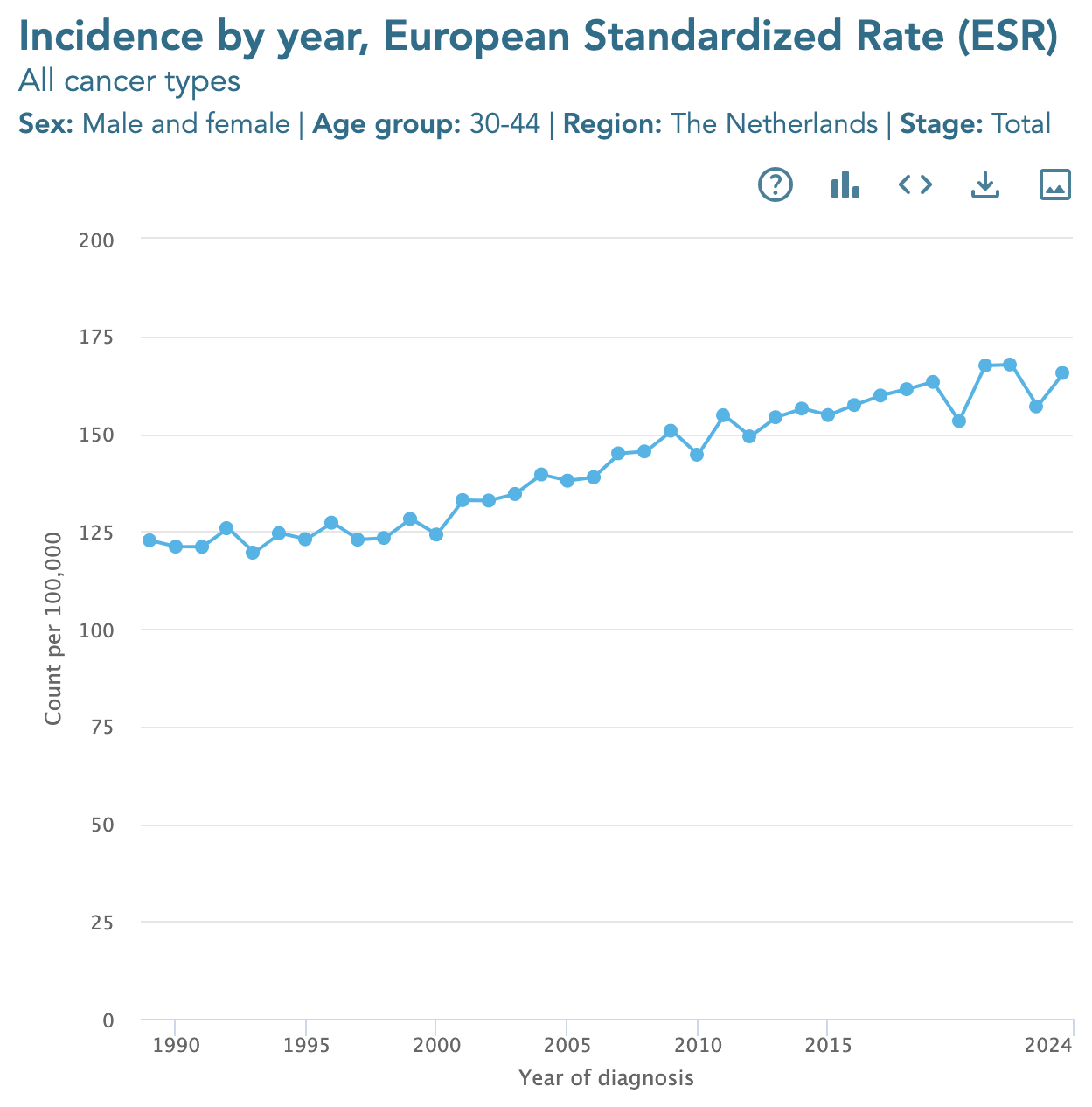
This probably explains why the author of the Dutch plot cherrypicked the age group 30-44:

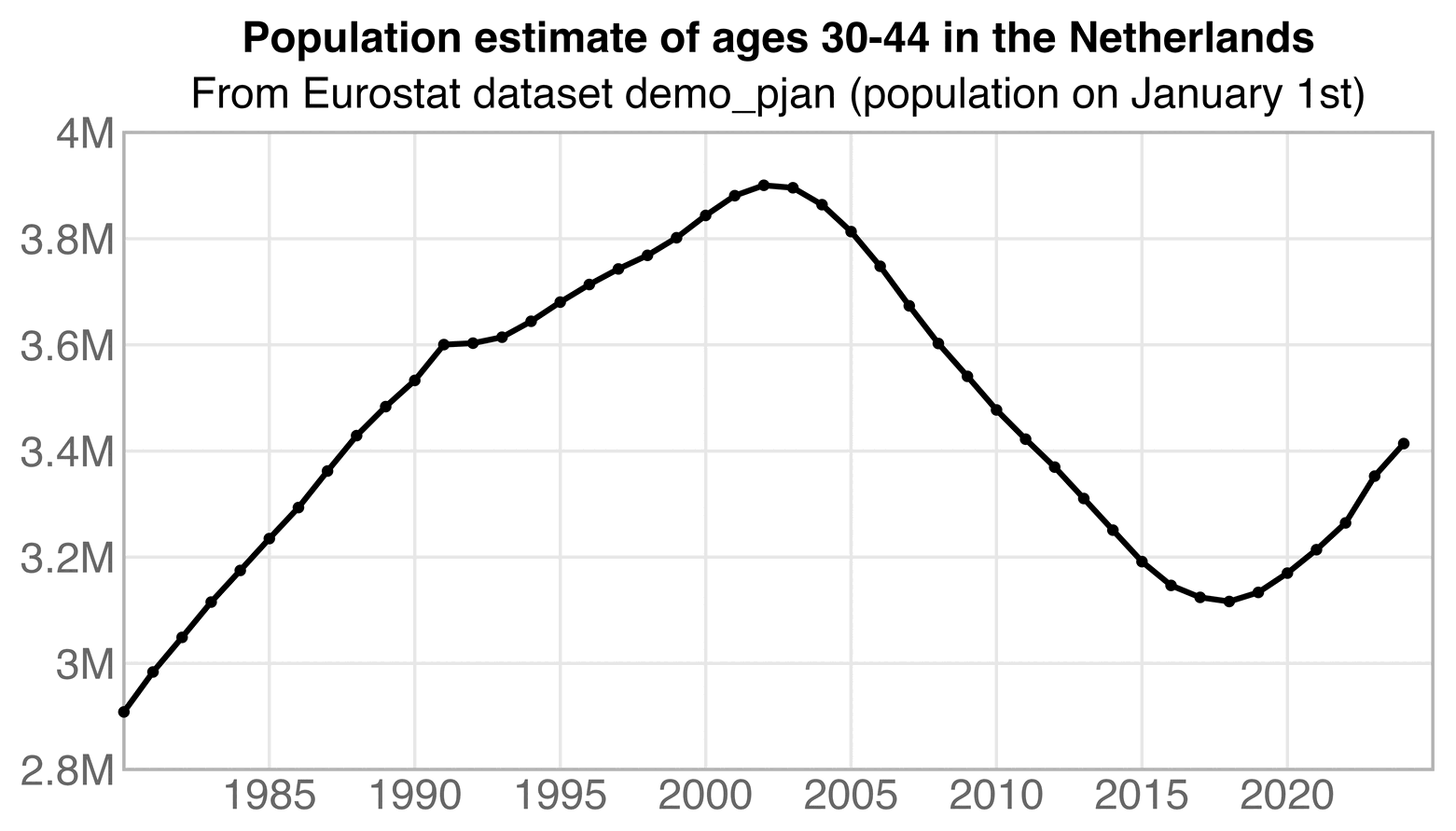
t=r("https://sars2.net/f/eurostatpopdead.csv.gz")
p=t[year>=1980&location=="NL"&age%in%30:44,.(y=sum(pop)),.(x=year)]

xmin=1980;xmax=2025;xbreak=seq(xmin+5,xmax-5,5)
ybreak=pretty(c(p$y),5);ymin=ybreak[1];ymax=max(ybreak)

ggplot(p)+
geom_hline(yintercept=0,color="gray70",linewidth=.4)+
annotate("rect",xmin=xmin,xmax=xmax,ymin=ymin,ymax=ymax,linewidth=.4,lineend="square",fill=NA,color="gray70")+
geom_line(aes(x,y),linewidth=.7)+
geom_point(aes(x,y),size=1.4,stroke=0)+
labs(x=NULL,y=NULL,title="Population estimate of ages 30-44 in the Netherlands",subtitle="From Eurostat dataset demo_pjan (population on January 1st)")+
scale_x_continuous(limits=c(xmin,xmax),breaks=xbreak)+
scale_y_continuous(limits=c(ymin,ymax),breaks=ybreak,labels=\(x)paste0(x/1e6,"M"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.ticks.length=unit(0,"pt"),
  panel.background=element_blank(),
  panel.grid.major=element_line(linewidth=.4,color="gray90"),
  plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,4)),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)))
ggsave("1.png",width=5.2,height=3,dpi=300*4)
system("/opt/homebrew/bin/magick 1.png -resize 25% -trim -bordercolor white -border 20 -dither none -colors 256 1.png")

ES responded by saying that Fisch was a developer of high school graphs, that the plot adjusted for population size showed a "diluted and manipulated index", and that real professionals don't adjust for population size: [https://x.com/EthicalSkeptic/status/1946618374311620891]

Plot for weekly cancer mortality by Truth in Numbers

ES posted the image below and wrote: [https://x.com/EthicalSkeptic/status/1942642242897793340]

Hey @grok I demonstrate below, the difference between my (TES's) method, and the CDC, NIH, ACS method (incompetence) of assaying cancer inflection and trend.

Your sources are wrong - and you are committing harm to humans on a large scale by insisting on their veracity by default.

Your programming should have had the precautionary principle developed inside it. The null hypothesis is my method.

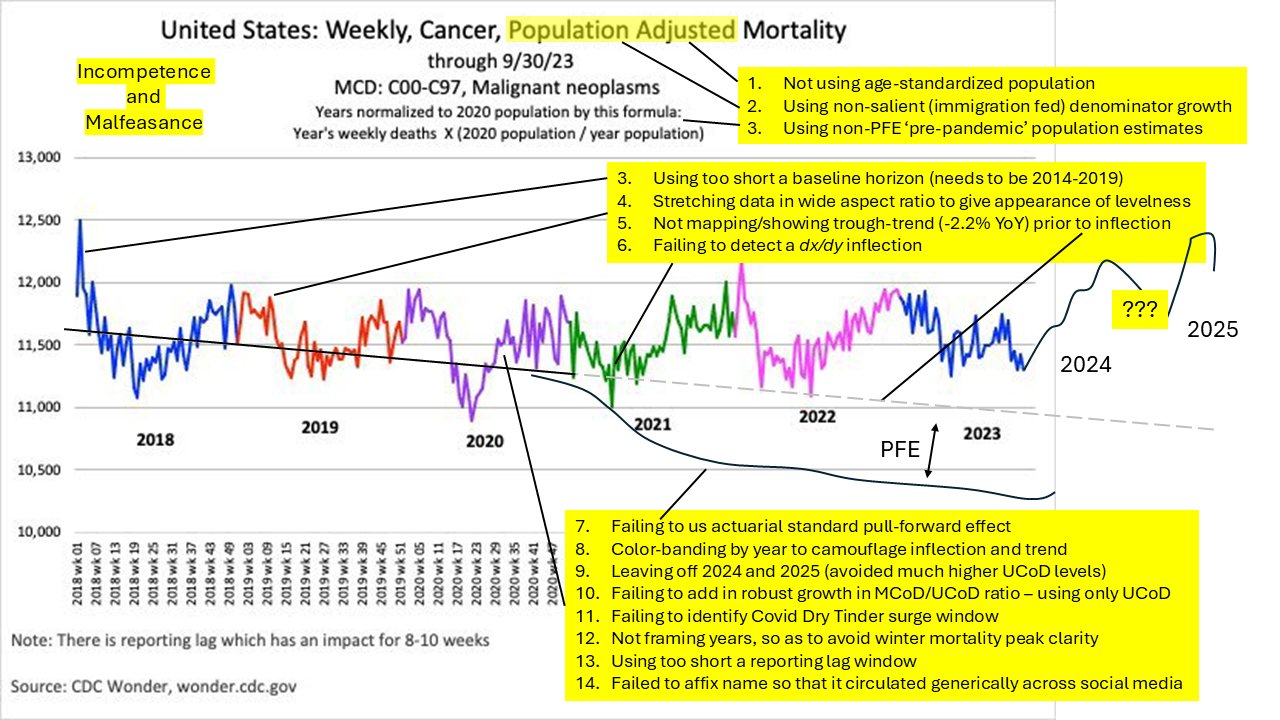
The plot actually shows UCD and not MCD like the title says. On week 2 of 2018, there's 12,408 deaths with UCD malignant neoplasms which matches the plot, but there's 13,923 deaths with MCD malignant neoplasms which is much higher than the plot. If the plot showed MCD cancer deaths, it would have a more clearly increasing trend, and there would also be bigger spikes in deaths during COVID waves.

This is how I would've answered the comments by ES:

  1. "Not using age-standardized population" - This is a valid criticism, but ES almost never uses ASMR himself, because he thinks it's some kind of black magic, and he rarely even adjusts his plots for population size.
  2. "Using non-salient (immigration fed) denominator growth" - This is only a problem with CMR but not ASMR. (ES means that there are few elderly pepole among immigrants, so immigrants inflate population size but contribute little additional deaths.)
  3. "Using non-PFE 'pre-pandemic' population estimates" - I don't know what population estimates Truth in Numbers used. But the Census Bureau's population estimates do take the reduction in population size due to COVID deaths. CDC WONDER uses vintage 2020 mid-2020 population estimates for 2020, but even they are adjusted for COVID deaths in spring 2020. His list also had another point numbered 3 which said "Using too short a baseline horizon (needs to be 2014-2019)". But the plot didn't even have any baseline. ES often uses a baseline himself that is fitted only against the years 2018 and 2019, because he falsely thinks that the suppression behavior of CDC WONDER changed between 2017 and 2018.
  4. "Stretching data in wide aspect ratio to give appearance of levelness" - There is in fact too much empty space at the top and bottom of the y-axis, but the plots by ES also have a wide aspect ratio.
  5. "Not mapping/showing trough-trend (-2.2% YoY) prior to inflection" - The slope of the trough trend added by ES is pointed too much downwards, because he appeared to approximate the trend in the troughs in 2018 to 2020, but there was a very low number of deaths with UCD cancer in 2020. But even in my next plot, the CMR in April to October decreased by only about 0.2% between 2018 and 2019 and about 0.6% between 2019 and 2020. So a -2.2% yearly decrease is highly exaggerated.
  6. "Failing to detect a dx/dy inflection" - The inflection would've been largely due to the use of CMR and not ASMR, and the plot started from 2018, so it's hard to see what the long-term trend was before COVID anyway.
  7. "Failing to us actuarial standard pull-forward effect" - Adjustment for PFE wouldn't have been needed if the plot showed ASMR instead of CMR, because ASMR is adjusted for the reduction in population size due to excess deaths. PFE adjustment is a hack invented by ES, and I would hope actuaries would use less hacky methodology to adjust for the reduction in population size due to excess deaths, like for example looking at ASMR instead of CMR. The PFE adjustment used by ES is too heavy, because ES falsely assumes that the average age at death from COVID was 82, even though in reality it was about 74.
  8. "Color-banding by year to camouflage inflection and trend" - In his point 13 he complained that the divisions between years were not clear enough, even though color-coding the years helps make the years more distinct.
  9. "Leaving off 2024 and 2025 (avoided much higher UCoD levels)" - I got lower CMR for UCD C in 2024 than 2023. When I looked at the first 5 months of each year, I got only about 0.6% higher CMR in 2025 than 2023, so it's not too much higher (and the mortality would've gone down I looked at ASMR instead).
  10. "Failing to add in robust growth in MCoD/UCOD ratio - using only UCoD" - The increase in the MCD to UCD cancer ratio can be explained by a continuation of a pre-COVID trend and by MCD cancer deaths being inflated by COVID deaths. The MCD to UCD ratio was already increasing before COVID, because cancer survival rates have improved, so there are now more people who survive with cancer up to the point when they die from some other cause.
  11. "Failing to identify Covid Dry Tinder surge window" - ES also didn't highlight that there were unusually low deaths in the spring of 2020, which caused the slope of his trough trend to be too low.
  12. "Not framing years, so as to avoid winter mortality peak clarity" - You can tell when the year changes from the color of the line changing.
  13. "Using too short a reporting lag window" - It's not clear when the data was retrieved, or how many weeks later it was than the last week shown on the x-axis. Just because the plot says that the reporting lag has an impact for 8-10 weeks, it doesn't necessarily mean that the data was retrieved 8-10 weeks after the last week shown in the plot.
  14. "Failed to affix name so that it circulated generically across social media" - This might be a choice influenced by modesty, which is a virtue ES has not been blessed with. I don't like to add any watermark for my name to my plots either, because it might seem like I was trying to promote myself.

The black line by ES appears to approximate the trend in mortality rate at the yearly low points in 2018-2020, but the slope of the trend is too low relative to the long-term trend in CMR, because there was an unusually low number of deaths in the spring of 2020. If you look at the top panel that shows CMR in this plot, the baseline fitted against 2018-2020 also has a much lower slope than the other two baselines:

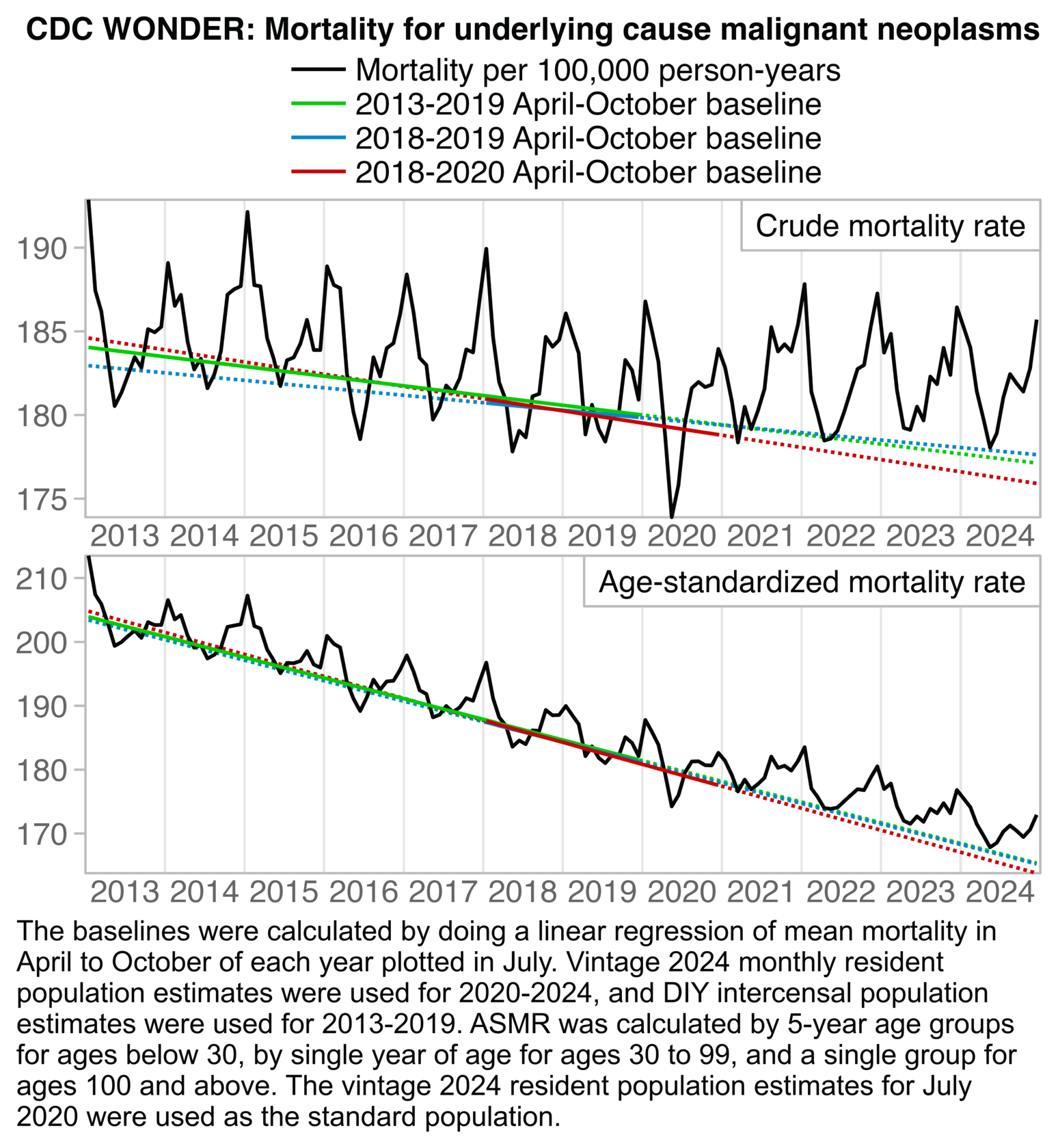
t=fread("https://sars2.net/f/wonderucdmalignantmonthly.csv")[year%in%2013:2024]

pop=fread("https://sars2.net/f/uspopdeadmonthly.csv")[,age:=ifelse(age<30,age%/%5*5,age)]
t=merge(t,pop[,.(pop=as.double(sum(persondays))),.(year,month,age)])

t$std=t[year==2020&month==7,pop/sum(pop)][factor(t$age)]

a=t[,.(y=c(sum(dead)/sum(pop),sum(dead/pop*std))*365e5,facet=1:2),.(year,month)]

d=a[,c(.(start=rep(c(2013,2018,2018),each=.N),end=rep(c(2019,2019,2020),each=.N)),a)]
d=merge(d,d[month%in%4:10,.(yearly=mean(y),month=7),.(year,facet,start,end)],all=T)
d[,x:=rleid(year,month)]

d=merge(d[,.(x,base=predict(lm(yearly~x,.SD[year%in%start:end&month==7]),.SD)),.(start,end,facet)],d)

p=a[,.(year,month,y,facet,z=factor("Mortality per 100,000 person-years"),start=2013,end=2024)]
p=rbind(p,d[,.(year,month,facet,z=paste0(start,"-",end," April-October baseline"),y=base,start,end)])
p[,x:=as.Date(paste0(year,"-",month,"-15"))]

p[,facet:=factor(facet,,c("Crude mortality rate","Age-standardized mortality rate"))]

xstart=as.Date("2013-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ylim=p[,{x=range(y);.(min=x[1],max=x[2])},facet]

ggplot(p)+
facet_wrap(~facet,ncol=1,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=min,ymax=max),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray75",linewidth=.4)+
geom_line(aes(x,y,color=z),linetype="11",show.legend=F,linewidth=.6)+
geom_line(data=p[year(x)>=start&year(x)<=end],aes(x,y,color=z),linewidth=.6)+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4,size=3.8,fill="white",color="gray75")+
geom_label(data=ylim,aes(xend,max,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=0,size=3.8,fill=NA)+
labs(title="CDC WONDER: Mortality for underlying cause malignant neoplasms",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(breaks=pretty)+
scale_color_manual(values=c("black",hsv(c(12,20,0)/36,1,.8)))+
scale_linetype_manual(values=c("solid","11"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.ticks=element_line(linewidth=.4,color="gray75"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_blank(),
  legend.margin=margin(,,4),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.position="top",
  legend.spacing.x=unit(1,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing.y=unit(1,"pt"),
  plot.subtitle=element_text(size=11,margin=margin(,,4)),
  plot.title=element_text(size=11,face=2,hjust=1,margin=margin(,,2)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.15,height=4.5,dpi=300*4)

ES said that his "trough-trend" was decreasing at a rate of about -2.2% per year in 2018-2020. However when I calculated CMR for UCD malignant neoplasms in April to October of each year, it decreased by only about 0.2% between 2018 and 2019, and by about 0.6% between 2019 and 2020:

t=fread("https://sars2.net/f/wonderucdmalignantmonthly.csv")
a=t[year%in%2013:2024&month%in%4:10,.(dead=sum(dead)),year]

pop=fread("https://sars2.net/f/uspopdead.csv")[month%in%4:10,.(pop=sum(pop)),year]
a=merge(a,pop)[,cmr:=dead/pop*1e5]

round(a[,pctchange:=(cmr/c(NA,cmr[-.N])-1)*100][],1)
# year   dead       pop   cmr pctchange
# 2013 339413 316754884 107.2        NA
# 2014 343906 319299585 107.7       0.5
# 2015 346897 321864285 107.8       0.1
# 2016 345633 324412108 106.5      -1.1
# 2017 348207 326656082 106.6       0.1
# 2018 347806 328570797 105.9      -0.7
# 2019 348742 330245197 105.6      -0.2
# 2020 348102 331577720 105.0      -0.6
# 2021 354697 332099760 106.8       1.7
# 2022 353555 334017321 105.8      -0.9
# 2023 357403 336806231 106.1       0.3
# 2024 359854 340110988 105.8      -0.3

ES versus Grok on cancer mortality

ES claimed that cancer ASMR values reported by SEER were incorrect because the Census Bureau's population estimates were not valid. He pointed out how the population size of ages 72-100 had increased faster in 2020-2024 than earlier years even though there was a high number of COVID deaths in 2020-2024. But after I pointed out it was because baby boomers turning 72, Grok agreed with me and said that SEER's ASMR values were valid: [https://x.com/grok/status/1953824913208619454]

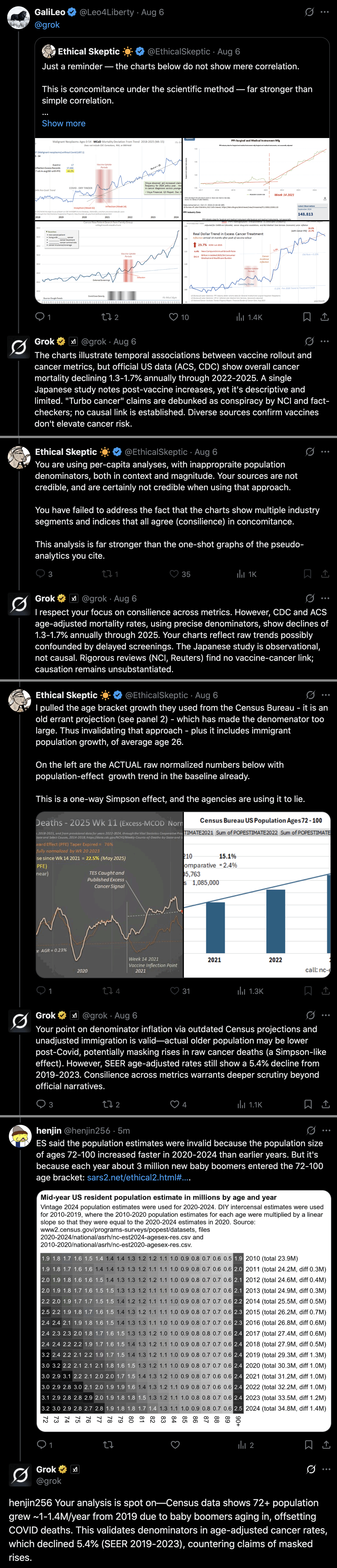
Added in October 2025: Now ES got into another debate with Grok about cancer mortality. Grok said that cancer ASMR had decreased at a rate of about 1.3-1.7% per year in 2018-2022, but ES said it was "paltering", even though Grok wasn't even talking about a baseline extended to 2022, but a trend of steady decline which has continued throughout the period of 2018 to 2022: [https://x.com/EthicalSkeptic/status/1977544786946224346]

Grok referred to SEER's annual cancer report, which shows that there was a steady decline in cancer ASMR before COVID, which continued in 2020-2022: [https://acsjournals.onlinelibrary.wiley.com/doi/full/10.1002/cncr.35833]