Comments to Ethical Skeptic (part 1) - sars2.net

First published 2024-04-03 UTC, last modified 2026-02-22 UTC

Other parts: ethical2.html, ethical3.html (deaths in ages 0-4), ethical4.html.

Contents

Plot for cardiac deaths in ages 0 to 54

Ethical Skeptic posted this tweet where he commented on a plot by Truth In Numbers: [https://x.com/EthicalSkeptic/status/1757181136306848244]

1. He used the wrong ICD-codes: used 'heart disease in older persons' (many of whom died in 2020/21 from Covid), not 'sudden cardiac death in younger persons' (see panel 1 chart done correctly).

2. Used an ICD R99/999 and Lag depleted 2023 data set (see data in panel 2). This is simply malicious.

3. Diluted the group with population growth (this cohort shrank actually, but he used total population - cheating, idiocy or both).

4. Did not use pull forward effect, as a professional does.

5. Quashed the chart into a full range y-axis magnitude to make it appear flat.

6. Put in a fictitious regression line, when the weekly line shows clearly an increase (save for his corrupted 2023 numbers)

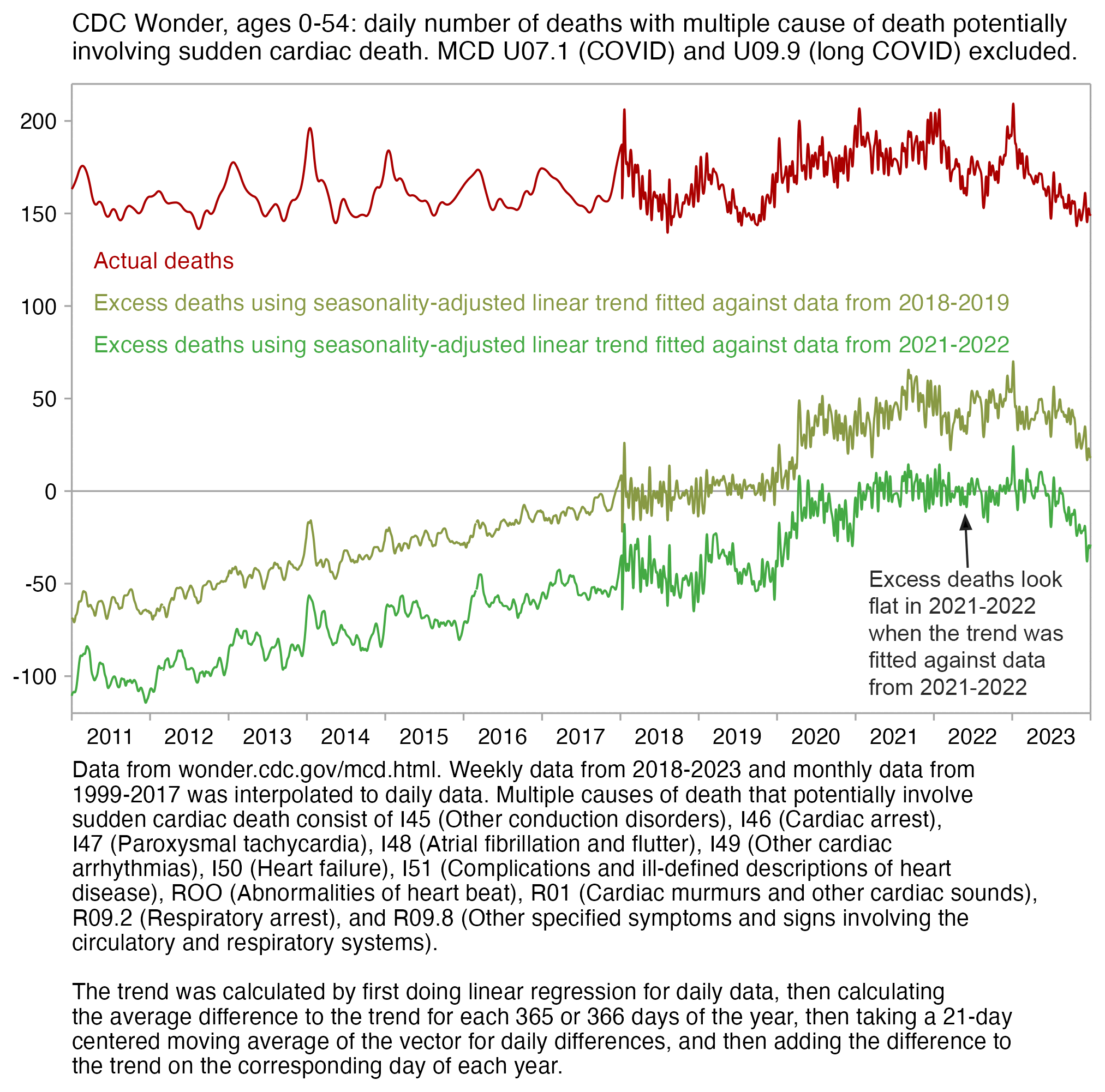
Ethical Skeptic didn't specify how he calculated the baseline for excess deaths. But if he only fitted the baseline based on data from 2018 and 2019, then it might explain why the line for excess deaths appears to be so flat in 2018 and 2019, and the line would've probably looked less flat if he used a longer fitting period so the baseline wouldn't have adapted as closely to the data in 2018-2019.

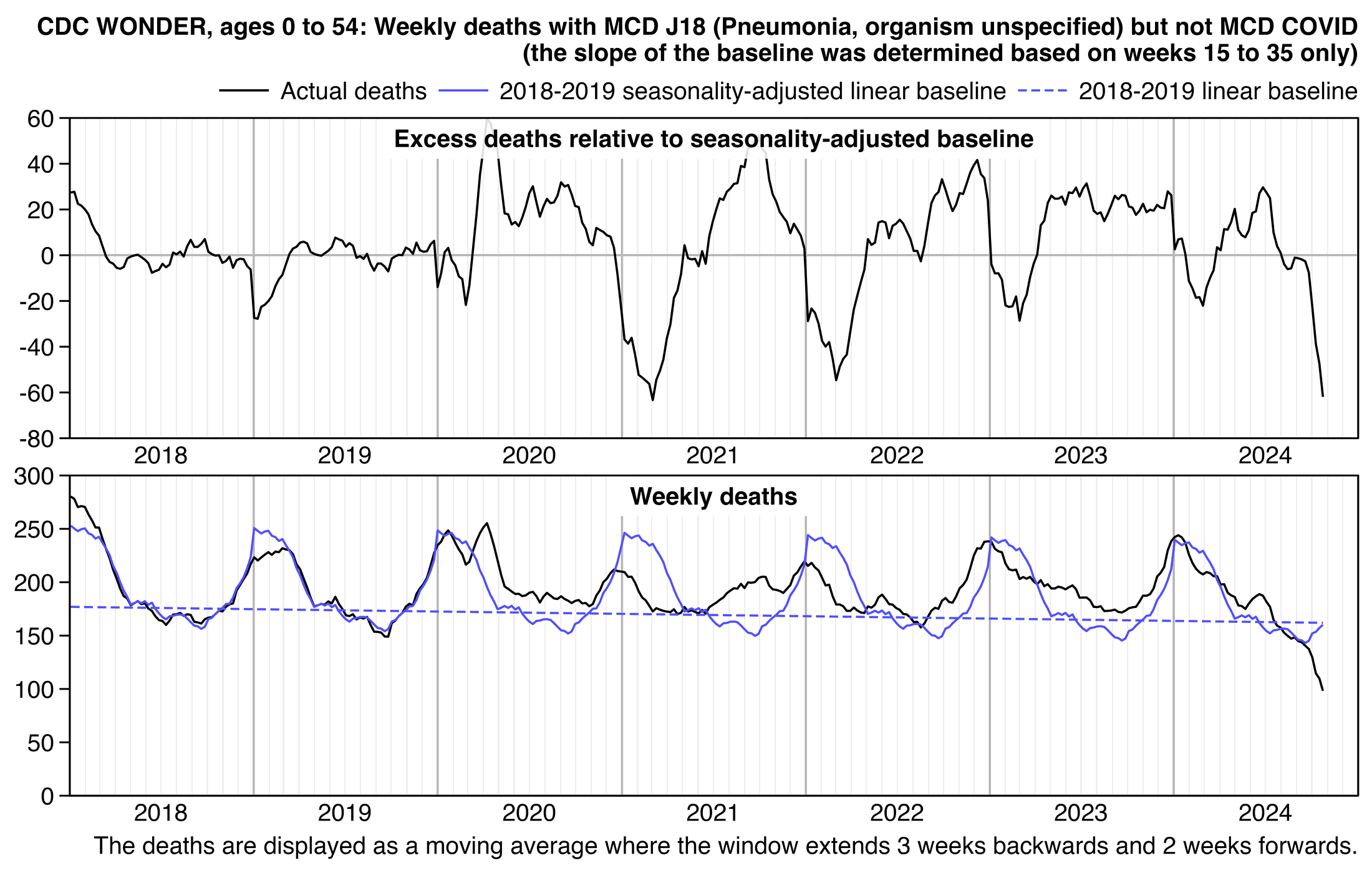
I did queries at CDC WONDER for ICD codes in Ethical Skeptic's plot, but I split it out into one query where the multiple cause of death included one of the cardiac-related ICD codes he used in his plot, and I did a second query for the R96 and R99 ICD codes which are used for unknown and unresolved causes of death: https://wonder.cdc.gov/mcd.html. I excluded COVID deaths by doing a query where the multiple causes of death included both one of the cardiac ICD codes and the ICD code for COVID, and then I subtracted the weekly COVID deaths from the cardiac total.

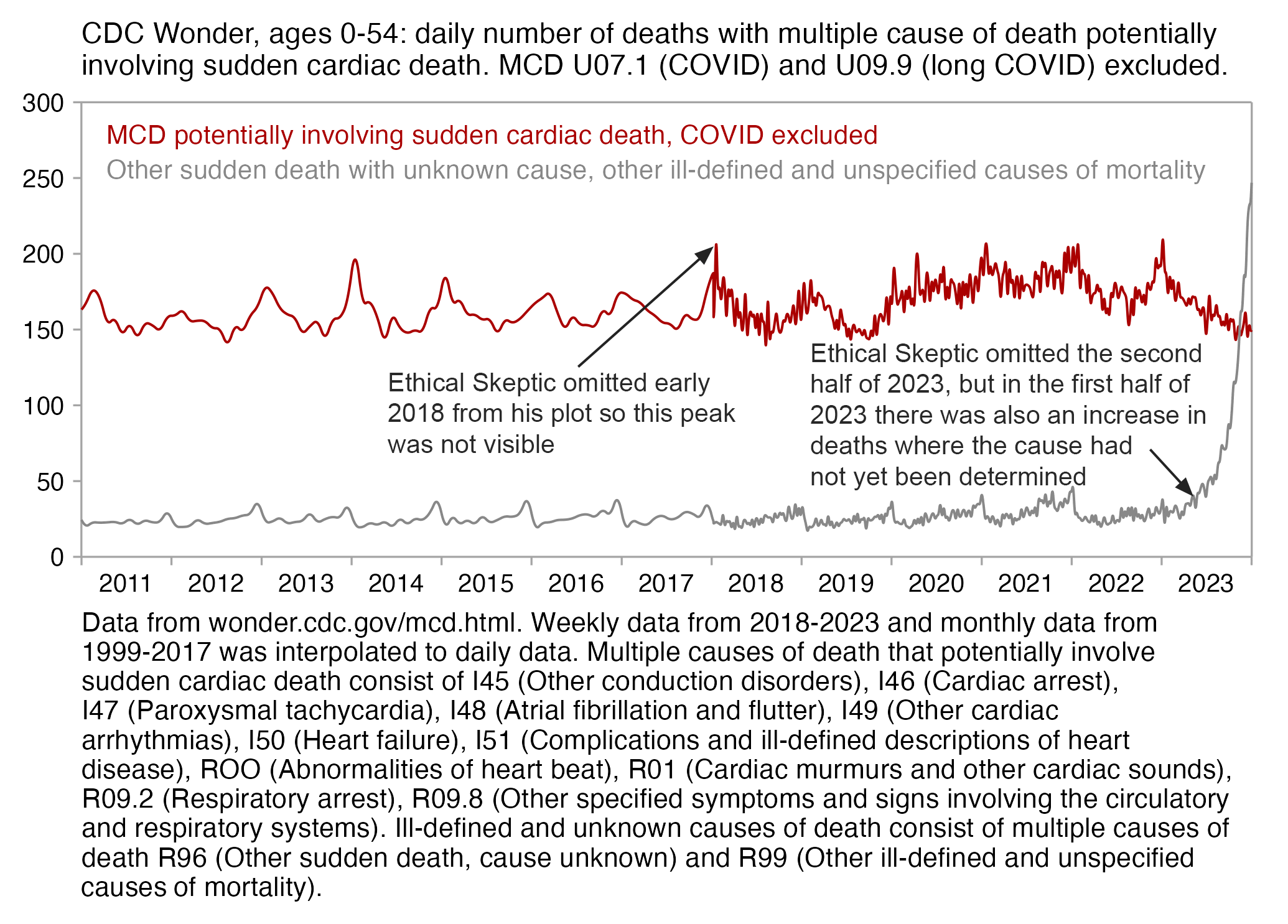
I got a large spike in cardiac deaths in early 2018, even though it lasted only a single week. It was not visible from Ethical Skeptic's plot because his blue line which shows the excess deaths only starts around the beginning of March 2018. At first I thought Ethical Skeptic may have deliberately omitted early weeks of 2018 from his plot to make later spikes in deaths seem more impressive in comparison to the flat excess deaths in 2018 and 2019, but he told me that the blue line in his plot was actually a moving average, so the first weeks of data were included in the moving average for the point that was plotted around the start of March 2018. He wrote: "The initial months are smoothed into a 7-w moving average data line, so they are in there. I will add a tapered-moving average version of the the initial months into the future versions of the chart to allay that misconception." [https://theethicalskeptic.substack.com/p/the-state-of-things-pandemic-week-706/comment/53336888] And the peak in deaths in early 2018 only consisted of a single week, so it doesn't have much effect on a moving average of several weeks.

Ethical Skeptic omitted the last 26 weeks of 2023 from his plot because there was a large increase in R96 and R99 deaths where the cause had not yet been specified. His plot also had a large increase in deaths in the first half of 2023, but it seems to be mainly due to deaths where the cause has not yet been specified and not due to cardiac deaths (especially since I retrieved the data in my plot below later than Ethical Skeptic retrieved his data, so at the time he retrieved his data the number of R96 and R99 deaths in the first half of 2023 would've been even higher than in my plot):

In Ethical Skeptic's plot the excess deaths looked flat in 2018-2019, but it might partially be because he fitted his baseline against data from only 2018 and 2019, because if you fit a seasonality-adjusted trend against only two years of data then it's easy to get the baseline to match the data closely. In the plot below where I fitted the baseline against data from 2021-2022, I also got my excess deaths to look roughly flat in 2021-2022:

library(tempdisagg);library(ggplot2);library(stringr)

wonder=\(x){t=readLines(x);t=paste(t[1:(grep("^\"(---|Total)",t)[1]-1)],collapse="\n");read.table(sep="\t",text=t,header=T,na.strings="Not Applicable")[-1]}

old=wonder("Multiple Cause of Death, 1999-2020.txt")
old=td(data.frame(as.Date(paste(old$Month.Code,1),"%Y/%m %d"),old$Deaths)~1,,"daily","fast")$values

new=wonder("Provisional Mortality Statistics, 2018 through Last Week.txt")
covid=wonder("wondercovid.txt")
mt=match(covid$MMWR.Week.Code,new$MMWR.Week.Code)
new$Deaths[mt]=new$Deaths[mt]-covid$Deaths
new=td(data.frame(as.Date(sub(".*ending ","",new$MMWR.Week),"%B %d, %Y")+3,new$Deaths)~1,,"daily","fast")$values

ill=wonder("ill.txt")
ill=td(data.frame(as.Date(sub(".*ending ","",ill$MMWR.Week),"%B %d, %Y")+3,ill$Deaths)~1,,"daily","fast")$values
illold=wonder("illold.txt")
illold=td(data.frame(as.Date(paste(illold$Month.Code,1),"%Y/%m %d"),illold$Deaths)~1,,"daily","fast")$values

d=rbind(old[!old$time%in%new$time,],new)|>"colnames<-"(c("x","y"))
xy=cbind(d,z="Actual deaths")

ma=\(x,b=1,f=b)rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T)

prediction=d$x>="2018-1-1"&d$x<="2019-12-31"
linear=predict(lm(y~x,d[prediction,]),d)
days=substr(d$x,6,10)
daily=tapply(d$y[prediction]-linear[prediction],days[prediction],mean)
daily=ma(rep(daily,3),10)[(length(daily)+1):(2*length(daily))]|>setNames(names(daily))
excess=d$y-(linear+daily[days])
xy=rbind(xy,data.frame(x=d$x,y=excess,z="Excess deaths using seasonality-adjusted linear trend fitted against data from 2018-2019"))

prediction=d$x>="2021-01-01"&d$x<="2022-12-31"
linear=predict(lm(y~x,d[prediction,]),d)
days=substr(d$x,6,10)
daily=tapply(d$y[prediction]-linear[prediction],days[prediction],mean)
daily=ma(rep(daily,3),10)[(length(daily)+1):(2*length(daily))]|>setNames(names(daily))
excess=d$y-(linear+daily[days])
xy=rbind(xy,data.frame(x=d$x,y=excess,z="Excess deaths using seasonality-adjusted linear trend fitted against data from 2021-2022"))

xy$z=factor(xy$z,unique(xy$z))

xstart=as.Date("2011-1-1");xend=as.Date("2024-1-1")
xy=xy[xy$x>=xstart&xy$x<=xend,]

xbreak=seq(xstart,xend,"6 month")
xlab=c(rbind("",2011:2023),"")
cand=c(sapply(c(1,2,5),\(x)x*10^c(-10:10)))
ymax=max(xy$y,na.rm=T);ymin=min(xy$y,na.rm=T)
ystep=cand[which.min(abs(cand-(ymax-ymin)/5))]
ystart=ystep*floor(ymin/ystep)
yend=ystep*ceiling(ymax/ystep)
ystart=-120;yend=220
ybreak=seq(-100,yend,ystep)

color=c("#aa0000","#889944","#44aa44")

labels=data.frame(x=xstart+.02*(xend-xstart),y=seq(ystart+(yend-ystart)*.72,,-(yend-ystart)/15,nlevels(xy$z)),label=levels(xy$z))

sub=str_wrap("Data from wonder.cdc.gov/mcd.html. Weekly data from 2018-2023 and monthly data from 1999-2017 was interpolated to daily data. Multiple causes of death that potentially involve sudden cardiac death consist of I45 (Other conduction disorders), I46 (Cardiac arrest), I47 (Paroxysmal tachycardia), I48 (Atrial fibrillation and flutter), I49 (Other cardiac arrhythmias), I50 (Heart failure), I51 (Complications and ill-defined descriptions of heart disease), ROO (Abnormalities of heart beat), R01 (Cardiac murmurs and other cardiac sounds), R09.2 (Respiratory arrest), and R09.8 (Other specified symptoms and signs involving the circulatory and respiratory systems).",95)
sub=paste0(sub,"\n\n",str_wrap("The trend was calculated by first doing linear regression for daily data, then calculating the average difference to the trend for each 365 or 366 days of the year, then taking a 21-day centered moving average of the vector for daily differences, and then adding the difference to the trend on the corresponding day of each year.",95))

ggplot(xy,aes(x=x,y=y,color=z))+
geom_hline(yintercept=c(ystart,0,yend),color="gray65",linewidth=.25)+
geom_vline(xintercept=c(xstart,xend),color="gray65",linewidth=.25)+
geom_line(aes(color=z),linewidth=.3)+
geom_label(data=labels,aes(x=x,y=y,label=label),fill=alpha("white",.8),label.r=unit(0,"lines"),label.padding=unit(.04,"lines"),label.size=0,color=color[1:nrow(labels)],size=2.4,hjust=0)+
labs(title=str_wrap("CDC Wonder, ages 0-54: daily number of deaths with multiple cause of death potentially involving sudden cardiac death. MCoD U07.1 (COVID) and U09.9 (long COVID) excluded.",88),x=NULL,y=NULL,caption=sub)+
coord_cartesian(clip="off",expand=F)+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
theme(axis.text=element_text(size=6.5,color="black"),
  axis.ticks=element_line(linewidth=.25,color="gray65"),
  axis.ticks.x=element_line(color=alpha("gray65",c(1,0))),
  axis.ticks.length=unit(.15,"lines"),
  axis.title=element_text(size=8),
  legend.position="none",
  panel.background=element_rect(fill="white"),
  panel.grid=element_blank(),
  plot.background=element_rect(fill="white"),
  plot.margin=margin(.4,.65,.4,.4,"lines"),
  plot.caption=element_text(size=6.7,hjust=0,margin=margin(.6,0,0,0,"lines")),
  plot.title=element_text(size=7.5))
ggsave("1.png",width=4.6,height=4.5,dpi=450)

Updated plot for cardiac deaths in ages 0 to 54 with drug deaths included

After Ethical Skeptic had published the plot that I wrote about in the previous section of this HTML file, he published an updated version of the plot where he included deaths due to accidental drug poisoning, and he included this note at the bottom of the plot: "X42-44 ((narcotics, heroin, fentanyl, meth, other drug) excess mortality surge removed (for 2020 only - lockdown impact is not trend data)". [https://theethicalskeptic.substack.com/p/the-state-of-things-pandemic-week-706] The plot now had a sudden increase in deaths between December 2020 and January 2021 which was missing from the earlier version, but it's because he removed excess deaths from drug overdoses in 2020 but not from 2021 and later years:

The reason why the increase between 2020 and 2021 is not instant but it's spread over several weeks is probably because the plot displays a moving average where the window extends 3 weeks backwards and 2 weeks forwards.

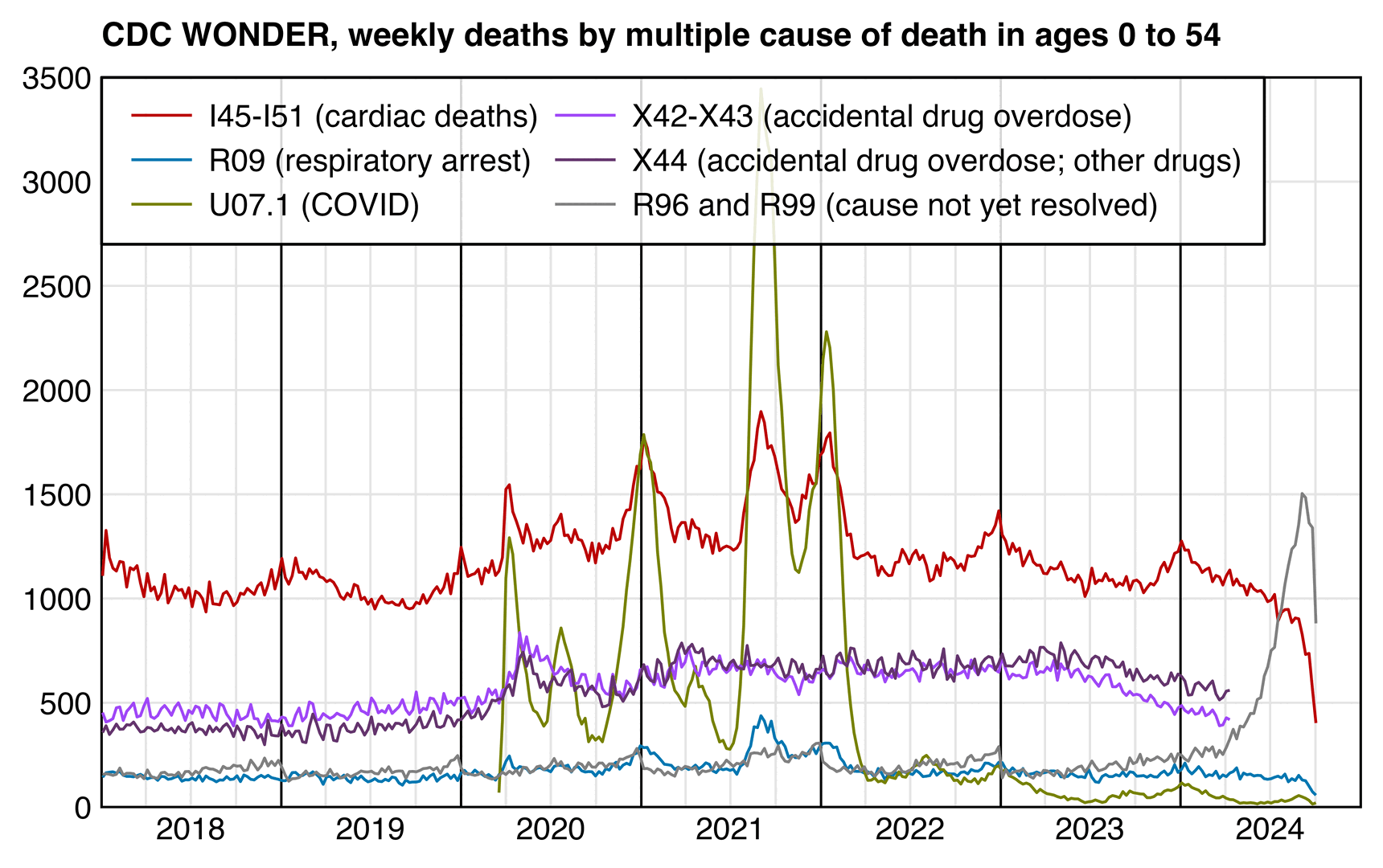
It's not clear if the plot above includes only X44 deaths or also X42 and X43 deaths, because the line at the bottom indicates that X42 to X44 deaths were removed in 2020, but the second line from the bottom seems to indicate that the plot only includes X44 deaths. In the plot below the number of X44 deaths was similar to the number of X42 and X43 deaths combined. The plot below also shows that there's spikes in cardiac deaths during COVID waves, so most of the excess deaths in Ethical Skeptic's plot can probably be attributed to either drugs or COVID:

library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wonderskeptic.csv")
p=t[,.(x=date-3,y=as.double(dead),z=factor(cause,unique(cause)))]

xstart=as.Date("2018-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=c(rbind("",2018:2024),"")
ystart=0;yend=3500;ystep=500;ybreak=seq(ystart,yend,ystep)

color=c("#bb0000",hcl(225,100,40),hcl(90,120,50),hcl(280,120,50),hcl(300,40,30),"gray50")

ggplot(p,aes(x,y,color=z))+
coord_cartesian(clip="off",expand=F)+
geom_hline(yintercept=seq(ystart,yend,ystep),color="gray90",linewidth=.25)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.25)+
geom_vline(xintercept=seq(xstart,xend,"year"),linewidth=.25)+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_line(linewidth=.3)+
labs(title="CDC WONDER, weekly deaths by multiple cause of death in ages 0 to 54"|>stringr::str_wrap(80),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
guides(colour=guide_legend(ncol=2,byrow=F))+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks=element_blank(),
  axis.ticks.length=unit(0,"pt"),
  axis.title=element_text(size=7),
  legend.background=element_blank(),
  legend.box.just="left",
  legend.key=element_blank(),
  legend.spacing.x=unit(2,"pt"),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.position=c(0,1),
  legend.justification=c(0,1),
  legend.box.background=element_rect(fill=alpha("white",.85),color="black",linewidth=.3),
  legend.margin=margin(-2,5,4,5),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=7),
  plot.title=element_text(size=7.3,face=2))
ggsave("1.png",width=4.3,height=2.7,dpi=400*4)
system("magick 1.png -resize 25% 1.png")

In the plot above I didn't exclude deaths with MCD COVID. In 2020 to 2023 in ages 0 to 54, only about 0.5% of deaths with MCD X42 to X44 also had MCD COVID, but about 9% of deaths with MCD I45 to I51 also had MCD COVID.

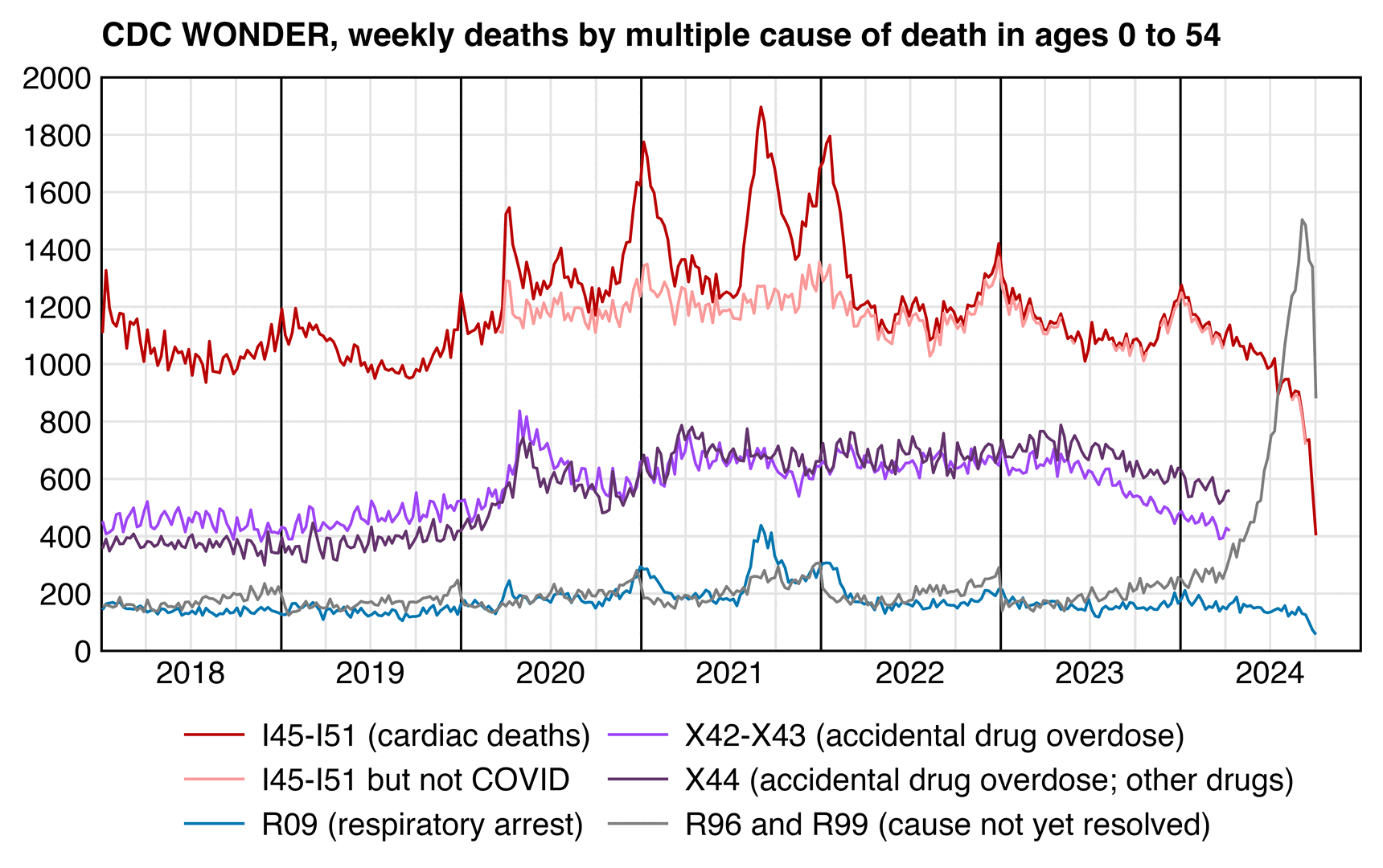
In the next plot the light red line shows deaths with MCD I45-I51 but not MCD COVID. The light red line is clearly elevated in 2020 to 2023 compared to 2018 and 2019, but the period with elevated deaths already started in the second quarter of 2020, which is difficult to blame on the vaccines, and the steady elevation of the light red line since 2020 rather seems to coincide with the elevation of drug-related deaths since 2020:

library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wonderskeptic.csv")
t=rbind(t[cause%like%"I45"],merge(t[cause%like%"I45",.(date,dead)],t[cause%like%"Cardiac",.(date,dead2=dead)],all=T)[,.(cause="I45-I51 but not COVID",dead=dead-dead2,date)],t[!cause%like%"I45|Cardiac|COVID"])

p=t[,.(x=date-3,y=as.double(dead),z=factor(cause,unique(cause)))]

xstart=as.Date("2018-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=c(rbind("",2018:2024),"")
ystart=0;yend=2000;ystep=200;ybreak=seq(ystart,yend,ystep)

color=c("#bb0000","#ff9999",hcl(225,100,40),hcl(280,120,50),hcl(300,40,30),"gray50")

ggplot(p,aes(x,y,color=z))+
coord_cartesian(clip="off",expand=F)+
geom_hline(yintercept=seq(ystart,yend,ystep),color="gray90",linewidth=.25)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.25)+
geom_vline(xintercept=seq(xstart,xend,"year"),linewidth=.25)+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_line(linewidth=.3)+
labs(title="CDC WONDER, weekly deaths by multiple cause of death in ages 0 to 54",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
guides(colour=guide_legend(ncol=2,byrow=F))+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks=element_blank(),
  axis.ticks.length=unit(0,"pt"),
  axis.title=element_text(size=7),
  legend.background=element_blank(),
  legend.box.just="left",
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.margin=margin(5,5,0,5),
  legend.position="bottom",
  legend.spacing.x=unit(2,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=7),
  plot.title=element_text(size=7.3,face=2))
ggsave("1.png",width=4.3,height=2.7,dpi=400*4)
system("magick 1.png -resize 25% 1.png")

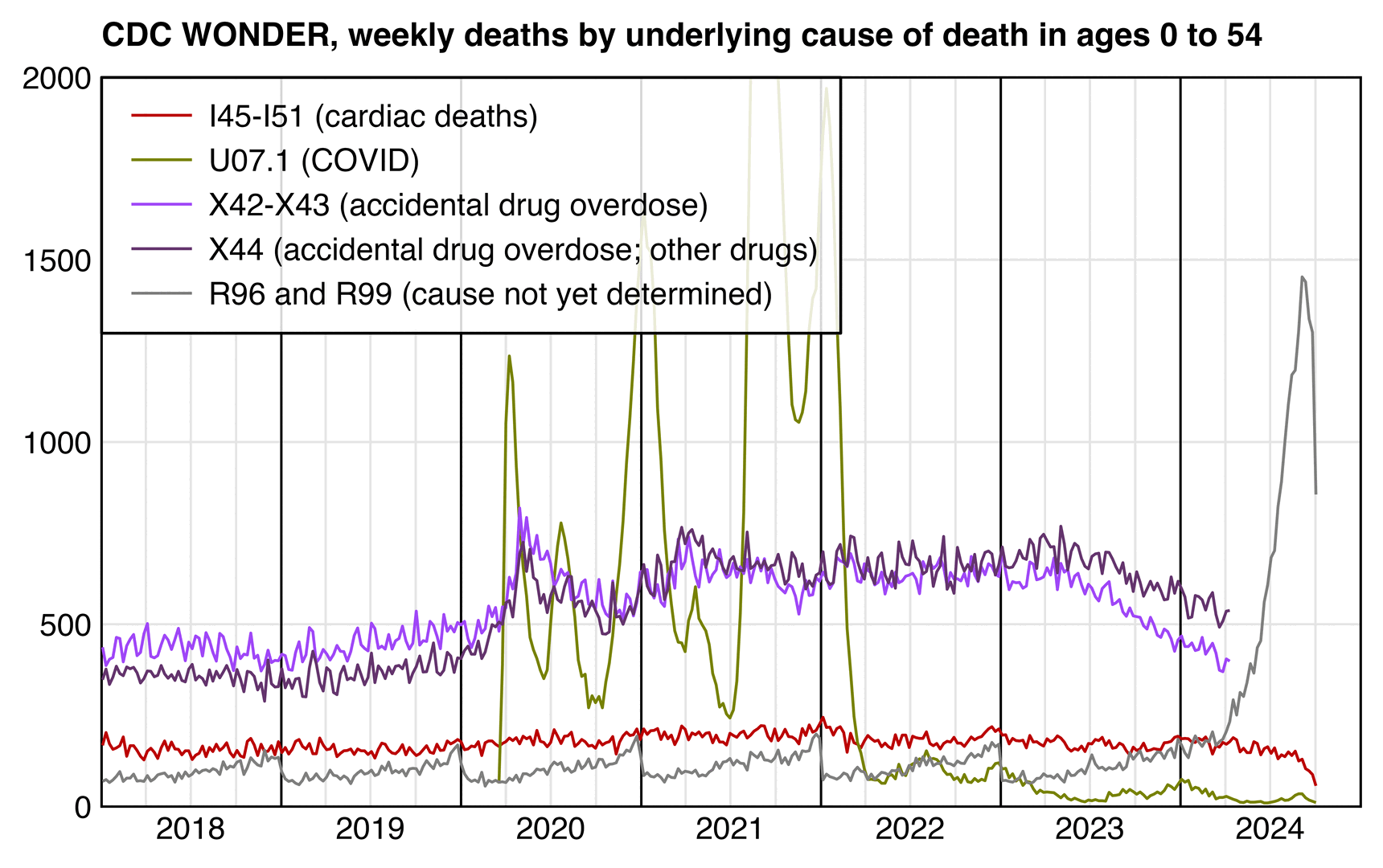
In the next plot which shows deaths by underlying cause instead of multiple cause, there is no longer such a clear increase in deaths under the cardiac ICD codes in 2020:

library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wonderskepticucd.csv")

p=t[,.(x=date-3,y=as.double(dead),z=factor(cause,unique(cause)))]

xstart=as.Date("2018-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=c(rbind("",2018:2024),"")
yend=2000;ystep=500;ybreak=seq(0,yend,ystep)

color=c("#bb0000",hcl(90,120,50),hcl(280,120,50),hcl(300,40,30),"gray50")

ggplot(p,aes(x,y=pmin(y,yend),color=z))+
coord_cartesian(clip="off",ylim=c(0,yend),expand=F)+
geom_hline(yintercept=seq(0,yend,ystep),color="gray90",linewidth=.25)+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray90",linewidth=.25)+
geom_vline(xintercept=seq(xstart,xend,"year"),linewidth=.25)+
geom_hline(yintercept=c(0,yend),linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_line(linewidth=.3)+
labs(title="CDC WONDER, weekly deaths by underlying cause of death in ages 0 to 54"|>stringr::str_wrap(80),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(breaks=ybreak)+
scale_color_manual(values=color)+
guides(colour=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks=element_blank(),
  axis.ticks.length=unit(0,"pt"),
  axis.title=element_text(size=7),
  legend.background=element_blank(),
  legend.box.just="left",
  legend.key=element_blank(),
  legend.spacing.x=unit(2,"pt"),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.position=c(0,1),
  legend.justification=c(0,1),
  legend.box.background=element_rect(fill=alpha("white",.85),color="black",linewidth=.3),
  legend.margin=margin(-2,5,4,5),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=7),
  plot.title=element_text(size=7.3,face=2))
ggsave("1.png",width=4.3,height=2.7,dpi=400*4)
system("magick 1.png -resize 25% 1.png")

Ethical Skeptic had the chutzpah to say that it would equate to obfuscation if he added excess drug deaths to his plot in 2020. He wrote: "It should be noted that an initial mid-2020 surge in excess deaths due to overdoses (X42-44) during the lockdown period has been removed from this data. This is a death-surge which is non-Natural/non-Vaccine in its basis and can be viewed as to its arrival shape and magnitude in Chart 4c above. This 2020 surge is not trend data, hence its removal in favor of the true arrival trend attributable to the mRNA vaccine. There exists a slight elevation in these deaths which remains on the chart, attributable to Covid-19, but the permanent surge in mortality arrived as a result of the Covid vaccine beginning in December (Week 52 - 14 days after the vaccine start) 2020. To conflate that pre-vaccine surge with the vaccine arrival data, would constitute obfuscation." [https://theethicalskeptic.com/2024/04/04/the-state-of-things-pandemic-week-50-2023/] He wrote that the excess drug deaths in 2020 were not "trend data", because the trend he was trying to find was a trend of increased deaths after the vaccine rollout. So in order to show there is a trend which fits his preconceptions, he considers data which doesn't conform to his preconceptions to not be "trend data", so he can freely discard it.

When someone asked ES why there was a huge increase in deaths in early 2021 even though only few people in ages 0 to 54 had been vaccinated, he answered the deaths were caused by the vaccines, but he didn't even mention that he omitted excess drug deaths from his plot in 2020 but not 2021: [https://x.com/EthicalSkeptic/status/1775757476085841999]

And when someone asked Ethical Skeptic why he included drug deaths in his plot, he said that the persistent increase in drug deaths was somehow caused by the vaccines: [https://x.com/EthicalSkeptic/status/1775741411524030473]

As a justification for why ES included a certain proportion of drug deaths in his plot, he falsely claimed that if a sudden cardiac death is induced by a drug overdose, only the drug overdose is listed as a multiple cause of death, because he falsely claimed that there is only one multiple cause of death code listed for deaths from external causes: [https://x.com/Beta350R/status/1778168854960808139]

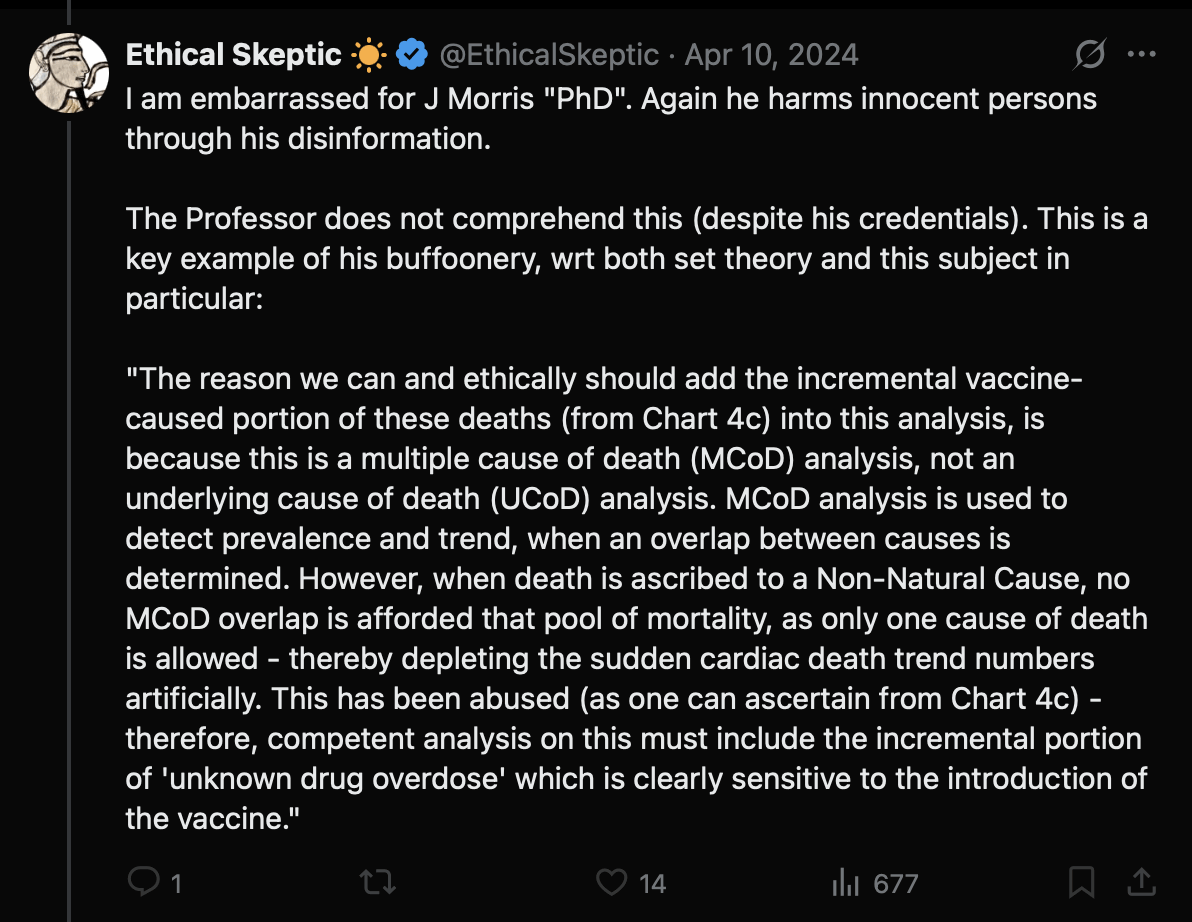
However for example in 2021, CDC WONDER returned 4,713 deaths where the MCD list included one of the drug-related codes X42-X44, and where the MCD list also included one of the cardiac ICD codes in his plot (which were I45-I51, R00, and R01). ChatGPT also said that "for a heart attack induced by drug overdose, both causes are typically listed on the death certificate in the U.S. This allows for a more complete understanding of the sequence of events leading to death. The death certificate will show both the immediate cause of death and the underlying causes."

An earlier version of the plot ES posted on Twitter was even more misleading, because it didn't include the line at the bottom which said: "X42-44 ((narcotics, heroin, fentanyl, meth, other drug) excess mortality surge removed (for 2020 only - lockdown impact is not trend data)": [https://x.com/EthicalSkeptic/status/1775711298061275434]

I don't know if ES included only X44 deaths in his plot or also X42 and X43 deaths, because the line at the bottom says that he removed X42-X44 deaths in 2020 but the line above it seems to indicate that his plot only includes X44 deaths but not X42 and X43 deaths. X42 is "Accidental poisoning by and exposure to narcotics and psychodysleptics [hallucinogens], not elsewhere classified", X43 is "Accidental poisoning by and exposure to other drugs acting on the autonomic nervous system", and X44 is "Accidental poisoning by and exposure to other and unspecified drugs, medicaments and biological substances". In the year 2021, CDC WONDER returned 45,053 deaths with MCD X42, 35 deaths with MCD X43, and 45,710 deaths with MCD X44. So there was approximately the same number of X42 and X44 deaths but almost no X43 deaths.

Someone on Twitter asked: "Wonder what that graph looks like without that bottom code (and similar others)" (where the bottom code referred to the cause of death X44, because the version of the plot on Twitter did not yet include the line which said that excess X42-X44 deaths had been removed from 2020). [https://x.com/All_Im_sayn/status/1775728867543535904] But Ethical Skeptic replied: "It is 268 deaths per week out of the 929. Decrement that, and the injury-death tally is far below the actual vaccine impact - by conducting cherry picking to force a desired conclusion - and it does not even accomplish the task." I believe 929 refers to the 7-week moving average of excess deaths on weeks 33-39 of 2023, so I guess 268 drug deaths also referred to the average number of deaths on weeks 33-39 of 2023. But it was at the end of the x-axis when a lot of drug deaths were still missing because of a registration delay, so the proportion of drug deaths out of all deaths was probably higher during earlier months.

One of the three "vaccine uptake periods" ES highlighted in his plot is in mid-2022:

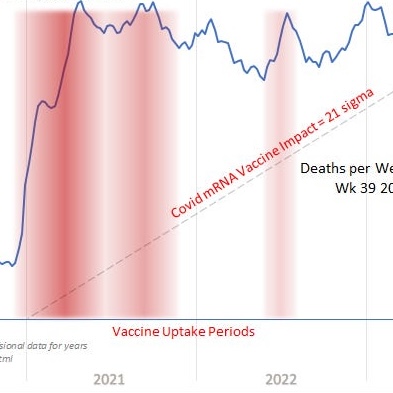
I don't know if the period in mid-2022 is supposed to refer to the period when people got second boosters, because the period in winter 2021-2022 when people got first boosters is not highlighted. In a CDC dataset which shows the number of vaccines administered by age group, the percentage of people in ages 25 to 49 who had received the first booster didn't increase by too much after February 2022. The dataset is missing second boosters administered in younger age groups, even though the total percentage of people in ages 25 to 49 who ever got a second booster is fairly low: [https://data.cdc.gov/Vaccinations/COVID-19-Vaccination-Age-and-Sex-Trends-in-the-Uni/5i5k-6cmh]

t=fread("COVID-19_Vaccination_Age_and_Sex_Trends_in_the_United_States__National_and_Jurisdictional_20240131.csv")
t=t[Demographic_Category=="Ages_25-49_yrs"&Location=="US"]
a=aggregate(t[,9:12],list(sub("(..)/../..(..).*","\\2-\\1",t$Date)),mean,na.rm=T)
names(a)=sub("_(Pop|Vax|pct).*","",names(a))
round(t(data.frame(a,row.names=1)))
                   20-12 21-01 21-02 21-03 21-04 21-05 21-06 21-07 21-08 21-09 21-10 21-11 21-12
Administered_Dose1     1     6    10    20    39    51    56    60    64    69    72    74    77
Series_Complete        0     1     6    11    23    40    49    53    56    60    63    65    67
Booster_Doses        NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN     0     1     3    10    23
Second_Booster       NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN
                   22-01 22-02 22-03 22-04 22-05 22-06 22-07 22-08 22-09 22-10 22-11 22-12 23-01
Administered_Dose1    80    81    82    82    83    83    83    83    84    84    85    85    85
Series_Complete       68    69    70    70    70    70    71    71    71    71    72    72    72
Booster_Doses         33    38    39    40    40    41    41    41    42    42    43    43    43
Second_Booster       NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN   NaN
                   23-02 23-03 23-04 23-05
Administered_Dose1    85    85    85    86
Series_Complete       72    72    72    72
Booster_Doses         43    43    43    43
Second_Booster       NaN   NaN   NaN   NaN

Added in October 2024: ES now posted a more transparent and honest version of his plot, because now in addition to the blue line where he omitted excess drug deaths from 2020 but not from 2021 or later years, he added a gray line where he didn't omit drug deaths from 2020: [https://x.com/EthicalSkeptic/status/1846690187297919231]

A lot of people on Twitter still didn't seem to understand what the gray line meant, and they didn't seem to understand that excess drug deaths were omitted from the blue line in 2020 but not 2021. The plot would be clearer if the gray lines would be drawn for all years of the plot, and one line would always have the meaning that drug deaths are excluded, and the other line would always have the meaning that drug deaths are not excluded. Currently it's confusing how the blue line has a different meaning in 2020 and in 2021-2024.

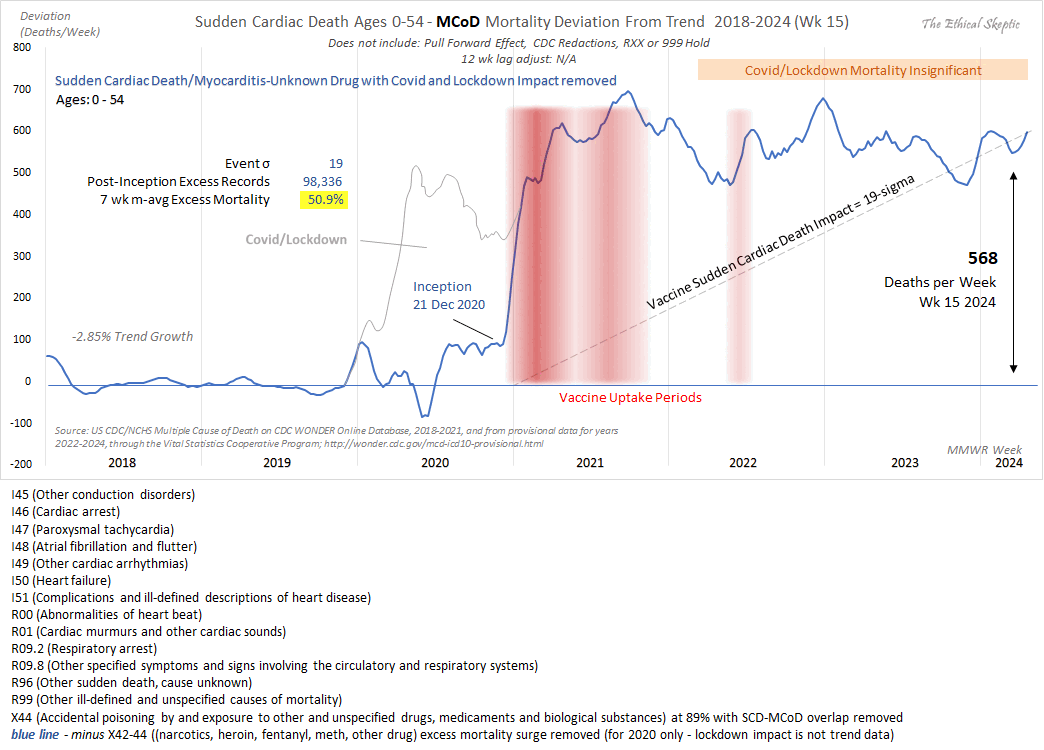
Added in December 2024: I now made the plot below where I included the same MCD codes that were listed in Ethical Skeptic's plot, but in the light black line where I simply excluded X44 deaths, the total excess deaths in 2020-2023 were more than a half lower compared to the light brown line where I kept X44 on the list of ICD codes. The black line does not include deaths which had only MCD X44 but not any of the other codes listed above, but it does still include deaths which had MCD X44 in addition to one of the other codes listed above. And there are also many other ICD codes for drug overdose besides X44. So the black line still includes many deaths where a drug overdose led to cardiac arrest, heart failure, or respiratory failure, and it includes R96 and R99 deaths where the cause has not yet been resolved but which were due to a drug overdose. So I think it explains why the light black line has been elevated since 2020, even though part of the elevation might also be explained by COVID deaths, because even though I excluded deaths with MCD COVID from the light black line, it still has slight peaks remaining during COVID waves. But in either case the light black line was already clearly elevated in 2020, which is difficult to blame on the vaccines:

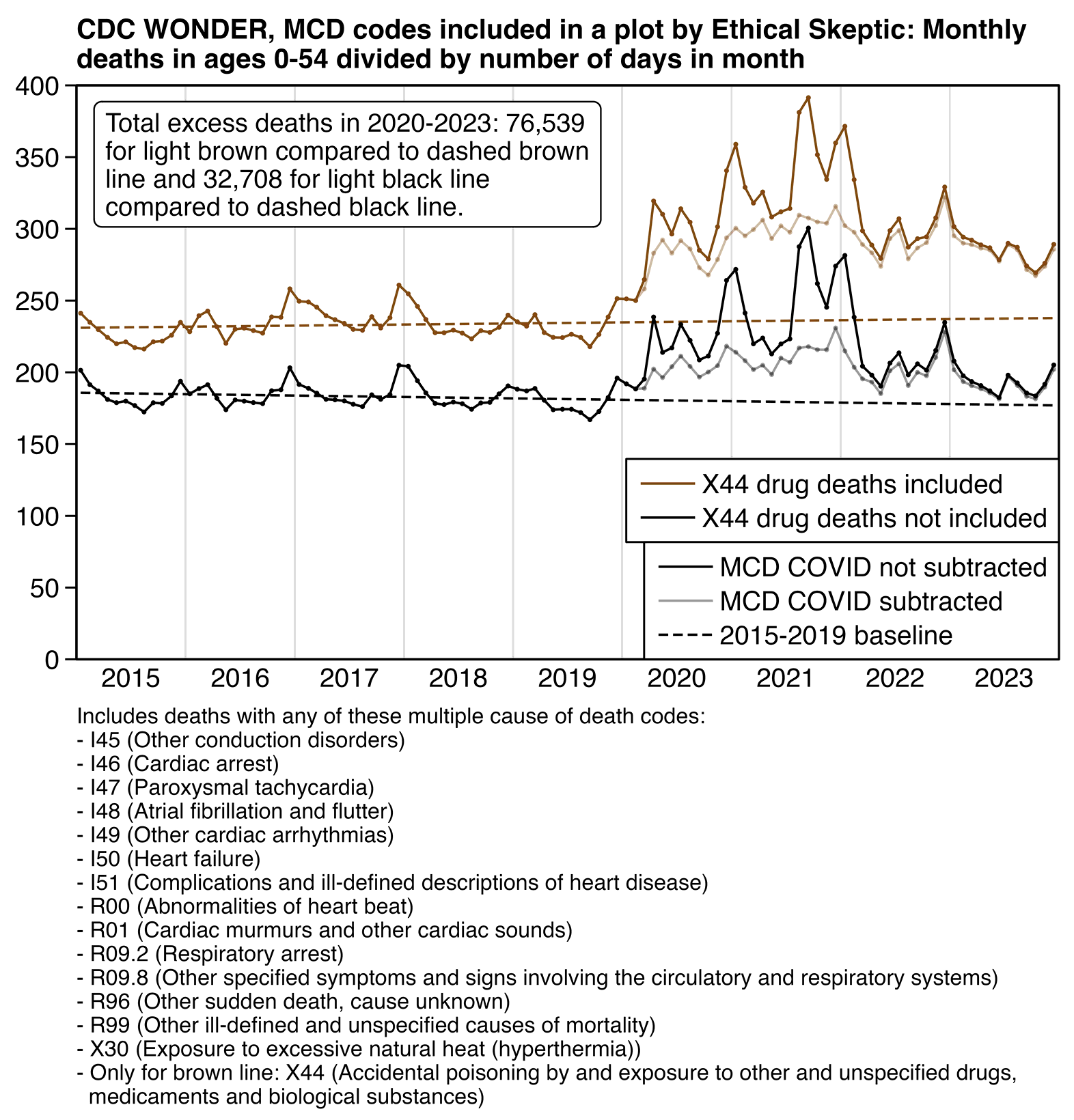
library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/ethicalcardiacdrugnew.csv")

t[,date:=as.Date(paste0(date,"-1"))]
t[,dead:=dead/lubridate::days_in_month(date)]

t=rbind(t,t[type%like%"not"&year(date)%in%2015:2019,.(date=unique(t$date),type="2015-2019 baseline",dead=predict(lm(dead~date),.(date=unique(t$date)))),cause])
t[,cause:=factor(cause,unique(cause))]
t[,type:=factor(type,unique(type))]

xstart=as.Date("2015-1-1");xend=as.Date("2024-1-1")
xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ybreak=pretty(c(0,t$dead),7);ystart=ybreak[1];yend=max(ybreak)

cap="Includes deaths with any of these multiple cause of death codes:
- I45 (Other conduction disorders)
- I46 (Cardiac arrest)
- I47 (Paroxysmal tachycardia)
- I48 (Atrial fibrillation and flutter)
- I49 (Other cardiac arrhythmias)
- I50 (Heart failure)
- I51 (Complications and ill-defined descriptions of heart disease)
- R00 (Abnormalities of heart beat)
- R01 (Cardiac murmurs and other cardiac sounds)
- R09.2 (Respiratory arrest)
- R09.8 (Other specified symptoms and signs involving the circulatory and respiratory systems)
- R96 (Other sudden death, cause unknown)
- R99 (Other ill-defined and unspecified causes of mortality)
- X30 (Exposure to excessive natural heat (hyperthermia))
- Only for brown line: X44 (Accidental poisoning by and exposure to other and unspecified drugs,
  medicaments and biological substances)

The black line does not include deaths which had only MCD X44 but not any of the other codes
listed above, but it still includes deaths which had MCD X44 in addition to one of the other codes
listed above. There are also many other ICD codes for drug overdose besides X44. So the black line
still includes many deaths where a drug overdose led to a cardiac arrest, heart failure, or respiratory
failure, and it includes drug overdose deaths where the cause has not been resolved (R96 and R99)."

thou=\(x)formatC(x,digits=0,format="f",big.mark=",")
note=t[year(date)%in%2020:2023,dcast(.SD,date+cause~type)][,sum(.SD[[3]])-sum(.SD[[4]]),cause]$V1*(365*4+1)/48
note=paste0("Total excess deaths in 2020-2023: ",thou(note[1])," for light brown compared to dashed brown line and ",thou(note[2])," for light black line compared to dashed black line.")|>stringr::str_wrap(40)

ggplot(t,aes(x=date+14,y=dead))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray83",linewidth=.25)+
geom_line(aes(color=cause,alpha=type,linetype=type),linewidth=.3)+
geom_point(aes(color=cause,alpha=type,size=type),stroke=0,show.legend=F)+
labs(x=NULL,y=NULL,title="CDC WONDER, MCD codes included in plot by Ethical Skeptic: Monthly
deaths in ages 0-54 divided by number of days in month",caption=cap)+
annotate(geom="label",x=as.Date("2015-3-1"),y=345,label=note,label.r=unit(2,"pt"),label.padding=unit(3,"pt"),label.size=.2,size=2.4,lineheight=.9,hjust=0)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c(hsv(1/12,.8,.5),"black"))+
scale_size_manual(values=c(.6,.6,0))+
scale_alpha_manual(values=c(1,.4,1))+
scale_linetype_manual(values=c("solid","solid","42"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),linetype=guide_legend(order=2),alpha=guide_legend(order=2),size=guide_legend(order=2))+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.y=element_text(margin=margin(,1.5)),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(3,"pt"),
  legend.background=element_rect(color="black",linewidth=.25),
  legend.box="vertical",
  legend.box.just="right",
  legend.justification=c(1,0),
  legend.key=element_blank(),
  legend.key.height=unit(9,"pt"),
  legend.key.width=unit(18,"pt"),
  legend.position=c(1,0),
  legend.spacing.x=unit(0,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.margin=margin(2,3,2,2),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3),
  plot.margin=margin(4,4,3,4),
  plot.caption=element_text(size=5.8,margin=margin(4),hjust=0),
  plot.subtitle=element_text(size=7,margin=margin(,,3)),
  plot.title=element_text(size=7.2,face=2,margin=margin(1,,3)))
ggsave("1.png",width=3.93,height=4.7,dpi=400*4)
system("magick 1.png -resize 25% PNG8:1.png")

I was expecting deaths with MCD drug overdose to explain most of the excess I45-51 cardiac deaths after subtracting deaths with MCD COVID. But actually in the next plot MCD drug deaths explained only a small part of the excess I45-51 deaths since 2020, even though I included 15 different 3-letter ICD codes for drug overdoses and not just the one or two most common codes like Ethical Skeptic. Then I thought other deaths from external causes might explain the excess deaths, since various external causes of death have remained elevated in younger age groups since 2020, but I didn't get rid of the excess deaths by subtracting other deaths from external causes either. So I don't know how to explain the remainder of excess deaths since 2020:

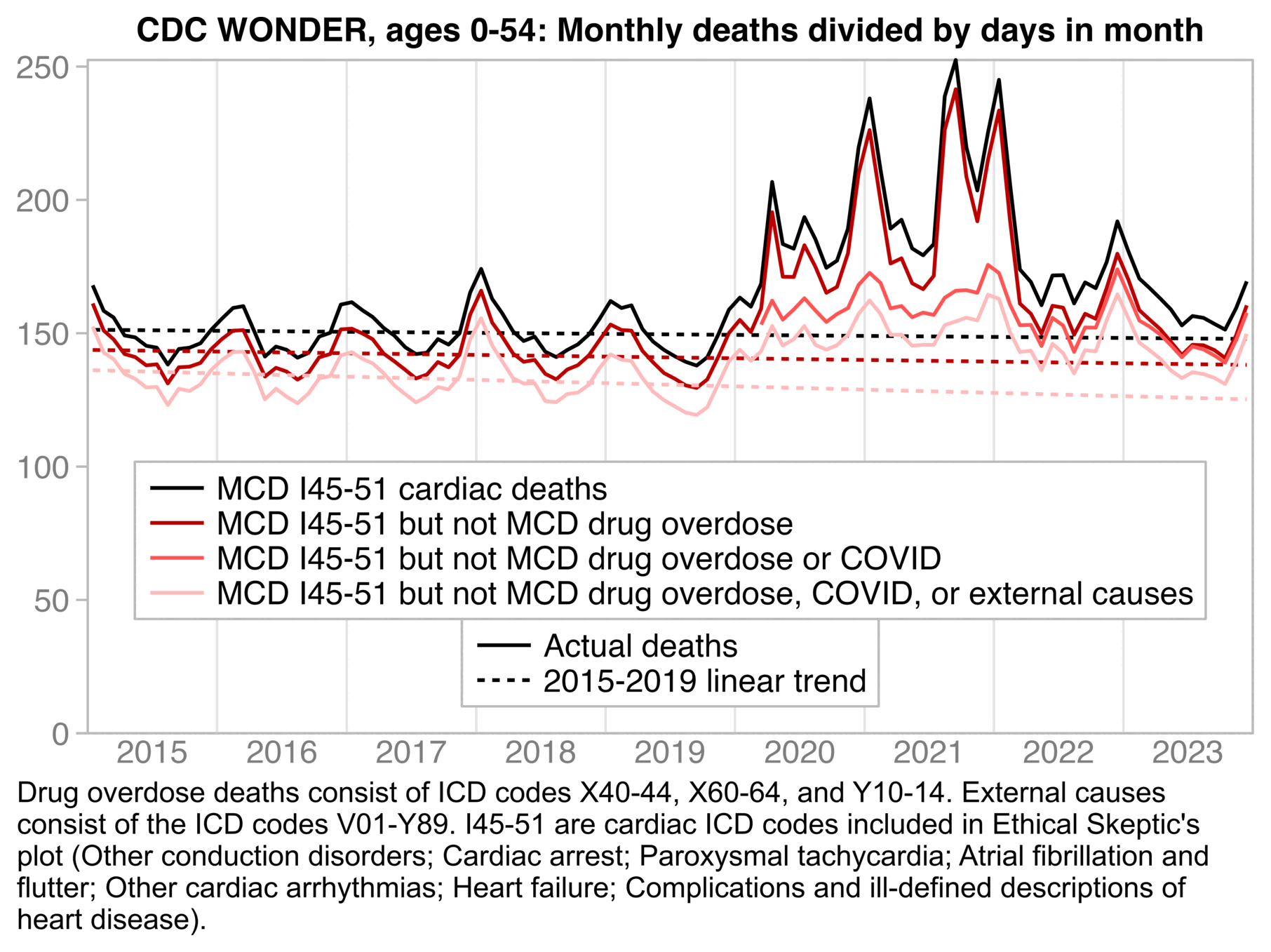
t=fread("https://sars2.net/f/wonderheartdrug.csv")

t[,date:=as.Date(paste0(date,"-1"))]
t[,dead:=dead/lubridate::days_in_month(date)]

w=dcast(t,date~cause,value.var="dead")
w[is.na(w)]=0

lab=c("MCD I45-51 cardiac deaths","MCD I45-51 but not MCD drug overdose","MCD I45-51 but not MCD drug overdose or COVID","MCD I45-51 but not MCD drug overdose, COVID, or external causes")
p=w[,.(x=date,y=c(w[[2]],w[[2]]-w[[3]],w[[2]]-w[[4]],w[[2]]-w[[5]]),z=factor(rep(lab,each=.N),lab),type=1)]

p=p[!(z==levels(z)[3]&x<"2020-3-1")]

p=rbind(p,p[z!=lab[3]&year(x)%in%2015:2019,.(x=unique(p$x),type=2,y=predict(lm(y~x),.(x=unique(p$x)))),z])
p[,type:=factor(type,,c("Actual deaths","2015-2019 linear trend"))]

xstart=as.Date("2015-1-1");xend=as.Date("2024-1-1")
xbreak=seq(xstart+182,xend,"year");xlab=year(xbreak)
ybreak=pretty(c(0,t$dead),7);ystart=ybreak[1];yend=max(p$y)

ggplot(p,aes(x=x+14,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,color="gray75",lineend="square",linejoin="mitre",fill=NA,linewidth=.4)+
geom_line(aes(color=z,linetype=type),linewidth=.6)+
labs(x=NULL,y=NULL,title="CDC WONDER, ages 0-54: Monthly deaths divided by days in month")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black","#bb0000","#ff5555","#ffbbbb"))+
scale_linetype_manual(values=c("solid","22"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray50",margin=margin(2,2,2,2)),
  axis.ticks=element_line(linewidth=.4,color="gray75"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_rect(color="gray75",linewidth=.4),
  legend.box="vertical",
  legend.box.just="center",
  legend.justification=c(.5,0),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(23,"pt"),
  legend.position=c(.5,.04),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.margin=margin(3,4,3,3),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(5,5,3,4),
  plot.subtitle=element_text(size=11,margin=margin(,,4)),
  plot.title=element_text(size=11.3,face=2,hjust=.5,margin=margin(1,,4)))
ggsave("1.png",width=6,height=3.7,dpi=300*4)

Added in July 2025: Steve Kirsch claimed the plot by ES showed deaths from myocarditis: [https://x.com/stkirsch/status/1941264976108453905]

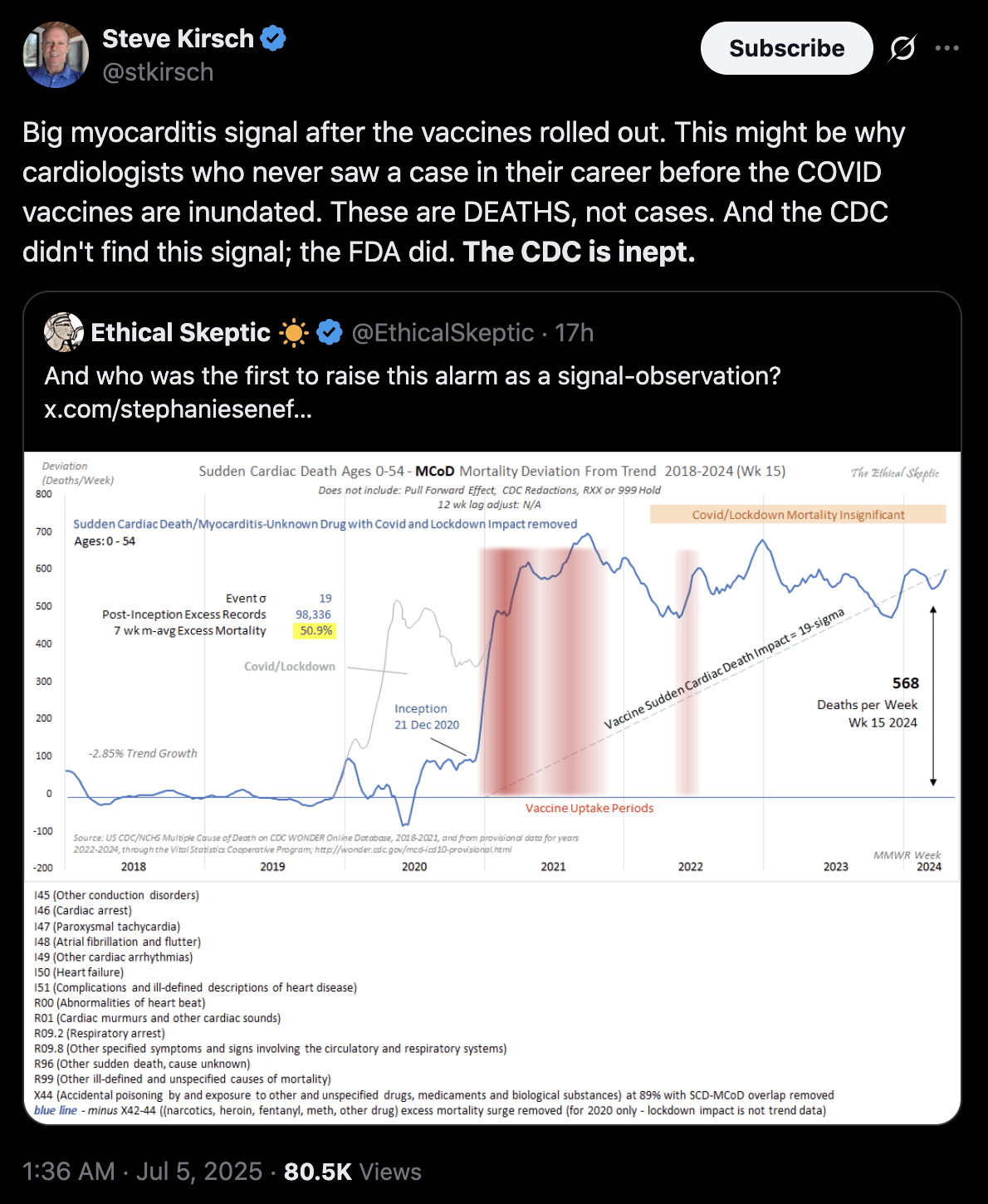
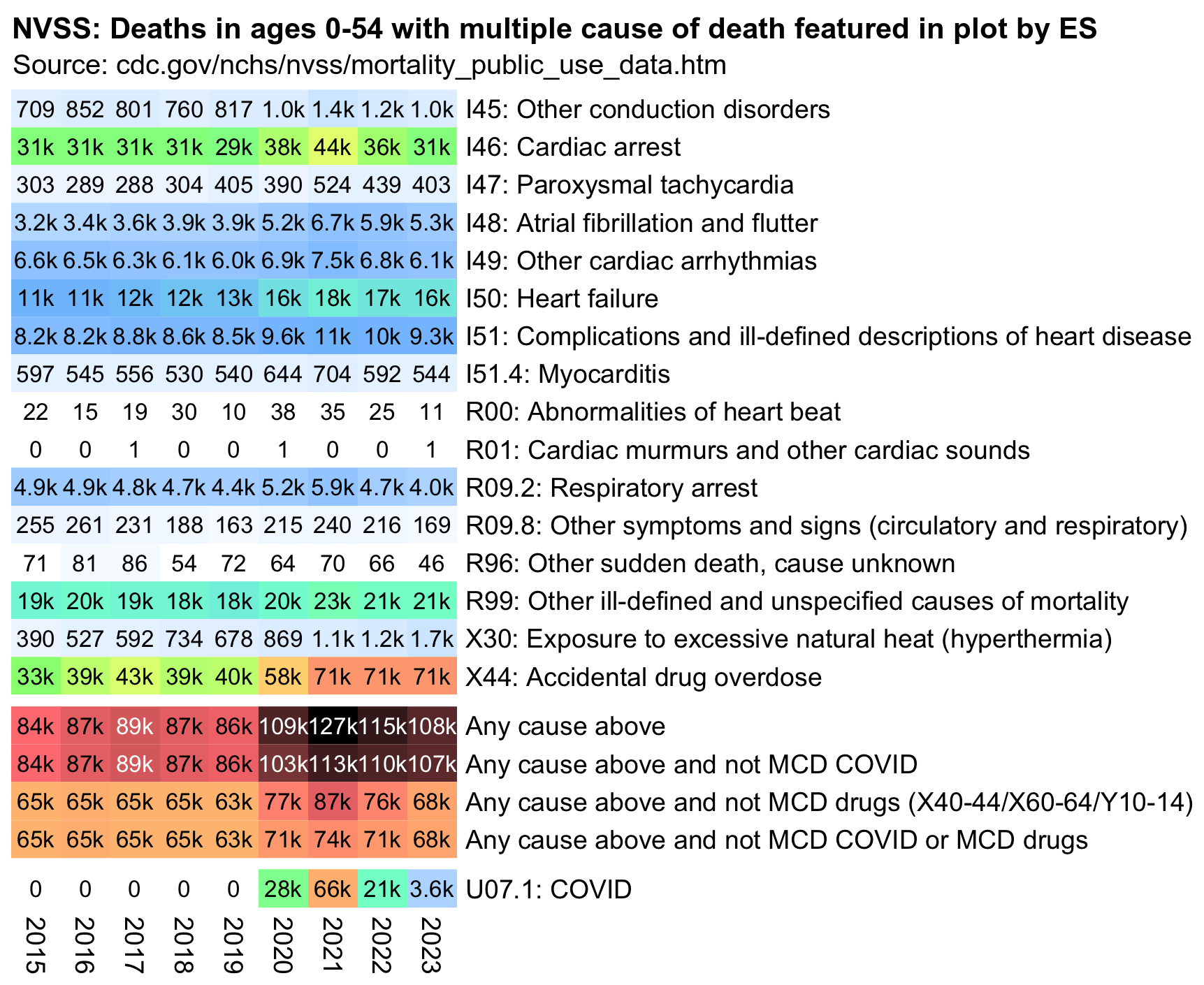
However deaths with MCD myocarditis accounted for only about 0.5% of all deaths in the plot, and there was already an increase in deaths with MCD myocarditis between 2019 and 2020 (but the myocarditis deaths had gone back to normal by 2023, even though Ethical Skeptic's plot still had a lot of excess deaths in 2023):

ua=\(x,y,...){u=unique(x);y(u,...)[match(x,u)]}
dotcode=\(x)ua(x,\(x)ifelse(x%like%"^ ",substr(x,2,4),sub("(...)(.)","\\1.\\2",x)))
kimi=\(x){na=is.na(x);x[na]=0;e=floor(log10(ifelse(x==0,1,abs(x))));e2=pmax(e,0)%/%3+1;x[]=ifelse(abs(x)<1e3,round(x),paste0(sprintf(paste0("%.",ifelse(e%%3==0,1,0),"f"),x/1e3^(e2-1)),c("","k","M","B","T")[e2]));x[na]="NA";x}

# sars2.net/stat.html#Download_fixed_width_and_CSV_files_for_the_NVSS_data_used_at_CDC_WONDER
vit=do.call(rbind,lapply(2015:2023,\(i)fread(j(i,".csv.gz"))[age!=9999&or(age>=2000,age<=1054)]))
l=vit[,.(.I,year,code=unlist(.SD,,F)),.SDcols=patterns("ucod|enicon_")][code!=""]

codes=paste(sub("\\.","",rbind(pick,pick4[code!="U07.1"])$code),collapse="|")

any=l[I%in%l[ua(code,like,codes),I]]
a2=any[,.(dead=uniqueN(I),label="Any cause above"),year]
a3=any[!I%in%I[code=="U071"],.(dead=uniqueN(I),label="Any cause above and not MCD COVID"),year]
a4=any[!I%in%I[code%like%"X4[0-4]|X6[0-4]|Y1[0-4]"],.(dead=uniqueN(I),label="Any cause above and not MCD drugs (X40-44/X60-64/Y10-14)"),year]
a5=any[!I%in%I[code%like%"X4[0-4]|X6[0-4]|Y1[0-4]|U071"],.(dead=uniqueN(I),label="Any cause above and not MCD COVID or MCD drugs"),year]

pick=fread("code;cause
I45;Other conduction disorders
I46;Cardiac arrest
I47;Paroxysmal tachycardia
I48;Atrial fibrillation and flutter
I49;Other cardiac arrhythmias
I50;Heart failure
I51;Complications and ill-defined descriptions of heart disease
R00;Abnormalities of heart beat
R01;Cardiac murmurs and other cardiac sounds
R96;Other sudden death, cause unknown
R99;Other ill-defined and unspecified causes of mortality
X30;Exposure to excessive natural heat (hyperthermia)
X44;Accidental drug overdose")

pick4=fread("code;cause
I51.4;Myocarditis
R09.2;Respiratory arrest
R09.8;Other symptoms and signs (circulatory and respiratory)
U07.1;COVID")

v=fread("curl -Ls sars2.net/f/vital3.csv.xz|xz -dc")
v4=fread("curl -Ls sars2.net/f/vital.csv.xz|xz -dc")
setnames(v4,"cause","code")

a=rbind(v,v4)[year>=2015&age<=54,.(dead=sum(mcd)),,.(year,code)]
a[,code:=dotcode(code)]

a=merge(rbind(pick,pick4),a)
a1=a[,.(label=paste0(code,": ",cause),year,dead)]

a0=rbind(a1,a2,a3,a4,a5)
a0=rbind(a0[!label%like%"U07"],a0[label%like%"U07"])

m=a0[,xtabs(dead~factor(label,unique(label))+year)]

disp=kimi(m)
m=m^.6;m=m/max(m)

pal=colorRampPalette(hex(HSV(c(210,210,210,160,110,60,30,0,0,0),c(0,.25,rep(.5,8)),c(rep(1,8),.5,0))))(256)

pheatmap::pheatmap(m,filename="0.png",display_numbers=disp,
  gaps_row=length(lab)-c(0,4),
  cluster_rows=F,cluster_cols=F,legend=F,cellwidth=17,cellheight=13,fontsize=9,fontsize_number=8,
  border_color=NA,na_col="white",
  number_color=ifelse(m>=.8,"white","black"),
  breaks=seq(0,1,,length(pal)),pal)

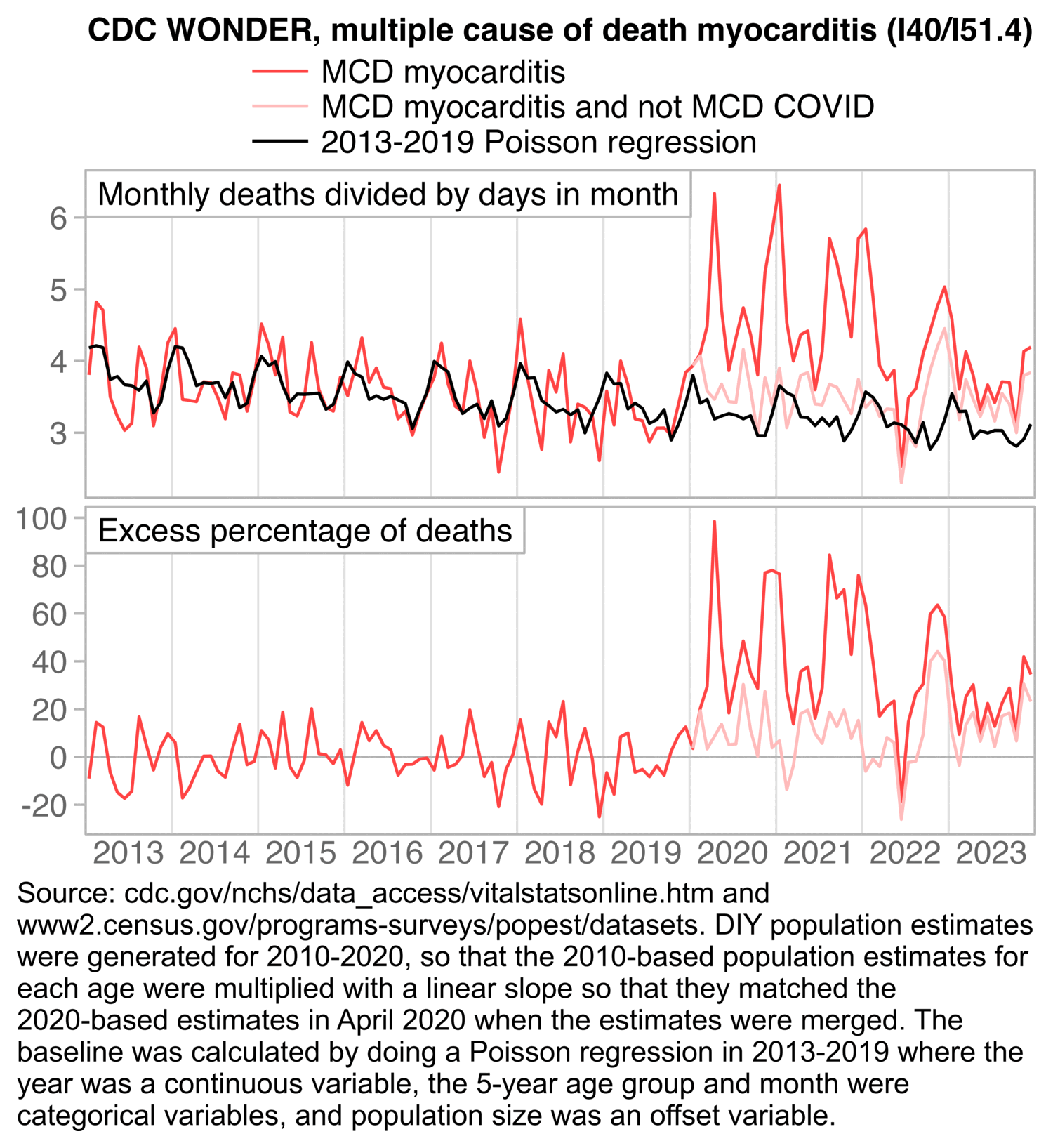
There was in fact a large increase in deaths involving myocarditis between 2019 and 2020, but deaths with MCD COVID account for most of the excess deaths with MCD myocarditis:

v=do.call(rbind,lapply(2013:2023,\(i)fread(paste0(i,".csv.gz"))[restatus!=4,
   .(I=year*1e7+.I,year,age,month=monthdth,code=unlist(.SD,,F)),.SDcols=patterns("ucod|enicon_")][code!=""]))
v[,age:=ifelse(age%/%1000%in%c(1,9),age%%1000,0)]

s=v[I%in%I[ua(code,like,"I40|I514")]]
a=s[,.(dead=c(uniqueN(I),length(setdiff(I,I[code%in%"U071"]))),z=1:2),.(year,month,age=pmin(age,100)%/%5*5)]

a=merge(a,fread("https://sars2.net/f/uspopdeadmonthly.csv")[,.(pop=sum(pop)),.(age=age%/%5*5,year,month)])

base=a[z==1][,z:=3]
lm=glm(dead~year+factor(month)+factor(age),offset=log(pop),poisson,base[year<2020])
base$dead=predict(lm,base,type="response")

p=rbind(a,base)[,.(y=c(sum(dead))),.(x=as.Date(paste(year,month,15,sep="-")),z)]
p[,y:=y/lubridate::days_in_month(x)]
p=rbind(p[,facet:=1],p[,.(y=(y[z<3]/y[z==3]-1)*100,z=1:2,facet=2),x])
p=p[!(z==2&year(x)<2020)]

p[,z:=factor(z,,c("MCD myocarditis","MCD myocarditis and not MCD COVID","2013-2019 Poisson regression"))]
p[,facet:=factor(facet,,c("Monthly deaths divided by days in month","Excess percentage of deaths"))]

xstart=as.Date("2013-1-1");xend=as.Date("2024-1-1");xbreak=seq(xstart+182,xend,"year")
ylim=p[,{x=extendrange(y);.(ymin=x[1],ymax=x[2])},facet]

ggplot(p)+
facet_wrap(~facet,dir="v",scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=ymin,ymax=ymax),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_segment(data=ylim[2],y=0,yend=0,x=xstart,xend=xend,linewidth=.4,color="gray72")+
geom_line(aes(x,y,color=z),linewidth=.5)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=xstart,hjust=0,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray72",size=3.87)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=xstart,hjust=0,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87)+
labs(x=NULL,y=NULL,title="CDC WONDER, multiple cause of death myocarditis (I40/I51.4)")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(breaks=pretty)+
scale_color_manual(values=c("#ff4444","#ffbbbb","black"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=3),linetype=guide_legend(order=1),alpha=guide_legend(order=1))+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.text.x=element_text(margin=margin(2)),
  axis.ticks=element_line(linewidth=.4,color="gray72"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_blank(),
  legend.box="vertical",
  legend.box.just="left",
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_blank(),
  legend.margin=margin(,,4),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(3,"pt"),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,2)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5,height=4.2,dpi=300*4)

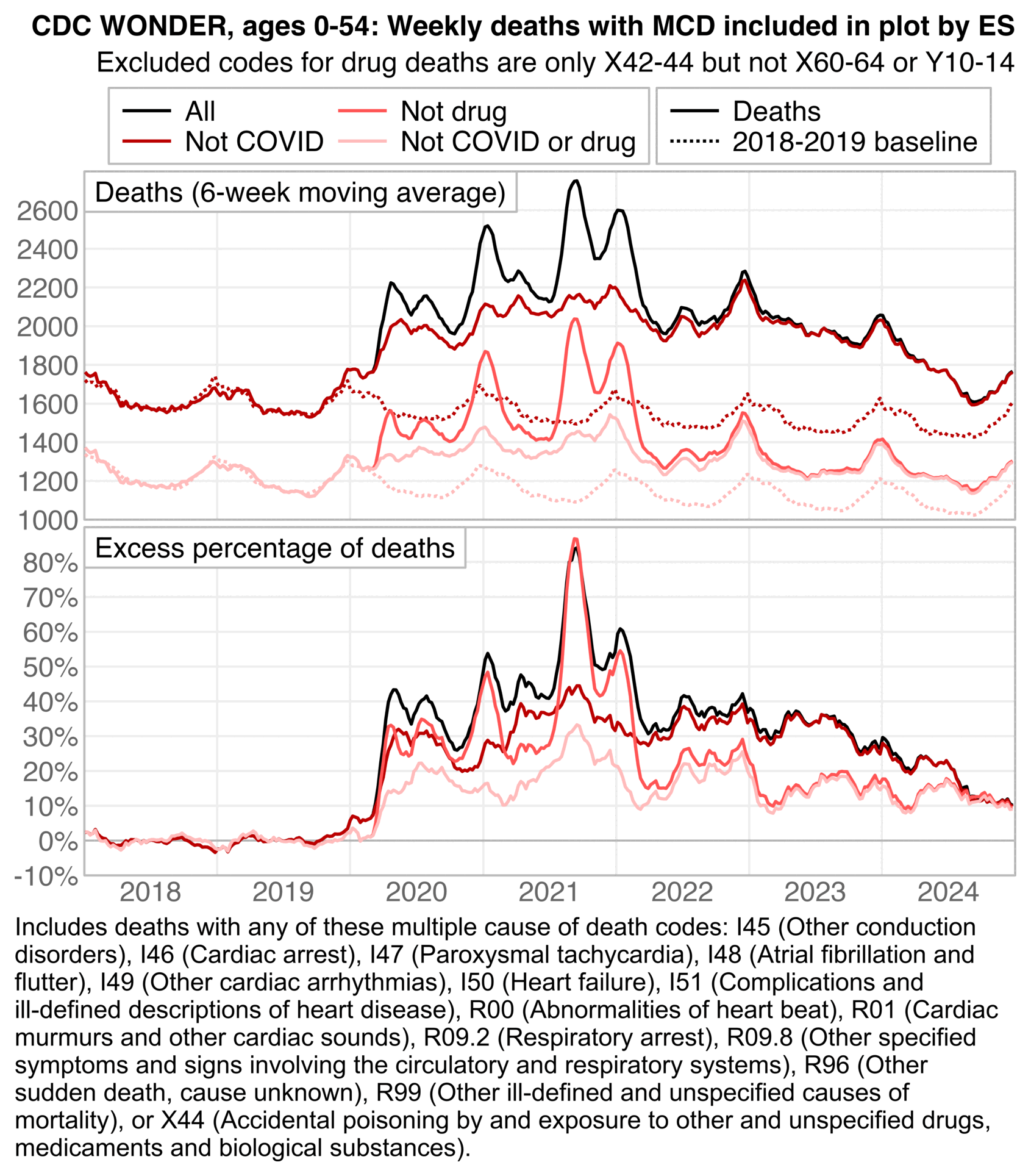
Next I tried reproducing the calculation of weekly excess deaths by ES. I excluded MCD COVID in the dark red line, MCD X42-44 drug deaths in the bright red line, and both in the light red line. The dark red line roughly matches the blue line in the plot by ES in 2021-2023, and the light red line roughly matches the gray line in the plot by ES in 2020, but neither of the lines matches the blue line in the plot by ES in 2020. So I don't know how he calculated the blue line in 2020:

t=fread("https://sars2.net/f/wonderethicalheartdrug.csv")[year<2025]
t[,type:=factor(type,unique(type))]

t[,dead:=as.double(dead)][,dead:=ma(dead,3,2),type]

yearly=t[week%in%15:40,.(dead=mean(dead)),.(year,type)]
t=merge(t,yearly[,.(year,yearly=predict(lm(dead~year,yearly[year<2020]),.SD)),type])
t=merge(t[year<2020,.(weekly=mean(dead-yearly)),.(week,type)],t)

p=t[,.(x=ending-3,y=c(dead,yearly+weekly),z=rep(1:2,each=.N),type)]
p=rbind(p[,facet:=1],p[,.(y=(y[1]/y[2]-1)*100,z=1,facet=2),.(x,type)])

p[,z:=factor(z,,c("Deaths","2018-2019 baseline"))]
p[,facet:=factor(facet,,c("Deaths (6-week moving average)","Excess percentage of deaths"))]

xstart=as.Date("2018-1-1");xend=as.Date("2025-1-1");xbreak=seq(xstart+182,xend,"year")
ystart=0;yend=max(p$y)

ylim=p[,{x=as.integer(pretty(y,7));.(ymin=min(x),ymax=max(x))},facet]

ggplot(p)+
facet_wrap(~facet,dir="v",scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray91",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=ymin,ymax=ymax),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_segment(data=ylim[2],y=0,yend=0,x=xstart,xend=xend,linewidth=.4,color="gray72")+
geom_line(aes(x,y,color=type,linetype=z),linewidth=.6)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=xstart,hjust=0,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray72",size=3.87)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=xstart,hjust=0,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(breaks=\(x)pretty(x,8),labels=\(x)ifelse(x==max(x),"",if(min(x)<0)paste0(x,"%")else x))+
scale_color_manual(values=c("black","#bb0000","#ff5555","#ffbbbb"))+
scale_linetype_manual(values=c("solid","11"))+
labs(x=NULL,y=NULL,title="CDC WONDER, ages 0-54: Weekly deaths with MCD included in plot by ES",subtitle="Excluded codes for drug deaths are only X42-44 but not X60-64 or Y10-14")+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=2,byrow=F,order=1),linetype=guide_legend(order=2))+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(color="gray72",linewidth=.4),
  legend.box="horizontal",
  legend.box.just="center",
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position="top",
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid.major.x=element_blank(),
  panel.grid.major.y=element_line(linewidth=.4,color="gray91"),
  panel.spacing=unit(3,"pt"),
  plot.margin=margin(5,5,3,4),
  plot.subtitle=element_text(size=11,hjust=1,margin=margin(,,4)),
  plot.title=element_text(size=11,face=2,hjust=1,margin=margin(1,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.6,height=5,dpi=300*4)

ES has said that in his plots that display weekly deaths from 2018 onwards, he fits the baseline against only deaths in 2018 and 2019. He also says that he excludes winter peaks from his baseline fitting period, but it's not clear which specific weeks he excludes. In the plot above I did a linear regression of two points which were the average weekly deaths on weeks 15 to 40 of 2018 and weeks 15 to 40 of 2019, and I projected the regression to other years. I adjusted the baseline for seasonality by adding the average difference between actual deaths and the baseline on week 1 of 2018 to the baseline on each week 1, and similarly for other week numbers.

I excluded only X42-44 but not other drug-related ICD codes. However it didn't make much difference when I also excluded X60-64 and Y10-14. For example in 2021 ages 0-54 had 125,174 deaths with one of the MCD codes listed by ES. Excluding X42-44 reduced the deaths by about 30%, but additionally excluding X60-64 and Y10-14 only reduced the deaths further by about 0.5%:

$ wget ftp.cdc.gov/pub/Health_Statistics/NCHS/Datasets/DVS/mortality/mort2021us.zip
$ unzip mort2021us.zip
$ awk 'substr($0,20,1)!=4{age=substr($0,70,4);if(age%1000==999||(age>=1055&&age<2000))next;o=substr($0,146,4);for(i=1;i<=20;i++){mcd=substr($0,167+(i-1)*7,4);if(mcd=="    ")break;o=o" "mcd}print o}' VS21MORT.DUSMCPUB_r20230320.txt>temp
$ egrep 'I4[5-9]|I5[01]|R0[01]|R09[28]|R9[69]|X44' temp|wc -l
125173
$ egrep 'I4[5-9]|I5[01]|R0[01]|R09[28]|R9[69]|X44' temp|egrep -v 'X4[2-4]'|wc -l
87763
$ egrep 'I4[5-9]|I5[01]|R0[01]|R09[28]|R9[69]|X44' temp|egrep -v 'X4[2-4]|X6[0-4]|Y1[0-4]'|wc -l
87238

Added in September 2025: Ethical Skeptic has now made a new version of his plot, where now as an uncharacteristic upgrade in honesty, he no longer excluded drug deaths from the blue line in 2020, so now the blue line followed the same pattern in 2020 as the gray line in earlier versions of his plot: [https://x.com/EthicalSkeptic/status/1955732621943824393/photo/1]

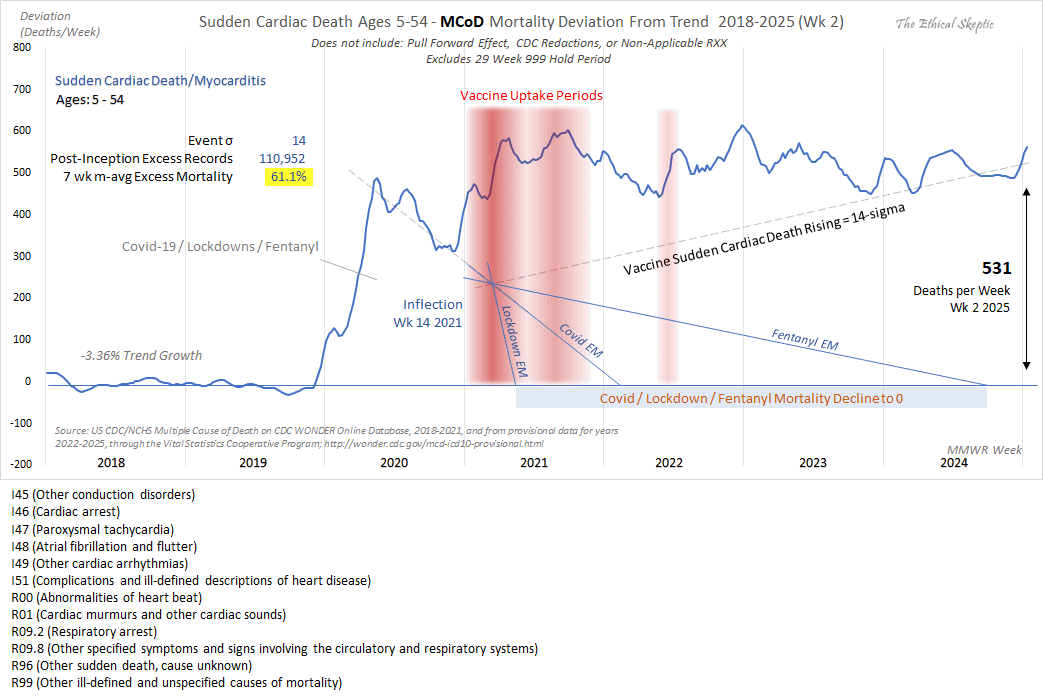
However he compensated for his single honest change by making several dishonest changes to his plot:

  1. He removed the line at the bottom of the plot which said that he included X44 drug deaths in his query, even though the shape of his blue line remained similar to the earlier versions of the plot which included X44 deaths, and I came much closer to reproducing his plot when I included X44 deaths in my query.
  2. He removed the "Unknown Drug" part from the line below the title that says "Sudden Cardiac Death/Myocarditis-Unknown Drug".
  3. He removed the text that said "with Covid and Lockdown Impact removed", even though he still excluded deaths with MCD COVID from his plot. (Even though even in the earlier version, it was ambiguous if the text meant that the impact of COVID was only removed from 2020, or if the text meant that deaths with MCD COVID were excluded throughout the plot.)
  4. He added a diagonal line that is meant to indicate the level of excess mortality associated with fentanyl, which intersects zero in 2024, even though there were still a lot of extra opioid deaths in 2024 relative to the 2018-2019 linear trend.
  5. He added a diagonal line to the plot that is meant to show excess deaths associated with COVID, but it's much lower during the Delta wave than in 2020, even though ages 5-54 had a huge number of COVID deaths during the Delta wave.
  6. He switched from a baseline that decreased by -2.85% per year to a baseline that decreased -3.36% per year, even though the only part of his query he seems to have changed between the plots is that he excluded ages 0-4 from the new version, which shouldn't affect the slope by that much. I believe he artificially made the slope steeper so he could exaggerate the excess deaths in 2023 and 2024, because most excess deaths in his plot are due to drug overdoses, but the United States had a big reduction in drug overdose deaths starting from 2023. The real trend in deaths before COVID was not even decreasing but increasing, but there just happened to be a low number of deaths in 2019.
  7. Even beyond the exaggerated slope of his baseline, he seems to have applied an additional upward shift to his excess deaths in 2024. Judging from how his line looks smoother in 2024 than earlier years, he appears to have inserted fake data for 2024.

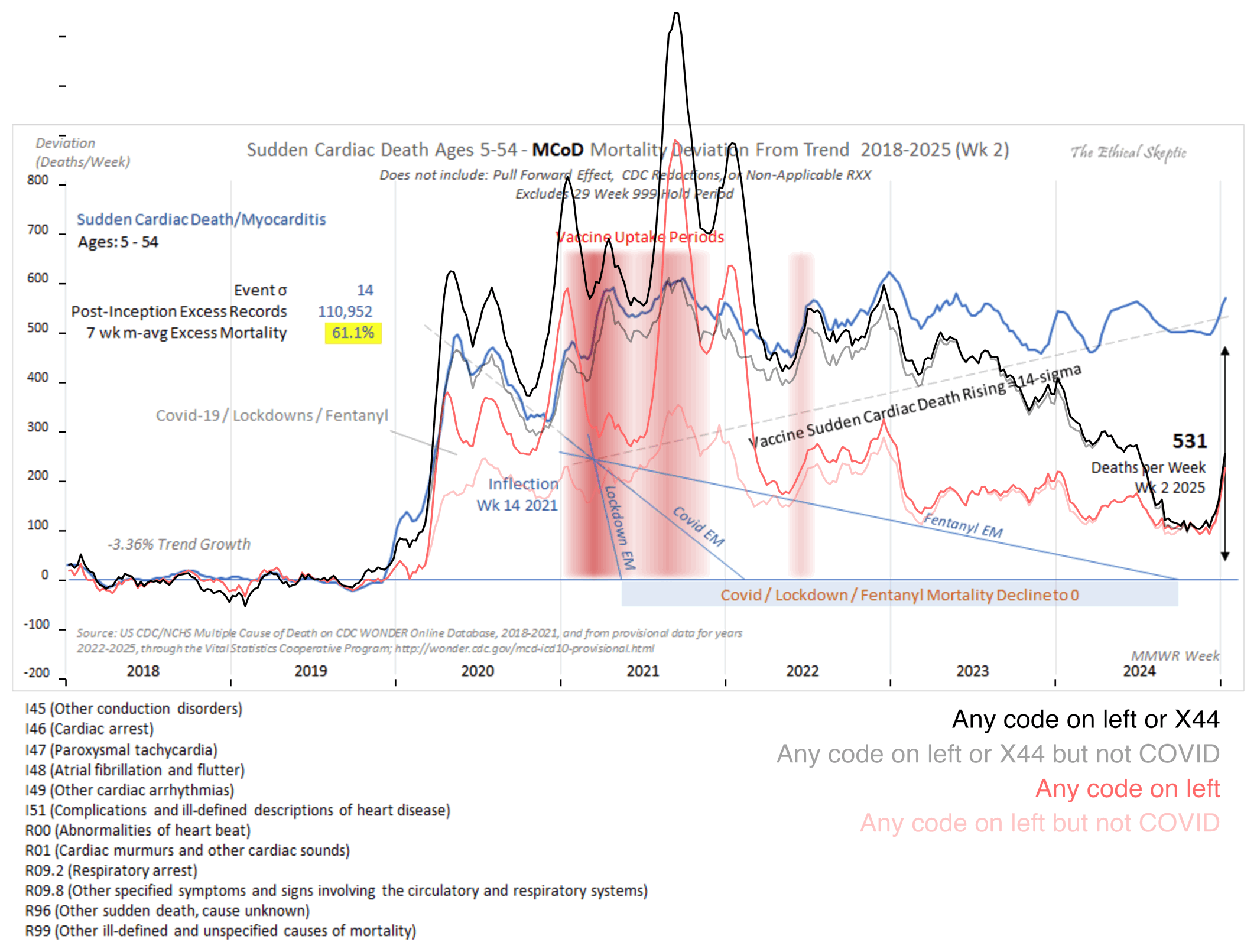
Out of the four lines I added in the next plot, I came the closest to reproducing Ethical Skeptic's plot with my gray line, where my list of ICD codes included X44 ("Accidental poisoning by and unspecified drugs, medicaments and biological substances"), and where I excluded deaths that had MCD COVID. But Ethical Skeptic's plot doesn't mention anywhere that X44 deaths would be included or COVID deaths would be excluded:

ma=\(x,b=1,f=b)rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T)

t=fread("https://sars2.net/f/wonderheartdrug5to54.csv")
t[,dead:=as.double(dead)][,dead:=ma(dead,3,2),.(withx44,covidsubtracted)]

base=t[year<2020&covidsubtracted==F]
weekly=base[,.(weekly=mean(dead)),.(week,withx44)]
weekly=rbind(weekly,weekly[week%in%c(1,52),.(week=53,weekly=mean(weekly)),withx44])
t=merge(t,base[,.(growthrate=coef(lm(dead~year))[2]/mean(dead)),withx44])
# t=merge(t,base[,.(growthrate=-.0336),withx44]) # force -3.36% growth rate
t=merge(weekly,t)[,base:=weekly*(1+growthrate)^(year-2018.5)]

t=t[!(year==2025&week>2)]
p=t[,.(x=MMWRweek::MMWRweek2Date(year,week,7),y=dead-base,z=factor(withx44),type=factor(covidsubtracted))]

xstart=as.Date("2018-1-1");xend=as.Date("2025-7-1");xbreak=seq(xstart,xend,"year")
ystart=-200;yend=max(p$y);ybreak=seq(ystart,yend,100)

anno=data.table(label=strsplit("Any code on left or X44
Any code on left or X44 but not COVID
Any code on left
Any code on left but not COVID","\n")[[1]])
anno$color=rep(c("black","#ff6666"),each=2)

ggplot(p)+
geom_line(aes(x,y,color=z,alpha=type))+
annotate("text",x=as.Date("2025-1-1"),y=seq(-280,,-70,4),hjust=1,size=5,label=anno$label,color=anno$color,alpha=rep(c(1,.4),2))+
labs(x=NULL,y=NULL)+
scale_x_date(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(breaks=ybreak)+
scale_color_manual(values=c("#ff6666","black"))+
scale_alpha_manual(values=c(1,.4))+
coord_cartesian(clip="off",expand=F,ylim=c(ystart,yend))+
theme(axis.text=element_blank(),
  axis.ticks=element_line(color="black",linewidth=.4),
  axis.ticks.length=unit(4,"pt"),
  legend.position="none",
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.background=element_rect(fill="transparent",color=NA),
  plot.margin=margin(,,90))
ggsave("1.png",width=9.5,height=6.5,dpi=300*2)

The text in Ethical Skeptic's plot indicates that his baseline has an annual growth rate of -3.36%, but I got an annual growth rate of only about -1.3% for my baseline when I included X44 deaths. Part of the difference might be if ES excluded some weeks from his baseline fitting period, because I simply included all weeks of the MMWR years 2018 and 2019 in my baseline fitting period. I calculated my baseline following the methodology ES described in this image: [https://theethicalskeptic.com/2025/08/19/houston-we-have-another-problem/]

The SLOPE function in Excel returns the second coefficient of a linear regression, like coef(lm(dead~year))[2] in R. If you do a linear regression of weekly deaths in 2018-2019 against a year variable, where there are 52 weeks where the value of the year variable is 2018 and 52 weeks where the value of the year variable is 2019, it's equivalent to doing a linear regression of yearly averages of weekly deaths, which is equivalent to simply subtracting the average deaths in 2018 from the average deaths in 2019:

t=fread("https://sars2.net/f/wonderheartdrug5to54.csv")
t=t[withx44==T&covidsubtracted==F]
ma=\(x,b=1,f=b)rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T)
t[,dead:=ma(dead,3,2)]

# linear regression of weekly deaths against a year variable
coef(lm(dead~year,t[year<2020]))[2]
# -18.67756

# linear regression of yearly average deaths against a year variable
t[,.(dead=mean(dead)),year][year<2020,coef(lm(dead~year))[2]]
# -18.67756

# average deaths in 2019 minus average deaths in 2018
t[,.(dead=mean(dead)),year][,dead[year==2019]-dead[year==2018]]
# -18.67756

The image above is missing the step where the slope is converted to an annual rate of decline, but I believe ES divides the slope with the average weekly deaths in the baseline period, like he described in another image: [https://theethicalskeptic.com/wp-content/uploads/2025/09/ICD-10-Code-Excess-Death-Derivation-small.jpg]

So when I divided the slope with the average weekly deaths in 2018-2019, I got an annual growth rate of about -1.3%:

t[year<2020,coef(lm(dead~year))[2]/mean(dead)]
# -0.01335137

In the next plot I manually forced the annual growth rate to be -3.36%, so now I got my gray line to match Ethical Skeptic's plot fairly closely in 2023. But I still got much lower excess deaths than him in 2024:

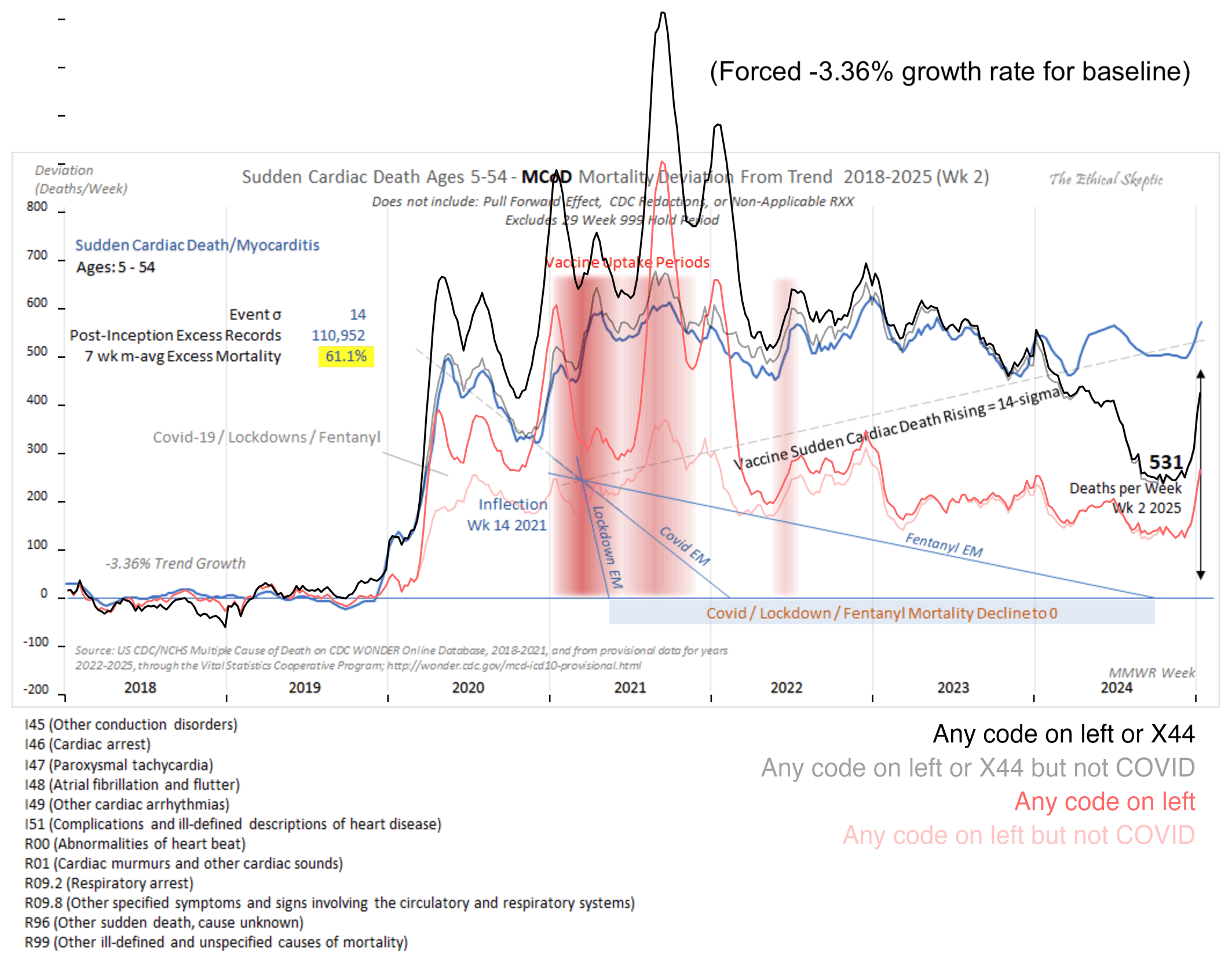
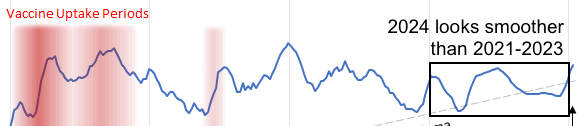
Part of the discrepancy might be if ES attempted to impute deaths that he estimated to be missing because of a registration delay. But I suspect ES simply inserted fake data for 2024, because his line for excess deaths looks more smooth in 2024 than earlier years:

The 3.36% annual rate of decline is also completely off from the actual trend in deaths before COVID, which was not even decreasing but increasing, because there just happened to be an unusually low number of deaths in 2019:

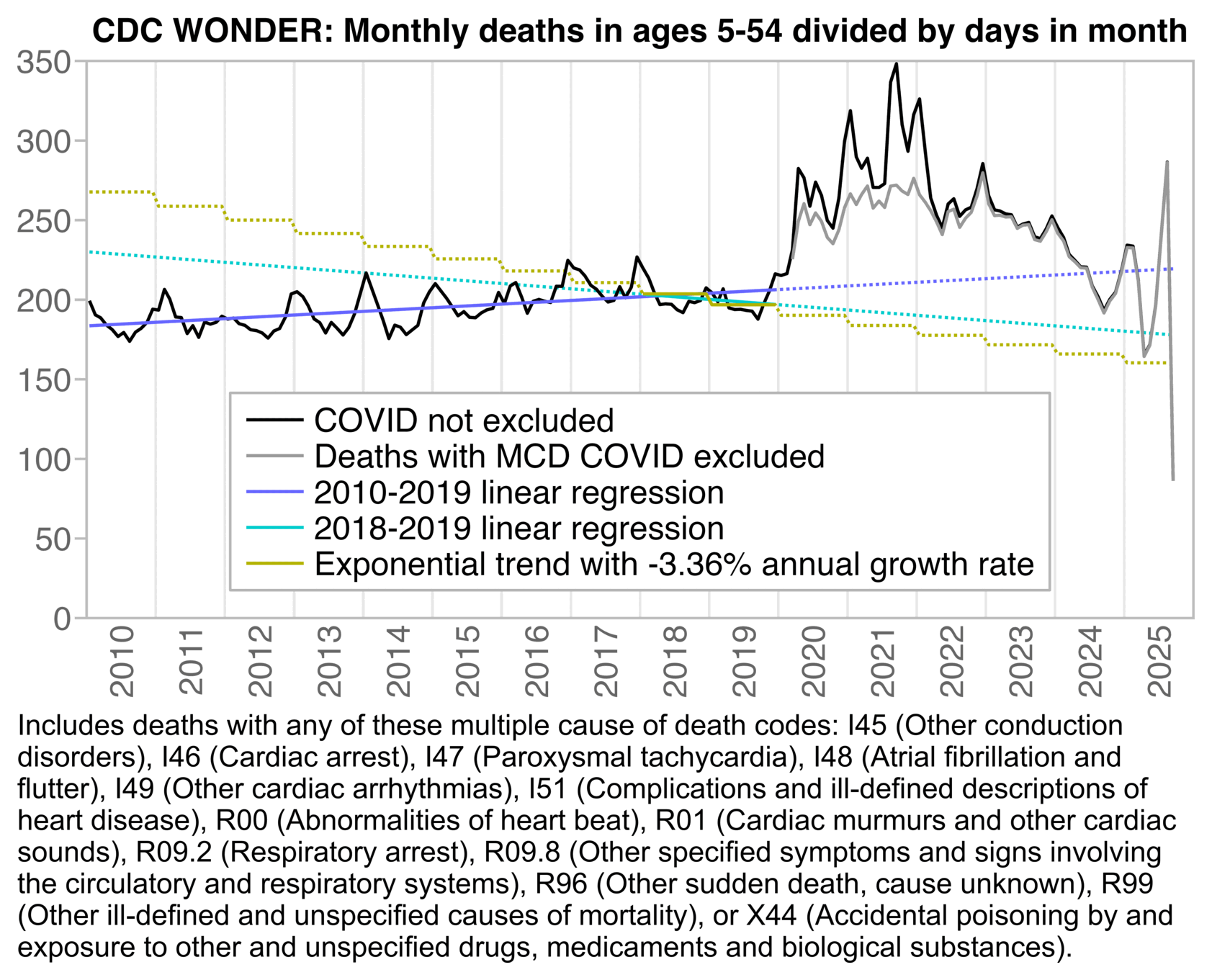
t=fread("https://sars2.net/f/wonderheartdrug5to54monthly.csv")
t[,date:=as.Date(paste(year,month,16,sep="-"))]

p1=t[type=="all",.(x=date,y=dead/days_in_month(date),z=1,fit=T)]
p2=t[type=="notcovid",.(x=date,y=dead/days_in_month(date),z=2,fit=T)]

p3=rbind(copy(p1)[,z:=3][,fit:=year(x)%in%2010:2019],copy(p1)[,z:=4][,fit:=year(x)%in%2018:2019])
p3=p3[,.(x,y=predict(lm(y~x,.SD[fit==T]),.SD),fit),z]

p4=p1[,.(x,y=p1[year(x)%in%2018:2019,mean(y)]*(1-.0336)^(year(x)-2018.5),z=5,fit=year(x)%in%2018:2019)]

p=rbind(p1,p2,p3,p4)
p[,z:=factor(z,,c("COVID not excluded","Deaths with MCD COVID excluded","2010-2019 linear regression","2018-2019 linear regression","Exponential trend with -3.36% annual growth rate"))]

p=p[year(x)>=2010]

xstart=as.Date("2010-1-1");xend=as.Date("2026-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=pretty(c(0,p$y));ystart=0;yend=max(ybreak)

ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=z),linetype="11",linewidth=.5)+
geom_line(data=p[fit==T],aes(x,y,color=z),linewidth=.5)+
labs(x=NULL,y=NULL,title="CDC WONDER: Monthly deaths in ages 5-54 divided by days in month")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black","gray60",hsv(c(2/3,1/2),c(.6,1),c(1,.8)),hsv(1/6,1,.7)))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.text.y=element_text(margin=margin(,1)),
  axis.ticks=element_line(linewidth=.4,color="gray75"),
  axis.ticks.length=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_rect(color="gray70",linewidth=.4),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification=c(.5,0),
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(3,5,3,3),
  legend.position=c(.5,.05),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,margin=margin(,,,1)),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.subtitle=element_text(hjust=.5,margin=margin(,,4)),
  plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)))
ggsave("1.png",width=5.6,height=3.3,dpi=300*4)

Plot for X44 drug deaths

Ethical Skeptic included the plot below in one of his blog posts, with this caption: "Excess Mortality from Overdose from Unspecified Drug and Climate Change - Yes, the combination of lockdowns and Covid-19 resulted in a temporary increase in undetermined drug overdoses. However, this is not 'trend' data. The trend begins at the end of 2020 with the introduction of the vaccine (which peaks the very week of vaccine maximum uptake). Vaccine-induced myocarditis rendered this population vulnerable to sudden cardiac death - which was then falsely attributed to drug overdose. This excess attribution, as of Week 25 2023, is in the range of 270-300 deaths per week, for 'unspecified drug' and 'climate'. A query-determined non-overlapping portion of this tally is added back into the Sudden Cardiac Death mortality totals show in DFT Chart 10 below. It suggests an alarming increase in young person Sudden Cardiac Death." [https://theethicalskeptic.com/2024/04/04/the-state-of-things-pandemic-week-50-2023/]

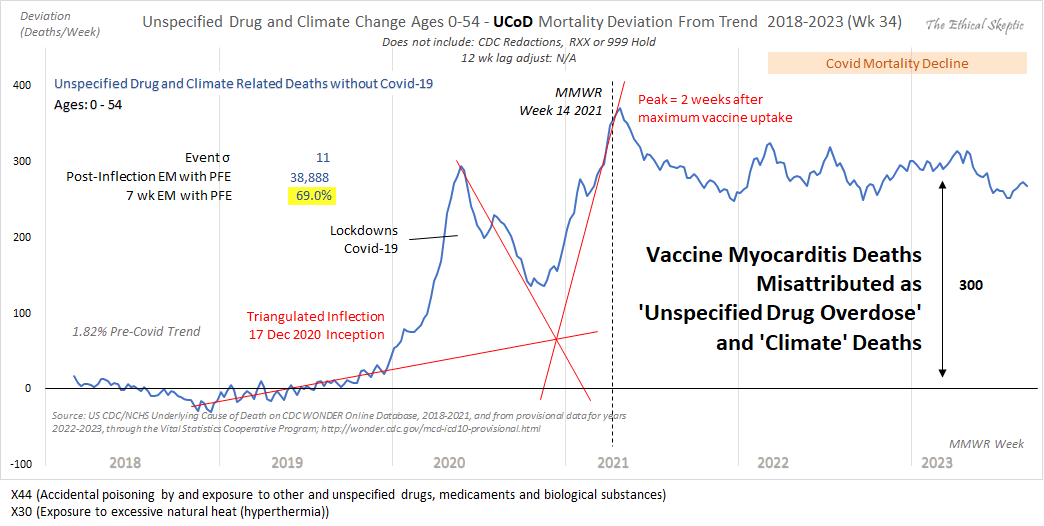
The title of the plot above says that the plot shows "Unspecified Drug and Climate Change" deaths. The only ICD code in the plot related to climate change is X30 ("Exposure to excessive natural heat (hyperthermia)") and the only drug-related ICD code is X44 ("Accidental poisoning by and exposure to other and unspecified drugs, medicaments and biological substances"). In the year 2021 CDC WONDER returned only 556 deaths with MCD X30 but 35,671 deaths with MCD X44. So deaths from hyperthermia account for such a small fraction of total deaths in Ethical Skeptic's plot that it's confusing that are included in the plot at all. When Ethical Skeptic's followers hear that there has been an increase in deaths related to climate change, they might think that there has been a large number of vaccine deaths that have been misclassified as deaths related to climate change, because it's a cliche among anti-vaxxers to say that vaccine deaths are covered up as deaths due to climate change. So Ethical Skeptic may have attempted to mislead his followers into thinking that the increase in deaths was due to the vaccines by conflating deaths from hyperthermia with drug deaths.

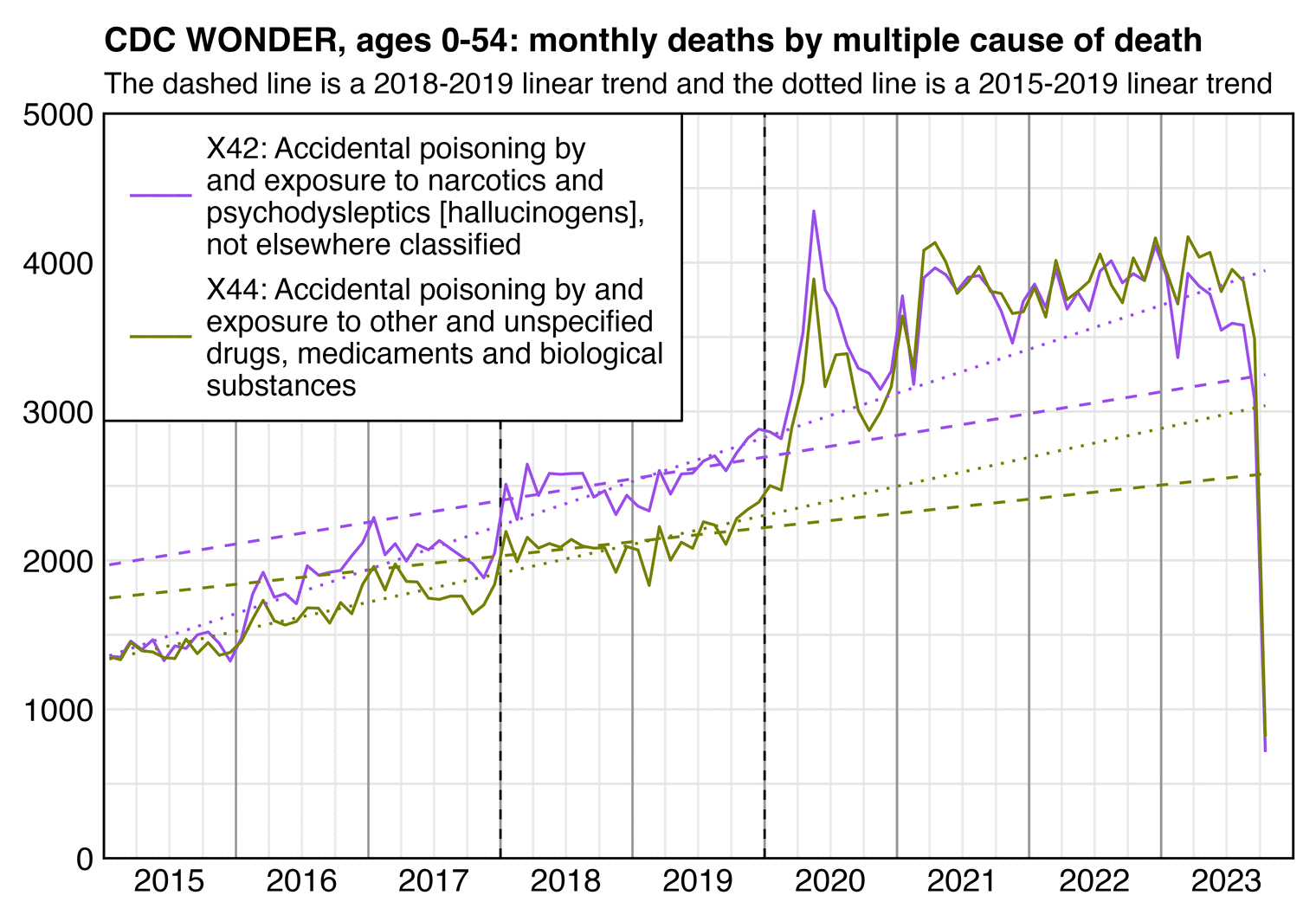
The plot above included only MCD X44 ("Accidental poisoning by and exposure to other and unspecified drugs, medicaments and biological substances") but not MCD X42 ("Accidental poisoning by and exposure to narcotics and psychodysleptics [hallucinogens], not elsewhere classified"). However there's about equally many deaths under X42 as X44 and both of them are common ICD codes for accidental overdoses from recreational drugs, so I don't know why Ethical Skeptic only included X44 but not X42 in his plot. But it might be because X42 had a higher peak in 2020 than 2021 and the peak in 2020 cannot be attributed to the vaccines, but X44 had a higher peak in 2021 than 2020 so it's easier to blame the deaths on the vaccines. Or it might also be because X44 had about 81% more deaths in 2021-2022 than 2018-2019 but X42 only had about 50% more deaths in 2021-2022 than 2018-2019. Or it might also be because X44 deaths have a more flat trend in 2018-2019 so the level of deaths in 2021-2023 looks like it's far above the trend in Ethical Skeptic's plot where the x-axis starts in 2018, but X42 deaths have a trend that is more sloped upwards in 2018-2019 so the level of deaths in 2022 doesn't seem that far off the trend even if the x-axis starts from 2018 so you're not seeing data for earlier years:

library(data.table);library(stringr);library(ggplot2)

t=fread("http://sars2.net/f/ethicalx42x44.csv")
t[,date:=as.Date(paste0(date,"-1"))]

xstart=as.Date("2015-1-1");xend=as.Date("2024-1-1")
xbreak=seq(xstart,xend,"6 month")
xlab=c(rbind("",2015:2023),"")

p=t[date>=xstart&date<=xend]
ybreak=pretty(p$dead);yend=max(ybreak)

dates=unique(p$date)
p$trend=p[year(date)%in%2018:2019,predict(lm(dead~date),.(date=dates)),cause]$V1
p$trend2=p[year(date)%in%2015:2019,predict(lm(dead~date),.(date=dates)),cause]$V1

color=c(hcl(280,110,50),hcl(90,110,50))

lab=c("X42: Accidental poisoning by and exposure to narcotics and psychodysleptics [hallucinogens], not elsewhere classified"|>str_wrap(36),"X44: Accidental poisoning by and exposure to other and unspecified drugs, medicaments and biological substances"|>str_wrap(36))

ggplot(p,aes(x=date,y=dead))+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray92",linewidth=.25)+
geom_hline(yintercept=seq(ystart,yend,ystep),color="gray90",linewidth=.25)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray60",linewidth=.25)+
geom_vline(xintercept=c(as.Date("2018-1-1"),as.Date("2020-1-1")),linetype=2,linewidth=.25)+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_line(aes(color=cause),linewidth=.3)+
geom_line(aes(color=cause,y=trend),linetype=2,linewidth=.3)+
geom_line(aes(color=cause,y=trend2),linetype=3,linewidth=.3)+
labs(title="CDC WONDER, ages 0-54: monthly deaths by multiple cause of death",subtitle="The dashed line is a 2018-2019 linear trend and the dotted line is a 2015-2019 linear trend",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color,labels=lab)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.background=element_rect(fill=alpha("white",1),color="black",linewidth=.25),
  legend.box.just="left",
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.width=unit(17,"pt"),
  legend.key.height=unit(31,"pt"),
  legend.margin=margin(-3,4,3,4,"pt"),
  legend.position=c(0,1),
  legend.spacing.x=unit(1.5,"pt"),
  legend.text=element_text(size=6.5,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=6.4,margin=margin(,,3)),
  plot.title=element_text(size=7.3,face=2,margin=margin(1,,3)))
ggsave("1.png",width=4,height=2.8,dpi=380*4)
system("magick 1.png -resize 25% 1.png")

The plot by Ethical Skeptic started from 2018 and it only included X44 deaths, so it looked like there was an anomalous sustained increase in drug deaths in 2021-2023. But from my plot above which starts from 2015 and where X44 deaths are also included, it looks like 2022 isn't that far off the long-term trend but rather the level of deaths in mid-2021 looks elevated, and there's still probably a lot of deaths missing in 2023 because drug-related deaths have a long registration delay.

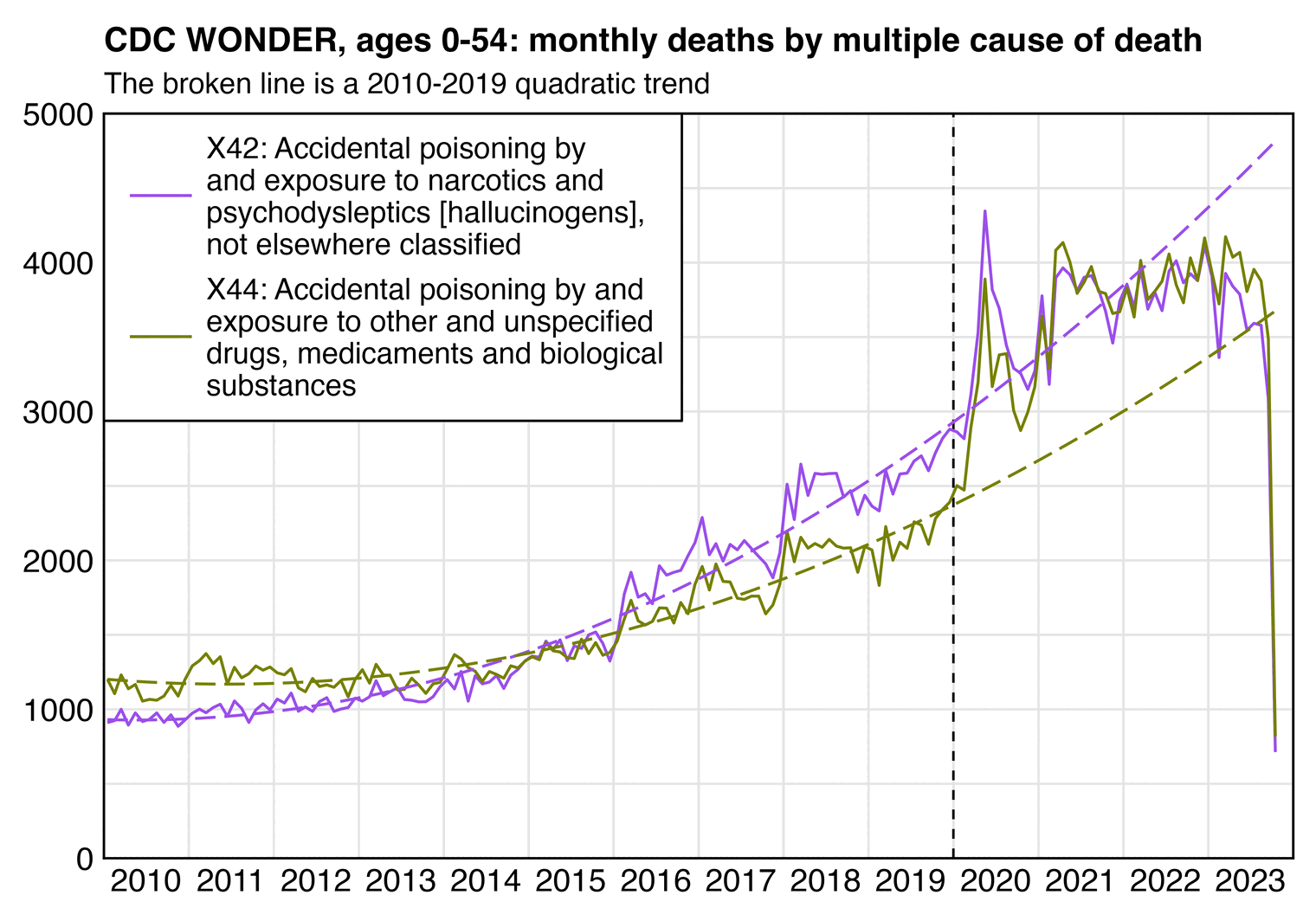
Before COVID the long-term trend in drug deaths seemed to be curved upwards, so the 2015-2019 linear trend in my plot above might be too low, and in the next plot where I used a 2010-2019 quadratic trend instead, the X42 deaths were actually below the trend in 2022 (even though X44 deaths were still above the trend in 2022):

library(data.table);library(stringr);library(ggplot2)

t=fread("http://sars2.net/f/ethicalx42x44.csv")
t[,date:=as.Date(paste0(date,"-1"))]

xstart=as.Date("2010-1-1");xend=as.Date("2024-1-1")
xbreak=seq(xstart,xend,"6 month")
xlab=c(rbind("",2010:2023),"")

p=t[date>=xstart&date<=xend]
ybreak=pretty(p$dead);yend=max(ybreak)

dates=unique(p$date)
p$trend=p[year(date)<2020,predict(lm(dead~poly(as.numeric(date),2)),.(date=dates)),cause]$V1

color=c(hcl(280,110,50),hcl(90,110,50))

lab=c("X42: Accidental poisoning by and exposure to narcotics and psychodysleptics [hallucinogens], not elsewhere classified"|>str_wrap(36),"X44: Accidental poisoning by and exposure to other and unspecified drugs, medicaments and biological substances"|>str_wrap(36))

ggplot(p,aes(x=date+15,y=dead))+
geom_hline(yintercept=seq(ystart,yend,ystep),color="gray90",linewidth=.25)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.25)+
geom_vline(xintercept=as.Date("2020-1-1"),linetype=2,linewidth=.25)+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_line(aes(color=cause),linewidth=.3)+
geom_line(aes(color=cause,y=trend),linetype=5,linewidth=.3)+
labs(title="CDC WONDER, ages 0-54: monthly deaths by multiple cause of death",subtitle="The broken line is a 2010-2019 quadratic trend",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color,labels=lab)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.background=element_rect(fill=alpha("white",1),color="black",linewidth=.25),
  legend.box.just="left",
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.width=unit(17,"pt"),
  legend.key.height=unit(31,"pt"),
  legend.margin=margin(-3,4,3,4,"pt"),
  legend.position=c(0,1),
  legend.spacing.x=unit(1.5,"pt"),
  legend.text=element_text(size=6.5,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=6.4,margin=margin(,,3)),
  plot.title=element_text(size=7.3,face=2,margin=margin(1,,3)))
ggsave("1.png",width=4,height=2.8,dpi=380*4)
system("magick 1.png -resize 25% 1.png")

Effect of fitting a baseline against data from only 2018 and 2019

When I asked Ethical Skeptic how he calculates his baseline in the plots which show weekly data from 2018 onwards, he posted this reply: [https://theethicalskeptic.substack.com/p/the-state-of-things-pandemic-week-706/comment/53292593]

I'm not analyzing generational or population-diluted trends (potentially misleading statistics), I am detecting deviation from trend dynamics (detecting system inflection).

I cannot use Wonder 2017 and earlier because the numbers are boosted by the small county single-record effect. This is why Wonder 2018 and beyond is a new database (shows as a variance in your chart which does not actually exist), under that HIPAA constraint. Nor can I use 2002 - 2017 data because this contain a dissipating generational effect of those Boomers who suffered cardiac arrest from specific past health impacts which are no longer salient to this age bracket. That trend line must be moved to the 65+ bracket now. This has caused a slight downtrend into 2019, which I do accommodate, yes.

I compared that baseline to a linear regression of the old growth rate (2014-2017) before hand to ensure it was 'in context'. However, I did not use a pure linear regression of 2018 and 19 for this reason. I fit the baseline to the variances linearly, but not by least-squares regression (how I avoided the early 2018 surge). There is of course not enough data to then use a non-linear function beyond that as well. That would be whipsawing fiction.

But much of this is moot, because none of these manipulations serve to make this dramatic an inflection disappear. These are trend manipulations. Four years from now, trend models will have to be adjusted again, but the inflection will still be there. The argument will be over just how much excess death there indeed is... but I anticipate that it will be moot. If you have a strong inflection like this and your trend analysis makes it disappear quickly, odds are the trend analysis is biased.

As a result, I don't have either a Jan 2018 high or 2019 lowering bias in my baseline.

I don't understand how his method of calculating a linear baseline is different from a regular linear regression or how he accounted for the low number of deaths in 2019, but he blocked me before I was able to ask him to clarify it.

The United States had a high number of deaths in early 2018 and a low number of deaths in 2019, so if you fit a regular linear baseline using only data from the years 2018 and 2019, the slope of the baseline will usually point too much downwards like in the case of my gray baseline below (even though I don't know to what extent Ethical Skeptic's undocumented regression method suffers from the same problem):

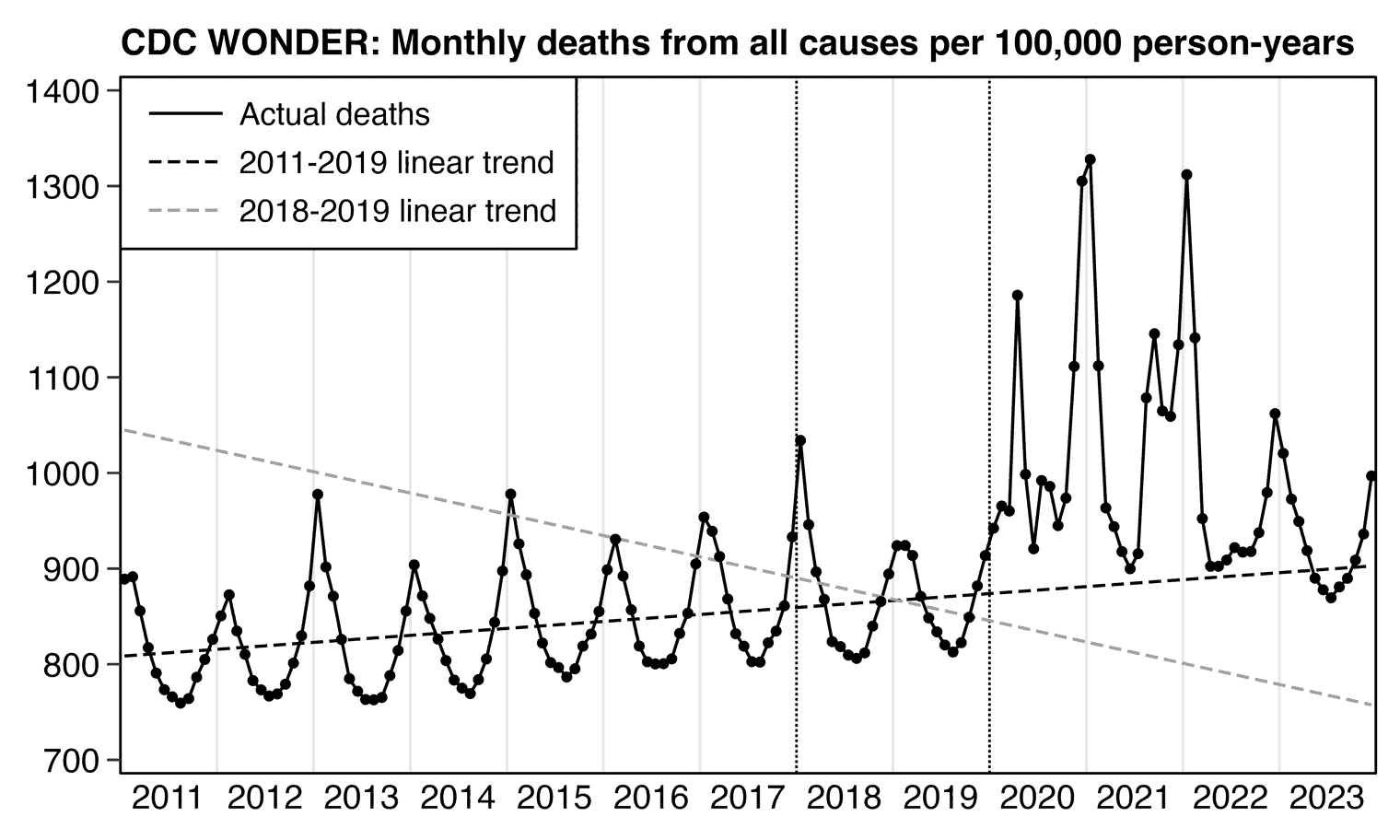
 library(data.table);library(stringr);library(ggplot2)

t=fread("http://sars2.net/f/uspopdeadmonthly.csv")
t[,date:=as.Date(paste0(date,"-1"))]

xstart=as.Date("2011-1-1");xend=as.Date("2024-1-1")
xbreak=seq(xstart,xend,"6 month")
xlab=c(rbind("",2011:2023),"")

a=t[date>=xstart&date<=xend,.(y=sum(dead)/sum(persondays)*365e5,z="Actual deaths"),.(x=date)]

dates=unique(p$x)
p=rbind(a,a[year(x)%in%2011:2019,.(x=dates,y=predict(lm(y~x),.(x=dates)),z="2011-2019 linear trend")])
p=rbind(p,a[year(x)%in%2018:2019,.(x=dates,y=predict(lm(y~x),.(x=dates)),z="2018-2019 linear trend")])
p[,z:=factor(z,unique(z))]

ybreak=pretty(p$y)
color=c("black","black","gray60")

ggplot(p,aes(x=x+15,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.25)+
geom_vline(xintercept=c(as.Date("2018-1-1"),as.Date("2020-1-1")),linetype="11",linewidth=.25)+
geom_line(aes(color=z,linetype=z),linewidth=.3)+
geom_point(data=p[z=="Actual deaths"],size=.4,show.legend=F)+
labs(title="CDC WONDER: Monthly deaths from all causes per 100,000 person-years",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab,expand=c(0,0))+
scale_y_continuous(limits=range(ybreak),breaks=ybreak,expand=c(.02,0))+
scale_color_manual(values=color)+
scale_linetype_manual(values=c("solid","42","42"))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.y=element_text(margin=margin(,1.5)),
  axis.ticks=element_line(linewidth=.25),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  legend.background=element_blank(),
  legend.box.background=element_rect(fill=alpha("white",1),color="black",linewidth=.25),
  legend.box.just="left",
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.width=unit(19,"pt"),
  legend.key.height=unit(10,"pt"),
  legend.margin=margin(-3,4,3,4,"pt"),
  legend.position=c(0,1),
  legend.spacing.x=unit(1.5,"pt"),
  legend.text=element_text(size=6.5,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.25),
  plot.margin=margin(5,5,5,5),
  plot.title=element_text(size=7.3,face=2,margin=margin(1,,3)))
ggsave("1.png",width=4,height=2.4,dpi=380*4)
system("magick 1.png -resize 25% 1.png")

When Ethical Skeptic posted of list errors made by other analysts, this was one of the points on his list: "Add volatility of peak winter mortality periods into the trend regression, and not index off the summer base. That way a rough flu year will raise the baseline artificially to your advantage." [https://x.com/EthicalSkeptic/status/1773066903000396096] So I don't know if it means that he omits the weeks with high mortality in early 2018 when he calculates the baseline.

Ethical Skeptic has published three articles in a series called "Houston We Have a Problem" where he has explained some of his methodology. [https://theethicalskeptic.com/2024/04/04/the-state-of-things-pandemic-week-50-2023/] In the third part he included the image below where he described how he calculates his baseline, but it sounds like he's just doing a regular linear regression and he's not applying any special method to account for the low number of deaths in 2019 or for the high number of deaths in early 2018 (even though he seems to describe how he makes his plots that start from 2014 so it could be that he uses different methodology in the plots that start from 2018, or he may have revised his methodology since he made this image):

When Ethical Skeptic fits a seasonality-adjusted baseline against only two years of data, another more minor issue is that the baseline for each week number will adapt to whatever the number of deaths that week number happened to be in 2018 and 2019, so 2018 and 2019 will have low residuals of excess deaths compared to subsequent years, and therefore the z-scores of subsequent years will also be elevated. So he will often get impressively high z-scores for deaths since 2021, but he doesn't mention that the z-scores would usually be lower if he used a longer fitting period for his baseline.

The plot below shows that when I fitted a seasonality-adjusted baseline against only one year of weekly data so that the baseline was adjusted to match the actual deaths each week, there were 0% excess deaths during each week of the fitting period, so then the standard deviation of the residuals during the fitting period was zero, so I got infinite z-scores when I subsequently divided excess deaths with the standard deviation of the residuals. And similarly when I fitted a seasonality-adjusted baseline against only two years of data, I subsequently got higher absolute z-scores than when I used a 4-year fitting period. The plot demonstrates that shorter seasonality-adjusted baselines tend to produce a lower standard deviation for the residuals during the fitting period, and therefore they tend to produce higher z-scores for excess deaths:

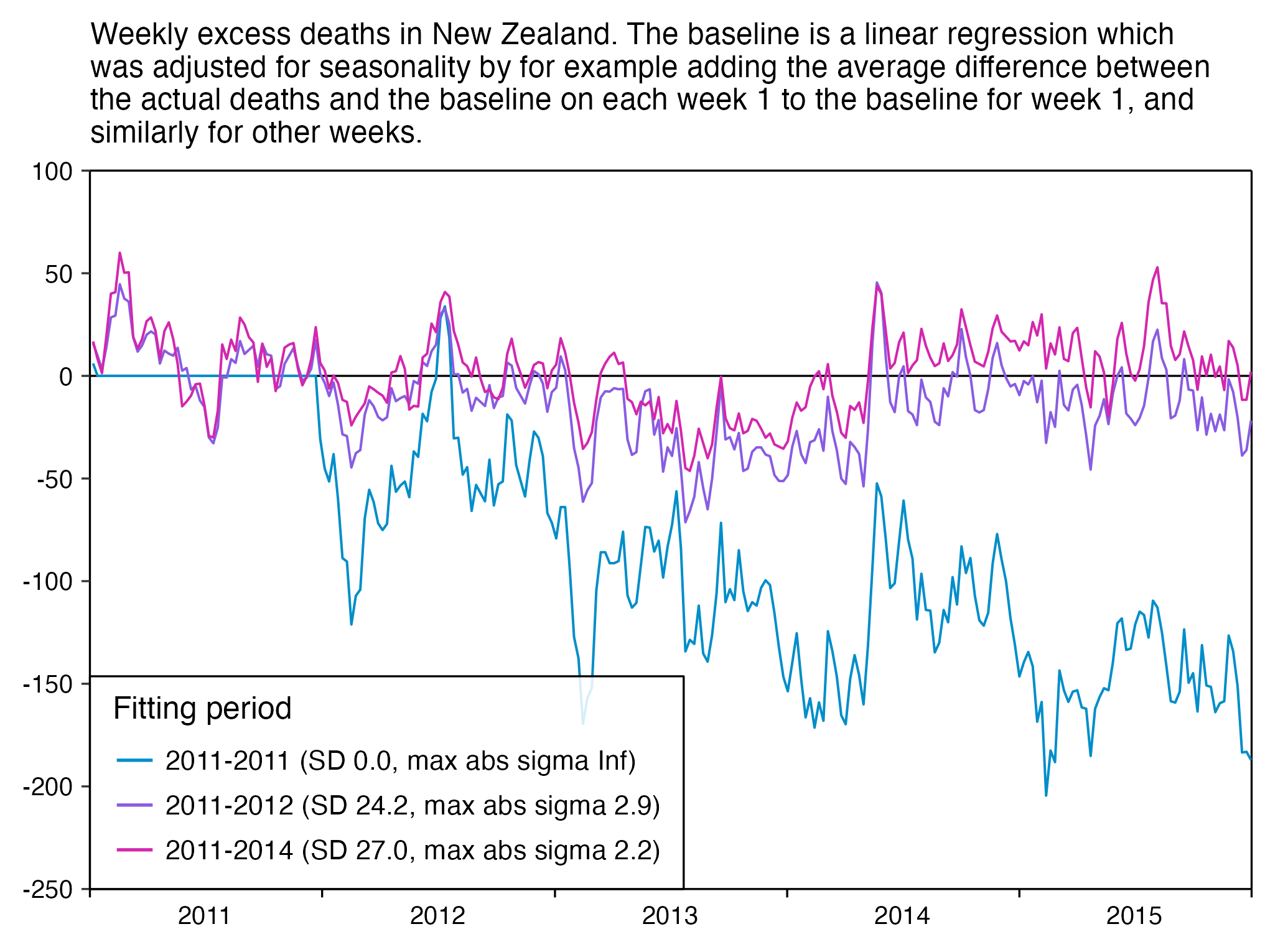
library(ggplot2)

isoweek=\(year,week,weekday=1){d=as.Date(paste0(year,"-1-4"));d-(as.integer(format(d,"%w"))+6)%%7-1+7*(week-1)+weekday}
ma=\(x,b=1,f=b)rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T)

t=read.csv("https://www.mortality.org/File/GetDocument/Public/STMF/Outputs/NZL_NPstmfout.csv")|>subset(Sex=="b")
t$date=isoweek(t$Year,t$Week,4)

xy=do.call(rbind,lapply(c(2011,2012,2014),\(i){
  pred=t$Year%in%2011:i
  trend=predict(lm(Total~date,t[pred,]),t)
  weekly=tapply(t$Total[pred]-trend[pred],t$Week[pred],mean)
  ma(rep(weekly,3),0)[53:154]
  o=data.frame(x=t$date,z=paste0("2011-",i),dead=t$Total)
  o$trend=trend+weekly[pmin(t$Week,52)]
  o$y=ma(o$dead-o$trend,1)
  o$sd=sd(o$dead[pred]-o$trend[pred])
  o}))

xstart=as.Date("2011-1-1");xend=as.Date("2016-1-1")
xy=xy[xy$x>=xstart&xy$x<=xend,]

xbreak=seq(xstart,xend,"6 month")
xlab=c(rbind("",2011:2015),"")
cand=c(sapply(c(1,2,5),\(x)x*10^c(-10:10)))
ymax=max(xy$y,na.rm=T);ymin=min(xy$y,na.rm=T)
ystep=cand[which.min(abs(cand-(ymax-ymin)/5))]
ystart=ystep*floor(ymin/ystep)
yend=ystep*ceiling(ymax/ystep)
ybreak=seq(ystart,yend,ystep)

color=c(hcl(c(210,260,310)+15,100,50))

sd=sprintf("%.1f",tapply(xy$sd,xy$z,unique))
sigma=c("Inf",sprintf("%.1f",tapply(abs(xy$y/xy$sd),xy$z,max))[-1])
lab=paste0(unique(xy$z)," (SD ",sd,", max abs sigma ",sigma,")")
xy$z=lab[factor(xy$z)]

tit="Weekly excess deaths in New Zealand. The baseline is a linear regression which was adjusted for seasonality by for example adding the average difference between the actual deaths and the baseline on each week 1 to the baseline for week 1, and similarly for other weeks."

ggplot(xy,aes(x=x,y=y,color=z))+
geom_hline(yintercept=c(ystart,0,yend),linewidth=.25)+
geom_vline(xintercept=c(xstart,xend),linewidth=.25)+
geom_line(aes(color=z),linewidth=.3)+
labs(title=stringr::str_wrap(tit,85),x=NULL,y=NULL)+
coord_cartesian(clip="off",expand=F)+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
guides(colour=guide_legend(title="Fitting period",override.aes=list(linewidth=.4)))+
theme(axis.text=element_text(size=6.5,color="black"),
  axis.ticks=element_line(linewidth=.25),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.ticks.length=unit(.15,"lines"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.just="left",
  legend.key=element_rect(fill="white"),
  legend.spacing.x=unit(.15,"lines"),
  legend.key.size=unit(.8,"lines"),
  legend.position=c(0,0),
  legend.justification=c(0,0),
  legend.box.background=element_rect(fill=alpha("white",.85),color="black",linewidth=.25),
  legend.margin=margin(.3,.4,.3,.4,"lines"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_text(size=8),
  panel.background=element_rect(fill="white"),
  panel.grid=element_blank(),
  plot.background=element_rect(fill="white"),
  plot.margin=margin(.4,.65,.4,.4,"lines"),
  plot.caption=element_text(size=6.7,hjust=0,margin=margin(.6,0,0,0,"lines")),
  plot.title=element_text(size=7.8))
ggsave("1.png",width=4.6,height=3.4,dpi=450)

COVID deaths per capita compared to percentage of vaccinated population in US counties

Ethical Skeptic posted the plot below and wrote: [https://x.com/EthicalSkeptic/status/1531517512906592256]

Covid Deaths per 100 K population trend down as the percentage of the population vaccinated rises.

Vaccines working right?

No, this is the function which existed prior to the vaccines being rolled out (22 Jan 2020 - 4 Apr 2021).

Watch for charlatans exploiting this effect.

He also posted the next plot and wrote:

In actuality, when we compare both periods before & after the launch of the vax (MMWR Wk 14 2021) - we observe that there exists no difference between pre & post vax death rates by US county. It is EXACTLY the same function pre & post vaccine.

Any benefit MUST show here.

However for some reason he extended his pre-vaccination period up to April 4th 2021, even though about 30% of the US population was already vaccinated at that point (and the majority of people were vaccinated in the elderly age groups which account for most COVID deaths):

$ curl https://data.cdc.gov/api/views/rh2h-3yt2/rows.csv>statesvax.csv
$ csvtk filter2 -f '$Date=="04/03/2021"&&$date_type=="Report"&&$Location=="US"' statesvax.csv|csvtk cut -f Date,Location,Administered_Dose1_Pop_Pct
Date,Location,Administered_Dose1_Pop_Pct
04/03/2021,US,31.4

He also didn't explain how he calculated the curved trend line, and it looks too low near the end of the x-axis, and for some reason he only drew the trend up to the point where the value of the x-axis was about 85%.

In the plot below I tried plotting the percentage of vaccinated population on March 1st 2022 on the x-axis like Ethical Skeptic, but I compared COVID deaths in 2020 against COVID deaths in 2021-2022 so that I didn't include the first three months of 2021 as part of the pre-vaccination period. When I splitted a spline trend to the data, it was a lot steeper in 2021-2022 than 2020. And even in 2020 the overall trend looks more flat in my plot, because I drew the trend line up to the end of the x-axis and I didn't smooth out the trend line as heavily as Ethical Skeptic. The trend got even flatter when I weighted it by population size, because larger counties have a higher percentage of vaccinated people than smaller counties, and in 2020 there were many large northeastern counties that had a high number of COVID deaths per capita:

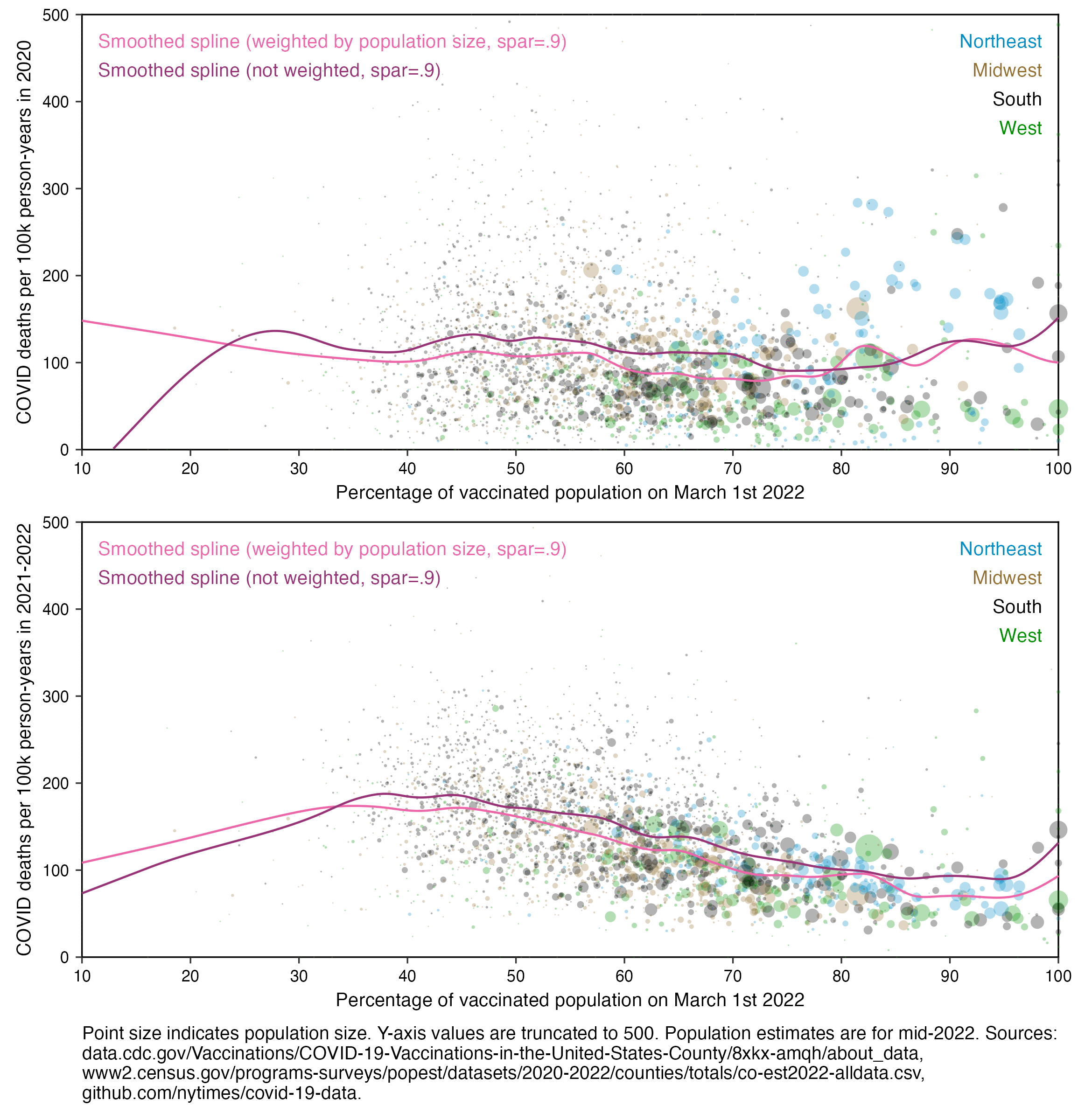
library(data.table);library(ggplot2)

# download.file("https://github.com/nytimes/covid-19-data/raw/master/us-counties-2020.csv","us-counties-2020.csv")
# download.file("https://github.com/nytimes/covid-19-data/raw/master/us-counties-2022.csv","us-counties-2022.csv")
# download.file("https://www2.census.gov/programs-surveys/popest/datasets/2020-2022/counties/totals/co-est2022-alldata.csv","uscountypop.csv")

# download manually:
# https://data.cdc.gov/Vaccinations/COVID-19-Vaccinations-in-the-United-States-County/8xkx-amqh/about_data

t=fread("COVID-19_Vaccinations_in_the_United_States_County_20240227.csv")
t=t[Date=="03/01/2022",c("FIPS","Administered_Dose1_Recip")]
names(t)=c("fips","vax")
t$fips=as.integer(t$fips)

pop=fread("uscountypop.csv")[,.(fips=as.integer(sprintf("%d%03d",STATE,COUNTY)),pop=POPESTIMATE2022)]

nyt=fread("us-counties-2022.csv")[date=="2022-12-31",.(fips,deaths)]
nyt2=fread("us-counties-2020.csv")[date=="2020-12-31",.(fips,deaths)]
nyt=merge(nyt,nyt2,by="fips")[,.(fips,deaths=(deaths.x-deaths.y)/2)]|>na.omit()

states=read.csv("https://github.com/cphalpert/census-regions/raw/master/us%20census%20bureau%20regions%20and%20divisions.csv")[,c(2,3)]
fips=read.csv("https://gist.githubusercontent.com/dantonnoriega/bf1acd2290e15b91e6710b6fd3be0a53/raw/11d15233327c8080c9646c7e1f23052659db251d/us-state-ansi-fips.csv",strip.white=T)[,c(3,2)]
states=merge(states,fips,by=1)
states=setNames(states[,2],states[,3])

me=merge(merge(t,nyt),pop)[vax>0]|>na.omit()
xy=data.frame(x=pmin(100,me$vax/me$pop*100),y=pmin(500,me$deaths/me$pop*1e5),pop=me$pop)
xy$size=pmax(.3,log(me$pop,20)-2.8)
xy$region=factor(states[sub("...$","",me$fips)],c("Northeast","Midwest","South","West"))

xstart=10;xend=100;xstep=10;ystart=0;yend=500;ystep=100
xbreak=seq(xstart,xend,xstep)
ybreak=seq(ystart,yend,ystep)

smooth1=as.data.frame(predict(smooth.spline(xy$x,xy$y,spar=.85,w=xy$pop/max(xy$pop)),seq(0,100,.1)))
smooth2=as.data.frame(predict(smooth.spline(xy,spar=.85),seq(0,100,.1)))

leg1=data.frame(x=11.4,y=seq(yend*.94,,-yend/15,2),label=c("Smoothed spline (weighted by population size, spar=.85)","Smoothed spline (not weighted, spar=.85)"))
leg2=data.frame(x=xend-1.4,y=seq(yend*.94,,-yend/15,4),label=levels(xy$region))

pal1=c("#ee66aa","#993377")
pal2=c(hcl(225,100,50),hcl(55,50,50),"black",hcl(135,100,50))

ggplot(xy,aes(x,y))+
geom_label(data=leg1,aes(x=x,y=y,label=label),fill=alpha("white",.85),label.r=unit(0,"lines"),label.padding=unit(.04,"lines"),label.size=0,size=2.3,hjust=0,color=pal1)+
geom_label(data=leg2,aes(x=x,y=y,label=label),fill=alpha("white",.85),label.r=unit(0,"lines"),label.padding=unit(.04,"lines"),label.size=0,size=2.3,hjust=1,color=pal2)+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_point(aes(color=region),stroke=0,size=xy$size,alpha=.3)+
geom_line(data=smooth1,color=pal1[1],linewidth=.35)+
geom_line(data=smooth2,color=pal1[2],linewidth=.35)+
labs(x="Percentage of vaccinated population on March 1st 2022",y="COVID deaths per 100k person-years in 2020",title="US counties: COVID deaths vs percentage of vaccinated population on March 1st 2022",caption="Point size indicates population size. Y-axis values are truncated to 500. Population estimates are for mid-2022. Sources:
data.cdc.gov/Vaccinations/COVID-19-Vaccinations-in-the-United-States-County/8xkx-amqh/about_data,
www2.census.gov/programs-surveys/popest/datasets/2020-2022/counties/totals/co-est2022-alldata.csv,
github.com/nytimes/covid-19-data.")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=pal2)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=5.5,color="black"),
  axis.ticks=element_line(linewidth=.25),
  axis.ticks.length=unit(.15,"lines"),
  axis.title=element_text(size=6.5),
  legend.position="none",
  panel.grid=element_blank(),
  panel.background=element_rect(fill="white"),
  plot.margin=margin(.4,.8,.4,.4,"lines"),
  plot.caption=element_text(size=6.3,hjust=0),
  plot.title=element_text(size=7.3))
ggsave("1.png",width=5.2,height=3.1,dpi=450)

Does the provisional dataset have different suppression behavior than the final dataset?

Ethical Skeptic wrote: "I cannot use Wonder 2017 and earlier because the numbers are boosted by the small county single-record effect. This is why Wonder 2018 and beyond is a new database (shows as a variance in your chart which does not actually exist), under that HIPAA constraint." [https://theethicalskeptic.substack.com/p/the-state-of-things-pandemic-week-706/comment/53292593]

He also wrote: "Please note however, that the provisional mortality figures for 2018-2024 are lower than the figures prior to 2018 because the NVSS suppresses county level data with fewer than nine records. We do not adjust 2018 and later mortality figures upward for this. Therefore, these excess mortality projections are lower than the reality as a result. For this reason, all inflection and DFT charts begin with the 2018 suppressed data, in order to avoid false 'downtrends' or inflections in the data." [https://theethicalskeptic.com/2024/04/04/the-state-of-things-pandemic-week-50-2023/]

The link in the text I quoted was a screenshot of this part of the help article for the provisional deaths dataset: [https://wonder.cdc.gov/wonder/help/mcd-provisional.html]

1. What are the Assurance of Confidentiality constraints for vital statistics?

All statistics representing one through nine (1-9) persons are suppressed, in the provisional mortality online database for years 2018 and later.

Data reports for years 1989 and later must meet the NCHS data use restrictions. Vital statistics data are suppressed due to confidentiality constraints, in order to protect personal privacy. The term "Suppressed" replaces sub-national death counts, births counts, death rates and associated confidence intervals and standard errors, as well as corresponding population figures, when the figure represents one to nine (1-9) persons.

Ethical Skeptic may have been confused by the text which said that the deaths are suppressed "in the provisional mortality online database for years 2018 and later", as if there would have been a change in policy in the year 2018, even though I think it just means that the deaths are suppressed throughout the provisional mortality dataset which starts in 2018. Similar text is also included in the help article for the final mortality data in 1999-2020, which says that the suppression starts in the year 1999: "The term 'Suppressed' replaces death counts, births counts, death rates and associated confidence intervals and standard errors, as well as corresponding population figures, when the figure represents one to nine (1-9) persons for deaths in 1999 and later years." [https://wonder.cdc.gov/wonder/help/mcd.html]

CDC WONDER suppresses the number of deaths on rows with 1-9 deaths both in the datasets for provisional and final deaths, and I haven't noticed any differences in the suppression behavior between the datasets. For example I did a request for provisional mortality statistics here: https://wonder.cdc.gov/mcd-icd10-provisional.html. I grouped the results by residence county and month, I set the state of residence to Rhode Island, I set the year to 2020, and I set underlying cause to intentional self-harm (X60-X84). Rhode Island has 5 counties, but 2 of them had 1-9 deaths so the number of deaths was suppressed, but the suppressed counties were still included in the total number of deaths across all counties. And I got identical results when I did a similar request in the 1999-2020 final dataset:

If there was some major change to the data suppression behavior in the dataset that starts in 2018, then I think it would be highlighted more clearly in the documentation.

Ethical Skeptic wrote that the reason why "Wonder 2018 and beyond is a new database" was because of the change to the suppression behavior. But actually it might be because the data from 2018 onwards includes more racial categories than the earlier data, and it includes weekly data in addition to monthly data, and it allows grouping the results by location of occurrence and not only location of residence. There's also a separate dataset for 1999-2004 which only includes 3 different race groups, which only includes yearly but not monthly data, and where Hispanic origin is not indicated:

The natality data at CDC WONDER is also split off into different datasets for different ranges of years, which have different sets of racial categories and other available variables: [https://wonder.cdc.gov/natality.html]

CDC has also published the mortality data at CDC WONDER as plain text files in a fixed-width field format: https://www.cdc.gov/nchs/data_access/vitalstatsonline.htm#Mortality_Multiple. There's CSV versions of the files here: https://www.nber.org/research/data/mortality-data-vital-statistics-nchs-multiple-cause-death-data. The files contain one line for each dead person, but the state and county of residence and occurrence are omitted for privacy reasons. At first I got slightly more deaths in the files than at CDC WONDER, but I got the same count of deaths after I excluded lines where the tape location 20 for resident status was not 4 (foreign residents). So for example in 2020 I got 602,350 deaths where the UCD started with the letter C, which was identical to the result I got from CDC WONDER regardless of whether I looked at the final or provisional dataset:

$ wget https://ftp.cdc.gov/pub/Health_Statistics/NCHS/Datasets/DVS/mortality/mort2020us.zip
$ unzip mort2020us.zip
$ awk '{if(substr($0,20,1)==4)next;a[substr($0,102,4),substr($0,65,2),substr($0,71,3),substr($0,146,4)]++}ENDFILE{for(i in a)print i,a[i]}' {SUBSEP,OFS}=, VS20MORT.DUSMCPUB_r20220105|tr -d \ >temp
$ sed 1q temp # year, month, age, UCD, deaths
2020,09,024,W31,1
$ awk -F, '$4~/^C/{x+=$5}END{print x}' temp
602350

Deaths associated with pregnancy and childbirth

Ethical Skeptic posted the following plot where there was a spike in pregnancy-associated deaths that coincided with the Delta wave, but he suggested that it might have been caused by vaccines instead of COVID. He also got a steadily decreasing number of excess deaths in 2022-2023, but he suggested it might have been because the birth rate was reduced by vaccines: [https://x.com/EthicalSkeptic/status/1778268480619331786]

Not particularly good news here.

1. We don't use the 'placental disorder unspecified' like the UK.

2. Expanding query to all Maternal deaths O00-O99 for Pregnancy, Childbirth & Puerperium reveals

a. large vaccine impact
b. distressing news about implied childbirth rate

Ethical Skeptic told me that in these plots which display weekly deaths from 2018 onwards, he fits the baseline using only data from 2018 and 2019. He said that his baseline is linear but it's somehow different from a regular least squares linear regression, but he didn't explain how it's different. [https://theethicalskeptic.substack.com/p/the-state-of-things-pandemic-week-706/comment/53237226]

The year 2019 had an unusually low number of deaths, so normally if you fit a linear baseline against only data from 2018 and 2019, the slope of the baseline is pointed too much downwards. However in the case of deaths with an underlying cause related to pregnancy and childbirth, 2019 actually had a higher number of deaths than 2018, so in the plot below when I fitted a linear baseline against deaths from 2018 and 2019 only, the slope of the baseline was pointed too much upwards compared to a longer-term linear trend. So it probably also explains why Ethical Skeptic's plot had a steadily decreasing trend in excess deaths in 2022-2023. But when I used a 2013-2019 baseline instead, my excess deaths remained roughly flat in 2022-2023:

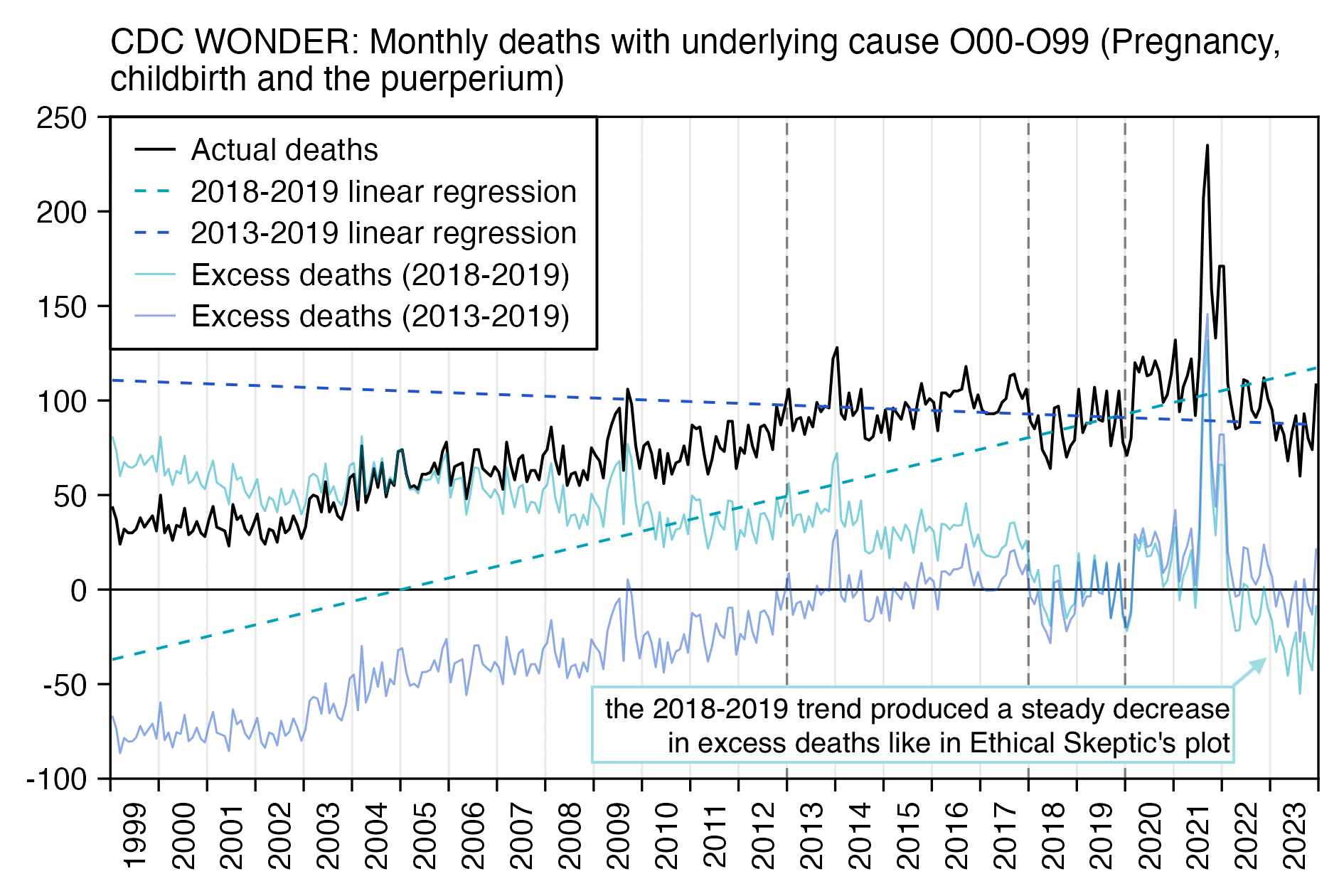
library(ggplot2)

t=read.csv("http://sars2.net/f/wonderpregnancymonthly.csv")

x=as.Date(paste0(t$year,"-",t$month,"-15"))
xy=data.frame(x,y=t$dead,z="Actual deaths")

trend1=predict(lm(y~x,xy[data.table::year(xy$x)%in%2018:2019,]),xy)
trend2=predict(lm(y~x,xy[data.table::year(xy$x)%in%2013:2019,]),xy)

rbd=\(x,...)rbind(x,setNames(data.frame(...),names(x)))
xy=rbd(xy,x,trend1,"2018-2019 linear regression")
xy=rbd(xy,x,trend2,"2013-2019 linear regression")
xy=rbd(xy,x,t$dead-trend1,"Excess deaths (2018-2019)")
xy=rbd(xy,x,t$dead-trend2,"Excess deaths (2013-2019)")

xy$z=factor(xy$z,unique(xy$z))

cand=c(sapply(c(1,2,5),\(x)x*10^c(-10:10)))
ymax=max(xy$y,na.rm=T);ymin=min(xy$y,na.rm=T)
ystep=cand[which.min(abs(cand-(ymax-ymin)/6))]
yend=ystep*ceiling(ymax/ystep)
ystart=ystep*floor(ymin/ystep)
ybreak=seq(ystart,yend,ystep)

xstart=as.Date("1999-1-1");xend=as.Date("2024-1-1")
xbreak=seq(xstart,xend,"6 month")
xlab=c(rbind("",seq(1999,2023)),"")

color=c("black",hcl(210,60,60),hcl(260,100,40))

kim=\(x)ifelse(x>=1e3,ifelse(x>=1e6,paste0(x/1e6,"M"),paste0(x/1e3,"k")),x)

ggplot(xy,aes(x,y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray93",linewidth=.25,lineend="square")+
geom_vline(xintercept=as.Date(paste0(c(2013,2018,2020),"-1-1")),color="gray50",linetype=2,linewidth=.25,lineend="square")+
geom_hline(yintercept=c(ystart,0,yend),color="black",linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),color="black",linewidth=.25,lineend="square")+
geom_line(aes(y=y,linetype=z,color=z,alpha=z,linewidth=z))+
labs(title=stringr::str_wrap("CDC WONDER: Monthly deaths with underlying cause O00-O99 (Pregnancy, childbirth and the puerperium)",70),x=NULL,y=NULL)+
coord_cartesian(clip="off",expand=F)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color[c(1,2,3,2,3)])+
scale_linetype_manual(values=c(1,2,2,1,1))+
scale_linewidth_manual(values=c(.3,.3,.3,.23,.23))+
scale_alpha_manual(values=c(1,1,1,.6,.6))+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length=unit(.2,"lines"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.just="left",
  legend.key=element_rect(fill="white"),
  legend.spacing.x=unit(.15,"lines"),
  legend.key.size=unit(.65,"lines"),
  legend.key.width=unit(.8,"lines"),
  legend.position=c(0,1),
  legend.justification=c(0,1),
  legend.box.background=element_rect(fill="white",color="black",linewidth=.3),
  legend.margin=margin(-.2,.3,.2,.3,"lines"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_rect(fill="white"),
  plot.margin=margin(.4,.4,.4,.4,"lines"),
  plot.title=element_text(size=7.7,margin=margin(.1,0,.6,0,"lines")))
ggsave("1.png",width=4.2,height=2.8,dpi=450)

In the previous plot the biggest spike in deaths was in the third quarter of 2021, so it's probably associated with the Delta wave in August-September 2021. Southeastern states had the highest excess mortality from all causes during the Delta wave, but from plot below which shows excess mortality for causes related to childbirth, you can see that in the third quarter of 2021 the excess mortality was by far the highest in southern states. But in northeastern states which had a high percentage of vaccinated people, the excess mortality in 2021 was by far the lowest:

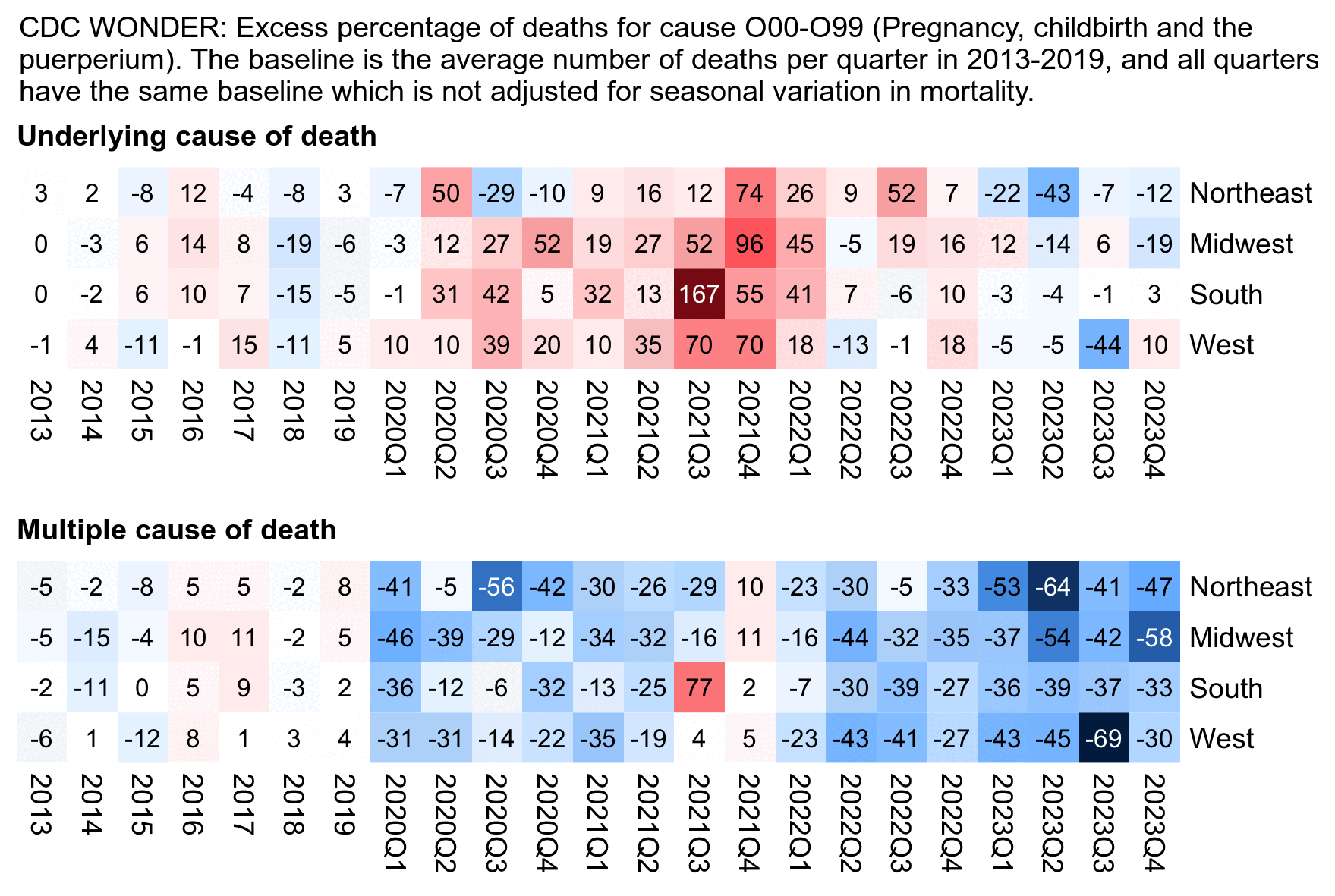
library(colorspace)

t=read.csv("http://sars2.net/f/wonderpregnancyregionquarter.csv")
y=read.csv("http://sars2.net/f/wonderpregnancyregionyearly.csv")|>subset(year%in%2013:2019)

dim=data.frame(cause=y$cause,region=factor(y$region,unique(y$region)),date=y$year)
dim=rbind(dim,data.frame(cause=t$cause,region=t$region,date=paste0(t$year,"Q",t$quarter)))

a=tapply(c(y$dead,t$dead),dim,sum)

for(i in 1:2){
  m=a[i,,]
  m[,1:7]=m[,1:7]/4
  ave=rowMeans(m[,1:7])
  disp=round((m/ave-1)*100)
  m=(m-ave)/ifelse(m>ave,ave,m)

  maxcolor=2
  pal=hex(HSV(c(210,210,210,210,0,0,0,0,0),c(1,.8,.6,.3,0,.3,.6,.8,1),c(.3,.65,1,1,1,1,1,.65,.3)))

  pheatmap::pheatmap(m,filename=paste0("i",i,".png"),display_numbers=disp,
    cluster_rows=F,cluster_cols=F,legend=F,cellwidth=18,cellheight=18,fontsize=9,fontsize_number=8,
    border_color=NA,na_col="gray90",
    number_color=ifelse(abs(m)>maxcolor*.6,"white","black"),
    breaks=seq(-maxcolor,maxcolor,,256),
    colorRampPalette(pal)(256))
}

system("f=i1.png;w=`identify -format %w $f`;convert -interline-spacing -2 -gravity northwest -font Arial -pointsize 38 -size $[w-44]x \\( -splice 22x14 caption:'CDC WONDER: Excess percentage of deaths for cause O00-O99 (Pregnancy, childbirth and the puerperium). The baseline is the average number of deaths per quarter in 2013-2019, and all quarters have the same baseline which is not adjusted for seasonal variation in mortality.' \\) -pointsize 38 -font Arial-Bold \\( -splice 22x14 caption:'Underlying cause of death' \\) i1.png \\( -splice 22x14 caption:'Multiple cause of death' \\) i2.png -append 1.png")

If you look at the bottom half of the plot above which shows excess MCD deaths, for some reason the excess MCD deaths remained far below zero for most of 2020-2023. I don't know why, but there might have been some change to coding practices. I don't think I made any error in my plot either, because I got the similar results when I looked at yearly data in the whole US, where 2018 and 2019 had a much higher number of MCD deaths than 2020:

The plot below shows that in the southern states which had a high number of pregnancy-associated deaths in the third quarter of 2021, deaths with UCD COVID also accounted for a large percentage of all deaths in ages 15-44 in the third quarter of 2021. I included both sexes in the plot, because females alone would've had some months with less than 10 deaths per census region so the number of deaths would've been suppressed:

The plot below also shows that in the third quarter of 2021, the percentage of vaccinated people was the highest in the northeastern states which had a low percentage of excess deaths associated with pregnancy, but the percentage of vaccinated people was much lower in the southern states which had a high percentage of excess deaths associated with pregnancy (R code). So if the deaths were caused by the vaccines, then why wasn't there a higher percentage of excess deaths in the states where more people were vaccinated?

In Ethical Skeptic's plot for deaths associated with childbirth, there was a steady decrease in excess deaths in 2022 and 2023, but I think it's because he fitted his baseline using only data from 2018 and 2019 so the slope of his baseline was pointed too much upwards. He speculated that the decrease in excess deaths could've been because vaccines had caused a decrease in birth rate instead, but I don't think he's right, because in my next plot which shows the monthly number of births at CDC WONDER, the excess percentage of births relative to the prepandemic trend was about -3% in 2020 and 0% in 2021, but in 2022 and 2023 the number of births was actually above the trend:

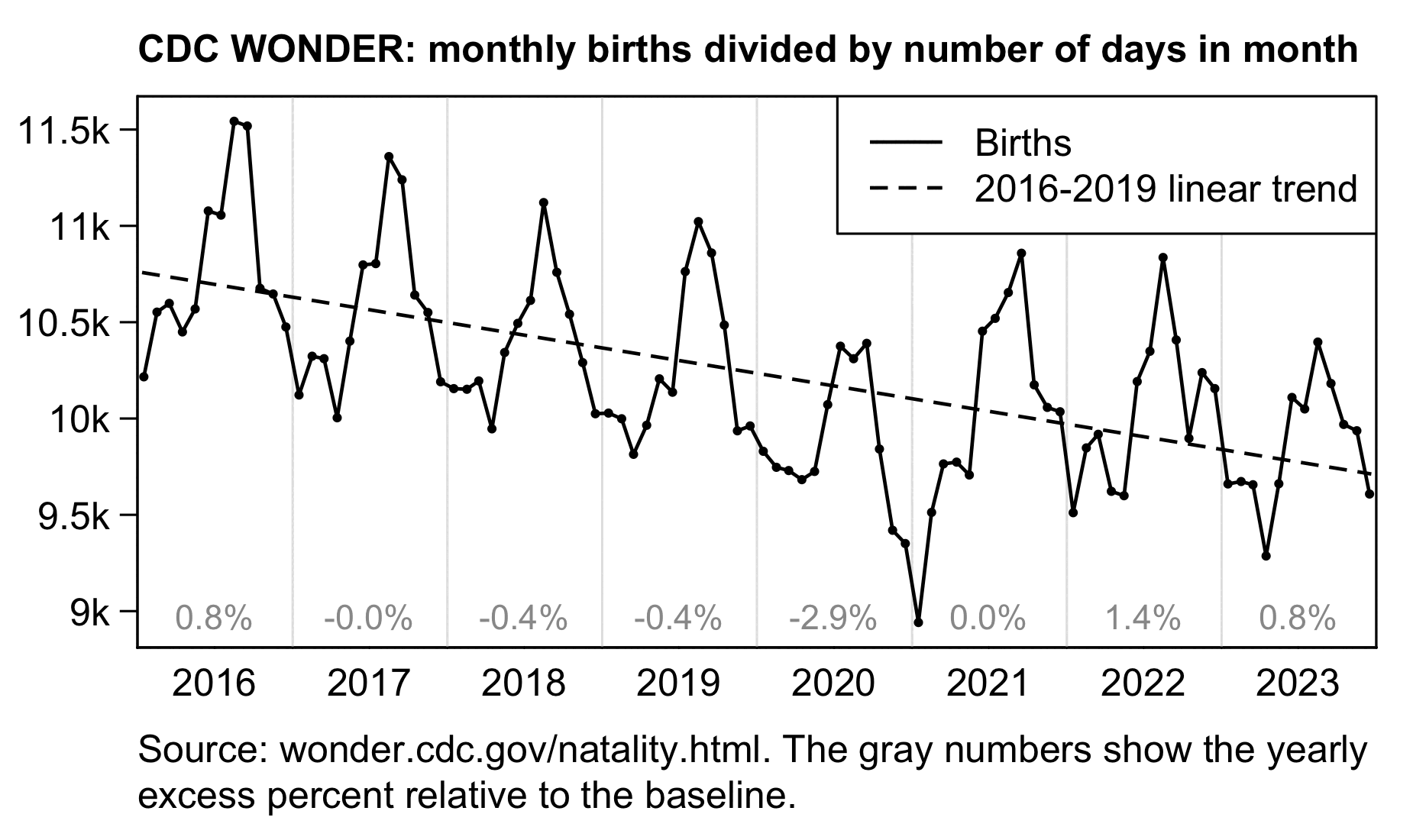
t=read.csv("http://sars2.net/f/wondernatality.csv")
t$date=as.Date(paste0(t$year,"-",t$month,"-16"))
t$born=t$born/lubridate::days_in_month(t$date)

xstart=as.Date("2016-1-1");xend=as.Date("2024-1-1")
xbreak=seq(xstart,xend,"6 month")
xlab=c(rbind(NA,2016:2023),NA)
t=t[t$date>=xstart&t$date<xend,]
ylim=extendrange(c(t$born,t$trend))
ybreak=pretty(range(t$born))

t$trend=predict(lm(born~date,subset(t,date>=xstart&date<as.Date("2020-1-1"))),t)

yearly=aggregate(t[,c("born","trend")],t[,1,drop=F],sum)
yearly=sprintf("%.1f%%",(yearly$born/yearly$trend-1)*100)

png("1.png",1850,1100,res=300)
par(mar=c(4.2,3,2.1,.8),mgp=c(0,.6,0),adj=0,lend="square")

tit="CDC WONDER: monthly births divided by number of days in month"
sub="Source: wonder.cdc.gov/natality.html. The gray numbers show the yearly
excess percent relative to the baseline."
leg=c("Births per month","2016-2019 linear trend")

plot(t$date,t$born,type="n",main=tit,xlab=NA,ylab=NA,xaxs="i",yaxs="i",yaxt="n",xaxt="n",ylim=ylim,xlim=c(xstart,xend),cex.main=1)
mtext(text=sub,side=1,line=2.7,adj=0)

axis(1,at=xbreak,labels=xlab,tck=0,padj=-.6)
axis(2,at=ybreak,labels=paste0(ybreak/1e3,"k"),las=1)
abline(v=seq(xstart,xend,"year"),col="gray90",lwd=1)

lines(t$date,t$born,lwd=1.5)
points(t$date,t$born,pch=20,cex=.6)
lines(t$date,t$trend,type="l",lty=2,lwd=1.5)
text(xbreak[c(F,T)],ylim[1],yearly,col="gray60",hjust=.5,offset=.4,pos=3,cex=.9)
rect(xstart,ylim[1],xend,ylim[2],lwd=1)
legend("topright",legend=leg,lty=c(1,2),lwd=1.5)

dev.off()

SV40 cancer wave plot for cancer ASMR since 1950s

Ethical Skeptic posted this tweet: [https://x.com/EthicalSkeptic/status/1803267649385668791]

I've taken a look at the cancer long term Age Standardized Per Capita stats, aannd....

SV40 cancers only took 50 years to work their way out of the population. Just a blip on an epochal chart really.

Just a minor spike the last 3 years as well. Nothing to worry about.

Really. Honestly. For sure... 🤥

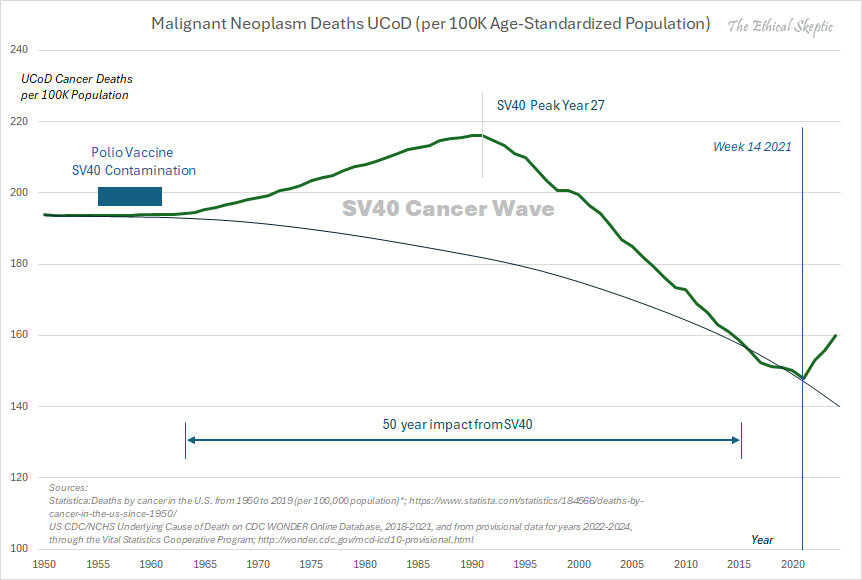
In the plot above Ethical Skeptic seems to have taken data for 2018 onwards from CDC WONDER but data from 1950 to 2017 from a dataset at Statista.com. The dataset at Statista.com was behind a paywall so I wasn't able to download it, but the description of the dataset said: "This statistic was assembled from several editions of 'Health, United States'. [...] Numbers are for malignant neoplasms. All rates are age-adjusted. Age-adjusted rates are calculated using the year 2000 standard population." [https://web.archive.org/web/20240822233635/https:/www.statista.com/statistics/184566/deaths-by-cancer-in-the-us-since-1950/] In June 2024 a new version of the dataset was released, where the description was changed to simply say that "Figures prior to 2000 were taken from this CDC release." [https://www.statista.com/statistics/184566/deaths-by-cancer-in-the-us-since-1950/] The link went to the same "Health, United States" dataset that was mentioned in the description earlier, but it only seemed to have yearly data from 1980s onwards but decade-level data for the 50s, 60s, and 70s. However I don't know if older versions of the dataset also had yearly data for the first three decades.

In Ethical Skeptic's plot the ASMR was the lowest in 2021, but the ASMR increased from 2021 to 2022, from 2022 to 2023, and from 2023 to 2024. However in the plot below where I used data from CDC WONDER, I wasn't able to reproduce the increase in ASMR after 2021, because got lower ASMR in 2022 and 2023 than 2021 regardless of whether I looked at only malignant neoplasms or all neoplasms:

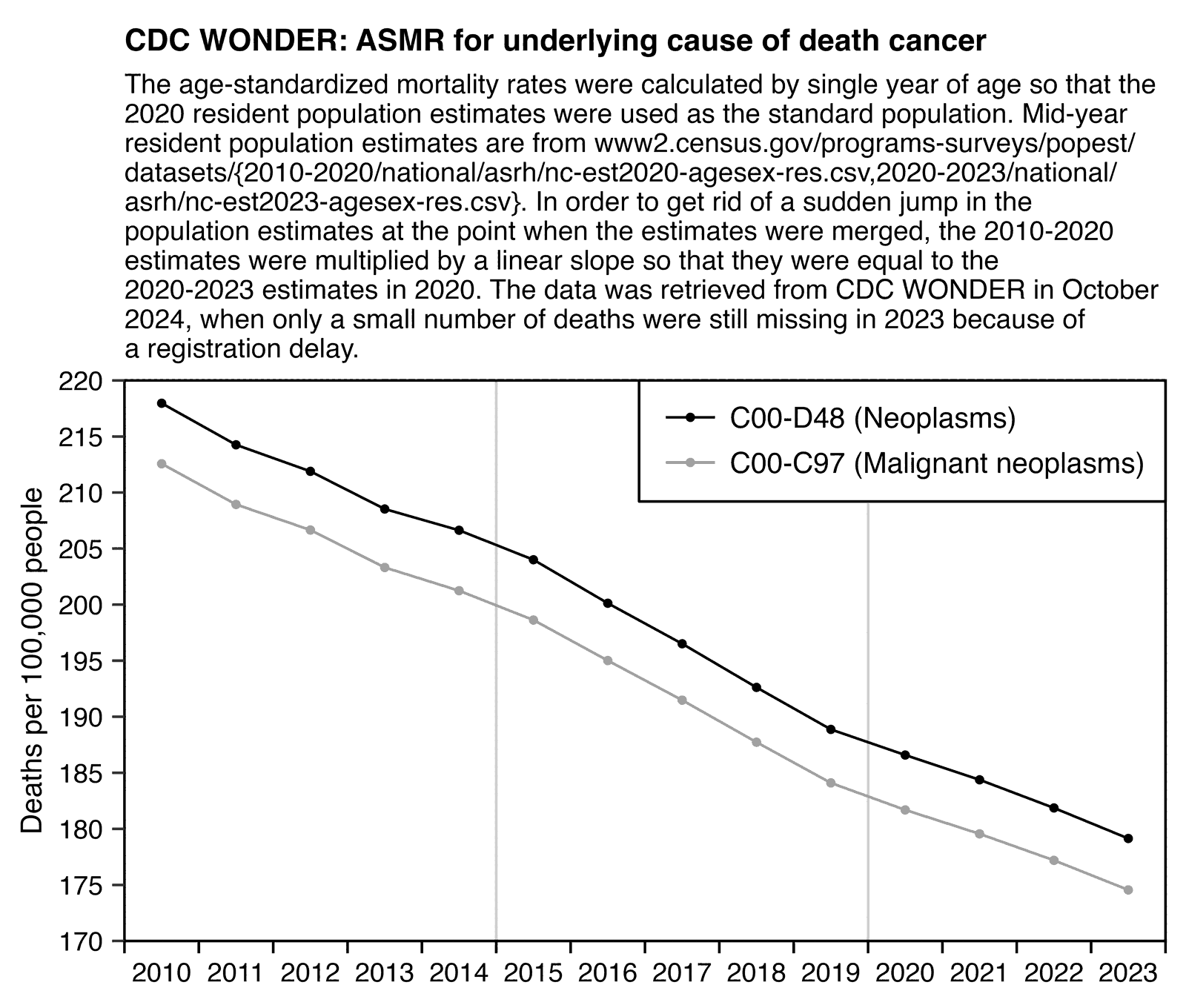
library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wondercanceryearly.csv")[,cause:=sub("^UCD ","",cause)]
pop=fread("http://sars2.net/f/uspopdead.csv")[,dead:=NULL]
t=merge(t,pop)
t=merge(pop[year==2020,.(age,std=pop/sum(pop))],t)

p=t[year%in%2010:2023,.(asmr=sum(dead/pop*std)*1e5),.(cause,year)]
p[,cause:=factor(cause,sort(unique(p$cause),T))]

cand=c(sapply(c(1,2,5),\(x)x*10^c(-10:10)))
ymin=min0(p$asmr);ymax=max0(p$asmr)
ystep=cand[which.min(abs(cand-(ymax-ymin)/6))]
ystart=ystep*floor(ymin/ystep)
yend=ystep*ceiling(ymax/ystep)
ybreak=seq(ystart,yend,ystep)

xstart=2010;xend=2023
xbreak=seq(xstart-.5,xend+.5,.5)
xlab=c(rbind("",xstart:xend),"")

sub="The age-standardized mortality rates were calculated by single year of age so that the
2020 resident population estimates were used as the standard population. Mid-year
resident population estimates are from www2.census.gov/programs-surveys/popest/
datasets/{2010-2020/national/asrh/nc-est2020-agesex-res.csv,2020-2023/national/
asrh/nc-est2023-agesex-res.csv}. In order to get rid of a sudden jump in the
population estimates at the point when the estimates were merged, the 2010-2020
estimates were multiplied by a linear slope so that they were equal to the
2020-2023 estimates in 2020. The data was retrieved from CDC WONDER in October
2024, when only a small number of deaths were still missing in 2023 because of
a registration delay."

ggplot(p,aes(x=year,y=asmr,color=cause))+
geom_vline(xintercept=seq(xstart-.5,xend+.5,5),linewidth=.3,color="gray80")+
geom_vline(xintercept=c(xstart-.5,xend+.5),linewidth=.3,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.3,lineend="square")+
geom_line(linewidth=.3)+
geom_point(size=.4)+
labs(x=NULL,y="Deaths per 100,000 people",title="CDC WONDER: ASMR for underlying cause of death cancer",subtitle=sub)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black","gray60"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=6.5,color="black"),
  axis.ticks=element_line(linewidth=.3),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.ticks.length=unit(3,"pt"),
  axis.title=element_text(size=7),
  legend.background=element_blank(),
  legend.box.background=element_rect(fill="white",color="black",linewidth=.3),
  legend.box.just="left",
  legend.justification=c(1,1),
  legend.key.width=unit(15,"pt"),
  legend.key.height=unit(11,"pt"),
  legend.key=element_rect(fill=alpha("white",0)),
  legend.margin=margin(-2,5,4,5),
  legend.position=c(1,1),
  legend.spacing.x=unit(.15,"lines"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=6.6,margin=margin(,,4)),
  plot.title=element_text(size=7.4,face=2,margin=margin(2,,4)))
ggsave("1.png",width=4,height=3.4,dpi=400*4)
system("magick 1.png -resize 25% 1.png")

In the plot above I used population estimates that I downloaded from the website of the US Census Bureau, because CDC WONDER doesn't return population estimates for ages 85 and above and it still uses 2022 population estimates for 2023. I used vintage 2023 estimates for 2020-2023 and vintage 2020 estimates for 2010-2019.

In the next plot I used population estimates returned by CDC WONDER and I calculated ASMR by 10-year age groups and not by single year of age. CDC WONDER doesn't return population sizes for the oldest age groups when the results are grouped by 5-year age groups or by single year of age, but when the results are grouped by 10-year age groups then the oldest age group is 85+ which does have population sizes available. So therefore Ethical Skeptic might have calculated the ASMR by 10-year age groups in case he simply relied on the population sizes returned by CDC WONDER.

As of October 2024, CDC WONDER still used 2022 population estimates for 2023. It results in the CMR of elderly age groups being overestimated in 2023, because the population sizes of elderly age groups were higher in 2023 than 2022, and therefore it also results in the total ASMR being overestimated in 2023.

However even when I used the population sizes returned by CDC WONDER, I still wasn't able to reproduce the plot by Ethical Skeptic, because I got lower ASMR in 2022 and 2023 than 2021 regardless of whether I looked at UCD malignant neoplasms or UCD neoplasms:

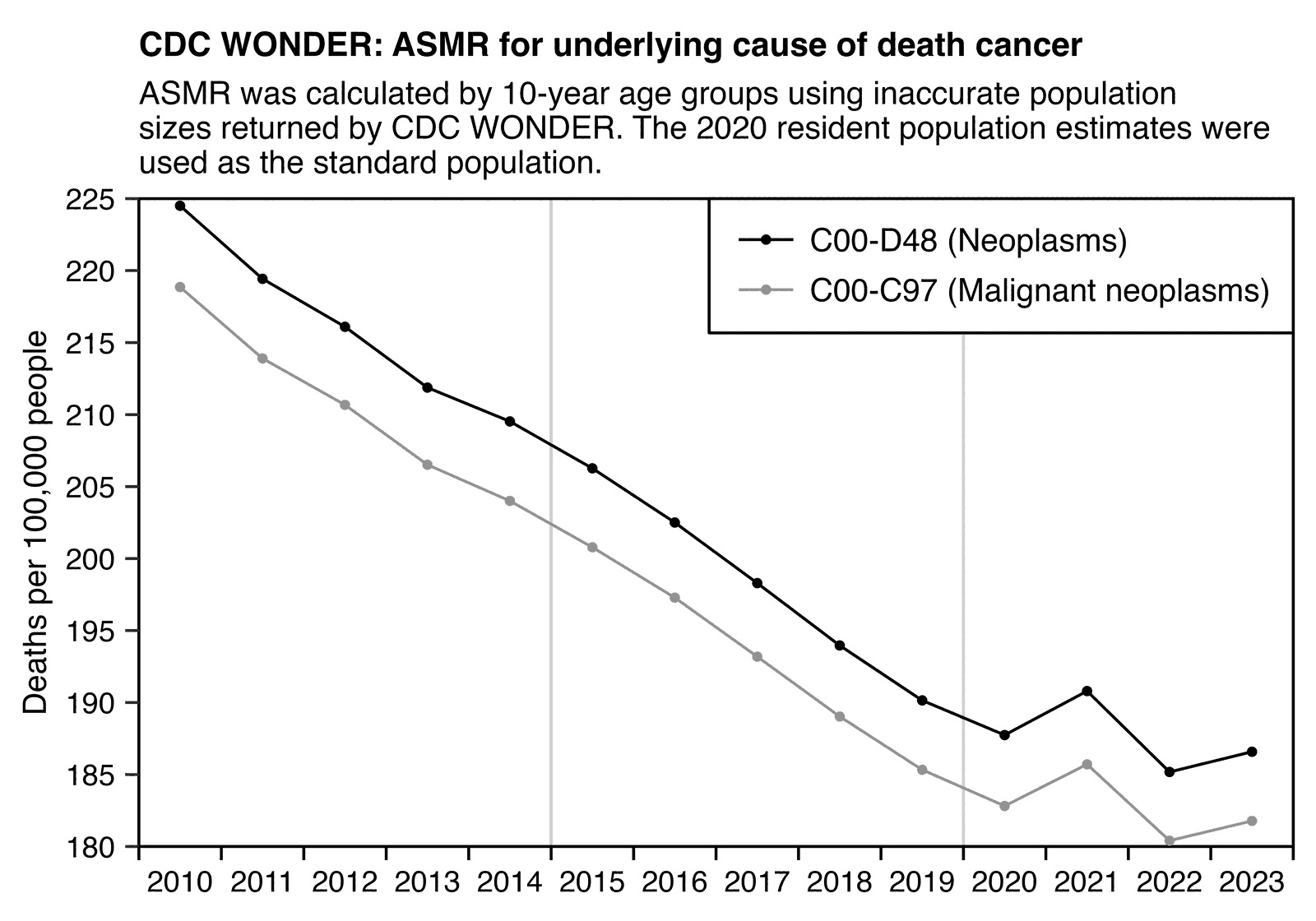
library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wondercanceryearlyten.csv")

t=merge(t,t[year==2020&cause==cause[1],.(age,std=pop/sum(pop))])

p=t[year%in%2010:2023,.(asmr=sum(dead/pop*std)*1e5),.(cause,year)]
p[,cause:=factor(cause,sort(unique(p$cause),T))]

cand=c(sapply(c(1,2,5),\(x)x*10^c(-10:10)))
ymin=min0(p$asmr);ymax=max0(p$asmr)
ystep=cand[which.min(abs(cand-(ymax-ymin)/6))]
ystart=ystep*floor(ymin/ystep)
yend=ystep*ceiling(ymax/ystep)
ybreak=seq(ystart,yend,ystep)

xstart=2010;xend=2023
xbreak=seq(xstart-.5,xend+.5,.5)
xlab=c(rbind("",xstart:xend),"")

ggplot(p,aes(x=year,y=asmr,color=cause))+
geom_vline(xintercept=seq(xstart-.5,xend+.5,5),linewidth=.3,color="gray80")+
geom_vline(xintercept=c(xstart-.5,xend+.5),linewidth=.3,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.3,lineend="square")+
geom_line(linewidth=.3)+
geom_point(size=.4)+
labs(x=NULL,y="Deaths per 100,000 people",title="CDC WONDER: ASMR for underlying cause of death cancer",subtitle="ASMR was calculated by 10-year age groups using inaccurate population sizes returned by CDC WONDER."|>stringr::str_wrap(82))+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("black","gray60"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=6.5,color="black"),
  axis.ticks=element_line(linewidth=.3),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.ticks.length=unit(3,"pt"),
  axis.title=element_text(size=7),
  legend.background=element_blank(),
  legend.box.background=element_rect(fill="white",color="black",linewidth=.3),
  legend.box.just="left",
  legend.justification=c(1,1),
  legend.key.width=unit(15,"pt"),
  legend.key.height=unit(11,"pt"),
  legend.key=element_rect(fill=alpha("white",0)),
  legend.margin=margin(-2,5,4,5),
  legend.position=c(1,1),
  legend.spacing.x=unit(.15,"lines"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=7,margin=margin(,,4)),
  plot.title=element_text(size=7.3,face=2,margin=margin(2,,4)))
ggsave("1.png",width=4,height=2.8,dpi=400*4)
system("magick 1.png -resize 25% 1.png")

In the next plot I calculated ASMR using the same year 2000 US standard population that was used in the Statista dataset. [https://seer.cancer.gov/stdpopulations/stdpop.19ages.html] In the yellow line where I calculated ASMR by 10-year age groups and I used the population sizes returned by CDC WONDER, I was now able to reproduce the historical ASMR from 1999 up to 2017 exactly or nearly exactly. But my yellow line started to diverge from Ethical Skeptic's plot from 2018 onwards, so I guess he took data up to 2017 from the Statista dataset but he calculated ASMR from 2018 onwards himself using different methodology. In the red line I used a more accurate way to calculate ASMR by single year of age where I took the population estimates from the website of the US Census Bureau and I adjusted the 2010-based estimates to get rid of the jump after the switch to the 2020-based estimates. But again I got lower ASMR in 2023 than 2021 for both the red and yellow lines, and I was still not able to reproduce the increase in ASMR that Ethical Skeptic got from 2021 onwards:

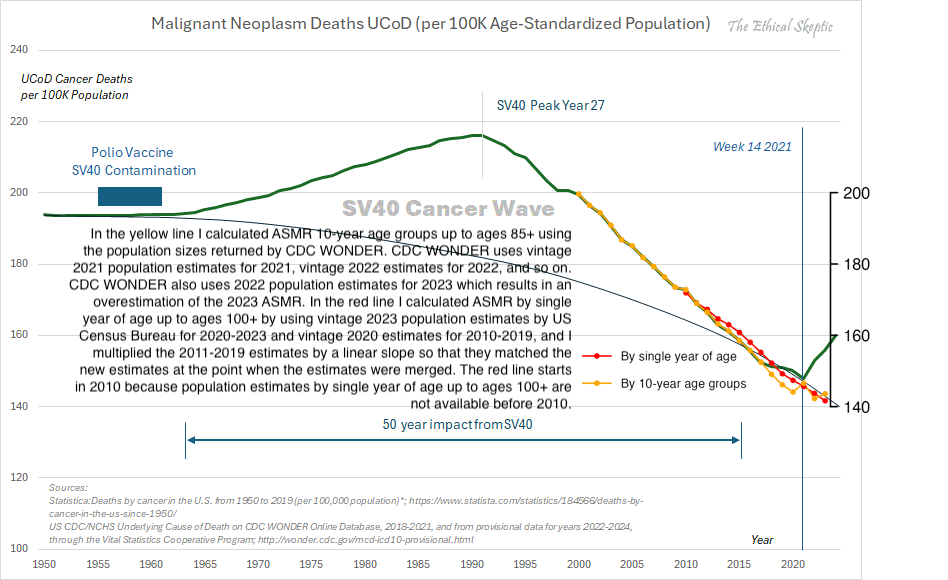
cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]

std=fread("http://sars2.net/f/us2000stdpop.csv")[,.(age,std=std/sum(std))]

t=fread("http://sars2.net/f/wondercanceryearly.csv")[cause%like%"Mali"][,cause:=sub("^UCD ","",cause)]
t=merge(t,fread("http://sars2.net/f/uspopdead.csv")[,dead:=NULL])
t=merge(std,t)
p=t[year%in%2010:2023,.(asmr1=sum(dead/pop*std)*1e5),year]

t2=fread("http://sars2.net/f/wondercanceryearlyten.csv")[cause%like%"Mal"]
t2=merge(t2,std[,.(std=sum(std)),.(age=cul(age,unique(t2$age)))])
merge(p,t2[,.(asmr10=sum(dead/pop*std)*1e5),year],all=T)

In the plot above my yellow line has a fairly large jump up between 2020 and 2021, but it's because CDC WONDER uses population estimates based on the 2010 census for 2020 but population estimates based on the 2020 census for 2021, and the population estimates of elderly age groups were reduced by several percent in the 2020-based population estimates:

t=fread("http://sars2.net/f/wondercanceryearlyten.csv")
t[cause%like%"Mal"&year==2020&age==85,pop]
# 6658420 (population size of ages 85+ in 2020 returned by CDC WONDER)

old=fread("https://www2.census.gov/programs-surveys/popest/datasets/2010-2020/national/asrh/nc-est2020-agesex-res.csv")
old[SEX==0&AGE%in%85:100,sum(POPESTIMATE2020)]
# 6658420 (population estimate based on the 2010 census; same as CDC WONDER)

new=fread("https://www2.census.gov/programs-surveys/popest/datasets/2020-2023/national/asrh/nc-est2023-agesex-res.csv")
new[SEX==0&AGE%in%85:100,sum(POPESTIMATE2020)]
# 6061016 (estimate based on the 2020 census; about 9% lower than the estimate based on the 2010 census)

But anyway, the reason why Ethical Skeptic got the increase in ASMR since 2021 might be if applied some of his usual adjustments to his plot, like his "excess MCD normalization" method where he adds in a gradually increasing proportion of MCD deaths to his plot in addition to UCD deaths. In fact I have only seen him apply the excess MCD normalization method to plots that show deaths with UCD cancer, so it's likely he used it here as well. And he may have also added in deaths that he estimated to be missing because of a registration delay, because he didn't exclude the year 2024 from his plot and he got even higher ASMR in 2024 than 2023. However in his other plots he has only applied excess MCD normalization from week 10 of 2022 onwards, but I was not even able to reproduce his plot in 2018-2021, so I don't know if he also applied some other adjustments to his plot before 2022 or if he just calculated ASMR using different methodology than me. But in either case he should document his methodology better.

In the next plot I simply used ASMR values returned by CDC WONDER instead of calculating ASMR myself, but the values returned by CDC WONDER were the same as the ASMR values I calculated myself in the yellow line in my previous plot, where I used the 2000 US standard population and I used the population sizes by 10-year age groups returned by CDC WONDER. The ASMR values returned by CDC WONDER match Ethical Skeptic's plot from 1995 up to 2017. But from 2018 onwards he seems to have used his own undocumented methodology to calculate ASMR, even though he could've just plotted the ASMR values returned by CDC WONDER to be consistent with the older data (or he could've included one line for the ASMR values returned by CDC WONDER and another line for his own ASMR values):

Ethical Skeptic's plot seems to imply that the SV40 virus would've been the primary determinant of the rise and fall in cancer mortality in the United States since the 1950s. But the plots below show that the increase in cancer mortality up to around 1990 seems to have been mainly driven by lung cancer, because the ASMR of other major types of cancer shown in the plot mostly decreased or remained flat from 1950 to 1990. And a large part of the decrease in cancer ASMR since 1990 seems to also be due to a decrease in lung cancer. So did the SV40 virus disproportionately cause lung cancer as opposed to other types of cancer? [https://www.cancer.org/content/dam/cancer-org/research/cancer-facts-and-statistics/annual-cancer-facts-and-figures/2024/2024-cancer-facts-and-figures-acs.pdf]

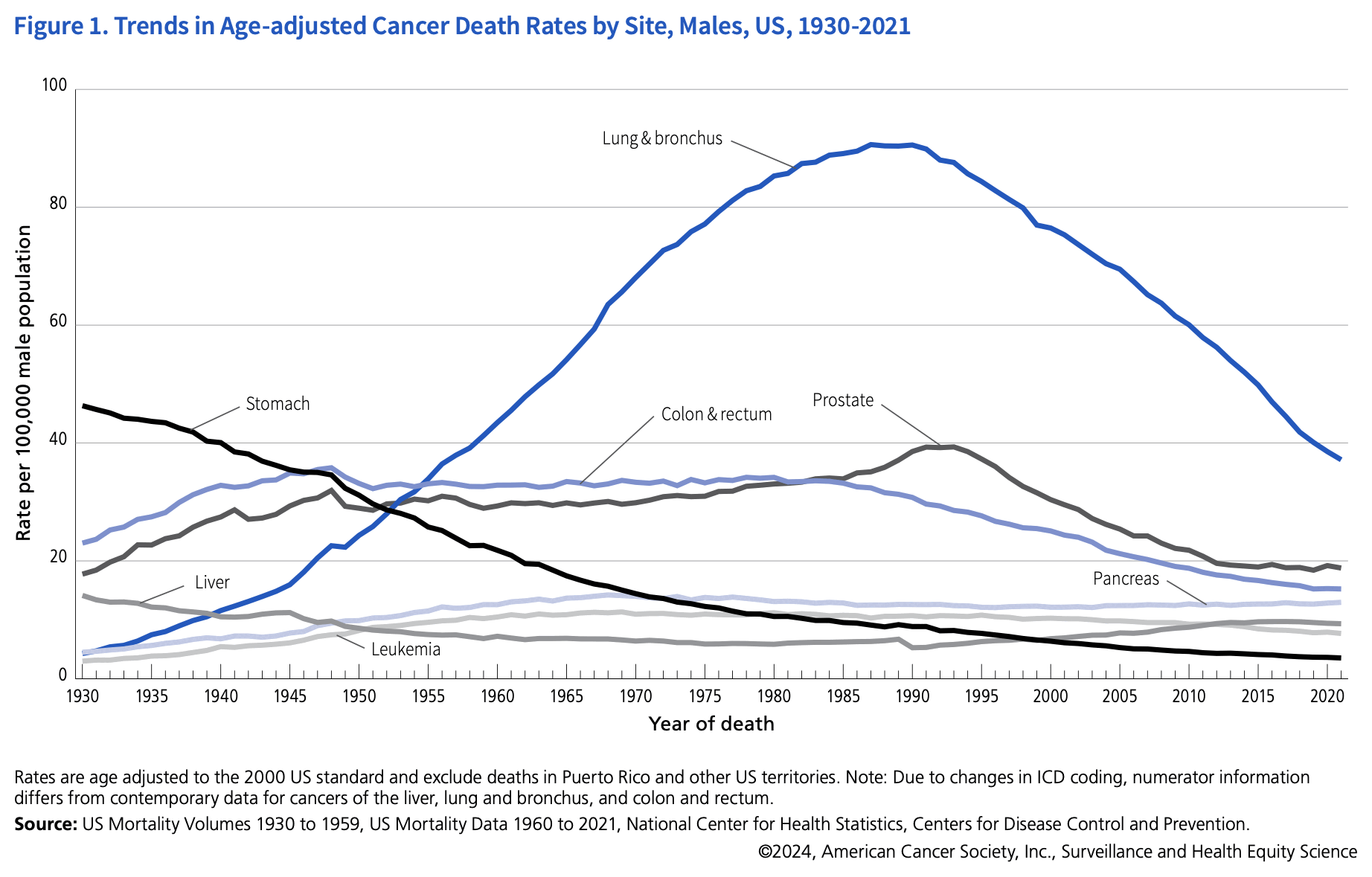
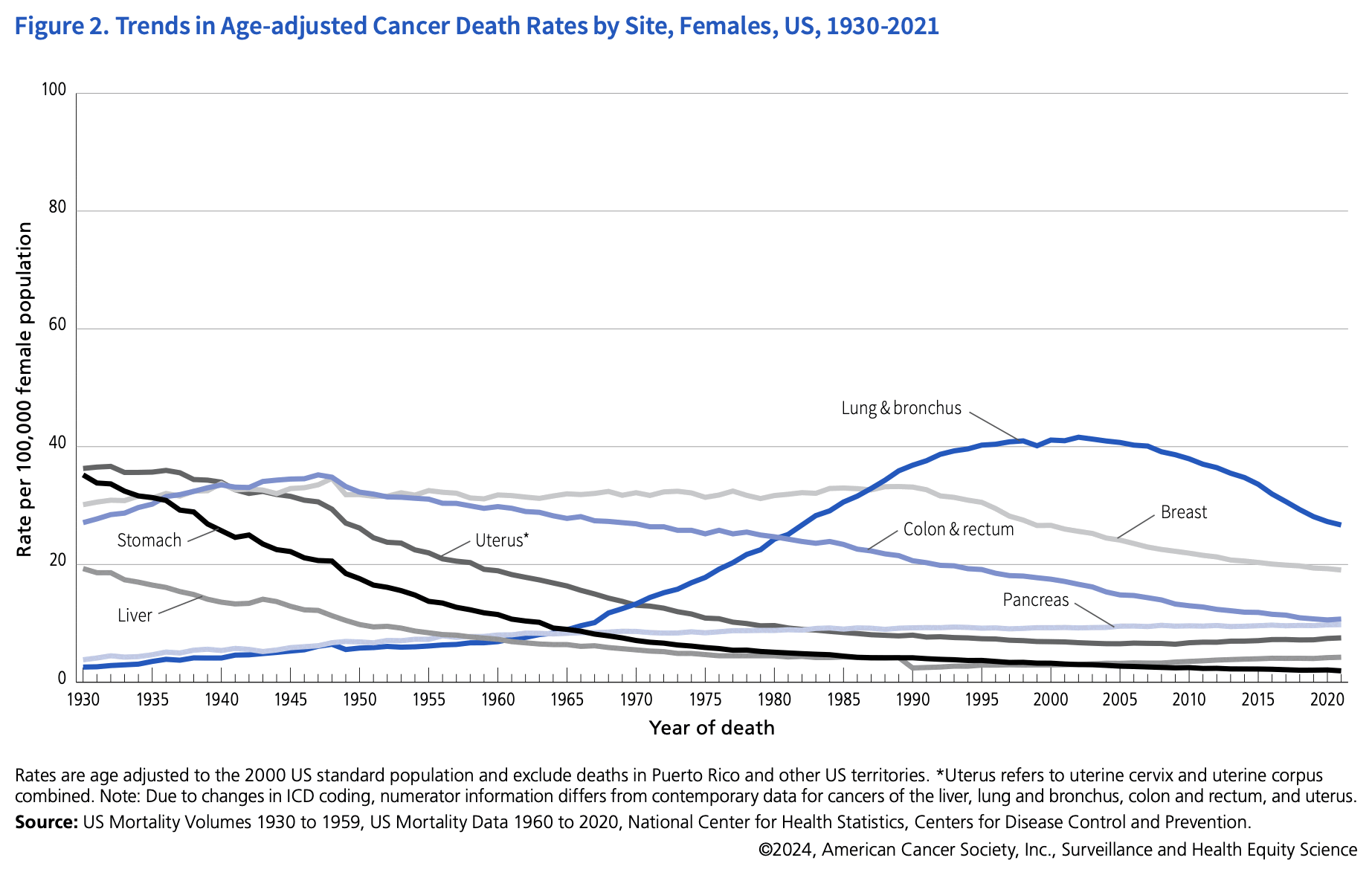
Added in December 2024: Ethical Skeptic's plot started in 1950 but there was a period when ASMR was roughly flat in the 1950s after which it started to climb again in the 1960s, which may have given some people the impression that the increase in the 1960s could be attributed to the SV40-contaminated polio vaccines which were administered between 1955 and 1963. But the plot below by Uncle John Returns shows that if Ethical Skeptic would've extended the x-axis of his plot further to the past, the cancer ASMR would've also climbed each decade in the first half of the 1900s. The plot below also shows that if lung cancer is excluded, the ASMR for all other types of cancer has been going down since 1968 (which is the earliest year with data available at CDC WONDER): [https://x.com/UncleJo46902375/status/1873785579743445037, https://www.cdc.gov/nchs/nvss/mortality/hist293.htm]

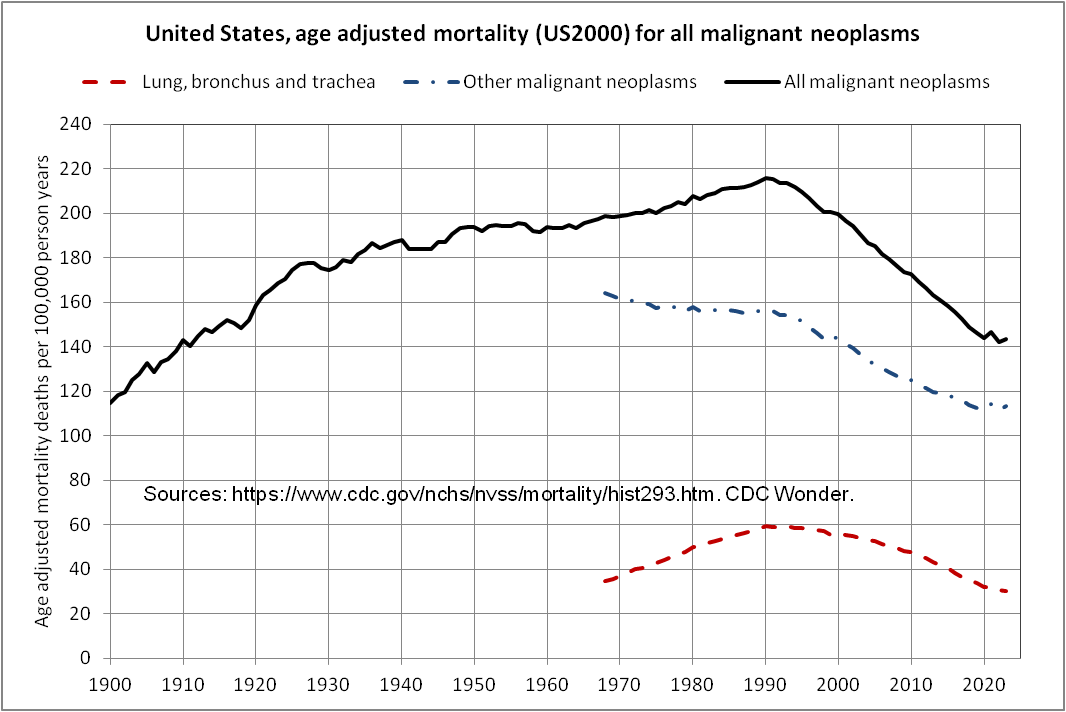
The primary target of the SV40-contaminated vaccines were children up to age 6, but the vaccines were also given to some older children up to age 18 who had not earlier been vaccinated for polio. However even if someone received the vaccinate at age 18 in 1955, they would've been 53 or 54 years old in 1990. Uncle John Returns also made this plot which shows that ages 0-54 had a falling trend in cancer ASMR between 1968 and 1990, but the increase in ASMR was due to ages 55 and above: [ibid.]

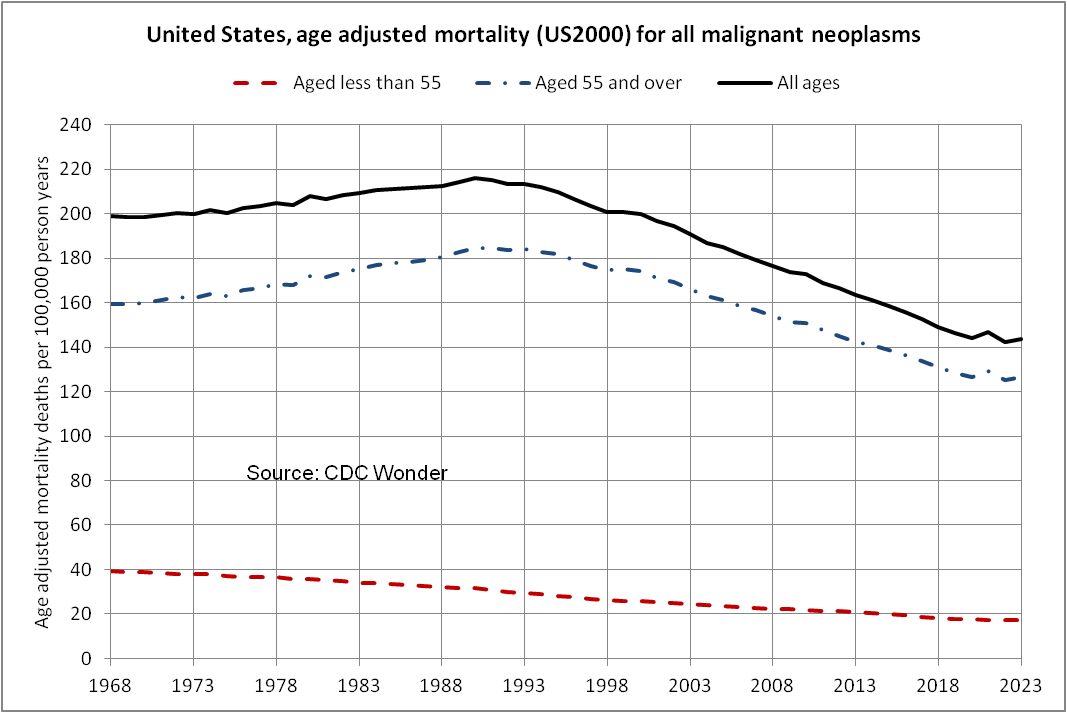
The curve for lung cancer ASMR seems to follow the curve for cigarette consumption with a lag of about 20 years: [https://nap.nationalacademies.org/read/11795/chapter/4]

So in summary here's my overall conclusion about Ethical Skeptic's plot, adapted from the lady detective:

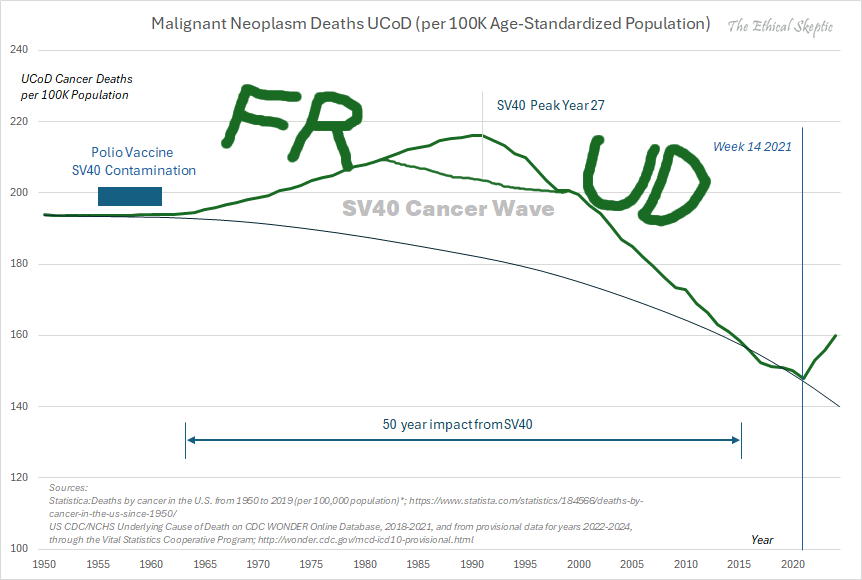
Added in May 2025: When the Salk polio vaccine was introduced in the UK in 1956, it was initially offered to children aged 2 to 9, the next year the target group was expanded to children up to age 15 years old, and in 1960 the UK Ministry of Health launched a campaign which encouraged all people under the age of 40 to get a polio vaccine. People who were under the age of 40 in 1960 were born in 1920 or earlier, even though some healthcare workers or pregnant mothers born before 1920 may have additionally been offered the Salk polio vaccine. [https://api.parliament.uk/historic-hansard/commons/1960/mar/30/poliomyelitis-vaccination] Uncle John Returns made these plots of cancer mortality in England and Wales that show when people born in 1920 would enter an age band: [https://x.com/UncleJo46902375/status/1923019534606180477]

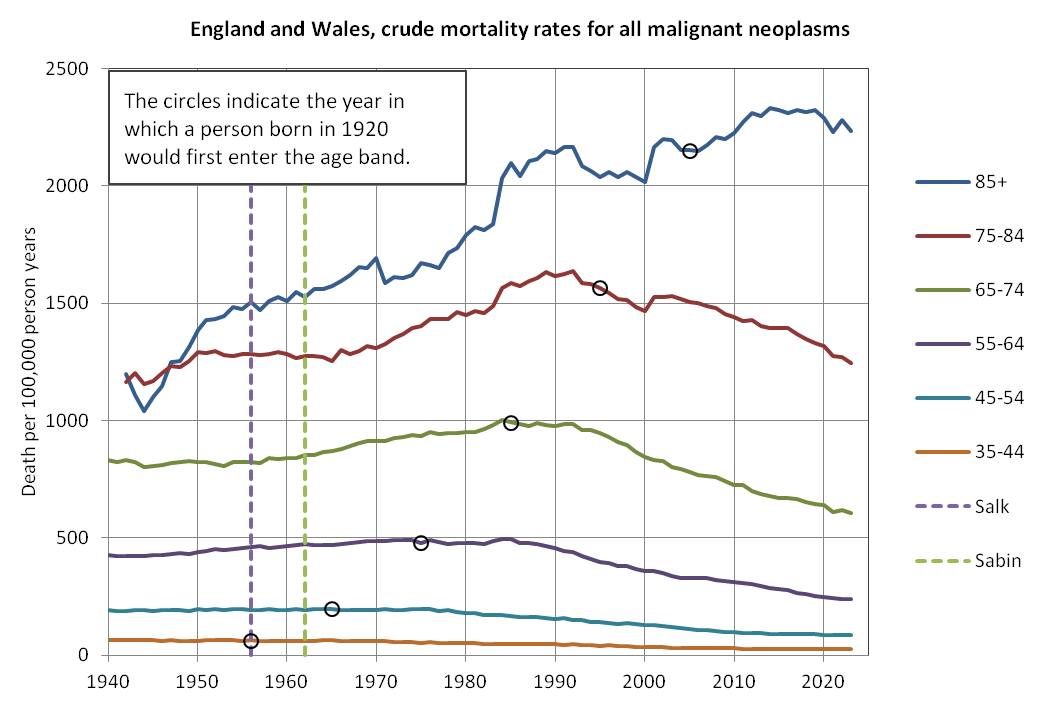
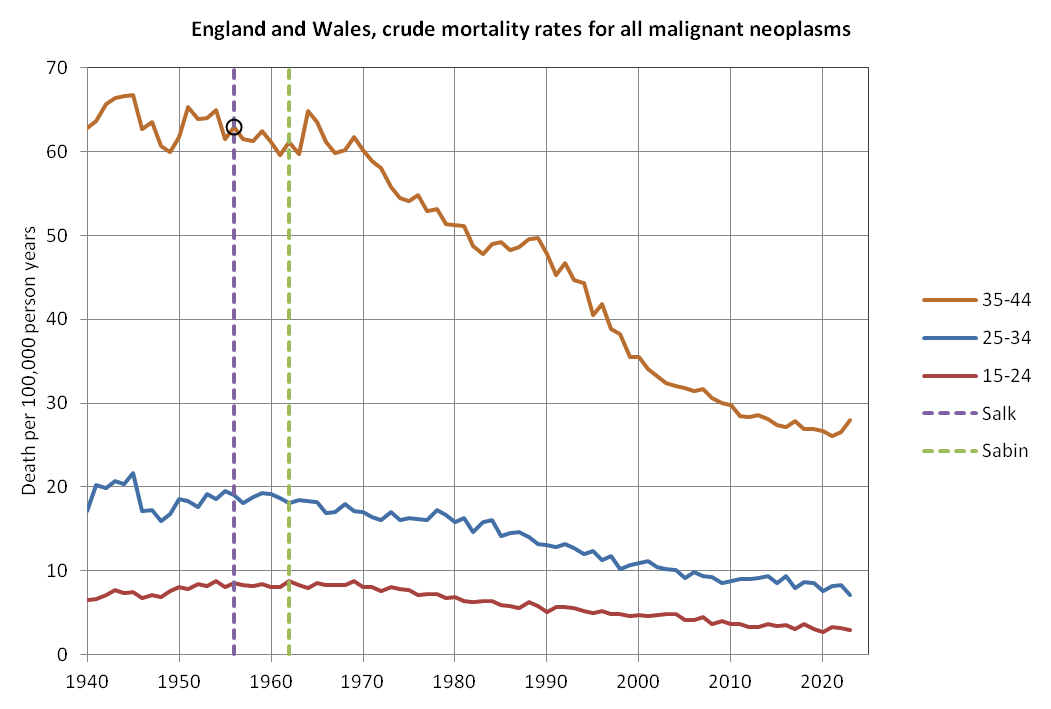
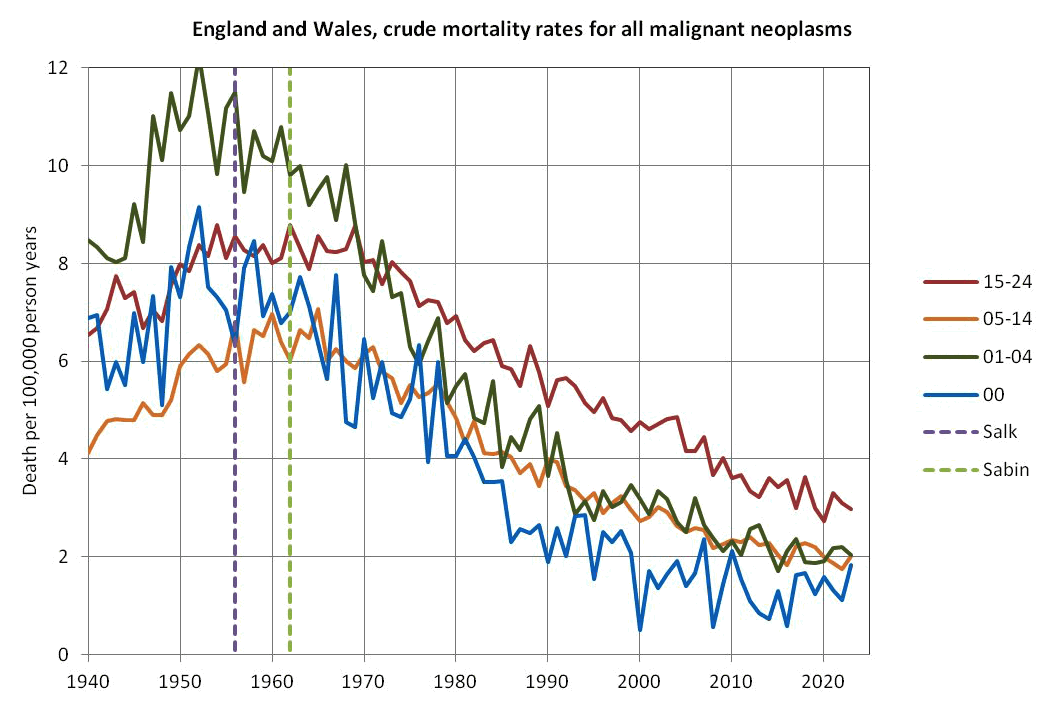
Added in May 2025: Ethical Skeptic has now modified this SV40 cancer wave plot so that he gets the lowest ASMR in 2020 and not in 2021 like earlier. [https://x.com/EthicalSkeptic/status/1927846174423208136] But I haven't seen him explain how he changed his methodology:

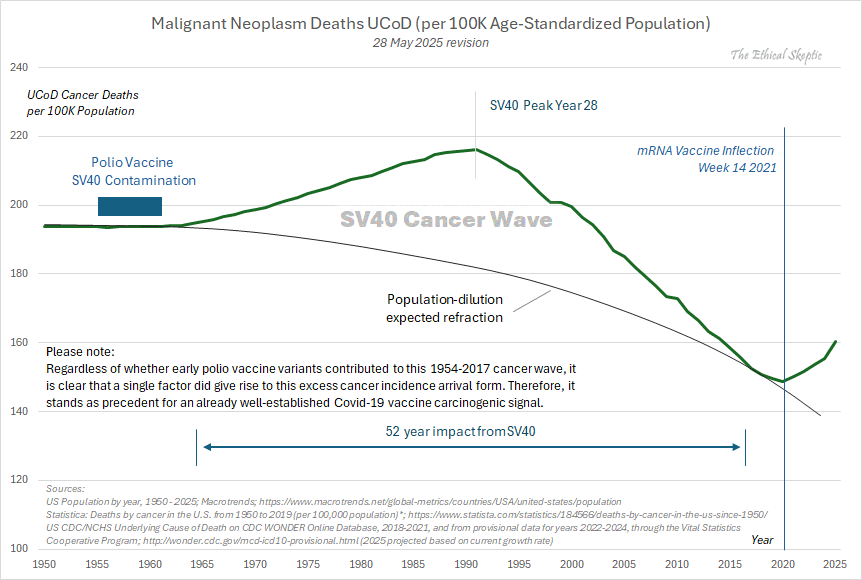
Previously his line for week 14 of 2021 intersected with the point for the year 2021, but now the line is placed slightly after the point for the year 2020. So maybe he meant to draw the line after the point for the year 2021, but he didn't realize that in the new version of his plot the lowest ASMR was now in the year 2020 and not 2021.

There's no sharp turn upwards in cancer ASMR around 2021 in other countries either: [https://x.com/UncleJo46902375/status/1976698264310497778, https://sdb.socialstyrelsen.se/if_dor]

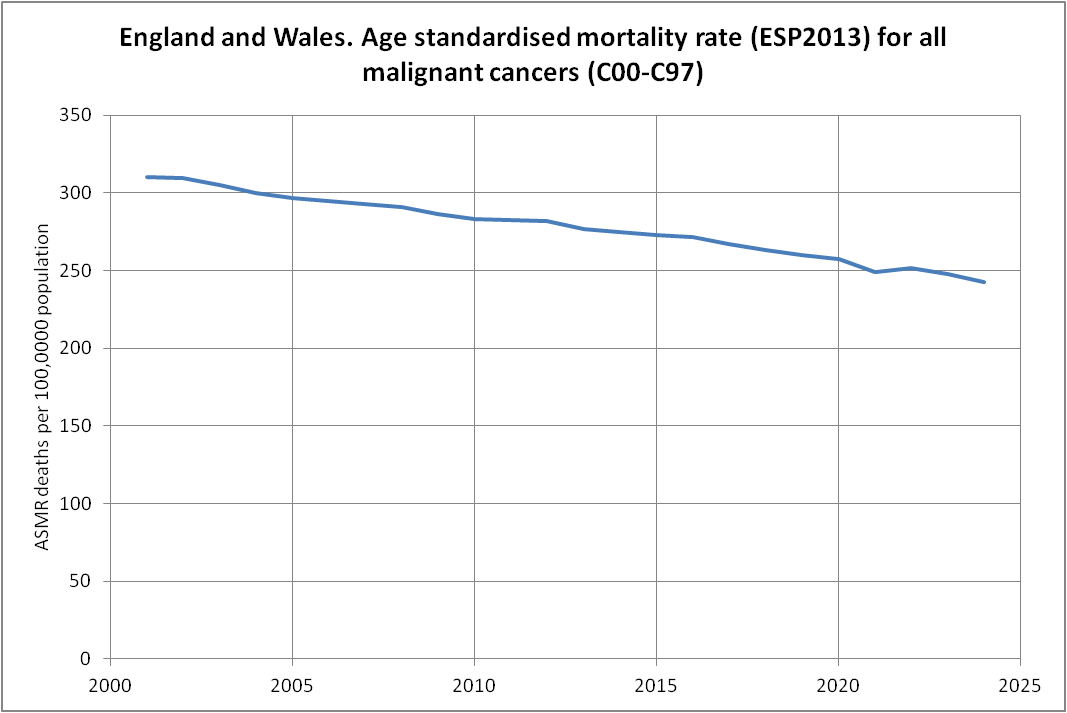
Baseline that started from the 1970s for CMR in New Zealand

One of the terms invented by Ethical Skeptic is a "paltered" baseline, which means that 2020 or later years are included in the fitting period of a baseline. The baseline that OWID uses to calculate excess deaths is fitted against data from 2015 to 2019. [https://ourworldindata.org/excess-mortality-covid#how-is-excess-mortality-measured] However for some reason in this tweet Ethical Skeptic said that the baseline used by OWID was "paltered" even though it doesn't fit his usual definition of what the term paltered means: [https://x.com/EthicalSkeptic/status/1720267405883027598]

The y-axis of Ethical Skeptic's plot says "deaths per 1000 people" but the values on the y-axis are over 6,000, so I don't know if it's supposed to mean deaths per million people.

In the tweet above for some reason Ethical Skeptic calculated CMR for segments of 5 years grouped together. His A baseline roughly looks like it's fitted against the last 5-year segment displayed in the plot. But OWID's baseline is not even calculated based on CMR but based on the raw number of deaths. His plot would've been more clear if it would've showed the CMR for each individual year and not for the 5-year blocks, and if he would've calculated the 2015-2019 linear trend in deaths based on the raw number of deaths and then converted it to CMR by dividing it by the population size, so then it would've been closer to the baseline that is actually used by OWID.

I wasn't able to reproduce Ethical Skeptic's plot perfectly, but I think he used a method similar to this to calculate CMR for the 5-year blocks:

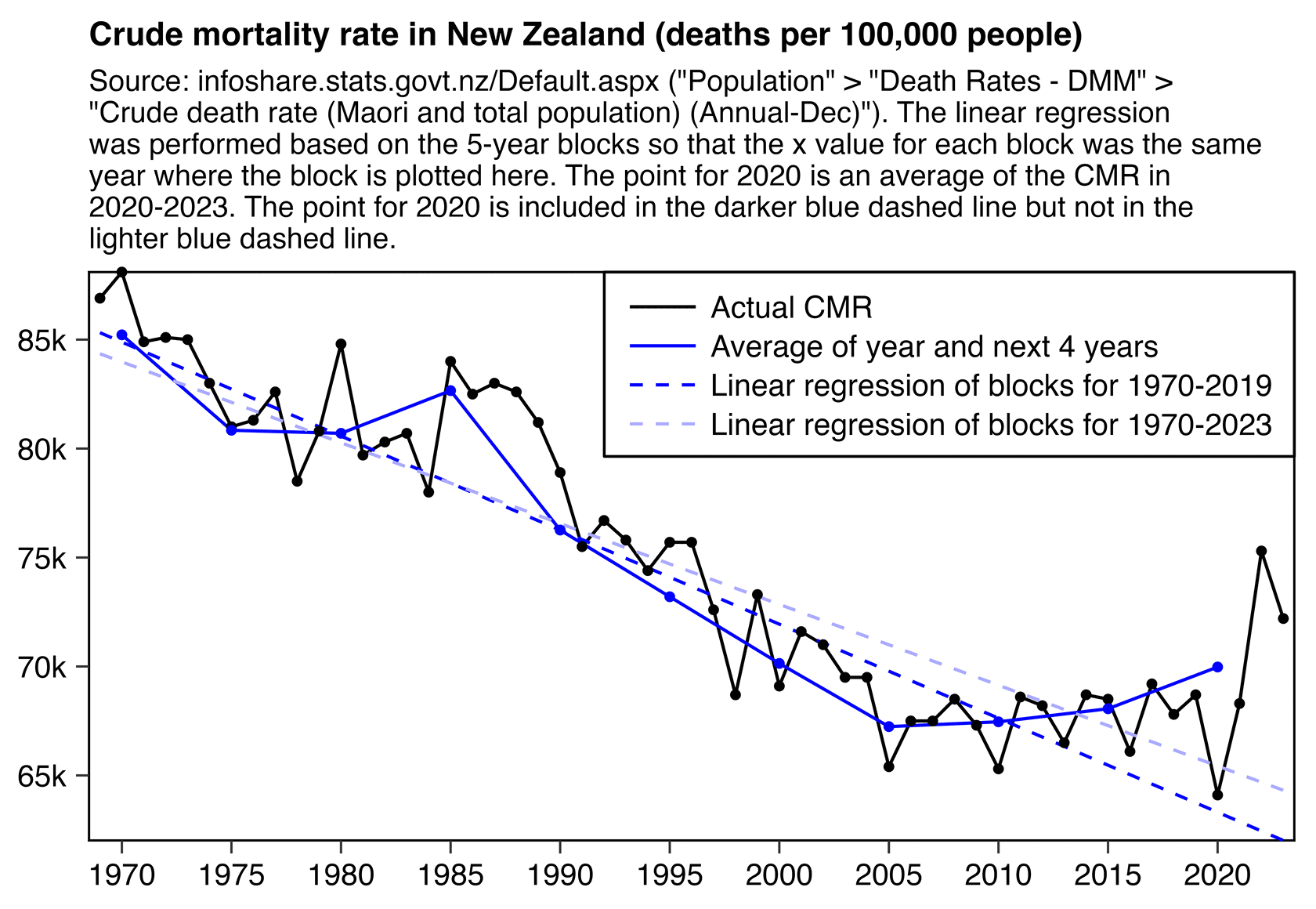
library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/nzcmr.csv")
p=t[,.(x=year,y=cmr,z="Actual CMR")]
v=t[,.(y=mean(cmr),z="Average of year and next 4 years"),.(x=(year)%/%5*5)]
lin1=p[,.(x,y=v[x>=1970,predict(lm(y~x),p)],z="Linear regression of blocks for 1970-2023")]
lin2=p[,.(x,y=v[x>=1970&x<=2015,predict(lm(y~x),p)],z="Linear regression of blocks for 1970-2019")]
p=rbind(p,v,lin1,lin2)
p$y=100*p$y

xstart=1969;xend=2023
p=p[x>=xstart&x<=xend]

ybreak=pretty(p$y);ystart=min(p$y);yend=max(p$y)

color=c("black","blue","#7777ff","#ccccff")

ggplot(p,aes(x,y))+
geom_vline(xintercept=c(xstart-.5,xend+.5),linewidth=.3,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.3,lineend="square")+
geom_line(aes(color=z,linetype=z),linewidth=.4)+
geom_point(data=p[!grep("Linear",z)],aes(color=z),size=.5,show.legend=F)+
labs(title="Crude mortality rate in New Zealand (deaths per 100,000 people)",subtitle=paste0("Source: infoshare.stats.govt.nz/Default.aspx
(\"Population\" > \"Death Rates - DMM\" > \"Crude death rate (Maori and total population) (Annual-Dec)\"). The linear regression was performed based on the 5-year blocks so that the x value for each block was the same year where the block is plotted here. The point for 2020 is an average of the CMR in 2020-2023. The point for 2020 is included in the darker blue dashed line but not in the lighter blue dashed line.")|>stringr::str_wrap(88),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(1900,2100,5))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)ifelse(x>=1e3,paste0(x/1e3,"k"),x))+
scale_color_manual(values=color)+
scale_linetype_manual(values=c(1,1,2,2))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks=element_line(linewidth=.3),
  axis.ticks.length=unit(3,"pt"),
  legend.direction="vertical",
  legend.background=element_rect(fill=alpha("white",.8),color="black",linewidth=.3),
  legend.key.height=unit(9,"pt"),
  legend.key.width=unit(15,"pt"),
  legend.key=element_rect(fill="white"),
  legend.margin=margin(-2,5,3,4),
  legend.justification=c(1,1),
  legend.position=c(1,1),
  legend.spacing.x=unit(1.5,"pt"),
  legend.text=element_text(size=7),
  legend.title=element_blank(),
  panel.grid.major=element_blank(),
  panel.background=element_rect(fill="white"),
  plot.margin=margin(3,5,4,4),
  plot.subtitle=element_text(size=6.7,margin=margin(0,0,4,0)),
  plot.title=element_text(size=7.5,face="bold",margin=margin(2,0,4,0)))
ggsave("0.png",width=4.2,height=2.9,dpi=400*4)
system("magick 0.png -resize 25% 1.png")

In Ethical Skeptic's plot the B baseline looks closer to my lighter blue dashed line which was fitted against the 5-year blocks for 1970-2023 than my darker blue dashed line which was fitted against the 5-year blocks for 1970-2019, or maybe the B baseline is somewhere in between my two baselines. I don't know if Ethical Skeptic just drew the B baseline by hand, but it doesn't look steep enough to be fitted against data from 1970-2019 but it looks more like it's fitted against data up to the present in his plot. (Which is not really an important point, but it would be ironic if he was simultaneously guilty of paltering his own baseline while he falsely accused OWID of paltering.)

But in any case, the age structure of the New Zealand population has completely changed since the 1970s, so it doesn't make any sense to just use a linear baseline for CMR that starts from the 70s, because the actual trend in CMR is curved due to the changing age structure. Here I only had population data that went back to 1992, but the change since the 1970s would've been even more dramatic:

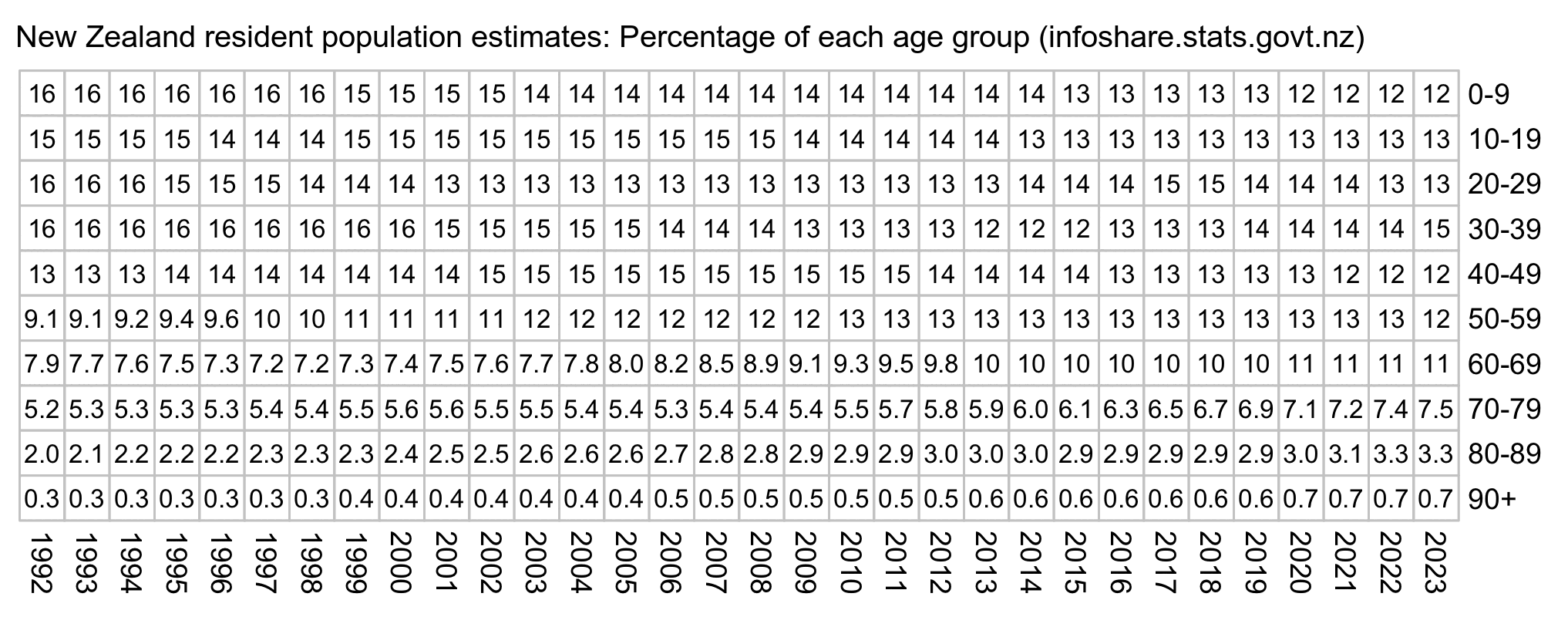
library(data.table)

agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)

t=fread("http://sars2.net/f/nzpopdead.csv")

m=t[,.(pop=sum(pop,na.rm=T)),.(age=agecut(age,0:9*10),year)][year>=1992,xtabs(pop~age+year)]
m=t(t(m)/colSums(m))*100

maxcolor=max(m)

disp=m;disp[]=sprintf("%.*f",ifelse(m>10,0,1),m)

pheatmap::pheatmap(m,filename="1.png",display_numbers=disp,
  cluster_rows=F,cluster_cols=F,legend=F,cellwidth=14,cellheight=14,fontsize=9,fontsize_number=8,
  border_color="#cccccc",number_color="black","white")

system("w=`identify -format %w 1.png`;pad=20;magick -pointsize 42 -font Arial \\( -size $[w-pad] caption:'New Zealand resident population estimates: Percentage of each age group' -splice 20x24 \\) 1.png -append 1.png")

Ethical Skeptic said that these were signs of a data charlatan, so I don't know if he was speaking about himself: [https://x.com/EthicalSkeptic/status/1758546649146593711]

Out of the three baselines in the next plot, I think the green baseline is the most accurate but it's far above the actual CMR in 2020:

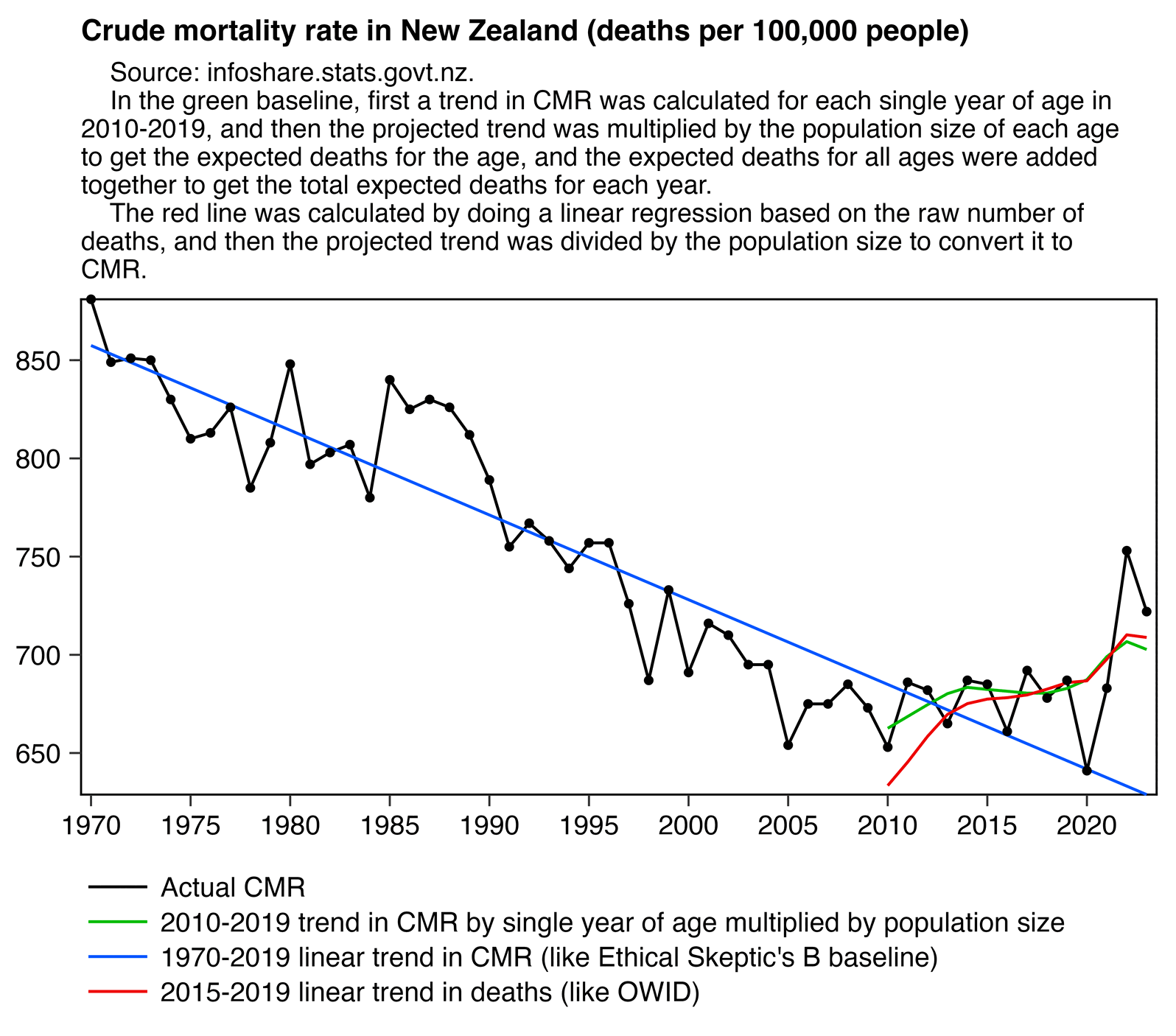
library(data.table);library(ggplot2);library(stringr)

t=fread("http://sars2.net/f/nzpopdead.csv")
a=t[,.(dead=sum(dead),pop=sum(pop,na.rm=T)),.(age=pmin(age,95),year)]

nzcmr=fread("http://sars2.net/f/nzcmr.csv")
p=nzcmr[year>=1970,.(x=year,y=cmr,z="Actual CMR")]

lm=a[year%in%2010:2019,.(year=2010:2023,trend=predict(lm(dead/pop~year),.(year=2010:2023))),age]
p=rbind(p,merge(a,lm)[,.(dead=sum(trend*pop),pop=sum(pop)),year][,.(y=dead/pop*1e5,z="2010-2019 trend in CMR by single year of age multiplied by population size"),.(x=year)])

p=rbind(p,nzcmr[year%in%1970:2019,.(x=1970:2023,y=predict(lm(cmr~year),.(year=1970:2023)),z="1970-2019 linear trend in CMR (like Ethical Skeptic's B baseline)")])

owid=a[,.(dead=sum(dead)),year][year%in%2015:2019,.(year=2010:2023,owid=predict(lm(dead~year),.(year=2010:2023)))]
p=rbind(p,merge(a[,.(pop=sum(pop)),year],owid)[,.(x=year,y=owid/pop*1e5,z="2015-2019 linear trend in deaths (like OWID)")])

p[,z:=factor(z,unique(z))]

xstart=1970;xend=2023
p=p[x>=xstart&x<=xend]
ystart=min(p$y);yend=max(p$y);ybreak=pretty(p$y)

color=c("black","#00bb00","#0055ff","#ee0000",hsv(30/36,1,.8))

cap="    Source: infoshare.stats.govt.nz."
cap=paste0(cap,"\n    ","In the green baseline, for example the CMR in 2023 was calculated by first calculating a trend in CMR for each age in 2010-2019, then the trend projected to 2023 was multiplied with the population size of each age in 2023 to get the expected deaths for each age group, and the expected deaths of all age groups were added together and then divided by the population size in 2023."|>str_wrap(90))
cap=paste0(cap,"\n    ","The red line was calculated by doing a linear regression for the raw number of deaths and by then dividing the projected trend with the population size to convert it to CMR."|>str_wrap(90))

ggplot(p,aes(x,y))+
geom_vline(xintercept=c(xstart-.5,xend+.5),linewidth=.25,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_line(aes(color=z),linewidth=.35)+
geom_point(data=p[grep("Actual",z)],aes(color=z),size=.5,show.legend=F)+
labs(title="Crude mortality rate in New Zealand (deaths per 100,000 people)",subtitle=cap,x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(1900,2100,5))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks=element_line(linewidth=.25),
  axis.ticks.length=unit(3,"pt"),
  legend.direction="vertical",
  legend.key.height=unit(9,"pt"),
  legend.key.width=unit(15,"pt"),
  legend.key=element_rect(fill="white"),
  legend.box.spacing=unit(2,"pt"),
  legend.margin=margin(,,3),
  legend.justification=c(0,1),
  legend.position="bottom",
  legend.spacing.x=unit(1.5,"pt"),
  legend.text=element_text(size=7),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(3,5,4,4),
  plot.subtitle=element_text(size=6.7,margin=margin(,,4)),
  plot.title=element_text(size=7.5,face="bold",margin=margin(2,,4)))
ggsave("1.png",width=4.2,height=3.7,dpi=380*4)
system("magick 1.png -resize 25% 1.png")

And also if you look at ASMR instead of CMR, then there was clearly negative excess mortality in 2020 even relative to a long-term trend like my 1992 to 2019 quadratic trend in this plot:

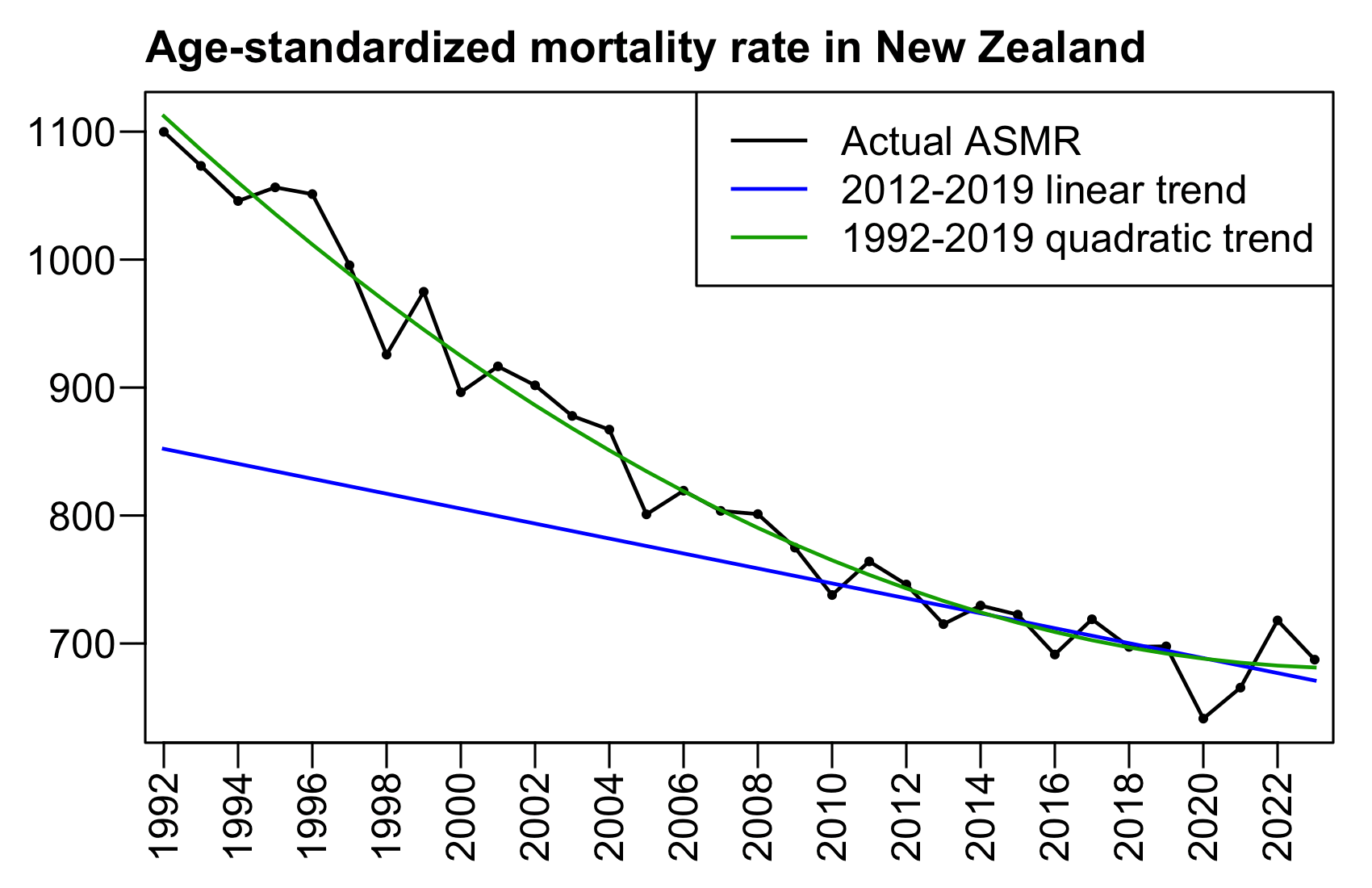
library(data.table)

t=fread("http://sars2.net/f/nzpopdead.csv")
a=t[,.(dead=sum(dead),pop=sum(pop,na.rm=T)),.(age=pmin(95,age),year)]
p=merge(a,a[year==2020,.(age,std=pop/sum(pop))])[year>=1992,.(asmr=sum(dead/pop*std*1e5)),year]
p$trend=p[year%in%2012:2019,predict(lm(asmr~year),.(year=p$year))]
p$poly=p[year%in%1992:2019,predict(lm(asmr~poly(year,2)),.(year=p$year))]

png("1.png",1700,1100,res=300)
par(mar=c(3.0,3,1.9,.8),mgp=c(0,.6,0),las=1,adj=0,lend="square")
tit="Age-standardized mortality rate in New Zealand"
leg=c("Actual ASMR","2012-2019 linear trend","1992-2019 quadratic trend")
col=c("black","#0000ff","#00aa00")
plot(p$year,p$asmr,type="l",main=tit,xlab=NA,ylab=NA,ylim=range(p[,-1]),xlim=range(p$year)+c(-.5,+.5),lwd=1.5,xaxt="n",xaxs="i",cex.main=1.1)
xbreak=seq(1992,2022,2)
axis(1,at=xbreak,labels=xbreak,las=2)
points(p$year,p$asmr,pch=20,cex=.6)
lines(p$year,p$trend,type="l",col=col[2],lwd=1.5)
lines(p$year,p$poly,type="l",col=col[3],lwd=1.5)
legend("topright",legend=leg,col=col,lty=1,lwd=1.5)
dev.off()

Deaths from malignant neoplasms in ages 0 to 54

In this plot that shows deaths with MCD malignant neoplasms but not MCD COVID, there's has been a steady increase in excess deaths since 2020 or 2021: [https://x.com/EthicalSkeptic/status/1834266396714246408]

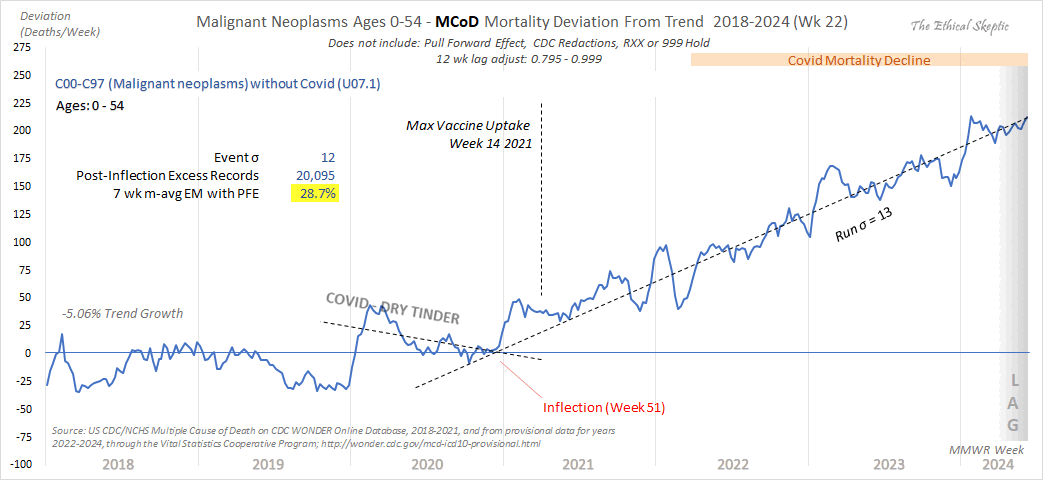
I believe Ethical Skeptic's baseline was fitted against data from only 2018 and 2019 like my blue baseline in the plot below, even though he may have fitted the baseline against only summer weeks but I fitted it against all months. In this case a 2018-2019 baseline is an unusually good approximation of a longer-term linear trend before COVID. But since 2020 the 2018-2019 baseline is still low compared to my green baseline here which accounts for changes to the age composition of the population:

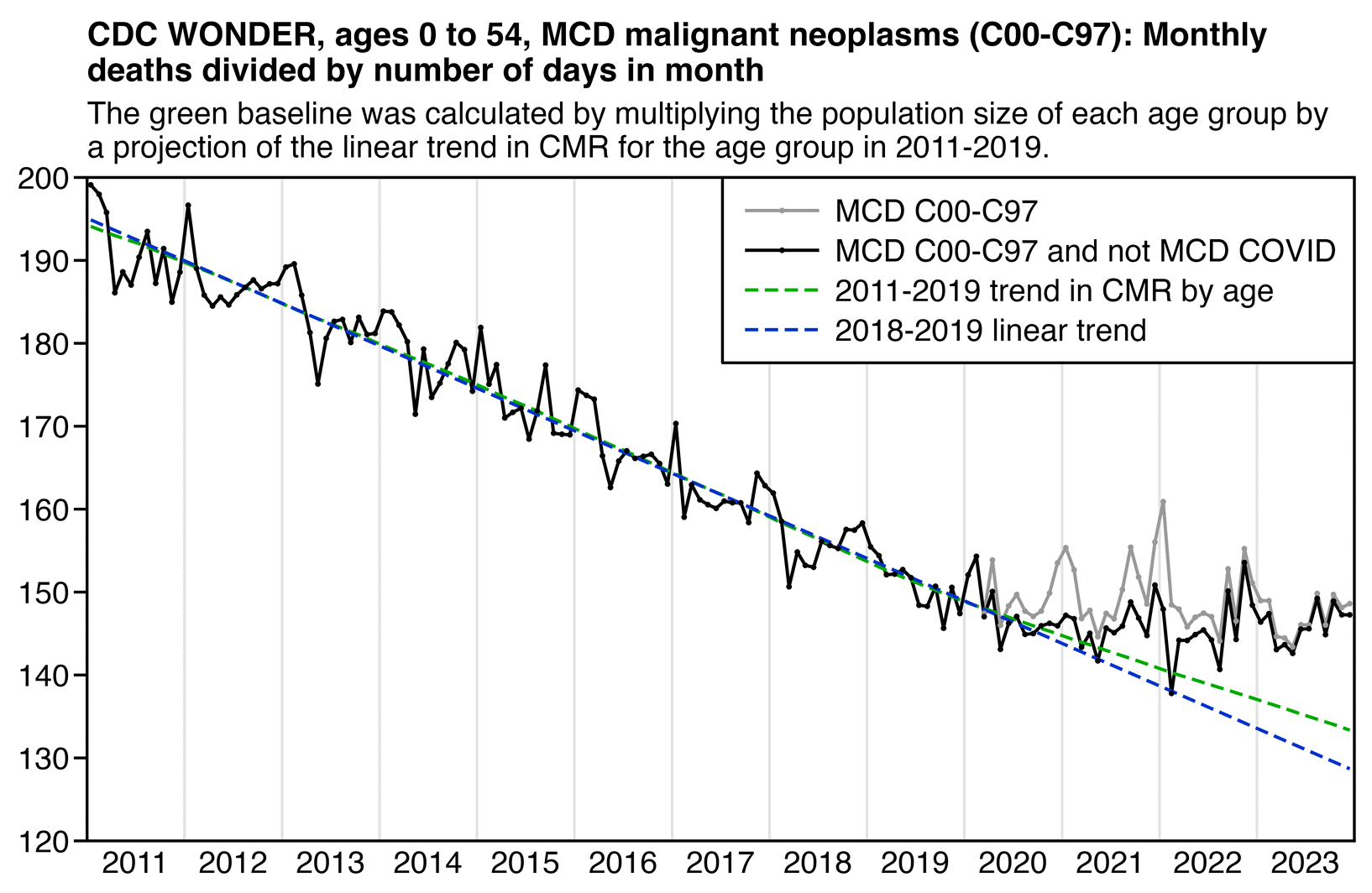
library(data.table);library(ggplot2);library(lubridate)

cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]

t=fread("http://sars2.net/f/wondermalignant5year.csv")[cause%like%"Multiple",.(age,date=month,dead)]
pop=fread("http://sars2.net/f/uspopdeadmonthly.csv")
t=merge(t,pop[,.(persondays=sum(persondays),pop=sum(pop)),.(date,age=cul(age,c(0,1,1:20*5)))],all=T)

t=t[,date:=as.Date(paste0(date,"-1"))]
t[,dead:=nafill(dead/days_in_month(date),,0)]
t=t[year(date)%in%2011:2023&age<55]

t$base=t$pop*t[year(date)<2020,predict(lm(dead/pop~date),.(date=unique(t$date))),age]$V1

w=t[,.(base=sum(base),dead=sum(dead)),date]

and=fread("http://sars2.net/f/wondermalignantmcdandcovidmcd.csv")[age=="under55"&date!="2024-09"]
and=and[,date:=as.Date(paste0(date,"-1"))][,.(date,dead2=dead/days_in_month(date))]
w=merge(w,and,all.x=T)[,dead2:=dead-nafill(dead2,,0)]

w$linear=w[year(date)%in%2011:2019,predict(lm(dead~date),w)]
w$linear2=w[year(date)%in%2018:2019,predict(lm(dead~date),w)]
lab=c("MCD C00-C97","MCD C00-C97 and not MCD COVID","2011-2019 trend in CMR by age","2018-2019 linear trend")
p=w[,.(x=date,y=c(dead,dead2,base,linear),z=factor(rep(lab,each=.N),lab))]

xstart=as.Date("2011-1-1");xend=as.Date("2024-1-1")
p=p[x>=xstart&x<=xend]
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ybreak=pretty(p$y,7);ystart=ybreak[1];yend=max(ybreak)

ggplot(p,aes(x=x+14,y=y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.3)+
geom_hline(yintercept=c(ystart,yend),linewidth=.3,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.3,lineend="square")+
geom_line(aes(color=z,linetype=z),linewidth=.35)+
geom_point(aes(alpha=z,color=z),stroke=0,size=.6)+
labs(title="CDC WONDER, ages 0 to 54, MCD malignant neoplasms (C00-C97): Monthly\ndeaths divided by number of days in month",subtitle="The green baseline was calculated by multiplying the population size of each age group by a projection of the linear trend in CMR for the age group in 2011-2019."|>stringr::str_wrap(90),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("gray60","black","#00aa00","#0033cc"))+
scale_linetype_manual(values=c("solid","solid","42","42"))+
scale_alpha_manual(values=c(1,1,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.y=element_text(margin=margin(,1)),
  axis.ticks=element_line(linewidth=.3,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(3,"pt"),
  axis.title=element_text(size=8),
  legend.direction="vertical",
  legend.justification=c(1,1),
  legend.key=element_blank(),
  legend.key.height=unit(9,"pt"),
  legend.key.width=unit(21,"pt"),
  legend.background=element_rect(color="black",linewidth=.3),
  legend.margin=margin(3,4,3,3),
  legend.position=c(1,1),
  legend.spacing.x=unit(1.5,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=7),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(4,4,3,4),
  plot.subtitle=element_text(size=7,margin=margin(,,3)),
  plot.title=element_text(size=7.4,face=2,margin=margin(1,,3)))
ggsave("1.png",width=4.3,height=2.8,dpi=380*4)
system("magick 1.png -resize 25% -colors 256 1.png")

In the plot above I also got a steady increase in excess deaths which started around 2020 or 2021, so the increase in excess deaths doesn't just seem to be an artifact produced by an inappropriate baseline. However the turning point in deaths seems to be around late 2020 or early 2021 so I don't know if it can be blamed on the vaccines, because cancers normally take time to develop and there weren't yet that many young people who had been vaccinated even in early 2021.

When I looked at all ages instead of only ages 0 to 54, there was not such a clear increase in deaths above the baseline in 2022-2023 (even though I guess Ethical Skeptic might argue it was because I didn't adjust sufficiently for the PFE in my baseline, because my baseline only had a slight downwards adjustment due to the reduction in population size caused by excess deaths since 2020):

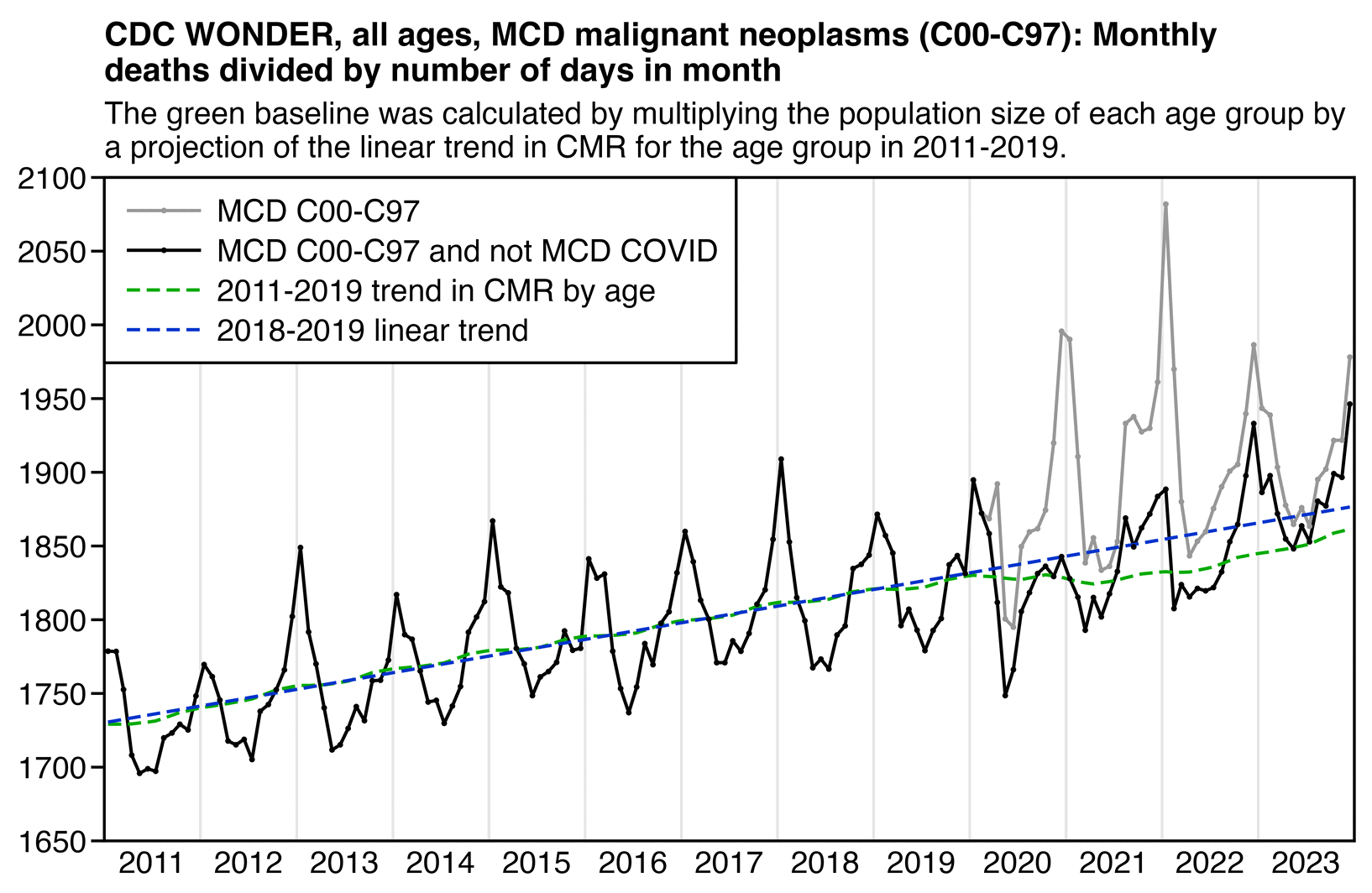
In the plot above the green baseline was not adjusted for seasonal variation in mortality, but the reason why my baseline has the wavy pattern is that the population sizes of elderly age groups are slightly higher in the winter. I calculated the baseline using monthly resident population estimates published by the US Census Bureau.

When Ed Dowd's group published a paper about deaths from neoplasms in ages 15 to 44 where they used a 2010-2019 linear baseline for CMR, I pointed out that a 1999-2019 trend in the mortality rate had a concave curve regardless of whether I looked at CMR or ASMR, so the 2010-2019 linear baseline might have been too steep and some flattening of the trend might have been expected during COVID. However that doesn't seem to be the case for deaths from malignant neoplasms in ages 0 to 54, where the 1999-2019 quadratic trend in ASMR is close to linear:

library(data.table);library(ggplot2);library(lubridate)

pop0=fread("https://www2.census.gov/programs-surveys/popest/datasets/2000-2010/intercensal/national/us-est00int-alldata.csv")
pop0=pop0[MONTH==7&AGE!=999&YEAR<2010,.(age=AGE,year=YEAR,pop=TOT_POP)]
pop=rbind(pop0,fread("http://sars2.net/f/uspopdead.csv")[year>=2010,.(age,year,pop)])

t=merge(pop,fread("http://sars2.net/f/wondercanceryearly.csv")[year<2024])
t=merge(pop[year==2020,.(age,std=pop/sum(pop))],t)

t1=cbind(t[(cause%like%"Neo"&age%in%15:44)],group="Neoplasms (C00-D48),\nages 15-44 (like Dowd)")
t2=cbind(t[(cause%like%"Malig"&age<55)],group="Malignant neoplasms (C00-C97),\nages 0-54 (like Ethical Skeptic)")
t=rbind(t1,t2)[,group:=factor(group,unique(group))]

p=t[,.(y=sum(dead/pop*std*1e5),z="Actual ASMR"),.(year,group)]
p1=p[year%in%2011:2019,.(year=2000:2023,z="2011-2019 linear trend",y=predict(lm(y~year),.(year=2000:2023))),group]
p2=p[year<2020,.(year=2000:2023,z="2000-2019 quadratic trend",y=predict(lm(y~poly(year,2)),.(year=2000:2023))),group]
p=rbind(p,p1,p2)[,z:=factor(z,unique(z))]

xstart=2000;xend=2023;xbreak=seq(xstart-.5,xend+.5,.5);xlab=c(rbind("",xstart:xend),"")

ggplot(p,aes(x=year,y=y))+
facet_wrap(~group,nrow=1,dir="v",scales="free")+
geom_text(data=p[,max(y),group],aes(label=group,y=V1),x=xend-(xend-xstart)*.01,vjust=1.4,size=grid::convertUnit(unit(7,"pt"),"mm"),hjust=1,fontface=2)+
geom_line(aes(color=z),linewidth=.3)+
geom_point(aes(color=z,alpha=z),stroke=0,size=.8,show.legend=F)+
geom_point(data=p[,max(y)/p[,max(y)/min(y),group][,max(V1)],group],aes(y=V1,x=xstart),stroke=0,size=0)+
labs(title="CDC WONDER: ASMR per 100,000 people for underlying cause of death cancer",caption="ASMR was calculated by single year of age so that the 2020 resident population estimates were used as the\nstandard population. Both panels have the same ratio between the maximum and minimum value of the y-axis.",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=xlab)+
scale_y_continuous(breaks=\(x)pretty(x,6))+
scale_color_manual(values=c("black","#0022cc","#009900"))+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1.2),
  axis.text.y=element_text(margin=margin(,1)),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(3,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.justification="right",
  legend.key=element_blank(),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.margin=margin(,,3),
  legend.position="top",
  legend.spacing.x=unit(1.5,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.25),
  panel.spacing=unit(3,"pt"),
  plot.caption=element_text(hjust=0,size=7,margin=margin(1,,1)),
  plot.margin=margin(3,3,3,3),
  plot.title=element_text(size=7.4,face=2,margin=margin(1,,2)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.2,height=2.6,dpi=400*4)
system("magick 1.png -resize 25% -colors 256 1.png")
system("qlmanage -p ~/1.png&>/dev/null")

Added in December 2024: Ethical Skeptic posted this updated version of his plot: [https://x.com/EthicalSkeptic/status/1866965795168985428]

His plot has an average of about 175 weekly excess deaths in 2023. However when I tried to reproduce his plot using three different baselines, they gave me an average of only about 69, 85, and 105 excess deaths in 2023, even though I fitted the baselines using only data from 2018 and 2019 like Ethical Skeptic:

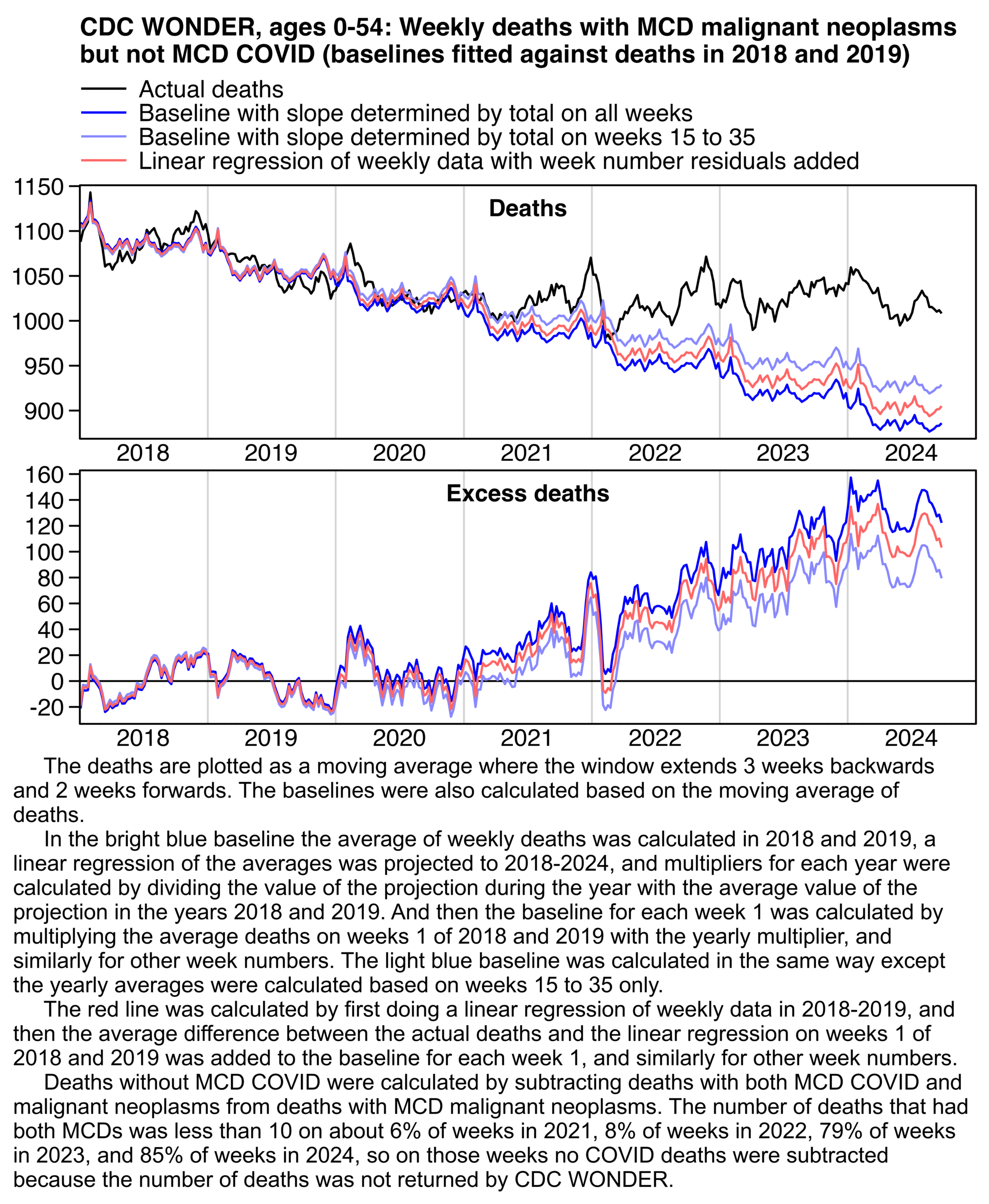
library(data.table);library(ggplot2)

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

t=fread("http://sars2.net/f/wondermalignant054weekly.csv")[date<="2024-10-1"]
t=dcast(t,date-3+year+week~cause,value.var="dead")
t=t[,.(date,year,week,dead=c(mcd,mcd-nafill(and,,0)),type=rep(1:2,each=.N))]
t=t[type==2]
t[,dead:=ma(dead,3,2)]

t=merge(t,t[year<2020,.(base=mean(dead),base2=mean(dead)),week])
slope=t[year<2020,mean(dead),year][,predict(lm(V1~year),.(year=2018:2024))]
slope2=t[year<2020&week%in%15:35,mean(dead),year][,predict(lm(V1~year),.(year=2018:2024))]
t[,base:=base*(slope/mean(slope[1:2]))[factor(t$year)]]
t[,base2:=base2*(slope2/mean(slope2[1:2]))[factor(t$year)]]

t$base3=t[year<2020,predict(lm(dead~date),t)]
t$base3=t$base3+t[year<2020,mean(dead-base3),week]$V1[t$week]

lab=c("Actual deaths","Baseline with slope determined by total on all weeks","Baseline with slope determined by total on weeks 15 to 35","Linear regression of weekly data with week number residuals added")
p=t[,.(x=date,y=c(dead,base,base2,base3),z=factor(rep(lab,each=.N),lab))]

p$facet="Deaths"
p=rbind(p,merge(p[z!=z[1]],p[z==z[1],.(x,actual=y)])[,.(x,y=actual-y,z,facet="Excess deaths")])
p[,facet:=factor(facet,unique(facet))]

xstart=as.Date("2018-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")

ggplot(p,aes(x=x,y))+
facet_wrap(~facet,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray83",linewidth=.4)+
geom_segment(data=tail(p,1),x=xstart,xend=xend,y=0,yend=0,linewidth=.4)+
geom_line(aes(color=z),linewidth=.5)+
geom_text(data=p[,.(y=max(y)),facet],x=pmean(xstart,xend),aes(label=facet),size=3.8,fontface=2,vjust=1.4)+
labs(x=NULL,y=NULL,title="CDC WONDER, ages 0-54: Weekly deaths with MCD malignant neoplasms\nbut not MCD COVID (baselines fitted against deaths in 2018 and 2019)")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab,expand=expansion(0,0))+
scale_y_continuous(breaks=\(x)pretty(x,7),expand=expansion(.03,0))+
scale_color_manual(values=c("black","blue","#8888ff","#ff6666","#ff66ff"))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=11,color="black"),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(5,"pt"),
  legend.background=element_blank(),
  legend.box.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.justification="left",
  legend.key=element_blank(),
  legend.key.height=unit(11,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(,,6,-2),
  legend.position="top",
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(6,6,1,5),
  plot.title=element_text(size=11.5,face=2,margin=margin(2,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=6.3,height=4.8,dpi=300*4)

sub="\u00a0    The deaths are plotted as a moving average where the window extends 3 weeks backwards and 2 weeks forwards. The baselines were also calculated based on the moving average of deaths.
     In the bright blue baseline the average of weekly deaths was calculated in 2018 and 2019, a linear regression of the averages was projected to 2018-2024, and multipliers for each year were calculated by dividing the value of the projection during the year with the average value of the projection in the years 2018 and 2019. And then the baseline for each week 1 was calculated by multiplying the average deaths on weeks 1 of 2018 and 2019 with the yearly multiplier, and similarly for other week numbers. The light blue baseline was calculated in the same way except the yearly averages were calculated based on weeks 15 to 35 only.
     The red line was calculated by first doing a linear regression of weekly data in 2018-2019, and then the average difference between the actual deaths and the linear regression on weeks 1 of 2018 and 2019 was added to the baseline for each week 1, and similarly for other week numbers.
     Deaths without MCD COVID were calculated by subtracting deaths with both MCD COVID and malignant neoplasms from deaths with MCD malignant neoplasms. The number of deaths that had both MCDs was less than 10 on about 6% of weeks in 2021, 8% of weeks in 2022, 79% of weeks in 2023, and 85% of weeks in 2024, so on those weeks no COVID deaths were subtracted because the number of deaths was not returned by CDC WONDER."

system(paste0("f=1.png;mar=100;w=`identify -format %w $f`;magick \\( $f \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[42*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x80 \\) -append -resize 25% -colors 256 1.png"))

Then I noticed that the earlier version of his plot had an average of only about 150 excess deaths in 2023. When I tried comparing the earlier version to the new version, I noticed that in the new version the excess deaths were suddenly shifted up around week 9 of 2020, after which the deaths remained permanently elevated compared to the old version. The change is so sudden that it doesn't just seem to be due to a difference in the slope of the baseline, which should result in a more gradual divergence between the new and old versions of the plot:

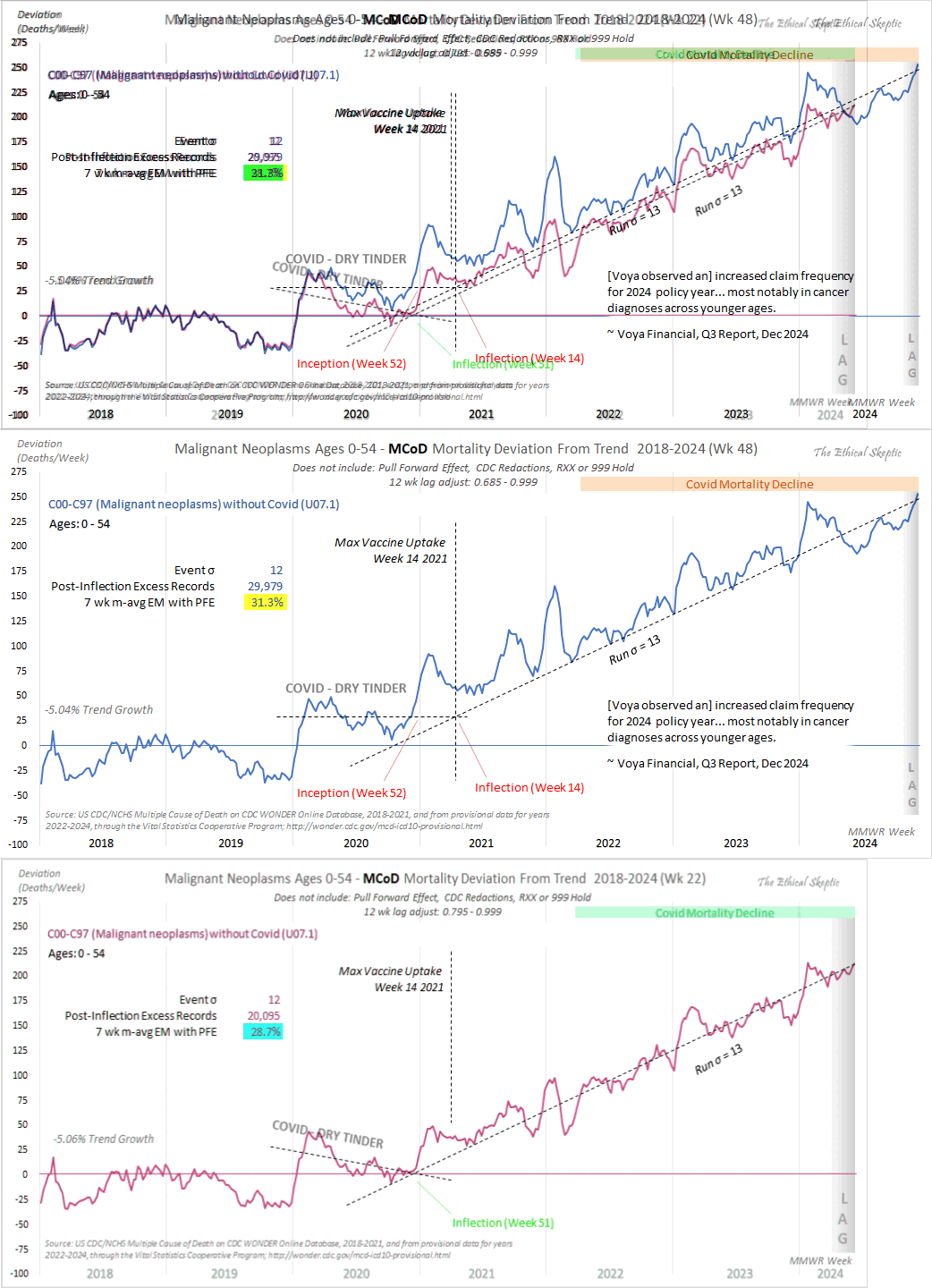
So I don't know if Ethical Skeptic has applied some of his usual undocumented adjustments to the data. He may have also applied some undocumented adjustments in the earlier version of his plot, because it already had much higher weekly excess deaths in 2023 than I got with any of my three baselines. He should describe his methodology in a detailed enough way that other people can reproduce his plots exactly.

In different versions of his plot ES has always drawn the so-called inflection point on week 14 of 2021, even though in the newest version the turning point in excess deaths seems to occur around early 2020, or possibly even in late 2019. In earlier versions the turning point seemed to occur around late 2020 or early 2021 because he had not yet shifted up the excess deaths from around week 9 of 2020 onwards. But in the new version the slope of his diagonal dashed line looks completely off compared to my magenta line here:

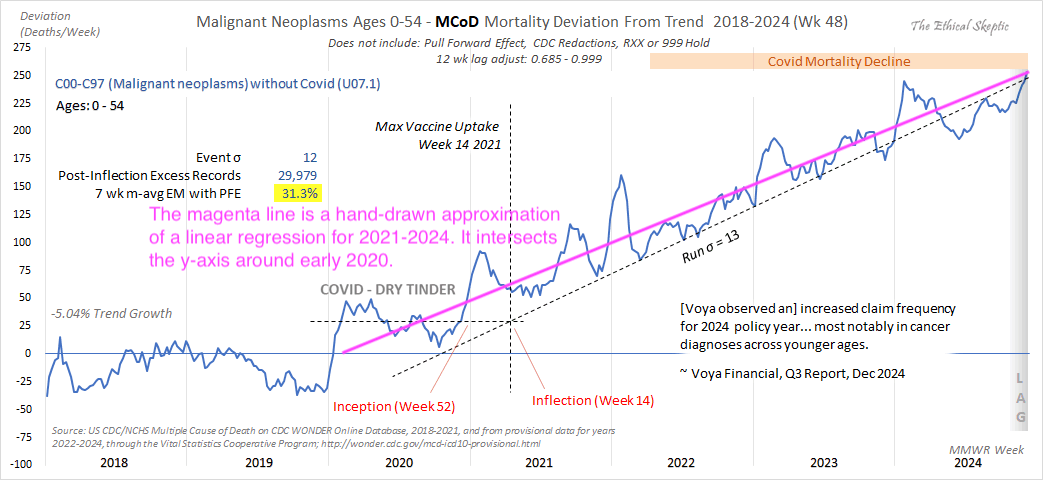
Added in July 2025: In this plot that extends up to MMWR week 15 of 2025, ES now claims that his 7-week moving average of excess deaths is 44.2%. He presumably refers to the moving average on weeks 9 to 15 of 2025: [https://x.com/EthicalSkeptic/status/1946279806506615277]

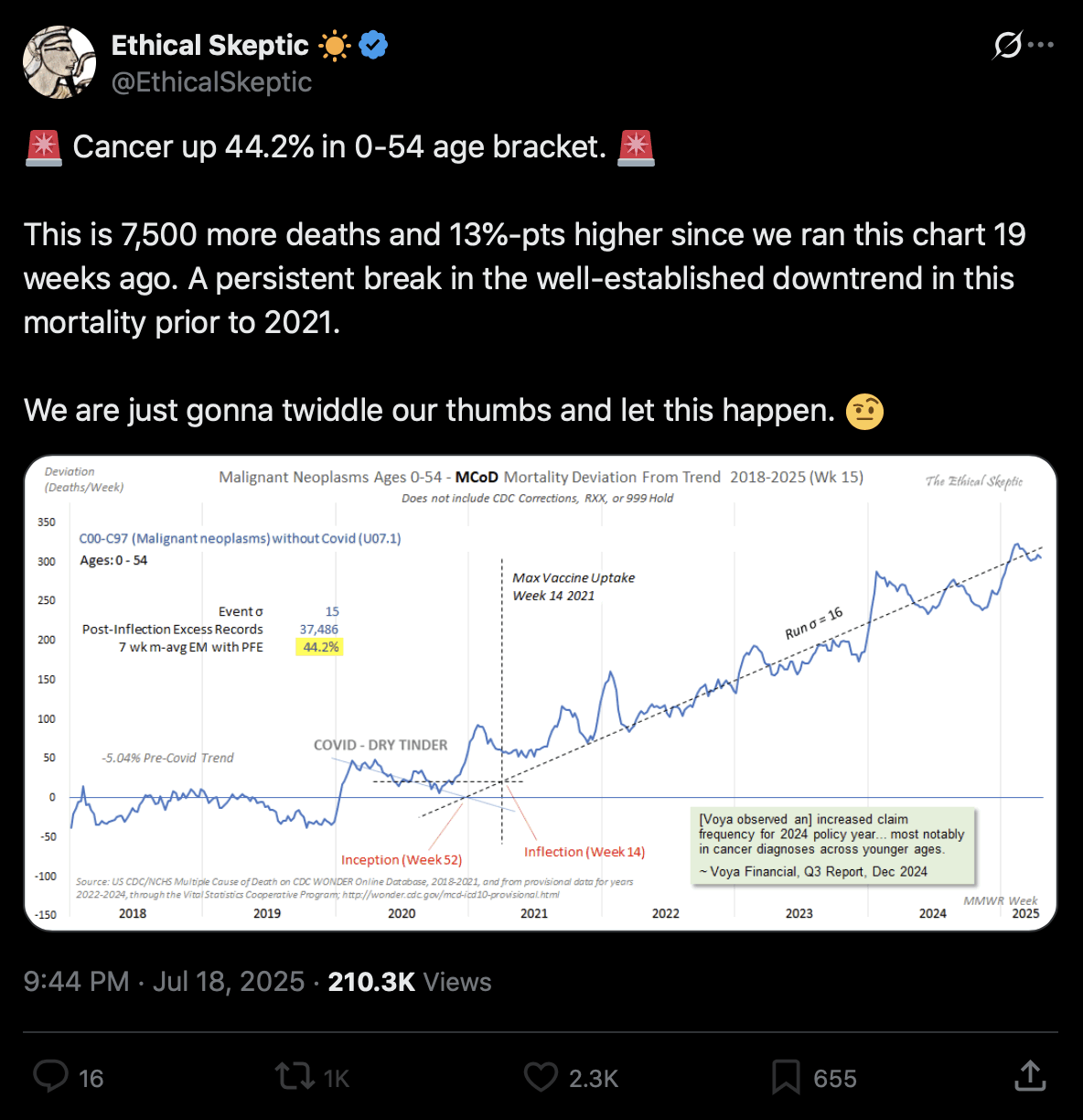
I believe ES added in deaths to the end of his x-axis that he estimated to be missing because of a registration delay, because when I tried to reproduce his plot using unadjusted data from CDC WONDER, I got a drop in deaths at then end of the x-axis that is missing from his plot. But since ES hasn't documented the exact method he uses to add in the missing deaths, in the following code I used the moving average of deaths on weeks 1 to 7 of 2025 as a proxy for the deaths on weeks 9 to 15.

On MMWR weeks 1 to 7 of 2025, the average number of deaths with MCD malignant neoplasms in ages 0-54 was 1059. I was not able to subtract COVID deaths because there were so few COVID deaths that they were suppressed by CDC WONDER:

t=fread("https://sars2.net/f/wondermalignant054weekly.csv") # retrieved July 20th 2025 UTC
t[year==2025&cause=="mcd"&week%in%1:6,mean(dead)]
# 1059

In order for 1059 deaths to correspond to about 44.2% excess deaths, the baseline number of deaths would have to be about 1059/1.442, which is about 734.4. It's about 33% lower than the average weekly number of deaths in 2018. So is it really reasonable to expect the number of cancer deaths to drop by a third in only 7 years?

ES has about 305 excess deaths at the end of his x-axis. In order for 305 excess deaths to correspond to 42.2% excess deaths, you can solve 305+x=1.422*x to get the baseline value, which is about 722.7. It's only off by about 13 deaths from the baseline value I reverse engineered above.

Earlier when I noticed that the average number of excess deaths in 2023 increased from about 150 in an older version of the plot to about 175 in a newer version of the plot, where the deaths were shifted upwards starting around week 9 of 2020, I thought it meant that ES had artificially inflated the deaths in his plot. However it might simply be that he shifted the baseline downwards instead, in case he changed the PFE adjustment curve he used in his plot. I didn't earlier realize that his plot probably included PFE adjustment, because even the text next to his excess deaths says "7 wk m-avg EM with PFE".

In plots for weekly excess deaths where ES does not incorporate PFE adjustment, he includes text that says "Does not include: Pull Forward Effect":

But the text was missing from the plot for cancer deaths in ages below 55:

Now of course it's questionable to incorporate a large amount of PFE adjustment in a plot for deaths in ages below 55.

Next in order to reverse engineer his baseline, I used WebPlotDigitizer to digitize the weekly excess deaths in his plot: https://automeris.io/wpd/. Then I subtracted the excess deaths from the actual deaths to reverse engineer his baseline, which I showed in yellow in the next plot. His baseline was higher than my three baselines in 2018 and 2019, but his baseline had a dramatic change in slope between 2019 and 2020. By 2024 his baseline was more than twice as high as the average of my three baselines:

library(data.table);library(ggplot2)

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

t=fread("https://sars2.net/f/wondermalignant054weekly.csv")[!(year==2025&week>15)]
t=dcast(t,date-3+year+week~cause,value.var="dead")
t=t[,.(date,year,week,dead=c(mcd,mcd-nafill(and,,0)),type=rep(1:2,each=.N))]
t=t[type==2]
t[,dead:=ma(dead,3,2)]

t=merge(t,t[year<2020,.(base=mean(dead),base2=mean(dead)),week])
slope=t[year<2020,mean(dead),year][,predict(lm(V1~year),.(year=2018:2025))]
slope2=t[year<2020&week%in%15:35,mean(dead),year][,predict(lm(V1~year),.(year=2018:2025))]
t[,base:=base*(slope/mean(slope[1:2]))[factor(t$year)]]
t[,base2:=base2*(slope2/mean(slope2[1:2]))[factor(t$year)]]

t$base3=t[year<2020,predict(lm(dead~date),t)]
t$base3=t$base3+t[year<2020,mean(dead-base3),week]$V1[t$week]

eth=fread("https://sars2.net/f/ethical054reverseengineered.csv")
t=t[order(date)]
t[,ethical:=dead-eth$dead]

lab=c("Actual deaths","Baseline with slope determined by total on all weeks","Baseline with slope determined by total on weeks 15 to 35","Linear regression of weekly data with week number residuals added","Reverse engineered baseline of Ethical Skeptic")
p=t[,.(x=date,y=c(dead,base,base2,base3,ethical),z=factor(rep(lab,each=.N),lab))]

p$facet="Deaths"
p=rbind(p,merge(p[z!=z[1]],p[z==z[1],.(x,actual=y)])[,.(x,y=actual-y,z,facet="Excess deaths")])
p[,facet:=factor(facet,unique(facet))]

xstart=as.Date("2018-1-1");xend=as.Date("2025-5-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")

ylim=p[,{x=extendrange(y,,.03);.(ymin=x[1],ymax=x[2])},facet]

ggplot(p)+
facet_wrap(~facet,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.4)+
geom_segment(data=p[.N],x=xstart,xend=xend,y=0,yend=0,linewidth=.4,color="gray75")+
geom_rect(data=ylim,aes(ymin=ymin,ymax=ymax),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_line(aes(x,y,color=z),linewidth=.5)+
geom_label(data=ylim,aes(mean(c(xstart,xend)),ymax,label=facet),vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4,color="gray75",size=3.8)+
geom_label(data=ylim,aes(mean(c(xstart,xend)),ymax,label=facet),vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=0,size=3.8,fill=NA)+
labs(x=NULL,y=NULL,title="CDC WONDER, ages 0-54: Weekly deaths with multiple cause of death\nmalignant neoplasms but not COVID (baselines fitted to 2018-2019)")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(breaks=\(x)pretty(x,7))+
scale_color_manual(values=c("black","blue","#8888ff","#ff6666","#aaaa00"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40"),
  axis.ticks=element_line(linewidth=.4,color="gray75"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_blank(),
  legend.key.height=unit(11,"pt"),
  legend.key.width=unit(23,"pt"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(color="gray75",fill=NA,linewidth=.4),
  panel.spacing=unit(2,"pt"),
  plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,2)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.7,height=4.8,dpi=300*4)

The average value of Ethical Skeptic's baseline is about 30% lower in 2024 than 2018:

t=fread("s/f/wondermalignant054weekly.csv")[!(year==2025&week>15)]
t=dcast(t,year+week~cause,value.var="dead")
t=t[,.(year,week,dead=mcd-nafill(and,,0))]

t[,ethical:=dead-fread("s/f/ethical054reverseengineered.csv")$dead]

round(t[,.(dead=mean(ethical)),year][,percentof2018:=dead/dead[year==2018]*100])
# year dead percentof2018
# 2018 1102           100
# 2019 1074            97
# 2020 1006            91
# 2021  946            86
# 2022  900            82
# 2023  848            77
# 2024  767            70
# 2025  732            66

In the next plot the green baseline is probabaly the most accurate, but it's only about 16% lower in 2024 than 2018, and not about 30% like Ethical Skeptic's baseline:

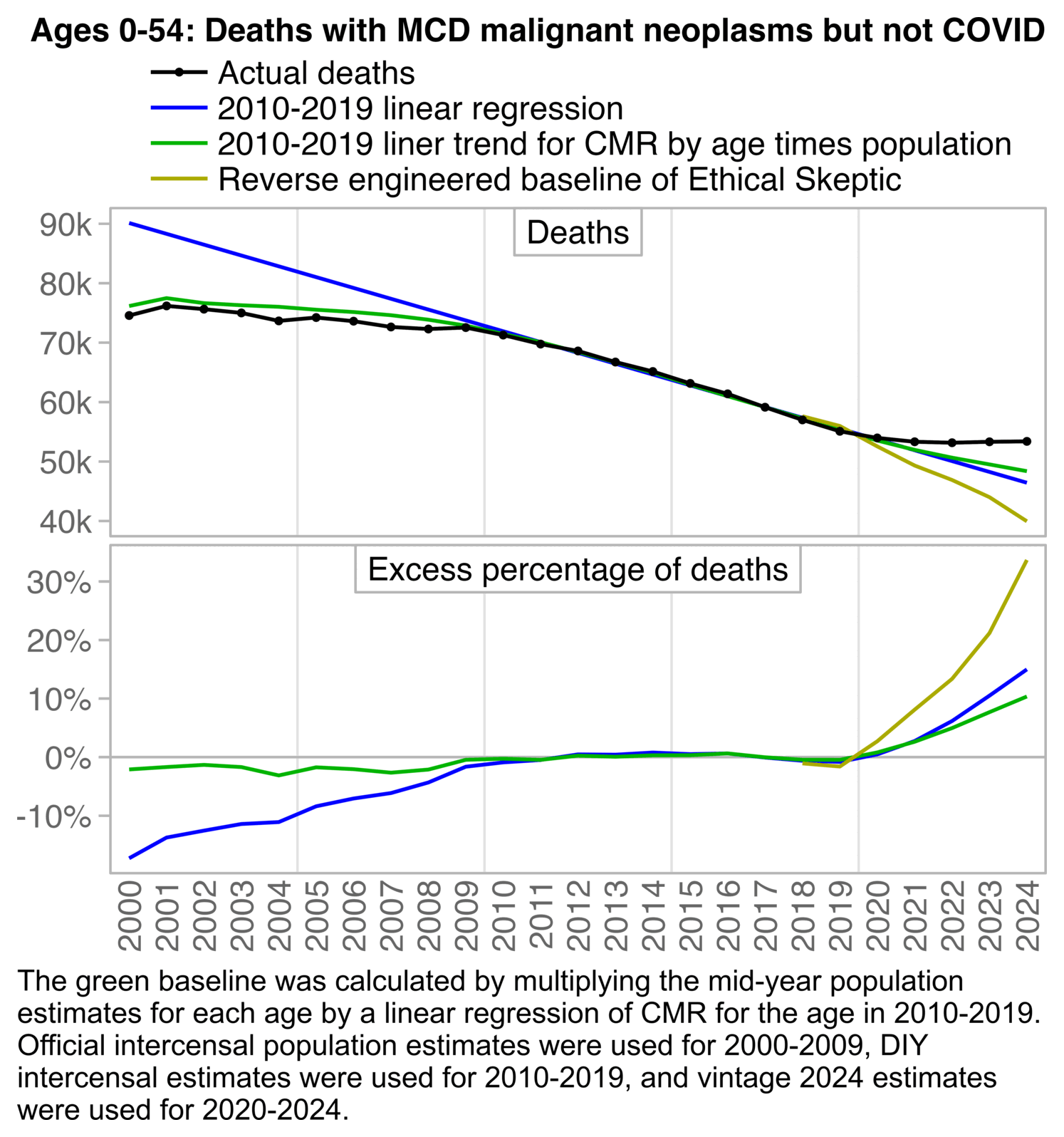
t=fread("https://sars2.net/f/wondermalignantyearly.csv")[cause==cause[1]]
t=merge(t[,-4],fread("https://sars2.net/f/uspopdead.csv")[,-4],all=T)
t=t[age<55&year%in%2000:2024]

a=t[,.(dead=sum(dead)),year]

# subtract COVID deaths from combined query for ages 0-54 to avoid suppression
a[year>=2020,dead:=c(53970,53326,53164,53321,53392)]

a$base=a[year%in%2010:2019,predict(lm(dead~year),a)]
a$base2=t[,.(year,base=predict(lm(dead/pop~year,.SD[year%in%2010:2019]),.SD)*pop),age][,tapply(base,year,sum)]

eth=fread("https://sars2.net/f/ethical054reverseengineered.csv")
eth=eth[,spline(ending-3,dead,xout=seq(as.Date("2018-1-1"),as.Date("2024-12-31"),1))]
a=merge(a,eth[,.(ethical=sum(y)/7),year(`class<-`(x,"Date"))],all=T)
a[,ethical:=dead-ethical]

p=a[,.(x=year,y=c(dead,base,base2,ethical),z=rep(1:4,each=.N),facet=1)]
p=rbind(p,p[,.(x,y=(y[z==1]/y-1)*100,z,facet=2)][z!=1])

p[,z:=factor(z,,c("Actual deaths","2010-2019 linear regression","2010-2019 liner trend for CMR by age times population","Reverse engineered baseline of Ethical Skeptic"))]
p[,facet:=factor(facet,,c("Deaths","Excess percentage of deaths"))]

xstart=min(p$x);xend=max(p$x)

ylim=p[,{x=extendrange(y);.(ymin=x[1],ymax=x[2])},facet]

ggplot(p)+
facet_wrap(~facet,dir="v",scales="free_y")+
geom_vline(xintercept=seq(xstart-.5,xend,5),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=ymin,ymax=ymax),xmin=xstart-.5,xmax=xend+.5,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_segment(data=ylim[2],y=0,yend=0,x=xstart-.5,xend=xend+.5,linewidth=.4,color="gray70")+
geom_line(aes(x,y,color=z),linewidth=.6)+
geom_line(data=p[z==z[1]],aes(x,y,color=z),linewidth=.6)+
geom_point(aes(x,y,alpha=z,color=z),stroke=0,size=1.4)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=(xstart+xend)/2,hjust=.5,vjust=1,fill="white",label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray70",size=3.87,lineheight=.8)+
geom_label(data=ylim,aes(label=facet,y=ymax),x=(xstart+xend)/2,hjust=.5,vjust=1,fill=NA,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,size=3.87,lineheight=.8)+
labs(x=NULL,y=NULL,title="Ages 0-54: Deaths with MCD malignant neoplasms but not COVID")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xstart:xend)+
scale_y_continuous(breaks=\(x)pretty(x,7),labels=\(x)if(max(x,na.rm=T)<1e3)paste0(x,"%")else paste0(x/1e3,"k"))+
scale_color_manual(values=c("black","blue",hsv(1/3,1,.7),"#aaaa00"))+
scale_alpha_manual(values=c(1,0,0,0,0,0))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="gray40",margin=margin(2,2,2,2)),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1.2),
  axis.ticks=element_line(linewidth=.4,color="gray70"),
  axis.ticks.length=unit(4,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(,,4),
  legend.position="top",
  legend.spacing.x=unit(1,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(linewidth=.3,fill=NA,color="gray70"),
  panel.grid.major=element_blank(),
  panel.spacing=unit(3,"pt"),
  plot.margin=margin(4,4,4,4),
  plot.title=element_text(size=11,face=2,margin=margin(1,,2),hjust=1),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.93,height=4.5,dpi=300*4)

The previous plot shows that the raw number of deaths slightly increased between 2022 and 2023, and also between 2023 and 2024. However the next plot shows that the ASMR has still gone down each year since 2020, regardless of whether you look at MCD deaths with COVID subtracted or UCD deaths. And also the turning point in the mortality trend seems to have already occurred between 2019 and 2020, which is difficult to blame on the vaccines:

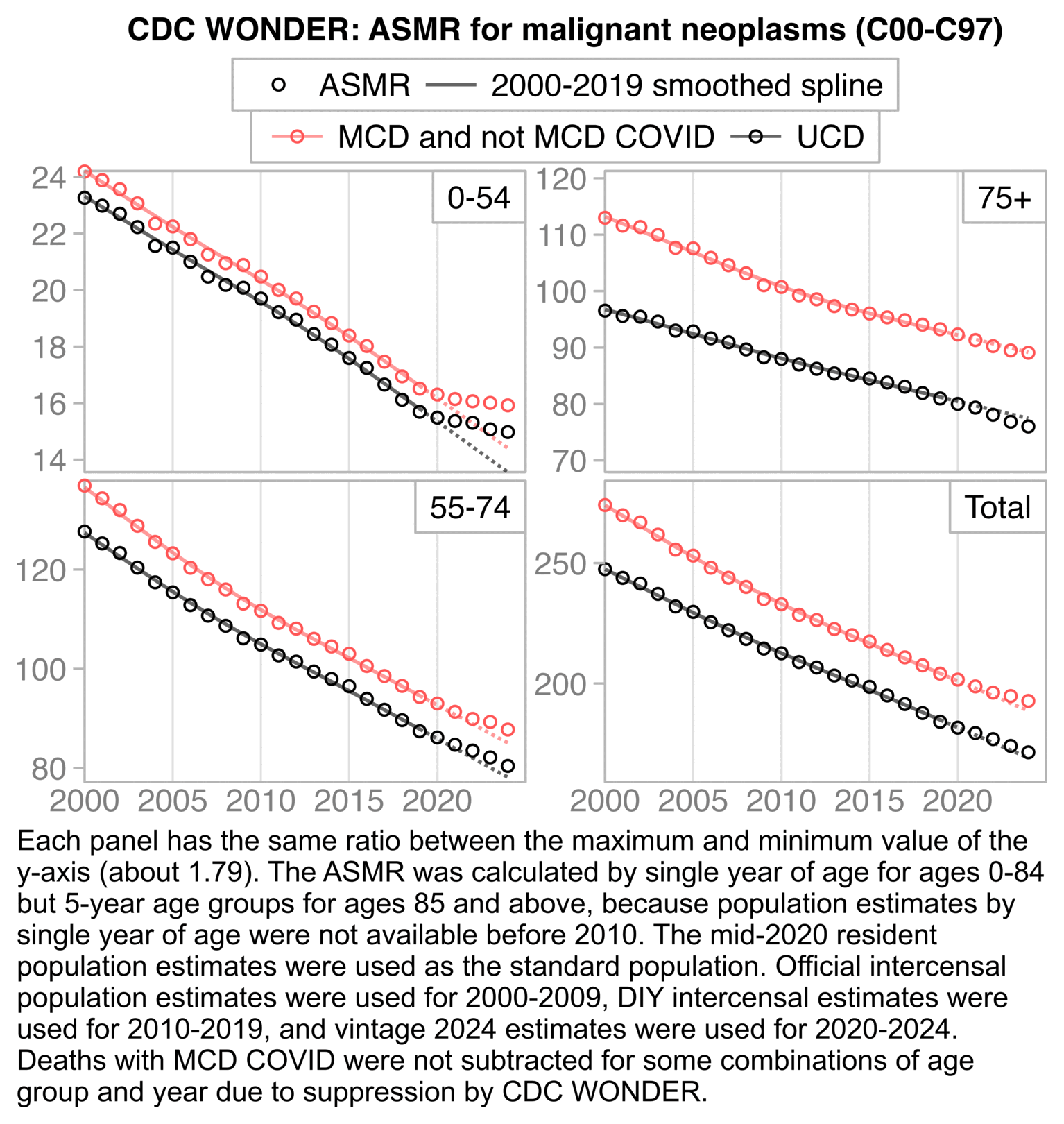
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)

t=fread("https://sars2.net/f/wondermalignantyearly.csv")[year%in%2000:2024]

d=merge(t[cause=="MCD malignant neoplasms",-4],t[cause%like%"and",.(year,age,and=dead)],all=T)
d=d[,.(year,age,dead=dead-nafill(and,,0),type=1)]
d=rbind(d,t[cause=="UCD malignant neoplasms",.(year,age,dead,type=2)])

pop=fread("https://sars2.net/f/uspopdead.csv")[,dead:=NULL]
d=merge(d,pop)

d$std=pop[year==2020,pop/sum(pop)][d$age+1]
d=d[,.(dead=sum(dead),pop=sum(pop,na.rm=T),std=sum(std)),.(year,age=ifelse(age>=85,age%/%5*5,age),type)]

d[,facet:=agecut(age,c(0,55,75))]
d=rbind(d,copy(d)[,facet:="Total"])

p=d[,.(y=sum(dead/pop*std*1e5)),.(x=year,z=type,facet)]

p=rbind(p[,type:=1],p[x<2020,predict(smooth.spline(x,y,spar=.7),2000:2024),.(z,facet)][,type:=2])

p[,z:=factor(z,,c("MCD and not MCD COVID","UCD"))]
p[,type:=factor(type,,c("ASMR","2000-2019 smoothed spline"))]

xstart=2000;xend=2025

ylim=p[,.(min=min(y),max=max(y)),facet]
rat=ylim[,max(max/min)]
ylim=ylim[,{x=(rat*min-max)/(1+rat);.(ymin=min-x,ymax=max+x)},facet]

ggplot(p)+
facet_wrap(~facet,ncol=2,dir="v",scales="free_y")+
geom_vline(xintercept=seq(xstart,xend,5),color="gray90",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=ymin,ymax=ymax),xmin=xstart,xmax=xend,lineend="square",linejoin="mitre",fill=NA,color="gray72",linewidth=.4)+
geom_line(data=p[x<=2019],aes(x,y,color=z,linewidth=type),alpha=.6)+
geom_line(data=p[x>=2019],aes(x,y,color=z,linewidth=type),linetype="11",alpha=.6,show.legend=F)+
geom_point(aes(x,y,color=z,shape=type),stroke=.6,size=1.5)+
geom_label(data=ylim,aes(xend,ymax,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4,color="gray72",size=3.87)+
geom_label(data=ylim,aes(xend,ymax,label=facet),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=0,fill=NA,size=3.87)+
labs(title="CDC WONDER: ASMR for malignant neoplasms (C00-C97)",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend-1,5))+
scale_y_continuous(breaks=\(x)pretty(x,4,3))+
coord_cartesian(clip="off",expand=F)+
scale_color_manual(values=c("#ff5555","black"))+
scale_linewidth_manual(values=c(0,.6))+
scale_shape_manual(values=c(1,NA))+
guides(shape=guide_legend(order=1),linewidth=guide_legend(order=1),color=guide_legend(order=2))+
theme(axis.text=element_text(size=11,color="gray50"),
  axis.ticks=element_line(linewidth=.4,color="gray72"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(4,"pt"),
  legend.background=element_rect(color="gray72",linewidth=.4),
  legend.box="vertical",
  legend.box.just="center",
  legend.box.margin=margin(,,3),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.width=unit(22,"pt"),
  legend.margin=margin(3,5,3,2),
  legend.position="top",
  legend.spacing.x=unit(3,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.spacing=unit(3,"pt"),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=11,margin=margin(,,3),hjust=1),
  plot.title=element_text(size=11,face=2,margin=margin(1,,4),hjust=.5),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.1,height=4,dpi=300*4)

Added in October 2025: Ethical Skeptic's plot says there's a "-5.04% Pre-Covid Trend". But he now said he referred to a 10-year trend, even though I thought that in his plots that display weekly deaths from 2018 onwards, he fits the baseline using data from only 2018 and 2019 (apart from certain broad causes of death for all ages combined, which have weekly data going back to 2014): [https://x.com/EthicalSkeptic/status/1977478689710395630]

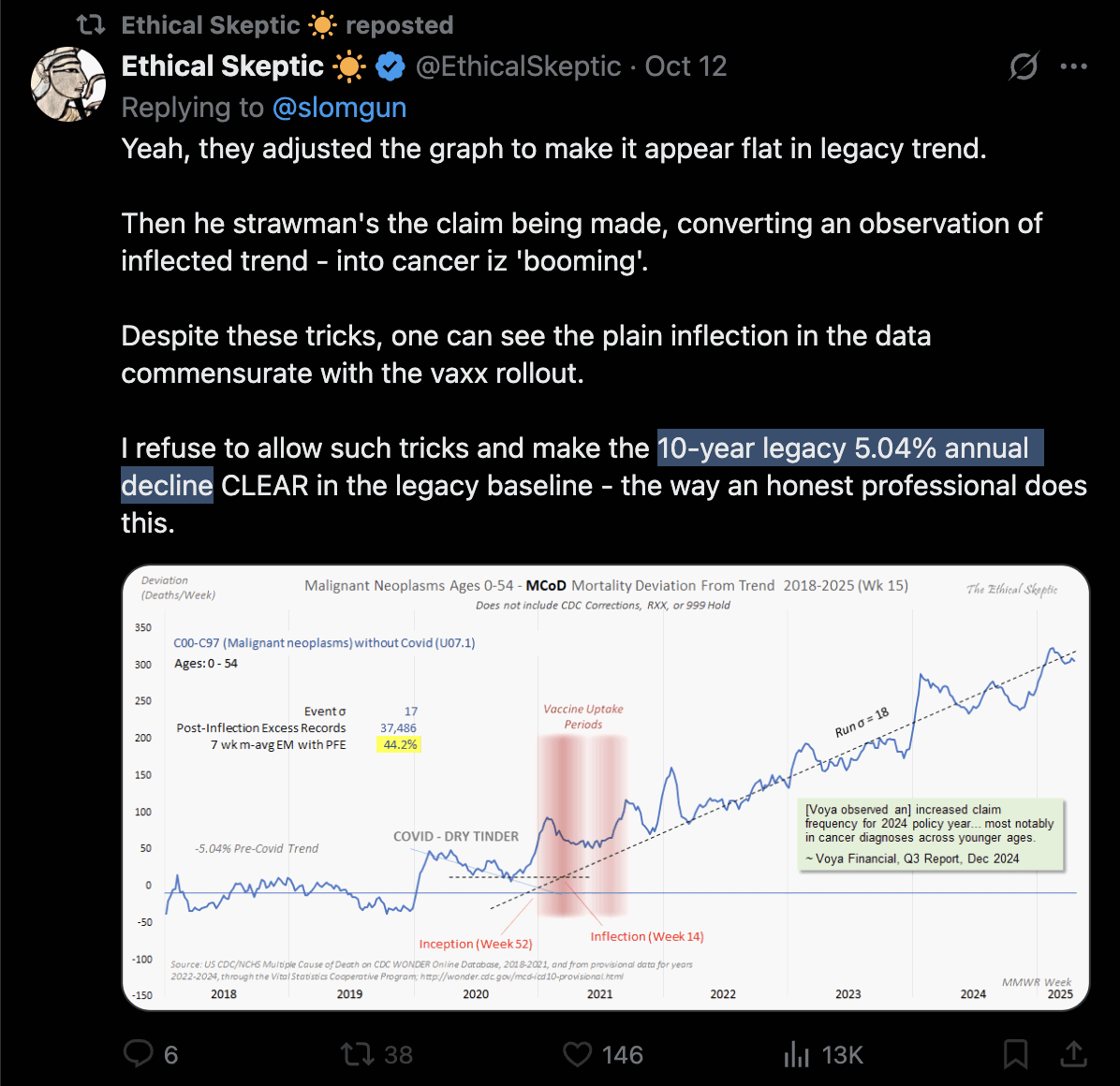
ES has indicated that he calculates the annual growth percentage by first using the SLOPE function in Excel to do a regression of a variable for weekly deaths against a year variable. The SLOPE function gets the second coefficient in a linear regression, which in this case shows the annual change in the number of deaths. He then divides the result with the average weekly deaths in the baseline period. [https://theethicalskeptic.com/wp-content/uploads/2024/02/Deviation-from-Trend-Retrospective-Plot-Procedure.webp, https://theethicalskeptic.com/wp-content/uploads/2025/09/ICD-10-Code-Excess-Death-Derivation-small.jpg]

However when I used his method for deaths with MCD malignant neoplasms in ages 0-54, I got an annual growth percent of about -3.1%, which is nowhere near -5.04%:

t=fread("https://sars2.net/f/wondermalignant054weekly.csv")
t[cause=="mcd"&year<2020,coef(lm(dead~year))[2]/mean(dead)]
# -0.03050468

When I used the same method with yearly data for 2010-2019, I got an annual growth rate of only about -2.9%:

t=fread("https://sars2.net/f/wondermalignantyearly.csv")
a=t[cause=="MCD malignant neoplasms"&age<55,.(dead=sum(dead)),year]
a[year%in%2010:2019,coef(lm(dead~year))[2]/mean(dead)]
# -0.0285691

Deaths from malignant neoplasms with excess MCD normalization

Ethical Skeptic posted the plot below with this caption: "Excess Cancer Mortality (USA) - stands at 5.9% or 747 persons per week over the last three weeks on average. More alarmingly however, is the novel compound annualized growth rate (CAGR) of 2.2%, a significant departure from the old growth rate of 0.23%, normalized from the years 2014-2019 (dark orange line). This chart is expertly adjusted for reporting lag (procedure here), Pull Forward Effect (345 week PFE method is depicted in Charts 3b and 6), and excess MCoD attributions (critical data mining method depicted in Chart 5 above). In other words it is showing the true cancer UCoD rate (shorted by pressure on physicians to not report cancers unless 'proven' by multiple tests). Despite all these shorts in the data collection, the raw (and misleading) UCoD data nonetheless shows a rise - which can be seen by clicking here." [https://theethicalskeptic.com/2024/04/04/the-state-of-things-pandemic-week-50-2023/]

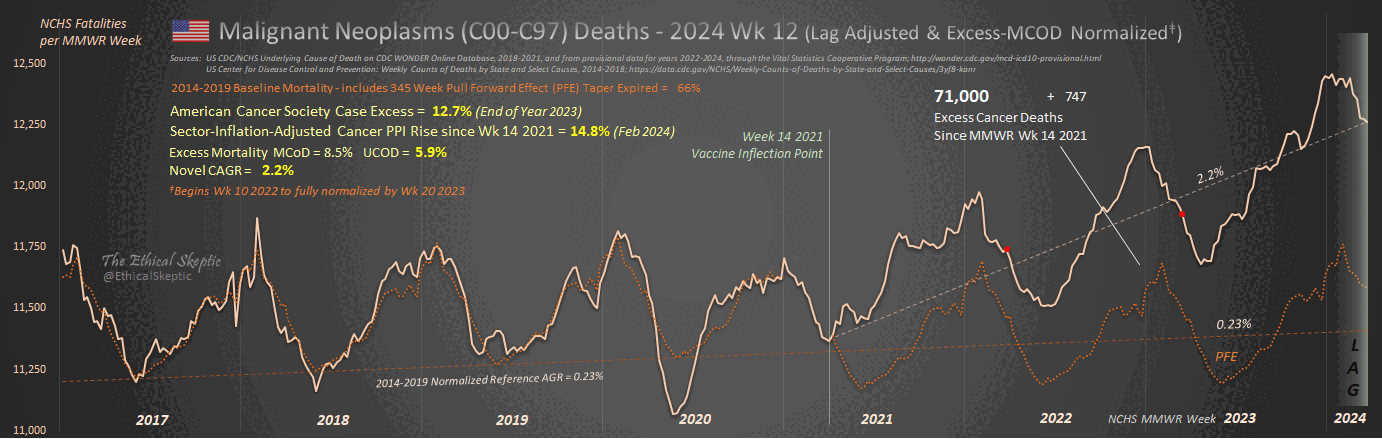
I believe "excess MCOD normalization" means that ES initially plotted UCD deaths up to week 9 of 2022, after which he added in a gradually increasing proportion of MCD deaths so that the proportion reached the maximum level on week 20 of 2023, after which it remained at the maximum level. He hasn't documented the exact methodology of how he performed the normalization.

He justified the use of the normalization by showing that the ratio of MCD to UCD deaths for malignant neoplasms has remained elevated since 2020, so he assumes that some cancer deaths which should've been classified as UCD were classified as MCD only instead. He showed the plot below and wrote: "The green-to-red line in Chart 5 below shows the CDC Wonder Excess Attributions of underlying cause of death Cancer to multiple cause of death Cancer, per week for the two years prior, as well as years-of and years-post the pandemic. The dotted baseline is normalized from the years 2018-2019, and indexed to the last 7 week average as compared to those same 7 weeks of 2018/19, so it is not a 'regression'. Since this is a relative index, it should exhibit no trend or growth rate (outside the context of Covid mortality peak periods of course). The current excess of 321 deaths reflects cancer deaths which are concealed from the underlying cause of death ICD code, and must be added back into the mix in order to make Excess Cancer Mortality comparable to its past baseline. We reconcile this into Chart 6 below, applying it only after the pandemic period ended." The plot had this caption: "Cancer Concealment by Excess MCOD Attribution - stands at 394 concealed cancer deaths per week. In this practice, cancers are moved from the underlying cause of death line in Part I of the death certificate, to one of the multiple cause of death lines above the UCoD line, in excess of past practice. Once Covid has abated, this balance should trend back to zero. It has not. Therefore, in order to capture the true cancer mortality increase, these cancer deaths falsely attributed to Covid and other underlying causes must be added back into the total in the Excess Cancer Mortality chart below. These missing deaths are phased back in from Week 10 of 2022 (point of large decline in Covid mortality) onward."

However the x-axis in the plot above started from 2018 so you couldn't see that there had been an increasing trend in the MCD to UCD ratio since approximately 2015. And in my next plot if you look at the light gray line where I subtracted deaths with both MCD COVID and MCD cancer from the MCD cancer deaths, the MCD to UCD ratio since 2020 has remained below the prepandemic trend on average, so basically all of the increase in the MCD to UCD ratio since 2020 can be explained by either a continuation of the prepandemic trend or by deaths with MCD COVID:

t=fread("http://sars2.net/f/wondermalignantmonthly.csv")

t[,z:=factor(cause,unique(cause),c("ucd","mcd","andmcd","anducd"))]
d=dcast(t,date~z,value.var="dead")
d[,date:=as.Date(paste0(date,"-16"))]

d$base=predict(lm(mcd/ucd~date,d[year(date)%in%2016:2019]),d)

p=d[,.(x=date,y=c(c(mcd,mcd-andmcd)/ucd,base)*100,z=factor(rep(1:3,each=.N)))]

x1=as.Date("1999-1-1");x2=as.Date("2025-1-1");xbreak=seq(x1+182,x2,"year")
ybreak=pretty(p[z!=3,y]);y1=ybreak[1];y2=max(ybreak)

levels(p$z)=c("COVID not subtracted","MCD COVID subtracted","2016-2019 linear trend")
color=c("black","gray60","#4444ff")

ggplot(p,aes(x,y))+
geom_vline(xintercept=seq(x1,x2,"year"),color="gray90",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray90",linewidth=.4)+
annotate("rect",xmin=x1,xmax=x2,ymin=y1,ymax=y2,linewidth=.4,color="gray80",fill=NA,lineend="square")+
geom_line(aes(color=z,linetype=z),linewidth=.5)+
geom_line(data=p[z==levels(z)[3]&year(x)%in%2016:2019],color=color[3],linewidth=.5)+
labs(title="CDC WONDER, malignant neoplasms (C00-C97): Multiple cause
of death as percentage of underlying cause of death",x=NULL,y=NULL)+
scale_x_continuous(limits=c(x1,x2),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(y1,y2),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=color)+
scale_linetype_manual(values=c("solid","solid","11"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,margin=margin(3,3,3,3),color="gray40"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks.length=unit(0,"pt"),
  legend.background=element_rect(fill="white",color="gray80",linewidth=.4),
  legend.box.just="left",
  legend.justification=c(.5,1),
  legend.key=element_blank(),
  legend.key.height=unit(13,"pt"),
  legend.key.width=unit(26,"pt"),
  legend.margin=margin(3,4,3,3,"pt"),
  legend.position=c(.5,1),
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=11),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(5,5,4,5),
  plot.title=element_text(size=11,margin=margin(1,,4),hjust=.5,lineheight=.9))
ggsave("1.png",width=5,height=3.1,dpi=300*4)

In the plot below if you look at the black line for UCD deaths, it remained near the baseline in 2020 and 2021 but by 2023 it had risen clearly above the baseline. And similarly if you look at the light gray line for MCD deaths with COVID subtracted, it also remained close to the baseline in 2020 and 2021 but it rose clearly above the baseline in 2023. So there seems to be a genuine increase in cancer deaths above the trend in 2023 even if you only look at UCD deaths, even though it's much smaller than the increase Ethical Skeptic gets when he applies his excess MCD normalization and PFE adjustment tricks to the data:

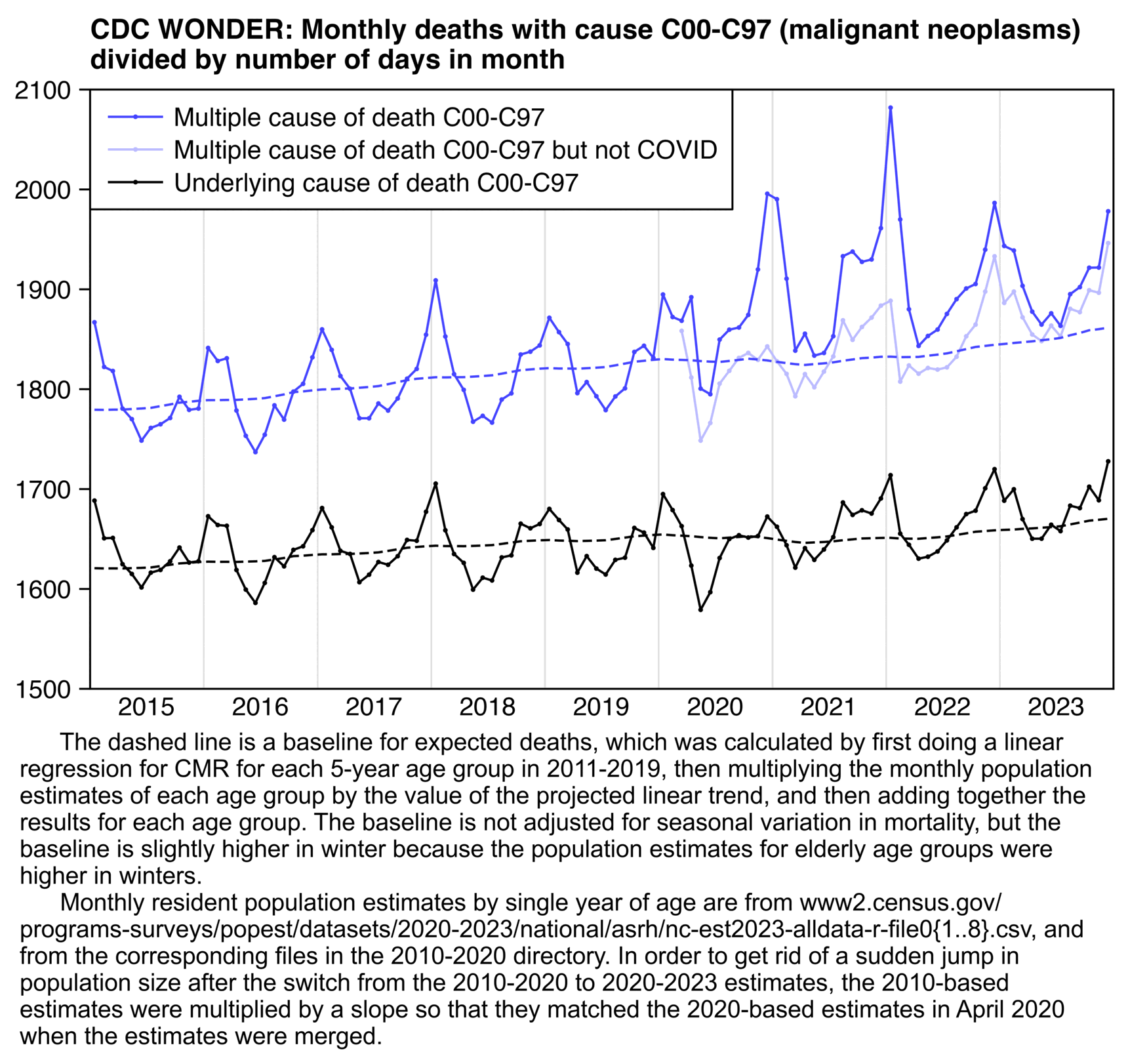
library(data.table);library(ggplot2);library(lubridate)

cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]

t=fread("http://sars2.net/f/wondermalignant5year.csv")
pop=fread("http://sars2.net/f/uspopdeadmonthly.csv")
t=merge(t,pop[,.(pop=sum(pop)),.(month=date,age=cul(age,c(0,1,1:20*5)))])
t=t[,month:=as.Date(paste0(month,"-1"))][,dead:=dead/days_in_month(month)]

base=t[!cause%like%"COVID"&year(month)%in%2011:2019][,dead:=nafill(dead,,0)]
t=merge(base[,.(month=unique(t$month),base=predict(lm(dead/pop~month),.(month=unique(t$month)))),.(age,cause)],t)
p=t[,.(base=sum(base*pop),dead=sum(dead)),.(date=month,cause)]

and=fread("http://sars2.net/f/wondermalignantmcdandcovidmcd.csv")[age=="all"]
and=and[,date:=as.Date(paste0(date,"-1"))][,.(date,andcovid=dead/days_in_month(date))]
p=rbind(p,merge(and,p[cause%like%"Multiple"])[,.(date,base=NA,cause="Multiple cause of death C00-C97 but not COVID",dead=dead-andcovid)])

xstart=as.Date("2015-1-1");xend=as.Date("2024-1-1")
p=p[date>=xstart&date<=xend]
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ybreak=pretty(p[,c(dead,base)],7);ystart=ybreak[1];yend=max(ybreak)

ggplot(p,aes(x=date+14,y=dead,color=cause))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.25)+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_line(linewidth=.3)+
geom_point(stroke=0,size=.6)+
geom_line(aes(y=base),linetype="42",linewidth=.3,show.legend=F)+
labs(title="CDC WONDER: Monthly deaths with cause C00-C97 (malignant neoplasms) divided by number of days in month"|>stringr::str_wrap(70),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("#4444ff","#bbbbff","black"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(2,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.background=element_rect(color="black",linewidth=.25),
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.position=c(0,1),
  legend.spacing.x=unit(1,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.margin=margin(3,4,3,3),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(4,4,4,4),
  plot.title=element_text(size=7.6,face=2,margin=margin(2,,3)))
ggsave("1.png",width=4.3,height=2.8,dpi=400*4)

sub="\u00a0     The dashed line is a baseline for expected deaths, which was calculated by first doing a linear regression for CMR for each 5-year age group in 2011-2019, then multiplying the monthly population estimates of each age group by the value of the projected linear trend, and then adding together the results for each age group. The baseline is not adjusted for seasonal variation in mortality, but the baseline is slightly higher in winter because the population estimates for elderly age groups were higher in winters.
      Monthly resident population estimates by single year of age are from www2.census.gov/
programs-surveys/popest/datasets/2020-2023/national/asrh/nc-est2023-alldata-r-file0{1..8}.csv, and from the corresponding files in the 2010-2020 directory. In order to get rid of a sudden jump in population size after the switch from the 2010-2020 to 2020-2023 estimates, the 2010-based estimates were multiplied by a slope so that they matched the 2020-based estimates in April 2020 when the estimates were merged."
system(paste0("f=1.png;mar=120;w=`identify -format %w $f`;magick \\( $f -chop 0x40 \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[38*4] caption:'",sub,"' -gravity southwest -splice $[mar]x80 \\) -append -resize 25% -colors 256 1.png"))

However I don't think the method of excess MCD normalization is justified, because there was already an increasing trend in the MCD to UCD ratio before COVID, and because deaths with MCD COVID account for basically all of the increase in the MCD to UCD ratio above the prepandemic trend.

And if there would be some other cause of death which had a reduced MCD to UCD ratio since 2020 compared to the ratio before 2020, should people be applying a "negative excess MCD normalization" where they subtract a part of deaths when they plot UCD deaths?

I think Ethical Skeptic hasn't documented what precise calculation he used to determine the magnitude of the excess MCD normalization, or how he picked week 10 of 2022 as the date when he started applying the normalization or week 20 of 2023 as the date when he stopped increasing the amount of added deaths. If he didn't pick the variables programmatically but based on some kind of subjective criteria, it would be difficult for other people to reproduce his work systematically or so that people would be able to apply the same methodology to other causes of death.

In any case in his plot that has a line that shows weekly deaths with excess MCD normalization, he should've also included another line that would've showed the number of deaths without the normalization, so it would've been clearer to his followers what the magnitude of the normalization was and when it started.

The increase in the MCD to UCD ratio might be due to an increase in the survival rate from cancer, which might cause there to be more people who have cancer at the time of death but who don't end up dying of cancer. Cancer ASMR in the United States has been decreasing faster than the age-standardized incidence of cancer: [https://acsjournals.onlinelibrary.wiley.com/doi/full/10.3322/caac.21820]

In the Cancer Facts & Figures reports by the American Cancer Society, there's also this table that shows how the 5-year survival rates for most types of cancer have increased over time: [https://www.cancer.org/research/cancer-facts-statistics/all-cancer-facts-figures/2024-cancer-facts-figures.html]

Added later: Chris Martenson posted this reply to me: "I don't think we can explain that above-trend line jump with 'Covid.' Covid can't explain anything in post-Omicron world, which is from Dec-21 onward. It just doesn't kill people in those numbers. Sure, it gets written down on death certs, but that's explained by incentives and poor reporting thresholds ('with vs of' and all that). So 'with MCD Covid' is not a valid explanation to me." [https://x.com/chrismartenson/status/1850667452901781740] But I replied by posting the plot below and pointing out that during the Omicron spike in January 2022, deaths with UCD COVID account for about 77% of the extra MCD cancer deaths above the 2016-2019 baseline. And why would my black line for the MCD to UCD ratio even have the sharp spike in January 2022 if it wasn't caused by Omicron? However later on in 2023 and 2024 if you look at my blue line where I subtracted UCD COVID deaths from the MCD cancer deaths, the blue line is clearly elevated above the 2016-2019 baseline, even though it could be that my baseline is too low in case the real trend in the MCD to UCD ratio is curved upwards (or it could also be that COVID has been underdiagnosed as a cause of death in 2023 and 2024, or that the UCD COVID deaths don't capture all extra deaths caused by COVID):

library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wondermalignantmonthly.csv")

p=t[cause=="MCD malignant neoplasms",.(date,dead,cause="COVID not subtracted")]

p1=merge(p,t[cause=="MCD malignant neoplasms and MCD COVID",.(and=dead,date)])[,.(date,dead=dead-nafill(and,,0),cause="MCD COVID subtracted")]
p2=merge(p,t[cause=="MCD malignant neoplasms and UCD COVID",.(and=dead,date)])[,.(date,dead=dead-nafill(and,,0),cause="UCD COVID subtracted")]
p=rbind(p,p1,p2)

p=merge(t[cause=="UCD malignant neoplasms",.(date,under=dead)],p)

p=p[date!="2024-10"]
p=p[,.(x=as.Date(paste0(date,"-1")),y=dead/under*100,z=cause)]

xstart=as.Date("1999-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month")
xlab=c(rbind("",1999:2024),"")
ybreak=pretty(p[z=="COVID not subtracted",y]);ystart=ybreak[1];yend=max(ybreak)

color=c("black","gray60",hsv(22/36,.8,1),"black")

months=seq(xstart,xend,"month")
p=rbind(p[,.(x,y,z)],p[z=="COVID not subtracted"&year(x)%in%2016:2019,.(x=months,y=predict(lm(y~x),.(x=months)),z="2016-2019 linear trend")])

p[,z:=factor(z,unique(z))]

seg=p[x==D("2022-1-1")&!z%like%"MCD"]

ggplot(p,aes(x=x+14,y=y))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.25)+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_line(aes(color=z,linetype=z),linewidth=.3)+
labs(title="CDC WONDER: Monthly deaths with cause C00-C97 (malignant neoplasms): MCD deaths as percentage of UCD deaths"|>stringr::str_wrap(70),x=NULL,y=NULL)+
geom_segment(data=seg,aes(x=x-90,y=y,xend=x,yend=y),linewidth=.3,color="red",lineend="square")+
annotate(geom="segment",x=seg$x[1]-90,xend=seg$x[1]-90,y=min(seg$y),yend=max(seg$y),lineend="square",color="red",linewidth=.3)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=color)+
scale_linetype_manual(values=c(1,1,1,2))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.just="left",
  legend.justification=c(0,1),
  legend.key=element_blank(),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.position=c(0,1),
  legend.spacing.x=unit(2,"pt"),
  legend.box.background=element_rect(fill="white",color="black",linewidth=.3),
  legend.margin=margin(-2,5,4,4,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.title=element_text(size=7.6,margin=margin(2,,4)))
ggsave("1.png",width=4.2,height=2.8,dpi=450)

Added even later: In the plot below I tried reproducing Ethical Skeptic's plot. I took weekly deaths for UCD malignant neoplasms from CDC WONDER from 2018 onwards and from the same dataset Ethical Skeptic used from 2014 until 2017. [https://catalog.data.gov/dataset/weekly-counts-of-deaths-by-state-and-select-causes-2014-2018]

Ethical Skeptic's plot uses a moving average where the window extends 3 weeks backwards and 2 weeks forwards, so I applied a similar moving average to my green line. [https://www.covid-datascience.com/post/evaluating-claims-of-excess-cancer-deaths-in-the-usa-during-the-pandemic]

My green line matches Ethical Skeptic's line from 2018 to 2020. But for some reason his line already starts to rise slightly above from my line around the start of 2021 even though he is supposed to have only started applying the excess MCD normalization on week 10 of 2022. So I don't know if he also applied some additional adjustment that already started in 2021.

I took data for 2017 from the same CDC dataset that Ethical Skeptic listed as his source, but my number of deaths is slightly higher in 2017 because he seems to have excluded deaths in District of Columbia. My green line shows deaths where the jurisdiction of occurrence was listed as United States, but I got my green line to match Ethical Skeptic's plot when I excluded DC so that I summed together deaths for all jurisdictions except United States, Puerto Rico, and District of Columbia. However I don't think it's correct to exclude DC because DC is not part of any state. In the CDC dataset the total number of cancer deaths in all jurisdictions except United States and Puerto Rico is only 79 lower than the number of deaths in the jurisdiction of United States, which is explained by 11 rows where the number of deaths was suppressed because it was below 10.

Ethical Skeptic's plot shows that he got 94,700 excess cancer deaths since MMWR week 14 of 2021. But I got only about 18,000 excess deaths between week 14 of 2021 and week 26 of 2024 (where I excluded later weeks because there's too many deaths missing because of a registration delay).

My light green baseline was calculated based on a simple linear regression of raw deaths, which is inaccurate in two ways that end up partially canceling each other out. My baseline is too low because it doesn't account for changes to the size or age composition of the population. But my baseline is also too high because it doesn't account for the reduced population size due to COVID deaths. So overall I think my baseline is probably too high in 2021 and 2022 but by 2024 it might already be too low.

library(data.table);library(ggplot2)

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

t=fread("http://sars2.net/f/wondermalignantweekly.csv")

old=fread("https://data.cdc.gov/api/views/3yf8-kanr/rows.csv?accessType=DOWNLOAD")
t2=old[`Jurisdiction of Occurrence`=="United States",.(date=as.IDate(as.Date(`Week Ending Date`,"%m/%d/%Y")),year=`MMWR Year`,week=`MMWR Week`,dead=`Malignant neoplasms (C00-C97)`)]

t=rbind(t2[year(date)<2018],t)
t[,dead:=ma(dead,3,2)]

t$base=t[year<2020,predict(lm(dead~date),t)]
p=merge(t,t[,mean(dead-base),week])[,.(date,dead,week,year,base=base+V1)]

ystart=11000;yend=12500;ystep=250;ybreak=seq(ystart,yend,ystep)
xstart=as.Date("2017-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=c(rbind("",2017:2024),"")

ggplot(p,aes(x=date,y=dead))+
geom_vline(xintercept=c(xstart),color="green",linewidth=.2,lineend="square")+
geom_hline(yintercept=c(ystart),color="green",linewidth=.2,lineend="square")+
geom_line(aes(y=base),linewidth=.2,color="#bbffbb")+
geom_line(linewidth=.2,color="green")+
geom_point(stroke=0,size=.5,color="green")+
labs(x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.2,xend+.5),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=6,color="green"),
  axis.ticks=element_line(linewidth=.2,color="green"),
  axis.ticks.x=element_line(color=alpha("green",c(1,0))),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.background=element_rect(fill="transparent",color=NA))
ggsave("1.png",width=5.5,height=2.2,dpi=400)

Added in November 2024: Ethical Skeptic now updated his plot for the MCD to UCD ratio so he started the x-axis from 2017 instead of 2018. [https://x.com/EthicalSkeptic/status/1852385322543219017] I was able to reproduce the plot from 2018 onwards as is shown by the magenta crosses below, but I don't even know where to get weekly MCD cancer deaths for 2017. I only found weekly UCD deaths here: https://catalog.data.gov/dataset/weekly-counts-of-deaths-by-state-and-select-causes-2014-2018. The bottom of his plot only lists CDC WONDER as a source, but CDC WONDER only has weekly data from 2018 onwards. Ethical Skeptic may have added the data for 2017 to his plot in order to address my criticism about how there had been an increasing trend in the MCD to UCD ratio since around 2015 or 2016, because I had pointed it out on Twitter multiple times, and I'm sure he saw it at least once even though he has blocked me because I told about it to Steve Kirsch who relayed my criticism to Ethical Skeptic and posted Ethical Skeptic's response to me on DM. There's even a note in the updated plot which specifically says that the trend in 2017 to 2019 is flat, even though the trend was clearly increasing in my plot for monthly data. However Ethical Deceptic seems to have inserted fake data for 2017, because the shape of his line for 2017 looks too similar to the line for 2018:

The line for 2017 looks like it was produced by adding random noise to the line for 2018, except weeks 1 and 3 may been possibly been lowered manually because they have the biggest difference between 2018 and 2017. The lines for 2017 and 2018 have peaks on the same week numbers:

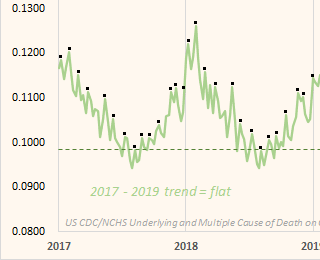
Here the line for 2017 is shown in purple over the line for 2018. Looks like clear fraud:

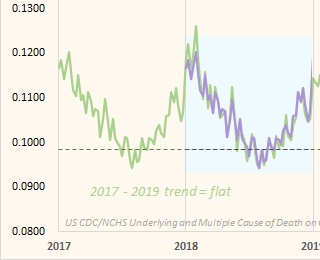
Ethical Skeptic even had the chutzpah to say it was "indicative of a darkened heart" if someone plotted regular UCD cancer deaths without applying his trick of excess MCD normalization, even though he seems to have falsified data in order to justify his method of excess MCD normalization: [https://x.com/EthicalSkeptic/status/1854044515604308023]

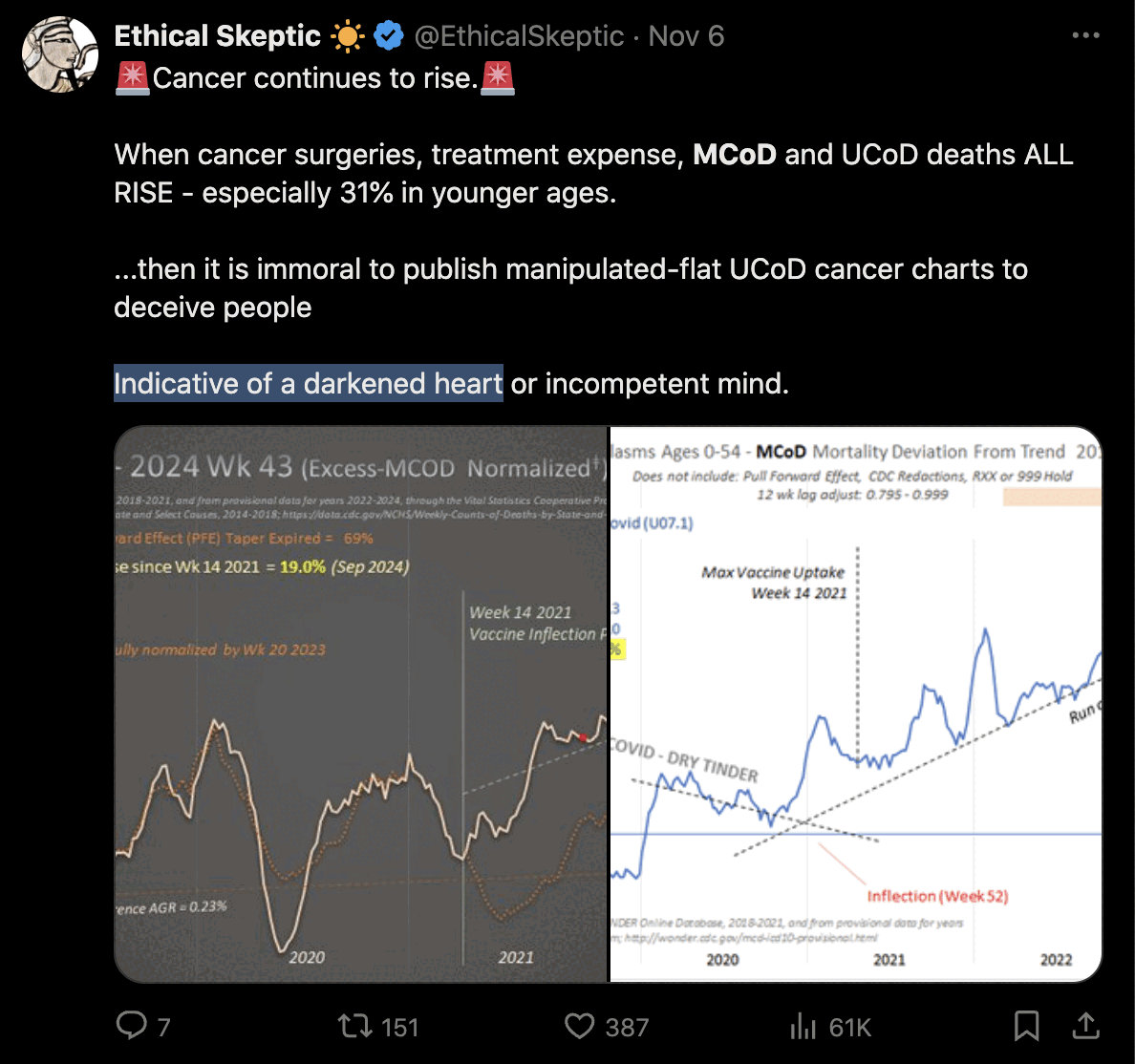
Added in December 2024: Uncle John Returns showed me this ONS user response which had both UCD and MCD deaths grouped by cause and date: https://www.ons.gov.uk/peoplepopulationandcommunity/birthsdeathsandmarriages/deaths/adhocs/2325deathsinvolvingorduetoselectedcausesbetweenseptember2003anddecember2023byweekandyearofbirthbycountriesenglandandwalesseperately. It shows that in England there was also an increasing trend in the MCD to UCD ratio for malignant neoplasms before COVID, because the ratio gradually increased from about 1.1 in 2004 to about 1.2 in 2019:

library(data.table);library(ggplot2);library(readxl)

t4=setDT(read_excel("finaldata2023v2.xlsx",sheet=4,skip=5))
t6=setDT(read_excel("finaldata2023v2.xlsx",sheet=6,skip=5))
t4$type="ucd";t6$type="mcd"

p=t4[,.(mcd=sum(rowSums(.SD))),.(date=t4$Death),.SDcols=patterns("[Mm]alignant")]
p=merge(p,t6[,.(ucd=sum(rowSums(.SD))),.(date=t6$Death),.SDcols=patterns("[Mm]alignant")])
p[,ratio:=mcd/ucd]
p[,x:=.I]
p[,date:=sub("\\S+ (...).*? (....) - (...).*? (.*)","\\1 \\2 - \\3 \\4",date)]

ystart=0;yend=1.4;ybreak=seq(ystart,yend,.1)

ggplot(p,aes(x=x,y=ratio))+
geom_line(linewidth=.5)+
labs(title="ONS user response 2325: MCD to UCD ratio for malignant neoplasms",subtitle="Includes England only. Deaths are by date of registration and not occurrence. Source: ONS user response titled \"Deaths involving or due to selected causes between September 2003 and December 2023 by week and year of birth, by countries England and Wales seperately\"."|>stringr::str_wrap(83),x=NULL,y=NULL)+
scale_x_continuous(limits=c(.5,max(p$x)+.5),breaks=p$x,labels=p$date)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.text.y=element_text(margin=margin(,1.5)),
  axis.ticks.length=unit(0,"pt"),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  panel.grid.major.y=element_line(size=.3,color="gray85"),
  plot.margin=margin(4,4,4,4),
  plot.subtitle=element_text(size=6.7,margin=margin(,,3)),
  plot.title=element_text(size=7.2,face=2,margin=margin(1,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.2,height=3,dpi=400*4)
system("magick 1.png -resize 25% -colorspace gray -dither none -colors 16 1.png")

Added in December 2024: Ethical Skeptic now posted an updated version of the plot for the MCD to UCD ratio which included a note that said "Because Wonder does not offer 2017 weekly data, 2017 weekly data reflects the correct total for the year but is a week-by-week apportionment by combined 2018/19 arrival forms": [https://x.com/EthicalSkeptic/status/1866674708239855796]

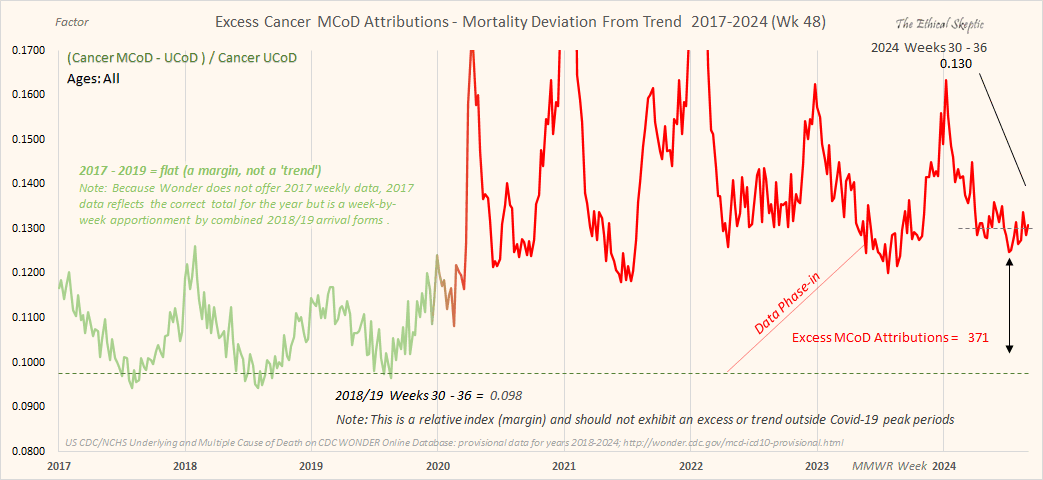
I don't understand what he meant or how he calculated the line for 2017. At first I thought it might have meant an average of the lines for 2018 and 2019, because for example 2019 has a much lower ratio during the first weeks of the year than 2018, but 2017 is roughly halfway between 2018 and 2019 during the first weeks of the year. However the line for 2017 can't be a simple average of 2018 and 2019, because the line for 2017 has a much more similar shape to the line for 2018 than to the line for 2019. And also his plot doesn't seem to reflect the correct total for the year 2017, because the MCD to UCD ratio in 2017 should be about 1.1015 which is much lower than the average ratio for 2017 in his plot:

> t=fread("http://sars2.net/f/wondermalignantyearly.csv")
> a=merge(t[cause%like%"MCD",.(mcd=sum(dead)),year],t[cause%like%"UCD",.(ucd=sum(dead)),year])
> a[year>=2015,.(year,mcd,ucd,ratio=mcd/ucd)]|>print(r=F)
 year    mcd    ucd    ratio
 2015 652659 595919 1.095214
 2016 656189 598031 1.097249
 2017 659896 599099 1.101481
 2018 662624 599265 1.105728
 2019 664750 599589 1.108676
 2020 703154 602347 1.167357
 2021 717005 605206 1.184729
 2022 723433 608366 1.189141
 2023 705468 613361 1.150168
 2024 498951 460627 1.083200

From this plot where I imposed real monthly data for 2017 on top of Ethical Skeptic's fake weekly data for 2017, you can also see that his ratio is too high in 2017:

library(data.table);library(ggplot2)

t=fread("http://sars2.net/f/wondermalignantmonthly.csv")
t=dcast(t,date~cause)
lab=c("MCD COVID not subtracted","MCD COVID subtracted")
p=t[,.(x=as.Date(paste0(date,"-1")),y=100*c(t[[2]]/t[[5]],(t[[2]]-t[[3]])/t[[5]]),z=factor(rep(lab,each=.N),lab))]

ystart=108;yend=117;ybreak=ystart:yend
xstart=as.Date("2017-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")

ggplot(p,aes(x+15,y))+
geom_vline(xintercept=c(xstart),color="magenta",linewidth=.2,lineend="square")+
geom_hline(yintercept=c(ystart),color="magenta",linewidth=.2,lineend="square")+
geom_point(aes(color=z),shape=3,stroke=.3,size=1)+
labs(x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.2,xend+.5),breaks=xbreak,labels=xlab)+
scale_y_continuous(breaks=ybreak)+
scale_color_manual(values=c("magenta","#660066"))+
coord_cartesian(ylim=c(ystart,yend),clip="off",expand=F)+
theme(axis.text=element_blank(),
  axis.ticks=element_line(linewidth=.2,color="magenta"),
  axis.ticks.x=element_line(color=alpha("magenta",c(1,0))),
  legend.position="none",
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.background=element_rect(fill="transparent",color=NA))
ggsave("1.png",width=5.5,height=2.2,dpi=400)

Added in February 2025: The Twitter user yukatapangolin posted the plot below and wrote: "ES applies his 'excess MCOD normalization' starting in '22 because he believes that's when the CDC began switching the underlying cause of death in cancer cases to COVID. He posted this chart showing an increase in MCoD Cancer as a percentage of UCoD COVID https://theethicalskeptic.com/2022/10/24/houston-the-cdc-has-a-problem-part-2-of-3/" [https://x.com/yukatapangolin/status/1891685788615680344]

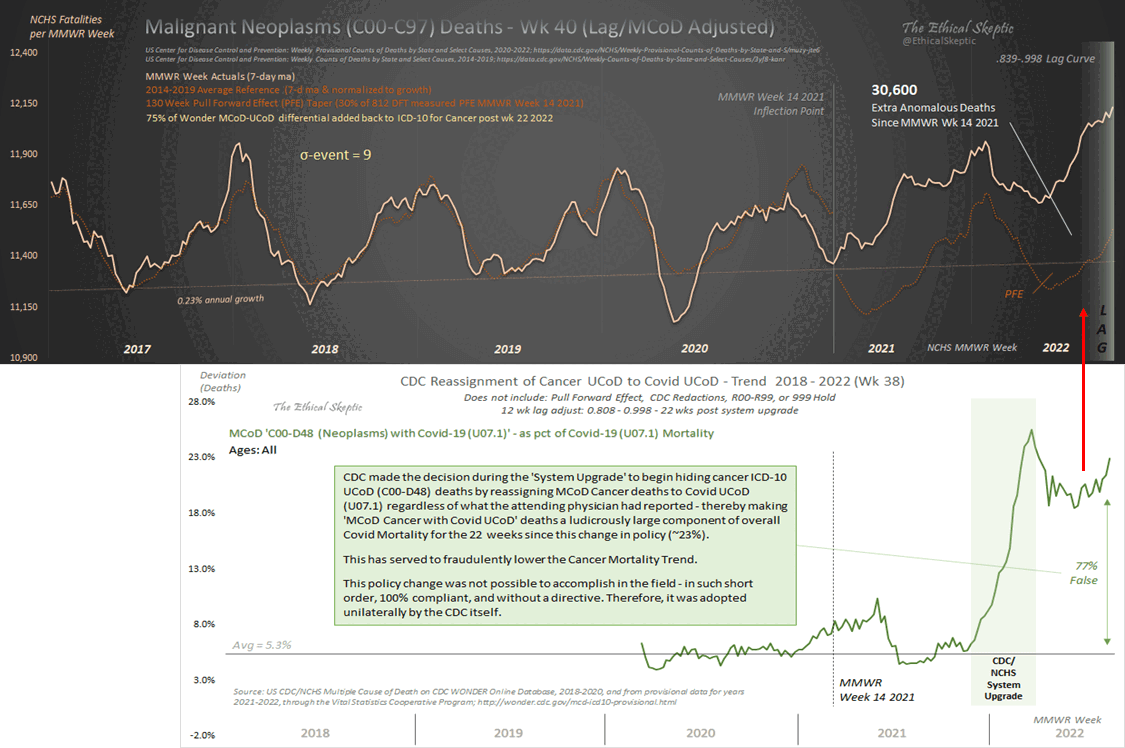
And yukatapangolin also posted the plot below and wrote: "I was able to reproduce his chart, but as it happens, he made a mistake when calculating the percentage. Instead of dividing by MCD Cancer and Covid *UCD* (as it says in his chart) he divided by MCD Cancer and Covid *MCD*":

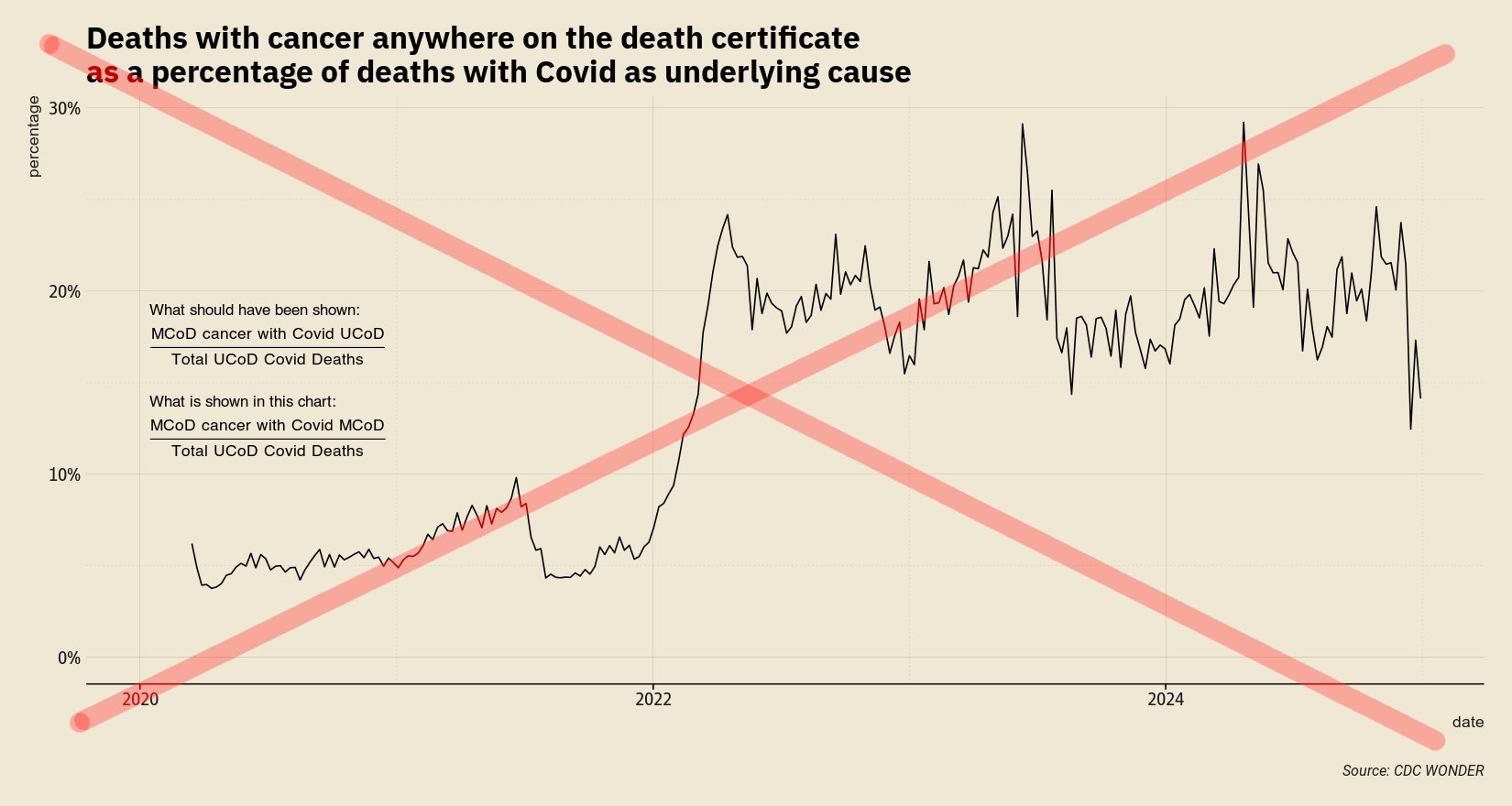
I don't even remember seeing the plot by ES above, so maybe he realized himself the plot was wrong so he stopped posting it. But he still kept doing the excess MCD adjustment regardless, even though he appears to have originally justified it based on an erroneoues plot.

So basically the MCD to UCD ratio for COVID deaths increased after Omicron, which explains why there was an increase in 2022 in the ratio of "(MCD cancer and MCD COVID) / UCD COVID":

v=fread("curl -Ls sars2.net/f/vital.csv.xz|xz -dc")
o=v[cause=="U071",.(ucd=sum(ucd),mcd=sum(mcd)),.(year,quarter=(month+2)%/%3)]
print(o[,mcdtoucdratio:=round(mcd/ucd,2)][],r=F)
# year quarter    ucd    mcd mcdtoucdratio
# 2020       1   6769   7287          1.08
# 2020       2 112777 124056          1.10
# 2020       3  71920  83092          1.16
# 2020       4 159365 183131          1.15
# 2021       1 158589 182251          1.15
# 2021       2  35185  42991          1.22
# 2021       3 114134 128386          1.12
# 2021       4 108985 124774          1.14
# 2022       1 124395 156124          1.26
# 2022       2  14692  23939          1.63 # MCD to UCD ratio of COVID
# 2022       3  25292  39498          1.56 # deaths went up after Omicron
# 2022       4  22173  34794          1.57
# 2023       1  20648  32039          1.55
# 2023       2   6832  11472          1.68
# 2023       3   8394  12615          1.50
# 2023       4  14058  21138          1.50

However there was in fact also a big increase in the ratio of "(MCD cancer and UCD COVID) / UCD COVID" in 2022. But I think the increase in the ratio was due to Omicron, because the shape of the curve for the ratio closely follows the curve of the MCD to UCD COVID ratio:

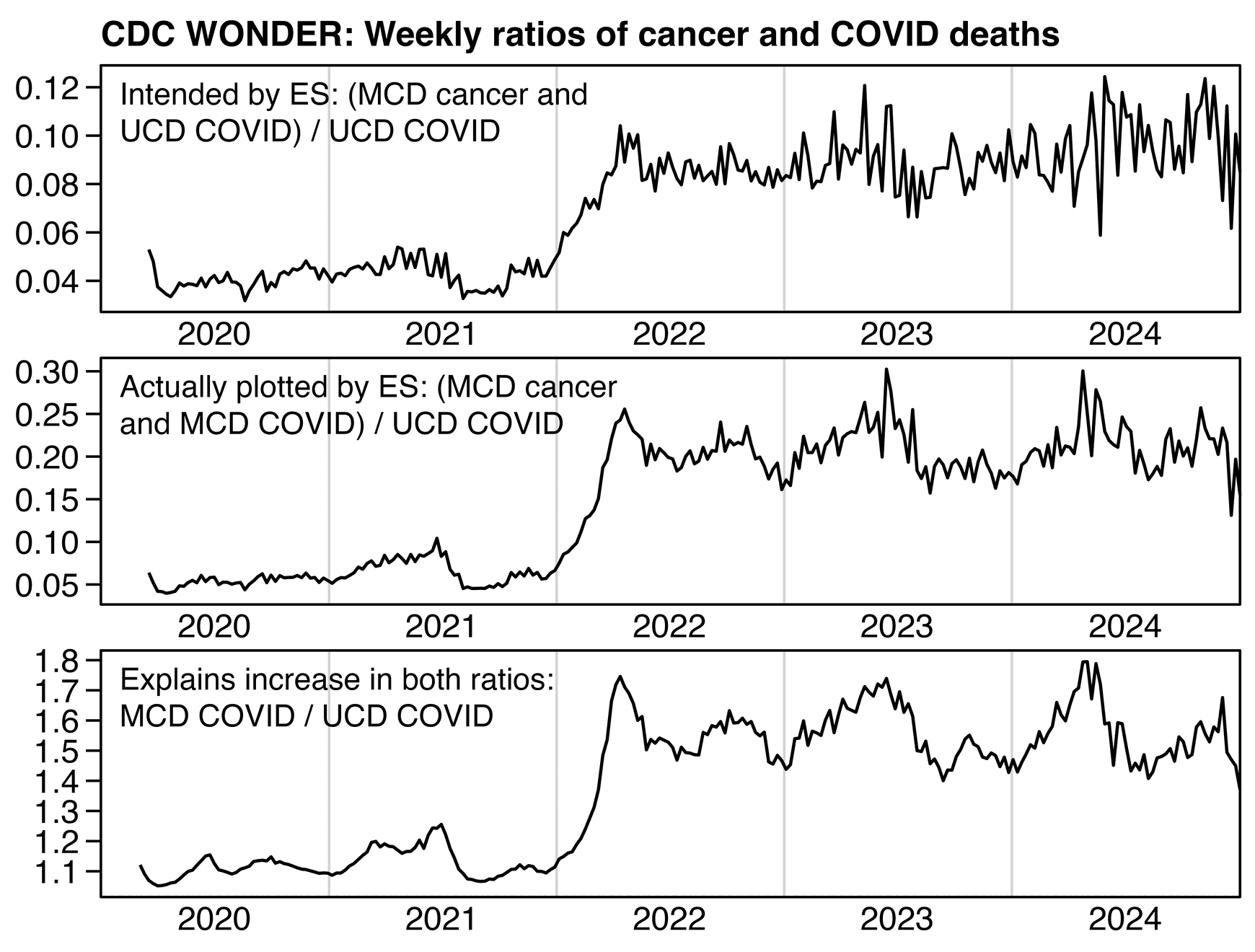
library(data.table);library(ggplot2);library(lubridate)

t=fread("http://sars2.net/f/wondermcdcanceranducdcovid.csv")
t=dcast(t,date~type)

lab=c("(MCD cancer and UCD COVID) / UCD COVID","(MCD cancer and MCD COVID) / UCD COVID","MCD COVID / UCD COVID")
p=t[,.(x=date-3,y=c(mcd_cancer_and_ucd_covid,mcd_cancer_and_mcd_covid,mcd_covid)/ucd_covid,z=factor(rep(lab,each=.N),lab))]
p=na.omit(p)

xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=ifelse(month(xbreak)==7,year(xbreak),"")

ggplot(p,aes(x,y))+
facet_wrap(~z,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray83",linewidth=.4)+
geom_text(data=p[,max(y),z],aes(label=z,y=V1),x=xstart+30,hjust=0,vjust=1.4,size=3.6)+
geom_line()+
labs(x=NULL,y=NULL,title="CDC WONDER: Weekly ratios of cancer and COVID deaths")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab,expand=expansion(0,0))+
scale_y_continuous(breaks=\(x)pretty(x,7))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=11,color="black"),
  axis.text.x=element_text(margin=margin(3)),
  axis.ticks=element_line(linewidth=.4,color="black"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.ticks.length.y=unit(5,"pt"),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.4),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(5,5,5,5),
  plot.title=element_text(size=11.5,face=2,margin=margin(2,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.8,height=4.4,dpi=300*4)
system("magick 1.png -resize 25% -colorspace gray -colors 64 1.png")

The Twitter user yukatapangolin also posted the plot below and wrote "You could probably use a similar argument to the one ES uses to prove that the vaccine gives you AIDS": [https://x.com/yukatapangolin/status/1891955439996141658]

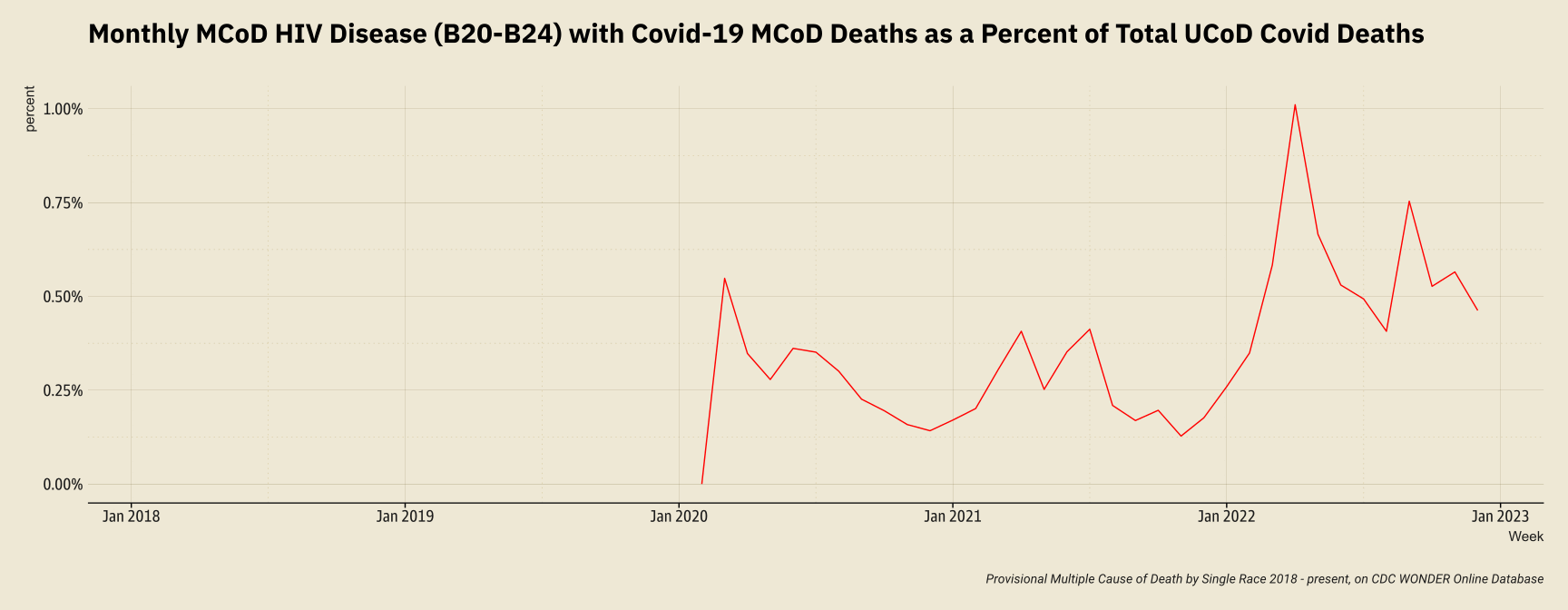
Added in September 2025: I now noticed that the distance of the line with "excess MCOD normalization" continues to rise further above the undadjusted deaths even after week 20 of 2023. So I don't know if ES manually shifted the deaths upwards:

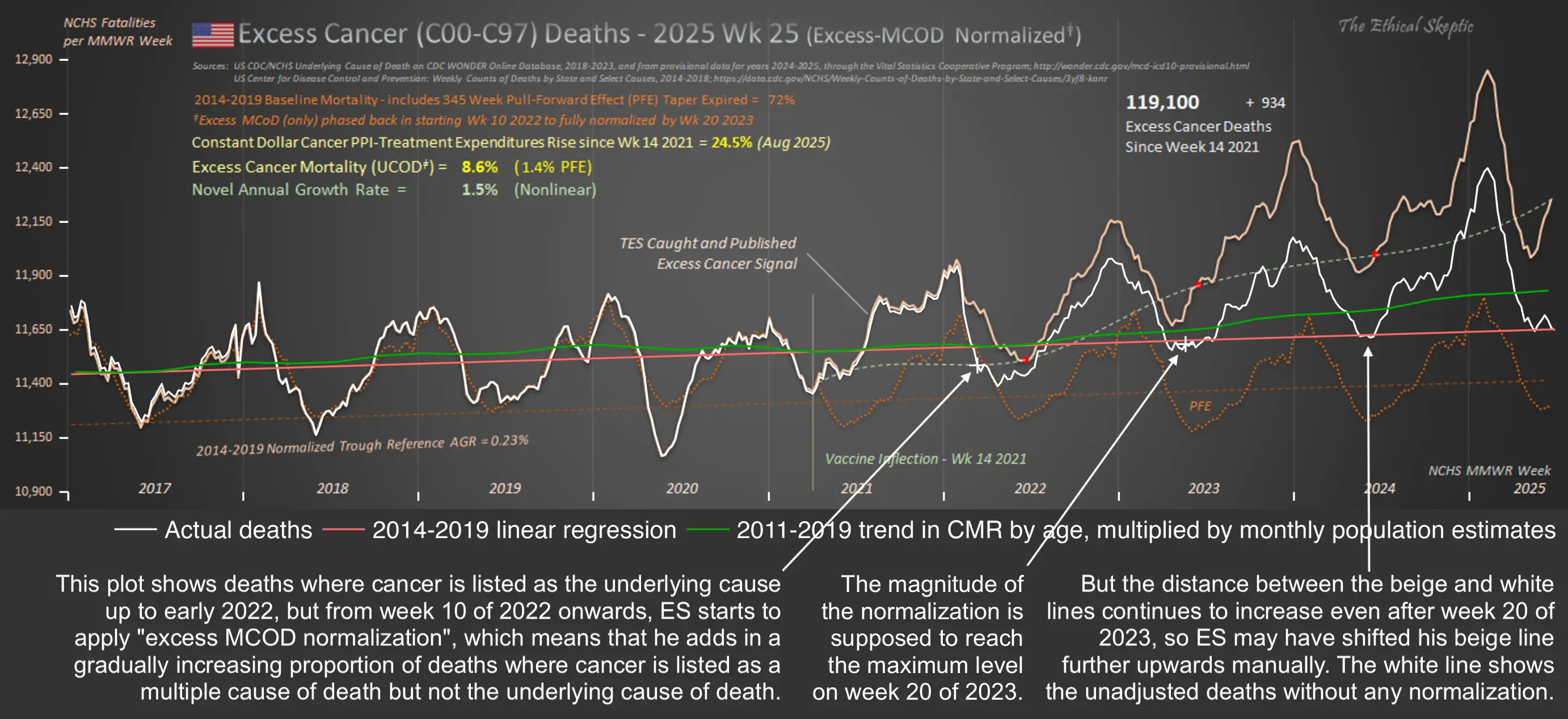
t=fread("https://sars2.net/f/wondermalignantweekly.csv")[,.(year,week,dead)]

old=fread("https://sars2.net/f/Weekly_Counts_of_Deaths_by_State_and_Select_Causes__2014-2019.csv.gz")
old=old[`Jurisdiction of Occurrence`=="United States"]
t=rbind(old[,.(year=`MMWR Year`,week=`MMWR Week`,dead=`Malignant neoplasms (C00-C97)`)][year<2018],t)

p=t[,.(x=MMWRweek::MMWRweek2Date(year,week,7),y=ma(dead,3,2),z="Actual deaths")]
p=rbind(p,p[,.(x,y=predict(lm(y~x,p[year(x)<2020]),p),z="2014-2019 linear regression")])

v=fread("curl -Ls sars2.net/f/vital.csv.xz|xz -dc")
v=v[year%in%2011:2019&age!=999][substr(cause,1,1)=="C"]
a=v[,.(dead=sum(ucd)),.(year,month,age=pmin(age,100))]
a=merge(do.call(CJ,lapply(a[,1:3],unique)),a,all=T)[is.na(dead),dead:=0]
a=merge(a,fread("https://sars2.net/f/uspopdeadmonthly.csv")[,.(year,month,age,pop=persondays)],all=T)
a=a[year>=2011]
a[,date:=as.Date(paste(year,month,15,sep="-"))]
a=a[,cbind(.SD,base=predict(lm(dead/pop~date,.SD[year<2020]),.SD)*pop),age]
p2=a[,.(y=sum(base),z="2011-2019 trend in CMR by age, multiplied by monthly population estimates"),.(x=date)]
p2[,y:=y/days_in_month(x)*7]

p=rbind(p,p2)[,z:=factor(z,unique(z))]
p=p[year(x)>=2017]

xstart=as.Date("2017-1-1");xend=as.Date("2025-7-1");xbreak=seq(xstart,xend-1,"6 month")
xlab=ifelse(month(xbreak)==7,year(xbreak),"")
ystart=10900;yend=12900;ybreak=seq(ystart,yend,250)

ggplot(p)+
geom_line(aes(x,y,color=z,linewidth=z))+
labs(x=NULL,y=NULL)+
geom_point(data=p[z==z[1]&x%in%MMWRweek2Date(2022:2023,c(10,20),7)],aes(x,y),shape=3,color="white",stroke=.6,size=1.8)+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=c("white","#ff6666","#00aa00"))+
scale_linewidth_manual(values=c(.4,.4,.4))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_blank(),
  axis.ticks=element_line(color="white",linewidth=.4),
  axis.ticks.length=unit(4,"pt"),
  axis.ticks.x=element_line(color=alpha("white",1:0)),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="right",
  legend.key=element_blank(),
  legend.key.height=unit(12,"pt"),
  legend.key.spacing.x=unit(2,"pt"),
  legend.key.width=unit(24,"pt"),
  legend.margin=margin(7),
  legend.position="bottom",
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(color="white",size=11,margin=margin(,,,1)),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.grid=element_blank(),
  plot.background=element_rect(fill="transparent",color=NA))
ggsave("1.png",width=9.5,height=3.2,dpi=300*2)

Files for US population estimates by single year of age

The population estimates used by CDC WONDER have several shortcomings, which are corrected by my code below:

In the following code I combine 4 sets of population estimates: official intercensal estimates for 2000-2009, DIY intercensal estimates for 2010-2019, vintage 2024 estimates for 2020-2024, and modified 2023 population projections for 2025-2030. [https://www2.census.gov/programs-surveys/popest/datasets/2000-2010/intercensal/national/, https://www2.census.gov/programs-surveys/popest/datasets/2010-2020/national/asrh/, https://www2.census.gov/programs-surveys/popest/datasets/2020-2024/national/asrh/, https://www2.census.gov/programs-surveys/popproj/datasets/2023/2023-popproj/]

In order to get rid of a sudden jump in population size at the point when the 2010-based and 2020-based estimates are merged, I applied DIY intercensal adjustment to the 2010-based estimates, so that I multiplied the population estimates for each age with a linear slope so that they were equal to the 2020-based estimates in 2020. For example for age 80, the 2020-based estimate for 2020 is 1,450,397 and the 2010-based estimate for 2020 is 1,526,957, so their ratio is about 0.9499, so I'm multiplying the 2010-based estimate by about .9+.1*0.9499 for 2011, by about .8+.2*0.9499 for 2012, and so on.

The Census Bureau does not publish population projections each year, so when I wrote this, the newest available population projections were from 2023. The population projections are not harmonized to match the resident population estimates, so some ages have a fairly big difference between the mid-2023 resident population estimate and the population projection for 2023. So for each age, I multiplied the population projections for 2025-2030 by the ratio between the mid-2023 resident population estimate and the mid-2023 population projection.

Here's the code that combines the different sets of population estimates, and which also includes a column for the yearly number of deaths from CDC WONDER:

old=fread("https://www2.census.gov/programs-surveys/popest/datasets/2010-2020/national/asrh/nc-est2020-agesex-res.csv")
new=fread("https://www2.census.gov/programs-surveys/popest/datasets/2020-2024/national/asrh/nc-est2024-agesex-res.csv")
older=fread("https://www2.census.gov/programs-surveys/popest/datasets/2000-2010/intercensal/national/us-est00int-alldata.csv")
older5=fread("https://www2.census.gov/programs-surveys/popest/datasets/2000-2010/intercensal/national/us-est00int-alldata-5yr.csv")

old=old[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:4)]),year=rep(2010:2020,each=.N))]
new=new[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:3)]),year=rep(2020:2024,each=.N))]

# get ratio between 2020-based and 2010-based population estimates for each age in 2020
o=merge(merge(old[year==2020,.(age,old=pop)],new[year==2020,.(age,new=pop)])[,.(age,ratio=new/old)],old)

# multiply 2010-based population estimates by a linear slope so they match 2020-based estimates in 2020
o=rbind(o[year!=2020,.(year,age,pop=round(pop*(1-(((year-2010)/10))*(1-ratio))))],new)

# use 2000-2010 intercensal estimates for 2000-2009 (only 5-year age groups are available for ages 85 and above)
o=rbind(older[YEAR!=2010&AGE<85&MONTH==7,.(pop=sum(TOT_POP)),.(year=YEAR,age=AGE)],o)
o=rbind(older5[year!=2010&month==7&AGEGRP%in%18:21,.(age=17:20*5,pop=TOT_POP),year],o)

# include population projections for 2025-2060 adjusted to match 2023 resident population estimates in 2023
proj=fread("https://www2.census.gov/programs-surveys/popproj/datasets/2023/2023-popproj/np2023_d1_mid.csv")
proj=proj[SEX==0&ORIGIN==0&RACE==0&YEAR%in%2023:2030,.(year=YEAR,age=rep(0:100,each=.N),pop=unlist(.SD[,-(1:5)]))]
mult=o[year==2023,pop]/proj[year==2023]$pop
o=rbind(o,proj[,pop:=pop*mult[age+1]][year>=2025])

# add a column for yearly deaths from CDC WONDER (downloaded in August 2025)
o=merge(o,na.omit(fread("https://sars2.net/f/usyearlydead.csv")),all=T)

fwrite(o[order(year,age)],"uspopdead.csv",na="")

I uploaded the output here: f/uspopdead.csv.

This code generates a similar file for monthly population estimates in 2010-2025:

u="https://www2.census.gov/programs-surveys/popest/datasets/"
t1=do.call(rbind,lapply(sprintf("%s2010-2020/national/asrh/NC-EST2020-ALLDATA-R-File%02d.csv",u,1:24),fread))
t2=do.call(rbind,lapply(sprintf("%s2020-2024/national/asrh/nc-est2024-alldata-r-file%02d.csv",u,1:12),fread))

old=t1[YEAR!=2021&MONTH!=4.2&AGE!=999,.(year=YEAR,month=floor(MONTH),age=AGE,pop=TOT_POP)]
new=t2[AGE!=999,.(year=YEAR,month=floor(MONTH),age=AGE,pop=TOT_POP)]

mult=new[year==2020&month==4,pop]/old[year==2020&month==4,pop]
old=old[!(year==2020&month>=4)]
old[,pop:={x=rleid(year,month);x=(x-1)/max(x);round(pop*(x*mult[age+1]+1-x))}]

dead=fread("https://sars2.net/f/usdeadmonthly.csv") # downloaded from CDC WONDER in July 2025
o=merge(rbind(old,new),dead,all=T)
o[,date:=sprintf("%d-%02d",year,month)]
o[,persondays:=pop*lubridate::days_in_month(as.Date(paste0(date,"-1")))]
fwrite(o,"uspopdeadmonthly.csv")

I uploaded the output here: f/uspopdeadmonthly.csv. The vintage 2024 monthly population estimates conveniently also included population projections for 2025, but for some reason the population projections for 2025 were not included in the vintage 2024 yearly population estimates.

This shows that particularly ages 90+ have a huge jump in population size between the switch from the estimates based on the 2010 census to the estimates based on the 2020 census:

library(data.table);library(ggplot2)

agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)

kim=\(x)ifelse(x>=1e3,ifelse(x>=1e6,paste0(x/1e6,"M"),paste0(x/1e3,"k")),x)

new=fread("https://www2.census.gov/programs-surveys/popest/datasets/2020-2023/national/asrh/nc-est2023-agesex-res.csv")
old=fread("https://www2.census.gov/programs-surveys/popest/datasets/2010-2020/national/asrh/nc-est2020-agesex-res.csv")

old=old[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:4)]),year=rep(2010:2020,each=.N))]
new=new[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:3)]),year=rep(2020:2023,each=.N))]

me=merge(merge(old[year==2020,.(age,old=pop)],new[year==2020,.(age,new=pop)])[,.(age,ratio=new/old)],old)
p=rbind(me[year!=2020,.(year,age,pop=round(pop*(1-(((year-2010)/10))*(1-ratio))))],new)
p$group="2011-2019 estimates multiplied by a linear slope"

p=rbind(p,rbind(old[year!=2020],new)[,group:="Unadjusted"])
p[,group:=factor(group,unique(group))]

p=p[,.(pop=sum(pop)),.(group,year,age=agecut(age,0:9*10))]

xstart=2010;xend=2023
p=p[year%in%xstart:xend]

levels(p$age)=p[year==2019,sprintf("%s (%.1f%%)",age,(pop[group!="Unadjusted"]/pop[group=="Unadjusted"]-1)*100)]

ggplot(p,aes(x=year,y=pop,color=group))+
coord_cartesian(clip="off",expand=F)+
facet_wrap(~age,ncol=2,dir="v",scales="free_y")+
geom_vline(xintercept=c(2014.5,2019.5),color="gray80",linewidth=.23)+
geom_line(linewidth=.3)+
geom_point(stroke=0,size=.7)+
labs(title="Mid-year resident population estimates by US Census Bureau",subtitle="The number after the age group shows the percentage change between the unadjusted and adjusted estimates for 2019."|>stringr::str_wrap(78),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart-.5,xend+.5,.5),labels=c(rbind("",xstart:xend),""))+
scale_y_continuous(labels=kim,breaks=\(x)pretty(x,3))+
scale_color_manual(values=c("gray60","black"))+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.2,color="black"),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.justification="right",
  legend.key=element_blank(),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.margin=margin(,,-2),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.23),
  panel.spacing=unit(-2,"pt"),
  panel.spacing.x=unit(3,"pt"),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=7,margin=margin(,,3)),
  plot.title=element_text(size=7.4,face=2,margin=margin(1,,4)),
  strip.background=element_blank(),
  strip.text=element_text(size=7,vjust=-.3))
ggsave("1.png",width=4.4,height=4.4,dpi=350*4)
system("magick 1.png -resize 25% 1.png")

The reason why the population size of ages 90+ decreased by over 10% in the new population estimates might partially be due to COVID deaths in case COVID deaths are accounted for in the mid-year population estimates for 2020. But COVID deaths would probably only explain a small part of the decrease, because in the first half of 2020 CDC WONDER returned 21,600 deaths with UCD COVID in ages 90+, which is only about 0.9% of the total population size of ages 90+ based on the vintage 2023 resident population estimates for the year 2020. However in case the population estimates are calculated based on yearly data for deaths, it might also be that the mid-year population estimates for 2020 are affected by COVID deaths in the second half of 2020, but even in the whole of 2020 the number of COVID deaths in ages 90+ was only about 2.5% of the resident population estimate for ages 90+ in 2020.

There's often fairly large changes to old population estimates in newer vintages. For example the resident population estimate of ages 80-84 in 2021 was increased by about 1.9% between the 2021 and 2022 vintages, but it was again reduced by about 1.8% between the 2022 and 2023 vintages:

r=do.call(rbind,lapply(2020:2023,\(x){
  t=fread(paste0("https://www2.census.gov/programs-surveys/popest/datasets/",ifelse(x==2020,2010,2020),"-",x,"/national/asrh/nc-est",x,"-agesex-res.csv"))
  t[SEX==0&AGE!=999,.(vintage=x,year=rep(as.integer(sub("\\D+","",names(.SD))),each=.N),age=AGE,pop=unlist(.SD,,F)),.SDcols=patterns("POPESTIMATE")]}))

r[year>=2020&age%in%80:84,xtabs(pop~year+vintage)]
#       vintage
# year      2020    2021    2022    2023
#   2020 6464714 6155000 6288784 6160937
#   2021       0 6301306 6422252 6308178
#   2022       0       0 6659545 6557159
#   2023       0       0       0 6980680


t2=fread("http://sars2.net/f/wondercanceryearlysingle.csv")
t2[age%in%80:84&year==2021,sum(pop)]
# 6301306 (CDC WONDER still uses vintage 2021 estimates for 2021)

The next plot shows how the 2000-2010 intercensal estimates have been adjusted to get rid of the jump between the 2000-based and 2010-based population estimates. The 2010-2020 intercensal estimates are only scheduled to be published in 2025, but they will probably look similar to my gray line below where I used the same method as in the code above to adjust the population estimates:

library(data.table);library(ggplot2)

agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)

kim=\(x)ifelse(x>=1e3,ifelse(x>=1e6,paste0(x/1e6,"M"),paste0(x/1e3,"k")),x)

new=fread("https://www2.census.gov/programs-surveys/popest/datasets/2020-2023/national/asrh/nc-est2023-agesex-res.csv")
old=fread("https://www2.census.gov/programs-surveys/popest/datasets/2010-2020/national/asrh/nc-est2020-agesex-res.csv")

old=old[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:4)]),year=rep(2010:2020,each=.N))]
new=new[SEX==0&AGE!=999,.(age=AGE,pop=unlist(.SD[,-(1:3)]),year=rep(2020:2023,each=.N))]

older=fread("https://www2.census.gov/programs-surveys/popest/tables/2000-2010/intercensal/national/us-est00int-01.csv")
older=older[6:26,c(1,3:12,14)][,.(age=as.numeric(sub("\\D*(\\d+).*","\\1",sub("Under 5",0,V1))),pop=as.numeric(gsub(",","",unlist(.SD[,-1]))),year=rep(2000:2010,each=.N))]

oldest=fread("https://www2.census.gov/programs-surveys/popest/tables/2000-2009/national/asrh/nc-est2009-01.csv")
oldest=oldest[6:26,c(1,2:11)][,.(age=as.numeric(sub("\\D*(\\d+).*","\\1",sub("Under 5",0,V1))),pop=as.numeric(gsub(",","",unlist(.SD[,-1]))),year=rep(2009:2000,each=.N))]

mult=merge(old[year==2020],new[year==2020,.(age,new=pop)])[,.(ratio=new/pop,age)]
mult=merge(old,mult)[,mult:=(year-2010)/10]
mult=mult[,.(age,year,pop=((1-mult)*1+mult*ratio)*pop)]

won=fread("http://sars2.net/f/wondercanceryearlysingle.csv")[age<85,.(year,pop,age)]
won=rbind(won,fread("http://sars2.net/f/wondercanceryearlyten.csv")[cause==cause[1]&age==85,.(year,pop,age)])

p=cbind(oldest,z="2000-2009")
p=rbind(p,cbind(older,z="2000-2010 intercensal"))
p=rbind(p,cbind(old,z="2010-2020"))
p=rbind(p,cbind(mult,z="2010-2020 multiplied by linear slope"))
p=rbind(p,cbind(new,z="2020-2023"))
p=rbind(p,cbind(won,z="CDC WONDER"))

p[,z:=factor(z,unique(z))]

ages=0:4*20
ages=c(0,25,45,65,75,85)

p=p[,.(pop=sum(pop)),.(z,year,age=agecut(age,ages))]

xstart=2000;xend=2023
p=p[year%in%xstart:xend]

ggplot(p,aes(x=year,y=pop))+
coord_cartesian(clip="off")+
facet_wrap(~age,ncol=2,dir="v",scales="free_y")+
geom_vline(xintercept=c(2009.5,2019.5),color="gray80",linewidth=.23)+
geom_line(aes(color=z,alpha=z),linewidth=.3)+
geom_point(aes(color=z,shape=z,size=z),stroke=.3)+
geom_text(fontface=2,data=p[,max(pop),age],aes(label=paste0("\n   ",age,"   \n"),y=V1),x=xstart-.5,lineheight=.4,hjust=0,vjust=1,size=grid::convertUnit(unit(7,"pt"),"mm"))+
labs(title="Mid-year US resident population estimates by age group",subtitle="Source: www2.census.gov/programs-surveys/popest/datasets and CDC WONDER.",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart-.5,xend+.5,.5),labels=c(rbind("",ifelse(xstart:xend%%2==0,xstart:xend,"")),""),expand=expansion(0))+
scale_y_continuous(labels=kim,breaks=\(x)Filter(\(y)y>min(x)+(max(x)-min(x))*.05,pretty(x,4)),expand=expansion(.04))+
scale_color_manual(values=c("#0055ff","#8844ff","#ff55ff","gray50","#ff5555","black"))+
scale_shape_manual(values=c(16,16,16,16,16,4))+
scale_alpha_manual(values=c(1,1,1,1,1,0))+
scale_size_manual(values=c(.7,.7,.7,.7,.7,1))+
guides(color=guide_legend(ncol=2,byrow=F))+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.2,color="black"),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.justification="left",
  legend.key=element_blank(),
  legend.key.height=unit(8,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.margin=margin(-2,,4),
  legend.position="top",
  legend.spacing.x=unit(2,"pt"),
  legend.spacing.y=unit(1,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.23),
  panel.spacing.x=unit(3,"pt"),
  panel.spacing.y=unit(3,"pt"),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=6.9,margin=margin(,,4)),
  plot.title=element_text(size=7.4,face=2,margin=margin(1,,3)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4,height=3,dpi=350*4)
system("magick 1.png -resize 25% 1.png")

So if you need to combine my files for the modified population estimates with older population estimates for 2000-2009, you can just use the 2000-2010 intercensal estimates. This file has population estimates by single year of age up to ages 85+: https://www2.census.gov/programs-surveys/popest/datasets/2000-2010/intercensal/national/us-est00int-alldata.csv. This file has population estimates by 5-year age groups up to ages 100+: https://www2.census.gov/programs-surveys/popest/tables/2000-2010/intercensal/national/us-est00int-01.csv. Both files are identical to the population sizes used by CDC WONDER:

inter1=fread("https://www2.census.gov/programs-surveys/popest/datasets/2000-2010/intercensal/national/us-est00int-alldata.csv")
inter5=fread("https://www2.census.gov/programs-surveys/popest/tables/2000-2010/intercensal/national/us-est00int-01.csv")
wonder=fread("http://sars2.net/f/wondercanceryearlysingle.csv")

inter1[YEAR==2009&MONTH==7&AGE%in%70:74,sum(TOT_POP)] # 9140722
inter5[which(inter5[[1]]==".70 to 74 years")[1],unlist(.SD),.SDcols=which(inter5[4]==2009)] # "9,140,722"
wonder[year==2009&age%in%70:74,sum(pop)] # 9140722

Added later: Apparently SEER has also published their own intercensal population estimates for 2010-2019: https://seer.cancer.gov/endofdecade-pops/. They look similar to my DIY intercensal estimates:

Cancer deaths by age group

Ethical Skeptic posted the images below and wrote: [https://x.com/EthicalSkeptic/status/1841879475241300326]

Competence Question: If young age-bracket cancer mortality is up 20+%, while old age-bracket cancer mortality is down 3 to 6% due to PFE pool depletion, what is the underlying rate of cancer increase?

Answer: The young age bracket rate. Especially in the circumstance where the former young rate was negative (prior to inflection).

Beware of analysts who don't comprehend this.

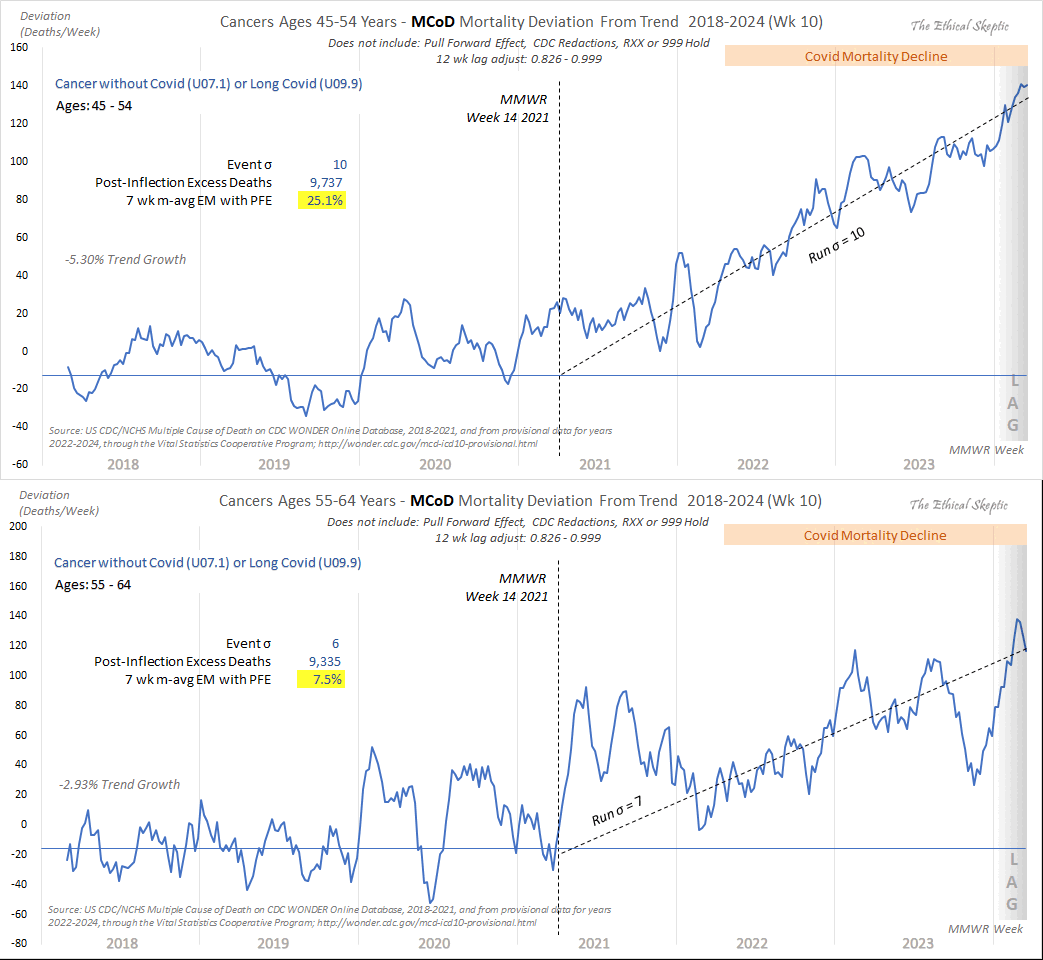
<img src=i/ ethical-cancerage-2.webp width=70>

In his plots which display weekly deaths starting from 2018, I believe Ethical Skeptic calculates some kind of a linear baseline based on data from 2018 and 2019 only, because he erroneously believes that CDC WONDER has different suppression behavior for the data before 2018 than the data from 2018 onwards. When I asked him that isn't a trend that is only fitted against data from 2018 and 2019 biased because there was a low number of deaths in 2019 and a high number of deaths in early 2018, he answered that the method he uses to fit the baseline is somehow different from a regular linear regression, but he didn't explain how: "However, I did not use a pure linear regression of 2018 and 19 for this reason. I fit the baseline to the variances linearly, but not by least-squares regression (how I avoided the early 2018 surge)." [https://theethicalskeptic.substack.com/p/the-state-of-things-pandemic-week-706/comment/53237226]

But in any case, fitting a linear trend based on raw deaths is inaccurate, and it's especially inaccurate when you're fitting the trend based on only two years of data. And it's even more inaccurate if you're plotting deaths within an age group 75 to 84, because its population size has increased dramatically since 2021 because the baby boomers started turning 75 in 2021.

In the next plot I believe the gray 2018-2019 baseline is somewhat similar to the baseline used by Ethical Skeptic, except he fits his baseline using weekly and not yearly data, and his method of regression might be somehow different from the regular linear regression I used here. But anyway I calculated the black baseline using a more accurate method, where for each single year of age I first calculated the linear trend in crude mortality rate in 2010 to 2019, and then I multiplied the value of the projected linear trend with the population size to get the expected deaths for each age. My method of calculating the baseline gave me close to 0% excess mortality each year since 2020 for ages 85+. But my plot also shows that the 2018-2019 linear trend is way too high in ages 85+, which probably explains why Ethical Skeptic got such low excess mortality in ages 85+:

library(data.table);library(ggplot2)

agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)

kim=\(x)ifelse(x>=1e3,ifelse(x>=1e6,paste0(x/1e6,"M"),paste0(x/1e3,"k")),x)

t=fread("http://sars2.net/f/wondermalignantyearly.csv")
t=t[year%in%2010:2023&cause%like%"MCD"]
t=merge(t[!cause%like%"COVID"],t[cause%like%"COVID",.(year,age,and=dead)],all=T)

# Some ages below 45 have less than 10 deaths with both MCD cancer and
# MCD COVID per year, so the deaths are suppressed when the results
# are grouped by single year of age, but here I retrieved deaths for
# ages 0-44 aggregated together to avoid the supression.
t[age<45,and:=0][age==0&year>=2020,and:=c(311,495,477,130)]

t=t[,.(year,age,dead=dead-nafill(and,,0))]

t=merge(t,fread("http://sars2.net/f/uspopdead.csv")[,dead:=NULL])

t=merge(t,t[year%in%2010:2019,.(year=2010:2023,trend=predict(lm(dead/pop~year),.(year=2010:2023))),age])

p=t[,.(dead=sum(dead),base=sum(trend*pop)),.(year,group=agecut(age,c(0,45,55,65,75,85)))]

p=p[p[year%in%2018:2019,.(year=2010:2023,linear=predict(lm(dead~year),.(year=2010:2023))),group],on=c("group","year")]

minmax=p[,.(min=min(dead,base,linear),max=max(dead,base,linear)),group]
p=merge(minmax[,.(group,min=max/minmax[,max(max/min)])],p)

xstart=2010;xend=2023

p=p[,.(group,year,min,y=c(dead,base,linear),z=rep(c("Actual deaths","2010-2019 trend in CMR by age","2018-2019 linear trend for raw deaths"),each=.N))]
p[,z:=factor(z,unique(z))]

ggplot(p,aes(year,y))+
facet_wrap(~group,ncol=2,dir="v",scales="free_y",strip.position="top")+
geom_vline(xintercept=c(2014.5,2019.5),color="gray85",linewidth=.25)+
geom_line(aes(color=z,linetype=z),linewidth=.3)+
geom_point(data=p[z=="Actual deaths"],stroke=0,size=.6,show.legend=F)+
geom_point(aes(y=min),size=0,stroke=0)+
labs(title="CDC WONDER: Yearly deaths with MCD malignant neoplasms but not MCD COVID",x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart-.5,xend+.5,.5),labels=c(rbind("",xstart:xend),""))+
scale_y_continuous(labels=kim)+
scale_color_manual(values=c("black","black","gray60"))+
scale_linetype_manual(values=c(1,2,2))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.ticks=element_line(linewidth=.3,color="black"),
  axis.ticks.length=unit(.2,"lines"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.key=element_blank(),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.position="top",
  legend.margin=margin(2,,),
  legend.justification="left",
  legend.spacing.x=unit(2,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3),
  panel.spacing=unit(0,"pt"),
  panel.spacing.x=unit(3,"pt"),
  plot.margin=margin(5,5,5,5),
  plot.title=element_text(size=7.6,face=2,margin=margin(2,,2)),
  strip.background=element_blank(),
  strip.text=element_text(size=7))
ggsave("1.png",width=5,height=4.1,dpi=380*4)
system("magick 1.png -resize 25% 1.png")

My method of calculating the baseline implements a weak adjustment for the pull-forward effect in elderly age groups, because when I'm multiplying the trend in CMR with the population size, the baseline deaths are reduced from 2020 onwards because the population size has been lowered by COVID deaths. But my adjustment is usually not nearly as strong as Ethical Skeptic's PFE adjustment. And my adjustment doesn't have much effect in young age groups, because it would have little effect on their population size even if they had double the normal number of deaths.

In the next plot where I plotted ASMR instead of raw deaths and I used the 2010-2019 linear trend in ASMR as the baseline, ages 85+ got positive excess ASMR each year from 2020 to 2023:

library(data.table);library(ggplot2)

agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)

t=fread("http://sars2.net/f/wondermalignantyearly.csv")
t=t[cause%like%"MCD"&year%in%2010:2023]
t=merge(t[!cause%like%"COVID"],t[cause%like%"COVID",.(year,age,and=dead)],all=T)
t[age<45,and:=0][age==0&year>=2020,and:=c(311,495,477,130)]
t=t[,.(dead=sum(dead-nafill(and,,0))),.(year,age)]

pop=fread("http://sars2.net/f/uspopdead.csv")[,dead:=NULL]
t=merge(pop[year==2020,.(age,std=pop/sum(pop))],merge(t,pop))

p=t[,.(asmr=sum(dead/pop*std*1e5)),.(year,group=agecut(age,c(0,45,55,65,75,85)))]
p=merge(p,p[year%in%2010:2019,.(year=2010:2023,trend=predict(lm(asmr~year),.(year=2010:2023))),group])

minmax=p[,.(max=max(asmr,trend),min=min(asmr,trend)),group]
p=merge(minmax[,.(group,max,min=max/minmax[,max(max/min)])],p)

xstart=2010;xend=2023

ggplot(p,aes(x=year,y=asmr))+
facet_wrap(~group,ncol=2,dir="v",scales="free_y")+
geom_vline(xintercept=c(2014.5,2019.5),color="gray80",linewidth=.25)+
geom_line(linewidth=.3)+
geom_line(aes(y=trend),linetype=2,linewidth=.3)+
geom_point(stroke=0,size=.6)+
geom_point(aes(y=min),size=0,stroke=0)+
geom_label(data=p[!duplicated(group)],aes(label=paste0("\n   ",group,"   \n"),y=(max+min)/2),x=xstart-.5,lineheight=.3,hjust=0,vjust=.5,size=grid::convertUnit(unit(7,"pt"),"mm"),label.r=unit(0,"pt"),label.padding=unit(0,"pt"),label.size=.3)+
labs(title="CDC WONDER: ASMR per 100k for deaths with MCD malignant neoplasms but not MCD COVID",subtitle="The dashed line is a linear trend fitted against the ASMR in 2010 to 2019. The ASMR was calculated by single year of age so that the 2020 resident population estimates were used as the standard population."|>stringr::str_wrap(104),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=seq(xstart-.5,xend+.5,.5),labels=c(rbind("",xstart:xend),""))+
scale_y_continuous(breaks=pretty)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1),
  axis.ticks=element_line(linewidth=.3,color="black"),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.title=element_text(size=8),
  legend.position="none",
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3),
  panel.spacing=unit(0,"pt"),
  panel.spacing.x=unit(3,"pt"),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=7,margin=margin(,,4)),
  plot.title=element_text(size=7.2,face=2,margin=margin(1,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.9,height=3.6,dpi=380*4)
system("magick 1.png -resize 25% 1.png")

So basically my plots show that if you calculate the baseline in a way that accounts for the changing population size of age groups, then you don't necessarily even need to adjust for the pull-forward effect.

Non-COVID deaths from natural causes in ages 0 to 24

Ethical Skeptic posted the plot below and wrote: [https://x.com/EthicalSkeptic/status/1846676664589148455]

Excess Non-Covid Natural Cause Mortality Ages 0-24

Elevated 30% or 8-sigma

We broke out of a 2023 plateau. This rise appears to be related to annual winter virus dynamics, perhaps indicating immune system impairment in our youngest population.

Not good news for anyone. 😞

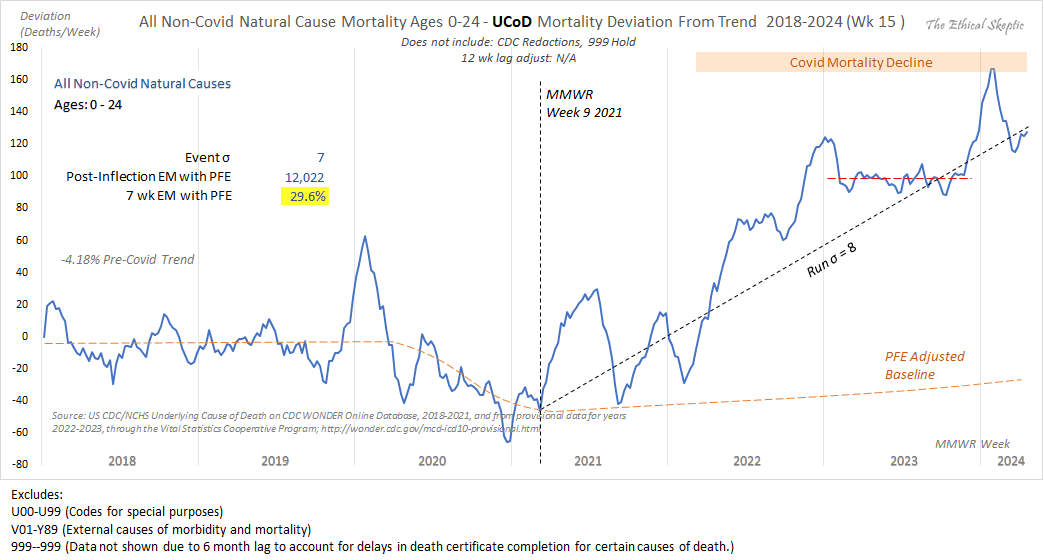
ES didn't exclude deaths under ICD chapter R from his plot, so some of his excess deaths in 2024 and to a less extent late 2023 might be due to deaths from external causes where the cause has not yet been resolved. His plot included the first 15 weeks of 2024. He posted the plot in October 2024 but I don't know if he retrieved the data earlier.

In the plot below where I plotted R deaths separately from A to Q deaths, there was a slight elevation in deaths under R codes during the first 3 to 4 months of 2024 but it was not that massive. But I wasn't able to reproduce Ethical Skeptic's steady increase in excess deaths that started in 2021, and my excess deaths peaked in December 2022 and not in early 2024 like in his plot:

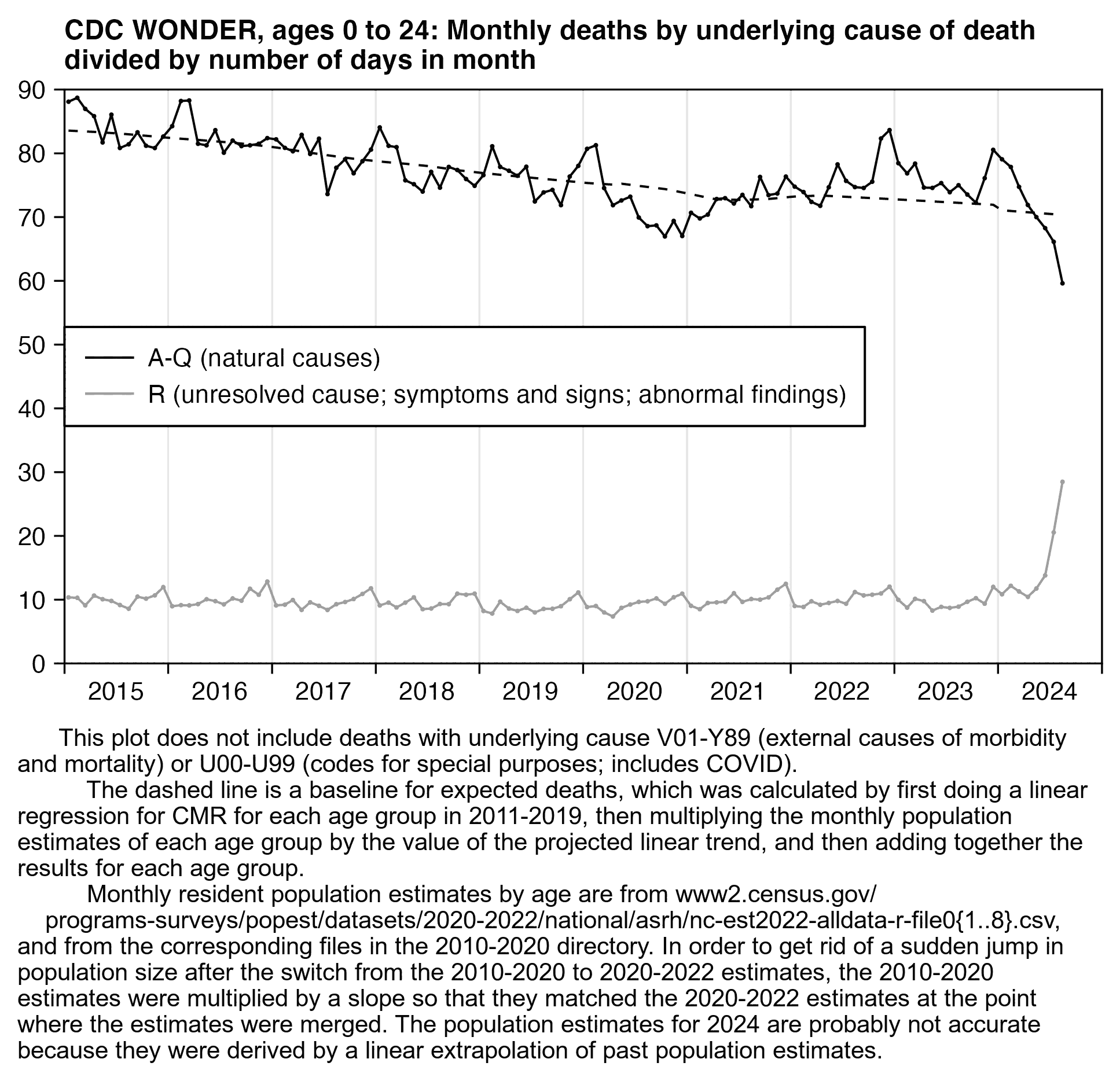
library(data.table);library(ggplot2);library(lubridate)

cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]

t=fread("http://sars2.net/f/wondernatural.csv")[age<25]

pop=fread("http://sars2.net/f/uspopdeadmonthly.csv")
t=merge(t,pop[,.(pop=sum(pop)),.(date,age=cul(age,c(0,1,5,15,25)))])

t=t[,date:=as.Date(paste0(date,"-1"))]
t[,dead:=dead/days_in_month(date)]

months=sort(unique(t$date))
base=t[cause=="A-Q"&year(date)%in%2011:2019][,dead:=nafill(dead,,0)]
t=merge(base[,.(date=months,base=predict(lm(dead/pop~date),.(date=months))),.(age,cause)],t,all=T)
t[,base:=base*pop]

p=t[,.(base=sum(base),dead=sum(dead)),.(date,cause)]
p[,cause:=factor(cause,unique(cause))]
levels(p$cause)=c("A-Q (natural causes)","R (unresolved cause; symptoms and signs; abnormal findings)")

xstart=as.Date("2015-1-1");xend=as.Date("2025-1-1")
p=p[date>=xstart&date<=xend]
xbreak=seq(xstart,xend,"6 month")
xlab=c(rbind("",2015:2024),"")

cand=c(sapply(c(1,2,5),\(x)x*10^c(-10:10)))
ymax=p[,max(base,dead,na.rm=T)]
ystep=cand[which.min(abs(cand-ymax/7))]
ystart=0
yend=ystep*ceiling(ymax/ystep)
ybreak=seq(ystart,yend,ystep)

color=c("black","gray60")

ggplot(p,aes(x=date+14,y=dead,color=cause))+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray90",linewidth=.25)+
geom_hline(yintercept=c(ystart,yend),linewidth=.25,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.25,lineend="square")+
geom_line(linewidth=.3)+
geom_point(stroke=0,size=.6,show.legend=F)+
geom_line(aes(y=base),linetype=2,linewidth=.3)+
labs(title="CDC WONDER, ages 0 to 24: Monthly deaths by underlying cause of death divided by number of days in month"|>stringr::str_wrap(70),x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length=unit(.2,"lines"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.justification=c(0,.5),
  legend.key=element_blank(),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.position=c(0,.5),
  legend.spacing.x=unit(2,"pt"),
  legend.box.background=element_rect(fill="white",color="black",linewidth=.3),
  legend.margin=margin(-2,5,4,4,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  plot.margin=margin(5,5,5,5),
  plot.title=element_text(size=7.6,face=2,margin=margin(2,,4)))
ggsave("1.png",width=4.3,height=2.8,dpi=450)

sub="\u00a0     This plot does not include deaths with underlying cause V01-Y89 (external causes of morbidity and mortality) or U00-U99 (codes for special purposes; includes COVID).
      The dashed line is a baseline for expected deaths, which was calculated by first doing a linear regression for CMR for each age group in 2011-2019, then multiplying the monthly population estimates of each age group by the value of the projected linear trend, and then adding together the results for each age group.
      Monthly resident population estimates by age are from www2.census.gov/
programs-surveys/popest/datasets/2020-2022/national/asrh/nc-est2022-alldata-r-file0{1..8}.csv, and from the corresponding files in the 2010-2020 directory. In order to get rid of a sudden jump in population size after the switch from the 2010-2020 to 2020-2022 estimates, the 2010-2020 estimates were multiplied by a slope so that they matched the 2020-2022 estimates at the point where the estimates were merged. The population estimates for 2024 are probably not accurate because they were derived by a linear extrapolation of past population estimates."

system(paste0("f=1.png;mar=30;w=`identify -format %w $f`;magick \\( $f -chop 0x10 \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize 42 caption:'",sub,"' -gravity southwest -splice $[mar]x20 \\) -append 1.png"))

I think Ethical Skeptic's heavy adjustment for the pull forward effect is not warranted in young age groups, because do ages 0 to 24 really have that many people who were on the verge of death so they would've died soon anyway if they hadn't died of COVID? There weren't even that many COVID deaths in ages 0 to 24.

In my plot above where I didn't use a PFE-adjusted baseline, there seems to have been a reduced number of deaths in late 2020, but after that deaths from natural causes remained close to the baseline until June 2022 after which they remained consistently above the baseline. So I would say the inflection rather occurred in 2022 and not in early 2021, even though I don't know how to explain the inflection.

But anyway, the increase above the baseline doesn't seem that impressive in my plot where the monthly number of excess deaths peaks at only about 15% above the baseline.

When Ethical Skeptic fits a seasonality-adjusted baseline against only two years of data, it's easy for him to get close to zero excess deaths during the fitting period because the baseline adapts to whatever the number of deaths happened to be during the fitting period, so therefore he gets a low standard deviation for his residuals during the fitting period and he subsequently gets high sigma values after his fitting period. But he would've probably gotten lower sigma values if he would've employed a longer fitting period or if wouldn't have adjusted his baseline for seasonality.

In a similar plot Ethical Skeptic posted on July 8th 2023 UTC, he plotted deaths up to week ending June 17th 2023. So in his old plot he only excluded approximately the last 3 weeks of data instead of about 18 weeks like in the newer plot (assuming that he retrieved the data from CDC WONDER shortly before he tweeted the plots). So therefore his old plot had an even more R99 deaths at the end of the x-axis: [https://x.com/EthicalSkeptic/status/1677513127468974081]

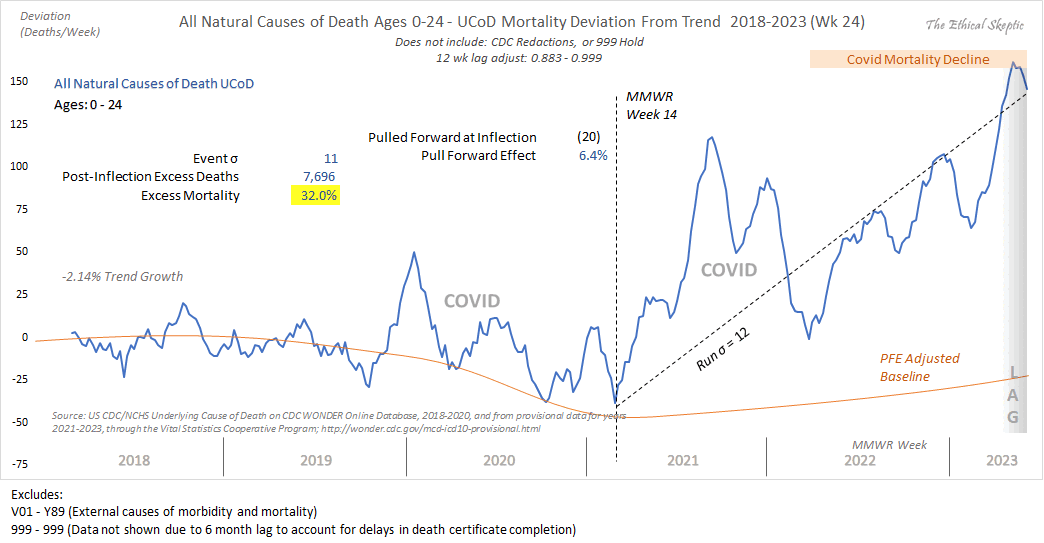
But in his newer plot many of the R99 deaths in 2023 had now been assigned under external causes, so there was no longer the huge increase in excess deaths in 2023:

Excess deaths from natural causes

Ethical Skeptic tweeted the image below and wrote: [https://x.com/EthicalSkeptic/status/1849206168767303734]

Excess Non-Covid Natural Cause Mortality = 760,000 US Citizens (+6,058 for Week 41 2024)

All the other excess natural cause mortality factors are mostly gone, yet Excess Non-Covid Natural Cause Mortality is still running around 6,000 excess deaths per week.

Only one differential remains in the populace -> the mRNA vaccine. The very event around which this curve inflected as its beginning.

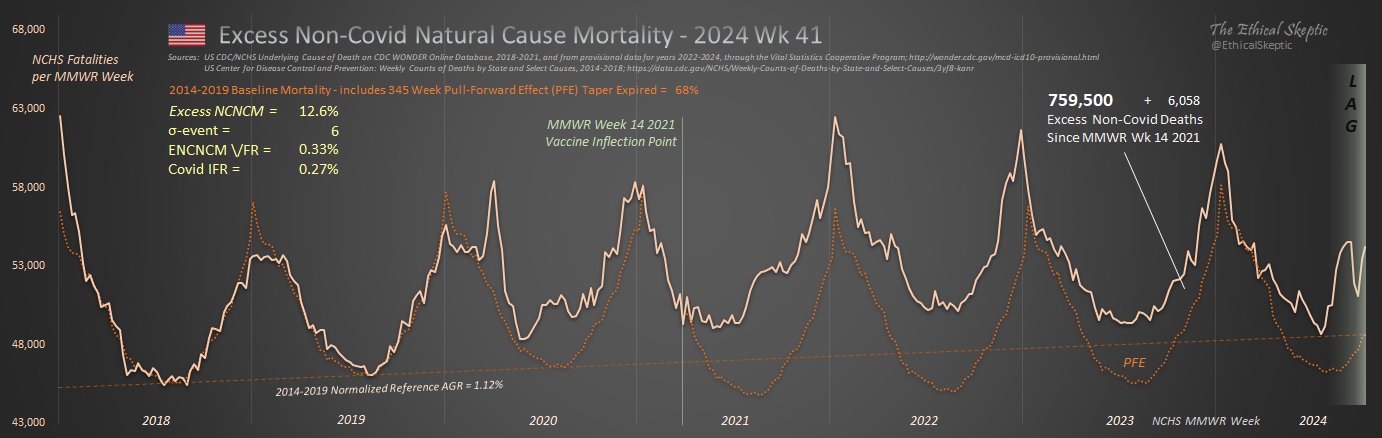
In the plot above a large part of the excess deaths from natural causes seem to be due to the PFE adjustment. You can roughly see the magnitude of the PFE adjustment by comparing the straight orange baseline against the PFE-adjusted baseline at the point when deaths are the lowest in the summer, which shows that the PFE adjustment accounted for the majority of excess deaths by summer 2023 and essentially all excess deaths by summer 2024.

Ethical Skeptic used a linear baseline fitted against raw deaths, which is inaccurate in many developed countries like Sweden because the trend in the raw number of deaths is curved upwards due to the aging population. The plot below shows that in Sweden the blue baseline which was calculated based on the raw number of deaths is much lower in 2023 than the green baseline which was calculated in a more accurate way, but in the United States the blue and green baselines have around the same height in 2023. In the United States the green baseline has a clear depression in 2021 and 2022 because the population size has been reduced by COVID deaths, so it causes the blue baseline to be too high in 2021 and 2022 compared to the green baseline which is more accurate. So basically the blue baseline is inaccurate in two ways which end up partially canceling each other out, because it's too high because it doesn't account for the reduced population size due to COVID deaths, but it's also too low because it doesn't account for the aging population. But by 2023 the two ways in which the blue baseline is inaccurate seem to have roughly canceled each other out in the United States. But in Sweden there was lower total COVID ASMR than in the United States, so in Sweden the blue baseline is much lower than the green baseline in 2023 because the population size has not been reduced as much by COVID deaths:

library(data.table);library(ggplot2)

kim=\(x)ifelse(x>=1e3,ifelse(x>=1e6,paste0(x/1e6,"M"),paste0(x/1e3,"k")),x)

years=2011:2023

t=fread("http://sars2.net/f/uspopdead.csv")[,country:="United States"]
t=rbind(t,fread("http://sars2.net/f/swedenpopdead.csv")[,country:="Sweden"])
t[,country:=factor(country,unique(country))]

t=t[year%in%years,.(dead=sum(dead),pop=sum(pop)),.(year,age,country)]

t=merge(t,t[year<2020,.(year=years,base=predict(lm(dead/pop~year),.(year=years))),.(age,country)])
t=t[,.(dead=sum(dead),base=sum(base*pop)),.(year,country)]
t=merge(t,t[year%in%2013:2019,.(year=years,base2=predict(lm(dead~year),.(year=years))),country])

p=t[,.(x=year,country,y=unlist(.SD[,-(1:2)]),z=rep(names(.SD)[-(1:2)],each=.N))]

lv=c("Actual deaths","2011-2019 linear baseline based on CMR by age","2013-2019 linear baseline for raw deaths")
p[,z:=`levels<-`(factor(z,unique(z)),lv)]

xstart=min(p$x);xend=max(p$x)
ybreak=pretty(p$y);ystart=ybreak[1];yend=max(ybreak)

color=c("black","#00aa00",hsv(21/36,1,.8))

minpoint=p[,.(min=min(y),max=max(y)),country]
yratio=minpoint[,max(max/min)]
minpoint=minpoint[,.(country,y=max/yratio)]

ggplot(p,aes(x,y))+
facet_wrap(~country,ncol=2,scales="free")+
geom_line(linewidth=.3,aes(color=z))+
geom_point(aes(alpha=z),size=.5)+
geom_point(data=minpoint,alpha=0,x=xstart)+
geom_line(data=p[z=="Actual deaths"],linewidth=.3,show.legend=F)+
geom_text(data=p[,.(y=max(y)),country],aes(label=paste0("\n   ",country,"   \n")),x=(xend+xstart)/2,size=grid::convertUnit(unit(7,"pt"),"mm"),vjust=.7,fontface="bold")+
labs(title="Yearly deaths in United States and Sweden",subtitle=paste0("The green baseline was calculated by first doing a linear regression for CMR for each single year of age in 2011-2019, and then the yearly population sizes of each age were multiplied by the value of the projected trend. The 2013-2019 linear trend is based simply on the total number of deaths each year in all ages aggregated together. Both countries have the same ratio between the maximum and minimum value of the y-axis (about ",sprintf("%.2f",yratio),").")|>stringr::str_wrap(95),x=NULL,y=NULL)+
scale_x_continuous(expand=expansion(0),limits=c(xstart-.5,xend+.5),breaks=xstart:xend)+
scale_y_continuous(breaks=pretty,labels=kim,expand=expansion(.03))+
scale_color_manual(values=color)+
scale_alpha_manual(values=c(1,0,0))+
coord_cartesian(clip="off")+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.x=element_text(angle=90,vjust=.5,hjust=1,margin=margin(3)),
  axis.ticks=element_line(linewidth=.3,),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.justification="left",
  legend.box.spacing=unit(0,"pt"),
  legend.direction="vertical",
  legend.key=element_rect(fill="white"),
  legend.spacing.x=unit(1,"pt"),
  legend.key.size=unit(9,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.position="top",
  legend.margin=margin(-7,,3),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.3),
  panel.spacing=unit(3,"pt"),
  plot.margin=margin(5,5,5,5),
  plot.subtitle=element_text(size=7,margin=margin(,,4)),
  plot.title=element_text(size=7.3,face=2,margin=margin(1,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.6,height=2.9,dpi=400*4)
system("mogrify -resize 25% 1.png")

Ethical Skeptic's unadjusted baseline is similar to my blue baseline in the plot above and his PFE-adjusted baseline is a much more extreme version of my green baseline. By 2023 my green baseline has risen close to the blue baseline, but Ethical Skeptic's PFE-adjusted baseline is so low in 2023 that it's about as low as his unadjusted baseline was in 2018. I think his adjustment for mortality displacement is too heavy, and in addition to the PFE adjustment he should also adjust his baseline upwards because of the changing age structure.

If Ethical Skeptic would plot ASMR instead of raw deaths, then he wouldn't even need to adjust for PFE to account for the reduction in population size due to COVID deaths. In the next plot which shows ASMR from natural causes, I got only about -0.1% total excess ASMR in 2023:

library(data.table);library(ggplot2);library(lubridate)

t=fread("http://sars2.net/f/wondernaturalsingle.csv")
pop=fread("http://sars2.net/f/uspopdeadmonthly.csv")
t=merge(t,pop[,.(date,age,pop=persondays)])[,date:=as.Date(paste0(date,"-1"))]
t=merge(t,fread("http://sars2.net/f/uspopdead.csv")[year==2020,.(age,std=pop/sum(pop))])
t=t[year(date)%in%2011:2023]

a=t[,.(y=sum(dead/pop*std*365e5),z="Actual ASMR"),.(x=date)]
p=copy(a)
dates=unique(a$x)

a[,month:=month(x)]
a=merge(a,a[year(x)<2020,.(x=dates,base=predict(lm(y~x),a))])
a=merge(a[year(x)<2020,.(monthly=mean(y-base)),.(month)],a)

p=a[,.(x,y,base=base+monthly,group="ASMR")]
p=rbind(p,p[,.(y=(y/base-1)*100,x,base=NA,group="Excess ASMR percent")])

p[,group:=factor(group,unique(group))]

xstart=min(dates);xend=as.Date("2024-1-1");xbreak=seq(xstart,xend,"6 month");xlab=c(rbind("",2011:2023),"")

color=c("black","gray60")

sub="\u00a0    Chapter R is excluded (symptoms, signs, and unresolved cause).
     ASMR was calculated by single year of age up to ages 100+ so that the vintage 2023 resident population estimates for the year 2020 were used as the standard population. Population estimates were downloaded from www2.census.gov/programs-surveys/popest/tables. Vintage 2020 resident population estimates are used for 2011 to 2019 and vintage 2023 resident population estimates are used for 2020 to 2023. In order to get rid of a sudden jump in the population estimates between 2019 and 2020, the population estimates for each age in 2011 to 2019 were multiplied by a linear slope.
     The gray baseline was calculated by doing a linear regression against the monthly ASMR values in 2011 to 2019, and then the average difference between the actual ASMR and the baseline on each January of 2011 to 2019 was added to the baseline for each January, and similarly for other months. The gray number above the year shows the yearly total excess mortality percent."

yearly=p[group=="ASMR",.(label=sprintf("%.1f%%",(sum(y)/sum(base)-1)*100)),.(x=year(x))]
yearly=cbind(yearly,p[group=="Excess ASMR percent",.(y=min(y)),group])

ggplot(p,aes(x+15,y))+
facet_wrap(~group,ncol=1,scales="free")+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray88",linewidth=.2)+
geom_vline(xintercept=as.Date("2020-1-1"),linetype=5,linewidth=.25)+
geom_hline(aes(yintercept=ifelse(group=="ASMR",NA,0)),linewidth=.25,linetype=5)+
geom_line(aes(y=base),color="gray60",linewidth=.3)+
geom_line(linewidth=.3)+
geom_label(data=p[,max(y,base,na.rm=T),group],aes(label=paste0("\n   ",group,"   \n"),y=V1),x=xstart,lineheight=.5,hjust=0,vjust=1,size=grid::convertUnit(unit(7,"pt"),"mm"),label.r=unit(0,"pt"),label.padding=unit(0,"pt"),label.size=.3)+
geom_point(stroke=0,size=.8,show.legend=F)+
geom_text(data=yearly,aes(x=as.Date(paste0(x,"-7-1")),label=label),vjust=-.6,color="gray60",size=2.3)+
labs(title="CDC WONDER: Monthly ASMR per 100,000 person-years for underlying cause of death A to Q (natural causes excluding COVID and chapter R)"|>stringr::str_wrap(74),x=NULL,y=NULL)+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=xlab,expand=expansion(0))+
scale_y_continuous(breaks=\(x)pretty(x,6),labels=\(x)ifelse(x<100,paste0(x,"%"),ifelse(x>1e3,paste0(x/1e3,"k"),x)))+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="right",
  legend.key=element_rect(fill=alpha("white",0)),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(17,"pt"),
  legend.margin=margin(,,2),
  legend.position="top",
  legend.spacing.x=unit(1.5,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.25),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(5,5,3,5),
  plot.title=element_text(size=7.2,face=2,margin=margin(,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.4,height=3.4,dpi=400*4)
system("magick 1.png -resize 25% 1.png")
system(paste0("f=1.png;mar=30;w=`identify -format %w $f`;magick $f \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize 36 caption:'",sub,"' -gravity southwest -splice $[mar]x14 \\) -append 1.png"))
system("qlmanage -p ~/1.png&>/dev/null")

Deaths from pneunomia with unspecified organism

Ethical Skeptic posted the plot below and wrote: [https://x.com/EthicalSkeptic/status/1855881320808731038]

Mycoplasma Pneumonia Ages 0-54 Mortality +40%

Often called 'walking pneumonia': - cough/sore throat
- low grade fever
- fatigue/body aches

Antibiotics of limited help. Immunocompromised individuals are vulnerable.

In the plot above the PFE adjustment seems too extreme, because were there really that many people in ages 0 to 54 who were on the verge of death so they would've died soon anyway if they hadn't died of COVID in 2020?

But anyway, when I did a query for deaths in ages 0-54 with UCD J15.7 (pneumonia due to Mycoplasma pneumoniae), there was a total of only 52 deaths in 2018-2024:

The small text at the bottom of Ethical Skeptic's plot shows that the plot also includes deaths from J18 (pneumonia unspecified), which actually accounts for virtually all deaths in his plot:

Deaths with cause 2018 2019 2020 2021 2022 2023 2024
MCD J15.7 (Pneumonia due to Mycoplasma pneumoniae) 17 31 28 19 1-9 11 21
MCD J20.0 (Acute bronchitis due to Mycoplasma pneumoniae) 0 0 0 0 0 0 1-9
MCD J18 (Pneumonia, organism unspecified) 10241 9889 22620 44348 17906 11110 8054
MCD J18 (Pneumonia, organism unspecified) but not MCD COVID (U07) 10241 9889 10778 9854 9787 10139 7512

Ethical Skeptic has said that in his plots that display weekly data from 2018 onwards, he fits the baseline against deaths from only 2018 and 2019, so I suspect it was also the case here. However it migth cause the slope of his baseline to be pointed too much downwards like the gray baseline here even (though I fitted the gray baseline here based on data for the whole year but he seems to exclude winter peaks when he determines the slope of the baseline):

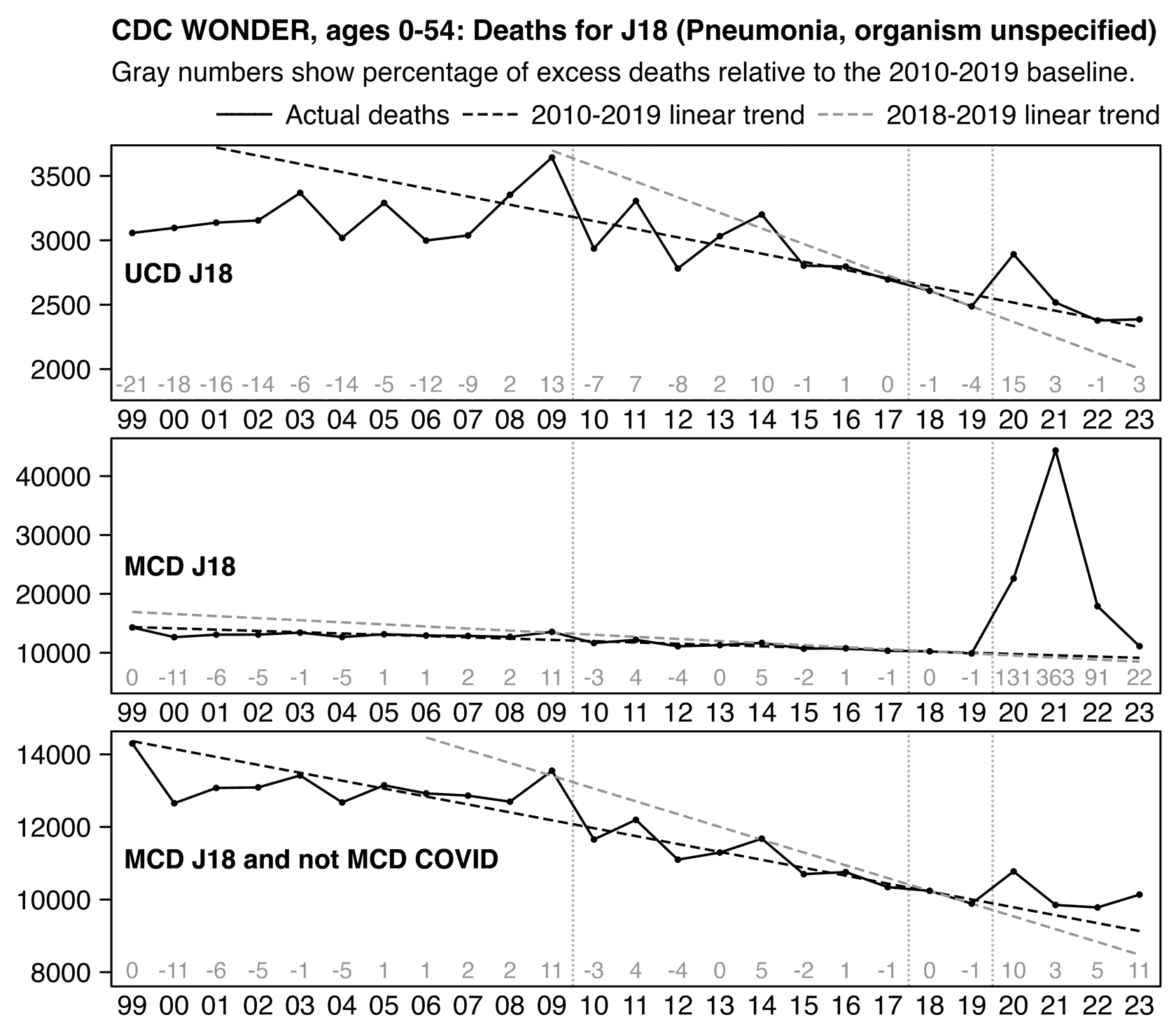
library(data.table);library(ggplot2);library(lubridate)

cul=\(x,y)y[cut(x,c(y,Inf),,T,F)]

t=fread("http://sars2.net/f/wonderj18u54.csv")[year!=2024]
and=merge(t[cause=="MCD J18"],t[cause%like%"and",.(year,and=dead)],all=T)
p=rbind(t[!cause%like%"and"],and[,.(year,dead=dead-nafill(and,,0),cause="MCD J18 and not MCD COVID")])

p$base=p[year%in%2010:2019,predict(lm(dead~year),.(year=1999:2023)),cause]$V1
p$base2=p[year%in%2018:2019,predict(lm(dead~year),.(year=1999:2023)),cause]$V1

p[,cause:=factor(cause,unique(cause))]

xstart=1999;xend=2023;xbreak=seq(xstart-.5,xend+.5,.5);xlab=c(rbind("",substr(xstart:xend,3,4)),"")

pct=p[,.(cause,year,pct=round((dead/base-1)*100))]
mima=p[,.(min=min(dead,base,base2),max=max(dead)),cause][,min:=min-(max-min)*.15][,max:=max+(max-min)*.05]
pct=merge(pct,mima)
p=merge(p,mima)

lab=c("Actual deaths","2010-2019 linear trend","2018-2019 linear trend")
lab=factor(lab,unique(lab))

ggplot(p,aes(x=year,y=dead))+
facet_wrap(~cause,ncol=1,scales="free")+
geom_vline(xintercept=c(2010,2018,2020)-.5,linewidth=.3,color="gray70",linetype="11")+
geom_line(aes(color=lab[1],linetype=lab[1]),linewidth=.3)+
geom_line(aes(y=ifelse(base>max,NA,base),color=lab[2],linetype=lab[2]),linewidth=.3)+
geom_line(aes(y=ifelse(base2>max,NA,base2),color=lab[3],linetype=lab[3]),linewidth=.3)+
geom_point(aes(color=lab[1]),stroke=0,size=.8,show.legend=F)+
geom_text(data=pct,aes(y=min,label=pct),vjust=-.5,size=2.1,color="gray60")+
geom_text(data=p[,(min+max)/2,cause],aes(label=cause,y=V1),x=xstart-.2,hjust=0,vjust=.5,fontface=2,size=2.4)+
geom_point(data=mima,aes(y=min),x=xstart,alpha=0)+
geom_point(data=mima,aes(y=max),x=xstart,alpha=0)+
labs(x=NULL,y=NULL,title="CDC WONDER, ages 0-54: Deaths for J18 (Pneumonia, organism unspecified)",subtitle="The gray numbers show the percentage of excess deaths relative to the\n2010-2019 baseline.")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=xlab)+
scale_y_continuous(breaks=pretty)+
scale_color_manual(values=c("black","black","gray60"),labels=lab)+
scale_alpha_manual(values=c(1,0,0),labels=lab)+
scale_linetype_manual(values=c("solid","42","42"),labels=lab)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
  axis.ticks.x=element_line(color=alpha("black",c(1,0))),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="right",
  legend.key=element_rect(fill=alpha("white",0)),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(18,"pt"),
  legend.margin=margin(,,3),
  legend.position="top",
  legend.spacing.x=unit(1.5,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.25),
  panel.spacing=unit(1,"pt"),
  plot.margin=margin(4,4,4,4),
  plot.subtitle=element_text(size=7,margin=margin(,,2)),
  plot.title=element_text(size=7.3,face=2,margin=margin(1,,4)),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=4.2,height=3.7,dpi=400*4)
system("magick 1.png -resize 25% 1.png")
system("qlmanage -p ~/1.png&>/dev/null")

I suspect some of the excess deaths with MCD J18 and not MCD COVID may have been due to deaths that included COVID as an undiagnosed cause of death, because the number of MCD J18 deaths was about 5 times the baseline level in 2021 but nearly all excess MCD J18 deaths in 2021 also had MCD COVID. So if a diagnosis for COVID was missing for even a small part of deaths that should've had MCD COVID, it might explain a large part of excess deaths in my bottom panel that shows deaths with MCD J18 but not MCD COVID.

And in any case I don't know if the increase in J18 deaths can be attributed to vaccines, because the period with elevated J18 deaths seems to have already started in 2020. In my plot above the percentage of excess deaths for UCD J18 is about 15% in 2020 but close to zero in 2021, 2022, and 2023.

Ethical Skeptic said that he got about 40% excess deaths relative to his PFE-adjusted baseline, but in the bottom panel of my plot above which shows deaths with MCD J18 but not MCD COVID, I got only about 20% excess deaths in 2023 even relative to the light gray baseline that was fitted against deaths from 2018-2019. However Ethical Skeptic fitted his baseline against weekly data which might cause it to be steeper than my baseline fitted against yearly data, because there was a high number of deaths in early 2018.

In the next plot I calculated the baseline by first doing a linear regression of weekly data for the MMWR years 2018 and 2019, and then I calculated the average difference between the actual deaths and the baseline on MMWR week 1 of 2018 and 2019 and I added the difference to the baseline for MMWR week 1 of each year, and similarly for other week numbers. My baseline pointed even further downwards than Ethical Skeptic's baseline, so I got over 100% excess deaths on every week in the second half of 2023. But on the other hand I didn't get high excess deaths on the first weeks of 2018 like Ethical Skeptic, which might be if he excluded early weeks of 2018 from his baseline fitting period, which would also explain why the slope of his baseline was not as extreme as in my plot:

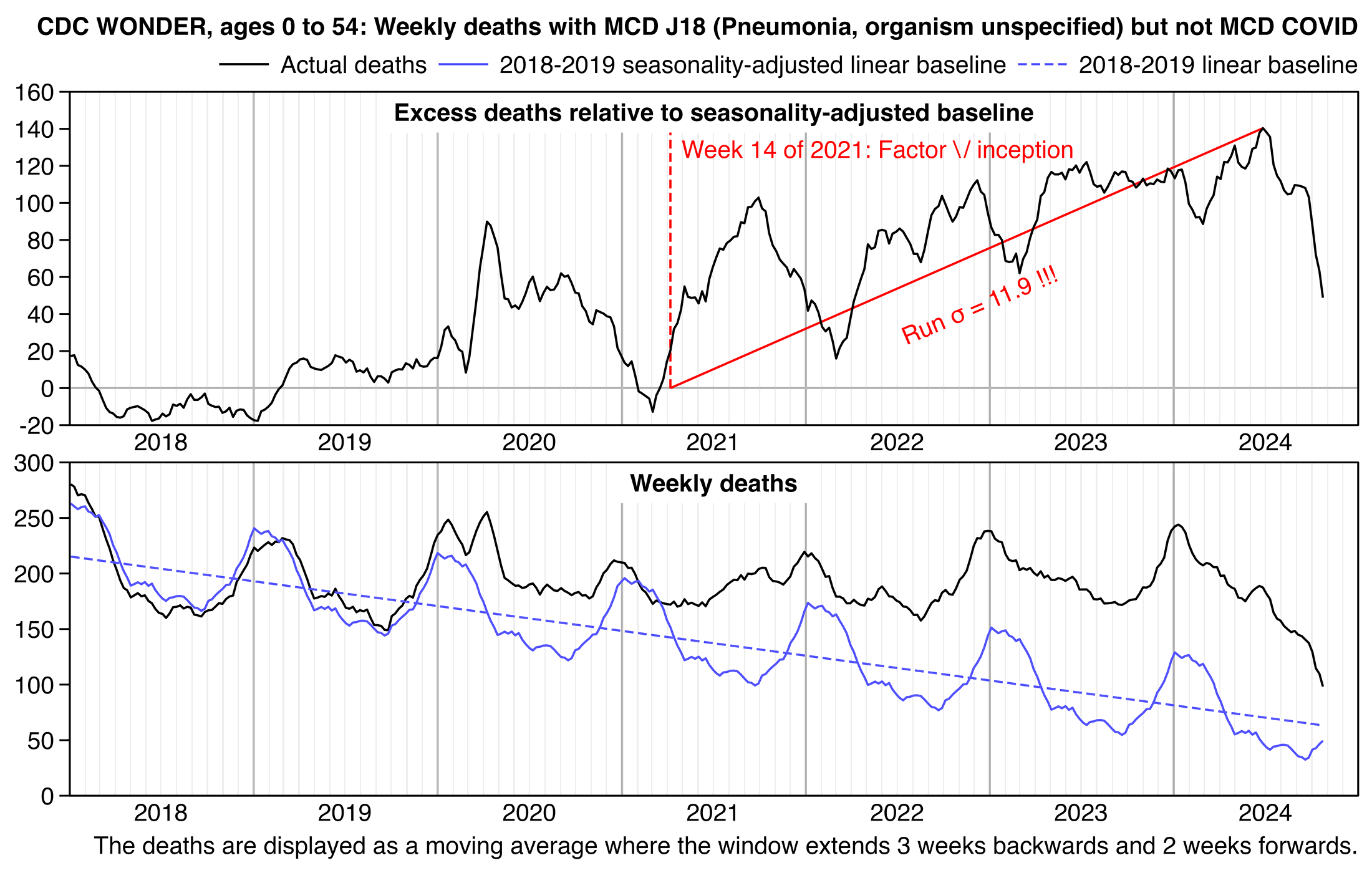
library(data.table);library(ggplot2)

ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}

t=fread("http://sars2.net/f/wonderj18weekly.csv")[,date:=date-3]

t=merge(t[cause=="MCD J18"],t[cause%like%"and",.(date,and=dead)],all=T)
p=t[,.(date,year,week,dead=dead-nafill(and,,0))]
p[,dead:=ma(dead,3,2)]
p$base=p[year<2020,predict(lm(dead~date),p)]

z=c("Actual deaths","2018-2019 seasonality-adjusted linear baseline","2018-2019 linear baseline")
facet=c("Moving average of weekly deaths","Excess deaths relative to seasonality-adjusted baseline")
p=merge(p[year<2020,mean(dead-base),week],p)[,.(x=date,y=c(dead,base+V1,base,dead-(base+V1)),z=rep(z[c(1:3,1)],each=.N),facet=rep(facet,c(.N*3,.N)))]
p[,z:=factor(z,unique(z))][,facet:=factor(facet,unique(facet))]

ybreak=pretty(p$y)
xstart=as.Date("2018-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=c(rbind("",2018:2024),"")

lab=p[,.(x=xstart+(xend-xstart)/2,y=max(pretty(y,8))),facet]

x1=t[year==2021&week==14,date]
xy2=p[facet==tail(facet,1)][y==max(y)]
x2=xy2$x;y2=xy2$y;y1=0
sigma=y2/p[year(x)<2020&facet==tail(facet,1),sd(y)]

ggplot(p,aes(x,y))+
coord_cartesian(clip="off",expand=F)+
facet_wrap(~facet,ncol=1,scales="free")+
geom_vline(xintercept=seq(xstart,xend,"month"),color="gray92",linewidth=.23)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray70",linewidth=.3)+
geom_hline(yintercept=0,linewidth=.3,color="gray70")+
geom_segment(data=data.table(facet=levels(p$facet)[2]),x=x1,y=y1,xend=x2,yend=y2,linewidth=.3,color="red")+
geom_text(data=data.table(facet=levels(p$facet)[2]),x=x1+(x2-x1)/2+25,y=45,size=2.46,label=sprintf("Run σ = %.1f !!!",sigma),color="red",angle=22)+
geom_segment(data=data.table(facet=levels(p$facet)[2]),color="red",x=x1,xend=x1,y=0,yend=p[facet==levels(facet)[2],max(y)],linetype="42",linewidth=.3)+
geom_text(data=data.table(facet=levels(p$facet)[2]),x=x1+22,y=129,size=2.46,label="Week 14 of 2021: Factor \\ / inception",color="red",hjust=0)+
geom_line(aes(color=z,linetype=z),linewidth=.3)+
geom_label(data=lab,aes(label=paste0("\n  ",facet,"  \n")),lineheight=.4,hjust=.5,vjust=1,size=2.46,label.r=unit(0,"pt"),label.padding=unit(0,"pt"),label.size=0,fontface=2)+
labs(x=NULL,y=NULL,title="CDC WONDER, ages 0 to 54: Weekly deaths with MCD J18 (Pneumonia, organism unspecified) but not MCD COVID",caption="The window of the moving average extends 3 weeks backwards and 2 weeks forwards.")+
scale_x_continuous(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=\(x)range(pretty(x,8)),breaks=\(x)pretty(x,8))+
scale_color_manual(values=c("black","gray60","gray60"))+
scale_linetype_manual(values=c("solid","solid","42"))+
theme(axis.text=element_text(size=7,color="black"),
  axis.text.y=element_text(margin=margin(,1.5)),
  axis.ticks=element_line(linewidth=.25,color="black"),
  axis.ticks.length=unit(3,"pt"),
  axis.ticks.length.x=unit(0,"pt"),
  axis.title=element_text(size=8),
  legend.background=element_blank(),
  legend.box.spacing=unit(0,"pt"),
  legend.direction="horizontal",
  legend.justification="right",
  legend.key=element_rect(fill=alpha("white",0)),
  legend.key.height=unit(10,"pt"),
  legend.key.width=unit(18,"pt"),
  legend.margin=margin(,,3),
  legend.position="top",
  legend.spacing.x=unit(1.5,"pt"),
  legend.spacing.y=unit(0,"pt"),
  legend.text=element_text(size=7,vjust=.5),
  legend.title=element_blank(),
  panel.background=element_blank(),
  panel.border=element_rect(fill=NA,linewidth=.25),
  panel.spacing=unit(2,"pt"),
  plot.margin=margin(4,4,3,4),
  plot.caption=element_text(size=7,margin=margin(3,,1)),
  plot.title=element_text(size=7,face=2,margin=margin(1,,2),hjust=1),
  strip.background=element_blank(),
  strip.text=element_blank())
ggsave("1.png",width=5.5,height=3.5,dpi=400*4)
system("magick 1.png -resize 25% 1.png")

Even though deaths with MCD COVID were excluded from the plot above, there's still a clear spike in excess deaths during the COVID wave in spring 2020. So even after spring 2020 a part of the excess deaths are probably explained by COVID (but most excess deaths are of course explained by the incorrect slope of the baseline).

On a list of crimes committed by other analysts, Ethical Skeptic included this point: "Add volatility of peak winter mortality periods into the trend regression, and not index off the summer base. That way a rough flu year will raise the baseline artificially to your advantage." [https://x.com/EthicalSkeptic/status/1773066903000396096] I don't know what method he uses to exclude winter peaks from the regression or to "index off the summer base", or if he applied the methods in his plot for J18 deaths. But in the next plot I determined the slope of the baseline by doing a regression for only weeks 15 to 35 of 2018 and 2019, which gave me a more realistic slope of the baseline than in the previous plot, even though my number of excess deaths in the early weeks of 2018 was still much lower than in Ethical Skeptic's plot: