Other parts: rootclaim.
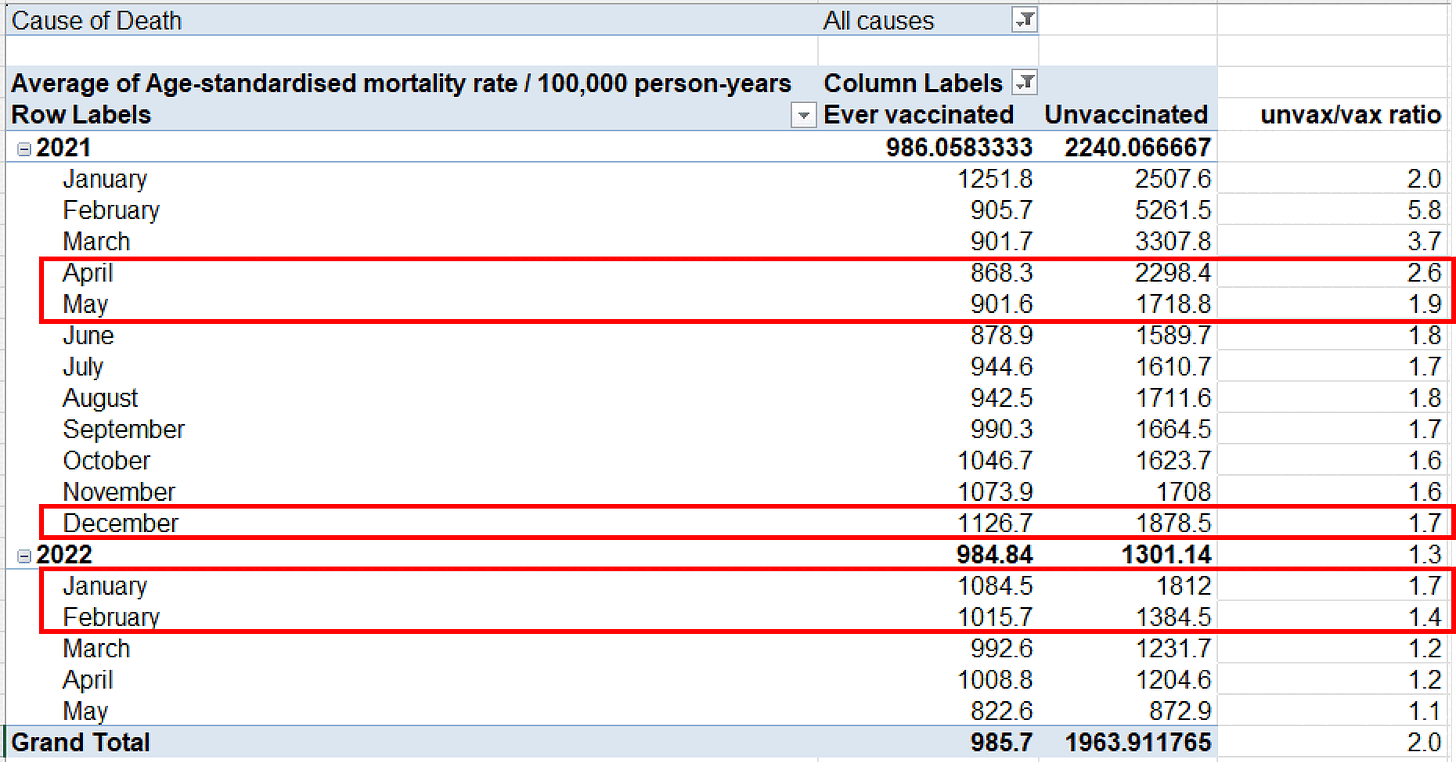
Kirsch posted this table of the English ONS data, where he pointed
out that in April to May 2021 when there was a low number of COVID
cases, the ratio between unvaccinated and vaccinated ASMR was higher
than in December 2021 to February 2022 when there was a high number of
COVID cases: [https://

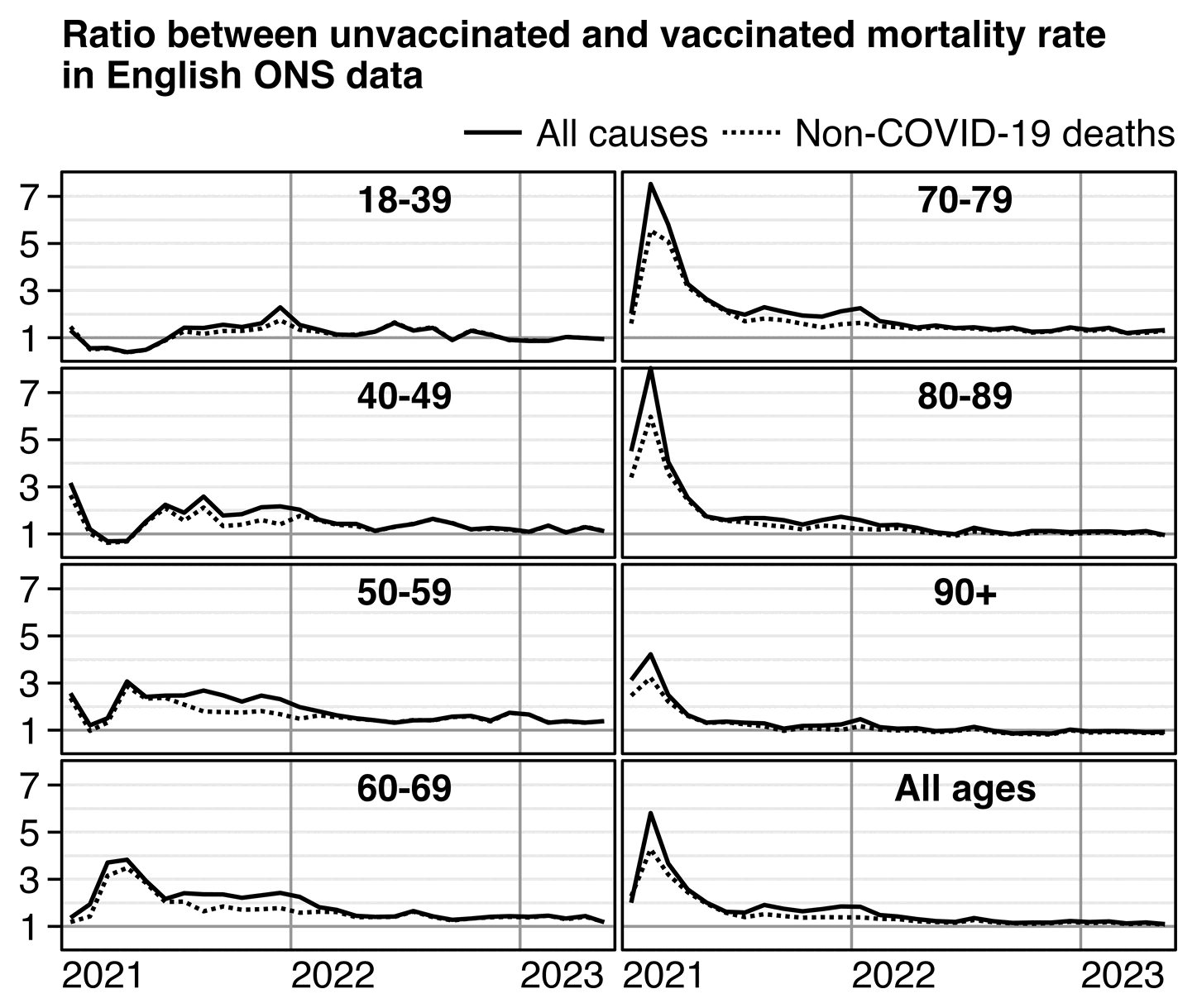
However in April to May 2021 there were still many people who had been recently vaccinated, so vaccinated people were still heavily impacted by the temporal healthy vaccinee effect (which is a term coined by Jeffrey Morris for the stronger form of HVE which lasts for the first weeks or months after vaccination, as opposed to the inherent HVE that remains in place even long after vaccination).
From the plot below you can roughly see the magnitude of the HVE from the dashed line which shows non-COVID ASMR. The plot below also shows that the ratio between unvaccinated and vaccinated ASMR was in fact elevated during the Delta peak in August 2021 and the COVID wave that peaked in December 2021 to January 2022. But in October 2021 when there was a lower number of COVID deaths than in the surrounding months, the ratio between unvaccinated and vaccinated ASMR was also lower than in the surrounding months:
t=fread(" http:// sars2. net/ f/ ons. csv") t=rbind( t[ ed==7& month< =" 2021- 03"], t[ ed==9])[ cause! =" Deaths involving COVID- 19"] t[, x: =as. Date( paste0( month, "- 15"))] t[, vax: =factor( status! =" Unvaccinated",, c( " Unvaccinated", " Vaccinated"))] a=t[ age! =" Total",.( cmr=sum( dead)/ sum( pop)),.( age, vax, x, cause)] p=a[,.( y=cmr[ 1]/ cmr[ 2]),.( age, x, cause)] p=rbind( p, t[ age==" Total" & status% like% " accin",.( y=asmr[ 1]/ asmr[ 2], age=" All ages"),.( x, cause)]) xstart=as. Date( " 2021- 1- 1"); xend=as. Date( " 2023- 6- 1"); xbreak=seq( xstart, xend, " year"); yend=max( p$ y) ggplot( p)+ facet_ wrap(~ age, dir=" v", ncol=2)+ geom_ hline( yintercept=2: 8, color=" gray91", linewidth=. 4)+ geom_ hline( yintercept=1, color=" gray60", linewidth=. 4)+ geom_ vline( xintercept=seq( xstart, xend, " year"), color=" gray60", linewidth=. 4)+ geom_ rect( data=p[, max( y), age], aes( xmin=xstart, xmax=xend, ymin=0, ymax=yend), linewidth=. 4, fill=NA, color=" black", lineend=" square")+ geom_ line( aes( x, y, linetype=cause), linewidth=. 6)+ geom_ text( data=p[, max( y), age], aes( x=as. Date( " 2022- 7- 1"), y=yend, label=age), hjust=. 5, fontface=2, vjust=1. 5, size=3. 8)+ labs( x=NULL, y=NULL, title=" Ratio between unvaccinated and vaccinated mortality rate\ nin English ONS data")+ scale_ x_ continuous( limits=c( xstart-. 5, xend+. 5), breaks=xbreak, labels=year( xbreak))+ scale_ y_ continuous( breaks=seq( 1, 7, 2))+ scale_ linetype_ manual( values=c( " solid", " 11"))+ scale_ alpha_ manual( values=c( 1, 0), guide=" none")+ coord_ cartesian( clip=" off", expand=F)+ guides( color=guide_ legend( order=1), linetype=guide_ legend( order=2))+ theme( axis. text=element_ text( hjust=0, size=11, color=" black"), axis. title=element_ text( size=11, face=2), axis. text. x=element_ text( margin=margin( 3)), axis. ticks=element_