
Links to earlier parts: czech.html, czech2.html, czech3.html. The files about the Rootclaim debate include additional analysis of the Czech data: rootclaim3.html, rootclaim4.html.
Kirsch told me on Twitter: "You have all failed to explain why in every age group where we have sufficient data. Moderna was significantly more deadly than Pfizer. it wasn't comorbidities because those didn't matter. So why was the death rate higher? Why can't you answer that simple question?" [https://x.com/stkirsch/status/1818053265357160918]
I told him that in the plot below if you look at the age groups 50-59 and above where there's a sufficient sample size of deaths, the Moderna-Pfizer ratio was close to 1.0 among people who got the first dose in the 4th quarter of 2021. So did Moderna vaccines get less deadly in the 4th quarter?

library(data.table)
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
quar=\(x){u=unique(x);paste0(substr(u,1,4),"Q",(as.numeric(substr(u,6,7))-1)%/%3+1)[match(x,u)]}
ages=c(0,2:9*10)
t=fread("http://sars2.net/f/czbucketskeep.csv.gz")[dose<=1][,age:=pmin(age,95)]
t=merge(t[dose==1&vaxmonth>="2021-01"&vaxmonth<="2022-03"],t[,.(base=sum(dead)/sum(alive)),age])[,base:=base*alive]
t=t[,.(base=sum(base),dead=sum(dead),alive=sum(as.double(alive))),.(type,vaxmonth=quar(vaxmonth),age=agecut(age,ages))]
t=rbind(t,t[,.(base=sum(base),dead=sum(dead),alive=sum(alive),vaxmonth="Total"),.(age,type)])
t=rbind(t,t[,.(base=sum(base),dead=sum(dead),alive=sum(alive),age="Total"),.(vaxmonth,type)])
a=t[,tapply(dead/base,.(type,age,vaxmonth),c)]
m1=a["Moderna",,];m2=a["Pfizer",,]
m=(m1-m2)/ifelse(m1>m2,m2,m1)
pop=t[type%in%c("Moderna","Pfizer"),xtabs(alive~age+vaxmonth)]/365
disp=matrix(sprintf(ifelse(m1/m2>10,"%.1f","%.2f"),m1/m2),nrow(m))
hide=pmin(m1,m2)==0;m[hide]=NA;disp[is.na(m)]=""
exp=.7;m=abs(m)^exp*sign(m);maxcolor=10^exp
pheatmap::pheatmap(m,filename="i1.png",display_numbers=disp,
gaps_row=nrow(m)-1,gaps_col=ncol(m)-1,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=19,cellheight=19,fontsize=9,fontsize_number=8,
border_color=NA,na_col="gray90",
number_color=ifelse((abs(m)>.55*maxcolor)&!is.na(m),"white","black"),
breaks=seq(-maxcolor,maxcolor,,256),
colorRampPalette(hsv(rep(c(7/12,0),5:4),c(.9,.75,.6,.3,0,.3,.6,.75,.9),c(.4,.65,1,1,1,1,1,.65,.4)))(256))
rec=fread("Czech/data/CR_records.csv",showProgress=F)
pop=rec[grep("comirnaty|spikevax",ignore.case=T,OckovaciLatka_1),.N,.(age=agecut(2021-Rok_narozeni,ages),vaxq=quar(Datum_1))]
pop=rbind(pop,pop[,.(N=sum(N),age="Total"),vaxq])
pop=rbind(pop,pop[,.(N=sum(N),vaxq="Total"),age])
pop=xtabs(N~age+vaxq,pop)[rownames(m),colnames(m)]
exp2=.6;maxcolor2=max(pop[-nrow(pop),])
kimi=\(x){e=floor(log10(ifelse(x==0,1,abs(x))));e2=pmax(e,0)%/%3+1;p=!is.na(x)
x[p]=paste0(sprintf(paste0("%.",ifelse(e[p]%%3==0,1,0),"f"),x[p]/1e3^(e2[p]-1)),c("","k","M","B","T")[e2[p]]);x}
exp2=.6;maxcolor2=max(pop[-nrow(pop),-ncol(pop)])
pheatmap::pheatmap(pop^exp2,filename="i2.png",display_numbers=kimi(ifelse(pop==0,0,pop)),
gaps_row=nrow(m)-1,gaps_col=ncol(m)-1,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=19,cellheight=19,fontsize=9,fontsize_number=8,
border_color=NA,na_col="white",
number_color=ifelse(pop^exp2>maxcolor2^exp2*.45,"white","black"),
breaks=seq(0,maxcolor2^exp2,,256),
sapply(seq(1,0,,256),\(i)rgb(i,i,i)))
cap="Czech record-level data: Age-normalized Moderna-Pfizer mortality ratio by vaccination quarter and age group. Only first doses are included. The mortality rate was calculated from the day of the first dose up to the end of 2022. A baseline number of deaths was calculated for each single year of age by multiplying the person-days of the age by the total mortality rate for the age in 2020 to 2022 among all people who are included in the record-level data, and the baseline deaths for all ages within an age group were added together. The ratio was calculated as (Moderna_deaths / Moderna_baseline) / (Pfizer_deaths / Pfizer_baseline). The right side shows the number of people each quarter who received either a Pfizer or Moderna vaccine for their first dose."
system(paste0("magick i[12].png +append 0.png;w=`identify -format %w 0.png`;pad=24;convert -pointsize 42 -interline-spacing -3 -font Arial \\( -size $[w-pad*2]x caption:'",cap,"' -splice $[pad]x20 \\) 0.png -append 1.png"))
Kirsch has been saying that the Moderna-Pfizer ratio is consistently around 1.3 for all months of vaccination that have a sufficiently large sample size of vaccinated people (even though my age-normalized Moderna-Pfizer ratio was about 1.02 for people who got the first dose in November 2021, and there's about about 300,000 people who got a first dose from a Pfizer or Moderna vaccine in November 2021 so I think it's a sufficiently large sample size).
But Kirsch has generally been looking at first doses only. The plot below shows the results for the third dose instead. I used the same R script as in this section: czech2.html#Triangle_plot_of_Moderna_Pfizer_ratio.
The total Moderna-Pfizer ratio is below 1.0 for people who got the third dose during each month from March 2022 to August 2022, but it shouldn't just be random noise because there's a total of about 300,000 people who received a third shot from a Moderna or Pfizer vaccine during those months. So there appears to be a similar effect as with the first dose, where the late vaccinees have a lower Moderna-Pfizer ratio than the early vaccinees:

The monthly number of 4th doses peaked in October 2022. But for people who got a 4th dose in October 2022, the Moderna-Pfizer ratio was about 0.67:

I had forgotten to make these triangle plots for the third and fourth doses, but now I think these plots have become yet another nail in the coffin of Kirsch's theory that his Moderna-Pfizer ratio proved that Moderna vaccines were more deadly. Now of course it's possible that Moderna vaccines were actually more deadly, but I don't think Kirsch's Moderna-Pfizer ratio is the smoking gun piece of evidence that he makes it out to be.
In the file prehled-ockovacich-mist.csv which has
information about vaccination sites, the sites are classified under
these 5 types:
[https://ockodoc.mzcr.cz/wp-content/uploads/2024/01/231230_manual_crs.pdf]
| Abbreviation | Translation | Czech |
|---|---|---|
| OČM | standard vaccination site | standardní očkovací místo |
| DOČM | vaccination site for children | očkovací místo pro děti |
| VOČM | large-capacity vaccination site | velkokapacitní očkovací místo |
| SMPL | vaccination site for self-payers | očkovací místo pro samoplátce |
| WALKIN | mobile vaccination site | mobilní očkovací místo |
The file ockovani-profese.csv contains about 19 million
rows with one row for each administered dose, but when I tried joining
the file with the file for information about vaccination sites, only
about 7 million rows could be joined by the vaccinator ID. The joined
rows didn't include any row for a large-capacity vaccination site. And I
further excluded vaccination sites for children and I excluded vaccines
given to ages below 18, because children have little effect on overall
mortality but the pediatric vaccination sites distorted the overall
percentages of site types. But this shows the distribution of the
remaining 3 types of vaccination sites:
dlf=\(x,y,...){if(missing(y))y=sub(".*/","",x);for(i in 1:length(x))download.file(x[i],y[i],quiet=T,...)}
dlf("https://onemocneni-aktualne.mzcr.cz/api/v2/covid-19/ockovani-profese.csv") # about 4 GiB
dlf("https://onemocneni-aktualne.mzcr.cz/api/v2/covid-19/prehled-ockovacich-mist.csv") # about 20 kiB
pro=fread("ockovani-profese.csv")
mist=fread("prehled-ockovacich-mist.csv")
d=pro[,.N,.(vaxtype=vakcina,vaccinator=zarizeni_kod,age=vekova_skupina)]
d=d[!d$age%in%c("0-4","05-11","12-15","16-17")]
name1=unique(d$vaxtype);name2=rep("Other",length(name1))
name2[name1==""]=""
name2[grep("comirnaty",ignore.case=T,name1)]="Pfizer"
name2[grep("spikevax",ignore.case=T,name1)]="Moderna"
name2[grep("nuvaxovid",ignore.case=T,name1)]="Novavax"
name2[name1=="COVID-19 Vaccine Janssen"]="Janssen"
name2[name1=="VAXZEVRIA"]="AstraZeneca"
d$vaxtype=name2[match(d$vaxtype,name1)]
d=merge(unique(mist[,.(sitetype=ockovaci_misto_typ,vaccinator=nrpzs_kod)],by="vaccinator"),d)
m=d[sitetype!="DOČM",xtabs(N~vaxtype+sitetype)]
m=m[order(-rowSums(m)),]
round(m/rowSums(m)*100)
sitetype vaxtype OČM SMPL WALKIN # percentage of site types by manufacturer Pfizer 54 37 9 Moderna 66 20 14 Janssen 67 29 4 AstraZeneca 46 42 12 Novavax 65 32 3 Other 42 46 11
So Pfizer has a higher percentage of vaccination sites for self-payers than Moderna (SMPL), but Moderna has a higher percentage of standard vaccination sites (OČM) and walk-in sites. Which is yet another line of evidence that there are systematic biases in the distribution of vaccine doses by different manufacturers.
In this blog post where Hans-Joachim Kremer looked at US VAERS data, he got a higher ratio of deaths per adverse event reports for Pfizer than Moderna vaccines, so he pointed out that it conflicted with Kirsch's analysis of the Czech data: https://tkp.at/2024/08/06/spikevax-gefaehrlicher-als-comirnaty-steve-kirsch-greift-daneben/.
However it could be that Moderna had both a higher number of adverse event reports per dose than Pfizer and a higher number of deaths per dose than Pfizer, but the ratio of deaths per adverse event reports could've still been higher for Pfizer than Moderna. So he could've repeated the calculation so that he would've used doses administered instead of adverse event reports as the denominator.
I took the number of adverse event reports in Czechia per vaccine manufacturer from this spreadsheet: https://github.com/PalackyUniversity/batch-dependent-safety/blob/main/data/SUKL-batches-AE.xlsx. The spreadsheet only included the number of doses released but not the number of doses administered, so I calculated the number of doses administered from the record-level data. I only included doses administered up to July 4th 2023, which was the date when the authors who published the batch data wrote they received the data. But anyway, Moderna got a higher ratio than Pfizer for both deaths per doses administered and adverse event reports per doses administered:
rename=\(x){u=unique(x);o=rep("Other",length(u))
o[grep("comirnaty|pfizer",u,T)]="Pfizer"
o[grep("moderna|spikevax",u,T)]="Moderna"
o[grep("nuvaxovid|novavax",u,T)]="Novavax"
o[grep("janssen",u,T)]="Janssen"
o[grep("vaxzevria|astrazeneca",u,T)]="AstraZeneca"
o[match(x,u)]}
rec=fread("curl -Ls github.com/skirsch/Czech/raw/main/data/CR_records.csv.xz|xz -dc")
k=grep("Datum_",names(rec));k2=k+3
d=data.table(date=`class<-`(unlist(rec[,..k],,F),"Date"),type=rename(unlist(rec[,..k2],,F)))[!is.na(date)]
d=d[date<="2023-7-4",.(doses=.N),type]
f="SUKL-batches-AE.xlsx"
download.file("https://github.com/PalackyUniversity/batch-dependent-safety/raw/main/data/SUKL-batches-AE.xlsx",f)
s2=data.table(readxl::read_excel(f,sheet=2))
s2=s2[,.(reports=sum(no_reports),serious=sum(serious),dead=sum(deaths)),.(type=rename(name))]
o=merge(s2,d)
o[,deadpermildose:=dead/doses*1e6]
o[,reportspermildose:=reports/doses*1e6]
o[,deadpermilreport:=dead/reports*1e6]
dplyr::mutate_if(o[type!="Other"],is.double,round)[order(-doses)]|>print(r=F)
type reports serious dead doses deadpermildose reportspermildose deadpermilreport
Pfizer 10712 5183 134 15680944 9 683 12509
Moderna 1575 583 26 1643159 16 959 16508
AstraZeneca 1512 695 44 887601 50 1703 29101
Janssen 555 241 10 415077 24 1337 18018
Novavax 14 4 0 11190 0 1251 0
When I used Pfizer as the baseline, Moderna got about 1.9 times higher deaths per dose and about 1.4 times higher adverse event reports per dose, so the ratio of deaths per reports also ended up being higher for Moderna than Pfizer:
> round(o[type=="Moderna",-1]/o[type=="Pfizer",-1],3) reports serious dead doses deadpermildose reportspermildose deadpermilreport 1: 0.147 0.112 0.194 0.105 1.852 1.403 1.32
The spreadsheet didn't include information about age so I wasn't able to look at only specific age groups or normalize my calculation by age. In the record-level data the average age is about 7 years higher for people who got a Moderna vaccine for the first dose than people who got a Pfizer vaccine for the first dose. But earlier I got a correlation of only about 0.18 between the average age of people under a batch and the rate of deaths per batch that had been reported as adverse events: czech3.html#Batch_study_by_authors_from_Palack_University.
But anyway, next I tried looking at US VAERS data: https://vaers.hhs.gov/data/datasets.html. I got the number of doses administered per manufacturer in the United States from this JSON file: https://covid.cdc.gov/covid-data-tracker/COVIDData/getAjaxData?id=vaccination_data. It only included the cumulative number of doses administered up to May 10th 2023 which was when the data stopped being updated, when there were about 367 million doses administered for Pfizer and 232 million for Moderna. But I didn't find any source which showed the number of doses grouped by both vaccine manufacturer and age, so I wasn't able to adjust my calculation for age.
Moderna again got a higher rate of both deaths per dose and reports per dose than Pfizer. But unlike in the case of the Czech data, the Moderna-Pfizer ratio for deaths per dose was now lower than the ratio for reports per dose, so Pfizer got a higher ratio of deaths per reports:
names=read.csv(text="name,vaers,doses
Pfizer,PFIZER\\BIONTECH,366979906
Moderna,MODERNA,232147784
Janssen,JANSSEN,19007537
Novavax,NOVAVAX,89195
Unknown,UNKNOWN MANUFACTURER,890835")
# # this code is not needed because I added the number of doses from the API to the table above
# con=url("https://covid.cdc.gov/covid-data-tracker/COVIDData/getAjaxData?id=vaccination_data")
# j=jsonlite::fromJSON(readLines(con))$vaccination_data;close(con)
# names$doses=j[1,paste0("Administered_",ifelse(names$name=="Unknown","Unk_Manuf",names$name))]
va=do.call(rbind,lapply(2020:2024,\(i)fread(paste0(i,"VAERSDATA.csv"))))
va=merge(va,do.call(rbind,lapply(2020:2024,\(i)fread(paste0(i,"VAERSVAX.csv")))))
o=va[VAX_TYPE=="COVID19",.(reports=.N,dead=sum(DIED=="Y")),.(vaers=VAX_MANU)]
o=merge(o,names)[,.(name,reports,dead,doses)]
o[,deadpermildose:=dead/doses*1e6]
o[,reportspermildose:=reports/doses*1e6]
o[,deadpermilreport:=dead/reports*1e6]
o[order(-doses)]|>dplyr::mutate_if(is.double,round)|>print(r=F)
name reports dead doses deadpermildose reportspermildose deadpermilreport Pfizer 481402 10439 366979906 28 1312 21685 Moderna 469655 9821 232147784 42 2023 20911 Janssen 73454 1943 19007537 102 3864 26452 Unknown 7363 82 890835 92 8265 11137 Novavax 492 5 89195 56 5516 10163
This shows that the Moderna-Pfizer ratio is about 1.53 for reports per dose, 1.39 for deaths per dose, and 0.91 for deaths per report:
> round(o[name=="Moderna",-1]/o[name=="Pfizer",-1],3) reports dead doses deadpermildose reportspermildose deadpermilreport 1: 0.976 0.941 0.633 1.487 1.542 0.964
However ideally I should've adjusted these calculations for age. In VAERS the ratio of deaths per reports seems to approximately double between each 10-year age group from 30-39 up to 90+ (even though the ratio remains similar in ages 10-19, 20-29, and 30-39):
> va=do.call(rbind,lapply(2020:2024,\(i)fread(paste0(i,"VAERSDATA.csv"))))
> va=merge(va,do.call(rbind,lapply(2020:2024,\(i)fread(paste0(i,"VAERSVAX.csv")))))
> agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
> o=va[!is.na(AGE_YRS)&VAX_TYPE=="COVID19",.(dead=sum(DIED=="Y"),reports=.N),.(age=agecut(AGE_YRS,0:9*10))]
> o[order(age)][,deadper10kreport:=round(dead/reports*1e4)][]|>print(r=F)
age dead reports deadper10kreport
0-9 20 16389 12
10-19 107 54171 20
20-29 201 86426 23
30-39 362 135659 27
40-49 672 140188 48
50-59 1572 155711 101
60-69 3786 162128 234
70-79 5910 117297 504
80-89 5445 48294 1127
90+ 2446 12197 2005
Kremer divided the VAERS data into only two groups for ages 18-64 and 65+, so I wanted to check if I would get different results for more fine-grained age groups. However when I calculated a Moderna-Pfizer ratio for deaths per reports, the ratio was below 1 in all age 5-year groups above 50-54, and some of the younger age groups where the ratio was above 1 had wide confidence intervals:
> o=va[!is.na(AGE_YRS)&VAX_TYPE=="COVID19",.(dead=sum(DIED=="Y"),reports=.N),.(age=agecut(AGE_YRS,0:19*5),type=VAX_MANU)][order(age)] > o1=o[type=="MODERNA"];o2=o[type=="PFIZER\\BIONTECH"] > rate=(o1$dead/o1$reports)/(o2$dead/o2$reports) > ci=exp(log(rate)+outer(qnorm(.975)*sqrt(1/o1$dead-1/o1$reports+1/o2$dead-1/o2$reports),c(-1,1))) > o1[,.(age,rate,low=ci[,1],high=ci[,2])]|>mutate_if(is.double,round,2)|>print(r=F) age rate low high 0-4 1.47 0.40 5.47 5-9 0.00 0.00 NaN 10-14 2.31 0.79 6.78 15-19 0.53 0.32 0.89 20-24 0.83 0.52 1.35 25-29 1.22 0.82 1.81 30-34 0.88 0.61 1.28 35-39 1.13 0.86 1.48 40-44 0.87 0.68 1.13 45-49 0.95 0.77 1.18 50-54 1.02 0.86 1.22 55-59 0.88 0.77 1.00 60-64 0.86 0.77 0.95 65-69 0.74 0.68 0.80 70-74 0.72 0.66 0.77 75-79 0.79 0.73 0.85 80-84 0.71 0.66 0.76 85-89 0.78 0.72 0.84 90-94 0.94 0.86 1.03 95+ 0.91 0.80 1.02
Kremer's "proportional rate ratio" values were expressed as the ratio for Pfizer divided by the ratio for Moderna, so it's the opposite of the Moderna-Pfizer ratios that have been calculated by me and Kirsch. His PRR value for deaths divided by reports was about 1.014 for ages 18-64 and 1.278 for ages 65+:

At first I got about 27% more deaths in ages 65+ than Kremer but only
about 4% more reports. But then I realized it was probably because I
counted reports where the DIED column had the value
Y as deaths, but Kremer might have only counted reports
where one of the symptom fields included death, which also gave me about
18% fewer deaths in ages 65+ for Moderna and Pfizer combined:
> va=do.call(rbind,lapply(2020:2024,\(i)fread(paste0(i,"VAERSDATA.csv"))))
> va=merge(va,do.call(rbind,lapply(2020:2024,\(i)fread(paste0(i,"VAERSVAX.csv")))))
> symp=do.call(rbind,lapply(2020:2024,\(i)fread(paste0(i,"VAERSSYMPTOMS.csv"))))
> va$dead=va$VAERS_ID%in%symp$VAERS_ID[rowSums(symp[,c(1:5*2)]=="Death")==1]
> vae=va[AGE_YRS>=65&VAX_TYPE=="COVID19"&grepl("MOD|PFI",VAX_MANU)]
> vae[DIED=="Y",.N,VAX_MANU] # DIED column is Y
VAX_MANU N
1: MODERNA 7598
2: PFIZER\\BIONTECH 7520
> vae[dead==T,.N,VAX_MANU] # symptom columns include death
VAX_MANU N
1: MODERNA 6285
2: PFIZER\\BIONTECH 6138
I don't know which approach is better, but here when I counted reports where the symptom columns included death, I got similar PRR values as Kremer:
> young=va[AGE_YRS%in%18:64&VAX_TYPE=="COVID19",.(dead=sum(dead),reports=.N),.(type=VAX_MANU)]
> young=young[match(c("PFIZER\\BIONTECH","MODERNA"),type)]
> young
type dead reports
1: PFIZER\\BIONTECH 1503 283324
2: MODERNA 1458 273126
> young[1,dead/reports]/young[2,dead/reports]
[1] 0.99376 # PRR for ages 18 to 64 (Pfizer divided by Moderna)
> old=va[AGE_YRS>=65&VAX_TYPE=="COVID19",.(dead=sum(dead),reports=.N),.(type=VAX_MANU)]
> old=old[match(c("PFIZER\\BIONTECH","MODERNA"),type)]
> old
type dead reports
1: PFIZER\\BIONTECH 6138 105769
2: MODERNA 6285 142616
> old[1,dead/reports]/old[2,dead/reports]
[1] 1.3168 # PRR for ages 65 and above (Pfizer divided by Moderna)
VAERS also contains reports from European countries, but several fields including the country codes were scrubbed from European reports in November 2022. WelcomeTheEagle posted a version of the VAERS data here that was downloaded before the country codes were removed: https://www.vaersaware.com/post/vaers-nov-11th-downloadable-files. I used the data to calculate an age-normalized rate of adverse event reports in the Czech Republic. I took the number of doses administered in each age group from the record-level data, so that I only included doses administered up to November 11th 2022 which was the date of the old snapshot of VAERS.
In the old VAERS data you can select Czech reports by selecting rows
where the first two characters of the SPLTTYPE field are
CZ. At first I tried selecting rows where the
SYMPTOM_TEXT field matched identifiers like
CZ-CZSUKL-21010694, but it missed about 16% of all reports
where the SPLTTYPE field started with CZ.
There were only two reports where SYMPTOM_TEXT matched
\bCZ- but SPLTTYPE didn't start with
CZ, but one of them was a Belgian report that was linked to
an earlier Czech report of the same patient, and the other report was
missing the SPLTTYPE field.
There were only 5,247 rows where the SPLTTYPE column
started with CZ and the VAX_TYPE column was
COVID19, and about two thirds of the rows were missing the
age field. But among the remaining 1,871 rows, the age-standardized rate
of adverse event reports per doses administered was about 3.0 times
higher for Moderna than Pfizer, and the crude rate that was not adjusted
for age was about 2.9 times higher for Moderna than Pfizer:
age=\(x,y){class(x)=class(y)=NULL;(y-x-(y-789)%/%1461+(x-789)%/%1461)%/%365}
ua=\(x,y,...){u=unique(x);y(u,...)[match(x,u)]}
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
ages=c(0,30,40,50,seq(60,95,5))
rename=\(x){u=unique(x);o=rep("Other",length(u))
o[grep("comirnaty|pfizer",u,T)]="Pfizer"
o[grep("moderna|spikevax",u,T)]="Moderna"
o[grep("nuvaxovid|novavax",u,T)]="Novavax"
o[grep("janssen",u,T)]="Janssen"
o[grep("vaxzevria|astrazeneca",u,T)]="AstraZeneca"
o[match(x,u)]}
va=fread("AllVAERSDataCSVS/NonDomesticVAERSDATA.csv")
va=merge(va,fread("AllVAERSDataCSVS/NonDomesticVAERSVAX.csv"))
vae=va[grepl("^CZ",SPLTTYPE)&VAX_TYPE=="COVID19"]
rec=fread("Czech/data/CR_records.csv")
k=grep("Datum_",names(rec));k2=k+3
set.seed(0);d=rec[,.(birth=rep(ua(paste0(Rok_narozeni,"-1-1"),as.Date)+sample(0:364,.N,T),7))]
d$date=`class<-`(unlist(rec[,..k],,F),"Date")
d$type=rename(unlist(rec[,..k2],,F))
d=d[!is.na(date)&date<="2022-11-11"]
d[,age:=age(birth,date)]
d=d[,.(doses=.N),.(type,age=agecut(pmax(age,0),ages))]
std=fread("http://sars2.net/f/czcensus2021pop.csv")[,.(std=sum(pop)),.(age=agecut(age,ages))][,std:=std/sum(std)]
a=merge(d,vae[!is.na(AGE_YRS),.(reports=.N),.(type=rename(VAX_MANU),age=agecut(AGE_YRS,ages))])
o=merge(std,a)[,.(reports=sum(reports),doses=sum(doses),agestd=sum(reports/doses*std*1e6)),type]
o[,crude:=reports/doses*1e6][order(-doses)]|>print(r=F)
type reports doses agestd crude Pfizer 1369 15508487 86.98 88.27 # Pfizer has about 3.3 times as many reports as Moderna Moderna 415 1639762 258.43 253.09 Janssen 84 397696 205.40 211.22 Other 2 180 2590.57 11111.11
At first when I tried to select Czech VAERS reports by picking rows
where the age field was not missing and the SYMPTOM_TEXT
field matched \bCZ-, I got 199 reports for Moderna but 1210
for Pfizer. But now when I picked rows where the SPLTTYPE
field started with CZ instead, I got 415 reports for
Moderna but 1369 for Pfizer, so it approximately doubled the ratio of
Moderna reports to Pfizer reports. It might be because many of the
reports for Pfizer vaccines included an identifier like
CZ-PFIZER INC-2021285400 in the SYMPTOM_TEXT
field, but there wasn't a similar identifier for Moderna vaccines.
However it also seems to be a sign that there was somehow a different
reporting procedure used for Pfizer vaccines and Moderna vaccines.
In the previous block of code I only included VAERS reports where the age field was not missing. But now when I also included the reports where the age field was missing, Pfizer got about 9% higher crude rate of reports per dose than Moderna:
> allage=merge(d[,.(doses=sum(doses)),type],va[,.(reports=.N),.(type=rename(VAX_MANU))])
> allage[,crude:=reports/doses*1e6][order(-doses)]|>print(r=F)
type doses reports crude
Pfizer 15526217 4548 292.9 # Pfizer has about 10.3 times as many reports as Moderna
Moderna 1639762 441 268.9
Janssen 414410 244 588.8
Other 764 14 18324.6
In the output above Pfizer got about 10.3 times as many reports as Moderna but in the block of output before it the ratio was about 3.3. In the spreadsheet from the GitHub account of Palacký University I got an intermediate ratio of about 6.8. The Palacký spreadsheet includes about 2.7 times as many total reports as VAERS, so there might be some kind of a bias for which reports end up being submitted to VAERS:
> s2=data.table(readxl::read_excel("SUKL-batches-AE.xlsx",sheet=2))
> s2[,.(reports=sum(no_reports)),type=rename(name)][order(-reports)]|>print(r=F)
type reports
Pfizer 10712 # Pfizer has about 6.8 times as many reports as Moderna
Moderna 1575
AstraZeneca 1512
Janssen 555
Other 18
Novavax 14
For some reason in the Czech VAERS data, the percentage of reports
that was missing the age field was about 6% for Moderna but 70% for
Pfizer (even though in many of the reports where the age field was
missing, the age was still mentioned in the SYMPTOM_TEXT
field):
> va=fread("AllVAERSDataCSVS/NonDomesticVAERSDATA.csv")
> va=merge(va,fread("AllVAERSDataCSVS/NonDomesticVAERSVAX.csv"))
> vae=va[grepl("^CZ",SPLTTYPE)&VAX_TYPE=="COVID19"]
> vae[,.(reports=.N,missingagepct=mean(is.na(AGE_YRS))*100),VAX_MANU][order(-reports)]|>print(r=F)
VAX_MANU reports missingagepct
PFIZER\\BIONTECH 4548 69.899
MODERNA 441 5.896
JANSSEN 244 65.574
UNKNOWN MANUFACTURER 14 78.571
In the whole VAERS data the percentage of reports that was missing the age field was about 8.9% for Moderna but 9.7% for Pfizer (so it's not a major difference, but it might have still introduced a slight bias to Kremer's analysis where he only included reports within a certain age range):
> va=do.call(rbind,lapply(2020:2024,\(i)fread(paste0(i,"VAERSDATA.csv"))))
> va=merge(va,do.call(rbind,lapply(2020:2024,\(i)fread(paste0(i,"VAERSVAX.csv")))))
> va[VAX_TYPE=="COVID19",.(reports=.N,missingagepct=mean(is.na(AGE_YRS))*100),VAX_MANU][order(-reports)]|>print(r=F)
VAX_MANU reports missingagepct
PFIZER\\BIONTECH 481402 9.738
MODERNA 469655 8.871
JANSSEN 73454 18.101
UNKNOWN MANUFACTURER 7363 27.774
NOVAVAX 492 3.862
I also tried downloading the raw EudraVigilance data from here: https://howbad.info (direct link https://www.dropbox.com/scl/fi/mrzkrrg5391kevsrwex0e/eudra-vigilance3.zip?rlkey=eqg628elz9lqufpehh2ni3o9w). I ran this code to get the number of deaths and reports grouped by age, date, and manufacturer:
awk -F\\t '{sub(" .*","",$3);sub("More than 85 Years",85,$7);sub("Not Specified","",$7);sub("[- ].*","",$7);x=""}$12~/SPIKEVAX|MODERNA/{x="Moderna"}$12~/COMIRNATY|TOZINAMERAN/{x="Pfizer"}$12~/COVID-19 VACCINE ASTRAZENECA|VAXZEVRIA/{x="AstraZeneca"}$12~/COVID-19 VACCINE JANSSEN|JCOVDEN/{x="Janssen"}x{k=$3","x","$7;a[k]++;dead[k]+=$11~/Fatal - Results in Death/}END{for(i in a)print i","a[i]","dead[i]}' eudra-vigilance3/*|(echo date,type,age,reports,dead;sort -nk3|sort -sk2,2|sort -sk1,1)>eudra.csv
However in the EudraVigilance data Moderna got a higher rate of deaths per reports than Pfizer in all age groups:
eu=fread("http://sars2.net/f/eudra.csv")
eu=eu[,.(reports=sum(reports),dead=sum(dead)),.(age=ifelse(age<10,0,age),type)][order(age)]
eu=rbind(eu,eu[,.(reports=sum(reports),dead=sum(dead),age="Total"),type])
o=eu[type=="Moderna",.(age,Moderna_dead=dead,Moderna_reports=reports)]
o=cbind(o,eu[type=="Pfizer",.(Pfizer_dead=dead,Pfizer_reports=reports)])
o$Moderna_rate=o[,2]/o[,3]*1e6
o$Pfizer_rate=o[,4]/o[,5]*1e6
o$Moderna_Pfizer_ratio=o[,6]/o[,7]
o
| Age |
Moderna dead |
Moderna reports |
Pfizer dead |
Pfizer reports |
Moderna rate |
Pfizer rate |
Moderna-Pfizer ratio |
|---|---|---|---|---|---|---|---|
| 0 | 13 | 511 | 74 | 6436 | 25440 | 11498 | 2.21 |
| 12 | 26 | 2553 | 158 | 30958 | 10184 | 5104 | 2.00 |
| 18 | 1832 | 292765 | 3034 | 920149 | 6258 | 3297 | 1.90 |
| 65 | 3139 | 53245 | 5937 | 152645 | 58954 | 38894 | 1.52 |
| 85 | 1367 | 6259 | 4104 | 26633 | 218405 | 154095 | 1.42 |
| NA | 280 | 16845 | 1098 | 74500 | 16622 | 14738 | 1.13 |
| Total | 6657 | 372178 | 14405 | 1211321 | 17887 | 11892 | 1.50 |
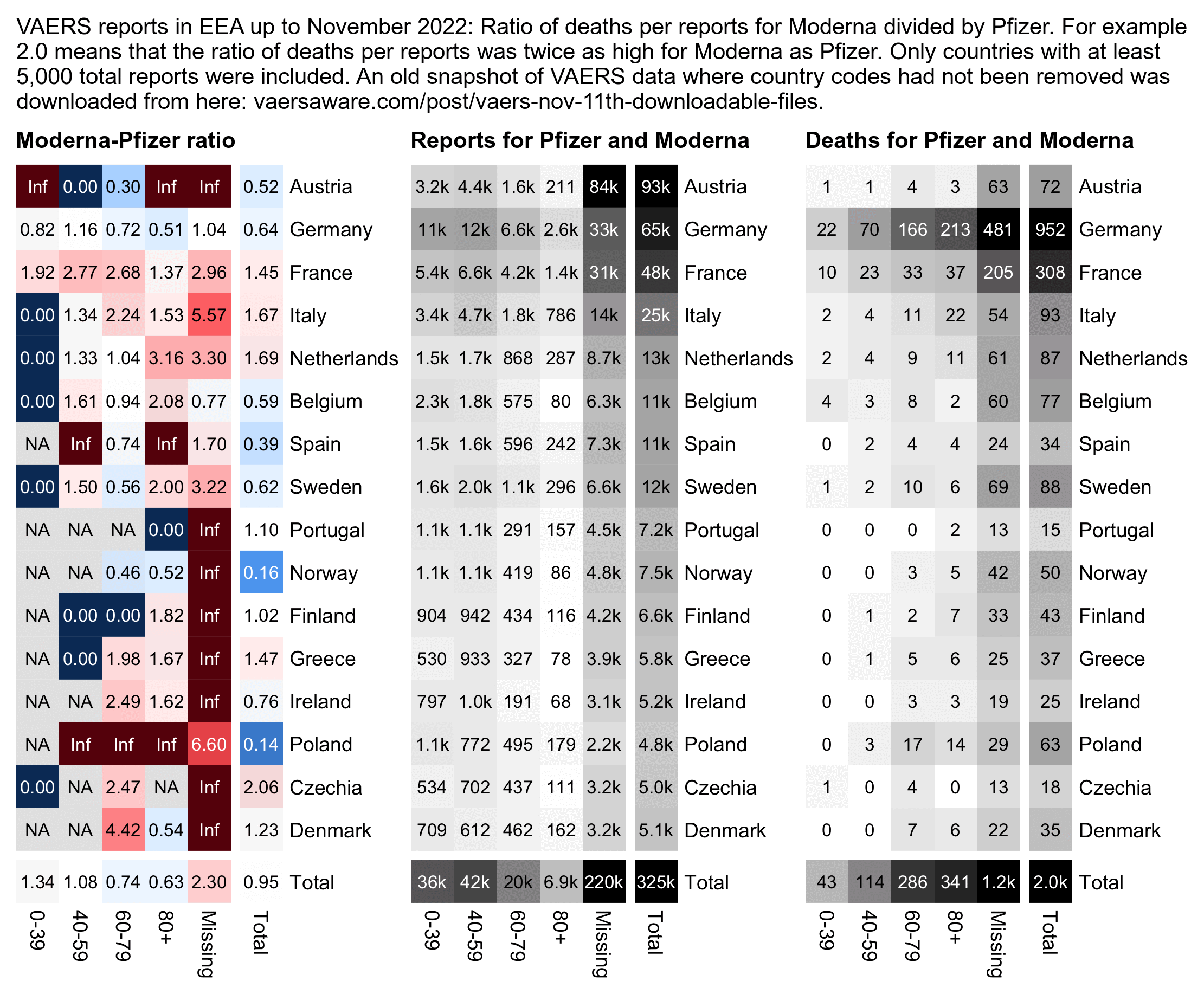
The next plot also shows that there's a lot of variance in the "proportional rate ratio" across European countries. Even if you only look at the column which shows the total ratio in all age groups and you look at the countries at the top of the plot which have the highest number of reports, the ratio is far below 1 in Austria and Germany but far above 1 in France, Italy, and Netherlands. The countries are sorted by the total number of reports, which was for some reason the highest in Austria:
library(data.table)
kimi=\(x){na=is.na(x);x[na]=0;e=floor(log10(ifelse(x==0,1,abs(x))));e2=pmax(e,0)%/%3+1;x[]=ifelse(abs(x)<1e3,round(x),paste0(sprintf(paste0("%.",ifelse(e%%3==0,1,0),"f"),x/1e3^(e2-1)),c("","k","M","B","T")[e2]));x[na]="NA";x}
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
iso2=fread("https://raw.githubusercontent.com/lukes/ISO-3166-Countries-with-Regional-Codes/master/all/all.csv")
iso2=setNames(iso2$name,iso2$`alpha-2`)
iso2["NL"]="Netherlands"
va=fread("AllVAERSDataCSVS/NonDomesticVAERSDATA.csv")
va=merge(va,fread("AllVAERSDataCSVS/NonDomesticVAERSVAX.csv"))
symp=fread("AllVAERSDataCSVS/NonDomesticVAERSSYMPTOMS.csv")
va$dead=va$VAERS_ID%in%symp$VAERS_ID[rowSums(symp[,c(1:5*2)]=="Death")==1]
va[,country:=substr(SPLTTYPE,1,2)]
eea=strsplit("AT BE BG HR CY CZ DK EE FI FR DE GR HU IE IT LV LT LU MT NL PL PT RO SK SI ES SE IS LI NO"," ")[[1]]
va=va[VAX_TYPE=="COVID19"&country%in%eea]
ages=c(0,40,60,80)
vae=va[,.(dead=sum(dead),reports=.N),.(type=VAX_MANU,country=iso2[country],age=agecut(AGE_YRS,ages))]
vae[is.na(age),age:="Missing"]
vae=vae[country%in%vae[,sum(reports),country][V1>=5e3,country]]
vae[,country:=factor(country,vae[,sum(reports),country][order(-V1),country])]
vae[,type:=factor(type,vae[,sum(reports),type][order(-V1),type])]
vae=rbind(vae,vae[,.(dead=sum(dead),reports=sum(reports),age="Total"),.(type,country)])
vae=rbind(vae,vae[,.(dead=sum(dead),reports=sum(reports),country="Total"),.(type,age)])
a=vae[,tapply(dead/reports*1e5,.(type,country,age),c)]
type1="MODERNA";type2="PFIZER\\BIONTECH"
m1=a[type1,,];m2=a[type2,,];m=(m1-m2)/ifelse(m1>m2,m2,m1)
disp=m1/m2;disp[]=sprintf("%.*f",ifelse(!is.na(disp)&disp>=10,1,2),disp);disp[is.na(m)]="NA"
maxcolor=10
zero=m1>0&m2==0;m[zero]=-maxcolor;disp[zero]="0.00"
inf=m1==0&m2>0;m[inf]=maxcolor;disp[inf]="Inf"
pal=hsv(rep(c(7/12,0),4:5),c(.9,.75,.6,.3,0,.3,.6,.75,.9),c(.4,.65,1,1,1,1,1,.65,.4))
pheatmap::pheatmap(m,filename="i1.png",display_numbers=disp,
gaps_col=ncol(m)-1,gaps_row=nrow(m)-1,cluster_rows=F,cluster_cols=F,legend=F,
cellwidth=19,cellheight=19,fontsize=9,fontsize_number=8,border_color=NA,na_col="gray90",
number_color=ifelse(!is.na(m)&abs(m)>.5*maxcolor,"white","black"),
breaks=seq(-maxcolor,maxcolor,,256),colorRampPalette(pal)(256))
mpop=vae[type%in%c(type1,type2),xtabs(reports~country+age)]
exp2=.6;maxcolor2=max(mpop[-nrow(mpop),-ncol(mpop)])
pheatmap::pheatmap(mpop^exp2,filename="i2.png",display_numbers=kimi(mpop),
gaps_row=nrow(m)-1,gaps_col=ncol(m)-1,cluster_rows=F,cluster_cols=F,legend=F,
cellwidth=19,cellheight=19,fontsize=9,fontsize_number=8,border_color=NA,na_col="white",
number_color=ifelse(mpop^exp2>maxcolor2^exp2*.45,"white","black"),
breaks=seq(0,maxcolor2^exp2,,256),sapply(seq(1,0,,256),\(i)rgb(i,i,i)))
mdead=vae[type%in%c(type1,type2),xtabs(dead~country+age)]
exp3=.6;maxcolor3=max(mdead[-nrow(mdead),-ncol(mdead)])
pheatmap::pheatmap(mdead^exp3,filename="i3.png",display_numbers=kimi(mdead),
gaps_row=nrow(m)-1,gaps_col=ncol(m)-1,cluster_rows=F,cluster_cols=F,legend=F,
cellwidth=19,cellheight=19,fontsize=9,fontsize_number=8,border_color=NA,na_col="white",
number_color=ifelse(mdead^exp3>maxcolor3^exp3*.45,"white","black"),
breaks=seq(0,maxcolor3^exp3,,256),sapply(seq(1,0,,256),\(i)rgb(i,i,i)))
cap="VAERS reports in EEA up to November 2022: Ratio of deaths per reports for Moderna divided by Pfizer. For example 2.0 means that the ratio of deaths per reports was twice as high for Moderna as Pfizer. Only countries with at least 5,000 total reports were included. An old snapshot of VAERS data where country codes had not been removed was downloaded from here: vaersaware.com/post/vaers-nov-11th-downloadable-files."
system(paste0("pad=20;pad2=30;w=`identify -format %w i1.png`;magick -font Arial-Bold -pointsize 42 -size $[w-pad*2]x \\( caption:'Moderna-Pfizer ratio' -splice $[pad]x20 i1.png -append \\) \\( caption:'Reports for Pfizer and Moderna' -splice $[pad]x20 i2.png -append \\) \\( caption:'Deaths for Pfizer and Moderna' -splice $[pad]x20 i3.png -append \\) -shave 14x +append -trim -bordercolor white -border $pad2 0.png;w=`identify -format %w 0.png`;magick -pointsize 42 -font Arial -interline-spacing -2 \\( -size $[w-pad2*2]x caption:'",cap,"' -splice $[pad2]x24 \\) 0.png -append 1.png"))
The raw data for EudraVigilance that can be downloaded from howbad.info doesn't show the country of the reports. But you can see the number of reports for each country from EMA's portal for EudraVigilance, if you go here, click "C", scroll to COVID vaccines, open the page for a vaccine brand, and click "Number of Individual Cases by EEA countries": https://www.adrreports.eu/en/search_subst.html. I compiled the data for all vaccine brands into this CSV file on August 8th 2024 UTC: f/eudracountry.csv.
I took the number of doses administered by manufacturer and country from OWID: https://raw.githubusercontent.com/owid/covid-19-data/master/public/data/vaccinations/vaccinations-by-manufacturer.csv. OWID was missing data for Greece and UK, and in the following analysis I also excluded Iceland because it was missing most administered doses at OWID.
In most countries Moderna got a higher rate of reports per dose than Pfizer (with the exception of Italy, Netherlands, Portugal, and a few small countries that have a small sample size):

library(data.table)
kimi=\(x){na=is.na(x);x[na]=0;e=floor(log10(ifelse(x==0,1,abs(x))));e2=pmax(e,0)%/%3+1;x[]=ifelse(abs(x)<1e3,round(x),paste0(sprintf(paste0("%.",ifelse(e%%3==0,1,0),"f"),x/1e3^(e2-1)),c("","k","M","B","T")[e2]));x[na]="NA";x}
owid=fread("https://raw.githubusercontent.com/owid/covid-19-data/master/public/data/vaccinations/vaccinations-by-manufacturer.csv")
owid=unique(owid[order(-date)],by=c("location","vaccine"))
owid=owid[,.(country=location,doses=total_vaccinations,type=vaccine)]
owid$type[owid$type=="Pfizer/BioNTech"]="Pfizer"
owid$type[owid$type=="Oxford/AstraZeneca"]="AstraZeneca"
owid$type[owid$type=="Johnson&Johnson"]="Janssen"
eu=fread("http://sars2.net/f/eudracountry.csv")
eu$country[eu$country=="Czech Republic"]="Czechia"
me=merge(eu,owid)[country!="Iceland"]
me[,country:=factor(country,me[,.(sum(doses)),country][order(-V1),country])]
me[,type:=factor(type,me[,.(sum(doses)),type][order(-V1),type])]
me=rbind(me,me[,.(reports=sum(reports),doses=sum(doses),country="Total"),type])
me=rbind(me,me[,.(reports=sum(reports),doses=sum(doses),type="Total"),country])
m=me[,tapply(reports/doses*1e4,.(country,type),c)]
m[is.infinite(m)]=NA;disp=kimi(m);exp=.7;maxcolor=200
pal=hsv(c(21,21,21,16,11,6,3,0,0,0)/36,c(0,.25,rep(.5,8)),c(rep(1,8),.5,0))
pheatmap::pheatmap(m^exp,filename="i1.png",display_numbers=disp,
gaps_row=nrow(m)-1,gaps_col=ncol(m)-1,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=20,cellheight=20,fontsize=9,fontsize_number=8,
border_color=NA,na_col="gray90",
number_color=ifelse(!is.na(m)&m^exp>maxcolor^exp*.8,"white","black"),
breaks=seq(0,maxcolor^exp,,256),
colorRampPalette(pal)(256))
m=me[,xtabs(doses~country+type)]
disp=kimi(m);exp=.7;maxcolor=max(m[-nrow(m),-ncol(m)])
pal=sapply(seq(1,0,,256),\(i)rgb(i,i,i))
pheatmap::pheatmap(m^exp,filename="i2.png",display_numbers=disp,
gaps_row=nrow(m)-1,gaps_col=ncol(m)-1,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=20,cellheight=20,fontsize=9,fontsize_number=8,
border_color=NA,na_col="gray90",
number_color=ifelse(!is.na(m)&m^exp>maxcolor^exp*.45,"white","black"),
breaks=seq(0,maxcolor^exp,,256),
colorRampPalette(pal)(256))
cap="Number of adverse event reports at EudraVigilance per 10,000 doses administered at OWID. The right side shows the number of doses administered. Source: adrreports.eu/en/search_subst.html (letter C, links for COVID vaccines), ourworldindata.org/grapher/covid-vaccine-doses-by-manufacturer (download CSV data)."
system(paste0("magick \\( i1.png -gravity east -chop 10x \\) \\( i2.png -gravity west -chop 10x \\) +append 0.png;w=`identify -format %w 0.png`;pad=20;magick -pointsize 42 -interline-spacing -2 -font Arial \\( -size $[w-pad*2]x caption:'",cap,"' -splice $[pad]x20 \\) 0.png -append 1.png"))
However I was not able to adjust my analysis for differences in the age distribution between vaccine brands. In the VAERS reports that are not missing the age field, most EEA countries have a higher average age for Moderna than Pfizer, even though in most countries the difference isn't as big as in the Czech Republic:
va=fread("AllVAERSDataCSVS/NonDomesticVAERSDATA.csv")
va=merge(va,fread("AllVAERSDataCSVS/NonDomesticVAERSVAX.csv"))
va[,country:=substr(SPLTTYPE,1,2)]
vae=va[VAX_TYPE=="COVID19",.(age=mean(AGE_YRS,na.rm=T),.N),.(type=VAX_MANU,country)]
o=vae[type=="MODERNA",.(country,Moderna_age=age,Moderna_N=N)]
o=merge(o,vae[type=="PFIZER\\BIONTECH",.(country,Pfizer_age=age,Pfizer_N=N)])
o$diff=o[,2]-o[,4]
o=o[country%in%strsplit("AT BE BG HR CY CZ DK EE FI FR DE GR HU IE IT LV LT LU MT NL PL PT RO SK SI ES SE IS LI NO"," ")[[1]]]
o[order(-Pfizer_N)][,c(1,2,4,6,3,5)]|>mutate_if(is.double,round,1)|>print(r=F)
country Moderna_age Pfizer_age diff Moderna_N Pfizer_N
AT 46.8 46.1 0.7 7179 85854
DE 49.7 49.4 0.3 9772 54896
FR 51.3 50.2 1.2 6781 41596
IT 49.2 48.0 1.2 5161 19949
NL 51.3 47.5 3.8 1743 11278
SE 49.9 49.7 0.3 2190 9454
ES 45.3 48.0 -2.7 2232 8977
BE 42.1 42.6 -0.5 2871 8285
PT 44.6 44.9 -0.3 885 6337
NO 44.5 46.3 -1.8 1563 5934
FI 45.6 47.1 -1.5 1059 5555
GR 49.6 47.8 1.8 676 5125
CZ 54.3 48.7 5.6 441 4548
IE 47.5 42.1 5.4 794 4408
PL 47.5 44.2 3.3 500 4300
DK 47.6 51.5 -3.9 861 4250
RO 46.5 41.2 5.3 180 1978
EE 55.7 49.4 6.3 104 1143
HR 47.7 44.7 3.0 178 1118
HU 61.8 49.2 12.6 93 1064
IS 41.2 47.6 -6.4 76 1048
SK 52.8 46.1 6.8 120 857
LT 53.1 47.8 5.4 63 830
SI 62.8 50.6 12.2 58 518
LU 45.7 43.4 2.3 117 457
LV 53.0 40.8 12.2 149 417
CY 43.2 45.5 -2.3 26 214
BG 46.2 46.5 -0.3 33 185
MT 43.2 50.9 -7.7 23 137
LI 44.0 72.0 -28.0 2 5
country Moderna_age Pfizer_age diff Moderna_N Pfizer_N
In February 2024 the Dutch Central Bureau of Statistics published a dataset for COVID and non-COVID ASMR by vaccination status: https://www.cbs.nl/nl-nl/longread/rapportages/2024/covid-vaccinatiestatus-en-sterfte/3-resultaten. It included one set of data where people were classified as vaccinated immediately after the first dose, and another set of data where people were generally only classified as vaccinated 2 weeks after the second dose (or 4 weeks after the first dose in the case of vaccine brands like Johnson & Johnson which had only one primary course dose).
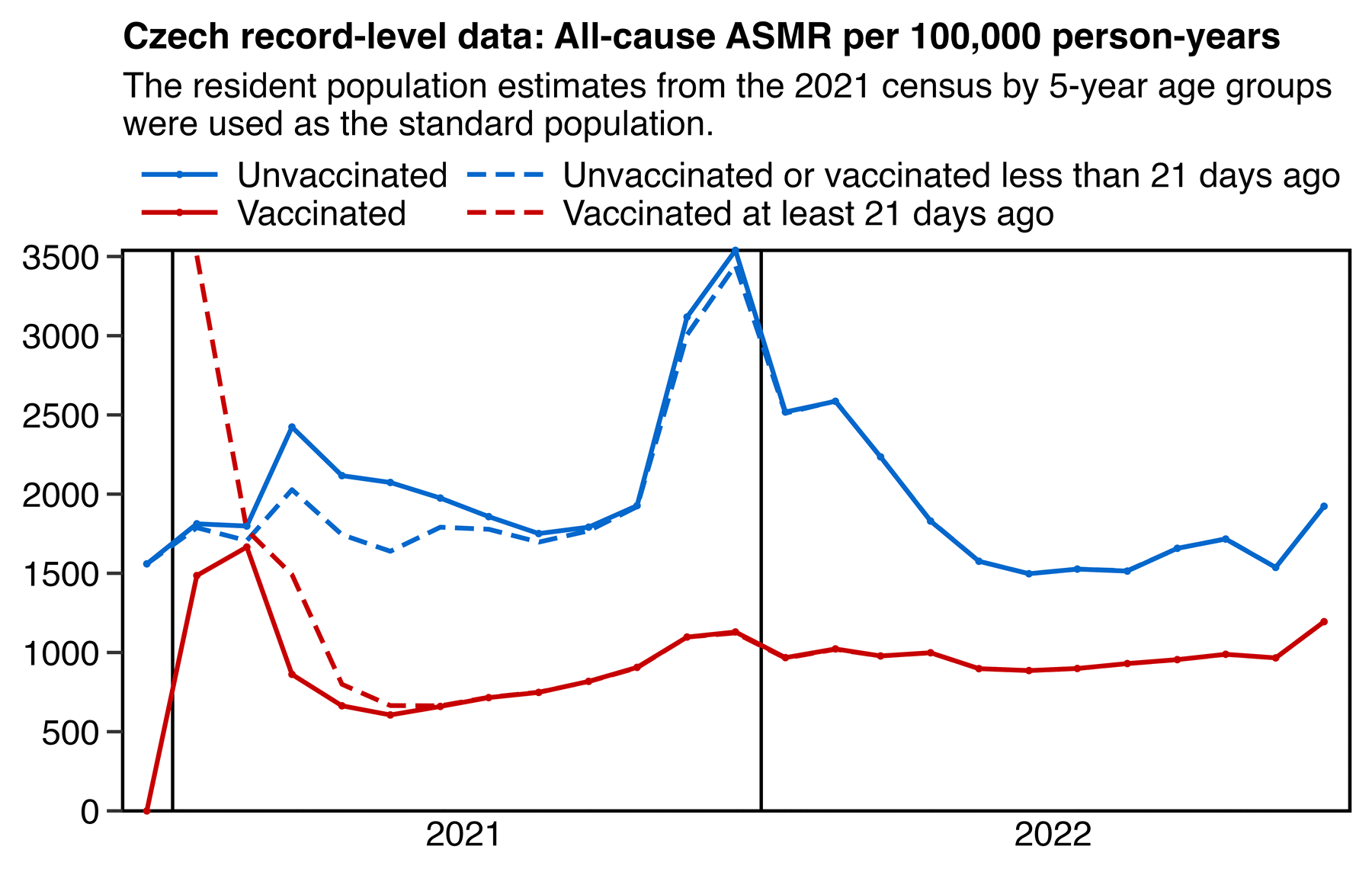
The classification delay reduced unvaccinated ASMR during the main rollout of the primary course doses from March to July 2021, so it resulted in a big advantage to unvaccinated people. In January and February 2021 the classification delay gave an advantage to vaccinated people because then there was a delay before the vulnerable groups of people were priorized during early rollout were counted as vaccinated, even though there were so few people who had been vaccinated during the first two months of 2021 that they don't have much impact on the total ASMR of vaccinated people: [statistic.html#Comparison_of_fully_vaccinated_and_vaccinated_ASMR]

Similarly in the Czech record-level data when I classified people as unvaccinated until 3 weeks from the first dose, it gave an advantage to unvaccinated people because it reduced the ASMR of unvaccinated people and it increased the ASMR of vaccinated people:
library(data.table);library(ggplot2)
b=fread("http://sars2.net/f/czbucketskeep.csv.gz")[dose<=1]
std=fread("http://sars2.net/f/czcensus2021pop.csv")[,.(std=sum(pop)),.(age=pmin(age,95)%/%5*5)][,std:=std/sum(std)]
p=copy(b)[,dose:=ifelse(dose==1,"Vaccinated","Unvaccinated")]
p=rbind(p,copy(b)[week<3,dose:=0][,dose:=ifelse(dose==1,"Vaccinated at least 21 days ago","Unvaccinated or vaccinated less than 21 days ago")])
p=p[,.(cmr=sum(dead)/sum(alive)*365e5),.(dose,age=pmin(age,95)%/%5*5,month)]
p=merge(std,p)[,.(asmr=sum(cmr*std)),.(dose,month)]
p[,dose:=factor(dose,unique(dose))]
p[,month:=as.Date(paste0(month,"-1"))]
xstart=as.Date("2020-12-1");xend=as.Date("2023-1-1")
p=p[month>=xstart&month<=xend]
xbreak=seq(as.Date("2021-7-1"),xend,"year");xlab=year(xbreak)
ystep=500;ystart=0;yend=max(p$asmr,na.rm=T);ybreak=seq(ystart,yend,ystep)
ggplot(p,aes(x=month+15,y=asmr))+
geom_vline(xintercept=seq(as.Date("2021-1-1"),as.Date("2023-1-1"),"year"),linewidth=.5)+
geom_vline(xintercept=c(xstart,xend),linewidth=.5,lineend="square")+
geom_hline(yintercept=c(ystart,yend),linewidth=.5,lineend="square")+
geom_line(aes(color=dose,linetype=dose),linewidth=.7)+
geom_point(aes(color=dose,alpha=dose),stroke=0,size=1.1)+
labs(x=NULL,y=NULL,title="Czech record-level data: All-cause ASMR per 100,000 person-years",subtitle="The resident population estimates from the 2021 census by 5-year age groups were used as the standard population."|>stringr::str_wrap(78))+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=hsv(c(21,0,21,0)/36,1,.8))+
scale_linetype_manual(values=c("solid","solid","42","42"))+
scale_alpha_manual(values=c(1,1,0,0))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=2,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(3)),
axis.ticks=element_line(linewidth=.5),
axis.ticks.length=unit(5,"pt"),
axis.ticks.length.x=unit(0,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.justification=c(0,0),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(30,"pt"),
legend.margin=margin(,,6),
legend.position="top",
legend.spacing.x=unit(3,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid=element_blank(),
plot.margin=margin(7,7,5,7),
plot.subtitle=element_text(size=11,margin=margin(,,4)),
plot.title=element_text(size=11.5,face="bold",margin=margin(,,5)))
ggsave("1.png",width=6,height=3.8,dpi=300*4)
system("mogrify -resize 25% -colors 256 1.png")
And in the English ONS data when I classified people as unvaccinated until 3 weeks from the first dose, it similarly gave a big advantage to unvaccinated people, because it reduced unvaccinated CMR in early 2021 when the first dose was rolled out (R code):

In an early version of the README file of Kirsch's GitHub repository about the Czech data, Kirsch wrote: "Vaccines were randomly distributed for those wishing to get vaxxed. [...] People were not allowed to select which vaccines they got. [...] The randomization of which vaccine someone got created a perfect real-world randomized clinical trial where we could compute the mortality rates for 1 year after Dose 2 for the two most popular vaccines." [https://github.com/skirsch/Czech/blob/5725ac1b64ede7124e00b72af68892f31736b349/README.md] After I showed him why his claim was likely wrong, he edited the README file to remove the claim.
However in August 2024 when Kirsch was on InfoWars, he resurrected his old claim that people were not allowed to choose if they got a Moderna or Pfizer vaccine. He said: "The only difference in the Czech Republic between getting a Pfizer shot and a Moderna shot is just pure luck. It was... you weren't allowed to choose, you were just assigned a brand. So it's effectively like the world's largest randomized trial." [https://x.com/RealAlexJones/status/1828912865107231096, time 45:51]
When I called Kirsch out for his comments on InfoWars, he asked me to show evidence that people were allowed to choose which vaccine type they got. But I showed him that there was a dropdown menu for choosing your preferred vaccine type in a form for registering a vaccination appointment: [https://ockodoc.mzcr.cz/wp-content/uploads/2023/07/manual_crs.pdf; translated with Yandex]

However I don't know if people were not initially allowed to choose the vaccine type, because an article dated May 2021 said: "You cannot currently choose which vaccine to get. Odds are you will get the Pfizer/BioNTech vaccine, as that one so far has been the most widely available, accounting for about three-fourths of the deliveries." [https://www.expats.cz/czech-news/article/vaccination-in-the-czech-republic-all-you-need-to-know]
Added in February 2025: Kirsch included my screenshot above in one of his earlier Substack posts about the Czech data, but for some reason now he again wrote: "But vaccine brands were QUASI-RANDOMLY distributed in the Czech Republic. People didn't get to choose. They got what was available. There was no systemic or systematic bias in the distribution." However someone from the Czech Republic corrected him in the comments and wrote: "Reservations for a specific 'vaccine' were possible through an online reservation system, which began operating about 2 months after the start of the vaccination campaign." [https://kirschsubstack.com/p/breaking-official-czech-record-level/comment/90222598]
I also posted this comment to Kirsch:
And also how do you differentiate whether the vaccines were distributed quasi-randomly or not quasi-randomly?
There's a bunch of biases like that Moderna recipients were older, had higher age-normalized comorbidity index, were vaccinated later, had higher age-normalized rate of vaccinators whose name matched "senior home", and so on. So at what point do those biases become severe enough that you would say the vaccines were not distributed quasi-randomly?
Or how do you differentiate between a systematic bias and a non-systematic bias? ChatGPT said that "Systematic bias leads to consistently skewed results in a particular direction, whereas nonsystematic bias results in random fluctuations around the true value." ChatGPT said that the effect of nonsystematic biases averages out over time, and as an example of a nonsystematic bias, ChatGPT gave that "If a scale sometimes overestimates or underestimates weight by small amounts in random ways, it introduces nonsystematic bias."
However in the case of the Czech data, the reason why Moderna recipients have higher average age than Pfizer recipients is not only due to random noise caused by a small sample size, or what ChatGPT suggested was a "nonsystematic bias", but the age distribution seems to be systematically skewed.
Tomáš Fürst posted this plot which shows that among people who were born in 1929 or earlier, vaccinated people had higher mortality than unvaccinated people starting from late 2021: [https://smis-lab.cz/2024/08/17/celkova-umrtnost-ceskych-obyvatel-dle-vakcinacniho-statutu-nejstarsi-rocniky/]

In the following code I took data from one of my buckets files where I had assigned a random birthday for each person so I could account for the aging of people over time with a sub-year precision. From the last column which shows the total mortality rate in 2021-2022, you can see that unvaccinated people had higher mortality than vaccinated people up to age 94, but in ages 95 and above vaccinated people had higher mortality:

b=fread("http://sars2.net/f/czbucketsdaily.csv.gz")
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(ifelse(head(y,-1)==y[-1]-1,"",paste0("-",y[-1]-1)),"+")),T,F)
ages=c(0:9*10,91:105)
a=b[date>="2021-1-1",.(alive=sum(alive),dead=sum(dead)),.(dose=pmin(dose,1),age=agecut(age,ages),month=substr(date,1,7))]
a=rbind(a,a[,.(dead=sum(dead),alive=sum(alive),month="Total"),.(dose,age)])
ar=a[,tapply(dead/alive,.(dose,age,month),c)]
m1=ar[1,,];m2=ar[2,,]
m=(m2-m1)/ifelse(m2>m1,m1,m2)*100
disp=round(m2/m1*100)
maxcolor=600;exp=.85
pheatmap::pheatmap(abs(m)^exp*sign(m),filename="0.png",display_numbers=disp,
gaps_col=ncol(m)-1,gaps_row=9,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=19,cellheight=19,fontsize=9,fontsize_number=8,
border_color=NA,na_col="gray90",
number_color=ifelse((abs(m)^exp>.55*maxcolor^exp)&!is.na(m),"white","black"),
breaks=seq(-maxcolor^exp,maxcolor^exp,,256),
colorRampPalette(hsv(rep(c(7/12,0),5:4),c(.9,.75,.6,.3,0,.3,.6,.75,.9),c(.4,.65,1,1,1,1,1,.65,.4)))(256))
cap="Czech record-level data: Vaccinated CMR as percentage of unvaccinated CMR"
system(paste0("w=`identify -format %w 0.png`;pad=24;convert -pointsize 42 -interline-spacing -3 -font Arial-Bold \\( -size $[w-pad*2]x caption:'",cap,"' -splice $[pad]x20 \\) 0.png -append 1.png"))
Elderly people who live in a senior home have higher ASMR than elderly people who live on their own, and I don't know if for example elderly people who live in a senior home are more likely to be vaccinated than age-matched elderly people who live on their own.
The plot above shows that for some reason in ages 104 and 105+ vaccinated people had more than 10 times as high mortality as unvaccinated people. For people who were born in 1917 so they turned 104 in 2022, people who were born near the end of the year were much more likely to be alive in 2022 than people who were born near the beginning of the year, but my code for assigning a random birthday distributed the birthdays evenly across the year which resulted in a fairly large bias in the case of the very oldest age groups. However it shouldn't matter that much here because I'm simply comparing vaccinated mortality rate against unvaccinated mortality rate. So I don't know how to explain the extremely high percentages in ages 104 and 105+.
But in any case Fürst could've mentioned that there was a sharp increase in the ratio of unvaccinated to vaccinated CMR around ages 94 to 95, but in younger ages unvaccinated people had higher mortality.
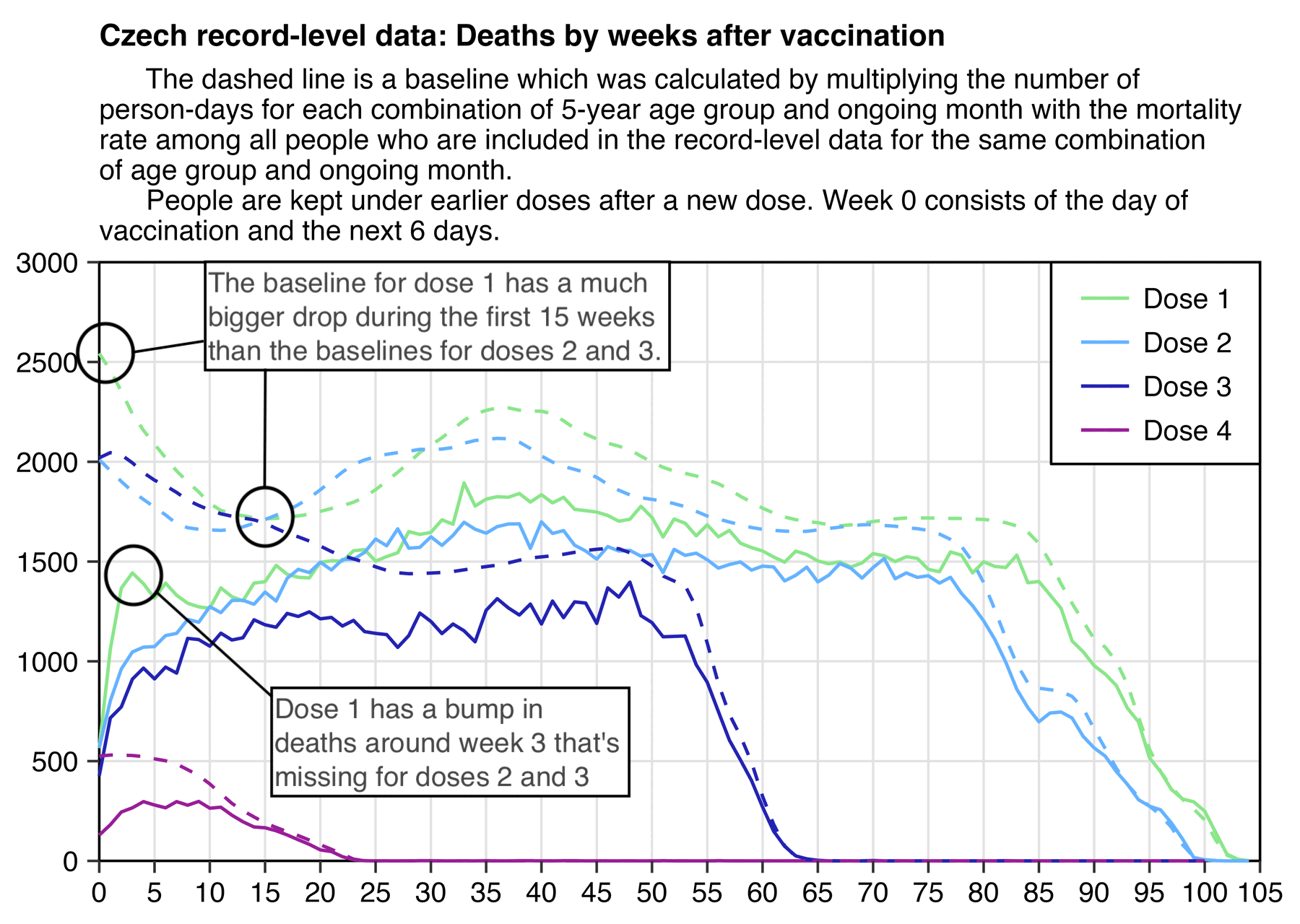
If you look at the raw number of deaths by weeks after vaccination but you don't normalize it for the background mortality rate, dose 1 seems to have a bump in deaths around weeks 2 to 10 that's missing for doses 2 and 3. But that's because during the first weeks after dose 1 the background mortality rate was falling rapidly because the COVID wave in early 2021 was passing by. So here when I calculated a baseline in a way where I accounted for the background mortality rate, the baseline for dose 1 has a much bigger drop during the first 15 weeks after vaccination than the baselines of doses 2 and 3:
library(data.table);library(ggplot2);library(stringr)
b=fread("http://sars2.net/f/czbucketskeep.csv.gz")[,age:=pmin(age,95)%/%5*5]
d=merge(b[dose%in%1:4],b[dose<=1,.(base=sum(dead)/sum(alive)),.(month,age)])[,base:=base*alive]
p=d[,.(y=sum(dead),base=sum(base),pop=sum(alive)),.(x=week,z=paste0("Dose ",dose))]
xstart=0;xend=105;xstep=5;ystart=0;yend=3000;ystep=500
color=hsv(c(12,21,24,30)/36,c(.4,.6,.8,.8),c(.9,1,.7,.6))
sub=paste0(" ","The dashed line is a baseline which was calculated by multiplying the number of person-days for each combination of 5-year age group and ongoing month with the mortality rate among all people who are included in the record-level data for the same combination of age group and ongoing month."|>str_wrap(90))
sub=paste0(sub,"\n ","People are kept under earlier doses after a new dose. Week 0 consists of the day of vaccination and the next 6 days."|>str_wrap(90))
ggplot(p,aes(x,y))+
geom_hline(yintercept=c(ystart,0,yend),linewidth=.3,lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.3,lineend="square")+
geom_line(aes(color=z),linewidth=.4)+
geom_line(aes(y=base,color=z),linetype=2,linewidth=.4)+
labs(title="Czech record-level data: Deaths by weeks after vaccination",subtitle=sub,x=NULL,y=NULL)+
scale_x_continuous(limits=c(xstart,xend),breaks=seq(xstart,xend,xstep))+
scale_y_continuous(limits=c(ystart,yend),breaks=seq(ystart,yend,ystep))+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
axis.ticks=element_line(linewidth=.3),
axis.ticks.length=unit(3,"pt"),
legend.background=element_rect(fill="white",color="black",linewidth=.3),
legend.justification=c(1,1),
legend.key.height=unit(11,"pt"),
legend.key.width=unit(15,"pt"),
legend.key=element_rect(fill="white"),
legend.margin=margin(-2,7,3,6),
legend.position=c(1,1),
legend.spacing.x=unit(2,"pt"),
legend.text=element_text(size=7),
legend.title=element_blank(),
panel.grid.major=element_line(linewidth=.3,color="gray90"),
panel.background=element_rect(fill="white"),
plot.margin=margin(4,10,4,4),
plot.subtitle=element_text(size=7,margin=margin(0,0,4,0)),
plot.title=element_text(size=7.5,face="bold",margin=margin(2,0,4,0)))
ggsave("0.png",width=4.5,height=3.2,dpi=400*4)
system("magick 0.png -filter lanczos2 -resize 25% 1.png")
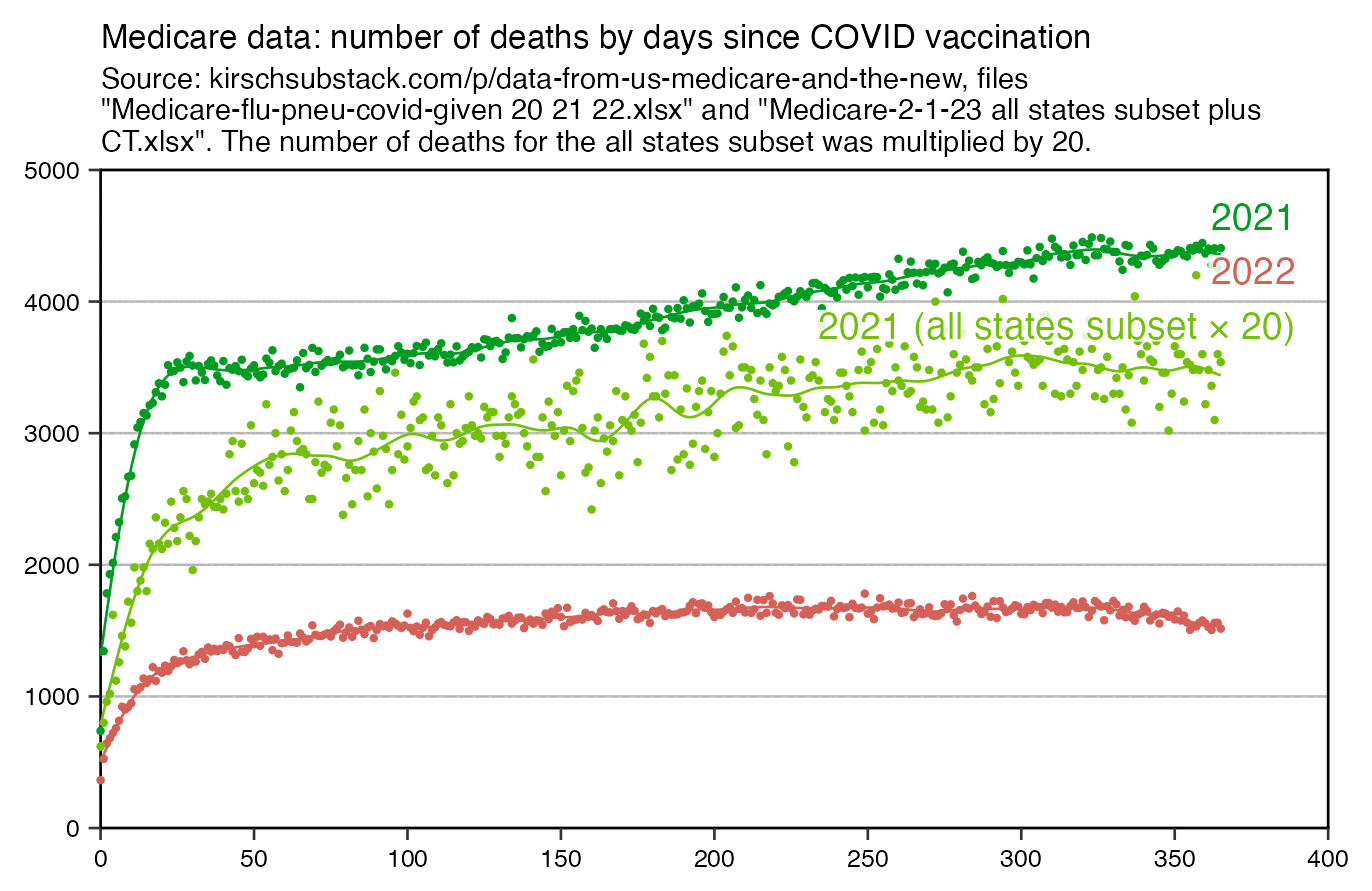
In the United States first doses were also given at a time when the COVID wave in early 2021 was passing by, which I think explains why the temporal HVE appears to last only about 3 weeks in Kirsch's Medicare data for 2021. But the temporal HVE seems to last longer in the Medicare data for 2022 which is missing the bump around the third week: [moar.html#US_Medicare_data]
Kirsch picked 9 batches that were given to at last 100 people in ages 70 to 74 in February 2021, and he then calculated a mortality rate for each batch during the first year from vaccination: [https://kirschsubstack.com/p/covid-vax-some-batches-increase-your]

Kirsch wrote that "there was >9X variation
between the most deadly Moderna vaccine batch and the safest Pfizer
vaccine batch". However actually the ratio of the two batches
that are shown in red in his table is only about 8.5 (from
.10989/.013001). The ratio becomes over 9 if you compare
the Moderna vaccines with a missing batch ID against the Pfizer batch
with the highest rate (.12/.013001). But I don't think it
makes sense to treat the doses with a missing batch ID as a distinct
batch.
But anyway, the sample sizes in his table are way too small because he restricted his analysis to only a single age group and a single month of vaccination.
In the code below I calculated a normalized excess mortality percent for each batch up to the end of 2022, so that I multiplied the number of person-days for each combination of 5-year age group and ongoing month with the mortality rate among all people who are included in the record-level data for the same combination of 5-year age group and ongoing month. I kept people included under a batch even after a dose from another batch.
I got about 19% excess mortality for the Moderna batch 300042721
which was Kirsch's batch with the highest mortality rate, and I got
about -16% excess mortality for the Pfizer batch EJ6797 which was
Kirsch's batch with the lowest mortality rate. So the Pfizer batch had
only about 1.39 times higher normalized mortality (from
119.64/86.28):
> library(data.table)
> download.file("http://sars2.net/f/czbucketsbatchkeep.csv.xz","czbucketsbatchkeep.csv.xz")
> b=fread("xz -dc czbucketsbatchkeep.csv.xz")[,age:=pmin(age,95)%/%5*5]
> a=merge(b[dose>0&batch!=""&type!="Other"],b[dose<=1,.(base=sum(dead)/sum(alive)),.(age,month)])[,base:=base*alive]
> a=a[,.(alive=sum(alive),dead=sum(dead),base=sum(base)),.(batch,age,type)]
> p=a[,.(excess=(sum(dead)/sum(base)-1)*100),.(batch,type)]
> print(p[batch%in%c("300042721","EJ6797")][order(-excess)],nrow=Inf)
batch type excess
1: 300042721 Moderna 19.63627
2: EJ6797 Pfizer -16.28020
I posted code for generating the czbucketsbatchkeep.csv
file here:
czech2.html#Statistics_by_batch.
In the code I assigned a random birthday to each person so that I could
model the aging of people with a daily precision.
Kirsch wrote that for people in ages 60 to 64 who got a second dose in June 2021, the Pfizer batch FC2473 got more than 3 times higher mortality rate within a year from vaccination than the Pfizer batch FD0168:

However using the code above my total normalized excess mortality was about -32% for the FC batch and about -39% for the FD batch, so there was not much difference. I included all doses instead of only second doses like Kirsch. I included all age groups and all vaccination months, and I calculated the excess mortality up to the end of 2022 and not during the first year from vaccination.
Kirsch got 48 deaths out of 6238 doses for the FC batch. The upper bound of the 95% confidence interval for the ratio is about twice as the high as the lower bound:
> as.numeric(prop.test(48,6238)$conf) [1] 0.005739933 0.010277757
In the following block of code I picked people who got a second dose from the FC or FD batch in June 2021 and I divided the number of deaths in the 365 days starting from the day of vaccination with the number of doses from the batch. I treated the age of each person as their year of birth subtracted from 2021. I kept people included under a batch even after they got a dose from another batch.
I converted the batch IDs to uppercase and stripped trailing spaces, which is what Kirsch also did. [https://github.com/skirsch/Czech/blob/main/code/vax.py#L59]
When I calculated the ratio of deaths per doses for each 5-year age group, the FD batch actually got a higher mortality rate than the FC batch in each age group from 65-69 to 85-89 (which all had a fairly large sample size of deaths):
rec=fread("CR_records.csv")
d=rec[,.(date=as.IDate(unlist(rec[,.SD,.SDcols=patterns("Datum_")],,F)),dead=DatumUmrti,age=2021-Rok_narozeni)]
d[,batch:=unlist(rec[,.SD,.SDcols=patterns("Sarze_")],,F)][,batch:=toupper(trimws(batch)),batch]
d$dose=rep(1:7,each=nrow(rec))
a=d[dose==2&date>="2021-06-01"&date<"2021-07-01"]
a=a[,.(dead=sum(!is.na(dead)&dead-date<365),doses=.N),.(batch,age=pmin(age,95)%/%5*5)]
a1=a[batch=="FC2473",.(age,dead1=dead,doses1=doses,rate1=dead/doses*1e5)]
a2=a[batch=="FD0168",.(age,dead2=dead,doses2=doses,rate2=dead/doses*1e5)]
o=merge(a1,a2)
o[,rate1vs2:=rate1/rate2]
o[,low:=exp(log(rate1vs2)-qnorm(.975)*sqrt(1/dead1+1/dead2))]
o[,high:=exp(log(rate1vs2)+qnorm(.975)*sqrt(1/dead1+1/dead2))]
print(round(o,2),row.names=F)
# FC2473 # FD0168 # FC vs FD with 95% CI age dead1 doses1 rate1 dead2 doses2 rate2 rate1vs2 low high 15 1 179 558.66 1 709 141.04 3.96 0.25 63.32 20 1 970 103.09 2 2280 87.72 1.18 0.11 12.96 25 0 1706 0.00 1 3469 28.83 0.00 0.00 NaN 30 2 2069 96.67 5 4877 102.52 0.94 0.18 4.86 35 1 2682 37.29 1 6452 15.50 2.41 0.15 38.46 40 8 4111 194.60 11 11006 99.95 1.95 0.78 4.84 45 16 4993 320.45 19 19186 99.03 3.24 1.66 6.29 50 29 4482 647.03 66 28524 231.38 2.80 1.81 4.33 55 38 5404 703.18 148 65597 225.62 3.12 2.18 4.45 60 84 8560 981.31 318 75389 421.81 2.33 1.83 2.96 65 240 31491 762.12 474 58382 811.89 0.94 0.80 1.10 # ratio below 1 70 203 16682 1216.88 301 17613 1708.96 0.71 0.60 0.85 # ratio below 1 75 109 3595 3031.99 213 6880 3095.93 0.98 0.78 1.23 # ratio below 1 80 54 934 5781.58 156 2365 6596.19 0.88 0.64 1.19 # ratio below 1 85 44 440 10000.00 115 1017 11307.77 0.88 0.62 1.25 # ratio below 1 90 36 160 22500.00 59 335 17611.94 1.28 0.84 1.93 95 18 46 39130.43 14 50 28000.00 1.40 0.70 2.81
My ratio in ages 60 to 64 was only about 2.33 and not 3.15 like in Kirsch's table. But I eventually figured out it was because of these three reasons:
df['date_1_'] regardless of the dose number:
df['days_until_death'] = (df[dod_col] - df['date_1_']).dt.days.round(0).
[https://github.com/skirsch/Czech/blob/eb8406c7c160f3951d798f5cd72a7c84901a60c4/code/vax.py#L117]
Kirsch fixed the bug after I pointed it out to him.Kirsch later added this section to his Substack post:

The plot above is a histogram where the y-axis values are always integers, so it's confusing how the y-axis labels include values like 0.5 and 1.5.
Kirsch wrote that "if the vaccines were safe, the mortality rates of the batches I looked at (given to a given group in a specific time period) must have a normal distribution". But that's not necessarily the case if there's confounding factors that vary across batches even after age and month of vaccination are controlled for.
Kirsch's plot had so few batches that it was difficult to even tell if his plot followed a normal distribution or not. And his sample size of total deaths was also fairly small because he only looked at vaccines given in March 2021, but he could've increased his sample size if he would've included all months of vaccination in his plot.
In the histogram plot below I calculated a normalized mortality rate for each batch the same way as earlier, except I plotted the mortality rate as a percentage of the baseline and not as excess mortality relative to the baseline (so now the values are the same as excess mortality values plus 100). I included only batches with at least 10,000 total person-years. But now in my histogram the distribution of mortality rates looks closer to a normal distribution than in Kirsch's plot (even though in plots like this which show excess mortality as a percentage of a baseline, the distribution is typically skewed because the values below 100% typically have a more narrow spread than the values above 100%):

b=fread("xz -dc czbucketsbatchkeep.csv.xz")[,age:=pmin(age,95)%/%5*5]
a=merge(b[dose>0&batch!=""&type!="Other"],b[dose<=1,.(base=sum(dead)/sum(alive)),.(age,month)])[,base:=base*alive]
a=a[,.(alive=sum(alive),dead=sum(dead),base=sum(base)),.(batch,age,type)]
keep=a[,sum(alive),batch][V1/365>=1e4,batch]
a=a[batch%in%keep,.(mort=sum(dead)/sum(base)*100),batch]
step=10;lev=seq(0,max(a$mort),step);yend=30
p=data.table(x=paste0("[",lev,",",lev+step,")"),y=as.integer(table(factor(a$mort%/%step*step,lev))))
p[,x:=factor(x,unique(x))]
png("1.png",1300,800,res=200)
par(mar=c(5,2.3,1.9,0),mgp=c(0,0.6,0))
tit="Histogram of batch mortality percentage relative to baseline"
barx=barplot(p$y,names.arg=p$x,main=tit,cex.main=1.1,xlab=NA,ylab=NA,lwd=1.5,las=2,space=0,ylim=c(0,yend))
text(x=barx,y=p$y-.01*yend,labels=p$y,pos=3,cex=0.8)
dev.off()
In the next plot I calculated ASMR using 5-year age groups but I didn't normalize it in any way for ongoing month or month of vaccination. I again included only batches with at least 10,000 person-years. However now the distribution looked less similar to a normal distribution:

b=fread("xz -dc czbucketsbatchkeep.csv.xz")
b[,age:=ifelse(age<25,0,pmin(age,95)%/%5*5)]
std=fread("czcensus2021pop.csv")[,.(std=sum(pop)),.(age=ifelse(age<25,0,pmin(age,95)%/%5*5))][,std:=std/sum(std)]
a=b[dose>0&batch!=""&type!="Other",.(dead=sum(dead),alive=sum(alive)),.(batch,age)]
a=merge(std,a)[alive/365>=1e4,.(asmr=sum(dead/alive*std*365e5)),batch]
step=50;max=max(a$asmr);lev=seq(0,max,step);yend=10
p=data.table(x=paste0("[",lev,",",lev+step,")"),y=as.integer(table(factor(a$asmr%/%step*step,lev))))
p[,x:=factor(x,unique(x))]
png("1.png",1300,800,res=200)
par(mar=c(5,2.3,1.9,0),mgp=c(0,.6,0))
tit="Histogram of batch ASMR"
barx=barplot(p$y,names.arg=p$x,main=tit,cex.main=1.1,xlab=NA,ylab=NA,lwd=1.5,las=2,space=0,ylim=c(0,yend))
text(x=barx,y=p$y-.01*yend,labels=p$y,pos=3,cex=.8)
dev.off()
Kirsch said that in my triangle plot which showed an age-normalized Moderna-Pfizer ratio by month of vaccination and ongoing month, the results were not statistically significant from July 2021 onwards: [https://kirschsubstack.com/p/a-closer-look-at-the-czech-data-confirms]

Kirsch seems to have determined statistical significance on each row of my heatmap by calculating the mean and standard deviation of each column and then looking at whether the mean was at least 2 standard deviations above 1, so for example in July 2021 he calculated the mean and standard deviation for a vector of monthly values like 0.64, 1.07, 1.72, 1.52, 0.88, and so on:

I don't think his approach was correct, because he should've taken into account the number of deaths and baseline deaths for Moderna and Pfizer vaccinees. I'm not sure if the following is the correct approach either, but when I asked ChatGPT how to calculate the confidence interval for the Moderna-Pfizer ratio for people vaccinated in July 2021, it gave me code like this, where the 95% CI was about 1.20 to 1.53 so the lower bound of the CI was still clearly above 1:
dead1=284;dead2=2266 base1=252.52;base2=2725.01 rate1=dead1/base1;rate2=dead2/base2 ratio=rate1/rate2 se1=sqrt(dead1)/base1;se2=sqrt(dead2)/base2 se=sqrt((se1/rate1)^2+(se2/rate2)^2) exp(log(ratio)+c(-1,1)*qnorm(.975)*se) # [1] 1.195500 1.530073
When I asked ChatGPT how to calculate whether the result was statistically significant, it said "To assess if the result is statistically significant, we check if the 95% confidence interval for the ratio excludes 1. If the interval excludes 1, it indicates that there is a statistically significant difference between the Moderna and Pfizer rates."
When I asked how to calculate a p-value for the result, ChatGPT answered: "To calculate the p-value, we need to test the null hypothesis that the ratio of the two rates is equal to 1. This can be done using a Wald test, which compares the observed value of the ratio to the null value (1), using the standard error of the ratio to compute a Z-score. The p-value is then obtained from the Z-score." And it gave me this code which gave me a p-value of about 2e-6:
z_score=log(ratio)/se 2*(1-pnorm(abs(z_score))) # [1] 1.6133e-06
Here when I applied the same method of calculating confidence intervals to all months of vaccination, I got fairly narrow confidence intervals up to January 2022:
b=fread("http://sars2.net/f/czbucketskeep.csv.gz")
b=b[month>="2020-12"&dose<=1][,age:=pmin(age,100)]
t=b[,.(dead=sum(dead),alive=as.numeric(sum(alive))),.(age,month,vaxmonth,type)]
t=merge(t,t[,.(base=sum(dead)/sum(alive)),age])[,base:=base*alive]
a=t[,.(dead=sum(dead),base=sum(base)),.(vaxmonth,type)]
a1=a[type=="Moderna",.(vaxmonth,dead1=dead,base1=base)]
a2=a[type=="Pfizer",.(vaxmonth,dead2=dead,base2=base)]
o=merge(a1,a2)
rate1=o[,dead1/base1];rate2=o[,dead2/base2]
o[,ratio:=rate1/rate2]
se1=o[,sqrt(dead1)/base1];se2=o[,sqrt(dead2)/base2]
se=sqrt((se1/rate1)^2+(se2/rate2)^2)
o[,low:=exp(log(ratio)-qnorm(.975)*se)]
o[,high:=exp(log(ratio)+qnorm(.975)*se)]
mutate_if(o,is.double,round,2)|>print(r=F)
vaxmonth dead1 base1 dead2 base2 ratio low high 2021-01 1515 744.34 18513 21218.40 2.33 2.21 2.46 2021-02 3501 3732.26 13979 19466.04 1.31 1.26 1.36 2021-03 4961 6404.36 19616 32300.32 1.28 1.24 1.32 2021-04 2887 3748.78 16321 26352.89 1.24 1.20 1.29 2021-05 2186 2433.25 12130 21496.87 1.59 1.52 1.67 2021-06 1674 1510.94 3761 5030.32 1.48 1.40 1.57 2021-07 284 252.52 2266 2725.01 1.35 1.20 1.53 2021-08 136 125.80 1080 1118.41 1.12 0.94 1.34 2021-09 157 93.80 744 586.62 1.32 1.11 1.57 2021-10 99 78.51 754 557.74 0.93 0.76 1.15 2021-11 282 222.76 2275 1838.82 1.02 0.90 1.16 2021-12 249 163.23 1306 871.66 1.02 0.89 1.17 2022-01 81 47.04 585 342.17 1.01 0.80 1.27 2022-02 13 8.14 125 55.09 0.70 0.40 1.25 2022-03 2 3.08 46 17.62 0.25 0.06 1.03 2022-04 0 0.81 19 10.48 0.00 NaN NaN 2022-05 0 0.45 20 8.44 0.00 NaN NaN 2022-06 0 0.25 12 4.52 0.00 NaN NaN 2022-07 2 0.77 10 4.49 1.17 0.26 5.34 2022-08 1 0.87 21 8.76 0.48 0.06 3.55 2022-09 1 0.53 20 7.98 0.76 0.10 5.66 2022-10 0 0.12 14 3.93 0.00 NaN NaN 2022-11 1 0.07 3 1.45 6.85 0.71 65.81 2022-12 0 0.00 0 0.26 NaN NaN NaN vaxmonth dead1 base1 dead2 base2 ratio low high
The record-level dataset contains an entry for a man whose year of birth is 1912 but who got vaccinated in 2023 when he would've been 110 or 111 years old:
> t=fread("curl https://github.com/skirsch/Czech/blob/main/data/CR_records.csv.xz|xz -dc")
> t[Rok_narozeni<1913,1:4]
Pohlavikod Rok_narozeni DatumUmrti Datum_1
1: M 1912 <NA> 2021-09-24
2: F 1912 2021-07-22 2021-02-11
3: F 1911 <NA> 2021-07-27
4: F 1911 2020-12-06 <NA>
5: F 1910 <NA> 2021-03-28
6: F 1912 2020-05-12 <NA>
7: F 1912 2021-10-22 <NA>
8: M 1912 <NA> 2023-11-29
9: F 1912 <NA> <NA>
10: F 1912 <NA> <NA>
11: F 1912 <NA> <NA>
12: F 1912 <NA> <NA>
However according to the Czech-language Wikipedia, there have not been male Czech citizens older than 107 years since at least 2010. [https://cs.wikipedia.org/wiki/Seznam_nejstar%C5%A1%C3%ADch_obyvatel_%C4%8Ceska]
In November 2024 ÚZIS (the Czech institute of health information and statistics) published a new dataset which contains columns for infections and hospitalizations. However the year of birth is only given in 5-year ranges and dates of vaccination and death are given on a weekly and not daily precision. SMIS published the following blog post about the data (translated from Czech): [https://smis-lab.cz/2024/11/07/dalsi-velka-datova-sada-uzis-zverejnena/]
After a long time, we received another large data set from ÚZIS. At first glance, this seems like a holy grail, as the field descriptions indicate that the data contains individual-level information on birth quintile, gender, calendar weeks of all covid vaccines, calendar week of death, and cause of death (covid/non-covid). In addition, the data includes information on tests and covid hospitalizations. No country in the world has yet (completely incomprehensible to us) published such a data set.
However, a closer look at the data raises many doubts.
1. The file contains 12,597,668 lines , which is suspiciously large. Even if the second, third, and other infections that are marked as duplicates in the data description are excluded, that leaves 12,125,969 rows, which is still a lot. There are not that many people in the Czech Republic, even if all the dead since 2020 are included.
2. The file does not contain an (anonymized) person identifier , so it is not possible to match lines that belong to the same person. It is therefore not possible to link the data on vaccination with the data on death and its cause. Therefore, it is also impossible to find out what duplications are the reason for the previous point.
3. When examining the "DatumUmrtiLPZ" column, we find that the numbers listed there approximately correspond to the course of death according to the CZSO. Until the end of 2022, the difference in the weekly number of deaths compared to the CZSO will not exceed one percent, but in the second half of 2024 it will already grow to tens of percent. Data on deaths are therefore usable until the end of 2023 at most. However, even the differences compared to the CZSO in the statistics for the weeks of 2020-2023 are suspicious and should not be there.
4. A far bigger problem, however, is that a total of 1,556,198 lines of the file contain no data (except for DCCI=0), i.e. neither birth nor gender data. Similarly, we have 63,606 rows that contain only the date of death, again without data on birth and sex. A substantial part of these deaths occurred in 2020, and when compared with the data from CSU, it is clear that these deaths actually occurred. Not only can these deaths not be matched to a cause of death, but they cannot even be assigned to a given age group and gender. It is therefore not possible to calculate any mortality rate, as it is always dramatically dependent on age and sex.
Thus, this data set is worthless for analysis. At the same time, its investigation already cost several statisticians hours of time. We will inform the ÚZIS about the problems described above through the applicant and request the publication of data in the same format as here, with the fact that the relevant period will be extended at least until the end of 2023 and a column will be added as to whether the death was caused by covid or not.
The file contains these columns:
| column | translation |
|---|---|
| ID | ID |
| Infekce | order of infection |
| Pohlavi | sex |
| RokNarozeni | year of birth |
| DatumPozitivity | date of positivity |
| DatumVysledku | date of result |
| Vylecen | week of recovery |
| Umrti | week of COVID death |
| Symptom | was symptomatic at time of test |
| TypTestu | type of test |
| Datum_Prvni_davka | first dose date |
| Datum_Druha_davka | second dose date |
| Datum_Treti_davka | third dose date |
| Datum_Ctvrta_davka | fourth dose date |
| Datum_Pata_davka | fifth dose date |
| Datum_Sesta_davka | sixth dose date |
| Datum_Sedma_davka | seventh dose date |
| OckovaciLatkaKod_Prvni_davka | first dose vaccine type code |
| OckovaciLatkaKod_Druha_davka | second dose vaccine type code |
| OckovaciLatkaKod_Treti_davka | third dose vaccine type code |
| OckovaciLatkaKod_Ctvrta_davka | fourth dose vaccine type code |
| OckovaciLatkaKod_Pata_davka | fifth dose vaccine type code |
| OckovaciLatkaKod_Sesta_davka | sixth dose vaccine type code |
| OckovaciLatkaKod_Sedma_davka | seventh dose vaccine type code |
| PrimPricinaHospCOVID | primary reason for COVID hospitalization |
| bin_Hospitalizace | was hospitalized |
| min_Hospitalizace | earliest week of hospitalization |
| dni_Hospitalizace | days of hospitalization |
| max_Hospitalizace | last week of hospitalization |
| bin_JIP | admitted to ICU |
| min_JIP | earliest week of ICU stay |
| dni_JIP | days in ICU |
| max_JIP | last week of ICU stay |
| bin_STAN | hospitalized at regular hospital ward |
| min_STAN | earliest week of regular ward stay |
| dni_STAN | days in regular ward |
| max_STAN | last week of regular ward stay |
| bin_Kyslik | received oxygen therapy |
| min_Kyslik | earliest week of oxygen therapy |
| dni_Kyslik | days of oxygen therapy |
| max_Kyslik | last week of oxygen therapy |
| bin_HFNO | received high-flow nasal oxygen therapy |
| min_HFNO | earliest week of HFNO |
| dni_HFNO | days of HFNO |
| max_HFNO | last week of HFNO |
| bin_UPV_ECMO | received ultra-protective ventilation/ECMO |
| min_UPV_ECMO | earliest week of UPV/ECMO |
| dni_UPV_ECMO | days of UPV/ECMO |
| max_UPV_ECMO | last week of UPV/ECMO |
| Mutace | variant |
| DatumUmrtiLPZ | week of death from any cause |
| Long_COVID | long COVID diagnosis date |
| DCCI | Deyo-Charlson Comorbidity Index |
The Infekce column indicates whether the entry is for a
person with no infection listed, or for the first, second, or third
infection of the person. So part of the reason why there are more rows
than people is probably because there's multiple rows for people with 2
or 3 infections. But I don't know why the maximum infection number is
only 3 though:
> t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv")
> t[,.N,Infekce]
Infekce N
1: NA 7800263
2: 1 4325706
3: 2 450511
4: 3 21188
The DCCI column shows a Deyo-Charlson Comorbidity Index at the time of a COVID case, so its value is zero for all people with no COVID case included:
> t[,.N,,.(DCCI,Infekce)]|>print(r=F)
DCCI Infekce N
0 NA 7800263
0 1 2865288
0 2 284733
0 3 11712
1 1 777793
1 2 93645
1 3 5005
2 1 310110
2 2 35398
2 3 2148
3 1 152020
3 2 15990
3 3 1009
4 1 83520
4 2 8110
4 3 524
5 1 136975
5 2 12635
5 3 790
There's about 1.6 million rows where the year of birth is missing. All except one of them are for people with no vaccine doses listed:
> t[RokNarozeni=="-",.N,OckovaciLatkaKod_Prvni_davka][N>0][order(-N)] OckovaciLatkaKod_Prvni_davka N 1: 1630991 # about 1.6 million rows for unvaccinated people 2: CO01 1 # one row for Pfizer
On most rows with a missing year of birth, all other fields including the date of death are also missing, but there's 63,695 rows where the year of birth is missing but the date of death is not missing (which are mostly for deaths in 2020):
> t[RokNarozeni=="-"&DatumUmrtiLPZ!="",.N,.(year=substr(DatumUmrtiLPZ,1,4))][order(year)] year N 1: 2020 37471 # most records with year of birth missing and date of death not missing are for deaths in 2020 2: 2021 9658 3: 2022 5522 4: 2023 6981 5: 2024 4063
If rows with a missing date of birth are excluded and rows for second and third infections are excluded, then the new UZIS dataset has only about 10.5 million rows, which is about half a million less than in the old record-level dataset:
> t[RokNarozeni!="-"&!(!is.na(Infekce)&Infekce>1),.N] [1] 10494977
The new UZIS dataset is missing about 15% of all deaths in 2020 even if you don't exclude the rows with a date of birth missing: [https://ec.europa.eu/eurostat/data/database, czech2.html#Deaths_by_ICD_code_region_age_group_and_year]
> rec=fread("CR_records.csv")
> reclev=rec[,.(reclev=.N),.(year=year(DatumUmrti))]
> eurostat=fread("http://sars2.net/f/czpopdead.csv")[,.(eurostat=sum(dead)),year]
> icd=fread("http://sars2.net/f/czicd.csv.gz")[,.(byicd=sum(dead)),year]
> me=merge(merge(reclev,eurostat),icd)
> ua=\(x,y,...){u=unique(x);y(u,...)[match(x,u)]}
> new=t[!(!is.na(Infekce)&Infekce>1),.(newuzis=.N),.(year=as.integer(substr(DatumUmrtiLPZ,1,4)))]
> merge(me,new,all=T)[year>=2020]|>print(r=F)
year reclev eurostat byicd newuzis
2020 129289 129289 129289 110177
2021 139890 139891 139891 139687
2022 120219 120219 120219 121464
2023 NA NA NA 113807
2024 NA NA NA 70941
However it's because the new dataset is missing all deaths in the first 9 weeks of 2020:
> t[,.N,DatumUmrtiLPZ][order(DatumUmrtiLPZ)][1:6] DatumUmrtiLPZ N 1: 12034894 2: 2020-10 2277 3: 2020-11 2289 4: 2020-12 2318 5: 2020-13 2290 6: 2020-14 2322
There's two different columns for the week of death:
Umrti (COVID death) and DatumUmrtiLPZ (date of
death LPZ). LPZ is the Czech death certificate registry.
[https://www.uzis.cz/index.php?pg=registry-sber-dat–ostatni-rezortni-registry–list-o-prohlidce-zemreleho]
There's 829 rows where the DatumUmrtiLPZ column is empty
but the Umrti column for a COVID death is not:
> t[DatumUmrtiLPZ!="",.N] # date of death in death certificate registry [1] 562774 > t[Umrti!="",.N] # date of COVID death [1] 43633 > t0[DatumUmrtiLPZ==""&Umrti!="",.N] # number of rows with only date of COVID death listed [1] 829
There are 354 rows where the date of death is not the same as the date of a COVID death, even though the difference is only one week in most cases:
> t[Umrti!=""&DatumUmrtiLPZ!=""&DatumUmrtiLPZ!=Umrti,.(DatumUmrtiLPZ,Umrti)]
DatumUmrtiLPZ Umrti
1: 2022-03 2022-04
2: 2021-12 2021-13
3: 2020-47 2020-48
4: 2021-11 2021-10
5: 2020-51 2020-52
---
350: 2021-15 2021-14
351: 2020-43 2020-44
352: 2021-06 2021-07
353: 2021-01 2021-02
354: 2022-44 2022-43
About 2,000 people have a date of positive test after a date of death, but in most cases the difference is only 1 or 2 weeks, so it might be if the date of positive tests is by reporting date:
> t[DatumUmrtiLPZ!=""&DatumUmrtiLPZ<DatumPozitivity,.(DatumPozitivity,DatumUmrtiLPZ)]
DatumPozitivity DatumUmrtiLPZ
1: 2024-03 2024-01
2: 2021-21 2021-18
3: 2020-45 2020-44
4: 2020-45 2020-44
5: 2020-18 2020-17
---
1745: 2021-48 2020-18
1746: 2021-12 2021-11
1747: 2023-21 2023-09
1748: 2021-14 2021-13
1749: 2022-05 2022-04
The DCCI column shows a value of the Deyo-Charlson Comorbidity Index at the time of a COVID case. The value is zero for all people with no COVID case listed, but at the time of the first case the value was zero for about 66% of all people:
> t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv")
> t[Infekce==1,.N,DCCI]|>print(r=F)
DCCI N
0 2865288
1 777793
2 310110
3 152020
4 83520
5 136975
A Czech study which employed the DCCI index said: "0 points indicate no disease, 1-2 points suggest a low level of severity, 3-4 points represent a moderate level of severity and a score of 5 or higher can be considered as the occurrence of multiple significant comorbidities". [https://www.sciencedirect.com/science/article/pii/S0965206X23000591] However in the UZIS data values of 5 and above seem to be listed as 5.
The average comorbidity index was about 0.73 for people with the
first dose type Comirnaty (CO01) but about 1.03 for people
with first dose type SPIKEVAX (CO02):
> rec=fread("Czech/data/CR_records.csv")
> k=grep("OckovaciLatka_",names(rec));k2=k-1
> codes=rec[,.(type=unlist(rec[,..k],,F),code=unlist(rec[,..k2],,F))][!duplicated(code)]
> a=t[Infekce==1,.(DCCI=mean(DCCI),.N),.(code=OckovaciLatkaKod_Prvni_davka)]
> merge(codes,a)[order(-N)][N>=1e3]
code type DCCI N
1: CO01 Comirnaty 0.7299204 2183923 # Pfizer
2: 0.4616843 1678946 # unvaccinated
3: CO02 SPIKEVAX 1.0274723 182293 # Moderna
4: CO04 COVID-19 Vaccine Janssen 0.6712624 152824
5: CO03 VAXZEVRIA 1.7055395 123531 # Astrazeneca
6: CO07 Nuvaxovid 0.5196774 3100 # Novavax
The comorbidity index peaks in people who were born in 1930-1934, so
this new dataset might reflect the actual level of comorbidities better
than the earlier file ockovani-profese.csv (where the
proportion of people who were indicated to have a chronic illness peaked
in ages 65-69 but it was very low in the oldest age groups, which might
be if information about chronic illness was not listed for people who
qualified to be vaccinated based on their age):
> t[Infekce==1,.(DCCI=mean(DCCI),.N),RokNarozeni][order(RokNarozeni)]|>print(r=F)
RokNarozeni DCCI N
- 0.03012425 11187
1860-1864 0.00000000 1
1865-1869 0.00000000 2
1870-1874 0.00000000 1
1875-1879 0.00000000 2
1880-1884 0.00000000 2
1890-1894 0.00000000 1
1895-1899 0.00000000 1
1900-1904 0.00000000 69
1905-1909 0.00000000 45
1910-1914 0.07142857 56
1915-1919 2.15384615 117
1920-1924 2.81595830 2494
1925-1929 3.08236062 13793
1930-1934 3.11992329 38066
1935-1939 2.92733054 60383
1940-1944 2.62483070 104105
1945-1949 2.24024614 151786
1950-1954 1.75856013 176516
1955-1959 1.31641930 194789
1960-1964 0.93541726 257143
1965-1969 0.72503103 289229
1970-1974 0.54189543 375757
1975-1979 0.42561725 431108
1980-1984 0.34186083 358409
1985-1989 0.28738798 332540
1990-1994 0.24863189 314119
1995-1999 0.22801030 232643
2000-2004 0.20644919 226230
2005-2009 0.16525787 291738
2010-2014 0.15856826 273346
2015-2019 0.13150042 153490
2020-2024 0.06051234 36538
RokNarozeni DCCI N
Next I calculated an age-normalized excess comorbidity percentage for each vaccine type. I excluded people with a year of birth missing.
I derived the expected total DCCI for each vaccine type by multiplying the number of people in each age group with the average DCCI index for the age group among all rows where the infection number was 1, and then I divided the actual total DCCI with the expected total DCCI, subtracted 1, and multiplied the result by 100. The excess comorbidity percentage was about -0.6% for Pfizer but 6.7% for Moderna, which supports my earlier hypothesis that a higher level of comorbidities explained why Moderna vaccinees had higher ASMR than Pfizer vaccinees:
> dcci=t[Infekce==1&RokNarozeni!="-",.(dcci=sum(as.numeric(DCCI)),.N),.(code=OckovaciLatkaKod_Prvni_davka,born=RokNarozeni)]
> dcci=merge(dcci[,.(base=sum(dcci)/sum(N)),born],dcci)[,base:=base*N]
> dcci=dcci[,.(excesspct=round((sum(dcci)/sum(base)-1)*100,1),N=sum(N)),code]
> merge(codes,dcci)[N>=1e3][order(-N)]|>print(r=F)
code type excesspct N
CO01 Comirnaty -0.6 2183923 # Pfizer
-1.4 1667759 # unvaccinated
CO02 SPIKEVAX 6.7 182293 # Moderna
CO04 COVID-19 Vaccine Janssen -3.5 152824
CO03 VAXZEVRIA 5.8 123531 # AstraZeneca
CO07 Nuvaxovid 0.3 3100 # Novavax
In almost all age groups the percentage of the highest DCCI value 5 was higher for Moderna than Pfizer:
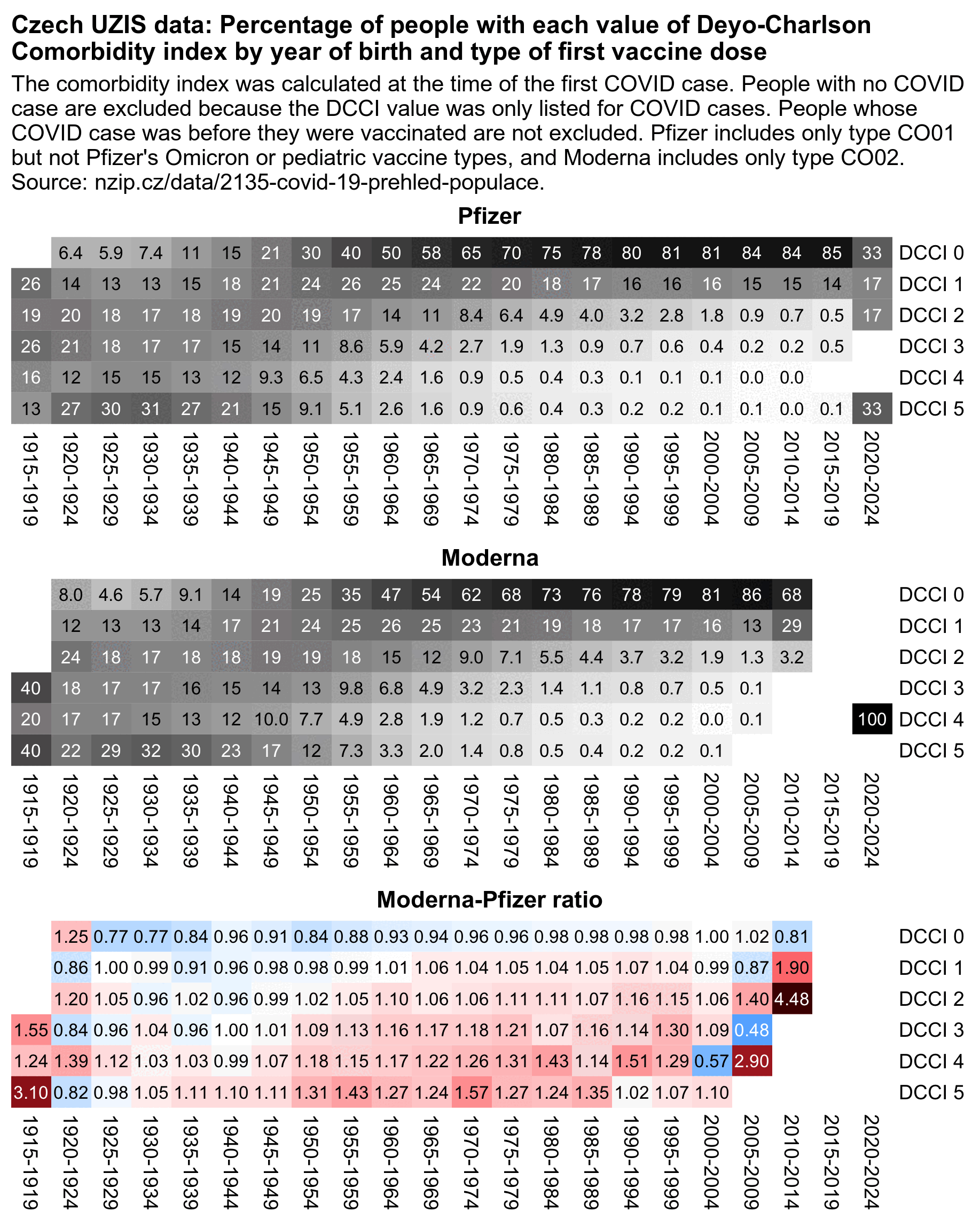
library(data.table)
t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv")
a=t[Infekce==1,.N,.(dcci=DCCI,born=RokNarozeni,code=OckovaciLatkaKod_Prvni_davka)]
a=a[!born%like%"19(05|10)"]
a=merge(a,a[,.(pop=sum(N)),.(born,code)])
a=a[code%in%c("CO01","CO02")]
a[,name:=factor(code,,c("Pfizer","Moderna"))]
m0=a[,tapply(N/pop*100,.(name,paste("DCCI",dcci),born),c)]
maxcolor=max(m0,na.rm=T)
pal=hsv(c(21,21,21,16,11,6,3,0,0)/36,c(0,.25,rep(.5,6),0),c(rep(1,8),.0))
pal=sapply(255:0/255,\(i)rgb(i,i,i))
exp=.5
for(i in 1:dim(m0)[1]){
m=disp=m0[i,,];disp=ifelse(m>=10,round(m),sprintf("%.1f",m))
pheatmap::pheatmap(m^exp,filename=paste0("i",i,".png"),display_numbers=disp,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=18,cellheight=14,fontsize=9,fontsize_number=8,
border_color=NA,na_col="white",
number_color=ifelse(m^exp>maxcolor^exp*.4,"white","black"),
breaks=seq(0,maxcolor^exp,,256),colorRampPalette(pal)(256))}
ar=a[,tapply(N/pop,.(code,paste("DCCI",dcci),born),c)]
m1=ar[1,,];m2=ar[2,,];m=(m2-m1)/ifelse(m2>m1,m1,m2)
disp=m2/m1;disp[]=sprintf("%.2f",disp)
pal=hsv(rep(c(21,0)/36,5:4),c(1,.8,.6,.3,0,.3,.6,.8,1),c(.3,.65,1,1,1,1,1,.65,.3))
maxcolor=3;exp=.7
pheatmap::pheatmap(sign(m)*abs(m)^exp,filename=paste0("i3.png"),display_numbers=disp,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=18,cellheight=14,fontsize=9,fontsize_number=8,
border_color=NA,na_col="white",
number_color=ifelse(abs(m)>maxcolor^exp*.5,"white","black"),
breaks=seq(-maxcolor^exp,maxcolor^exp,,256),colorRampPalette(pal)(256))
sub="The comorbidity index was calculated at the time of the first COVID case. People with no COVID case are excluded because the DCCI value was only listed for COVID cases. People whose COVID case was before they were vaccinated are not excluded. Pfizer includes only type CO01 but not Pfizer's Omicron or pediatric vaccine types, and Moderna includes only type CO02. Source: nzip.cz/data/2135-covid-19-prehled-populace."
system(paste0("w=`identify -format %w i1.png`;pad=14;convert -gravity northwest -pointsize 46 -interline-spacing -2 -font Arial-Bold -size $[w-pad*2]x \\( caption:'Czech UZIS data: Percentage of people with each value of Deyo-Charlson Comorbidity index by year of birth and type of first vaccine dose' -splice $[pad]x20 \\) \\( -size $[w-pad*2]x -font Arial -pointsize 42 caption:'",gsub("'","'\\\\''",sub),"' -splice $[pad]x10 \\) -pointsize 44 -font Arial-Bold -gravity north \\( caption:Pfizer -splice x12 \\( i1.png -chop x10 \\) caption:Moderna \\( i2.png -chop x10 \\) caption:'Moderna-Pfizer ratio' \\( i3.png -chop x10 \\) \\) -append 1.png"))
Based on the new CSV file published by UZIS in November 2024, it's now possible to calculate hospitalization rate by vaccine type.
In the following code in order to calculate an age-standardized hospitalization rate, I subtracted the start of the 5-year ranges of year of birth from 2020 to assign people to 5-year age groups based on their age on December 31st 2020 (because for example all people born in 1950-1954 belong to the age group 70-74 on December 31st 2020). I didn't bother accounting for the aging of people over time.
The new UZIS data is missing the year of birth of many unvaccinated people, even though it's not missing for any unvaccinated people with a date of hospitalization included. But I think the new data doesn't make it possible to see how many unvaccinated people there are for each combination of month and age, so I took the monthly number of people by vaccine type and age from one of my old bucket files for the record-level data, where I treated the number of vaccinated people in each age group at the end of 2022 as the number of vaccinated people for the rest of the dataset. (In my bucket file I accounted for the aging of people over time, but it shouldn't make much difference here.)
I assigned each hospitalization week to a hospitalization month based on the month of the Thursday of the week.
But anyway, the results below show that people who got a Janssen or AstraZeneca vaccine for the first dose had a high hospitalization rate during the COVID wave in November to December 2021. So it's consistent with my plot for all-cause ASMR by vaccination status where the spike in deaths during the last two months of 2021 was more pronounced for Janssen and AstraZeneca but more flat for Pfizer and Moderna.
In January 2021 vaccinated people had almost as high hospitalization rate as unvaccinated people, which might be because there had not been enough time for the immune response to build up after vaccination, or because vulnerable groups of people were priorized during the early rollout.

library(data.table);library(ggplot2)
t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv")
isoweek=\(year,week,weekday=7){d=as.Date(paste0(year,"-1-4"));d-(as.integer(format(d,"%w"))+6)%%7-1+7*(week-1)+weekday}
getweek=\(x)isoweek(as.integer(substr(x,1,4)),as.integer(substr(x,6,7)))
ua=\(x,y,...){u=unique(x);y(u,...)[match(x,u)]}
yemo=\(x){u=unique(x);format(u,"%Y-%m")[match(x,u)]}
t[min_Hospitalizace!="",hospweek:=ua(min_Hospitalizace,getweek)-3]
t[,date1:=ua(Datum_Prvni_davka,getweek)-3]
t[,type:=OckovaciLatkaKod_Prvni_davka]
t[type%in%c("CO01","CO08","CO09","CO16","CO20","CO21"),type:="Pfizer"]
t[type%in%c("CO02","CO12","CO15"),type:="Moderna"]
t[type=="CO03",type:="AstraZeneca"]
t[type=="CO04",type:="Janssen"]
t[type=="",type:="Unvaccinated"]
t[,type:=ifelse(!is.na(date1)&date1>hospweek,"Unvaccinated",type)]
t[RokNarozeni!="-",age:=pmin(100,(2020-as.integer(substr(RokNarozeni,1,4))))]
hosp=t[!type%like%"^CO"&!is.na(hospweek),.(hosp=.N),.(month=yemo(hospweek),type,age=ifelse(age<20,0,age))]
b=fread("http://sars2.net/f/czbucketskeep.csv.gz")
a=b[dose<=1,.(pop=sum(alive)),.(month,type=ifelse(type=="","Unvaccinated",type),age=ifelse(age<20,0,age%/%5*5))]
a=rbind(a,a[month=="2022-12",.(month=yemo(seq(as.Date("2023-1-1"),as.Date("2024-10-1"),"month")),pop),.(type,age)])
me=merge(a,hosp,all=T)[!type%in%c("Novavax","Other")]
me=merge(fread("http://sars2.net/f/czcensus2021pop.csv")[,.(std=sum(pop)),.(age=age%/%5*5)][,std:=std/sum(std)],me)
p=me[,.(hosp=sum(hosp/pop*std*365e5,na.rm=T)),.(month,type)][order(-type)]
p[,month:=as.Date(paste0(month,"-1"))]
p[,type:=factor(type,c("Unvaccinated","Pfizer","Moderna","AstraZeneca","Janssen"))]
xstart=as.Date("2020-1-1");xend=as.Date("2025-1-1")
xbreak=seq(xstart,xend,"6 month");xlab=c(rbind("",2020:2024),"")
ybreak=pretty(p$hosp,7);ystart=0;yend=max(ybreak)
color=c("black",hsv(c(240,355,330,204,36)/360,c(.94,.75,.8,.67,.64),c(.76,.82,.5,.87,.95)))
ggplot(p,aes(x=month+15,y=hosp))+
geom_vline(xintercept=seq(xstart,xend,"3 month"),color="gray85",linewidth=.3)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray65",linewidth=.3)+
geom_vline(xintercept=c(xstart,xend),linewidth=.3,lineend="square")+
geom_hline(yintercept=c(ystart,0,yend),linewidth=.3,lineend="square")+
geom_line(aes(color=type),linewidth=.4)+
geom_point(aes(color=type),size=.5)+
labs(title="Age-standardized hospitalization rate per 100,000 person-years",subtitle=paste0("The 2021 census population by 5-year age groups was used as the standard population, where ages below 20 were aggregated to a single age group.")|>stringr::str_wrap(80),x=NULL,y=NULL,color="First dose type")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=xlab)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
scale_color_manual(values=color)+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=7,color="black"),
axis.ticks=element_line(linewidth=.3),
axis.ticks.x=element_line(color=alpha("black",c(1,0))),
axis.ticks.length=unit(3,"pt"),
legend.background=element_rect(fill="white",color="black",linewidth=.3),
legend.direction="vertical",
legend.justification=c(1,1),
legend.key.height=unit(10,"pt"),
legend.key.width=unit(15,"pt"),
legend.key=element_blank(),
legend.margin=margin(3,5,3,4),
legend.position=c(1,1),
legend.spacing.x=unit(1.5,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=7),
legend.title=element_text(size=7,face=2,margin=margin(2,,3)),
panel.background=element_blank(),
plot.margin=margin(4,4,4,4),
plot.subtitle=element_text(size=6.7,margin=margin(,,4)),
plot.title=element_text(size=7.5,face="bold",margin=margin(1,,3)))
ggsave("1.png",width=4,height=2.2,dpi=380*4)
system("magick 1.png -resize 25% 1.png")
Here's my old plot for ASMR by vaccine type for comparison, where you can see that the spike in ASMR in the last two months of 2021 is more pronounced for Janssen and AstraZeneca which are viral vector vaccines but the spike is more flat for Moderna and Pfizer which are mRNA vaccines (even though the difference might not necessarily be due to efficacy, but it might also be if people with a higher COVID mortality risk were more likely to get certain types of vaccines): [czech2.html#ASMR_by_month_and_vaccine_type]
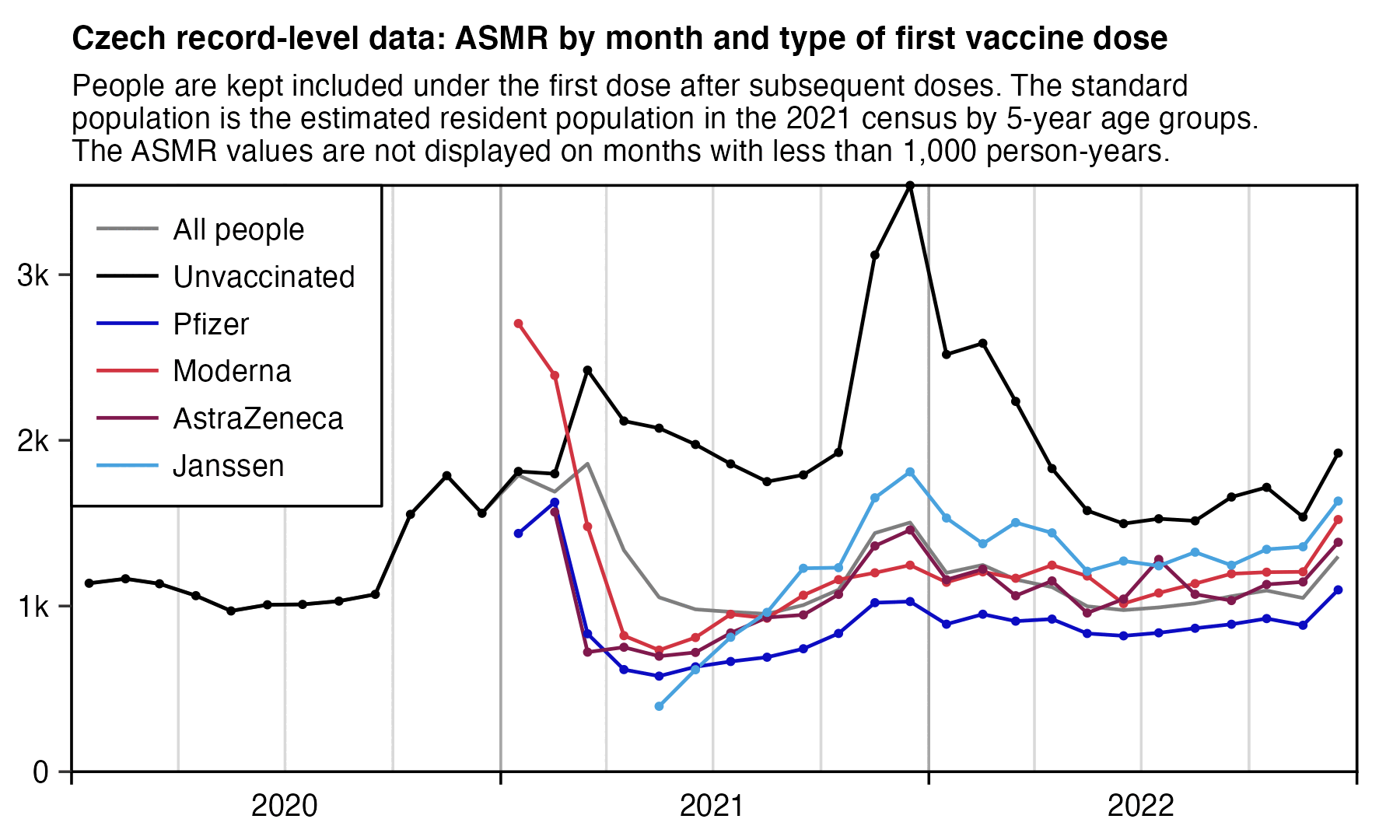
Earlier I have pointed out that in the winter of 2020 to 2021 when the Czech Republic had a pattern with three distinct humps in all-cause mortality, the third hump was lower than the first hump in ages 80+ but ages 40-59 and 60-79 followed the opposite pattern where the third hump was higher than the first hump. I thought it might have been because in ages 80+ about half of people had been vaccinated by the time of the third hump, but in ages 40-59 and 60-79 only a few people had been vaccinated by the time of the third hump.
When I looked at all-cause ASMR by vaccination status, the third hump was close to nonexistent in vaccinated people in ages 80+. But it wasn't necessarily because vaccines prevented COVID deaths, because it might have also been because there was a reduced number of deaths in recently vaccinated people due to the temporal HVE: [czech.html#Daily_deaths_and_vaccine_doses_by_age_group]
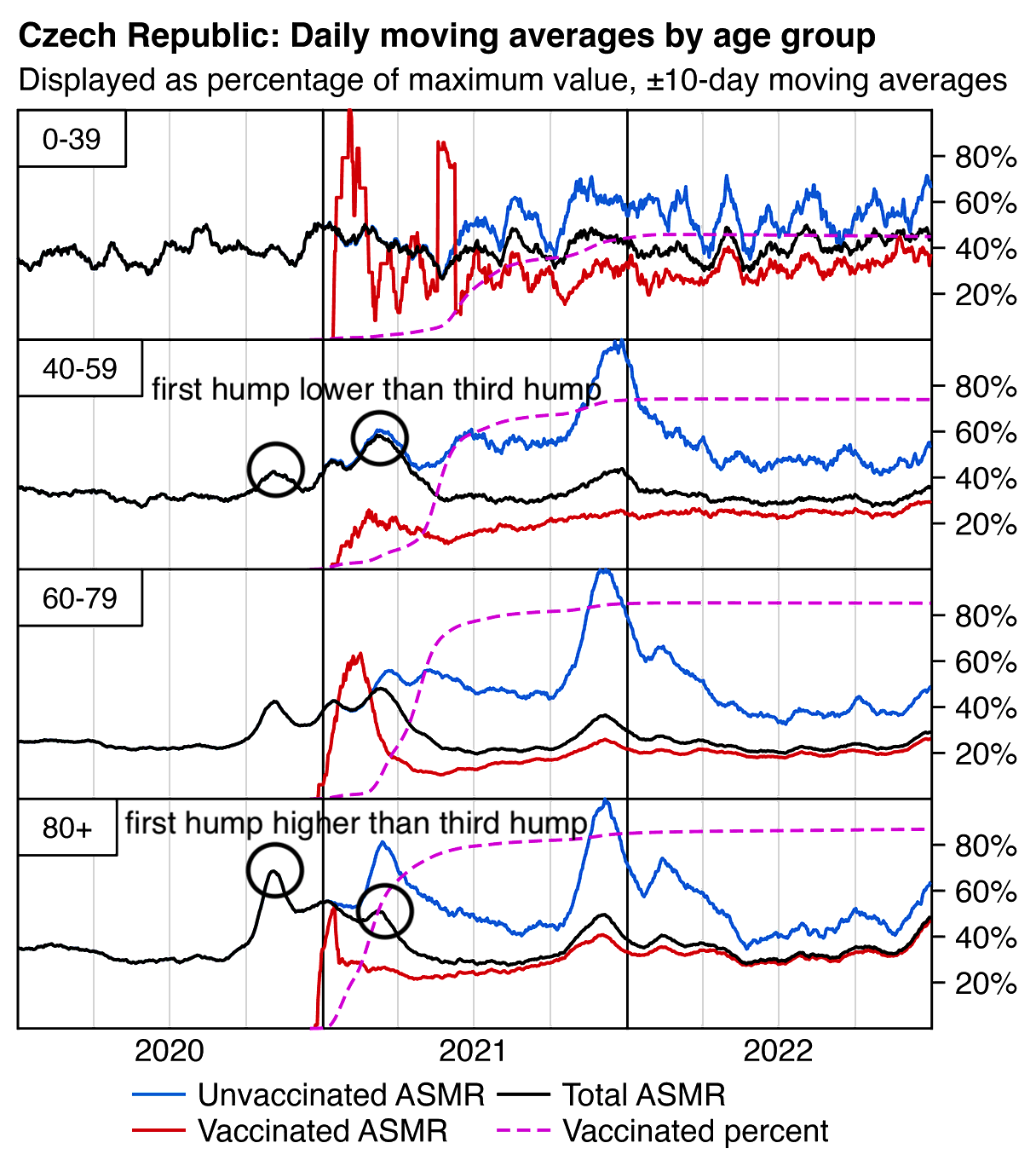
So therefore I wanted to check if COVID hospitalizations followed a similar pattern as all-cause deaths, because COVID hospitalizations are probably less affected by temporal HVE than all-cause mortality. But data for 2020 was missing from the datasets published by the Czech MoH for COVID hospitalizations by vaccination status.
However now based on the new UZIS dataset it's possible to calculate a hospitalization rate by age and vaccination status so that 2020 is included. It shows that among unvaccinated people in ages 80+, the third hump was higher than the first hump. But in ages 80+ if you look at both unvaccinated and vaccinated people combined, the reason why the third hump is so low appears to be that a high percentage of people had been vaccinated by the time of the third hump:

library(data.table);library(ggplot2)
ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
isoweek=\(year,week,weekday=7){d=as.Date(paste0(year,"-1-4"));d-(as.integer(format(d,"%w"))+6)%%7-1+7*(week-1)+weekday}
getweek=\(x)isoweek(as.integer(substr(x,1,4)),as.integer(substr(x,6,7)))
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
ages=c(0,40,60,80)
t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv")
t[,dose:=ifelse(Datum_Prvni_davka!=""&Datum_Prvni_davka<=min_Hospitalizace,1,0)]
t[RokNarozeni!="-",age:=pmin(100,(2020-as.integer(substr(RokNarozeni,1,4))))]
a=t[,.(hosp=.N),.(age,dose,week=min_Hospitalizace)]
b=fread("http://sars2.net/f/czbucketsdaily.csv.gz")
b=b[,.(pop=sum(alive)),.(week=format(date,"%G-%V"),dose=pmin(dose,1),age=pmin(90,age)%/%5*5)]
b=rbind(b,b[week=="2022-51",.(week=setdiff(a[week!=""&!week%like%2020,week],week),pop),.(dose,age)])
b=b[rowid(week,dose,age)==1]
a=merge(a,b)
a=a[!week%like%2024]
a=a[age!=0]
a=rbind(a,a[,.(hosp=sum(hosp),pop=sum(pop),dose=2),.(week,age)])
a=merge(fread("http://sars2.net/f/czcensus2021pop.csv")[,.(std=sum(pop)),.(age=age%/%5*5)][,std:=std/sum(std)],a)
p=a[,.(y=sum(hosp/pop*std/7*365e5)),.(age=agecut(age,ages),x=week,z=factor(dose,,c("Unvaccinated","Vaccinated","Unvaccinated and vaccinated")))]
ymax=p[,.(ymax=max(y)),age]
p=merge(p,ymax)[,.(x,y=y/ymax*100,age,z)]
pct=b[,.(pop=sum(pop)),.(week,age=agecut(age,ages),dose)]
pct=dcast(pct,week+age~dose,value.var="pop")[,`1`:=nafill(`1`,,0)]
pct=pct[week>=b[dose==1,min(week)]]
p=rbind(p,pct[,.(x=week,age,z="Vaccinated percent",y=`1`/(`0`+`1`)*100)])
xval=unique(format(seq(as.Date("2020-1-1"),as.Date("2023-12-31"),1),"%G-%V"))
p[,x:=as.integer(factor(x,xval))]
p=na.omit(p)
xstart=1;xend=max(p$x)
ggplot(p,aes(x))+
facet_wrap(~age,ncol=1,strip.position="top",dir="v",scales="free_y")+
geom_vline(xintercept=grep("-01",xval),linewidth=.4,color="gray66",lineend="square")+
geom_vline(xintercept=c(xstart,xend),linewidth=.4,lineend="square")+
geom_hline(yintercept=c(0,100),linewidth=.4,lineend="square")+
geom_line(aes(y=y,color=z,linetype=z),linewidth=.6)+
geom_label(data=ymax,aes(label=sprintf("\n Age %s (max %.0f) \n",age,ymax),y=100),x=xend,lineheight=.5,hjust=1,vjust=1,size=3.6,fill=alpha("white",1),label.r=unit(0,"pt"),label.padding=unit(0,"pt"),label.size=.4)+
labs(x=NULL,y=NULL,title="Czech Republic: Weekly age-standardized COVID hospitalization\nrate per 100,000 person-years",subtitle="Displayed as percentage of maximum value shown in parentheses")+
scale_x_continuous(limits=c(xstart,xend),breaks=grep("-26",xval),labels=2020:2023)+
scale_y_continuous(breaks=1:4*20,limits=c(0,100),labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c(hsv(c(7,0)/12,1,.8),"black",hsv(30/36,.5,1)))+
scale_linetype_manual(values=c("solid","solid","solid","42"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=2,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.ticks=element_line(color="black",linewidth=.4),
axis.text.x=element_text(margin=margin(4)),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="center",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(,,4),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid=element_blank(),
panel.spacing=unit(3,"pt"),
plot.margin=margin(5,5,5,5),
plot.subtitle=element_text(size=11,margin=margin(,,2)),
plot.title=element_text(size=11,face="bold",margin=margin(1,,4)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.3,height=5.3,dpi=300*4)
sub="The 2021 census population by 5-year age groups was used as the standard population. In the hospitalization data people were given a year of birth as a range of 5 years like 1950-1954, so here each person was assigned to a 5-year age group by subtracting the year of birth from 2020 so that aging over time was not accounted for. Ages 0-4 were excluded due to a small vaccinated population size which inflated the hospitalization rate on days with nonzero hospitalizations. Sources: nzip.cz/data/2135-covid-19-prehled-populace (hospitalizations) and github.com/PalackyUniversity/uzis-data-analysis (number of vaccinated and unvaccinated people by age)."
system(paste0("mar=$[24*4];w=`identify -format %w 1.png`;magick \\( 1.png -gravity southwest -chop 0x70 \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x$[20*4] \\) -append -resize 25% -colors 256 1.png"))
In the next plot I calculated the number of deaths within the first 52 weeks of the first vaccine dose grouped by the vaccine type, DCCI, and age group. There were 36 combinations of age group and DCCI which had at least 100 deaths, but in 30 of them Moderna got a higher mortality rate than Pfizer:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv")
weeks=u(format(seq(as.Date("2020-1-1"),as.Date("2024-12-31"),1),"%G-%V"))
t[,dead:=match(ifelse(DatumUmrtiLPZ=="",Umrti,DatumUmrtiLPZ),weeks)]
a=t[Infekce==1&RokNarozeni!="-",.(case=match(DatumPozitivity,weeks),first=match(Datum_Prvni_davka,weeks),dead,dcci=DCCI,code=OckovaciLatkaKod_Prvni_davka,born=RokNarozeni)]
a=a[!born%like%"19(05|10)"]
# a=a[case>=first] # exclude people with a case before the first dose
a=a[code%in%paste0("CO0",1:2),.(pop=.N,dead=sum((dead-first)%in%0:51,na.rm=T)),.(code,born,dcci)]
a[,cmr:=dead/pop*1e5]
# # compare combinations of DCCI and age with at least 100 total deaths
# a[a[,sum(dead),.(born,dcci)][V1>=100,.(born,dcci)],on=c("born","dcci")][,dcast(.SD,born+dcci~code,value.var="cmr")]
a[,name:=factor(code,,c("Pfizer","Moderna"))]
m0=a[,tapply(cmr,.(name,paste("DCCI",dcci),born),c)]
maxcolor=max(m0,na.rm=T)
pal=sapply(255:0/255,\(i)rgb(i,i,i))
exp=.5
for(i in 1:dim(m0)[1]){
m=disp=m0[i,,]
pheatmap::pheatmap(m^exp,filename=paste0("i",i,".png"),display_numbers=kimi(m),
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=18,cellheight=14,fontsize=9,fontsize_number=8,
border_color=NA,na_col="white",
number_color=ifelse(m^exp>maxcolor^exp*.4,"white","black"),
breaks=seq(0,maxcolor^exp,,256),colorRampPalette(pal)(256))}
ar=a[,tapply(cmr,.(code,paste("DCCI",dcci),born),c)]
m1=ar[1,,];m2=ar[2,,];m=(m2-m1)/ifelse(m2>m1,m1,m2)
disp=m2/m1;disp[]=ifelse(disp>=10,sprintf("%.1f",disp),sprintf("%.2f",disp))
pal=hsv(rep(c(21,0)/36,5:4),c(1,.8,.6,.3,0,.3,.6,.8,1),c(.4,.65,1,1,1,1,1,.65,.4))
maxcolor=8;exp=.7
pheatmap::pheatmap(sign(m)*abs(m)^exp,filename=paste0("i3.png"),display_numbers=disp,
cluster_rows=F,cluster_cols=F,legend=F,cellwidth=18,cellheight=14,fontsize=9,fontsize_number=8,
border_color=NA,na_col="white",
number_color=ifelse(abs(m)>maxcolor^exp*.5,"white","black"),
breaks=seq(-maxcolor^exp,maxcolor^exp,,256),colorRampPalette(pal)(256))
sub="The comorbidity index was calculated at the time of the first COVID case. People with no COVID case are excluded because the DCCI value was only listed for COVID cases. People whose COVID first case was before they were vaccinated are not excluded. Pfizer includes only type CO01 and Moderna includes only type CO02. Source: nzip.cz/data/2135-covid-19-prehled-populace."
system(paste0("w=`identify -format %w i1.png`;pad=14;convert -gravity northwest -pointsize 46 -interline-spacing -2 -font Arial-Bold -size $[w-pad*3]x \\( caption:'Czech UZIS data: Deaths per 100,000 people within 52 weeks from first dose (grouped by Deyo-Charlson comorbidity index, year of birth, and type of first vaccine dose) (people vaccinated after first COVID case are excluded)' -splice $[pad]x20 \\) \\( -size $[w-pad*3]x -font Arial -pointsize 42 caption:'",gsub("'","'\\\\''",sub),"' -splice $[pad]x10 \\) -pointsize 44 -font Arial-Bold -gravity north \\( caption:Pfizer -splice x12 \\( i1.png -chop x10 \\) caption:Moderna \\( i2.png -chop x10 \\) caption:'Moderna-Pfizer ratio' \\( i3.png -chop x10 \\) \\) -append 1.png"));qp()
In the following code I calculated a risk ratio within first the 52 weeks from vaccination, which was adjusted for both age group and vaccination week. I included only people with a COVID case listed because the comorbidity index was missing for people with no COVID case. Moderna got about 1.19 times higher risk ratio than Pfizer when I only normalized the rates by age and vaccination week, but the difference decreased to about 1.14 when I additionally normalized the rates by the comorbidity index:
t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv")
codes=setNames(rep("Other",26),sprintf("CO%02d",1:26))
codes[c(1,8,9,16,20,21,23)]="Pfizer"
codes[c(2,15)]="Moderna"
codes[3]="AstraZeneca"
codes[4]="Janssen"
codes[c(7,22)]="Novavax"
weeks=unique(format(seq(as.Date("2020-1-1"),as.Date("2024-12-31"),1),"%G-%V"))
d=t[Infekce==1] # exclude people with no case and keep only entry for first case
d[,date:=match(Datum_Prvni_davka,weeks)] # convert combination of year and week number to integer
d[,dead:=match(ifelse(DatumUmrtiLPZ=="",Umrti,DatumUmrtiLPZ),weeks)]
d=d[,.(date,dead,dcci=DCCI,type=codes[OckovaciLatkaKod_Prvni_davka],born=RokNarozeni)]
d=d[born!="-"&!born%like%"19(05|10)"] # exclude people with a missing or erroneous birthdate
d=d[date<min(grep("2023",weeks))] # exclude people with a first dose in 2023 and 2024
a=d[,.(dead=sum((dead-date)%in%0:51),pop=.N),.(date,type,born,dcci)] # include only first 52 weeks
# a=d[,.(dead=sum(dead>=date,na.rm=T),pop=.N),.(date,type,born,dcci)] # include whole observation period
a=merge(a,a[,.(base=sum(dead)/sum(pop)),.(date,born)])
a=merge(a[,.(base2=sum(dead)/sum(pop)),.(date,born,dcci)],a)
o=a[,.(dead=sum(dead),pop=sum(pop),rr_by_age_and_vaxweek=sum(dead)/sum(base*pop),rr_by_age_and_vaxweek_and_dcci=sum(dead)/sum(base2*pop)),type]
mutate_if(o,is.double,round,3)[order(-pop)]|>print(r=F)
type dead pop rr_by_age_and_vaxweek rr_by_age_and_vaxweek_and_dcci
Pfizer 14790 2183514 0.936 0.944
Moderna 2729 182240 1.115 1.073
Janssen 1395 152581 1.118 1.136
AstraZeneca 3474 123531 1.206 1.177
Novavax 9 3097 0.592 0.820
Other 0 8 0.000 0.000
When I did a Poisson regression to calculate the risk ratios instead, the Moderna-Pfizer ratio was about 1.26 when I only included age and vaccination week as variables in the regression, but the ratio decreased to about 1.20 when I also included DCCI as a variable:
a=d[,.(dead=sum((dead-date)%in%0:51),pop=.N),.(date,type,born,dcci)]
a=rbind(a,a[,.(dead=sum(dead),pop=sum(pop),type="Total"),.(date,born,dcci)])
a[,type:=relevel(factor(type),"Total")] # first factor level is used as baseline by glm
a[,date:=factor(date)] # treat vaccination week as categorical instead of continuous variable
a[,dcci:=factor(dcci)] # treat DCCI as categorical instead of continuous variable
lm=glm(dead~type+born+date,offset=log(pop),poisson,a)
lm2=glm(dead~type+born+date+dcci,offset=log(pop),poisson,a)
o=a[type!="Total",.(dead=sum(dead),pop=sum(pop)),type]
o$rr_by_age_and_vaxweek=o[,exp(coef(lm))[paste0("type",type)]]
o$rr_by_age_and_vaxweek_and_dcci=o[,exp(coef(lm2))[paste0("type",type)]]
mutate_if(o,is.double,round,3)[order(-pop)]|>print(r=F)
type dead pop rr_by_age_and_vaxweek rr_by_age_and_vaxweek_and_dcci
Pfizer 14790 2183514 0.916 0.926
Moderna 2729 182240 1.158 1.112
Janssen 1395 152581 1.155 1.174
AstraZeneca 3474 123531 1.297 1.257
Novavax 9 3097 0.541 0.604
Other 0 8 0.000 0.000
The new UZIS data makes it possible to plot number of hospitalizations by time since vaccination, which is a fairly rare type of plot I haven't seen in many studies.
Hospitalizations are reduced for several weeks before vaccination, which might be because people who had recently been hospitalized were recommended to not get vaccinated after hospitalization (and they would've already had natural immunity anyway).
For some reason there's also a spike in hospitalizations about 1-10 weeks after vaccination. At first I thought it might have been if a lot of people got vaccinated before the COVID wave that peaked in March 2021. But when I split out the data by the quarter of vaccination, the same spike occurred during all quarters except the third quarter when there were few hospitalizations in general. So I don't know if it's because recently vaccinated people somehow have an elevated risk of hospitalization:

weeks=unlist(sapply(2020:2024,\(i)sprintf("%d-%02d",i,1:ifelse(i==2020,53,52))))
t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv")
t[,date:=match(Datum_Prvni_davka,weeks)]
t[,hosp:=match(min_Hospitalizace,weeks)]
t=t[date%in%54:105]
t[,vaxq:={x=(date-54)%/%13*13+1;ifelse(date%in%54:105,paste0("Vaccinated week ",x,"-",x+12," of 2021"),NA)}]
p=na.omit(t[,.(y=.N,z="Total"),.(x=hosp-date)])
p=rbind(p,na.omit(t[,.(y=.N),.(x=hosp-date,z=vaxq)]))
xbreak=pretty(p$x,10);xstart=min(p$x);xend=max(p$x)
ybreak=pretty(p$y,7);ystart=0;yend=max(p$y)
ggplot(p,aes(x,y))+
geom_hline(yintercept=0,linewidth=.4)+
geom_line(aes(color=z),linewidth=.5)+
labs(x="Week of hospitalization minus week of first dose",y="Count of hospitalizations",title="Count of COVID hospitalizations in Czech Republic by weeks since\nfirst vaccine dose",subtitle="Includes only people vaccinated on weeks where the Thursday fell in 2021. Source: nzip.cz/data/2135-covid-19-prehled-populace."|>stringr::str_wrap(70))+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak)+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak)+
coord_cartesian(clip="off",expand=F)+
scale_color_manual(values=c("black",hsv(c(21,12,4,0)/36,.9,.7)))+
theme(axis.text=element_text(size=11,color="black"),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length=unit(5,"pt"),
axis.title=element_text(size=11,face=2),
legend.background=element_blank(),
legend.box.background=element_rect(color="black",linewidth=.4),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.justification=c(1,1),
legend.key=element_blank(),
legend.key.height=unit(14,"pt"),
legend.key.width=unit(26,"pt"),
legend.position=c(1,1),
legend.spacing.x=unit(3,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.margin=margin(5,5,5,5),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
plot.margin=margin(6,8,5,5),
plot.subtitle=element_text(size=11.5,margin=margin(,,5)),
plot.title=element_text(size=11.5,face=2,margin=margin(1,,5)))
ggsave("1.png",width=6,height=3.7,dpi=300*4)
system("magick 1.png -resize 25% PNG8:1.png")
However the spike in hospitalizations in the weeks following vaccination is lot smaller for second doses, because I guess a lot of people got hospitalized after the first dose but before they had time to get the second dose:

Kirsch did a blog post about how during a low-COVID period between weeks 21 to 40 of 2021, Moderna had about 1.5 times higher mortality rate than Pfizer within age groups: https://kirschsubstack.com/p/official-czech-republic-record-level.
I tried using the old record-level data to do a Poisson regression normalized for age and vaccination month, where I calculated the mortality risk in June to September 2021 and I only included people vaccinated before June 2021. But the relative risk was about 1.47 times higher for Moderna than Pfizer, so it roughly matches Kirsch's calculation:
b=fread("http://sars2.net/f/czbucketskeep.csv.gz")
a=b[vaxmonth<"2021-06"&month>="2021-06"&month<="2021-09"&dose<=1&type!="Other"]
a[dose==0,type:="Unvaccinated"]
a=a[,.(dead=sum(dead),pop=sum(alive)),.(type,age=factor(pmin(age,100)),vaxmonth)]
a[,type:=relevel(factor(type),"Unvaccinated")]
lm=glm(dead~type+age+vaxmonth,offset=log(pop),poisson,a)
o=a[,.(dead=sum(dead),pop=sum(pop)),type]
o$rr=o[,exp(coef(lm))[paste0("type",type)]]
se=sqrt(diag(vcov(lm)))
err=qnorm(.975)*se[paste0("type",o$type)]
o[,low:=exp(log(rr)-err)][,high:=exp(log(rr)+err)]
o[1,`:=`(rr=1,low=1,high=1)]
dplyr::mutate_if(o,is.double,round,3)[order(-pop)]|>print(r=F)
# type dead pop rr low high
# Unvaccinated 14515 634463184 1.000 1.000 1.000
# Pfizer 12446 379085660 0.294 0.282 0.308
# AstraZeneca 3838 53538740 0.405 0.383 0.427
# Moderna 2440 38525931 0.432 0.408 0.457
# Janssen 217 4977937 0.464 0.406 0.531
o[type=="Moderna",rr]/o[type=="Pfizer",rr]
# 1.46563
Kirsch posted this tweet: [https://x.com/stkirsch/status/1888449481668223379]

My plot didn't show IFR but CFR. But anyway the reason why the CFR went up in the first half of 2021 was because both deaths and cases were going down, but deaths were lagging about 2-3 weeks behind deaths. When I shifted the cases forwards by 3 weeks, the CFR went down in the first half of 2021 instead:

library(data.table);library(ggplot2)
ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
ages=c(10,40,60,80)
weeks=unique(format(seq(as.Date("2020-1-1"),as.Date("2024-12-31"),1),"%G-%V"))
t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
t=t[RokNarozeni!="-"]
t[,age:=pmin(100,(2020-as.integer(substr(RokNarozeni,1,4))))]
t=t[!is.na(age)]
t[,dead:=ifelse(DatumUmrtiLPZ=="",Umrti,DatumUmrtiLPZ)]
t[,dosecase:=ifelse(Datum_Prvni_davka!=""&Datum_Prvni_davka<=DatumPozitivity,1,0)]
t[,dosedead:=ifelse(Datum_Prvni_davka!="",1,0)]
a=t[DatumPozitivity!="",.(y=.N,z="case"),.(week=DatumPozitivity,dose=dosecase,age)]
t[,testlag:=match(dead,weeks)-match(DatumPozitivity,weeks)]
t[,hosplag:=match(dead,weeks)-match(max_Hospitalizace,weeks)]
a=rbind(a,t[pmax(testlag%in%0:3,hosplag%in%0:3)==1,.(y=.N,z="dead"),.(week=dead,dose=dosedead,age)])
w=dcast(a,age+week+dose~z,value.var="y")
w=merge(do.call(CJ,lapply(w[,1:3],unique)),w,all.x=T)
w[,case:=nafill(case,,0)][,dead:=nafill(dead,,0)]
w=w[,.(dead=sum(dead),case=sum(case)),.(age=agecut(age,ages),week=match(week,weeks),dose)]
w=rbind(w,w[,.(dead=sum(dead),case=sum(case),dose=2),.(age,week)])
lab=c("Unvaccinated","Vaccinated","Unvaccinated and vaccinated")
w[,z:=factor(dose,,lab)]
p=merge(w[,.(case=ma(case,2),x=week+3),.(age,z)],w[,.(dead=ma(dead,2),x=week),.(age,z)],all=T)
p[is.na(case),case:=0][is.na(dead),dead:=0]
p[,y:=ifelse(case<5,NA,dead/case*100)]
p=p[!is.na(age)]
p[y>100,y:=100]
xstart=1;xend=length(weeks)
ggplot(p,aes(x))+
facet_wrap(~age,ncol=1,strip.position="top",dir="v",scales="free_y")+
geom_vline(xintercept=grep("-01",weeks),linewidth=.4,color="gray66",lineend="square")+
geom_line(aes(y=y,color=z,linetype=z),linewidth=.6)+
geom_text(data=p[,.(ymax=max(y,na.rm=T)),age],aes(label=sprintf("\n Age %s \n",age),y=ymax*.87),x=mean(c(xstart,xend)),hjust=.5,size=3.9,fontface=2)+
labs(x=NULL,y=NULL,title="Czech Republic: Weekly percentage of COVID deaths per COVID\ncases (cases shifted 3 weeks forwards)")+
scale_x_continuous(limits=c(xstart,xend),breaks=grep("-26",weeks),labels=2020:2024)+
scale_y_continuous(breaks=\(x){y=pretty(x,4);y[y<max(x)*.9]},labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c(hsv(c(7,0)/12,1,.8),"black",hsv(30/36,.5,1)))+
scale_linetype_manual(values=c("solid","solid","solid","42"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=1,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.ticks=element_line(color="black",linewidth=.4),
axis.text.x=element_text(margin=margin(4)),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="right",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(,,5),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.grid=element_blank(),
panel.spacing=unit(3,"pt"),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,face="bold",margin=margin(1,,3)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.38,height=5.3,dpi=300*4)
sub="Each line shows a ±2-week moving average of deaths divided by a ±2-week moving average of cases, where the lines are not drawn on weeks where the ±2-week moving average of cases is below 5. COVID deaths are deaths where the difference between the week of death and week of positive test or hospitalization is 0-3 weeks, so many deaths classified as COVID deaths here were not actually due to COVID. The age groups were determined by subtracting the year of birth from 2020 so that aging over time was not accounted for. Source: nzip.cz/data/2135-covid-19-prehled-populace."
system(paste0("mar=$[24*4];w=`identify -format %w 1.png`;magick \\( 1.png -gravity southwest -chop 0x50 \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x$[20*4] \\) -append -resize 25% PNG8:1.png"))
The two previous plots show that regardless of whether I shifted the cases forwards or not, unvaccinated people had higher CFR than vaccinated people. Within age groups unvaccinated people had both higher COVID mortality rate than vaccinated people and a higher rate of COVID cases, but the difference in deaths was bigger than the difference in cases, which explains why unvaccinated people also had higher CFR.
In the two previous plots I treated deaths that occurred within three
weeks of a positive test or hospitalization as COVID deaths, because I
thought that the new UZIS dataset did not indicate which deaths were due
to COVID. However then I realized that the column Umrti
showed the week of death for COVID deaths but the column
DatumUmrtiLPZ showed the week of death for all-cause
deaths. But actually it doesn't seem to make too much difference which
definition for a COVID death I use, because when I determined the number
of COVID deaths based on the Umrti column, the result was
not much different from the number of deaths which occurred on the same
week as the last week of a COVID hospitalization:
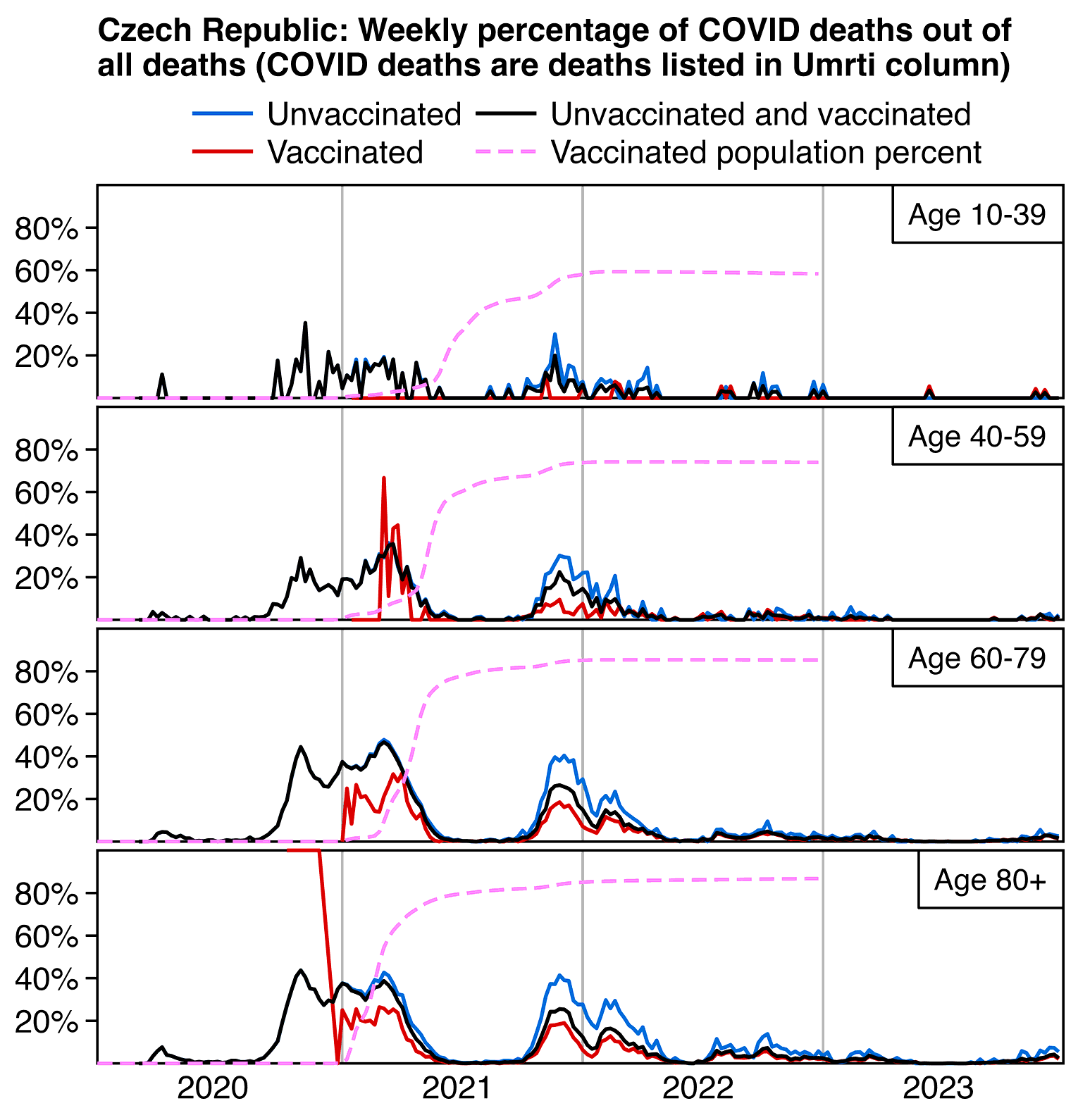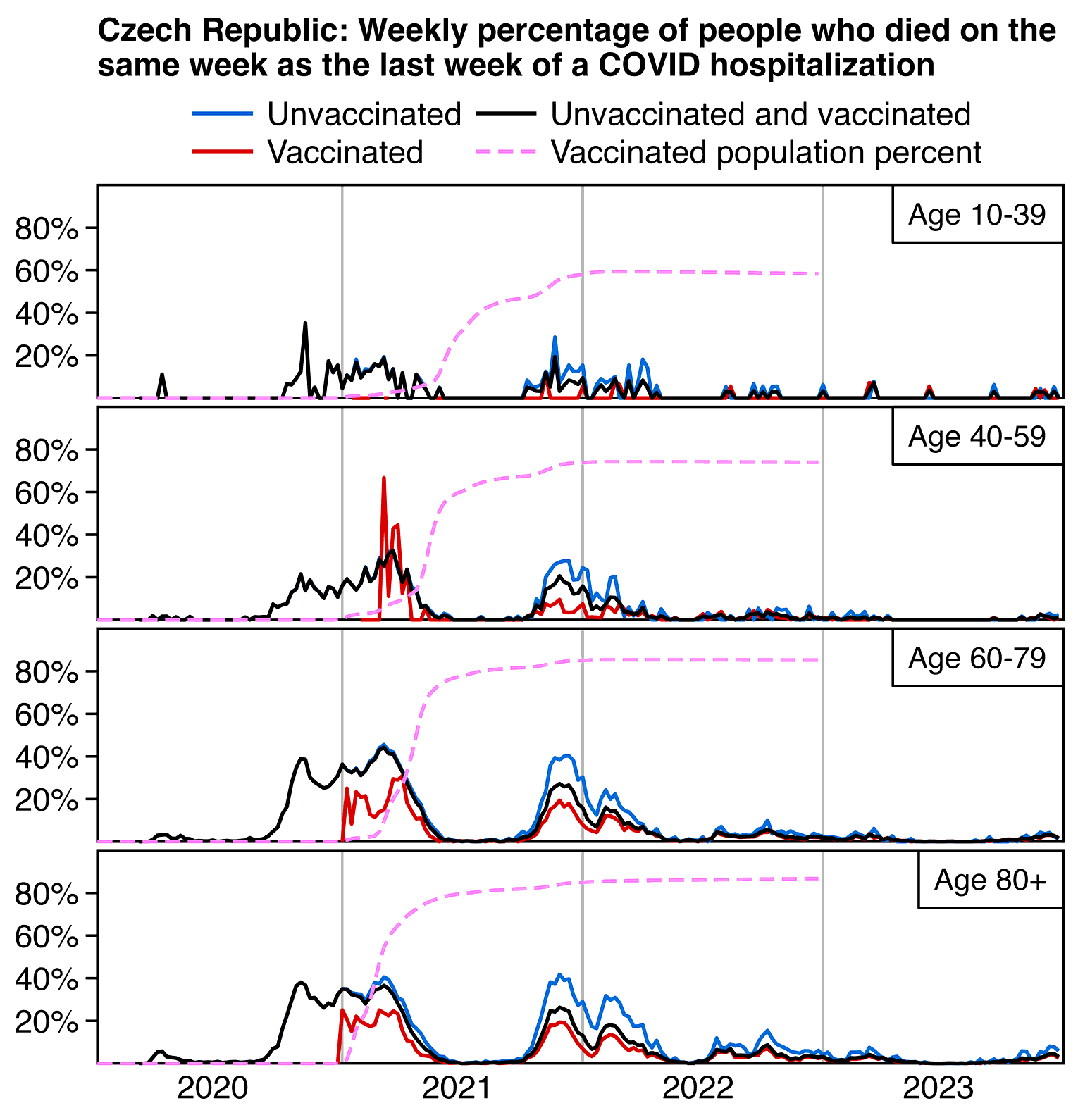
In the winter of 2020-2021 deaths and hospitalizations had a pattern with three distinct humps, where in ages 80+ where about half of people had been vaccinated by the time of the third hump, the third hump was lower than the first and second humps, but in younger age groups the third hump was not as low relative to the two earlier humps. However a similar pattern can be seen in the next plot for cases, where in ages 80+ the third hump was much lower than the first two humps, but in ages 60-79, 40-59, and 10-39 the third hump was about as high as the first two humps:

library(data.table);library(ggplot2)
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
ages=c(10,40,60,80)
weeks=unique(format(seq(as.Date("2020-1-1"),as.Date("2024-12-31"),1),"%G-%V"))
t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
t[RokNarozeni!="-",age:=pmin(100,(2020-as.integer(substr(RokNarozeni,1,4))))]
t[,dose:=ifelse(Datum_Prvni_davka!=""&Datum_Prvni_davka<=DatumPozitivity,1,0)]
a=t[DatumPozitivity!="",.(cases=.N),.(week=DatumPozitivity,dose,age)]
a=merge(do.call(CJ,lapply(a[,-4],unique)),a,all.x=T)[is.na(cases),cases:=0][]
b=fread("http://sars2.net/f/czbucketsdaily.csv.gz")
b=b[,.(pop=sum(alive)),.(week=format(date,"%G-%V"),dose=pmin(dose,1),age=pmin(90,age)%/%5*5)]
b=rbind(b,b[week=="2022-51",.(week=setdiff(a[week!=""&!week%like%2020,week],week),pop),.(dose,age)])
b=b[rowid(week,dose,age)==1]
a=merge(a,b)
a=a[!week%like%2024]
a=a[age>=10]
a=rbind(a,a[,.(cases=sum(cases),pop=sum(pop),dose=2),.(week,age)])
a=merge(fread("http://sars2.net/f/czcensus2021pop.csv")[,.(std=sum(pop)),.(age=age%/%5*5)][,std:=std/sum(std)],a)
lab=c("Unvaccinated","Vaccinated","Unvaccinated and vaccinated")
p=a[,.(pop=sum(pop),y=sum(cases/pop*std/7*365e5)),.(age=agecut(age,ages),week,z=factor(dose,,lab))]
p[pop<1e4,y:=NA]
ymax=p[,.(ymax=max(y,na.rm=T)),age]
p=merge(p,ymax)[,.(week,y=y/ymax*100,age,z)]
pct=b[,.(pop=sum(pop)),.(week,age=agecut(age,ages),dose)]
pct=dcast(pct,week+age~dose,value.var="pop")[,`1`:=nafill(`1`,,0)]
pct=pct[week>=b[dose==1,min(week)]]
p=rbind(p,pct[,.(week,age,z="Vaccinated percent",y=`1`/(`0`+`1`)*100)])
xval=unique(format(seq(as.Date("2020-1-1"),as.Date("2023-12-31"),1),"%G-%V"))
p=p[!is.na(age)]
p=p[week<="2024-01"]
p[,x:=match(week,weeks)]
ggplot(p,aes(x))+
facet_wrap(~age,ncol=1,strip.position="top",dir="v",scales="free_y")+
geom_vline(xintercept=grep("-01",weeks),linewidth=.4,color="gray66",lineend="square")+
geom_vline(xintercept=range(p$x),linewidth=.4,lineend="square")+
geom_hline(yintercept=c(0,100),linewidth=.4,lineend="square")+
geom_line(aes(y=y,color=z,linetype=z),linewidth=.6)+
geom_label(data=ymax,aes(label=sprintf("\n Age %s (max %.0f) \n",age,ymax),y=100),x=max(p$x),lineheight=.5,hjust=1,vjust=1,size=3.6,fill=alpha("white",1),label.r=unit(0,"pt"),label.padding=unit(0,"pt"),label.size=.4)+
labs(x=NULL,y=NULL,title="Czech Republic: Weekly age-standardized rate of COVID cases\nper 100,000 person-years",subtitle="Displayed as percentage of maximum value shown in parentheses")+
scale_x_continuous(limits=range(p$x),breaks=grep("-26",weeks),labels=2020:2024)+
scale_y_continuous(breaks=1:4*20,limits=c(0,100),labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c(hsv(c(7,0)/12,1,.8),"black",hsv(30/36,.5,1)))+
scale_linetype_manual(values=c("solid","solid","solid","42"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=2,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.ticks=element_line(color="black",linewidth=.4),
axis.text.x=element_text(margin=margin(4)),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="center",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(,,4),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.grid=element_blank(),
panel.spacing=unit(3,"pt"),
plot.margin=margin(5,5,5,5),
plot.subtitle=element_text(size=11,margin=margin(,,3)),
plot.title=element_text(size=11,face="bold",margin=margin(1,,5)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.3,height=5.3,dpi=300*4)
sub="The 2021 census population by 5-year age groups was used as the standard population. People were given a year of birth as a range of 5 years like 1950-1954, so here each person was assigned to a 5-year age group by subtracting the year of birth from 2020 so that aging over time was not accounted for. The resident population estimates in the 2021 census were used as the standard population. The age-standardized rates are not shown on days with population size below 10,000. Sources: nzip.cz/data/2135-covid-19-prehled-populace (cases) and github.com/PalackyUniversity/uzis-data-analysis (number of vaccinated and unvaccinated people by age)."
system(paste0("mar=$[24*4];w=`identify -format %w 1.png`;magick \\( 1.png -gravity southwest -chop 0x70 \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x$[20*4] \\) -append -resize 25% -colors 256 1.png"))
Added later: I now figured out a better method to calculate CFR which
doesn't require shifting deaths or cases, which is to simple look at the
proportion of cases by the DatumPozitivity column where the
Umrti column is not empty. But by that method the CFR also
went down during the first half of 2021:
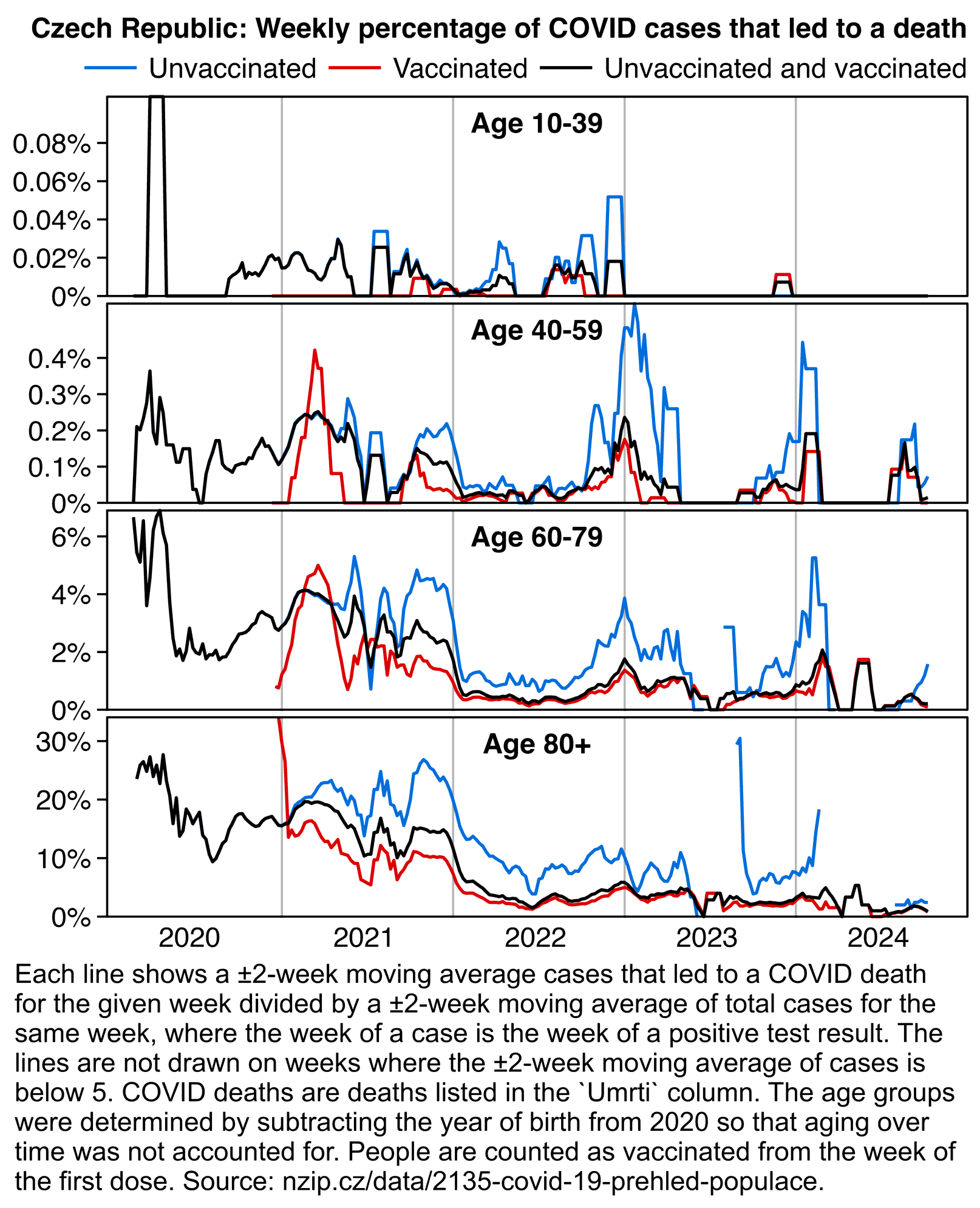
library(data.table);library(ggplot2)
ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
ages=c(10,40,60,80)
weeks=unique(format(seq(as.Date("2020-1-1"),as.Date("2024-12-31"),1),"%G-%V"))
t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
d=t[RokNarozeni!="-"]
d[,age:=pmin(100,(2020-as.integer(substr(RokNarozeni,1,4))))]
d=d[!is.na(age)]
d=d[DatumPozitivity!=""]
d[,dose:=as.integer(Datum_Prvni_davka!=""&Datum_Prvni_davka<=DatumPozitivity)]
a=d[,.(cases=.N,dead=sum(Umrti!="")),,.(week=DatumPozitivity,dose,age=agecut(age,ages))]
a=a[!is.na(age)]
a=merge(do.call(CJ,lapply(a[,1:3],unique)),a,all.x=T)
a[is.na(cases),cases:=0][is.na(dead),dead:=0]
a=rbind(a,a[,.(cases=sum(cases),dead=sum(dead),dose=2),.(week,age)])
p=a[,.(y=ifelse(ma(cases,2)<5,NA,ma(dead/cases*100,2)),week),.(dose,age)]
lab=c("Unvaccinated","Vaccinated","All people")
p[,z:=factor(dose,,lab)]
p[,x:=match(week,weeks)]
xstart=1;xend=length(weeks)
ggplot(p,aes(x,y))+
facet_wrap(~age,ncol=1,strip.position="top",dir="v",scales="free_y")+
geom_vline(xintercept=grep("-01",weeks),linewidth=.4,color="gray66",lineend="square")+
geom_line(aes(color=z),linewidth=.6)+
geom_text(data=p[,.(y=max(y,na.rm=T)),age],aes(label=sprintf("\n Age %s \n",age),y=y*.87),x=mean(c(xstart,xend)),hjust=.5,size=3.9,fontface=2)+
labs(x=NULL,y=NULL,title="Czech Republic: Weekly percentage of COVID cases that led to a death")+
scale_x_continuous(limits=c(xstart,xend),breaks=grep("-26",weeks),labels=2020:2024)+
scale_y_continuous(breaks=\(x){y=pretty(x,4);y[y<max(x)*.9]},labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c(hsv(c(7,0)/12,1,.8),"black",hsv(30/36,.5,1)))+
scale_linetype_manual(values=c("solid","solid","solid","42"))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=1,byrow=F))+
theme(axis.text=element_text(size=11,color="black"),
axis.ticks=element_line(color="black",linewidth=.4),
axis.text.x=element_text(margin=margin(4)),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="right",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(,,5),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.grid=element_blank(),
panel.spacing=unit(3,"pt"),
plot.margin=margin(5,5,5,5),
plot.title=element_text(size=11,hjust=1,face="bold",margin=margin(2,,3)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.38,height=5.3,dpi=300*4)
sub="Each line shows a ±2-week moving average cases that led to a COVID death for the given week divided by a ±2-week moving average of total cases for the same week, where the week is the week of a positive test result. The lines are not drawn on weeks where the ±2-week moving average of cases is below 5. COVID deaths are deaths listed in the `Umrti` column. The age groups were determined by subtracting the year of birth from 2020 so that aging over time was not accounted for. People are counted as vaccinated on the week of the first dose. Source: nzip.cz/data/2135-covid-19-prehled-populace."
system(paste0("mar=$[24*4];w=`identify -format %w 1.png`;magick \\( 1.png -gravity southwest -chop 0x50 \\) \\( -size $[w-mar*2]x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\'",sub),"' -gravity southwest -splice $[mar]x$[20*4] \\) -append -resize 25% PNG8:1.png"))
In December 2023 Kirsch published a spreadsheet he received from a source at HHS, which shows the daily number of deaths by vaccination status among people enrolled to Medicare. The dataset doesn't show the ages of people who died or the population sizes of each age group so I wasn't able to plot ASMR by vaccination status but I had to simply plot the raw deaths. But even the raw deaths show that the spike in deaths during the Delta wave was much more pronounced in unvaccinated people than vaccinated people: [rootclaim.html#Post_by_Spiro_Pantazatos_for_mortality_by_state_during_the_Delta_wave]
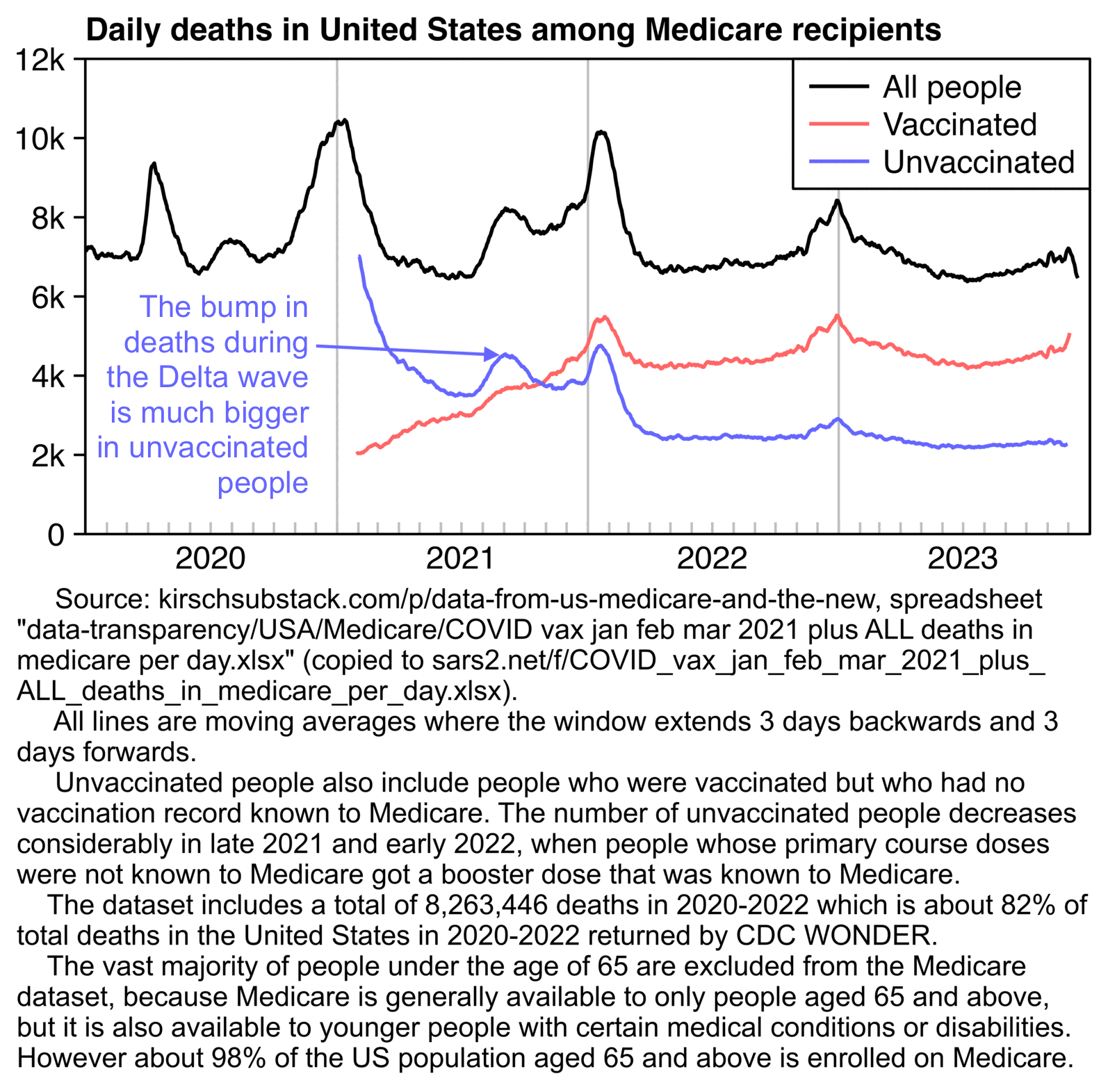
I also tried making a similar plot for the Czech data. In the Czech Republic the Delta wave only peaked around November to December 2021, but even from the top panel below which shows the raw number of deaths, you can see that the increase in deaths during the Delta wave was much more pronounced in unvaccinated people than vaccinated people:

library(data.table);library(ggplot2);library(readxl)
ma=\(x,b=1,f=b){x[]=rowMeans(embed(c(rep(NA,b),x,rep(NA,f)),f+b+1),na.rm=T);x}
ages=c(0,3:9*5,50:89,18:20*5)
t=fread("http://sars2.net/f/czbucketsdaily.csv.gz")
t[,z:=ifelse(dose==0,3,2)]
p=t[,.(y=as.double(sum(dead))),.(z,x=date)]
p=rbind(p,p[,.(y=sum(y),z=1),x])[,type:=1]
a=t[,.(dead=sum(dead),pop=sum(alive)),.(z,x=date,age=ages[findInterval(age,ages)])]
a=rbind(a,a[,.(dead=sum(dead),pop=sum(pop),z=1),.(x,age)])
a=merge(a,fread("http://sars2.net/f/czcensus2021pop.csv")[,std:=pop/sum(pop)][,.(std=sum(std)),.(age=ages[findInterval(age,ages)])])
p=rbind(p,a[,.(y=sum(dead/pop*std*365e5),type=2),.(x,z)])
p[,z:=factor(z,,c("All people","Vaccinated","Unvaccinated"))]
p[,type:=factor(type,,c("Deaths","Age-standardized mortality rate per 100,000 person-years"))]
p[,y:=ma(y,3),,.(type,z)]
xstart=as.Date("2020-1-1");xend=as.Date("2023-1-1")
xbreak=seq(xstart+182,xend,"year")
p=p[x%in%xstart:xend]
ybreak=pretty(c(0,p$y),7)
segx=seq(xstart,xend,"month")
ggplot(p,aes(x,y,z))+
facet_wrap(~type,dir="v",scales="free")+
geom_vline(xintercept=seq(xstart,xend,"month"),color="gray92",linewidth=.4)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="black",linewidth=.4)+
geom_line(aes(color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Daily deaths and ASMR in Czech Republic (±3-day moving average)")+
scale_x_continuous(limits=c(xstart-.5,xend+.5),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=\(x)c(0,max(x)*1.02),breaks=\(x)pretty(x,6))+
scale_color_manual(values=c("black","#ff6666","#6666ff"))+
coord_cartesian(clip="off",expand=F)+
theme(axis.text=element_text(size=11,color="black"),
axis.text.x=element_text(margin=margin(3)),
axis.ticks=element_line(linewidth=.4,color="black"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.box.background=element_blank(),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="right",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5),
legend.title=element_blank(),
panel.background=element_blank(),
panel.border=element_rect(fill=NA,linewidth=.4),
panel.spacing=unit(2,"pt"),
plot.margin=margin(5,5,5,5),
plot.title=element_text(hjust=1,size=11,face=2,margin=margin(2,,4)),
strip.background=element_blank(),
strip.text=element_text(margin=margin(,,4),size=11,hjust=0))
ggsave("1.png",width=5.3,height=4.3,dpi=300*4)
sub="Source: github.com/PalackyUniversity/uzis-data-analysis. People are counted as vaccinated from the day of the first dose. Partially vaccinated people are not excluded. The age groups used for ASMR were 0-14, single years of age for ages 50-89, and 5-year age groups for other ages. The resident population estimates in the 2021 census were used as the standard population."
system(paste0("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[43*4] caption:'",gsub("'","'\\\\'",sub),"' -splice x80 \\) -append -resize 25% -bordercolor white -border 24 -colors 256 1.png"))
This plot is basically the same as my earlier plot for a moving
average of daily ASMR, but I now plotted monthly ASMR instead. Both
plots are based on the czbuckets.csv.gz file generated by
the code here:
czech.html#Bucket_analysis.

agecut=\(x,y)cut(x,c(y,Inf),paste0(y,c(paste0("-",y[-1]-1),"+")),T,F)
ages=c(0,3:4*10,seq(50,95,5))
t=fread("http://sars2.net/f/czbuckets.csv.gz")
std=fread("http://sars2.net/f/czcensus2021pop.csv")
doses=c("Unvaccinated",paste("Dose",c(1:3,"4+")))
a=t[,.(dead=sum(dead),pop=sum(alive)),.(dose=factor(doses[pmin(dose,4)+1],doses),age=agecut(age,ages),month)]
a=rbind(a,a[dose!="Unvaccinated",.(dead=sum(dead),pop=sum(pop),dose="Vaccinated"),.(age,month)])
a=rbind(a,a[dose%like%"accinated",.(dead=sum(dead),pop=sum(pop),dose="All people"),.(age,month)])
a=merge(a,std[,.(std=sum(pop)),.(age=agecut(age,ages))][,std:=std/sum(std)])
p=a[,.(pop=sum(pop),y=sum(dead/pop*std*365e5)),.(x=as.Date(paste0(month,"-1")),z=dose)]
p[pop/365<1e3,y:=NA]
frac=p[!z%in%c("Vaccinated","All people"),.(frac=pop/sum(pop),z),x]
ybreak=pretty(p$y,8);ystart=0;yend=max(ybreak);xstart=min(p$x);xend=max(p$x)
pal=c(hcl(c(21,11,6,0,31)*10+15,90,70),"black","gray50")
ggplot(p,aes(x,y,color=z))+
geom_area(data=frac,aes(y=frac*yend*.9999,fill=z),linewidth=.15,show.legend=F,alpha=.3)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",fill=NA,color="black")+
geom_line(aes(linetype=z,linewidth=z))+
geom_point(aes(alpha=z),size=1)+
annotate("label",x=xstart,y=yend,hjust=0,vjust=1,size=3.8,label="ASMR per 100,000 person-years",label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4)+
annotate("label",x=xend,y=yend,hjust=1,vjust=1,size=3.8,label="Percentage of group",label.r=unit(0,"pt"),label.padding=unit(5,"pt"),label.size=.4)+
scale_x_date(breaks=unique(p$x)[c(T,F)],date_labels="%b\n%y")+
scale_y_continuous(limits=c(ystart,yend),breaks=seq(0,yend,1000),labels=\(i)ifelse(i<1000,i,paste0(i/1e3,"k")),sec.axis=sec_axis(trans=~./yend*100,labels=\(x)paste0(x,"%")))+
labs(x=NULL,y=NULL)+
ggtitle("Age-standardized mortality rate in Czech Republic")+
scale_color_manual(values=pal)+
scale_linetype_manual(values=rep(c("solid","42"),c(6,1)))+
scale_linewidth_manual(values=rep(c(.4,.6),c(6,1)))+
scale_alpha_manual(values=rep(1:0,c(6,1)))+
scale_fill_manual(values=pal)+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(nrow=2))+
theme(axis.text=element_text(size=10,color="black"),
axis.ticks=element_line(linewidth=.4),
axis.ticks.length=unit(3,"pt"),
axis.title=element_text(size=11),
legend.background=element_blank(),
legend.box.background=element_blank(),
legend.box.just="center",
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.key=element_rect(fill="white"),
legend.key.height=unit(13,"pt"),
legend.key.width=unit(26,"pt"),
legend.justification="center",
legend.margin=margin(,,3),
legend.position="top",
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=10.5),
legend.title=element_blank(),
panel.background=element_blank(),
plot.margin=margin(5,5,4,5),
plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,2)))
ggsave("1.png",width=5.6,height=3.7,dpi=300*4)
sub="Source: github.com/PalackyUniversity/uzis-data-analysis. The 2021 census population was used as the standard population, with age groups 0-29, 30-39, 40-49, 50-54, ..., 90-94, 95+."
system(paste0("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[44*4] caption:'",gsub("'","'\\\\''",sub),"' -splice x80 \\) -append -resize 25% -bordercolor white -border 24 -dither none -colors 256 1.png"))
In a PDF file Kirsch published in June 2025 as part of the Rootclaim debate, he now wrote that he regrets not having appreciated the effect of confounders when he compared the mortality of Moderna against Pfizer in the Czech data: [https://www.skirsch.com/covid/KIRSCH_COVID_shot_analysis.pdf]
In previous analyses of the Czech data, I found that the Moderna shots were more deadly than the Pfizer shots. That calculation was using the raw, unadjusted data.
In fact, in the Levi study, in the unadjusted FULL cohort, they found the same thing (that in the raw, unadjusted full cohort, Moderna appears to be more deadly):
However, after basic adjustments were made to the FULL COHORT (9M), they found that Pfizer was in fact more deadly (see the second line of the figure above).
And after doing extremely tight matching, it changed the adjusted full cohort by less than 0.5%, a tiny amount.
My earlier Czech analysis didn't do any of these adjustments. This is why in observational studies they do adjustments like these because sometimes they can flip the result.
The fact that the Levi study FULL cohort with basic adjustments nearly exactly matched the nearly exactly matched MATCHED cohort is extremely powerful.
The reality of course is that both vaccines were quite deadly. If Moderna was 100% safe as we have assumed in this analysis (since we don't know the absolute level of NCACM harm), most all the VAERS death reports would be for only one brand of vaccine; that just isn't the case.
This is a perfect example of why, when looking at observational data, basic adjustments to the raw data are necessary. I regret that I did not fully appreciate that before.
In 2024 Kirsch kept insisting that Pfizer and Moderna vaccines were distributed randomly and without bias in the Czech Republic, so the difference in mortality could not have been due to confounders, even though me and Uncle John Returns and Jeffrey Morris kept telling him otherwise.
In the first round of the Rootclaim debate in 2024, Kirsch wrote: [https://kirschsubstack.com/p/did-the-covid-vaccine-save-more-people]
The Czech Republic record-level data obtained under FOIA request from the Czech government showed that people who got the Moderna vaccine were 30% more likely to die within 1 year of the shot than people who got the Pfizer vaccine. The 30% difference appeared in all age groups where there was sufficient data and it happened during NON-COVID time periods. People tried to attack this claiming that it was due to distribution bias, but we showed that was false. The reason this is such an important study is because you cannot compare vaccinated with unvaccinated death rates due to selection bias. But in the Czech Republic, the vaccines were randomly assigned and nobody had any clue which one was safer. So there was no systematic or systemic bias. So how can the death rates be 30% higher in every age group with sufficient data? The only way that can happen is if the Moderna vaccine is more deadly. And in that document we show 8 different data points that are consistent with Moderna having a higher adverse event rate. We believe the higher death rate in Moderna vs. Pfizer is primarily due to the 100mcg dose vs. 30 mcg dose. The more poison, the more death. There have been very few brand comparison studies like this and what they do is adjust the numbers to make the death differences go away because their assumption going into it is that the vaccines should have equal mortality rates so they get rid of the differences statistically. This is raw data. You can't have a 30% higher death rate in nearly all 5 year age groups over 50. That's statistically unlikely to happen. And even if Pfizer was 100% safe, a 30% increase in ACM (over the first year from the shot) is a disaster.
However even though he summarized many of his earlier arguments in his new PDF, he no longer repeated his earlier claim that the Czech data showed that Moderna was more deadly than Pfizer.
USMortality posted this tweet: [https://x.com/USMortality/status/1975667010341425586]

I pointed out that the Alpha spike around March 2021 occurs around the same time in all age groups, even though young people got vaccinated later than old people. And the same thing applies to the Delta spike in November to December 2021, which Rancourt blamed on the vaccines:

t=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
t=t[RokNarozeni!="-"]
t=t[Infekce%in%c(1,NA)]
t[,born:=pmin(pmax(1920,as.integer(substr(RokNarozeni,1,4))),2000)]
t[,vax:=Datum_Prvni_davka]
t[,dose:=(vax!="")*1]
pop=t[vax!="",.(pop=.N,dose=1),.(week=vax,born)]
pop=rbind(pop,t[,.(week="2020-10",pop=.N,dose=0),born])
dead=t[,.(dead=.N),.(week=DatumUmrtiLPZ,dose,born)]
covid=t[,.(covid=.N),.(week=Umrti,dose,born)]
a=merge(covid,merge(dead,pop,all=T),all=T)[week!=""]
a=merge(do.call(CJ,lapply(a[,1:3],unique)),a,all=T);a[is.na(a)]=0
a[dose==0,pop:=pop-a[dose==1,pop]]
a[,pop:=cumsum(pop-dead),.(born,dose)]
a=a[,.(type=1:2,dead=dead-c(0,covid),pop),.(week,dose,born)]
a=rbind(a,a[,.(dead=sum(dead),pop=sum(pop),dose=2),.(week,born,type)])
a=a[,.(week,dead=ma(dead,2),pop=ma(pop,2)),.(type,born,dose)]
groups=c(1900,1935,1950,1970)
a[,group:=agecut(born,groups)]
a[,std:=tapply(pop,born,sum)[factor(born)]/sum(pop)]
iso=as.IDate(0:1e4*7);names(iso)=format(iso,"%G-%V")
p=a[,.(y=ifelse(pop<1e3,NA_real_,sum(dead/pop*std/7*365e5))),.(x=iso[week],type,dose,group)]
p[,type:=factor(type,,c("All causes","Not COVID"))]
p[,dose:=factor(dose,,c("Unvaccinated","Vaccinated","Total"))]
xmin=as.Date("2021-1-1");xmax=as.Date("2024-1-1")
p=p[x>=xmin&x<=xmax]
xbreak=seq(xmin+182,xmax,"year")
ylim=p[,.(max=max(y,na.rm=T)),group]
vax=t[,.(born,week=unlist(.SD,,F)),.SDcols=patterns("Datum_")]
vax=vax[,.(y=.N),.(born,week)]
vax=vax[week!="",.(y=sum(y)),.(group=agecut(born,groups),week)]
vax=merge(do.call(CJ,lapply(vax[,-3],unique)),vax,all=T)
vax[,y:=as.double(ma(nafill(y,,0),2))]
vax=merge(ylim,vax)[,.(x=iso[week],y=y/max(y)*max),group]
vaxlab="New vaccine doses (panel top is maximum)"
ggplot(p)+
facet_wrap(~group,ncol=2,dir="v",scales="free_y")+
geom_ribbon(data=vax,aes(x,ymin=0,ymax=y,fill=vaxlab),linewidth=0)+
geom_vline(xintercept=seq(xmin,xmax,"year"),color="gray75",linewidth=.4)+
geom_rect(data=ylim,aes(ymin=0,ymax=max),xmin=xmin,xmax=xmax,lineend="square",linejoin="mitre",fill=NA,color="gray75",linewidth=.4)+
geom_line(aes(x,y,color=dose,alpha=type),linewidth=.6)+
geom_label(data=ylim,aes(xmax,max,label=group),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=.4,color="gray72",fill="white",size=3.87,lineheight=.8)+
geom_label(data=ylim,aes(xmax,max,label=group),hjust=1,vjust=1,label.r=unit(0,"pt"),label.padding=unit(4,"pt"),label.size=0,fill=NA,size=3.87,lineheight=.8)+
labs(x=NULL,y=NULL,title="ASMR per 100,000 person-years in Czech Republic")+
scale_x_date(limits=c(xmin,xmax),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(breaks=\(x){y=pretty(x,4);y[y<max(x)*.98]},labels=\(x)ifelse(x>=1e3,paste0(x/1e3,"k"),x))+
scale_color_manual(values=c(hsv(2:3/3,.6,1),"black"))+
scale_fill_manual(labels=vaxlab,values="gray85")+
scale_alpha_manual(values=c(1,.4))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(order=1),alpha=guide_legend(order=1),fill=guide_legend(order=3))+
theme(axis.text=element_text(size=11,color="gray50"),
axis.text.y=element_text(margin=margin(,1.5)),
axis.ticks=element_line(linewidth=.4,color="gray75"),
axis.ticks.length.x=unit(0,"pt"),
axis.ticks.length.y=unit(4,"pt"),
legend.background=element_rect(color="gray70",linewidth=.4),
legend.box="vertical",
legend.box.just="center",
legend.box.margin=margin(,,3),
legend.box.spacing=unit(0,"pt"),
legend.direction="horizontal",
legend.justification="center",
legend.key=element_blank(),
legend.key.height=unit(13,"pt"),
legend.key.spacing.x=unit(2,"pt"),
legend.key.width=unit(26,"pt"),
legend.margin=margin(2.5,5.5,2.5,2.5),
legend.position="top",
legend.spacing.x=unit(3,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,vjust=.5,margin=margin(,,,2)),
legend.title=element_blank(),
panel.background=element_blank(),
panel.spacing.x=unit(2,"pt"),
panel.spacing.y=unit(3,"pt"),
plot.subtitle=element_text(size=11,hjust=.5,margin=margin(,,3)),
plot.title=element_text(size=11,face=2,hjust=.5,margin=margin(,,3)),
strip.background=element_blank(),
strip.text=element_blank())
ggsave("1.png",width=5.4,height=3.8,dpi=300*4)
system("mogrify -trim 1.png;magick 1.png \\( -size `identify -format %w 1.png`x -font Arial -interline-spacing -3 -pointsize $[42*4] caption:'All lines are ±2-week moving averages. ASMR was calculated by 5-year groups for year of birth, so that aging over time was not accounted for. People born in 2000 or later were grouped together, and people born in 1924 or earlier were grouped together. The total person-weeks for each age were used as the standard population. Due to a missing date of birth, unvaccinated people are missing about 10% of deaths, with slightly more deaths missing in early 2021. Source: nzip.cz/data/2135-covid-19-prehled-populace.' -splice x$[16*4] \\) -append -trim -resize 25% -bordercolor white -border 20 -dither none -colors 256 1.png")
If you exclude people with a year of birth missing, then even in 2022, the NZIP data is missing more than 10% of deaths in unvaccinated people. The proportion of missing deaths is temporarily reduced in the winter of 2021 to 2022, but I think it's because in the winter many unvaccinated people died of COVID, so their year of birth is available from ISIN if they have a COVID case listed at ISIN:

old=fread("xz -dc CR_records.csv.xz",showProgress=F)
a=old[,.(old=.N),.(week=format(DatumUmrti,"%G-%V"),dose=(!is.na(Datum_1))*1)]
new=fread("Otevrena-data-NR-26-30-COVID-19-prehled-populace-2024-01.csv.gz")
a2=new[Infekce%in%c(1,NA)&RokNarozeni!="-"][!(DatumUmrtiLPZ!=""&Datum_Prvni_davka>DatumUmrtiLPZ)]
a2=a2[,.(new=.N),.(week=DatumUmrtiLPZ,dose=(Datum_Prvni_davka!="")*1)]
iso=as.IDate(0:1e4*7);names(iso)=format(iso,"%G-%V")
p=merge(a,a2)[week!="2022-52"]
p=rbind(p,p[,.(old=sum(old),new=sum(new),dose=2),week])
p=p[,.(y=new/old*100,x=iso[week],z=factor(dose,c(1,2,0),c("Vaccinated","Total","Unvaccinated")))]
xstart=as.Date("2020-1-1");xend=as.Date("2023-1-1");xbreak=seq(xstart+182,xend,"year")
ybreak=0:11*10;ystart=0;yend=110
ggplot(p)+
geom_vline(xintercept=seq(xstart,xend,"year"),color="gray91",linewidth=.4)+
geom_hline(yintercept=ybreak,color="gray91",linewidth=.4)+
annotate("rect",xmin=xstart,xmax=xend,ymin=ystart,ymax=yend,linewidth=.4,lineend="square",linejoin="mitre",fill=NA,color="gray75")+
geom_line(aes(x,y,color=z),linewidth=.6)+
labs(x=NULL,y=NULL,title="Weekly deaths with year of birth not missing in NZIP data as\npercentage of deaths in FOI data")+
scale_x_date(limits=c(xstart,xend),breaks=xbreak,labels=year(xbreak))+
scale_y_continuous(limits=c(ystart,yend),breaks=ybreak,labels=\(x)paste0(x,"%"))+
scale_color_manual(values=c(hsv(0,.7,1),"black",hsv(2/3,.7,1)))+
coord_cartesian(clip="off",expand=F)+
guides(color=guide_legend(ncol=1,byrow=F))+
theme(axis.text=element_text(size=11,color="gray40"),
axis.text.y=element_text(margin=margin(,1.5)),
axis.ticks.length=unit(0,"pt"),
legend.background=element_rect(color="gray75",linewidth=.4),
legend.box.spacing=unit(0,"pt"),
legend.direction="vertical",
legend.justification=c(.5,.5),
legend.key=element_blank(),
legend.key.height=unit(12,"pt"),
legend.key.width=unit(24,"pt"),
legend.margin=margin(3,5,3,3),
legend.position=c(.5,.5),
legend.spacing.x=unit(2,"pt"),
legend.spacing.y=unit(0,"pt"),
legend.text=element_text(size=11,margin=margin(,,,2)),
legend.title=element_blank(),
panel.background=element_blank(),
plot.subtitle=element_text(hjust=.5,margin=margin(,,4)),
plot.title=element_text(size=11,hjust=.5,face=2,margin=margin(,,4)))
ggsave("1.png",width=5,height=3,dpi=300*4)
I'm not sure why the number of unvaccinated people with no year of birth is smaller than the number of unvaccinated people with no case. But ISIN might have the year of birth for unvaccinated people who got tested, but who tested negative so they weren't added as a case. ISIN has a "laboratory module" which includes negative tests, and which includes the date of birth: [https://vladci.cz/archive/covid/106/UZIS_2022-02_Struktura_NZIS_106.pdf]
